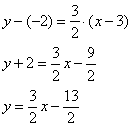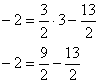Как составить уравнение прямой проходящей через точку если угловой коэффициент - AvtoShod.ru

В декартовых координатах каждая прямая
определяется уравнением первой степени
и, обратно, каждое уравнение первой
степени определяет прямую.

Уравнение
вида

(1)

называется
общим уравнением прямой.

Угол ,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:

Уравнение называется
уравнением прямой с угловым коэффициентом;
k — угловой коэффициент, b — величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.

Если
прямая задана общим уравнением

то
ее угловой коэффициент определяется
по формуле

Уравнение является
уравнением прямой, которая проходит
через точку (, )
и имеет угловой коэффициент k.

Если
прямая проходит через точки (, ), (, ),
то ее угловой коэффициент определяется
по формуле

Уравнение

является
уравнением прямой, проходящей через
две точки (, )
и (, ).

Если
известны угловые коэффициенты и двух
прямых, то один из углов между
этими прямыми определяется по формуле

Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:.

Признаком
перпендикулярности двух прямых является
соотношение
,
или .

Иначе говоря, угловые коэффициенты
перпендикулярных прямых обратны по
абсолютной величине и противоположны
по знаку.

4.Общее уравнение прямой

Уравнение

Ах+Ву+С=0

(где А, В, Смогут иметь любые
значения, лишь бы коэффициентыА,
Вне были нулями оба сразу)
представляетпрямую
линию. Всякую прямую можно
представить уравнением этого вида.
Поэтому его называютобщим уравнением
прямой.

Если А=0, то есть уравнение не
содержитх, то оно представляет
прямую,параллельную
оси ОХ.

Если В=0, то есть уравнение не
содержиту, то оно представляет
прямую,параллельную
оси ОY.

Когла Вне равно нулю, то общее
уравнение прямой можноразрешить
относительно ординаты у,
тогда оно преобразуется к виду

y=ax+b

(где a=-A/B; b=-C/B).

Аналогично, при Аотличным от
нуля общее уравнение прямой можно
разрешить относительнох.

Если С=0, то есть общее уравнение
прямой не содержит свободного члена,
то оно представляет прямую, проходящую
через начало координат

5. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом

Уравнение прямой, проходящей
через данную точку A(x₁, y₁)
в данном направлении, определяемом
угловым коэффициентом k,

y — y₁ = k(x — x₁). (1)

Это уравнение определяет
пучок прямых, проходящих через
точку A(x₁, y₁),
которая называется центром пучка.

6. уравнение прямой,
проходящей через две данные точки.

. Уравнение
прямой, проходящей через две точки: A(x₁, y₁)
и B(x₂, y₂),
записывается так:

(2)

Угловой коэффициент прямой, проходящей
через две данные точки, определяется
по формуле

(3)

7.
Уравнение прямой в отрезках

Если в общем уравнении
прямой ,
то разделив (1) на ,
получаем уравнение прямой в отрезках

где  ,  .
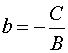
Прямая пересекает ось   в
точке  ,
ось   в
точке  .

8.
Формула: Угол между прямыми на плоскости

Уголα между
двумя прямыми, заданными
уравнениями: y=k₁x+b₁ (первая
прямая) и y=k₂x+b₂ (вторая
прямая), может быть вычислен по формуле
(угол отсчитывается от 1^й прямой
ко 2^й против
часовой стрелки):

tg(α)=(k₂-k₁)/(1+k₁k₂)

9. Взаимное
расположение двух прямых на плоскости.

Пусть сейчас
оба уравнения прямых
записаны в общем виде.

Теорема. Пусть

– общие уравнения двух
прямых на координатной плоскости
Оху. Тогда

1) если ,
то прямые и совпадают;

2) если ,
то прямые и

параллельные;

3) если ,
то прямые пересекаются.

Доказательство.
Условие равносильно
коллинеарности нормальных векторов данных
прямых:

.
Поэтому, если ,
то и прямыепересекаются.

Если же ,
то , , иуравнение прямой принимает
вид:

или ,
т.е. прямые совпадают.
Заметим, что коэффициент пропорциональности ,
иначе все коэффициенты общего уравнения были
бы равны нулю, что невозможно.

Если же прямые не
совпадают и не пересекаются, то остается
случай ,
т.е. прямые параллельны.

Теорема доказана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.

Здесь будет калькулятор

Уравнение прямой с угловым коэффициентом

y=kx+by=kx+b,

где kk — угловой коэффициент, а bb — свободный коэффициент.

Уравнения данного вида составляются следующим образом по формуле:

y−y0=k(x−x0)y-y_0=k(x-x_0),

где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.

Задача 1

Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.

Решение

Подставляем значения в формулу:

y−y0=k(x−x0)y-y_0=k(x-x_0)

y−2=1⋅(x−1)y-2=1cdot(x-1)

Приводим подобные слагаемые:

y=x+1y=x+1

Ответ

y=x+1y=x+1

Общее уравнение прямой

Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:

y−x−1=0y-x-1=0

Уравнение прямой по двум точкам

Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:

Уравнение прямой по двум точкам

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},

где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.

Задача 2

Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).

Решение

x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}

x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}

x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}

x−4=−y−12x-4=frac{-y-1}{2}

y+1=2⋅(4−x)y+1=2cdot(4-x)

y=8−2x−1y=8-2x-1

y=−2x+7y=-2x+7

Ответ

y=−2x+7y=-2x+7

Уравнение прямой при помощи точки и вектора нормали

Уравнение прямой по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.

Задача 3

Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).

Решение

x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,

x−7+40−5y=0x-7+40-5y=0

x−5y=−40+7x-5y=-40+7

x−5y=−33x-5y=-33

5y=x+335y=x+33

y=x5+335y=frac{x}{5}+frac{33}{5}

Проверка

Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.

8=75+3358=frac{7}{5}+frac{33}{5}

8=88=8 — верно, ответ правильный.

Ответ

y=x5+335y=frac{x}{5}+frac{33}{5}

Прямая в пространстве

Уравнение прямой, заданной в пространстве имеет такой вид:

Уравнение прямой в пространстве

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.

Задача 4

Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).

Решение

x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Проверка

Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:

1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.

Такой вид уравнения прямой называется каноническим.

Ответ

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Тест по теме “Составление уравнения прямой”

Источник

2.1. Уравнение прямой с угловым коэффициентом

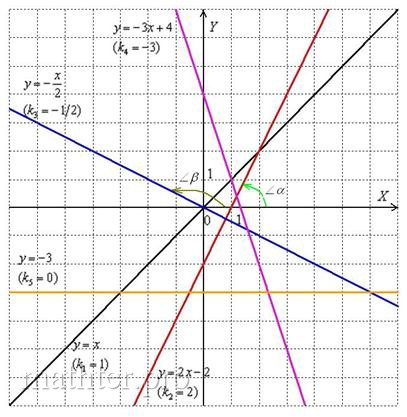
Прямая – это одна из простейших геометрических фигур. Она бесконечна:

и обозначается маленькими латинскими буквами , как вариант,
с подстрочным индексом, например, . Также прямую можно обозначить двумя различными точками, которые ей принадлежат, например, .

Прямую часто задают уравнением, и начнём мы опять со школьного материала. Всем известное «школьное» уравнение называется уравнением прямой с угловым коэффициентом . Вспомним геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:

Угловой коэффициент прямой равен тангенсу угла (см. Приложение Тригонометрия) между положительным направлением оси и данной прямой: . Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых:

Это «красная» прямая с коэффициентом . Согласно вышесказанному, (угол «альфа» обозначен зелёной дугой). Для «синей» прямой с справедливо равенство (угол «бета» обозначен коричневой дугой).

Если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Так, для «черной» прямой тангенс угла наклона равен , а сам угол наклона составляет:
радиан или 45 градусов, что хорошо видно по чертежу. Значения углов можно находить по Таблице или с помощью Калькулятора (Приложения в помощь).

Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс. При этом возможны следующие случаи:

1) Если угловой коэффициент отрицателен: , то линия, грубо говоря, идёт «сверху вниз». Примеры – «синяя» и «малиновая» прямые на чертеже.

2) Если угловой коэффициент положителен: , то линия идёт «снизу вверх». Примеры – «чёрная» и «красная» прямые на чертеже.

3) Если угловой коэффициент равен нулю: , то уравнение принимает вид , и соответствующая прямая параллельна оси . Пример – «жёлтая» прямая. Неформальный смысл уравнения: «игрек» ВСЕГДА (при любом «икс») равен «бэ».

4) Для семейства прямых , параллельных оси (на чертеже нет примера, кроме самой оси ), угловой коэффициент не определён. В данной ситуации , а тангенса угла 90 градусов не существует. Неформальный смысл уравнения: «икс» ВСЕГДА (при любом «игрек») равен «цэ».

Чем больше угловой коэффициент по модулю, тем круче идёт график прямой.

Рассмотрим прямые и . Здесь , поэтому прямая имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
В свою очередь, прямая более крутА, чем прямые .

Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой. Так, для прямых справедливо неравенство , таким образом, прямая более пологая.

Зачем эта информация? ~~Продлить ваши мучения.~~ Знания вышеперечисленных фактов позволяет немедленно увидеть свои ошибки, в частности, ошибки при построении графиков – когда на чертеже получилось явно «что-то не то». Желательно, чтобы вам сразу было понятно, что прямая весьма крутА и идёт «снизу вверх», а прямая – очень полога, близко прижата к оси и идёт «сверху вниз».

Сомневался, напоминать ли, но на всякий пожарный: как построить прямую, если известно её уравнение?

Для того чтобы построить прямую, нужно знать две её точки (любые). Их легко найти из уравнения. Рассмотрим, например, уравнение и выберем произвольное значение «икс», удобно взять , тогда: , и первая точка найдена: . Теперь выбираем другое значение , например, и находим – точка . Отмечаем точки на чертеже и аккуратно проводим линию по линейке.

Ах да, чуть не забыл: прямая вида называется прямой пропорциональностью. Она проходит через начало координат, и для её построения достаточно найти одну точку. На чертеже выше изображены две таких прямых + ось .

Как составить уравнение прямой с угловым коэффициентом?

Если известна точка , принадлежащая некоторой прямой, и угловой коэффициент этой прямой, то уравнение данной прямой выражается формулой:

Задача 59

Составить уравнение прямой с угловым коэффициентом , если известно, что точка принадлежит данной прямой.

Решение: уравнение составим по формуле . В данном случае:

Ответ:

Проверка выполняется элементарно. Во-первых, смотрим на полученное уравнение и убеждаемся, что наш угловой коэффициент на своём месте. Во-вторых, координаты точки должны удовлетворять данному уравнению. Подставим их в уравнение:

– получено верное равенство, значит, точка удовлетворяет полученному уравнению.

Вывод: уравнение найдено правильно.

Более хитрая задачка для самостоятельного решения:

Задача 60

Составить уравнение прямой, если известна её точка , а угол наклона к положительному направлению оси составляет .

Ну что же, прозвенел «последний звонок», отгремел выпускной бал (как это быстро у меня происходит ), и за воротами родной школы нас поджидает, собственно, аналитическая геометрия:

2.2.1. Общее уравнение и направляющий вектор прямой