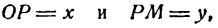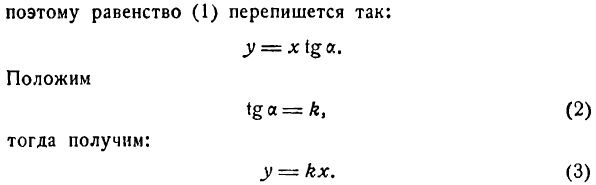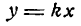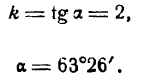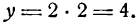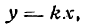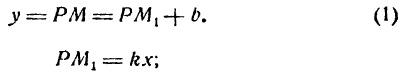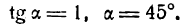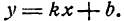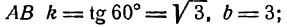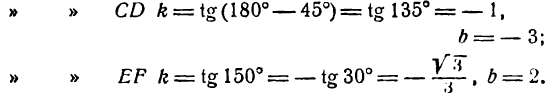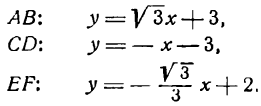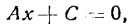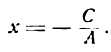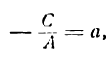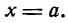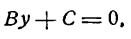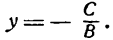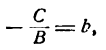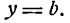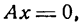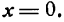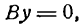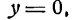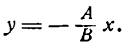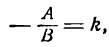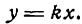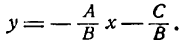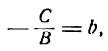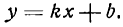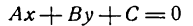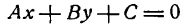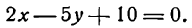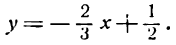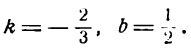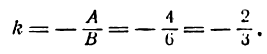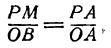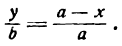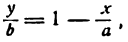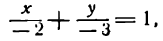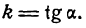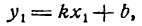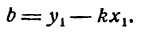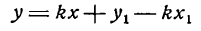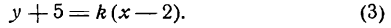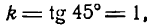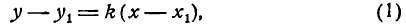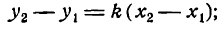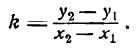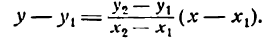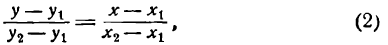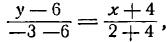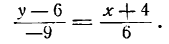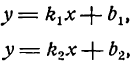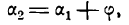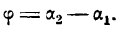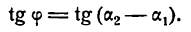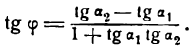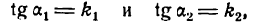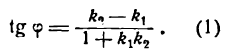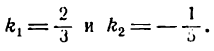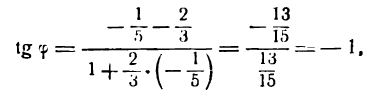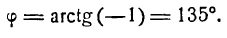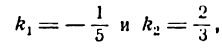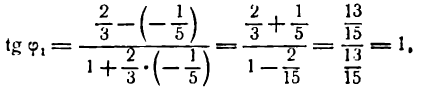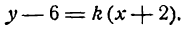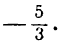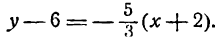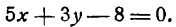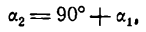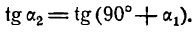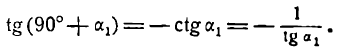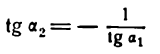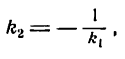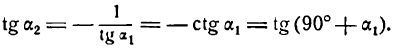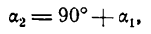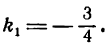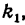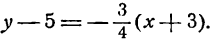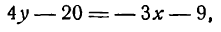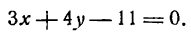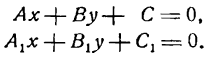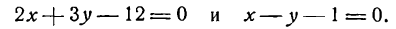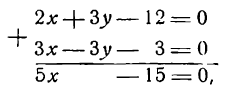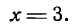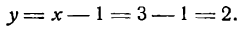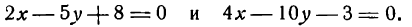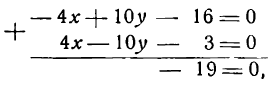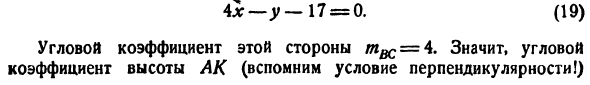Задача 32290 Найти уравнение прямой:
а) образующей с…
Условие

Найти уравнение прямой:
а) образующей с осью Ox угол pi/3 и пересекающей ось Oу в точке (0;–6)
б) параллельной оси Ох и отсекающей на оси Oу отрезок, равный 2
в) отсекающей на осях координат отрезки, равные 3 и 4.
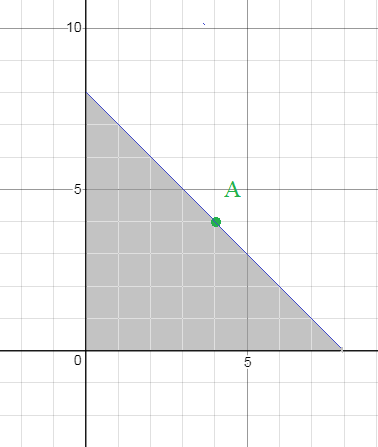
2) Составить уравнение прямой, проходящей через точку А(4;4) и отсекающей от координатного угла треугольник площадью S=4
предмет не задан
7478
Решение
★
а) Уравнение прямой y=kx+b
k_(прямой)=tgα
По условию α =(π/3)
k= tg (π/3)=sqrt(3)
y=sqrt(3)*x + b
Чтобы найти b подставим координаты точки
-6=sqrt(3)*0+b
b=-6
О т в е т. y=sqrt(3)*x — 6
б)О т в е т. y=2
в)
(x/3)+(y/4)=1
При х=0 получаем y=4 ( отрезок длины 4 на оси Оу)
При у=0 получаем х=3 ( отрезок длины 3 на оси Ох)
2.
(x/a)+(y/b)=1
Подставим A(4;4)
(4/a)+(4/b)=1
S=a*b/2
S=4
a*b=8
Система
{(4/a)+(4/b)=1
{a*b=8
{4*b+4*a=ab
{ab=8
{4b+4a=8
{ab=8
{b=2-a
{a*(2-a)=8
a^2-2a+8=0
D<0
нет решения.
Проверяйте данные задачи!
Самую маленькую площадь, будет иметь равнобедренный прямоуольный треугольник.
Прямая, проходящая через А, отсекает треугольник с катетами 8
Площадь такого треугольника 8*8/2=32
Написать комментарий
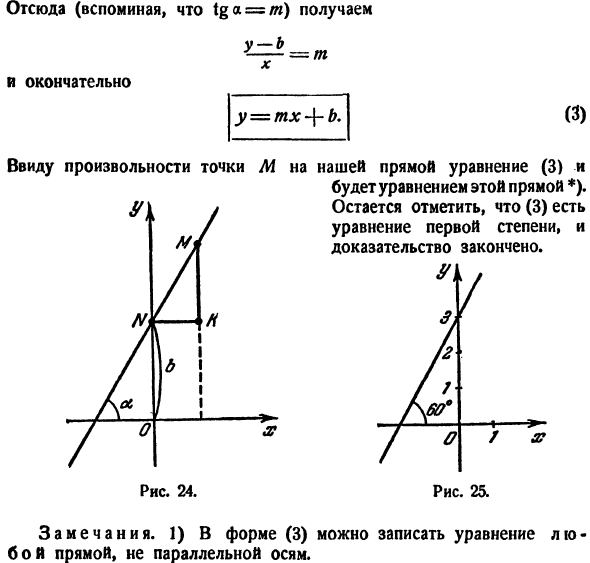
Уравнение прямой
Пусть прямая пересекает ось Оу в точке В (0; b) и образует с осью Ох
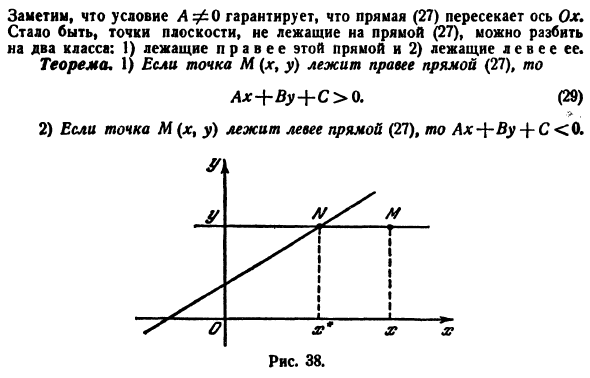
Итак, мы доказали, что координаты каждой точки прямой удовлетворяют уравнению (4.2). Нетрудно показать, что координаты любой точки, не лежащей на прямой, не удовлетворяют уравнению (4.2).
Уравнение (4.2) называется уравнением прямой с угловым коэффициентом.
Рассмотрим частные случаи уравнения (4.2).
- 1. Если b = 0, то получаем у = кх — уравнение прямой, проходящей через начало координат и образующей при к = tg а > О острый угол а с осью Ох, а при к = tg а ТО прямая перпендикулярна оси Ох (см.
рис. 4.6) и к = tg— не существует, т.е. вертикальная прямая не 2
имеет углового коэффициента. Предположим, что эта прямая отсекает на оси Ох отрезок, равный а. Очевидно, что уравнение такой прямой х = а (так как абсцисса любой точки прямой равна а), а уравнение оси Оу есть х = 0.
Уравнение прямой, проходящей через данную точку в данном направлении. Пусть прямая проходит через точку Мх(хх ,ух) и
образует с осью Ох угол а (рис. 4.7).
Так как точка Мх(хх,ух) лежит на прямой, то ее координаты удовлетворяют уравнению (4.2), т.е.
Вычитая равенство (4.3) из равенства (4.2), получим уравнение искомой прямой
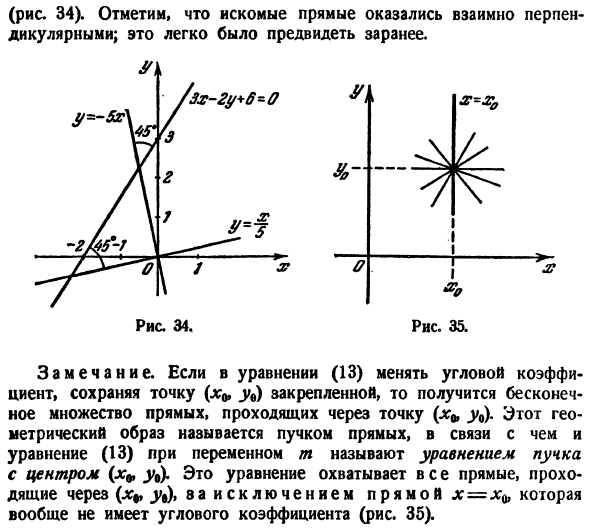
Уравнение пучка прямых. Если в уравнении (4.4) к — произвольное число, то это уравнение определяет пучок прямых, проходящих через точку Мх(хх,ух), кроме прямой, параллельной оси Оу и не имеющей углового коэффициента (рис. 4.8).
О Пример 4.2. 1. Составить уравнение
прямой, проходящей через точку А (3;—2):
а) под углом 135° к оси Ох б) параллельно оси Оу. 2. Найти уравнение пучка прямых.
Решение. 1. а) угловой коэффициент прямой k = tg 135° = — 1.
Уравнение прямой, проходящей через точку А (3; —2) (см. рис. 4.9), по формуле (4.4) имеет вид у + 2 = — 1 (х —3) или у = —х + 1.
- б) Уравнение прямой, параллельной оси Оу, х = 3.
- 2. Уравнение пучка прямых, проходящих через точку А (3; —2),
Для составления уравнения прямой Мх М2 (рис. 4.10) запишем уравнение пучка прямых, проходящих через точку Мх:
Так как точка М2 <х2,у2) лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М2 в уравнение пучка у2
хj) и найдем угловой коэффициент прямой
Теперь уравнение искомой прямой примет вид или
[> Пример 4.3. Составить уравнение прямой, проходящей через точки А (-5; 4) и В (3; —2).
Р е ш е н и е. По уравнению (4.6): —- = ———, откуда по
сле преобразований у = — х + —. ?
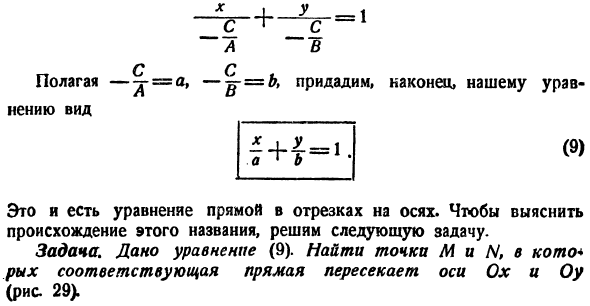
Уравнение прямой в отрезках. Найдем уравнение прямой по заданным отрезкам аФ 0 и b ф 0, отсекаемым на осях координат. Используя (4.6), уравнение прямой, проходящей через точки А <а;0) и В (0; Ь)
(рис. 4.11), примет вид — = —
или после преобразований
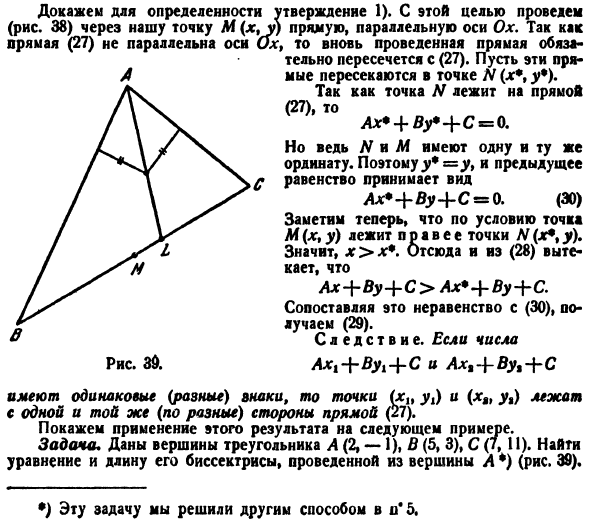
О Пример 4.4. Составить уравнение прямой, проходящей через точку А (2; —1), если эта прямая отсекает от положительной полуоси Оу отрезок, вдвое больший, чем на положительной полуоси Ох (рис. 4.12).
Р е ш е н и е. По условию b = 2а (а >0, b > 0). Подставляя это выражение в
уравнение (4.7), получим — + — = 1.
Так как точка А (2; —1) лежит на прямой, то ее координаты удовлетворяют 2 1
этому уравнению, т.е. — — — =1, от- а 2 а
Итак, уравнение искомой прямой имеет вид — + — = 1 или у = —2х + 3. ?
Общее уравнение прямой и его исследование. Рассмотрим уравнение первой степени с двумя переменными в общем виде
в котором коэффициенты А и В не равны одновременно нулю, т.е. А 2 + В 2 ф 0.
1. Пусть В ф 0. Тогда уравнение (4.8) можно записать в виде = А _ С
А/В, b = —С/В. Если А ф 0, С ф 0, то получим у = кх + b (уравнение прямой с угловым коэффициентом); если А ф 0, С = 0, то у = кх (уравнение прямой, проходящей через начало координат); если А = 0, С ф 0, то у = b (уравнение прямой, параллельной оси Оу); если А = 0, С = 0, то у = 0 (уравнение оси Ох).
2. Пусть В = 0, А ф 0. Тогда уравнение (4.8) примет вид С
х =—. Обозначим а = —С/А. Если С ф 0, то получим х = а
(уравнение прямой, параллельной оси Оу); если С = 0, то х = 0 (уравнение оси Оу).
Уравнение (4.8) называется общим уравнением прямой. Заметим, что в отличие от уравнения пучка прямых (4.4) общее уравнение (4.8) включает и уравнение любой вертикальной прямой, параллельной оси Оу.
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Уравнение прямой, проходящей через точку A ( — 2, 3) и образующей с осью Ох угол 45 градусов, 90 и 0?
Математика | 1 — 4 классы
Уравнение прямой, проходящей через точку A ( — 2, 3) и образующей с осью Ох угол 45 градусов, 90 и 0.
Поскольку уравнение прямой образует с осью OX угол в 45⁰, значит.
Угловой коэффициент прямой будет равен :
(угловой коэффициент это коэффициент при х в уравнении графика).
Для 90 градусов :
Уравнение прямой, проходящей через точку?
Уравнение прямой, проходящей через точку.
Срочно помогите?
Cоставить уравнение прямой проходящую через точку (0 ; — 2) и составляющей с положительным направлением оси ОХ такой же угол, что и прямая y = 3 / 7x — 3.
Напишите уравнение прямой , проходящей через точку N( — 2 ; 3) и параллельно оси х?
Напишите уравнение прямой , проходящей через точку N( — 2 ; 3) и параллельно оси х.
Написать уравнение прямой, проходящей через точку С(1 ; 2 ; 4) и перпендикулярной к оси ОY?
Написать уравнение прямой, проходящей через точку С(1 ; 2 ; 4) и перпендикулярной к оси ОY.
Опишите на алгеброическом языке : помогите плииииииииз ?
Опишите на алгеброическом языке : помогите плииииииииз !
А)Прямую, проходящую через точку 5 оси координат и параллельную оси абсцисс
Б) прямую проходящую через точку ( — 5 ; 2) и паралельную оси ординат.
Запишите уравнение прямой параллельной оси х и проходящей через точку (2 ; — 3)?
Запишите уравнение прямой параллельной оси х и проходящей через точку (2 ; — 3).
Составьте уравнение прямой проходящей через точку A (1 ; — 2) если она параллельна оси абсцисс?
Составьте уравнение прямой проходящей через точку A (1 ; — 2) если она параллельна оси абсцисс.
Составьте уравнение прямой, которая проходит через точку A(корень из 3 ; 5) и образует с положительным направлением оси абцисс угол 60 градусов?
Составьте уравнение прямой, которая проходит через точку A(корень из 3 ; 5) и образует с положительным направлением оси абцисс угол 60 градусов.
Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси Ох угол А — 45°?
Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси Ох угол А — 45°.
Составьте уравнение прямой, проходящей через точку (5 ; — 7) и образующей с осью Ox угол arctg( — 2)?
Составьте уравнение прямой, проходящей через точку (5 ; — 7) и образующей с осью Ox угол arctg( — 2).
На странице вопроса Уравнение прямой, проходящей через точку A ( — 2, 3) и образующей с осью Ох угол 45 градусов, 90 и 0? из категории Математика вы найдете ответ для уровня учащихся 1 — 4 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.
1)30 + 2 = 32 2)32 + 2 = 34 3)34 + 2 = 36 4)36 + 2 = 38 5)38 + 2 = 40 6)40 + 2 = 42 места в 7 ряду.
1 ряд — 30 2 ряд — 32 3 ряд — 34 4 ряд — 36 5 ряд — 38 6 ряд — 40 7 ряд — 42 Следовательно, в 7 ряду 42 мест.
То что угол это угол хDDD.
На каждого токаря приходится 738 : 6 = 123 деталей если одного токаря не будет бригада наточит 738 — 123 = 615 деталей БЕЗОБРАЗИЕ. Срыв плана. Лишение премии. ПОЛНЫЕ УБЫТКИ.
Русский знаеш ? А то я русскй.
За 5 шо спортсмен пробіг 15 м скільки він пробіг за 1 год Скільки м проїхав велосипедист, якщо продуктивність його праці на 1 год на 2 м більша ніж у спортсмена і він їхав 6 год.
3) 12 : 30 4) Футбольный Уроки в школе начинаются матч начинается в 8 часов утра в половине четвёртого.
111 × 11 — 111 + 1 = 1111.
1)48 6 = 8(км) — прошли пешком 2)48 2 = 24(км) — проехали на автобусе 3)48 — (24 + 
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-prjamoj-s-uglovym-koeffitsientom/
http://matematika.my-dict.ru/q/6240818_uravnenie-pramoj-prohodasej-cerez-tocku-a/
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямых, параллельных осям координат
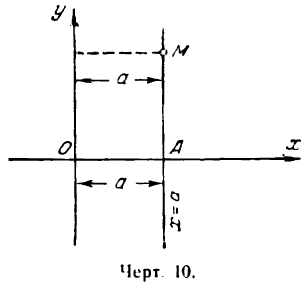
Возьмем прямую линию, параллельную оси Оу и проходящую на расстоянии а от нее (рис. 10).
Все точки этой прямой одинаково удалены от оси ординат на расстояние, равное а. Следовательно, для каждой точки прямой АМ абсцисса одна и та же, а именно:
х = а, (1)
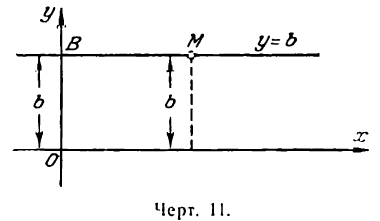
ордината же различна. Таким образом, уравнение (1) вполне определяет прямую, параллельную оси Оу, а потому оно является ее уравнением. Возьмем прямую, параллельную оси Ох, на расстоянии.
равном b от нее (рис. 11). Все точки этой прямой одинаково удалены от оси Ох на расстояние, равное b , т. е. любая точка прямой ВМ имеет постоянную ординату, а именно:
абсциссу же различную. Как видно, уравнение (2) вполне определяет прямую, параллельную оси Ох, а потому оно является ее уравнением.
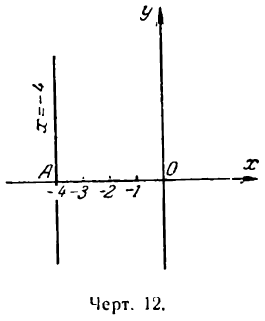
По уравнениям (1) и (2) можно построить соответствующие им прямые. Пусть, например, дана прямая х = — 4. Отложив на оси Ох отрезок ОА = — 4 (рис. 12) и проведя через точку А прямую, параллельную оси Оу, получим искомую прямую.
Уравнения осей координат
Возьмем уравнение прямой, параллельной оси Оу:
х = а
и станем в нем уменьшать абсолютную величину а, тогда прямая, определяемая этим уравнением, будет приближаться к оси Оу, оставаясь все время ей параллельной, и при а = 0 сольется с ней. Уравнение х = 0 является уравнением оси Оу.
Если же в уравнении у = b прямой, параллельной оси Ох, будем уменьшать абсолютную величину b то эта прямая станет приближаться к оси Ох, оставаясь ей параллельной, и при b = 0 с ней совпадет. Таким образом, уравнение у = 0 будет уравнением оси Ох.
Уравнение прямой, проходящей через начало координат
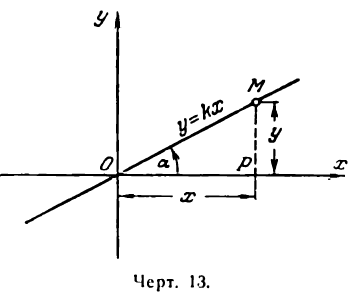
Проведем прямую через начало координат под углом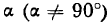
к оси Ох (рис. 13). Принято положительный угол а отсчитывать от положительного направления оси абсцисс в сторону, противоположную движению часовой стрелки (рис. 13), а отрицательный — по часовой стрелке.
Возьмем на проведенной прямой произвольную точку М (х; у). Опустив перпендикуляр МР на ось Ох, получим прямоугольный треугольник ОМР, из которого найдем:
Но
Координаты любой точки прямой ОМ удовлетворяют полученному уравнению; можно показать, что координаты любой точки, не лежащей на прямой ОМ, не удовлетворяют ему; поэтому оно является уравнением прямой ОМ. Итак,
есть уравнение прямой, проходящей через начало координат. В нем х и у — текущие координаты, а 
Определение:
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к положительному направлению оси Ох.
Величина 

Заметим, что при а = 90° углового коэффициента не существует, так как 90° не имеет числового значения.
Зная угловой коэффициент прямой у = 
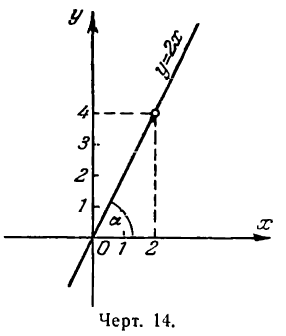
Пусть требуется построить прямую у= 2х.
Для этого найдем угол а из условия
откуда:
Построив при точке О найденный угол, мы и получим искомую прямую (рис. 14).
Построение этой прямой можно провести и проще.
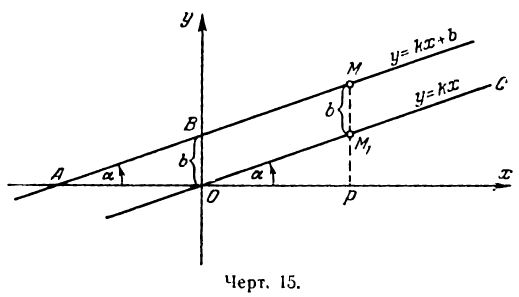
Известно, что положение прямой определяется двумя точками, поэтому для решения задачи нужно знать их координаты. В нашем же случае достаточно определить координаты одной точки, так как вторая (начало координат) нам известна. Для этого дадим х произвольное значение, например х = 2, тогда из уравнения прямой найдем:
Значения х = 2 и у = 4 и будут координатами точки, лежащей на данной прямой. Построив эту точку, проведем через нее и начало координат прямую линию (рис. 14).
Уравнение прямой с угловым коэффициентом и начальной ординатой
Пусть дана прямая ОС, проходящая через начало координат под углом а к положительному направлению оси Ох (рис. 15)
Ее уравнение имеет вид
где 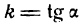
Проведем прямую 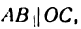
Но
Подставив значение РМ1 в равенство (1), получим уравнение прямой АВ в виде:
где 
Заметим что прямая 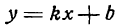
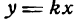
Уравнение 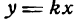
Зная угловой коэффициент 
Из данного уравнения имеем:
откуда
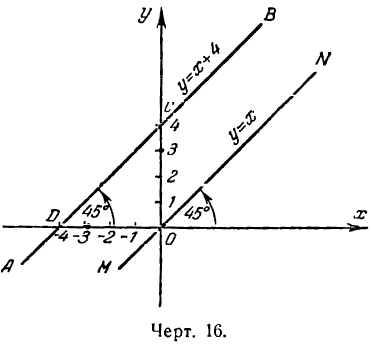
Проведем через начало координат прямую МN под углом в 45 градусов к положительному направлению оси Ох (рис. 16). На прямую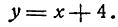
Как видно из уравнения ее пересекает ось Оу на расстоянии ОС, равном 4 единицам масштаба от начала координат.
Поэтому прямая АВ, проведенная через точку С параллельно прямой МN, и будет искомой.
Однако проще построить указанную прямую по двум ее точкам. Удобнее для этого брать точки пересечения прямой с осями координат. Одна из них — точка С пересечения прямой с осью Оу— дается самим уравнением, а именно С(0; 4). Для нахождения точки D пересечения этой прямой с осью Ох положим в данном уравнении y = 0, получим х = — 4; значит, прямая пересекает ось Ох в точке D (-4; 0). Строим точки С и D и проводим через них искомую прямую.
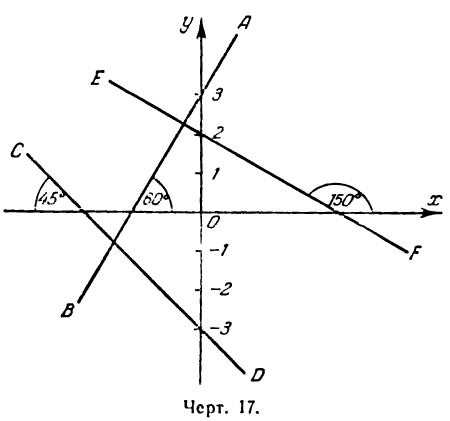
Пример:
Найти уравнения прямых АВ, СD и ЕF, изображенных на рис. 17.
Решение:
Чтобы написать уравнения данных прямых, нужно определить величины 
Для прямой АВ
Следовательно, уравнения данных прямых будут:
Общее уравнение прямой
В предыдущей лекции были выведены следующие виды уравнения прямой: уравнение прямой, параллельной оси Оу:
уравнение прямой, параллельной оси Ох:
уравнение оси Оу:
уравнение оси Ох:
уравнение прямой, проходящей через начало координат:
уравнение прямой с угловым коэффициентом и начальной ординатой:
Уравнения (1) — (6) исчерпывают все возможные положения прямой, поэтому можно сказать, что
всякая прямая линия определяется уравнением первой степени относительно текущих координат.
Покажем теперь, что указанные виды уравнения прямой можно получить из уравнения
при некоторых частных значениях коэффициентов А, В и С.
I. Если В = 0, то уравнение (7) обратится в следующее:
откуда
Положив
получим
Уравнение 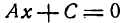
II. Если А = 0, то
отсюда
Положив
получим
Уравнение 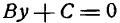
III. Если В = 0 и С = 0, то
отсюда
IV. Если А = 0 и С = 0, то
отсюда
V. Если С = 0, то
отсюда
Положим
тогда
Уравнение 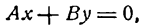
VI. Если ни один из коэффициентов уравнения (7) не равен нулю, то и в этом случае его можно преобразовать в знакомую нам форму уравнения прямой. Найдем из уравнения (7) значение у:
Положив
и
можем написать
Следовательно, уравнение
включает в себя все рассмотренные нами ранее уравнения прямой; поэтому оно называется общим уравнением прямой. Итак, всякое уравнение первой степени
при любых значениях коэффициентов А, В и С, исключая одновременное равенство А и В нулю, определяет прямую линию.
Пример:
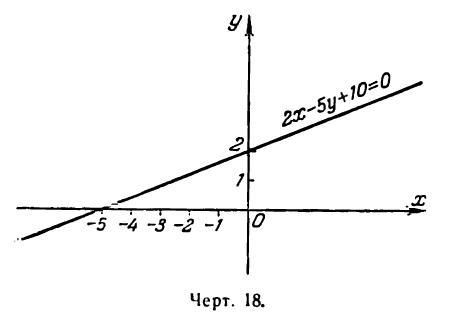
Построить прямую
Решение:
Проще всего построить прямую по двум ее точкам пересечения с осями координат. Положив в данном уравнении у = 0, получим х =- 5; координаты (-5; 0) и будут определять положение точки пересечения прямой с осью Ох. Для нахождения точки пересечения прямой с осью Оу положим в том же уравнении х = 0 тогда найдем у = 2; координаты искомой точки будут (0; 2).
Построив эти точки, проводим через них прямую 2х— 5у —10 = 0 (рис. 18).
Пример:
Найти угловой коэффициент и начальную ординату прямой 4х+ 6у — 3 = 0.
Решение:
Преобразуем это уравнение к виду
для этого находим:
6у = — 4х + 3,
отсюда
Сравнив полученное уравнение с уравнением 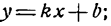
Угловой коэффициент можно найти и из равенства (8). Для этого, как видно, нужно коэффициент при х общего уравнения прямой разделить на коэффициент при у и частное
взять с противоположным знаком. Таким образом, в данном примере
Уравнение прямой в отрезках
Как мы уже знаем, положение прямой определяется или двумя точками или одной точкой и углом наклона прямой к оси Ох. Если прямая не параллельна ни одной из координатных осей и не проходит
через начало координат, то ее положение может быть определено и другими данными, например отрезками, которые она отсекает на осях. Выведем уравнение прямой для этого случая.
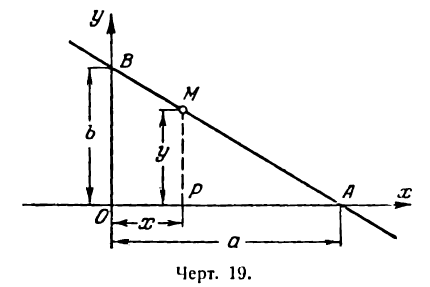
Пусть дана прямая, отсекающая на координатных осях отрезки ОА = а и ОВ = b (рис. 19).
Возьмем на этой прямой произвольную точку M (х; у) и проведем
МР 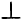
или
Разделив а — х почленно на а, будем иметь:
откуда
Можно показать, что координаты любой точки нашей прямой будут удовлетворять этому равенству, а потому его нужно рассматривать как уравнение прямой АВ.
В уравнение (1) входят отрезки а и b , отсекаемые прямой на осях; поэтому оно называется уравнением прямой в отрезках.
Величины а и b могут быть как положительными, так и отрицательными в зависимости от того, в какую сторону от начала координат откладываются отрезки а и b .
Пусть, например, дана прямая АВ (рис. 20). Здесь а = — 2, b = — 3; следовательно, уравнение прямой АВ запишется в таком виде:
По уравнению вида (1) Очень просто строится прямая. Для этого нужно только отложить на осях отрезки а и b взятые из уравнения, и через их концы провести прямую.
Заметим, что уравнение в отрезках легко получается из общего уравнения прямой: Ах + Ву + С= 0, если все коэффициенты общего уравнения отличны от нуля (иначе уравнение в отрезках не имеет смысла).
Уравнение пучка прямых
Пусть прямая АВ проходит через точку М(х1; у1) и образует угол а с положительным направлением оси Ох (рис. 21). Составим для прямой АВ уравнение вида
Для этого нужно найти величины 

Для нахождения b воспользуемся тем, что точка М лежит на прямой (1) и, следовательно, ее координаты удовлетворяют уравнению этой прямой.
Подставив в уравнение (1) вместо х и у их значения х1 и у1, а величину 
откуда
Уравнение (1) можем теперь записать в виде
или
Таково искомое уравнение прямой АВ; в нем 
Допустим, что через ту же точку M(х1; у1) проходит несколько прямых; тогда угол а наклона этих прямых к оси Ох, и также множитель 
В таком случае уравнение (2) будет определять уже не одну прямую, проходящую через данную точку M, а множество прямых, пересекающихся в эточке.
Совокупность всех прямых, проходящих через одну точку М, называется пучком прямых с центром в точке М. Таким образом, уравнение (2) с переменным 
Чтобы выделить из этого пучка прямую, образующую заданный угол с осью Ох, нужно в уравнении (2) вместо 
Выделим из этого пучка одну прямую, которая наклонена к положительному направлению оси Ох под углом а = 45°;
тогда
и уравнение (3) обратится в следующее:
или
Уравнение прямой, проходящей через две данные точки
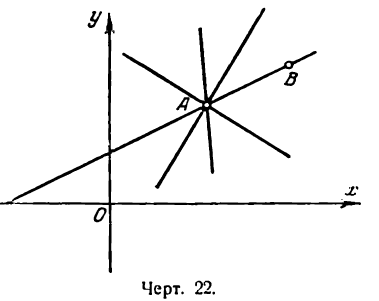
Пусть даны две точки A(х1; у1) и В(х2; у2); требуется найти уравнение прямой, проходящей через эти точки.
Если взять одну точку, например А, то через нее можно провести пучок прямых, уравнение которого будет:
где каждому значению 
Выделим из этого пучка прямую, которая проходит и через вторую точку В (рис. 22). Чтобы найти ее уравнение, необходимо определить угловой коэффициент. Для этого примем во внимание, что точка В лежит на искомой прямой, и потому ее координаты должны обращать уравнение (1)
в тождество при 
отсюда находим угловой коэффициент искомой прямой:
Уравнение (1) можно переписать так:
Преобразуем это уравнение, разделив обе части его на у2 — у1 получим:
гле х и у — текущие координаты. Равенство (2) является уравнением прямой, проходящей через две данные точки. Это, как и уравнение в отрезках, частный случай общего уравнения прямой.
Если х1 = х2 или у1 = у2, то формула (2) теряет смысл, так как делить на нуль нельзя. В этих случаях точки А и В лежат либо на прямой, параллельной оси Оу, либо на прямой, параллельной оси Ох. В первом случае уравнение прямой запишется в виде
х = х1
а во втором — в виде
у = у1
Пример:
Написать уравнение прямой, проходящей через две точки: А(—4; 6) и В(2; —3).
Решение:
Имеем:
х1 = —- 4, х2 = 2
и
у1 = 6, у2 = — 3.
Подставим эти значения в уравнение (2); получим:
или
Умножив обе части последнего уравнения на —18, будем иметь:
2у— 12 = — 3х— 12,
откуда
Зх + 2у = 0.
Пример:
Через две точки А( 3; 2) и В (5; 2) проходит прямая. Написать ее уравнение.
Решение:
Так как ординаты данных точек равны, то заключаем, что искомая прямая параллельна оси Ох, а потому ее уравнение будет
у = 2.
Угол между двумя прямыми
Пусть даны уравнения двух прямых:
y=klx+blt
где 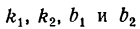
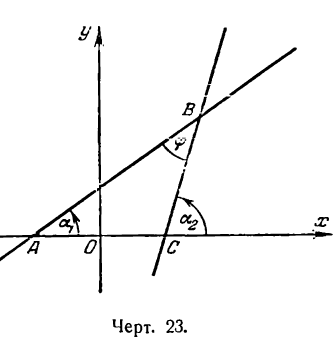
Обозначим углы, образуемые данными прямыми с положительным направлением оси Ох, через а1 и а2, а угол между этими прямыми через 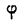
Угол а2, как внешний угол треугольника ABC, будет равен сумме внутренних, с ним не смежных, т. е.
откуда
Если углы равны между собой, то и тангенсы их равны друг другу, поэтому
Применяя формулу для тангенса разности двух углов, получим:
Но
Поэтому
Определив tg 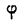
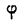
Пример:
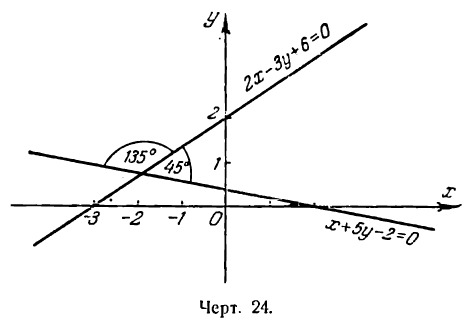
Определить угол между прямыми:
2х — 3у + 6 =0
и
х + 5у — 2=0.
Решение:
Из данных уравнений найдем угловые коэффициенты этих прямых :
Согласно формуле (1) имеем:
откуда
Полученный угол между прямыми тупой. Но если принять
то вычисляя 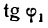
откуда 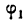
найденным тупым углом (рис. 24). Первое и второе значение угла будет ответом на вопрос задачи.
Условие параллельности прямых
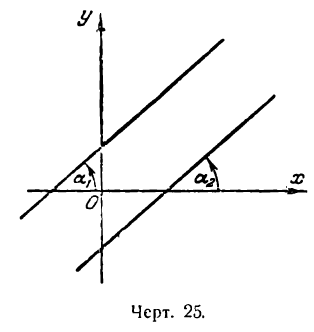
Если прямые параллельны между собой, то они образуют одинаковые углы а1 и а2 с положительным направлением оси Ох (рис. 25).
Из равенства углов а1 и а2 следует
или
Обратно, если 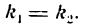
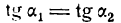
Итак, если прямые параллельны между собой, то их угловые коэффициенты равны (и наоборот).
Пример:
Написать уравнение прямой, проходящей через точку А (—2; 6) и параллельной прямой 5х—3у — 7 = 0.
Решение:
Через точку А проходит пучок прямых, среди которых находится искомая прямая. Следовательно, прежде всего пишем уравнение пучка прямых , проходящих через точку А:
Затем находим из данного в задаче уравнения прямой ее угловой коэффициент; применяя равенство (8) , получим:
Согласно условию параллельности угловой коэффициент искомой прямой тоже равен
Подставим найденное значение 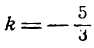
пучка:
Выполнив необходимые преобразования, получим искомое уравнение прямой:
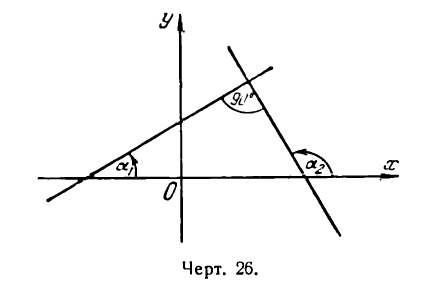
Условие перпендикулярности прямых
Пусть две прямые взаимно перпендикулярны и образуют с положительным направлением оси Ох углы а1 и а2 (рис. 26). В этом случае
отсюда
Но
Следовательно,
или
Обратно, если
то
Отсюда
т. е. данные прямые взаимно перпендикулярны.
Таким образом, если прямые взаимно перпендикулярны, то их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку (и наоборот).
Так, например, если у одной прямой угловой коэффициент
равен 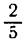
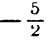
Пример:
Написать уравнение прямой, проходящей через точку А(—3; 5) и перпендикулярной прямой 4х — Зу—10 = 0.
Решение:
Через точку А проходит пучок прямых, среди которых находится и искомая прямая. Поэтому напишем сначала уравнение этого пучка
Чтобы выделить из него нашу прямую, нужно найти ее угловой коэффициент 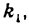
данной прямой равенством (1). Но 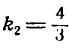
Подставив в уравнение (2) вместо 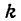
получим:
Это и есть искомое уравнение прямой. Преобразовав его, найдем:
или
Пересечение прямых
Пусть даны две прямые, определяемые уравнениями:
Требуется найти точку их пересечения.
Так как точка пересечения данных прямых есть их общая точка, то ее координаты должны удовлетворять как первому, так и второму уравнению, т. е. эти координаты должны быть общими корнями данных уравнений.
Чтобы найти эти корни, нужно, как известно из алгебры, решить совместно данные уравнения, рассматривая их как систему уравнений.
Пример:
Найти точку пересечения прямых
Решение:
Решим данные уравнения как систему. Умножив второе уравнение на 3 и сложив результат с первым уравнением, получим:
откуда
Зная х, находим у, например, из второго уравнения:
Пример:
Найти точку пересечения прямых
Решение:
Умножив все члены первого уравнения на —2 и сложив полученное уравнение со вторым, найдем:
что невозможно. Значит, данная система уравнений решений не имеет, а потому прямые, определяемые этими уравнениями, не имеют общих точек, т. е. данные прямые параллельны.
К этому же заключению можно прийти, сравнивая угловые коэффициенты данных прямых.
Дополнение к прямой линии
Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Изучение геометрических свойств линий начнем с простейшей из линий – прямой. Всякая прямая в декартовой системе координат может быть представлена уравнением первой степени и, обратно, всякое уравнение первой степени относительно Х и У определяет прямую линию.
Рассмотрим прямую, не параллельную осям координат. Положение ее на плоскости вполне определяется заданием Угла наклона прямой к оси ОХ и ординатой точки В пересечения прямой с осью ОY. Под углом наклона прямой к оси ОХ будем понимать тот угол, на который надо повернуть ось ОХ против часовой стрелки, чтобы она совпала с данной прямой (или оказалась параллельной ей). Обозначим этот угол через . Величину отрезка OB обозначим через b. Пусть
М (Х, У) – произвольная точка, лежащая на прямой (рисунок 1.3).
Рисунок 1.3
При движении точки по прямой ее координаты остаются все время связанными между собой некоторым условием. Выпишем это условие. Проведем прямые BK и МК, параллельные осям координат. Мы получили прямоугольный треугольник МВК, для которого верно соотношение
(1.5)
Тангенс угла наклона прямой к оси ОХ называется угловым коэффициентом прямой. Обозначим его буквой K, т. е. tg = K. Из рисунка 1.3 видно, что MK = Y – b, BK = X. Равенство (1.5) теперь можно записать в виде
,
Откуда, выразив y, окончательно получаем
y = Kx + B. (1.6)
Этому уравнению удовлетворяют лишь координаты точек, лежащих на рассматриваемой пря-мой, и оно нарушается, если точка не лежит на прямой. Таким образом, полученное уравнение (1.6) является уравнением заданной прямой линии.
Уравнение прямой вида (1.6) называется Уравнением прямой с угловым коэффициентом.
Уравнение (1.6) мы получили, считая, что прямая не параллельна осям координат.
Посмотрим, какое уравнение будет иметь прямая, параллельная какой-либо координатной оси (рисунок 1.4).
Рисунок 1.4
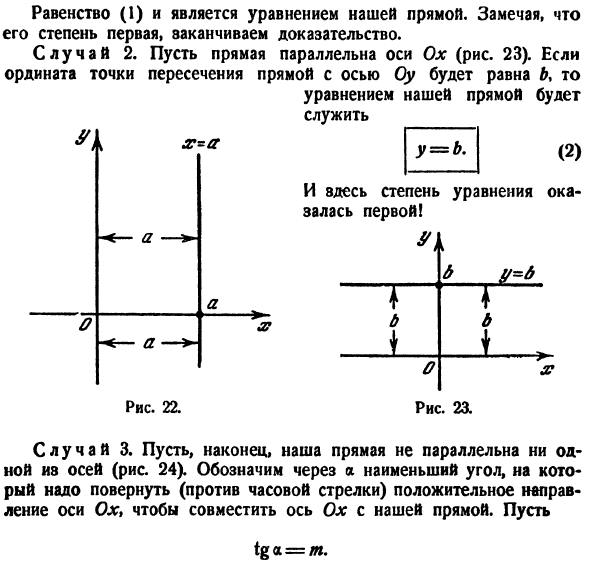
1. Пусть Прямая параллельна оси ОY. Обозначим через А абсциссу точки пересечения этой прямой с осью ОХ. Очевидно, любая точка прямой имеет абсциссу, равную А, если же точка не лежит на прямой, то ее абсцисса будет отлична от А. Следовательно, Уравнение этой прямой имеет вид
x = A. (1.7)
2. Пусть теперь Прямая параллельна оси ОХ. Ее угловой коэффициент K = 0. Считая этот случай частным, из Уравнения (1.6) получаем
Y = B. (1.8)
Итак, если прямая не параллельна осям координат, то ее уравнение может быть записано в форме (1.6). Если же прямая параллельна оси ОY, то ее уравнение можно записать в форме (1.7), уравнение прямой, параллельной оси ОХ, имеет вид (1.8). Все эти уравнения являются уравнениями первой степени относительно переменных Х и У. Таким образом, мы показали, что в декартовой системе координат всякая прямая может быть представлена уравнением первой степени.
Пример 1.3. Составить уравнение прямой, отсекающей на оси ОY отрезок B = 3 и составляющей с осью OX угол: 1) = 45°; 2)
= 135°.
Решение. 1. K = tg = tg 45° = 1. Уравнение прямой имеет вид Y = 1 × X + 3, или Y = X + 3.
2. К = tg = tg 135° = –1. Уравнение имеет вид Y = –X + 3.
| < Предыдущая | Следующая > |
|---|
Уравнением
прямой в отрезках называется
уравнение
вида
(4)
где
а
и b
– абсцисса и ордината точек пересечения
прямой с осями Ох
и Оу,
т.е. длины
отрезков,
отсекаемых прямой на координатных осях,
взятые с соответствующими знаками.
Пример
4. Общее
уравнение прямой 2х
– 3у
– 6 = 0 привести к уравнению в отрезках.
Решение:
запишем данное уравнение в виде 2х
– 3у=6
и разделим обе его части на свободный
член:
.
Это и есть уравнение данной прямой в
отрезках.
Пример
5. Через
точку А (1;2)
провести прямую, отсекающую на
положительных полуосях координат равные
отрезки.
Решение:
Пусть уравнение искомой прямой имеет
вид
По условию а=b.
Следова-тельно, уравнение принимает
вид х +
у =
а.
Так как точка А (1; 2) принадлежит этой
прямой, значит ее координаты удовлетворяют
уравнению х
+ у =
а;
т.е. 1 + 2 = а,
откуда а
= 3. Итак, искомое уравнение записывается
следующим образом: х
+ у = 3, или
х + у – 3
= 0.
Пример
6. Для прямой
написать
уравнение в отрезках. Вычислить площадь
треугольника, образованного этой прямой
и осями координат.
Решение:
Преобразуем данное уравнение следующим
образом:
,
или
.
В
результате получим уравнение
,
которое и
является уравнением данной прямой в
отрезках. Треугольник, образованный
данной прямой и осями координат, является
прямоугольным треугольником с катетами,
равными 4 и 3, поэтому его площадь равна
S
=
(кв.
ед.)

26
2.1.4 Уравнение прямой, проходящей через точку в данном направлении
Уравнение
прямой, проходящей через т.у А(ха;
уа)
и имеющей
угловой коэффициент k,
записывается в виде
у
– уа=k
(x
– xa).
(5)
Пример 7.
Составить уравнение прямой, проходящий
через точку (–2; 5) и образующей с осью
Ох
угол 45º.
Решение:
Угловой коэффициент искомой прямой k=
tg
45º = 1. Поэтому, воспользовавшись уравнением
(5), получаем у
– 5 = x
– (–2), или
х – у + 7
= 0.
2.1.5 Уравнение прямой, проходящей через две точки
Уравнение
прямой, проходящей через две точки т.
А (х1;
у1)
и т.В (х2;
у2),
имеет вид
(6)
Пример
8. Составить
уравнение прямой, проходящей через
точки А(–3;
5) и
В(7;
–2).
Решение:
Воспользуемся уравнением (6):
,
или
,
откуда 7х
+ 10у
– 29 = 0.
2.1.6 Нормальное уравнение прямой
Пусть
дана прямая С, проходящая через данную
точку Мо(Хо; Уо) и перпендикулярная
вектору
(А;В). Любой вектор
,
перпендикулярный данной прямой
,
называется ее нормальным
вектором.
Выберем
на прямой произвольную т. М(х;у).
Тогда
,
а значит их скалярное произведение
.
Это равенство можно записать в координатах
А(
х-хо
)+В( у-уо
)=0
(7)
Уравнение
(7) называется нормальным
уравнением прямой.
Пример
9.
Даны точки М1
(2;-1) и М2(4;
5). Написать уравнение прямой, проходящей
через
точку
М1
перпендикулярно
вектору
Решение:
Нормальный вектор искомой прямой
имеет
координаты (2;6), следовательно по формуле
(7) получим уравнение 2(х-2)+6(у+1)=0
или х+3у
+1=0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #