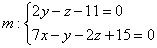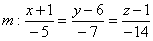vtg25 писал(а):
Не могу понять, как составить уравнение проекции прямой [math]frac{ x-1 }{ -1 }[/math] [math]=[/math][math]frac{ y }{ 3 }[/math] [math]=[/math][math]frac{ z+1 }{ 5 }[/math] на плоскость 5x-y+z-1=0
vtg25
При решении поставленной перед Вами задачи нужно исходить из того, что под проекцией обычно понимается ортогональная проекция. Значит, искомая проекция (которая в общем случае является прямой) принадлежит как заданной плоскости (плоскости проекции), так и плоскости, которая проходит через заданную прямую перпендикулярно к заданной плоскости.
Чтобы вывести уравнение второй (проецирующей) плоскости, воспользуемся тем, что ей принадлежит точка [math]M_0 left( 1;~0;~-1 right);[/math] вектор [math]vec{p}= left( -1;~3;~5 right)[/math] — направляющий вектор заданной прямой; вектор [math]vec{n}= left( 5;~-1;~1 right)[/math] — нормальный вектор плоскости проекции. Тогда получим
[math]begin{vmatrix} x-1 & -1 & 5 \ y & 3 & -1 \ z+1 & 5 & 1 end{vmatrix}=0,[/math]
[math](x-1)(3 cdot 1-(-1) cdot 5)-y((-1) cdot 1-5 cdot 5)+(z+1)((-1) cdot (-1)-5 cdot 3)=0,[/math]
[math]8(x-1)+26y-14(z+1)=0,[/math]
[math]8x+26y-14z-22=0,[/math]
[math]4x+13y-7z-11=0[/math]
— уравнение проецирующей плоскости.
Искомая проекция может быть задана системой уравнений, задающих плоскости проекции и проецирующую, то есть так:
[math]left{!begin{aligned}
& 5x-y+z-1=0, \
& 4x+13y-7z-11=0.
end{aligned}right.[/math]
Полученная система уравнений является ответом к задаче.
От указанной выше системы уравнений, задающих проекцию как результат пересечения двух плоскостей, можно перейти к её каноническим уравнениям. Для этого примем, например, что [math]z=0.[/math] Тогда получим систему уравнений
[math]left{!begin{aligned}
& 5x-y-1=0, \
& 4x+13y-11=0,
end{aligned}right.[/math]
решив которую, получим [math]x=frac{8}{23},[/math] [math]y=frac{17}{23},[/math] то есть точка [math]M left( frac{8}{23};~frac{17}{23};~0 right)[/math] принадлежит проекции. Направляющим вектором проекции является вектор, который перпендикулярен к нормальным векторам плоскостей проекции и проецирующей, то есть
[math]vec{l}=begin{vmatrix} vec{i} & vec{j} & vec{k} \ 5 & -1 & 1 \ 4 & 13 & -7 end{vmatrix}=((-1) cdot (-7)-1 cdot 13) vec{i}-(5 cdot (-7)-1 cdot 4) vec{j}+(5 cdot 13-(-1) cdot 4) vec{k}=[/math]
[math]=-6 vec{i}+39 vec{j}+69 vec{k},[/math]
поэтому канонические уравнения проекции суть
[math]frac{x-frac{8}{23}}{-6}=frac{y-frac{17}{23}}{39}=frac{z}{69},[/math]
или
[math]frac{x-frac{8}{23}}{-2}=frac{y-frac{17}{23}}{13}=frac{z}{23}.[/math]
Если Вы хотите воспользоваться моими расчётами, то не поленитесь, пожалуйста, проверить их хотя бы на отсутствие арифметических ошибок. Рекомендую Вам также посетить этот ресурс:
http://www.mathprofi.ru/zadachi_s_pryam … ostju.html
5.6.3. Как найти ортогональную проекцию прямой на плоскость?
г) Во-первых, что это за проекция?
Проведём очередную физкульт-пятиминутку:
Пожалуйста, найдите дома швабру и поместите её между ног. Представьте, что она бесконечна. Подбородок плотно прижат к груди. Теперь строго перпендикулярно смотрим вниз на швабру. при этом получается такое умное лицо…. Все выполнили задание? Тень от швабры – это и есть её ортогональная проекция на пол.
На чертеже выше наша «швабра» 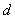
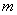
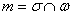
Другое дело, что часто требуется представить уравнения прямой в канонической форме, это стандартная задача:
Точка 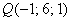
Таким образом, канонические уравнения проекции:
Как уже отмечалось, для решения этой задачи, не обязательно находить именно точку пересечения 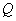
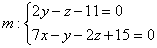
Есть и другой способ нахождения проекции, связанный с построением перпендикуляра к плоскости «сигма», но я тут прикинул, он вряд ли короче. Однако на всякий случай озвучу алгоритм, вдруг понадобится кому:
– находим точку пересечения прямой и плоскости: 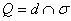
– берём произвольную точку 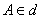
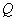
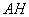
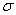
– находим основание перпендикуляра 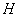
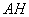
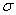
– составляем канонические уравнения проекции 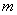
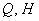
Задача 31787 Найти проекцию прямой (x–2)/5 = (y–3)/1.
Условие
Найти проекцию прямой (x–2)/5 = (y–3)/1 = (z+1)/2 на плоскость x+4y–3z+7=0
Решение
Точка (2;3;-1) принадлежит данной прямой.
Составим уравнение прямой || нормальному вектору плоскости
vector=(1;4;-3)
Найдем координаты точки K — точки пересечения этой прямой и плоскости
Решаем систему:
<(x-2)/1=(y-3)/4=(z-1)/(-3)
Обозначим отношение
(x-2)/1=(y-3)/4=(z-1)/(-3) = λ ⇒
получим параметрические уравнения прямой
x= λ +2
y= 4λ +3
z=-3 λ +1
подставим в уравнение плоскости
Найдем координаты точки В — точки пересечения данной прямой и данной плоскости.
Обозначим отношение
(x-2)/5=(y-3)/1=(z+1)/2=t ⇒
получим параметрические уравнения прямой
x=5t+2
y=t+3
z=2t+1
подставим в уравнение плоскости
Составляем уравнение прямой ВК, как уравнение прямой, проходящей через две точки
Ортогональнальная проекция прямой на плоскость.
Угол между прямой и плоскостью.
Теорема о трех перпендикулярах
Проекция прямой на плоскость
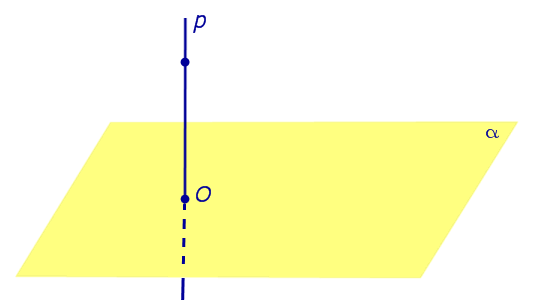
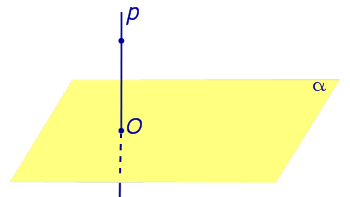
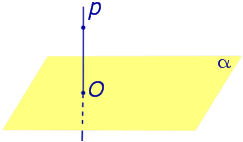
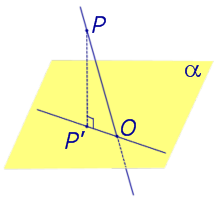
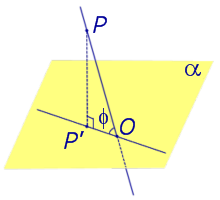
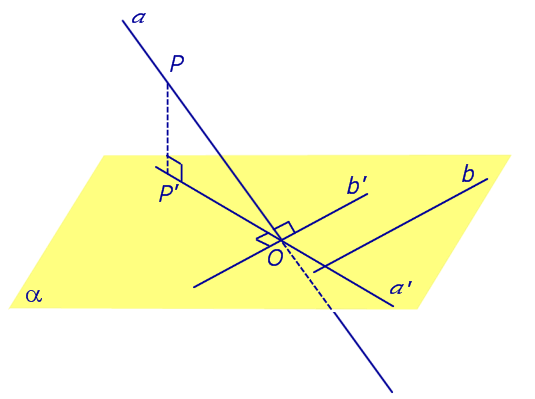
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
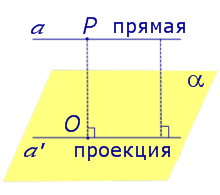
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
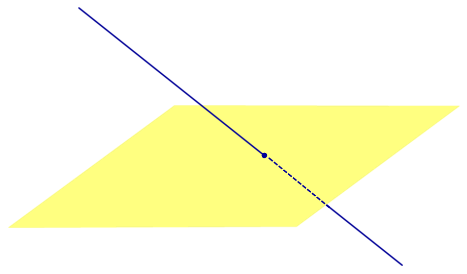
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
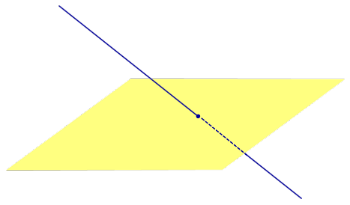
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
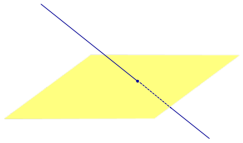
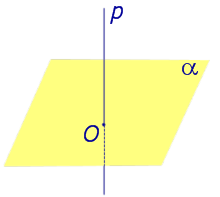
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Угол между прямой и плоскостью
Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.
| Фигура | Рисунок | Свойство проекции |
| Наклонная к плоскости α | 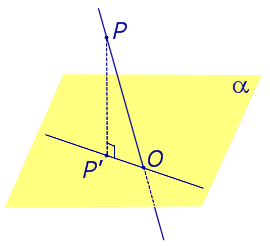 |
|
| Прямая, параллельная плоскости | 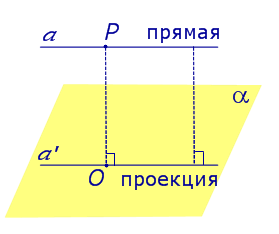 |
|
| Прямая, лежащая на плоскости | 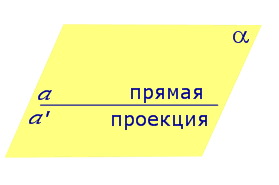 |
|
| Прямая, перпендикулярная к плоскости | 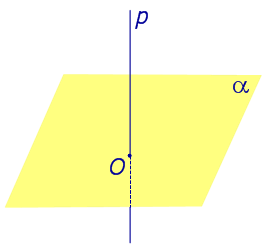 |
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
Теорема о трех перпендикулярах
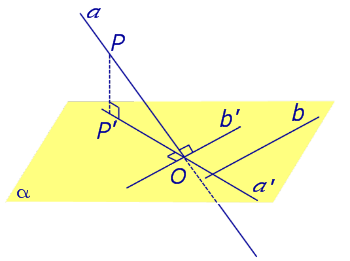
Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.
Доказательство. Рассмотрим следующий рисунок 3.
На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.
Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.
Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.
Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.
Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.
источники:
http://reshimvse.com/zadacha.php?id=31787
http://www.resolventa.ru/uslugi/uslugischoolsvib.htm
| Фигура | Рисунок | Определение |
| Наклонная к плоскости α | 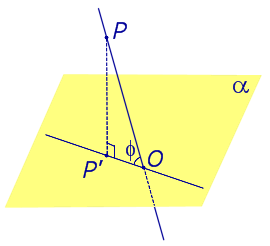 |
|
| Прямая, параллельная плоскости |  |
|
| Прямая, лежащая на плоскости |  |
|
| Прямая, перпендикулярная к плоскости |  |
Задача 31787 Найти проекцию прямой (x–2)/5 = (y–3)/1…
Условие
Найти проекцию прямой (x–2)/5 = (y–3)/1 = (z+1)/2 на плоскость x+4y–3z+7=0
предмет не задан
20148
Решение
★
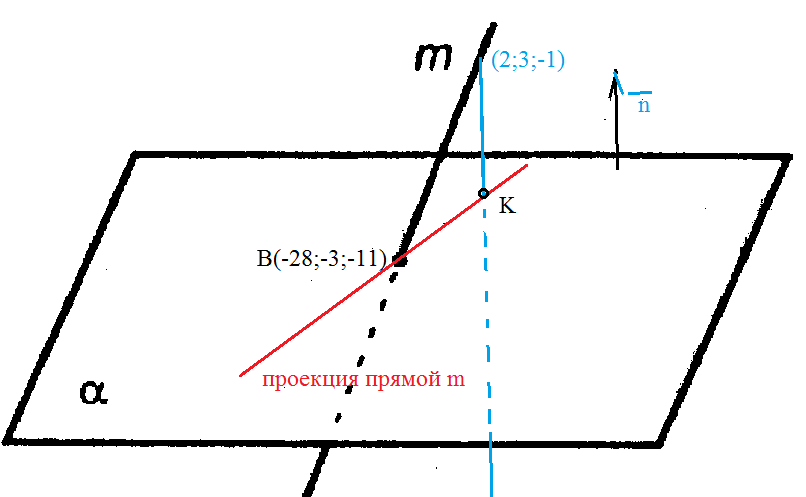
Точка (2;3;-1) принадлежит данной прямой.
Составим уравнение прямой || нормальному вектору плоскости
vector{n}=(1;4;-3)
(x-2)/1=(y-3)/4=(z-1)/(-3)
Найдем координаты точки K — точки пересечения этой прямой и плоскости
Решаем систему:
{(x-2)/1=(y-3)/4=(z-1)/(-3)
{x+4y-3z+7=0
Обозначим отношение
(x-2)/1=(y-3)/4=(z-1)/(-3) = λ ⇒
получим параметрические уравнения прямой
x= λ +2
y= 4λ +3
z=-3 λ +1
подставим в уравнение плоскости
( λ +2) +4*(4λ +3)-3*(-3 λ +1)+7=0
26 λ=-18
λ=-9/13
x_(К)=(-9/13)+2=
y_(К)=4*(-9/13)+3=
z_(К)=-3*(-9/13)+1=
Найдем координаты точки В — точки пересечения данной прямой и данной плоскости.
Решаем систему:
{(x-2)/5=(y-3)/1=(z+1)/2
{x+4y-3z+7=0
Обозначим отношение
(x-2)/5=(y-3)/1=(z+1)/2=t ⇒
получим параметрические уравнения прямой
x=5t+2
y=t+3
z=2t+1
подставим в уравнение плоскости
5t+2+4*(t+3)-3*(2t+1)+7=0
3t=-18
t=-6
x=5*(-6)+2=-28
y=-6+3=-3
z=2*(-6)+1=-11
В(-28; -3; -11)
Составляем уравнение прямой ВК, как уравнение прямой, проходящей через две точки
Написать комментарий
г) Во-первых, что это за проекция?
Проведём очередную физкульт-пятиминутку:
Пожалуйста, найдите дома швабру и поместите её между ног. Представьте, что она бесконечна. Подбородок плотно прижат к груди. Теперь строго
перпендикулярно смотрим вниз на швабру…, при этом получается такое умное лицо…. Все выполнили задание? Тень от швабры – это и есть её
ортогональная проекция на пол.
На чертеже выше наша «швабра» проведена малиновым цветом, а её
проекция, прямая – коричневым цветом. Легко заметить, что проекция задаётся
пересечением плоскостей: , и на самом деле ответ уже готов:
Другое дело, что часто требуется представить уравнения прямой в канонической форме, это стандартная
задача:
Точка , принадлежащая проекции, уже известна, осталось найти её
направляющий вектор. Для быстроты используем формулу:
Таким образом, канонические уравнения проекции:
Как уже отмечалось, для решения этой задачи, не обязательно находить именно точку пересечения (лишняя работа). Нас устроит любая точка, принадлежащая проекции, и её легко подобрать из системы
.
Есть и другой способ нахождения проекции, связанный с построением перпендикуляра к плоскости «сигма», но я тут прикинул, он
вряд ли короче. Однако на всякий случай озвучу алгоритм, вдруг понадобится кому:
– находим точку пересечения прямой и плоскости: (вот в этом способе уже
обязательно находим);
– берём произвольную точку , не совпадающую с точкой
) и опускаем из неё перпендикуляр
на плоскость
(см. следующие
параграфы);
– находим основание перпендикуляра (как пересечение прямой
и плоскости
);
– составляем канонические уравнения проекции по двум точкам:
.


| Оглавление |
Автор: Aлeксaндр Eмeлин
Skip to content
Если прямая представляется уравнениями
A1x + B1y + C1z + D1=0 (1)
A2x + B2y + C2z + D2=0 (2)
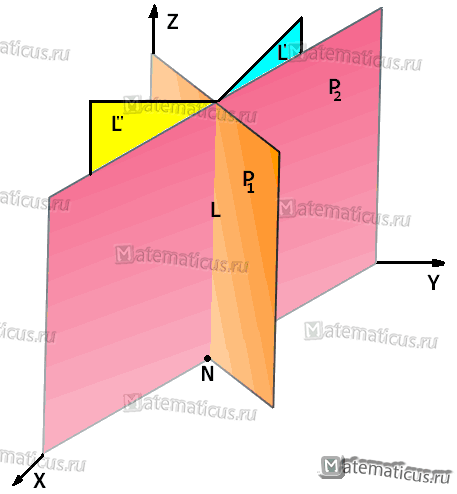
,где С1 и С2 одновременно не равны нулю (случай когда С1=С2= 0 рассмотрен ниже в примере 2). Чтобы найти проекцию прямой на плоскость XOY, необходимо исключить z из уравнений (1) и (2). Полученное уравнение (вместе с уравнением z=0) будет представлять искомую проекцию. Аналогично находятся проекции на плоскости для YOZ и ZOX.
Пример 1
Найти проекцию прямой L
2x+4y-3z-12=0
x-2у+4z-10=0
на плоскость ХОY.
Решение
Для того, чтобы исключить z, умножим первое уравнение на 4, а второе — на 3 и затем сложим. Получим:
4⋅(2x+4y-3z-12)+3⋅(x-2y+4z-10)=0
11x+10у-78=0
Это уравнение вместе с уравнением z=0 представляет проекцию L’ прямой L на плоскость XOY.
Пример 2
Найти проекции прямой L
2х-3у=0
х+у-4=0
на координатные плоскости.
Решение
В данных уравнениях отсутствует z, потому что плоскости Р1 и Р2 перпендикулярны (Р1⊥Р2) к плоскости XOY. Прямая L перпендикулярна к XOY и проектируется на плоскость XOY в точку N с координатой zN=0. Решая систему, находим значения xN=12/5, уN=8/5.
Уравнение проекции L’ на плоскость YOZ можно найти по общему способу, исключая х из уравнения. Получим у=8/5, то есть то же равенство, которое найдено выше для уN. Уравнение проекции L» на плоскость XOZ будет x=12/5
1772