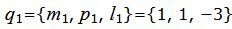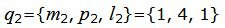Как составить уравнение плоскости проходящей через точку параллельно прямым

Уравнение плоскости, проходящей через точку и параллельной двум прямым

Плоскость, проходящая через данную точку М0(х0;у0;z0) и параллельная данным прямым K1 и K2 (при этом прямые K1 и K2 не параллельным между собой), выражается уравнением:


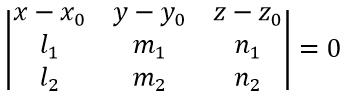
где l 1, m1, n1, l 2, m2, n2 — направляющие коэффициенты данных прямых.
Запись в векторной форме:

Примечание
Если данные прямые K1 и K2 параллельны между собой, то уравнение (1) имеет бесчисленное множество решений (получаем пучок плоскостей с осью, проходящей через точку М0 и параллельно данным прямым).

Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2, которые не параллельны:

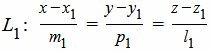. (1)
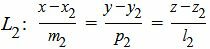. (2)

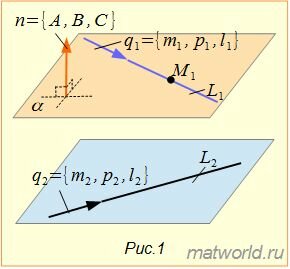
Задача заключается в построении уравнения плоскости α, проходящей через прямую L1 параллельно прямой L2(Рис.1).

Прамая L1 должна лежать на искомой плоскости α, следовательно точка M1 должна нежать на плоскости α.

Уравнение плоскости можно записать формулой

и поскольку M1(x1, y1, z1) принадлежит этой плоскости, то справедливо следующее равенство:

Для того, чтобы плоскость α проходила через прямую L1, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:

Для того, чтобы плоскость α была параллельна прямой L2, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q2 прямой L2, т.е. скалярное произведение этих векторов должен быть равным нулю:

Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:

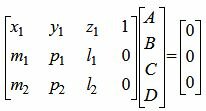
(7)

Решив однородную систему линейных уравнений (7) найдем частное решение. (как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L1 параллельно прямой L2.

Пример 1. Найти уравнение плоскости α, проходящей через прямую L1:

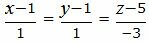(8)

паралленьно другой прямой L2 :

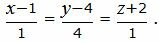(9)

Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(1, 1, 5) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= <1, 1, −3>прямой L1. Тогда уравнение плоскости должна удовлетворять условию:

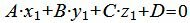(10)

а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:

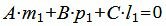(11)

Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:

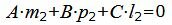(12)
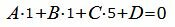(13)
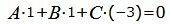(14)
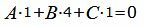(15)

Представим эти уравнения в матричном виде:

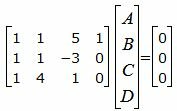(16)

Решим систему линейных уравнений (16) отностительно A, B, C, D:

(17)

Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= <−13/24,1/6,−1/8>то она может быть представлена формулой:

Подставляя значения A,B,C,D в (17), получим:

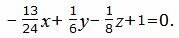(18)

Уравнение плоскости можно представить более упрощенном виде, умножив на число −24:

Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (19).

Пример 2. Найти уравнение плоскости α, проходящей через прямую L1:

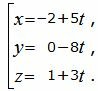(20)

Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(−2, 0, 1) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= <5, −8, 3>прямой L1. Тогда уравнение плоскости должна удовлетворять условию:

а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:

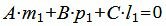(23)

Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:

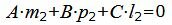(24)

Представим эти уравнения в матричном виде:

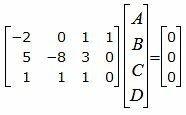(28)

Решим систему линейных уравнений (28) отностительно A, B, C, D:

(29)

Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= <11/35,2/35,−13/35>то она может быть представлена формулой:

Подставляя значения A,B,C,D в (30), получим:

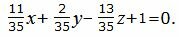(31)

Уравнение плоскости можно представить более упрощенном виде, умножив на число 35:

Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (32).

Математический портал

Nav view search

Navigation

Search

  • Вы здесь:
  • Home

Расстояние между двумя скрещивающимися прямыми.

Пусть $L_1: frac=frac=frac$ и $L_2: frac=frac=frac$ — две скрещивающиеся прямые. Расстояние $rho(L_1, L_2)$ между прямыми $L_1$ и $L_2$ можно найти по следующей схеме:

1) Находим уравнение плоскости $P,$ проходящей через прямую $L_1,$ параллельно прямой $L_2:$

Плоскость $P$ проходит через точку $M_1(x_1, y_1, z_1),$ перпендикулярно вектору $overline n=[overline s_1, overline s_2]=(n_x, n_y, n_z),$ где $overline s_1=(m_1, l_1, k_1)$ и $overline s_2=(m_2, l_2, k_2)$ — направляющие вектора прямых $L_1$ и $L_2.$ Следовательно, уравнение плоскости $P: n_x(x-x_1)+n_y(y-y_1)+n_z(z-z_1)=0.$

2) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_2$ до плоскости $P:$

Нахождение общего перпендикуляра скрещивающихся прямых.

Для нахождения общего перпендикуляра прямых $L_1$ и $L_2,$ необходимо найти уравнения
плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0;$

Тогда уравнение общего перпендикуляра имеет вид

Пример.

2.214.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Решение.

а) Если прямые $L_1$ и $L_2$ лежат в одной плоскости, то их направляющие вектора $overline(3, 4, -2),$ $overline(6, -4, -1),$ и вектор $overline l,$ соединяющий произвольную точку прямой $L_1$ и произвольную точку прямой $L_2$ компланарны. В качестве такого вектора $overline$ можно выбрать $overline(x_2-x_1, y_2-y_1, z_2-z_1).$ Проверим будут ли эти вектора компланарны.

Следовательно, вектора не компланарны и прямые не лежат в одной плоскости.

б) Запишем уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1.$ Эта плоскость проходит через точку $M_2(21, -5, 2)$ перпендикулярно вектору $overline n=[overline s_1, overline s_2].$

Таким образом, вектор $overline n$ имеет координаты $overline n(-12, -9, -36).$

Находим уравнение плоскости $$P:,, -12(x-21)-9(y+5)-36(z-2)=0Rightarrow$$ $$Rightarrow-12x-9y-36z+252-45+72=0Rightarrow -12x-9y-36z+279=0Rightarrow$$ $$Rightarrow 4x+3y+12z-93=0.$$

в) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_1$ до плоскости $P:$

Ответ: $frac<76><13>.$

г) Найдем уравнения плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Имеем, $M_1=(-7, -4, -3)in P_1,$

Таким образом, $$P_1: 54(x+7)-44(y+4)-7(z+3)=54x-44y-7z+378-176-21=$$ $$=54x-44y-7z+181=0.$$

Аналогично находим $P_2:$

Имеем, $M_2=(21, -5, 2)in P_2,$

Таким образом, $$P_1: -45(x-21)-76(y+5)+34(z-2)=-45x-76y+34z+945-380-68=$$ $$=-45x-76y+34z+497=0.$$

Ответ: $left<begin54x-44y-7z+181=0;\ -45x-76y+34z+497=0.endright. $

2.215.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Ответ: б) $4x+12y+12z+76=0;$

г) $left<begin53x-7y-44z-429=0;\ 105x-23y-48z+136=0.endright. $

источники:

http://matworld.ru/analytic-geometry/uravnenie-ploskosti5-online.php

http://mathportal.net/index.php/component/content/article/87-visshaya-matematika/analiticheskaya-geometriya/152-rasstoyanie-mezhdu-dvumya-skreshchivayushchimisya-pryamymi

Источник

Уравнение плоскости, проходящей через точку и параллельной двум прямым

Плоскость, проходящая через данную точку М0(х0;у0;z0) и параллельная данным прямым K1 и K2 (при этом прямые  K1 и K2 не параллельным между собой), выражается уравнением:

уравнения
где l1, m1, n1, l2, m2, n2 — направляющие коэффициенты данных прямых.
Запись в векторной форме:

 (r-r0)a1a2 = 0

  Примечание
Если данные прямые K1 и K2 параллельны между собой, то уравнение (1) имеет бесчисленное множество решений (получаем пучок плоскостей с осью, проходящей через точку М0 и параллельно данным прямым).

5115


Источник

Лучший ответ



0 Голосов

 Вячеслав Морг
Posted Январь 12, 2015 by Вячеслав Моргун

Решение: в условии задания даны уравнения двух прямых.
Рассмотрим уравнения
( frac{x}{1}=frac{y-1}{2}=frac{z-3}{8}) — каноническое уравнение прямой, где вектор ( vec{s_1} = (1;2;8)) — направляющий вектор (прямая параллельна этому вектору)
( frac{x+1}{4}=frac{y-1}{0}=frac{z+5}{2}) — каноническое уравнение прямой, где вектор (vec{s_2} = (4;0;2)) — направляющий вектор (прямая параллельна этому вектору) 
Получили два направляющих вектора, которые параллельны искомой плоскости.

Согласно условия задачи, плоскость проходит через заданную точку. Рассмотрим формулу уравнения плоскости, проходящую через заданную точку $$A(x-x_0)+B(y-y_0)+C(z-z_0) = 0 quad (1)$$ координаты ((x_0;y_0;z_0)) — известная точка,
координаты вектора (vec{N} = (A;B;C)) — вектор нормали к плоскости,
т.е. это уравнение плоскости , которая проходит через заданную точку, перпендикулярно данному вектору.

В условии задачи даны координаты точки, через которую проходит плоскость и есть два вектора, параллельные плоскости.

Воспользуемся свойством векторного произведения двух векторов 
Векторным произведением двух векторов: вектора (vec{a}) на вектор (vec{b}) называется вектор (vec{c}), который перпендикулярен векторам (vec{a}) и (vec{b}). 

Т.о. найдя векторное произведение ( vec{s_1}times vec{s_2} = vec{N}) мы найдем нужные координаты вектора нормали.
Найдем (vec{N}) 
$$vec{N} = vec{s_1}times vec{s_2} = left|begin{array}{c} i & j & k\ 1 &2 & 8 \ 4 & 0 & 2end{array}right| = i*2*2+j*8*4+k*1*0-k*2*4-i*8*0-j*1*2=4i+30j-8k$$ получили координаты (vec{N} = (4;30;-8))

Подставляем координаты точки и вектора в формулу (1)
$$4(x-2)+30(y+4)-8(z-3) = 0 => 2(x-2)+15(y+4)-4(z-3) = 0 =>$$$$2x-4+15y+60-4z+12 = 0 => 2x+15y-4z+68 = 0$$
Ответ: уравнение плоскости, проходящей через заданную точку, параллельно двум заданным прямым (2x+15y-4z+68 = 0)

Источник

Уравнение плоскости, проходящей через точку параллельно двум прямым

Материал из Циклопедии

Перейти к навигации
Перейти к поиску

Уравнение плоскости, параллельной двум неколлениарным направлениям // Виктор Глазнев [14:55]

Уравнение плоскости, проходящей через точку параллельно двум прямым, задаётся равенством нулю смешанного произведения вектора-разности радиусов-векторов точек и направляющих векторов прямых.

Обозначения[править]

Введём обозначения:

{displaystyle {bar {r}}=(x,y,z)} — радиус-вектор точки плоскости;

{displaystyle {bar {r}}_{0}=(x_{0},y_{0},z_{0})} — радиус-вектор точки;

{displaystyle {bar {s}}_{1}=(l_{1},m_{1},n_{1})} — направляющий вектор прямой;

{displaystyle {bar {s}}_{2}=(l_{2},m_{2},n_{2})} — направляющий вектор второй прямой.

Формулы:[править]

Векторная форма: {displaystyle left({bar {r}}-{bar {r}}_{0}right){bar {s}}_{1}{bar {s}}_{2}=0}.

Координатная форма:

{displaystyle {begin{vmatrix}x-x_{0}&y-y_{0}&z-z_{0}\l_{1}&m_{1}&n_{1}\l_{2}&m_{2}&n_{2}end{vmatrix}}=0Leftrightarrow }
{displaystyle Leftrightarrow {begin{vmatrix}m_{1}&n_{1}\m_{2}&n_{2}end{vmatrix}}(x-x_{0})-{begin{vmatrix}l_{1}&n_{1}\l_{2}&n_{2}end{vmatrix}}(y-y_{0})+{begin{vmatrix}l_{1}&m_{1}\l_{2}&m_{2}end{vmatrix}}(z-z_{0})=0}
  • Заметим, что формулы уравнения плоскости, проходящей через точку параллельно двум прямым, аналогичны формулам уравнения плоскости, проходящей через прямую параллельно прямой.

Уравнения плоскости:[править]

  • уравнение плоскости, проходящей через три точки;
  • уравнение плоскости, равноудалённой от двух точек;
  • уравнение плоскости, проходящей через две точки параллельно прямой;
  • уравнение плоскости, проходящей через две точки перпендикулярно плоскости;
  • уравнение плоскости, проходящей через точку и прямую;
  • уравнение плоскости, проходящей через точку перпендикулярно прямой;
  • уравнение плоскости, проходящей через точку параллельно плоскости;
  • уравнение плоскости, проходящей через точку параллельно двум прямым;
  • уравнение плоскости, проходящей через точку перпендикулярно двум плоскостям;
  • уравнение плоскости, проходящей через прямую параллельно прямой;
  • уравнение плоскости, проходящей через прямую перпендикулярно плоскости.

Литература[править]

  • Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.
  • Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.187.
Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти периметр квадрата внутри треугольника
  • Как найти ssh linux
  • Как найти инструкцию к алмазной мозаике
  • Vampire life как найти атаманшу
  • Как составить натюрморт с геометрическими фигурами

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии