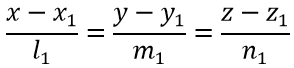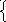Как составить уравнение плоскости проходящей через начало координат перпендикулярно прямой - AvtoShod.ru

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения

Задана точка M₀(x₀, y₀, z₀) и прямая L:

Построить уравнение плоскости α, проходящей через точку M₀ и перпендинулярной прямой L.

Решение. Уравнение плоскости, проходящей через точку M₀ и имеющий нормальный вектор n={A, B, C} имеет следующий вид:

Направляющий вектор прямой L имеет вид q={m, p, l}. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:

Упростим уравнение (3):

где D=−mx₀−px₀−lx₀.

Таким образом уравнение (4) определяет плоскость, проходящей через точку M₀(x₀, y₀, z₀) и перпендикулярной прямой (1).

Ответ. Уравнение плоскости прпоходящей через точку M₀(x₀, y₀, z₀) и перпендикулярной прямой (1) имеет вид (4).

Пример 1. Найти уравнение плоскости α, проходящую через точку M₀(3, −1, 2) и перпендикулярной прямой L:

Решение. Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n={A, B, C} представляется формулой (2).

Направляющий вектор прямой L имеет следующий вид: :

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:

Подставляя координаты точки M₀ и направляющего вектора q в (8), получим:

Упростим уравнение (9):

Ответ: Уравнение плоскости, проходящей через точку M₀(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).

Пример 2. Найти уравнение плоскости α, проходящую через точку M₀(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:

Решение. Приведем параметрическое уравнение (11) к каноническому виду:

Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n={A, B, C} представляется формулой:

Направляющий вектор прямой L имеет следующий вид:

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:

Подставляя координаты точки M₀ и направляющего вектора q в (13), получим:

Упростим уравнение (13):

Ответ. Уравнение плоскости, проходящей через точку M₀(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).

Источник

matematicus.ru

matematicus включает разделы – высшая математика, аналитическая геометрия в пространстве и на плоскости, теория вероятностей, Arduino, Android Studio, Excel, программирование, программы, Windows, ошибки, таблицы, формулы, примеры, физика, химия

Уравнение плоскости, проходящей через точку перпендикулярно к прямой

Плоскость, проходящая через данную точку М₀(х₀; у₀; z₀) и перпендикулярная к данной прямой:

имеет нормальный вектор N{ι₁, m₁, n₁} и представляется уравнением:

l₁(x-x₁) + m₁(y-y₁) + n₁(z-z₁)=0

или в векторной форме:

a₁(r−r₀)=0

Пример
Плоскость, проходящая через точку (9; -3; 7) и перпендикулярная к прямой:

$frac{x}{0} = frac{y}{4} = frac{{z — 3}}{4}$

, представляется уравнением:

4⋅(у+3)+4⋅(z-7)=0
4у+4z−16=0

4268

Источник

Уравнение плоскости, которая проходит через точку перпендикулярно прямой

1. Найти уравнение плоскости, которая проходит через точку , перпендикулярно прямой .

Решение.

Прямая имеет направляющий вектор . Плоскость, перпендикулярная прямой , также перпендикулярна ее направляющему вектору. То есть вектор является нормальным для искомой плоскости.

Уравнение плоскости, которая проходит через точку $(x_0, y_0, z_0)$ перпендикулярно вектору $(A, B, C)$ имеет вид

$A(x-x_0)+B(y-y_0)+C(z-z_0)=0.$

Уравнение плоскости, которая проходит через точку $(x_0, y_0, z_0)$ перпендикулярно вектору $(A, B, C)$ имеет вид

$A(x-x_0)+B(y-y_0)+C(z-z_0)=0.$

Запишем уравнение плоскости, проходящей через точку перпендикулярно вектору :

Ответ:

2. Напишите уравнение плоскости, проходящей через точку и параллельной плоскости :.

Решение.

Нормали параллельных плоскостей равны.

– уравнение плоскости, которая проходит через заданную точку перпендикулярно вектору .

Уравнение искомой плоскости:

Ответ: .

Источник

Задача 55893 Составить уравнение плоскости,…

Условие

Составить уравнение плоскости, проходящей через начало координат и перпендикулярной к прямой пересечения плоскости x-2y+4z-3=0 с плоскостью 0xz.

нет в списке ВУЗ
1391

Решение

★

Находим прямую пересечения плоскости x–2y+4z–3=0 с плоскостью 0xz.

Решаем систему:
[m]left{begin{matrix}
x-2y+4z-3=0\ y=0end{matrix}right.[/m]
⇒ получаем прямую, заданную как линия пересечения двух плоскостей.

Напишем ее каноническое уравнение .

Для этого подставим y=0 в первое уравнение

[m]left{begin{matrix}
x+4z-3=0\ y=0end{matrix}right.[/m]

и запишем первое уравнение как пропорцию

[m]left{begin{matrix}
x-3=-4z\ y=0end{matrix}right.[/m] ⇒ [m]left{begin{matrix}
frac{x-3}{4}=frac{z}{-1}\ y=0end{matrix}right.[/m] ⇒ [m]frac{x-3}{4}=frac{y}{0}=frac{z}{-1}[/m]

Получили каноническое уравнение прямой.

Направляющий вектор имеет координаты

(4;0;-1)

Этот направляющий вектор прямой становится нормальеым вектором плоскости, перпендикулярной прямой.

Значит надо написать уравнение плоскости, проходящей через точку (0;0;0)
с нормальным вектором (4:0;-1)

О т в е т. 4х-z=0

Написать комментарий

Источник

Основные виды
уравнений плоскости.

—общее
уравнение плоскости
;

2)
— уравнение плоскости, проходящей через
точкуМ₁(
x₁,
y₁,
z₁)
перпендикулярно нормальному вектору

;

—уравнение
плоскости в отрезках,
где а,
b,
с
— величины отрезков, отсекаемых
плоскостью на координатных осях Ох
,Оy,
Оz
соответственно ;

—уравнение
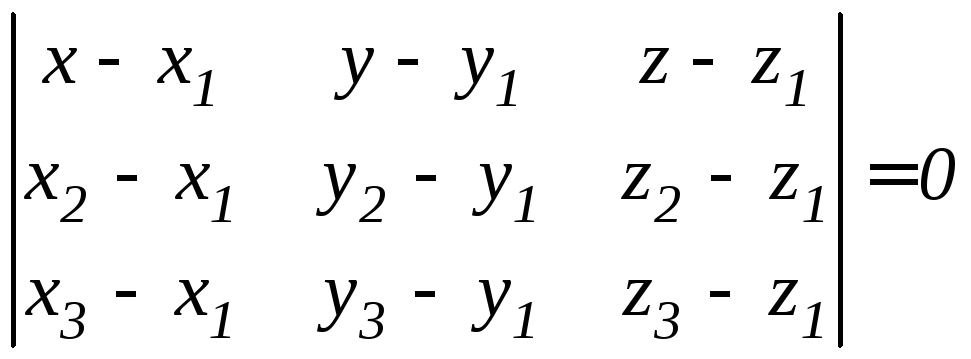
плоскости,
проходящей
через три точки
М₁(
x₁,
y₁,
z₁) , М₂(
x₂,
y₂,
z₂) , М₃(
x₃,
y₃,
z₃).

Основные виды
уравнений прямой.

—общее
уравнение прямой,
как пересечение двух плоскостей , где
направляющий вектор прямой находится
из векторного произведения нормальных
векторов плоскостей

;

—каноническое
уравнение прямой
или уравнение прямой , проходящей через
точку М₁(
x₁,
y₁,
z₁)
параллельно вектору ;.

— уравнение
прямой, проходящей через
две точки
М₁(
x₁,
y₁,
z₁) и
М₂(
x₂,
y₂,
z₂);

—векторное
уравнение прямой,
где
— радиус-вектор точки, лежащей на прямой,— направляющий вектор прямой, или в
параметрической форме.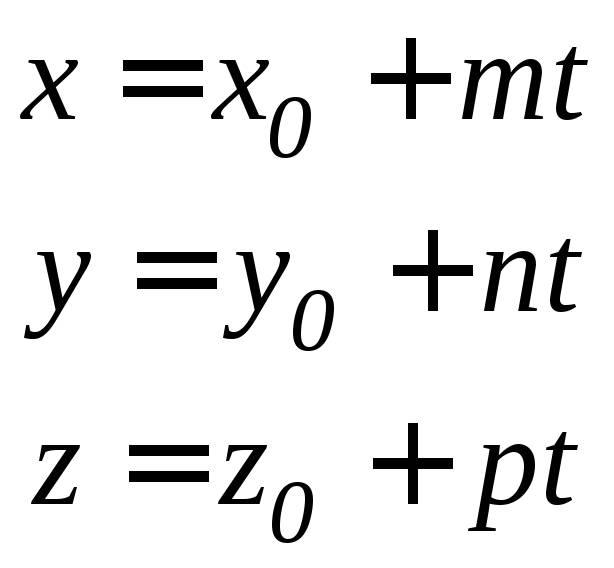

Расстояние
от точки
до плоскости

определяется по формуле.

Угол
между двумя прямыми,
заданными в канонической форме
, определяется
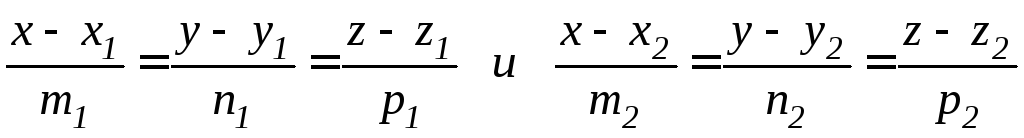
как угол между их направляющими векторами

Угол
между прямой

и
плоскостью
определяется так :

Задача.
Составить уравнение прямой, проходящей
через точку А(1,2,3)
параллельно прямой
.

Решение.
Так как прямые параллельны, значит
направляющий вектор для искомой прямой
будет таким же, как и для данной, т.е.
.
Поэтому применяем каноническое уравнение
прямой, проходящей через точкуА
(1,2,3)
параллельно вектору
, т.е..

Задача.
Составить уравнение прямой, проходящей
через точку А(2,-3,5)
параллельно прямой, заданной в виде
пересечения двух плоскостей:
.

Решение. Найдем направляющий вектор заданной прямой через векторное произведение нормальных векторов плоскостей

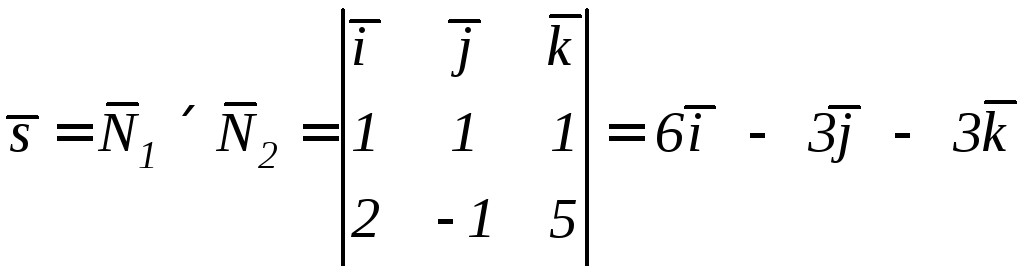
Тогда
каноническое уравнение прямой, проходящей
через точку А(2,-3,5)
параллельно вектору
будет.

Задача.
Дана пирамида АВСD
с вершинами
А(1,5,7),
В(-1,0,1), С
( 3,-2,4 ), D
( 0,1,-1 ). Найти
угол между ребром АD
и гранью
АВС .

Решение.
Найдем
уравнение грани АВС
, т.е.
уравнение плоскости, проходящей через
три точки А
,
В и С
.

Уравнение
ребра AD
— уравнение
прямой, проходящей через две точки А
и D
:

Тогда
угол между ребром и гранью будем находить
по формуле угла между прямой и плоскостью:

Задача.
Составить уравнение плоскости,
проходящей через точку А(1,2,3)
и через прямую, данную в виде пересечения
двух плоскостей

Решение.
Воспользуемся
уравнением пучка плоскостей, проходящих
через данную прямую
.
Так как плоскость должна проходить
через точкуА,
то, подставив ее координаты в уравнение
пучка, найдем λ
:

Теперь,
подставив λ
в уравнение
пучка, получим искомую плоскость:

Задача.
Найти точку
пересечения прямой
и плоскости
.

Решение.
Параметрически уравнения прямой
запишутся в виде
.
Далее, подставив в уравнение плоскости,
найдемt
:
.

По
данному t
найдем
координаты точки пересечения

Задание 4.1.

Даны
координаты вершин пирамиды АВСD.
Найти:

1)
Уравнение грани АВС;

2)
Уравнение высоты DM,
опущенной из точки D
на грань АВС;

3)
Длину высоты ДМ;

4)
Уравнение ребра DC;

5)
Угол наклона ребра DC
к плоскости АВС.

1.
А(-3;-2;-4), B(-4;2;-7),
C(5;0;3),
D(-1;3;0)

2.
A(2;-2;1), B(-3;0;-5), C(0;-2;-1), D(-3;4;2)

3.
A(5;4;1), B(-1;-2;-2), C(3;-2;2), D(-5;5;4)

4.
A(3;6;-2), B(0;2;-3), C(1;-2;0), D(-7;6;6)

5.
A(1;-4;1), B(4;4;0), C(-1;2;-4), D(-9;7;8)

6.
A(4;6;-1), B(7;2;4), C(-2;0;-4), D(3;1;-4)

7.
A(0;6;-5), B(8;2;5), C(2;6;-3), D(5;0;-6)

8.
A(-2;4;-6), B(0;-6;1), C(4;2;1), D(7;-1;-8)

9.
A(-4;-2;-5), B(1;8;-5), C(0;4;-4), D(9;-2;-10)

10.
A(3;4;-1), B(2;-4;2), C(5;6;0), D(11;-3;-12)

11.
A(2;1;3), B(3;-2;-4), C(-1;-3;-2), D(5;-3;4)

12.
A(4;1;1), B(-2;-1;3), C(1;-3;-4), D(6;-5;5)

13.
A(-3;-2;2), B(0;1;5), C(1;-2;-2), D(-1;9;-2)

14.
A(-1;0;4), B(2;2;5), C(3;2;4), D(2;3;1)

15.
A(-2;0;5), B(1;-4;-6), C(3;2;4), D(2;3;1)

16.
A(2;1;-1), B(0;3;-1), C(5;2;1), D(-2;-1;5)

17.
A(2;3;0), B(3;4;1), C(-2;5;-1), D(3;4;-5)

18.
A(-3;0;-4), B(2;7;2), C(4;-1;-1), D(-3;-2;7)

19.
A(1;-4;-4), B(-1;0;-3), C(2;5;1), D(5;6;-9)

20.
A(3;2;0), B(5;-2;-1), C(-4;3;-3), D(2;3;-3)

21.
A(1;1;1), B(6;3;2), C(0;7;1), D(2;3;4)

22.
A(1;0;-1), B(5;1;1), C(2;6;1), D(3;4;5)

23.
A(-1;2;0), B(8;1;1), C(2;7;-1), D(4;3;6)

24.
A(-1;-1;0), B(9;2;1), C(0;8;-1), D(4;4;7)

25.
A(0;1;0), B(8;2;1), C(1;7;2), D(3;5;1)

Задание 4.2.

Даны
координаты точек А,
В, С. Требуется:

1)
составить каноническое уравнение
прямой АВ;

2)
составить уравнение прямой, проходящей
через точку С
параллельно прямой АВ;

3)
составить уравнение плоскости, проходящей
через точку С
перпендикулярно
прямой АВ;

4)
найти следы этой плоскости на
координатных плоскостях.

1.
A(3;-1;5), B(7;1;1), C(4;-2;1). 2. A(-1;2;3), B(3;4;-1),
C(0;1;-1).

3.
A(2;-3;7), B(6;-1;3), C(3;-4;3). 4. A(0;-2;6), B(4;0;2),
C(1;-3;2).

5.
A(-3;1;2), B(1;3;-2), C(-2;0;-2). 6. A(-2;3;1), B(2;5;-3),
C(-1;2;-3).

7.
A(-4;0;8), B(0;2;4), C(-3;-1;4). 8. A(1;4;0), B(5;6;-4),
C(2;3;-4).

9.
A(4;-4;9), B(8;-2;5), C(5;-5;5). 10. A(5;5;4), B(9;7;0),
C(6;4;0).

11.
A(3;0;4), B(5;2;6), C(2;3;-3). 12. A(3;-2;2), B(-3;1;2),
C(-1;2;1).

13.
A(1;-1;1), B(-2;1;3), C(4;-5;-2). 14. A(3;-1;2), B(4;-1;-1),
C(2;0;2).

15.
A(-1;2;1), B(-3;1;2), C(3;-2;2). 16. A(9;-11;5), B(7;4;2),
C(-7;13;-3).

17.
A(2;4;-1), B(2;-4;2), C(3;6;0). 18. A(-4;-2;-5), B(1;8;-5),
C(0;4;-4).

19.
A(-2;4;-6), B(0;-6;1), C(4;2;1). 20. A(4;6;-1), B(7;2;4),
C(-2;0;-4).

21.
A(3;3;0), B(-1;2;-4), C(-9;7;8). 22. A(7;2;4), B(-2;0-4),
C(3;1;-4).

23.
A(8;2;5), B(2;6;-3), C(5;0;-6). 24. A(0;-6;1), B(4;2;1),
C(7;-1;-8).

25.
A(1;8;-5), B(0;4;-4), C(9;-2;-10).

Задание 4.3.

Даны
уравнение прямой в виде пересечения
двух плоскостей и координаты точки А.
Требуется:

1)
составить уравнение плоскости,
проходящей через данную прямую и точку
А;

2)
составить каноническое уравнение
прямой, проходящей через точку А
и параллельно оси ОX;

3)
найти угол между полученной прямой
и плоскостью;

4)
найти расстояние от начала координат
до плоскости.

1.
2x-y-3z=-1 A(3;0;2)

x+5y+z=0

2.
x+2y+3z=1 A(1;2;0)

2x-3y+2z=9

3.
x+y — z=1 A(-1;2;1)

8x+3y-6z=2

4.
x+y-z=-2 A(2;-3;0)

4x-3y+z=1

5.
2x+5y-3z=4 A(0;4;-2)

4x-3y+2z=9

6.
2x+7y-z=8 A(-3;0;5)

x+2y+z=4

7.
3x+4y+2z=8 A(1;3;0)

x+5y+z=0

8.
x-4y-2z=-3 A(5;1;-2)

3x+y+z=5

9.
x+y-z=1 A(-2;0;1)

x+2y+z=4

10.
3x+y+z=5 A(0;-5;2)

4x-3y+z=1

11.
x+4y-5z=-1 A(2;-1;2)

2x-y+3z=-2

12.
x+y-2z=-1 A(2;0;-1)

3x-y+z=2

13.
2x-y+z=3 A(1;1;-2)

2x+4y-z=4

14.
x+2y-3z=1 A(0;2;1)

2x-y+2z=-2

15.
3x-y+z=-2 A(1;-1;2)

x+2y-z=1

16.
2x-y+3z=6 A(1;2;4)

x+2y-z=-3

17.
3x+y+z=4 A(1;3;2)

x +3z=5

18.
3x+2y-5z=4 A(2;1;2)

x-2y+3z=4

19.
3x-5y+z=8 A(-1;2;3)

2x+y-z=-2

20.
2x-3y-3z=9 A(2;-5;3)

x-2y+z=-3

21.
x+y+z=3 A(1;1;7)

2x-3y+z=5

22.
x-y+2z=4 A(1;2;1)

2x+y+z=3

23.
x+y+2z=5 A(1;1;1)

3x+y+3z=-2

24.
x+2y-3z=3 A(1;2;0)

x+3y+z=2

25.
x+y+z=1 A(0;1;2)

x-3y+2z=10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения

Уравнение плоскости, которая проходит через точку перпендикулярно прямой

Задача 55893 Составить уравнение плоскости,…

Условие

Решение

Написать комментарий

Решение. Найдем направляющий вектор заданной прямой через векторное произведение нормальных векторов плоскостей

Не пропустите также: