Нахождение уравнения плоскости, проходящей через две параллельные прямые.
Прежде
чем получить уравнение
плоскости, проходящей через две заданные
параллельные прямые,
вспомним теорему: через две параллельные
прямые проходит единственная плоскость.
Эта теорема доказывается на основе
аксиомы о единственной плоскости,
проходящей через три заданные точки, с
использованием утверждения: если одна
из двух параллельных прямых пересекает
плоскость, то и другая прямая пересекает
эту плоскость.
Таким
образом, мы можем задать конкретную
плоскость в трехмерном пространстве,
указав две параллельные прямые, лежащие
в этой плоскости.
Очевидно,
что плоскость, проходящая через две
заданные параллельные прямые, совпадает
с плоскостью, проходящей через три
различные точки, две из которых лежат
на одной из заданных параллельных
прямых, а третья лежит на другой прямой.
Теперь
можно приступать к нахождению уравнения
плоскости, проходящей через две заданные
параллельные прямые.
Пусть
в трехмерном пространстве введена
прямоугольная система координат Oxyz,
заданы две параллельные прямые a и b и
требуется составить уравнение плоскости,
которая проходит через параллельные
прямые a и b.
Эта
задача, также как и задача о нахождении
уравнения плоскости, проходящей через
две заданные пересекающиеся прямые,
сводится к составлению уравнения
плоскости, проходящей через три точки.
Действительно, мы можем определить
координаты двух точек М1 и М2,
лежащих на одной из заданных параллельных
прямых, и координаты точки М3,
лежащей на другой прямой. После этого
нам лишь нужно написать уравнение
плоскости, проходящей через три
точки и
,
в виде 
Это уравнение является искомым уравнением
плоскости, проходящей через две заданные
параллельные прямые.
Нахождение
уравнения плоскости, проходящей через
заданную точку пространства параллельно
заданной плоскости.
Задача
нахождения уравнения плоскости,
проходящей через заданную точку
пространства параллельно заданной
плоскости, возникает из следующей
теоремы: через любую точку пространства,
не лежащую в данной плоскости, проходит
единственная плоскость, параллельная
данной. Доказательство этой теоремы
можно найти в учебнике геометрии
для 10—11
классов, указанном в конце статьи.
Пусть
в трехмерном пространстве
зафиксирована прямоугольная
система координат Oxyz,
в ней задана плоскость и
точка,
не лежащая в плоскости.
Поставим перед собой задачу: написать
уравнение плоскости,
проходящей через точкупараллельно
плоскости.
Решим
ее.
Нам
известно, что общее
уравнение плоскости,
проходящей через точку и
имеющей нормальный вектор плоскости,
имеет вид.
Таким образом, мы сможем записать
требуемое уравнение плоскости,
если определим координаты ее нормального
вектора.
При
изучении темы «нормальный
вектор плоскости»
мы отметили, что нормальный вектор одной
из двух параллельных плоскостей является
нормальным вектором второй плоскости.
Следовательно, в силу параллельности
плоскостей и
,
нормальным вектором плоскостиявляется
любой нормальный вектор заданной
плоскости.
Таким образом, задача составления
уравнения плоскости,
проходящей через заданную точкуМ1 параллельно
заданной плоскости,
сводится к определению координат
нормального вектора плоскости.
В свою очередь координаты нормального
вектора плоскостипроще
всего получить, если иметь перед глазами
общее уравнение плоскостивида
.
В этом случае коэффициентыA, B,C перед
переменными x, y, z являются
соответствующими координатами нормального
вектора плоскости .
Итак,
запишем алгоритм
нахождения уравнения плоскости ,
проходящей через заданную точкупараллельно
заданной плоскости:
Следует
заметить, что если точка М1 лежит
в плоскости ,
то, действуя по записанному алгоритму,
мы получим уравнение плоскости,
которая совпадает с плоскостью.
Нахождение
уравнения плоскости, проходящей через
заданную точку пространства перпендикулярно
к заданной прямой.
Поставим
перед собой следующую задачу.
Пусть
в трехмерном пространстве
зафиксирована прямоугольная
система координат Oxyz,
задана точка ,
прямаяa и
требуется написать уравнение плоскости ,
проходящей через точкуМ1 перпендикулярно
к прямой a.
Сначала
вспомним один важный факт.
На
уроках геометрии в средней школе
доказывается теорема: через заданную
точку трехмерного пространства проходит
единственная плоскость, перпендикулярная
к данной прямой (доказательство этой
теоремы Вы можете найти в учебнике
геометрии за 10—11 классы,
указанном в списке литературы в конце
статьи).
Теперь
покажем, как находится уравнение этой
единственной плоскости, проходящей
через заданную точку перпендикулярно
к заданной прямой.
Мы
можем написать общее
уравнение плоскости,
если нам известны координаты точки,
лежащей в этой плоскости, и координаты
нормального вектора плоскости.
В
условии задачи нам даны
координаты x1, y1, z1 точки М1,
через которую проходит плоскость .
Тогда, если мы найдем координаты
нормального вектора плоскости,
то мы сможем составить требуемое
уравнение плоскости, проходящей через
заданную точку перпендикулярно к
заданной прямой.
Любой направляющий
вектор прямой a представляет
собой нормальный вектор плоскости ,
так как он ненулевой и лежит на прямойa,
перпендикулярной к плоскости .
Таким образом, нахождение координат
нормального вектора плоскостисводится
к нахождению координат направляющего
вектора прямойa.
В
свою очередь, координаты направляющего
вектора прямой a могут
определяться различными способами,
зависящими от способа задания прямой a в
условии задачи. Например, если прямуюa в
прямоугольной системе координат
задают канонические
уравнения прямой в пространстве
вида 
уравнения прямой в пространстве вида 
то направляющий вектор этой прямой
имеет координатыax, ay и az;
если же прямая a проходит
через две точки и
,
то координаты ее направляющего вектора
определяются как.
Итак,
получаем алгоритм
для нахождения уравнения плоскости ,
проходящей через заданную
точкуперпендикулярно
к заданной прямойa:
Из
найденного общего уравнения плоскости
вида можно,
при необходимости, получитьуравнение
плоскости в отрезках и нормальное
уравнение плоскости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Все ответы
|
|
 |
|
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 37049 Составить уравнение плоскости,…
Условие
yelymcheav
2019-05-14 15:35:56
Составить уравнение плоскости, проходящей через две параллельные прямые x-2/3=y+1/2=z-3/-2
x-1/3=y-2/2=z+3/-2
предмет не задан
27139
Все решения
u821511235
2019-05-14 17:00:51

Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
В разделе 1 было получено уравнение плоскости проходящей через точку М0(x0,y0,z0) и с вектором нормали , где A2+B2+C2>0:
A(x – x0) + B(y – y0) + C(z – z0)=0. (*)
Рассмотрим теперь другие способы задания плоскости в пространстве.
Задача 1. Написать уравнение плоскости π, проходящей через три заданные точки М1(x1,y1,z1), М2(x2,y2,z2) и М3(x3,y3,z3) (рис. 5).
Рис. 5
Решение: Чтобы написать уравнение искомой плоскости, достаточно знать координаты какой-либо точки на плоскости и координаты вектора нормали (уравнение (*). Точкой на плоскости может быть любая из заданных точек М1, М2 или М3, а вектором нормали
может быть векторное произведение векторов [
].
Поставленную задачу можно решить другим способом. Пусть М(x, y,z) — текущая точка на плоскости π. Тогда векторы =(x-x1,y-y1,z-z1),
=(x2-x1,y2-y1,z2-z1) и
=(x3-x1,y3-y1,z3-z1) лежат на плоскости π (компланарны). Условие компланарности этих векторов (равенство нулю их смешанного произведения) задает уравнение искомой плоскости π:

Пример. Написать уравнение плоскости, проходящей через точки М1(1,1,1), М2(3,2,-1) и М3(4,1,0).
Для решения задачи воспользуемся вторым способом. Уравнение плоскости запишем в виде (21)

Разложив определитель по первой строке, получим

– уравнение искомой плоскости с
.
Заметим, что векторное произведение векторов =(2,1,–2) и
=(3,0,–1) коллинеарно вектору нормали
.
Действительно,

Задача 2. Написать уравнение плоскости π, проходящей через точку М0(x0,y0,z0) и прямую L (рис. 6): , если точка M0 не лежит на прямой L (иначе плоскость однозначно не определена). Точка М1(x1,y1,z1) принадлежит L, вектор
– направляющий вектор.
Рис. 6
Решение: Заданной точкой в уравнении (*) может быть любая из точек М1 или М0. Вектором нормали может служить векторное произведение векторов
и
:

Задача 3. Написать уравнение плоскости, проходящей через две параллельные прямые.
и
Т. M1 (x1,y1,z1),
Т. M2 (x2,y2,z2) ,
Вектор – направляющий вектор прямых L1,L2 (рис. 7).
Рис. 7
Вновь используем уравнение (*).
Точка на плоскости – любая из точек М1 или М2; вектором нормали =(A, B,C) может быть векторное произведение [
,
].
Задача 4. Доказать, что две прямые L1, L2 лежат в одной плоскости (пересекаются) и составить уравнение этой плоскости.
Решение задачи рассмотрим на примере.
Пусть и
.
1. Проверим, лежат ли прямые L1 и L2 в одной плоскости. Для этого убедимся, что векторы ,
и
компланарны.
Запишем параметрически заданную прямую L2 в каноническом виде
,
здесь М2(7,2,1) – точка на прямой L2, – ее направляющий вектор.
На прямой L1: М1(1,-2,5); . Вектор
=(6,4,–4) (рис. 8).
Рис. 8
Условием компланарности является равенство нулю смешанного произведения

Т. к. в полученном определителе две строки совпадают (при вычислении определителя общие множители первой строки и последнего столбца вынесены за знак определителя).
Итак, мы убедились, что прямые L1 и L2 пересекаются.
Точка плоскости π – любая из точек М1, М2 (возьмем, например, точку М1(1,–2,5)).
Вектор нормали =(А, B,C)= [
]=

+16
+13
.
Уравнение искомой плоскости π:
– 2(x – 1) + 16(y + 2) + 13(z – 5) = 0, или
2x – 16y – 13z + 31 = 0.
Задача 5. Определить взаимное расположение прямой L, заданной как пересечение двух непараллельных плоскостей:
L:
И плоскости π: A3x+B3y+C3z+D3=0.
Решение: Возможны следующие случаи:
А) прямая L и плоскость π не пересекаются (прямая параллельна плоскости и не имеет общих точек с плоскостью);
Б) прямая L пересекается с плоскостью в единственной точке;
В) прямая L лежит в плоскости – бесчисленное множество общих точек.
Эти задачи фактически были рассмотрены в разделе 2, когда прямая задавалась параметрическими или каноническими уравнениями.
Вообще говоря, нет надобности переходить от общего уравнения прямой к каноническому. Алгебраически задача сводится к исследованию и решению (если это возможно) системы уравнений

Решение этой системы определяет координаты общих точек прямой и плоскости.
Воспользуемся методом Крамера. Обозначим определитель системы (22)
А определитель Δ1, Δ2, Δ3, полученные из Δ с помощью столбца свободных членов, соответственно:

Если определитель , то система (22) имеет единственное решение, и оно определяется по формулам Крамера:
,
Имеет место случай (б).
Если определитель , а хотя бы один из определителей Δ1, Δ2 или Δ3 отличен от нуля, система (22) не имеет решения (не совместна). Геометрически это означает, что прямая и плоскость не имеют общих точек (параллельны) – случай (а).
Если же все определители Δ =Δ1=Δ2=Δ3=0, то система (22) имеет бесчисленное множество решений. Прямая L целиком лежит на плоскости π (случай в)).
Задача 6. Определить точку Q, симметричную точке M0(x0,y0,z0), относительно плоскости
π: Ax+By+Cz+D=0
Решение. Запишем алгоритм решения задачи.
1. Составим уравнение прямой L, проходящей через точку M0(x0,y0,z0) и перпендикулярной плоскости π. Направляющим вектором этой прямой послужит вектор нормали
.
2. Найдём точку пересечения M1(x1,y1,z1) прямой L и плоскости π (см. раздел 2).
3. Точка M1 является серединой отрезка M0Q, и координаты точек M0, M1 и Q связаны формулами: x1=,y1=
,z1=
, откуда найдем координаты точки Q(x0,y0,z0)
(рис. 9):
XQ=2×1 – x0, yQ=2y1 – y0, zQ=2z1 – z0.
Рис. 9
Аналогично решается и следующая задача.
Задача 7. Найти точку Q, симметричную точке M0(x0,y0,z0) относительно прямой
.
Решение.
1. Составим уравнение плоскости, проходящей через точку M0(x0,y0,z0) перпендикулярно прямой L. Вектором нормали к этой плоскости (A, B,C) возьмем направляющий вектор
=(l, m,n) прямой L.
π: l(x – x0) + m(y – y0) + n(z – z0)=0.
2. Найдем точку пересечения M1(x1,y1,z1) прямой L и плоскости π (см. раздел 2).
3. Точка M1 – середина отрезка M0Q, координаты точки Q определяются так же, как и в задаче 6.
| < Предыдущая | Следующая > |
|---|
плоскости
прямая
пересечения прямой и плоскости:
канонические уравнения прямой, проходящей через
точку М0(2; -4; -1) и
середину отрезка прямой
уравнение прямой, проходящей через точку М0(2; -3; -5) перпендикулярно
к плоскости
уравнение плоскости, проходящей через точку М0(1; -1; -1) перпендикулярно
к прямой
уравнение плоскости, проходящей через точку М0(1; -2; 1) перпендикулярно
к прямой
прямая
С прямая
A и D прямая
в плоскости
А и В плоскость
прямой
l и C прямая
плоскости
точки Р(2; -1; 3) на прямую
симметричную точке Р(4; 1; 6) относительно прямой
симметричную точке Р(2; -5; 7) относительно прямой,
проходящей через точки М1(5; 4; 6) и М2(-2; -17; -8).
точки Р(5; 2; -1) на плоскость
симметричную точке Р(1; 3; -4) относительно
плоскости
найти такую точку Р, сумма расстояний которой до
точек А(-1; 2; 5) и В(11; -16; 10) была бы наименьшей.
найти такую точку Р, разность расстояний которой
до точек M1(3; 2; -5), М2(8; -4; -13) была
бы наибольшей.
расстояний которой до точек А(3; -4; 7) и В(-5; -14; 17)
была бы наименьшей.
расстояний которой до точек М1(5; 2; -7) и М2(7; -25; 10) была
бы наибольшей.
движется прямолинейно и равномерно из
начального положения М0(15; -24; -16)
со скоростью v=12 в направлении
вектора s={-2; 2; 1}. Убедившись, что траектория точки
М пересекает плоскость
пересечения;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(28; -30; -27)
со скоростью v=12,5 по
перпендикуляру, опущенного из точки М0 на плоскость
уравнения движения точки М и определить:
ее траектории с этой плоскостью;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(11; -21; 20) в направлении вектора s={-1; 2; -2} со
скоростью v=12. Определить, за какое время она
пройдет отрезок своей траектории, заключенный
между параллельными плоскостями
расстояние d точки Р(1; -1; -2) от прямой
расстояние d от точки Р(2; 3; -1) до следующих прямых:
прямые
вычислить расстояние d между ними.
уравнение плоскости, проходящей через точку М1(1; 2; -3) параллельно
прямым
Доказать,
что уравнение плоскости, проходящей через точку
М0(x0; y0; z0) параллельно прямым ,
, может быть
представлено в следующем виде:
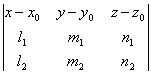
Доказать,
чо уравнение плоскости, проходящей через точки М1(x1; y1; z1) и М2(x2; y2; z2)
паралелльно прямой , может
быть представлено в следующем виде:
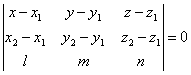
уравнение плоскости, проходящей через прямую
-2; 1).
Доказать,
что уравнение плоскости, проходящей через прямую
,
,
и точку М1(x1;
y1; z1), может быть
представлено в следующем виде:
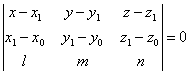
прямые
плоскости, и составить уравнение этой плоскости.
Доказать,
что если две прямые ,
пересекаются, то уравнение
плоскости, в которой они лежат, может быть
представлено в следующем виде:
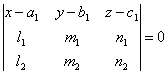
уравнение плоскости, проходящей через две
параллельные прямые
Доказать,
что уравнение плоскости, проходящей через две
параллельные прямые ,
,
и
,
,
, может быть
представлено в следующем виде:
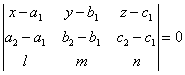
точки С(3; -4; -2) на плоскость, проходящую через
параллельные прямые
симметричную точке Р(3; -4; -6) относительно
плоскости, проходящей через М1(-6;
1; -5), М2(7; -2; -1) и М3(10; -7; 1).
симметричную точке Р(-3; 2; 5) относительно
плоскости, проходящей через прямые
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
параллельно прямой
,
,
, может быть представлено в следующем
виде:
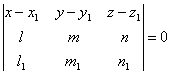
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
,
,
перпендикулярно к
плоскости , может быть представлено в следующем
виде:
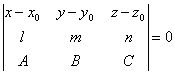
канонические уравнения прямой, которая проходит
через точку М0(3; -2; -4) параллельно плоскости
пересекает прямую
1082
проходит параллельно плоскостям
пересекает прямые
кратчайшее расстояние между двумя прямыми в
каждом из следующих случаев:









