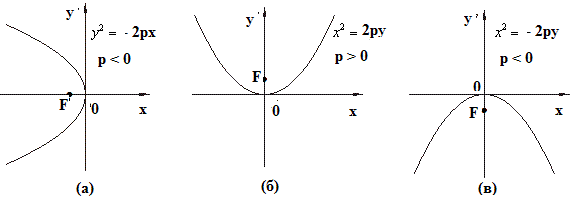Как составить уравнение параболы с 2 точками - AvtoShod.ru

Как легко составить уравнение параболы по графику

В данной статье репетитор по математике рассказывает о простом и эффективном способе составления уравнения параболы по её графику, которому вас не научат в школе. Дочитайте эту статью до конца или посмотрите видео с подробным объяснением, потому что эта информация может вам пригодиться на экзамене.

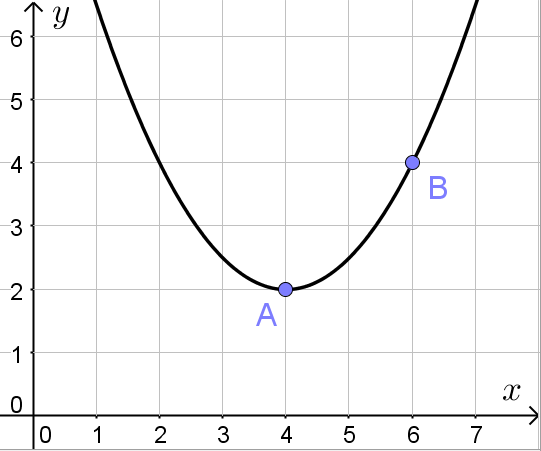
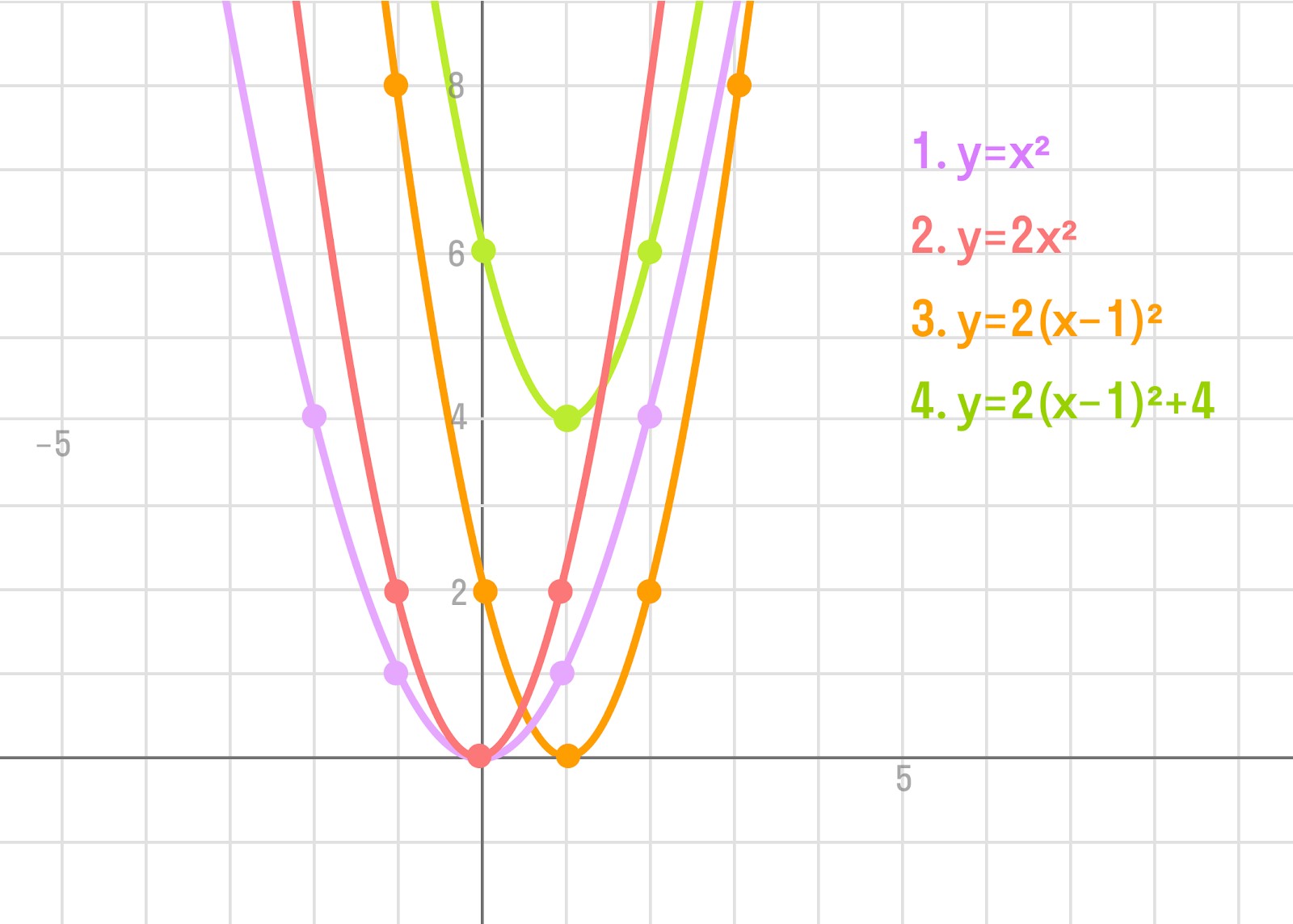
Задача состоит в том, чтобы по графику параболы (см. рисунок) определить коэффициенты a, b и c соответствующей квадратичной функции :

Существует стандартный и крайне неэффективный способ решения этой задачи. Он заключается в том, чтобы через координату вершины параболы связать коэффициенты a и b, используя формулу $x_B = -frac{b}{2a}$ . Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.

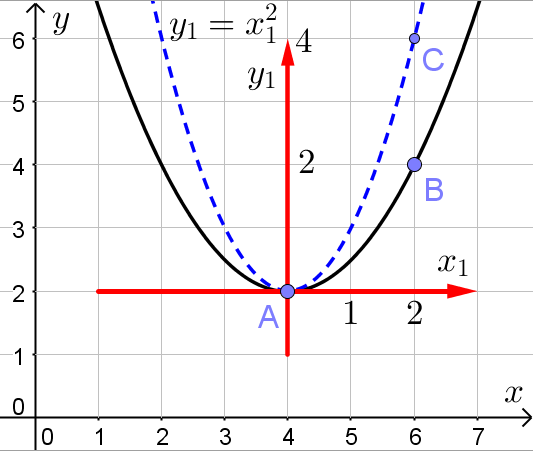
Мы не пойдём этим путём. Предлагаемый в данной статье способ намного более прост и изящен. Введём новую систему координат с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид: , где . Изобразим в новой системе координат график квадратичной функции (синяя пунктирная линия на рисунке):

Абсциссы точек C и B в новой системе координат равны. Ордината точки C в 2 раза больше ординаты точки B. Значит график исходной параболы в новой системе координат получен умножением на $frac{1}{2}$ всех ординат точек графика функции . Откуда получаем, что $a=frac{1}{2}$ . Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат: $y_1 = frac{1}{2}x_1^2$ .

Осталось перейти в исходную систему координат. Поскольку новая система координат получена путём параллельного переноса исходной системы координат на 4 единичных отрезка вправо и 2 единичных отрезка вверх, то в исходной системе координат наша парабола может быть представлена в виде следующего выражения:

$[ y = frac{1}{2}(x-4)^2+2 = frac{1}{2}x^2-4x+10. ]$

Как видите, данный способ требует минимум вычислений и фактически является полуустным. Запомните этот способ, он может пригодиться вам при решений задач из ЕГЭ, ОГЭ или вступительных экзаменов в вузы и школы с углубленным изучением математики.

Квадратичная функция. Построение параболы

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:

Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ: наглядно.

Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 в частном случае при b = 0, c = 0:

Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
Если старший коэффициент меньше нуля (a < 0), то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax 2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:

Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.

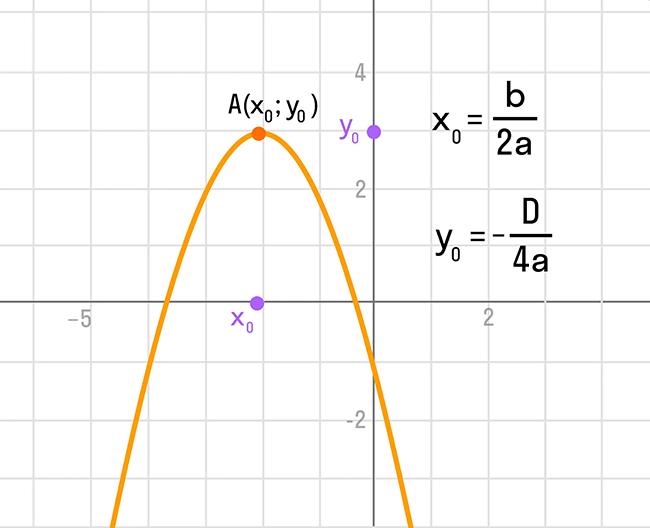
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Координаты вершины параболы:

Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.

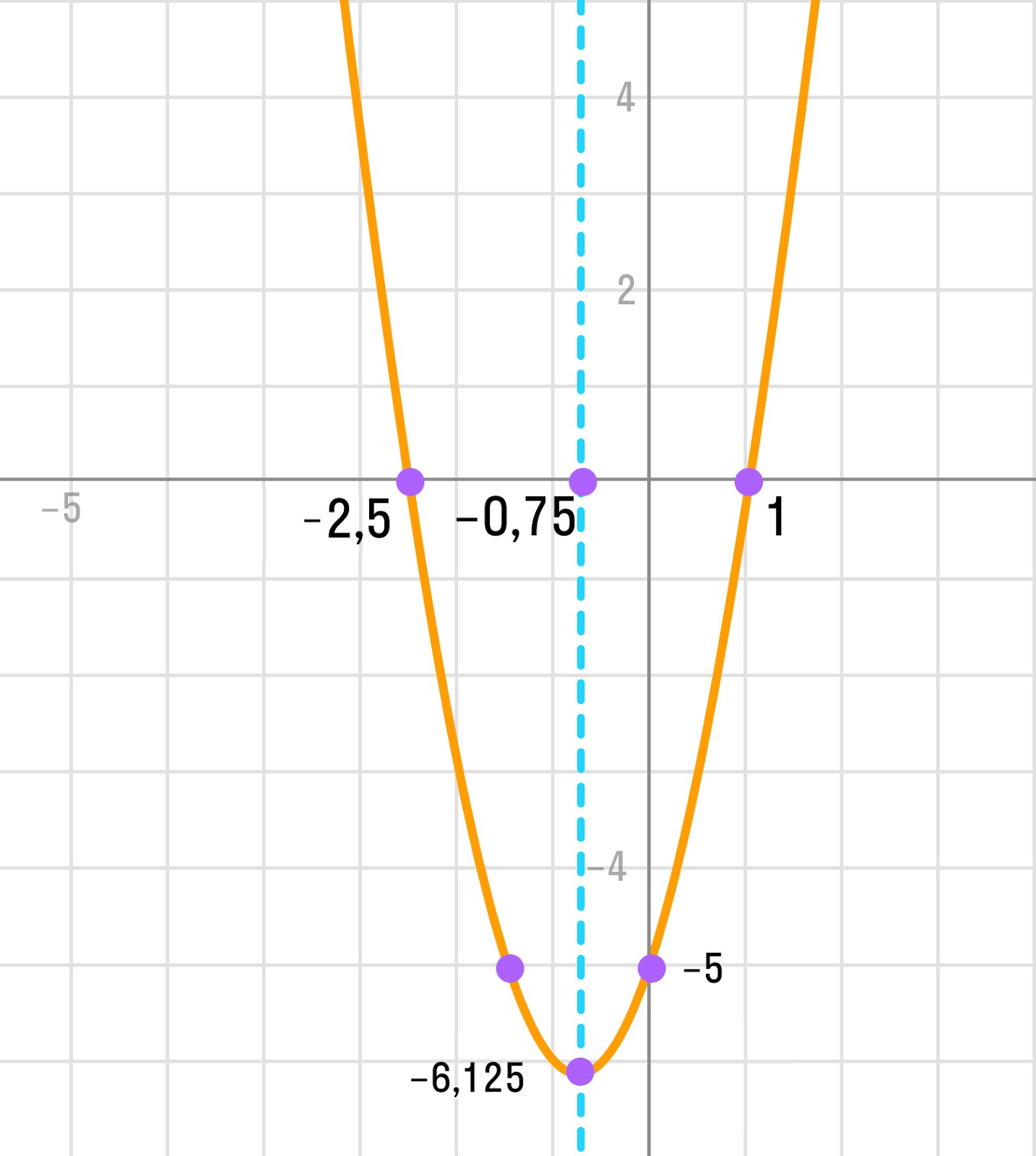
Нанесем эти точки на координатную плоскость и построим график параболы:

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x₀) + y₀, где x₀, y₀ — координаты вершины параболы.

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

построить график функции y = x 2 ,
умножить ординаты всех точек графика на 2,
сдвинуть его вдоль оси ОХ на 1 единицу вправо,
сдвинуть его вдоль оси OY на 4 единицы вверх.

Построить график параболы для каждого случая.

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид функции позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.

Отметим эти точки на координатной плоскости и соединим плавной прямой линией.

Как построить параболу

Соавтор(ы): Jake Adams. Джейк Адамс — репетитор и владелец онлайн-сервиса Simplifi EDU с офисом в Санта-Монике, Калифорния, который предлагает образовательные ресурсы и услуги репетиторов по предметам от уровня детского сада до колледжа, помощь в подготовке к тестам SAT и ACT и консультирование по вопросам поступления в колледж. Имеет более 14 лет опыта в качестве профессионального репетитора, нацелен на предоставление клиентам репетиторских услуг высочайшего качества и доступа к сети, объединяющей выскоквалифицированных репетиторов с высшим образованием из лучших колледжей страны. Получил диплом бакалавра по международному бизнесу и маркетингу в Университете Пеппердайна.

Количество источников, использованных в этой статье: 7. Вы найдете их список внизу страницы.

Источник

Как легко составить уравнение параболы по графику

Среда, 3 августа, 2016

$[ y = frac{1}{2}(x-4)^2+2 = frac{1}{2}x^2-4x+10. ]$

Статья написана репетитором по математике в Москве, Сергеем Валерьевичем

Источник

Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax²+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax²+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;

2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;

3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax²+bx+c=0;

Виды уравнений:

a) Полное квадратное уравнение имеет вид ax²+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax²+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax²+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

Как решать квадратные уравнения посмотреть тут.

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x²+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)²+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x²+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b²-4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x²+4x+3 значения
y=(-4)²+4*(-4)+3=16-16+3=3
y=(-3)²+4*(-3)+3=9-12+3=0
y=(-1)²+4*(-1)+3=1-4+3=0
y=(0)²+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x²+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)²+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x²+4x=0
Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x²+4x значения
y=0²+4*0=0
y=-(1)²+4*1=-1+4=3
y=-(3)²+4*3=-9+13=3
y=-(4)²+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x²-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)²-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x²-4=0
Неполное квадратное уравнение вида ax² +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x²=4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x²-4 значения
y=(-2)²-4=4-4=0
y=(-1)²-4=1-4=-3
y=1²-4=1-4=-3
y=2²-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

Источник

Парабола — это график функции описанный определённой формулой. Чтобы построить параболу нужно следовать формуле, определениям и уравнениям.

Парабола

Парабола – это множество точек плоскости, которые равноотделённые от заданной точки, что называется фокусом и заданной прямой под названием директриса.

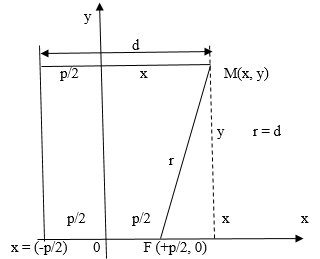
Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус на оси так, чтобы начало координат помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через расстояние от фокуса к директрисе, тогда у фокуса будут координаты , .

Для произвольной точки параболы расстояний , а расстояние к директрисе . По определению из рис. 1 видим, что , а ${r} = sqrt{x - {pover{2}}^2} + y^2$ и поэтому:

Рис. 1

$sqrt{(x - {pover{2}})^2 + y^2} = x + {pover{2}}to{x}^2 - 2 * {pover2}}x + {p^2over{4}} + y^2 = x^2 + 2 * {pover{2}}x + {p^2over{4}}$

(1)

– каноническое уравнение параболы.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Что такое вершина параболы

Вершина параболы – это парабола, которая проходит через точки . Если точка $M_{1}(x , y)$ принадлежит параболе, то и $M_{2}(x , -y)$ тоже принадлежит параболе, так как из:

$y^2 = 2pxto{(-y)^2 = 2px}$ .

Значит, парабола симметрична относительно оси , её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:

Чтобы найти вершину параболы, необходимо знать формулу: .

Давайте посмотрим, как данная формула действует, допустим дано уравнение:

Тогда:

, , . Чтобы найти величины , и , в квадратном уравнении коэффициент при , при , постоянная (коэффициент без переменной) = . Если взять тот же пример, , получается, что:

, , .

Форма и характеристики параболы

Исследуем за каноническим уравнением форму и расположение параболы:

1. В уравнении переменная входит в парной степени откуда получается, что парабола симметрична относительно оси . Ось – это ось, которая симметрична параболе.

2. Так как , тогда , откуда получается, что парабола расположена справа от оси .

3. При мы имеем , то есть парабола проходит через начало координат. Точка – это вершина параболы.

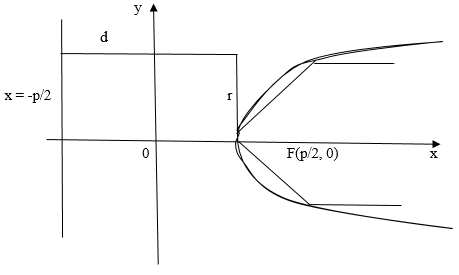
4. При увеличении значений переменной модуль тоже возрастает. Изобразим параболу на рисунке:

Рис. 2

5. В полярной системе координат, у канонического уравнения параболы такой вид:

6. Уравнение , , , тоже описывают параболы:

Рис. 3

Оптическое свойство параболы

У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси . Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.

При положительном уравнении:

описывают параболу симметричную относительно с вершиной в точке , ветви которой направлены влево (рис. 3 (а)).

Аналогично изложенному, уравнение и описывают параболы с вершиной в точке симметрично относительно , ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение решить относительно

$y = {1over{2p}}x^2$ и обозначить , тогда получим известное со школьного курса уравнение параболы . Теперь её фокусное расстояние .

Примеры решения

Задача

Найти координаты фокуса и составить уравнение директрисы параболы .

Решение

Сравнивая каноническое уравнение и данное , получим , , тогда. Так как уравнение директрисы , тогда в данном случае .

Ответ

координаты фокуса: , а уравнение директрисы параболы: .

Задача

Составить каноническое уравнение параболы:

а) с фокусом в точке ;

б) с фокусом в точке .

Решение

а). Так как фокус на положительной полуоси , тогда парабола симметрична относительно с вершиной в точке и , поэтому и согласно формуле (1) .

б). Фокус лежит на отрицательной полуоси с вершиной в точке , ветви направлены вниз, каноническое уравнение следует искать в виде . Фокусное расстояние параболы и уравнение запишется .

Ответ

а) каноническое уравнение параболы с фокусом в точке : ;

б) каноническое уравнение с фокусом в точке : .

Задача

Показать путём выделения полного квадрата, что уравнение – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.

Решение

Выделим относительно переменной полный квадрат

= $0to{4(x^2 - 3x)} + y + 6$ = $0to{4((x^2 - 2 * {3over{2}}x + {9over{4}}) - {9over{4}}) + y + 6$ = $0}to{4((x - {3over{2}}})^2 - 9 + y + 6$ = = $-4(x - {3over{2}})^2}to{(x - {3over{2}})^2}$ = .

Обозначим $y_{1} = y - 3$ , $x_{1} = x - {3over{2}}$ . Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку $O_{1}({3over{2}}, 3)$ , получим каноническое уравнение параболы ${x_{1}^2} = -{1over{4}}y_{1}$ .

Ветви этой параболы направлены вниз симметрично относительно оси $O_{1}Y_{1}$ , , – фокусное расстояние. В новой системе координат фокус находится в точке , уравнение директрисы в новой системе $y_{1} = {1over{16}}$ .

Повернёмся к старым координатам при помощи замены $y_{1} = y - 3$ , $x_{1} = x - {3over{2}}$ . Уравнение оси в новой системе $x_{1} = 0$ , а в старой – уравнение оси параболы.

Уравнение директрисы в новой системе координат $y_{1} = {1over{16}}$ , а в старой .

В новой системе $X_{1}O_{1}Y_{1}$ для фокуса $F(0, -{1over{16}}) x_{1} = 0$ , $y_{1} = -{1over{16}}$ , а в старой системе $x_{F} - {3over{2}} = 0to{x_{F}} = {3over{2}}$ , $y_{F} - 3 = -{1over{16}}to{y_{F} = -{1over{16}} + 3to{y_{F}} = {47over{16}}$ , то есть .

Ответ

Каноническое уравнение параболы – ${x_{1}^2} = -{1over{4}}y_{1}$ ;

вершина – ветви параболы направлены вниз;

$O_{1}Y_{1}$ , , $p_{2} = -{1over{16}}$ – фокусное расстояние, а фокус находится в точке ;

уравнение оси $x_{1} = 0$ ;

уравнение директрисы $y_{1} = {1over{16}}$ .

Источник

С квадратными уравнениями мы уже встречались в курсе алгебры (7)-го класса.

Квадратное уравнение — это уравнение второй степени. Общий вид квадратного уравнения

ax2+bx+c=0

, где (а, b, с) могут быть любыми числами и

a≠0

Применяя знания о функциях и их графиках, которые нам известны, мы можем решать некоторые квадратные уравнения. Рассмотрим (5) графических способов решения квадратного уравнения

x2−2x−8=0

Первый способ

Построим график функции

x2−2x−8=0

1. Имеем: (a = 1), (b = -2),

x0=−b2a=1,y0=f(1)=12−2−8=−9

. Значит, вершиной параболы служит точка ((1; -9)), а осью параболы является прямая (x = 1).

2. Возьмём на оси (x) две точки, симметричные относительно оси параболы, например, точки (x = -2) и (x = 4). Имеем (f(-2) = f(4) = 0). Построим на координатной плоскости точки ((-2; 0)) и ((4; 0)).

3. Построим параболу по точкам ((-2; 0)), ((1; -9)), ((4; 0)).

Корни уравнения

x2−2x−8=0

— это первые координаты точек, в которых функция равна нулю (то есть в которых график пересекает ось (х)); поэтому имеем решение:

x1=−2;x2=4

Второй способ

Запишем уравнение в другом виде

x2=2x+8

. Рассмотрим функции в левой и правой частях уравнения

y=x2;y=2x+8

. В одной системе координат построим их графики и найдём точки пересечения графиков:

Получили две точки:: (C(- 2; 4)) и (D(4; 16)). Решением уравнения будут первые координаты точек (C) и (D), имеем:

x1=−2;x2=4

Преобразуем уравнение к виду

x2−8=2x

. Построим в одной системе координат графики функций:

y=x2−8;y=2x

и определим точки их пересечения:

Получили две точки: (C(-2; — 4)) и (D(4; 8)). Решением уравнения будут первые координаты точек (C) и (D), то есть

x1=−2;x2=4

Четвёртый способ

Преобразуем уравнение к виду

x2−2x+1−9=0

и далее

x2−2x+1=9→x−12=9

.
Построим в одной системе координат параболу

y=x−12

, прямую (y = 9) и определим точки их пересечения:

Получили две точки: (C(-2; 9)) и (D(4; 9)). Решением уравнения будут первые координаты точек (C) и (D), поэтому

x1=−2;x2=4

Пятый способ

Так как (x=0) не является корнем уравнения, то разделим левую и правую части на (x):

x−2−8x=0;x−2=8x.

Рассмотрим функции в левой и правой частях уравнения

y=8x

, (y = x — 2) и определим точки их пересечения:

Получили две точки: (A (-2; -4)) и (B(4; 2)). Решением уравнения будут первые координаты точек (A) и (B), следовательно,

x1=−2;x2=4

Источник

Как легко составить уравнение параболы по графику

Квадратичная функция. Построение параболы

Построение квадратичной функции

Алгоритм построения параболы

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Как построить параболу

Как легко составить уравнение параболы по графику

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ПРАКТИЧЕСКАЯ ЧАСТЬ

Парабола

Что такое вершина параболы

Форма и характеристики параболы

Оптическое свойство параболы

Примеры решения

Не пропустите также: