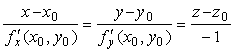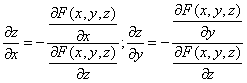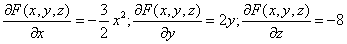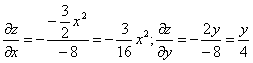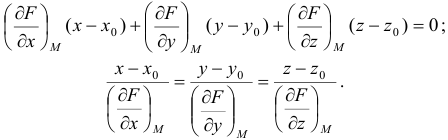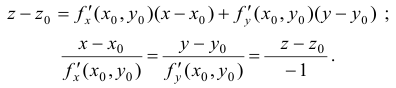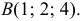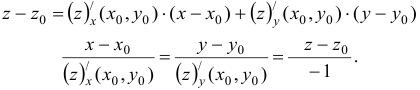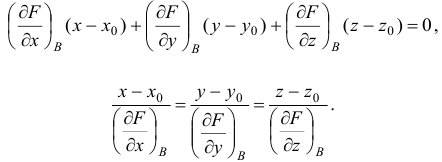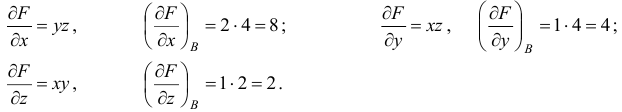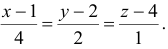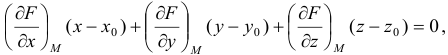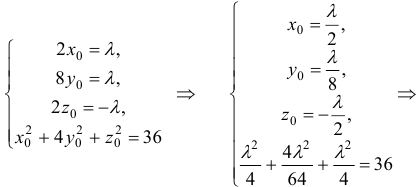Пусть поверхность
задана уравнением
Тогда уравнение
касательной плоскостив точкеимеет вид:
(18.16)
где
Нормальюк поверхности в точкеназывается прямая, проходящая через
точкуперпендикулярно к касательной плоскости
в этой точке.
Уравнение
нормалик поверхности (18.16) в точкеимеет вид:
(18.17)
Если поверхность
задана уравнением
(18.18)
и в точке
этой поверхности существуют частные
производныене равные нулю одновременно, то уравнение
касательной плоскости к поверхности
(18.18) в точкеимеет вид:
(18.19)
Уравнение нормали
к поверхности (18.18) в точке
имеет вид:
(18.20)
Пример
1. Поверхность
задана уравнением
Составить уравнение касательной
плоскости и уравнение нормали к
поверхности в точке
Решение.
Найдем
частные производные:
Их
значения в точке
равны
Найдем
соответствующее значение
функции для
Тогда
уравнение касательной плоскости примет
вид:
или
Уравнение нормали:
Пример
2. Составить
уравнение касательной плоскости и
нормали к поверхности
в точке
Решение.
Частные
производные имеют вид:
Их
значения в точке N0
равны:
Тогда
уравнение касательной плоскости в точке
N0:
или
Уравнение
нормали:
Пример
3. Составить
уравнения касательных плоскостей к
поверхности
параллельных плоскости
Решение.
Найдем
частные производные:
Так
как касательная плоскость параллельна
плоскости
то справедливо условие параллельности
плоскостей:
т. е.
Координаты
точек касания найдем из системы уравнений
Решая
систему, получаем:
Точки касания
имеют координаты:
и
Тогда уравнения
касательных плоскостей имеют вид:
Пример
4. Составить
уравнение касательной плоскости к
поверхности, заданной уравнением
где
в точке
Решение.
Поверхность
задана сложной функцией. Найдем частные
производные, используя формулы (18.11)
(см. § 18.3):
Их
значения в точке
соответственно равны:
Найдем
соответствующее значение
Тогда уравнение
касательной плоскости:
или
Пример
5. Записать
уравнение нормали к поверхности, заданной
уравнением
в точке
Решение.
Найдем
частные производные и вычислим их в
точке N0:
Уравнение
нормали в точке N0:

Равенство
нулю
означает, что касательная плоскость
параллельна осиОх,
а нормаль к ней лежит в плоскости
Задания
I уровень
1.1.Найдите
уравнение касательной плоскости и
нормали к поверхности, заданной функциейв точке
1)
2)
3)
4)
5)
6)
1.2.Найдите
уравнение касательной плоскости и
нормали к поверхности, заданной уравнениемв точке
1)
2)
3)
II уровень
2.1.Найдите
уравнения касательных плоскостей к
поверхностиперпендикулярных координатным плоскостям.
2.2.Составьте
уравнения касательных плоскостей к
поверхностипараллельных:
1) координатным
плоскостям; 2) плоскости
2.3.Составьте
уравнение касательной плоскости и
нормали к поверхности, заданной уравнениемгде
в точке
2.4.Найдите
точки на поверхности
в которых нормаль
к ее поверхности будет:
1) параллельна осям
координат;
2) перпендикулярна
осям координат.
III уровень
3.1.Определите,
в каких точках сферыкасательные плоскости к ней отсекают
на осях координат равные отрезки.
3.2.Найдите
точки эллипсоидав которых нормаль к его поверхности
образует равные углы с осями координат.
3.3. Выясните,
является ли плоскостьв точке
касательной:
1) к параболоиду
вращения
2) к конусу
3) к гиперболическому
параболоиду
3.4. Найдите
точки на поверхности
касательная
плоскость в которых к данной поверхности
будет:
1) параллельна
координатным плоскостям;
2) перпендикулярна
координатным плоскостям.
3.5.Докажите,
чтогде
– направляющие косинусы нормали к
поверхности
Соседние файлы в папке Часть 3
- #
- #
- #
- #
- #
- #
- #
- #
Касательная плоскость и нормаль к поверхности
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M0(x0,y0,z0) имеет вид:
Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z0 = f’x(x0,y0,z0)(x — x0) + f’y(x0,y0,z0)(y — y0)
По условию задачи x0 = 0 , y0 = 1 , тогда z0 = 5
Найдем частные производные функции z = x^3+5*y :
f’x(x,y) = (x 3 +5•y)’x = 3•x 2
f’x(x,y) = (x 3 +5•y)’y = 5
В точке М0(0,1) значения частных производных:
f’x(0;1) = 0
f’y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0
Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М0(1,0,1) значения частных производных:
f’x(1;0;1) = -3 /16
f’y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z — 1 = -3 /16(x — 1) + 0(y — 0) или 3 /16•x+z- 19 /16 = 0
Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
fx’(x, y) = (y/x + xy – 5x 3 )’x = – y/x 2 + y – 15x 2 ;
fy’ (x, y) = (y/x + xy – 5x 3 )’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
Пример №1 . Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z — z0 = f’x(x0,y0,z0)(x — x0) + f’y(x0,y0,z0)(y — y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’x(x,y) = (x 2 +3•x•y•+y 2 )’x = 2•x+3•y 3
f’x(x,y) = (x 2 +3•x•y•+y 2 )’y = 9•x•y 2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0
Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Математический анализ
- Касательная плоскость и нормаль к явно заданной поверхности.
Касательная плоскость и нормаль к явно заданной поверхности.
Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.
Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$
В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac=frac=frac<-1>.$$
Примеры:
7.229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=sin xcos y$ в точке $(pi/4, pi/4, pi/4).$
Решение.
Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac=frac=frac<-1>.$$
Находим частные производные:
$z’_x=(sin xcos y)’_x=cos xcos y;$
$z’_y=(sin xcos y)’_y=-sin xsin y;$
Таким образом, уравнение касательной плоскости: $$z-frac<pi><4>=frac<1><2>(x-frac<pi><4>)-frac<1><2>(y-frac<pi><4>)Rightarrow$$ $$frac<1><2>x -frac<1><2>y-z+frac<pi><4>=0.$$
7.232. Для поверхности $z=4x-xy+y^2$ найти уравнение касательной плоскости, параллельной плоскости $4x+y+2z+9=0.$
Решение.
Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0).$$
Находим частные производные:
Отсюда находим уравнение касательной плоскости: $$z-z_0=(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)Rightarrow$$ $$(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)-z+z_0=0.$$
Найдем точку поверхности $M(x_0, y_0, x_0)$ касательная плоскость к которой будет параллельна плоскости $4x+y+2z+9=0:$
Таким образом, уравнение касательной плоскости: $$z-11=(4-6)(x-frac<25><2>)+(-frac<25><2>+2cdot 6)(y-6)Rightarrow$$ $$z-11=-2(x-frac<25><2>)-frac<1><2>(y-6)Rightarrow 2x+frac<1><2>y+z-11-25-3=0Rightarrow$$ $$Rightarrow4x+y+2z-78=0.$$
7.233. а) Найти уравнения касательной плоскости и нормали к поверхности $x(y+z)(xy-z)+8=0$ в точке $(2, 1, 3).$
Решение.
Для поверхности $$F(x,y,z)=0,$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$
$F(x, y, z)=x(y+z)(xy-z)+8=x^2y^2-xyz+x^2yz-xz^2+8=0$
Находим частные производные:
Отсюда находим уравнение касательной плоскости: $$4(x-2)+14(y-1)-10(z-3)=0Rightarrow 4x+14y-10z+8.$$
Домашнее задание.
7.229. б) Найти уравнения касательной плоскости и нормали к поверхности $z=e^$ в точке $(1, pi/ 1/e).$
7.230. Найти расстояние от начала координат до касательной плоскости к поверхности $z=y tgfrac$ в точке $left(frac<pi a>right).$
7.233. б) Найти уравнения касательной плоскости и нормали к поверхности $2^+2^=8$ в точке $(2, 2, 1).$
7.234. Для поверхности $x^2-z^2-2x+6y=4$ найти уравнение нормали, параллельной прямой $frac<1>=frac<3>=frac<4>.$
Касательная плоскость и нормаль к поверхности.
Пусть поверхность задана в неявном виде: $F(x,y,z)=0$ и пусть точка $M_0(x_0,y_0,z_0)$ принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке $M_0$ таково:
Уравнение нормали имеет вид:
Если же уравнение поверхности задано в явном виде $z=f(x,y)$, то уравнение касательной плоскости имеет вид:
Уравнение нормали в случае явного задания поверхности таково:
Примечание (желательное для более полного понимания текста): показатьскрыть
Формулы (3) и (4) легко получить из формул (1) и (2). Если $z=f(x,y)$, то перенося $z$ в правую часть равенства получим: $f(x,y)-z=0$. Обозначая $F(x,y,z)=f(x,y)-z$, получим: $F_^<‘>=left(f(x,y)-zright)_^<‘>=f_^<‘>(x,y)-0=f_^<‘>(x,y)$. Аналогично и $F_^<‘>=left(f(x,y)-zright)_^<‘>=f_^<‘>(x,y)-0=f_^<‘>(x,y)$. Что же касается последней производной (т.е. производной по переменной $z$), то тут нужно учесть, что выражение $f(x,y)$ не содержит $z$, поэтому: $F_^<‘>=left(f(x,y)-zright)_^<‘>=0-1=-1$. Подставляя в формулы (1) и (2) вместо $F_^<‘>$, $F_^<‘>$, $F_^<‘>$ соответственно $f_^<‘>$, $f_^<‘>$ и $-1$ и получим формулы (3) и (4).
Найти уравнение касательной плоскости и нормали к поверхности $z=3x^2y^4-6xy^3+5x-4y+10$ в точке $M_0(-2;1;20)$.
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$, $y_0$, $z_0$ (координаты точки $M_0$) в нашем случае таковы: $x_0=-2$, $y_0=1$, $z_0=20$. Но перед тем, как переходить к решению, осуществим небольшую проверку. Убедимся, что точка $M_0$ действительно лежит на заданной поверхности. Эта проверка не является обязательной, но желательна, ибо ошибка в условиях подобных задач – дело вовсе не редкое. Подставим $x=x_0$, $y=y_0$ в уравнение нашей поверхности и убедимся, что $z_0$ действительно равно 20:
$$ z_0=3x_<0>^<2>y_<0>^<4>-6x_0y_<0>^<3>+5x_0-4y_0+10=3cdot (-2)^2cdot 1^4-6cdot (-2)cdot 1^3-4cdot 1+10=12+12-4=20. $$
Проверка пройдена, точка $M_0$ действительно лежит на заданной поверхности. Теперь найдём частные производные, т.е. $z_^<‘>$ и $z_^<‘>$:
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ в выражения частных производных:
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ <‘>left(x_0, y_0right)=-13$, $z_^ <‘>left(x_0, y_0right)=80$ в формулу (3) получим уравнение касательной плоскости:
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ <‘>left(x_0, y_0right)=-13$, $z_^ <‘>left(x_0, y_0right)=80$ в формулу (4) получим уравнение нормали:
Ответ: Касательная плоскость: $-13x+80y-z-86=0$; нормаль: $frac<-13>=frac<80>=frac<-1>$.
Найти уравнение касательной плоскости и нормали к поверхности $z=5sqrt-2xy-39$ в точке $M_0(3;-4;z_0)$.
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=3$, $y_0=-4$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
Теперь, как и в предыдущем примере, перейдём к нахождению частных производных $z_^<‘>$ и $z_^<‘>$. После того, как мы найдём эти производные в общем виде, укажем их значения при $x=x_0$ и $y=y_0$:
Подставляя $x_0=3$, $y_0=-4$, $z_0=10$, $z_^ <‘>left(x_0, y_0right)=11$, $z_^ <‘>left(x_0, y_0right)=-10$ в формулы (3) и (4) получим уравнения касательной плоскости и нормали:
Ответ: Касательная плоскость: $11x-10y-z-63=0$; нормаль: $frac<11>=frac<-10>=frac<-1>$.
Найти уравнение касательной плоскости и нормали к поверхности $3xy^2z+5xy+z^2=10xz-2y+1$ в точке $M_0(1;-2;3)$.
Перенесём все слагаемые в левую часть равенства и обозначим полученное в левой части выражение как $F(x,y,z)$:
Используем формулы (1) и (2). Значения $x_0$, $y_0$ и $z_0$ как и ранее обозначают координаты точки $M_0$, т.е. $x_0=1$, $y_0=-2$, $z_0=3$.
Проверим, действительно ли точка $M_0$ лежит на данной поверхности. Для этого подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражение $3xy^2z+5xy+z^2-10xz+2y-1$ и выясним, равен ли нулю полученный результат:
Итак, точка $M_0$ действительно лежит на данной поверхности. Естественно, что данная проверка не является обязательной, но она крайне желательна. Перейдём к дальнейшему решению. Нам нужно найти $F_^<‘>$, $F_^<‘>$ и $F_^<‘>$:
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражения частных производных:
Подставляя $x_0=1$, $y_0=-2$, $z_0=3$, $F_^ <‘>left(M_0right)=-4$, $F_^ <‘>left(M_0right)=-29$ и $F_^ <‘>left(M_0right)=8$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
Ответ: Касательная плоскость: $-4x-29y+8z-78=0$; нормаль: $frac<-4>=frac<-29>=frac<8>$.
Найти уравнение касательной плоскости и нормали к поверхности $z^3+4xyz=-3x^2+5y+7$ в точке $M_0(0;-3;z_0)$.
Поверхность задана в неявном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (1) и (2). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=0$, $y_0=-3$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
Перенесём все слагаемые в левую часть равенства:
Обозначим $F(x,y,z)=z^3+4xyz+3x^2-5y-7$ и применим формулы (1) и (2). Найдём частные производные первого порядка $F_^<‘>$, $F_^<‘>$ и $F_^<‘>$. После того, как мы найдём эти производные в общем виде, укажем их значения в точке $M_0$:
Подставляя $x_0=0$, $y_0=-3$, $z_0=-2$, $F_^ <‘>left(M_0right)=-24$, $F_^ <‘>left(M_0right)=-5$ и $F_^ <‘>left(M_0right)=12$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
Ответ: Касательная плоскость: $-24x-5y+12z+9=0$; нормаль: $frac<-24>=frac<-5>=frac<12>$.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
http://mathportal.net/index.php/matematicheskij-analiz/kasatelnaya-ploskost-i-normal-k-yavno-zadannoj-poverkhnosti
http://math1.ru/education/funct_sev_var/tannorm.html
Касательная плоскость и нормаль к явно заданной поверхности.
Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.
Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$
Уравнение нормали $$frac{x-x_0}{F_x'(x_0, y_0, z_0)}=frac{y-y_0}{F_y'(x_0, y_0, z_0)}=frac{z-z_0}{F_z'(x_0, y_0, z_0)}.$$
В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac{x-x_0}{f_x'(x_0, y_0)}=frac{y-y_0}{f_y'(x_0, y_0)}=frac{z-z_0}{-1}.$$
Примеры:
7.229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=sin xcos y$ в точке $(pi/4, pi/4, pi/4).$
Решение.
Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac{x-x_0}{f_x'(x_0, y_0)}=frac{y-y_0}{f_y'(x_0, y_0)}=frac{z-z_0}{-1}.$$
Находим частные производные:
$z’_x=(sin xcos y)’_x=cos xcos y;$
$z’_x(pi/4, pi/4)=cos frac{pi}{4}cos frac{pi}{4}=frac{1}{sqrt 2}cdotfrac{1}{sqrt 2}=frac{1}{2};$
$z’_y=(sin xcos y)’_y=-sin xsin y;$
$z’_y(pi/4, pi/4)=-sin frac{pi}{4}sin frac{pi}{4}=-frac{1}{sqrt 2}cdotfrac{1}{sqrt 2}=-frac{1}{2};$
Таким образом, уравнение касательной плоскости: $$z-frac{pi}{4}=frac{1}{2}(x-frac{pi}{4})-frac{1}{2}(y-frac{pi}{4})Rightarrow$$ $$frac{1}{2}x -frac{1}{2}y-z+frac{pi}{4}=0.$$
Уравнение нормали: $$frac{x-frac{pi}{4}}{frac{1}{2}}=frac{y-frac{pi}{4}}{-frac{1}{2}}=frac{z-frac{pi}{4}}{-1}.$$
Ответ: уравнение касательной плоскости: $frac{1}{2}x -frac{1}{2}y-z+frac{pi}{4}=0;$ уравнение нормали: $frac{x-frac{pi}{4}}{frac{1}{2}}=frac{y-frac{pi}{4}}{-frac{1}{2}}=frac{z-frac{pi}{4}}{-1}.$
7.232. Для поверхности $z=4x-xy+y^2$ найти уравнение касательной плоскости, параллельной плоскости $4x+y+2z+9=0.$
Решение.
Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0).$$
Находим частные производные:
$z’_x=(4x-xy+y^2)’_x=4-y;$
$z’_y=(4x-xy+y^2)’_y=-x+2y;$
Отсюда находим уравнение касательной плоскости: $$z-z_0=(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)Rightarrow$$ $$(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)-z+z_0=0.$$
Найдем точку поверхности $M(x_0, y_0, x_0)$ касательная плоскость к которой будет параллельна плоскости $4x+y+2z+9=0:$
$$frac{4-y_0}{4}=frac{-x_0+2y_0}{1}=frac{-1}{2}Rightarrow 4-y_0=-2Rightarrow y_0=6;$$ $$-x_0+12=-frac{1}{2}Rightarrow x_0=frac{25}{2};$$ $$z_0=4cdotfrac{25}{2}-frac{25}{2}cdot 6+6^2=50-75+36=11.$$
Таким образом, уравнение касательной плоскости: $$z-11=(4-6)(x-frac{25}{2})+(-frac{25}{2}+2cdot 6)(y-6)Rightarrow$$ $$z-11=-2(x-frac{25}{2})-frac{1}{2}(y-6)Rightarrow 2x+frac{1}{2}y+z-11-25-3=0Rightarrow$$ $$Rightarrow4x+y+2z-78=0.$$
Ответ: $4x+y+2z-78=0.$
7.233. а) Найти уравнения касательной плоскости и нормали к поверхности $x(y+z)(xy-z)+8=0$ в точке $(2, 1, 3).$
Решение.
Для поверхности $$F(x,y,z)=0,$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$
$F(x, y, z)=x(y+z)(xy-z)+8=x^2y^2-xyz+x^2yz-xz^2+8=0$
Находим частные производные:
$F’_x=(x^2y^2-xyz+x^2yz-xz^2+8)’_x=2xy^2-yz+2xyz-z^2;$
$F’_x(2, 1, 3)=4-3+12-9=4;$
$F’_y=(x^2y^2-xyz+x^2yz-xz^2+8)’_y=2x^2y-xz+x^2z;$
$F’_y(2, 1, 3)=8-6+12=14;$
$F’_z=(x^2y^2-xyz+x^2yz-xz^2+8)’_z=-xy+x^2y-2xz;$
$F’_z(2, 1, 3)=-2+4-12=-10.$
Отсюда находим уравнение касательной плоскости: $$4(x-2)+14(y-1)-10(z-3)=0Rightarrow 4x+14y-10z+8.$$
Ответ: $2x+7y-5z+4=0.$
Домашнее задание.
7.229. б) Найти уравнения касательной плоскости и нормали к поверхности $z=e^{xcos y}$ в точке $(1, pi/ 1/e).$
7.230. Найти расстояние от начала координат до касательной плоскости к поверхности $z=y tgfrac{x}{a}$ в точке $left(frac{pi a}{a, a, a}right).$
7.233. б) Найти уравнения касательной плоскости и нормали к поверхности $2^{x/z}+2^{y/z}=8$ в точке $(2, 2, 1).$
7.234. Для поверхности $x^2-z^2-2x+6y=4$ найти уравнение нормали, параллельной прямой $frac{x+2}{1}=frac{y}{3}=frac{z+1}{4}.$
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Касательная плоскость, параллельная другой плоскости
|
|||
|
К поверхности [math]x^{2}+2y^{2}+z^{2} =1[/math] провести касательную плоскость, параллельную плоскости [math]x — y +2z = 0[/math] [math]frac{partial f}{partial y} = 4y[/math] [math]frac{partial f}{partial z} = 2z[/math]
|
||
| Вернуться к началу |
|
||
|
Andrey82 |
Заголовок сообщения: Re: Касательная плоскость, параллельная другой плоскости
|
|
MihailM писал(а): У касательной плоскости к поверхности какой нормальный вектор? [math]N (1,2,1)[/math], так?
|
|
| Вернуться к началу |
|
|
searcher |
Заголовок сообщения: Re: Касательная плоскость, параллельная другой плоскости
|
|
Andrey82 писал(а): MihailM писал(а): У касательной плоскости к поверхности какой нормальный вектор? [math]N (1,2,1)[/math], так? И что, любая касательная плоскость ориентирована одинаково? В смысле, они все параллельны?
|
|
| Вернуться к началу |
|
|
searcher |
Заголовок сообщения: Re: Касательная плоскость, параллельная другой плоскости
|
|
Andrey82 searcher писал(а): И что, любая касательная плоскость ориентирована одинаково? В смысле, они все параллельны? Может я не к месту встрял, но я имел в виду, что у разных касательных плоскостей разный нормальный вектор, а у нужной нам нормальной плоскости вполне однозначный нормальный вектор и он в общем-то усматривается в условии.
|
|
| Вернуться к началу |
|
|
Andrey82 |
Заголовок сообщения: Re: Касательная плоскость, параллельная другой плоскости
|
|
Цитата: Andrey82 Стараюсь не путать)
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Касательная плоскость, параллельная оси z
в форуме Дифференциальное исчисление |
za-ek |
4 |
493 |
12 янв 2014, 03:12 |
|
Три вектора и параллельная плоскость
в форуме Аналитическая геометрия и Векторная алгебра |
AMAM55 |
10 |
616 |
01 апр 2015, 23:37 |
|
Плоскость, параллельная 2 векторам
в форуме Аналитическая геометрия и Векторная алгебра |
Scorpionddd |
1 |
562 |
06 окт 2013, 12:34 |
|
Прямая, параллельная плоскости
в форуме Аналитическая геометрия и Векторная алгебра |
hamham |
2 |
231 |
18 дек 2017, 22:14 |
|
Касательная плоскость
в форуме Дифференциальное исчисление |
w0nna |
1 |
92 |
29 май 2022, 13:11 |
|
Касательная плоскость
в форуме Дифференциальное исчисление |
w0nna |
4 |
166 |
29 май 2022, 15:33 |
|
Касательная плоскость
в форуме Дифференциальное исчисление |
searcher |
2 |
353 |
27 ноя 2016, 12:34 |
|
Касательная плоскость к сфере
в форуме Дифференциальное исчисление |
Slesher |
4 |
634 |
17 фев 2014, 18:50 |
|
Касательная плоскость к поверхности
в форуме Аналитическая геометрия и Векторная алгебра |
evaf |
20 |
623 |
19 сен 2017, 14:00 |
|
Касательная плоскость к сферам
в форуме Аналитическая геометрия и Векторная алгебра |
gashik |
23 |
2206 |
04 май 2014, 17:42 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Касательной плоскостью к поверхности в данной точке 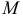
Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания.
Для поверхности 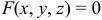
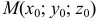
Для поверхности 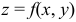
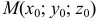
Пример №1
Составить уравнение касательной плоскости и нормали к поверхности:
а) 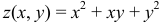
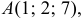
б) 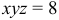
Решение:
а) Для составления уравнений касательной плоскости и нормали к поверхности 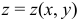
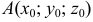
Из условия имеем: 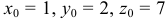
Подставляя значения частных производных и координат т. 
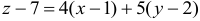
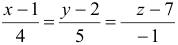
б) Для поверхности, заданной уравнением 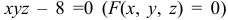
В нашем случае 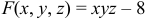
Уравнение касательной плоскости имеет вид: 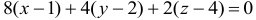
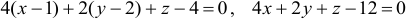
Уравнение нормали:
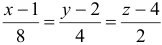
Пример №2
Определить плоскость, касательную к поверхности 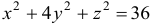
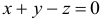
Решение:
Уравнение искомой плоскости имеет вид
где 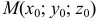
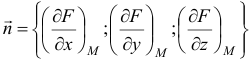
По условию 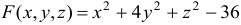
Так как искомая плоскость параллельна данной плоскости 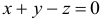
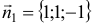
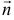
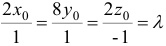
Поскольку точка 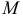
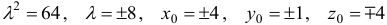
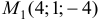
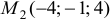
Для точки 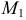
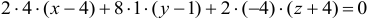
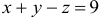
Для точки 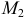
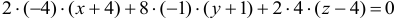
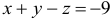
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы: