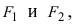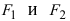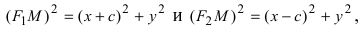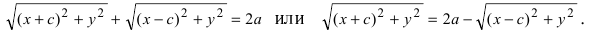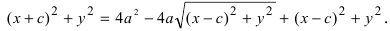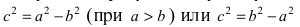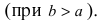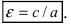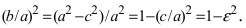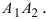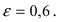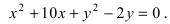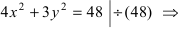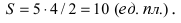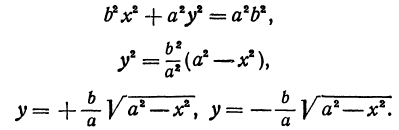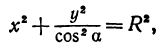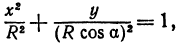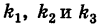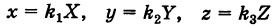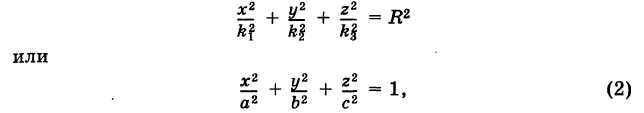A conic section can be defined as the set of points that describe the intersection of a right circular cone with a plane. The angle of intersection between the plane and the cone determines the shape of the conic section. When this angle is acute, that is, between 45° and 90°.
Alternatively, an ellipse can also be defined as such: a closed curve formed by a set of points whose sum of the distance from two fixed points is constant.
The standard equation of the ellipse whose center is (h, k) is,
Question: Determine the equation of the standard form of the ellipse given: The coordinates of two points P (p, q) and M (m, n), and the coordinates of the center, O (h, k).
Solution:
It is known that the standard equation of the ellipse is,
We have been provided the value of (h, k) in the question. Both P(p, q) and M(m, n) will satisfy the equation.
So, now we have two equations:
Equation 1:
Equation 2:
We can equate both the LHS of the equations (since the RHS is equal). Then, we get:
We can simplify this as:
Using the formula a2 – b2 = (a – b)×(a + b), we can simplify the equation further:
From this, we can get the relation between a and b as:
Now, we can plug this value in Equation 1 or Equation 2 to solve it finally.
Let us plug it into equation 1:
Finally, we can deduce that b is:
And hence, a is:
Given two points P (p, q) and M (m, n) of an ellipse with center (h, k), the equation of the ellipse in standard form is:
where,
and
Sample Problems
Problem 1: Given that the center of an ellipse is (5, 2) and the points A (3, 4) and B (5, 6) pass through the ellipse, form the standard equation of the ellipse.
Solution:
Given that center of the ellipse is (h, k) = (5, 2) and (p, q) = (3, 4) and (m, n) = (5, 6) are two points on the ellipse.
We can use the values of a and b from the above formula to create the standard equation as:
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving, we get a ≈ 2.31.
Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:
Solving, we get b = 4.
Therefore, the equation of the ellipse is:
Problem 2: A hypothetical ellipse has its center at (5, 8). The points A (9, 2) and B (7, 6) pass through the ellipse. Is it possible for such an ellipse to exist in the real plane? Explain your answer.
Solution:
Our hypothesis is that the ellipse exists.
Given that center of the ellipse is (h, k) = (5,
and (p, q) = (9, 2) and (m, n) = (7, 6) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation
We know that,
Substituting the values of p, q, h, k, m and n we get:
We cannot solve this and get a real value of a.
Therefore, our hypothesis is False. An ellipse with the given conditions cannot exist.
Problem 3: Given that the center of an ellipse is (1, 4) and the points A (2, 9) and B (12, 5) pass through the ellipse, form the standard equation of the ellipse.
Solution:
Given that center of the ellipse is (h, k) = (1, 4) and (p, q) = (2, 9) and (m, n) = (12, 5) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation:
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving, we get a ≈ 11.22.
Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:
Solving, we get b ≈ 5.02.
Therefore, the equation of the ellipse is:
Problem 4: A hypothetical ellipse has its center at (1, 3). The points A (8, 2) and B (7, 5) pass through the ellipse. Is it possible for such an ellipse to exist in the real plane? Explain your answer.
Solution:
Our hypothesis is that the ellipse exists.
Given that center of the ellipse is (h, k) = (1, 3) and (p, q) = (8, 2) and (m, n) = (7, 5) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation:
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving this, we get a ≈ 7.3.
Similarly, substituting the values of p, q, h, k, m, and n in the formula for b, we get:
Solving this, we get b ≈ 3.51.
As the values of a and b are real, our hypothesis is True. An ellipse that satisfies the given conditions can exist.
Problem 5: The center of an ellipse is at the Origin. The point (1, 5) lies on the ellipse. Does the point (11, 2) also lie on the ellipse?
Solution:
Our hypothesis is that an ellipse with a center at Origin (0, 0) passing through the points (11, 2) and (1, 5) exists.
Now, we can use the values of a and b from the above formula to create the standard equation
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving this, we get a ≈ 11.99.
Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:
Solving this, we get b ≈ 5.02.
As the values of a and b are real, our hypothesis is True. The point (11, 2) does lie on the ellipse.
Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
|
Первая координата |
|
Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр — половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей — большая полуось 

Эксцентриситет — коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия — отношение длин малой и большой полуосей
Перифокусное расстояние
Апофокусное расстояние
Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса |
 |
| Большая полуось эллипса |
|
8.48528137423857 |
| Малая полуось эллипса |
|
5.656854249492381 |
| Эксцентриситет эллипса |
|
0.8958064164776166 |
| Фокусное/фокальное расстояние |
|
32.2490309931942 |
| Коэффициент сжатия |
|
0.4444444444444444 |
| Координаты первого фокуса F1(x1:y1) |
|
-16.1245154965971 : 0 |
| Координаты второго фокуса F2(x2:y2) |
|
16.1245154965971 : 0 |
| Фокальный параметр |
|
3.5555555555555554 |
| Перифокусное расстояние |
|
1.875484503402901 |
| Апофокусное расстояние |
|
34.1245154965971 |
И еще один пример
Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.
Если мы введем данные в калькулятор получим
 |
| Большая полуось эллипса |
|
5.877538136328849 |
| Малая полуось эллипса |
|
NaN |
Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.
Таким образом по этим двум точкам, нельзя построить эллипс.
А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.
Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам
Удачных расчетов!
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 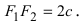
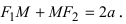
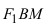
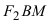
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 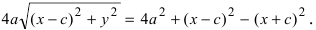
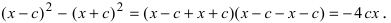
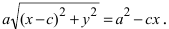
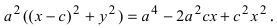
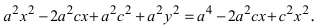
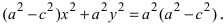
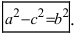
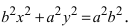
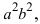
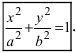
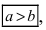
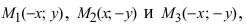
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 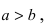
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 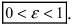
Если 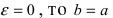
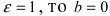
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 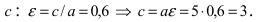
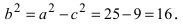
Пример:
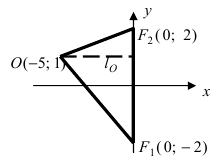
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 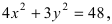
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
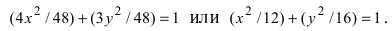
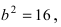
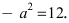
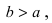
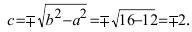
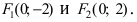
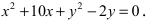
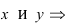
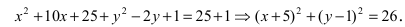
Построим в декартовой системе координат треугольник 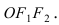
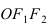
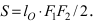
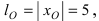
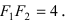
Эллипс в высшей математике
Рассмотрим уравнение
где 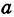
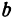
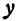
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
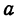

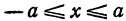
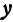
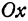
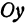
При 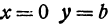
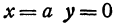
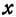

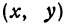
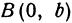
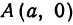
Полученная линия называется эллипсом. Число 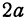
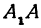
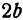
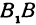
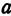
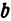
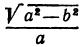
Пример:
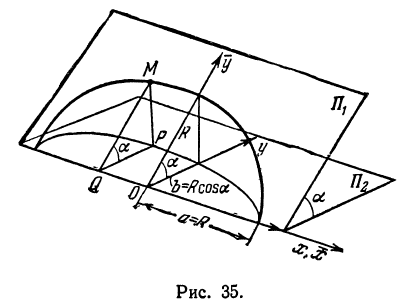
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 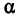
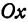
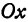
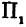
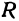
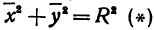
Пусть точка 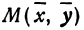
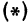
Обозначим проекцию точки 
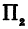
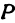
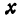
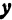


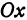
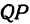
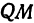
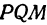
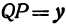
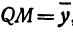
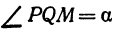
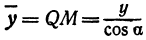


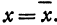
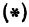
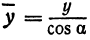
или
а это есть уравнение эллипса с полуосями 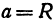
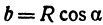
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 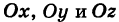
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 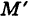
(рис. 206). Отсюда
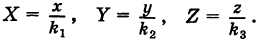
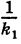
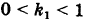
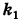
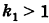
Подставляя эти формулы в уравнение (1), будем иметь
где 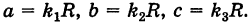
Величины 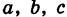
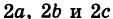
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
(схема 21)
Эллипсом называется
геометрическое место точек плоскости, сумма расстояний от каждой из которых до
двух данных точек этой плоскости, называемых
фокусами, есть величина постоянная, равная 2a.
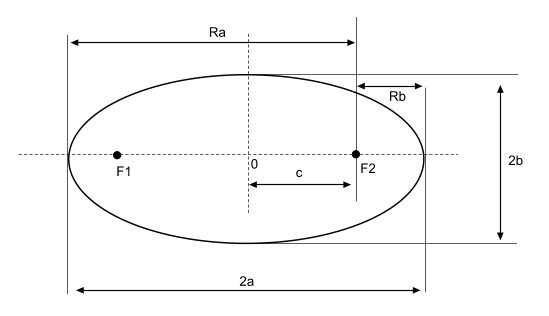
Обозначим фокусы через F1 и F2,
расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса до
фокусов – через 2a. По определению 2a>2c, то есть a>c .
Выберем систему координат
так, чтобы
фокусы F1 и F2
лежали на оси 0x, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы имют координаты: F1(–c;0) и F2(c;0). Пусть M(x;y) –
произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать
По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Так как, a>c, то a2–c2>0, то можно обозначить a2–c2=b2. Тогда
последнее уравнение имеет вид:

Это
уравнение равносильно первоначальному. Оно называется каноническим уравнением
эллипса – кривой
второго порядка.
Установим форму эллипса, пользуясь его каноническим
уравнением.
1. Уравнение (2.17) содержит x и y
только в четных степенях, поэтому
если точка (x;y)
принадлежит эллипсу, то
ему также принадлежат
точки (–x;y), (x;–y), (–x;–y). Отсюда: эллипс симметричен относительно осей 0x и 0y, а также
относительно точки O(0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат.
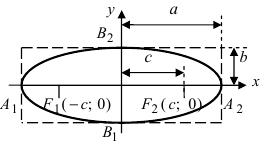
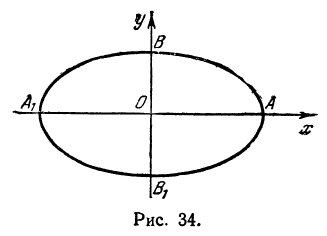
Положив y=0, найдем точки A1(a;0) и A2(–a;0), в которых ось 0x пересекает эллипс. Положив в уравнении
(2.17) x=0, находим точки пересечения эллипса с осью 0y: B1(0;b) и B2(0;–b). Точки A1, A2, B1, B2 называются вершинами эллипса. Отрезки А1А2,
В1В2, а также
их длины 2a и 2b – соответственно большая и малая оси эллипса (рис. 2.4).
3. Из уравнения (2.17) следует, что каждое слагаемое в
левой части не превосходит единицы,
т.е.:

Следовательно, все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми x= ± a
и y= ± b.
4. В уравнении (2.17) левая часть – сумма
неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет
уменьшаться, если |x| возрастает, |y|
уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму
овальной замкнутой кривой. Форма эллипса зависит от отношения
(2.17) принимает вид: x2+y2=a2. Отношение 

0<ε<1, так как 0<c<a.
Отсюда видно, что чем меньше эксцентриситет эллипса,
тем будет менее эллипс сплющенным; при ε=0 эллипс
превращается в окружность.
Пусть M(x;y) – произвольная точка эллипса с фокусами F1 и F2. Длины
отрезков |MF1|=r1 и |MF2|=r2 – фокальные
радиусы точки M, r1+r2=2a. Имеют место формулы: r1=a+εx и r2=a – εx.
Прямые 
эллипса.
Если r – расстояние от произвольной точки до какого–нибудь фокуса,
d –
расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение
постоянная, равная эксцентриситету эллипса: 
Из равенства a2–c2=b2
следует, что a>b. Если же
наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2b лежит на
оси 0y, а малая ось 2a – на оси 0x. Фокусы такого
эллипса находятся в точках F1(0;c) и F2(0;–c), где 
Пример 2.5. Составить уравнение линии, для каждой точки
которой отношение расстояний от нее до
точки A(3;0) и до прямой x=12, равно числу ε=0,5. Полученное
уравнение привести к простейшему виду.
Решение. Пусть M(x;y) – текущая (произвольная) точка искомого
геометрического множества точек. Опустим перпендикуляр MB на прямую
. Тогда точка B(12;y). По условию задачи

По формуле расстояния
двумя точками получаем:
Отсюда
Полученное уравнение представляет собой эллипс вида 
Определим фокусы эллипса F1(–c;0) и F2(c;0). Для эллипса справедливо равенство b2=a2–c2,
откуда c2=a2–b2 =9 и c=3. То есть,
F1(–3;0) и F1(3;0)–
фокусы эллипса (точки F2 и A совпадают).
Эксцентриситет эллипса
Примечание. Если эллипс (окружность) вращать вокруг одной из его
осей, то описываемая им поверхность будет эллипсоидом вращения (сферой)
Пример 2.6. В геодезии используется система географических координат,
основанная на понятии геоида. Геоид – поверхность Земли,
ограниченная уровенной поверхностью, продолженной под континенты. Поверхность
геоида отличается от физической поверхности Земли, на которой резко выражены
горы и океанические впадины.
Тело, поверхность которого более всего соответствует
поверхности геоида, имеет определенные размеры и ориентирована соответственно в
теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех
геодезических работ принят референц–эллипсоид Красовского с
параметрами a=6 378 245 м, b=6 356 863 м, α=1: 298,3.
Линия, проходящая вертикально через центр эллипсоида
является полярной осью. Линия, проходящая через центр эллипсоида,
перпендикулярно к полярной оси, – экваториальной осью. При пересечении
поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно
к полярной оси, образуется окружность, называемая экватором. Окружность,
полученная от пересечения поверхности эллипсоида плоскостью, параллельной
плоскости экватора, называется параллелью. Линия пересечения
поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную
ось, называется меридианом данной точки. Положение точки на земной поверхности
определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной
линией называется географической широтой. Для определения долгот
точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол
λ, составленный плоскостью меридиана,
проходящего через данную точку, и плоскостью начального меридиана, называется
географической долготой
Гипербола – геометрическое место точек плоскости, модуль разности расстояний от
каждой из которых до двух данных точек этой плоскости – фокусов, есть величина
постоянная, равная 2a.
Обозначим фокусы через
F1 и F2, расстояние между ними через 2c, а модуль
разности расстояний от каждой точки
гиперболы до фокусов через 2a. По определению 2a<2c, то есть a<c.
Выберем систему координат x0y так, чтобы фокусы F1 и F2 лежали на оси 0x, а начало координат совпало с серединой отрезка F1F2. Тогда фокусы будут иметь координаты F1(c;0) и F2(–c;0). На этой основе выведем уравнение гиперболы. Пусть M(x;y) – ее произвольная точка. Тогда по определению |MF1–MF2|=2a, то есть

где
b2=a2–c2.
Гипербола – линия 2–го порядка.
Установим форму гиперболы, исходя из ее канонического
уравнения.
1. Уравнение (2.18) содержит x и y только в
четных степенях. Следовательно, гипербола симметрична относительно осей координат
0x и 0y, и относительно точки O(0;0) – центра гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив в
уравнении (2.18) y=0, находим две точки пересечения гиперболы с осью 0x: A1(a;0) и A2(–a;0).
Положив в (2.18) x=0, получаем y2= – b2,
чего быть не может. Т.е. гипербола ось 0y не пересекает.
Точки A1(a;0) и A2(–a;0) – вершины гиперболы, а отрезок |A1A2|=2a – действительная ось. Отрезок |B1B2|=2b,
соединяющий точки B1(0;b) и B2(0;–b) – мнимая ось (рис. 2.6). Прямоугольник
со сторонами 2a и 2b – основной
прямоугольник гиперболы.
3. Из уравнения (2.18) следует, что уменьшаемое 
от прямой x=a (правая
ветвь гиперболы) и слева от прямой x=–a (левая
ветвь) (рис. 2.6).
4. Из уравнения (2.18) гиперболы видно, что
когда |x| возрастает, то |y| также
возрастает. Это
следует из того, что разность 
сохраняет значение, равноe единице. Следовательно, гипербола имеет форму,
состоящую из двух неограниченных ветвей.
Прямая L называется асимптотой некоторой неограниченной кривой, если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном
удалении точки M вдоль кривой
от начала координат.
Покажем, что гипербола 

данные прямые и гипербола (2.18) симметричны относительно координатных
осей, то достаточно рассмотреть только точки, расположенные в первой четверти.
Возьмем на прямой 
ту же абсциссу, что и точка M(x;y) на гиперболе 
Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка |MN| стремится
к нулю. Так как |MN| больше
расстояния d от точки M до прямой L, то d стремится к нулю тем более (и подавно). Следовательно, прямые

асимптоты гиперболы (рис. 2.7).
Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы.
Эксцентриситет гиперболы –
отношение расстояния между фокусами к величине её действительной оси,
обозначается ε: 
как у гиперболы c>a, то
эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как 
эксцентриситет гиперболы, тем меньше отношение 
значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет
равносторонней гиперболы равен 

,
для точек
правой ветви гиперболы имеют вид: r1=εx+a, r2=εx–a; для точек
левой ветви: r1=–(εx+a), r2=–(εx–a).
Прямые
гиперболы. Тот факт, что для гиперболы ε>1, то 
левая – между центром и левой вершиной. Директрисы
гиперболы имеют тоже свойство 
Уравнение 
на рисунке 2.7 пунктиром).
Значит, гиперболы

имеют общие
асимптоты. Такие гиперболы называются сопряженными.
Примечание. Если у кривой 2–го порядка смещен центр в некоторую
точку O’(x0;y0), то она
называется нецентральной кривой. Уравнение такой кривой имеет вид:
Примечание. При вращении гиперболы вокруг ее действительной оси
образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид
Подробно данные уравнения рассмотрены в теме:
«Исследование общего уравнения 2–ой степени» (смотри схему 10), частными
случаями которого являются данные формулы.
Вопросы
для самопроверки
фокусы которого лежат на оси абсцисс симметрично
относительно начала координат, зная, кроме того,
что: 444.1 его полуоси ранвы 5
и 2; 444.2 его большая ось
равна 10, а расстояние между фокусами 2c=8; 444.3 его малая ось равна
24, а расстояние между фокусами 2c=10; 444.4 расстояние между
его фокусами 2c=6 и эксцентриситет e=3/5. 444.5 его большая ось
равна 20, а эксцентриситет e=3/5. 444.6 его малая ось равна
10, а эксцентриситет e=12/13; 444.7 расстояние между
его директрисами равно 5 и расстояние между
фокусами 2c=4; 444.8 его большая ось
равна 8, а расстояние между директрисами равно 16; 444.9 его малая ось равна
6, а расстояние между директрисами равно 13; 444.10 расстояние между
его директрисами равно 32 и e=1/2. 445 Составить
уравнение эллипса, фокусы которого лежат на оси
ординат симметрично начала координат, зная,
кроме того, что: 445.1 его полуоси равны
соответственно 7 и 2; 445.2 его большая ось
равна 10, а расстояние между фокусами 2c=8; 445.3 расстояние между
его фокусами 2c=24 и эксцентриситет e=12/13. 445.4 его малая ось равна
16, а эксцентриситет e=3/5. 445.5 расстояние между
его фокусами 2c=6 и расстояние между директрисами
равно 50/3; 445.6 расстояние между
его директрисами равно 32/3 и эксцентриситет e=3/4. 446 Определить полуоси
каждого из следующих эллипсов: 446.1
эксцентриситет, уравнения директрис. 448 Вычислить площадь
четырехугольника, две вершины которого лежат в
фокусах эллипса
совпадают с концами его малой оси. 449 Дан эллипс
эксцентриситет, уравнения директрис. 450 Вычислить площадь
четырехугольника, две вершины которого лежат в
фокусах эллипса
концами его малой оси. 451 Вычислить
расстояние от фокуса F(c; 0) эллипса
односторонней с этим фокусом директрисы. 452 Пользуясь одним
циркулем, построить фокусы эллипса
что изображены оси координат и задана масштабная
единица). 453 На эллипсе
–3. 454 Определить, какие
из точек A1(-2; 3), A2(2; -2), A3(2;
-4), A4(-1; 3), A5(-4; -3), A6(3; -1), A7(3;
-2), A8(2; 1), A9(0; 15), A10(0; -16) лежат на эллипсе
внутри и какие вне его. 455 Установить, какие
линии опеределяются следующими уравнениями.
Изобразить эти линии на чертеже. 455.1
эллипса e=2/3, фокальный радиус точки М эллипса
равен 10. Вычислить расстояние от точки М до
односторонней с этим фокусом директрисы. 457 Эксцентриситет
эллипса e=2/5, расстояние от точки эллипса до
директрисы равно 20. Вычислить расстояние от
точки М до фокуса, односторонней с этой
директрисой. 458 Дана точка М1(2; -5/3) на эллипсе
уравнения прямых, на которых лежат фокальные
радиусы точки М1.
459 Убедившись, что
точка M1(-4; 2,4) лежит
на эллипсе
М1. 460 Эксцентриситет
эллипса e=1/3, центр его совпадает с началом
координат, один из фокусов (-2; 0). Вычислить
расстояние от точки М1 эллипса с абсциссой, равной 2, до
директрисы, односторонней с данным фокусом. 461 Эксцентриситет
эллипса e=1/2, центр его совпадает с началом
координат, одна из директрис дана уравнением x=16.
Вычислить расстояние от точки M1
эллипса с абсциссой, равной –4, до
фокуса, одностороннего с данной директрисой. 462 Определить точки
эллипса
правого фокуса равно 14. 463 Определить точки
эллипса
левого фокуса равно 2,5. 464 Через фокус эллипса
большой оси. Определить расстояния от точек
пересечения этого перпендикуляра с эллипсом до
фокусов. 465 Составить
уравнения эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если даны: 465.1 точка М1(
и его малая полуось b=3; 465.2 точка М1(2;
-2) эллипса и его большая полуось
a=4; 465.3 точки М1(4;
М2(
и его эксцентриситет e=2/3; 465.5 точка М1(2;
-5/3) эллипса и его эксцентриситет
e=2/3; 465.6 точка М1(8;
12) эллипса и расстояние r1=20
от нее до левого фокуса. 465.7 точка М1(
и расстояние между его директрисами, равное 10. 466 Определить
эксцентриситет e эллипса, если: 466.1 его малая ось видна
из фокусов под углом 600; 466.2 отрезок между
фокусами виден и вершин малой оси под прямым
углом; 466.3 расстояние между
директрисами в три раза больше расстояния между
фокусами; 466.4 отрезок
перпендикуляра, опущенного из центра эллипса на
его директрису, делится вершиной эллипса
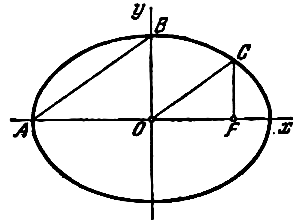
пополам. 467 Через фокус F
эллипса проведен перпендикуляр к его большой оси
(см. рис.). Определить, при каком значении
эксцентриситета эллипса отрезки
параллельны.
уравнение эллипса с полуосями a, b и центром C(x0, y0), если
известно, что оси симметрии эллипса параллельны
осям координат. 469 Эллипс касается оси
абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4).
Составить уравнение этого эллипса, зная, что его
оси симметрии параллельны координатным осям. 470 Точка С(-3; 2)
является центром эллипса, касающегося обеих
координатных осей. Составить уравнение этого
эллипса, зная, что его оси симметрии параллельны
координатным осям. 471 Установить, что
каждое из следующих уравнений определяет эллипс,
и найти координаты его центра С, полуоси,
эксцентриситет и уравнения директрис: 471.1
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже. 472.1
уравнение эллипса, зная, что: 473.1 его большая ось
равна 26 и фокусы суть F1(-10; 0), F2(14;0);
473.2 его малая ось равна
2 и фокусы суть F1(-1; -1), F2(1;
1);
473.3 его фокусы суть F1(-2; 3/3), F2(2; -3/2) и
эксцентриситет e=
473.4 его фокусы суть F1(1; 3), F2(3; 1) и
расстояние между директрисами равно
474 Составить уравнение эллипса, если известны его
эксцентриситет
фокус F (-4; 1) и уравнение соответствующей
директрисы
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(-4; 1) и уравнение
соответствующей директрисы
на эллипсе, фокус которого F(-1; -4), а
соответствующая директриса дана уравнением
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(3; 0) и уравнение
соответствующей директрисы
-1) лежит на эллипсе, фокус
которого F(1; 0), а соответствующая директриса дана
уравнением
-1) является концом малой оси
эллипса, фокусы которого лежат на прямой
уравнение этого эллипса, зная его эксцентриситет
e=
пересечения прямой
пересечения прямой
пересечения прямой
расположена прямая относительно эллипса:
пересекает ли, касается или проходит вне его,
если прямая и эллипс заданы следующими
уравнениями: 483.1
каких начениях m прямая
эллипса. 485 Вывести условие,
при котором прямая
уравнение касательной к эллипсу
точке M1(x1; y1). 487 Доказать, что
касательные к эллипсу
в концах одного и того же диаметра, параллельны.
(Диаметром эллипса называется его хорда,
проходящая через его центр). 488 Составить
уравнения касательных к эллипсу
прямой
уравнения касательных к эллипсу
к прямой
прямой
ближайшую к прямой
этой прямой. 492 Из точки А(10/3; 5/3)
проведены касательные к эллипсу
их уравнения. 493 Из точки С(10; -8)
проведены касательные к эллипсу
уравнение хорды, соединяющей точки касания. 494 Из точки Р(-16; 9)
проведены касательные к эллипсу
расстояние d от точки Р до хорды эллипса,
соединяющей точки касания. 495 Эллипс проходит
через точку А(4; -1) и касается прямой
уравнение этого эллипса при условии, что его оси
совпадают с осями координат. 496 Составить
уравнение эллипса, касающегося двух прямых
условии, что его ося совпадают с осями координат. 497 Доказать, чо
произведение расстояний от центра эллипса до
точки пересечения любой его касательной с
фокальной осью и до основания перпендикуляра,
опущенного из точки касания на фокульную ось,
если величина постоянная, равная квадрату
большой полуоси эллипса. 498 Доказать, что
произвдение расстояний от фокусов до любой
касательной к эллипсу равно квадрату малой
полуоси. 499 Прямая
эллипса, фокусы которого находятся в точках F1(-3;
0), F2(3; 0). Составить
уравнение этого эллипса. 500 Составить
уравнение эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
эллипсу
прямая, касающаяся эллипса в некоторой точке М,
составляет равные углы с фокальными радиусами F1M, F2M и проходит
вне угла F1MF2. 502 Из левого фокуса
эллипса
Ox направлен луч света. Известно, что
до эллипса, луч на него отразился. Составить
уравнение прямой, на которой лежит отраженный
луч. 503 Определить точки
пересечения эллипсов
эллипсы
в четырех точках, лежающих на окружности с
центром в начале координат, определить радиус R
этой окружности. 505 Плоскости
полуоси эллипса, полученного проектированием на
плоскость
плоскости
полуось которого равна 6, является проекцией
окружности радиуса R=12. Опредилть угол
эллипс и окружность. 507 Направляющей
круглого цилиндра является окружность радиуса
R=8. Определить полуоси эллипса, полученного в
сечении этого цилиндра плоскостью, наклоненной к
его оси под уголом
круглого цилиндра является окружность радиуса R=
цилиндра нужно его пересечь плоскостью, чтобы в
сечении получить эллипс с большой полуосью a=2. 509 Равномерным
сжатием (или равномерным растяжением) плоскости
к оси абсцисс называется такое преобразование
точек плоскости, при котором произвольная точка
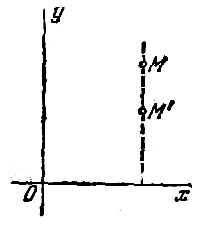
M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что
x’=x, y’=qy, где q>0 – постоянная, называемая
коэффициентом равномерного сжатия. Аналогично
рпи помощи уравнения x’=qx, y’=y определяется
равномерное сжатия плоскости к оси Oy (рис. 2).
Определить, в какую линию преобразуется
окружность
равномерного сжатия плоскости к оси абсцисс q=4/5.
равномерного сжатия плоскости к оси Oy равен 3/4.
Определить уравнение линии, в которую при таком
сжатии преобразуется эллипс
линии, в которую преобразуется эллипс
равномерных сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ox и Oy равны соответственно 4/3 и
6/7. 512 Определить
коэффициент q равномерного сжатия плоскости к
оси Ox, при котором эллипс
в эллипс
коэффициент q равномерного сжатия плоскости к
оси Oy, при котором эллипс
в эллипс
коэффициенты q1, q2 двух последовательных равномерных
сжатий плоскости к осям Ox и Oy, при которых
эллипс

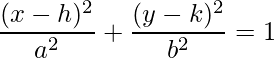


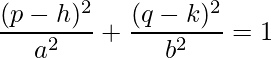
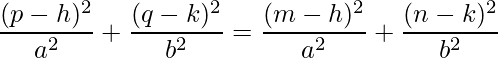
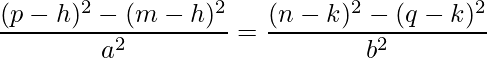
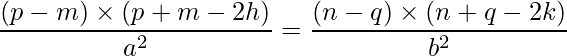
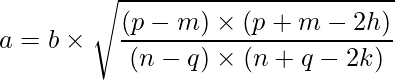
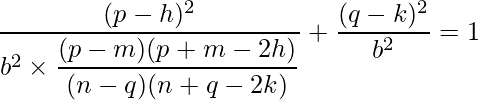
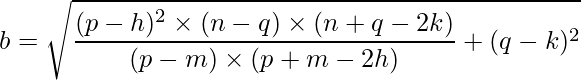
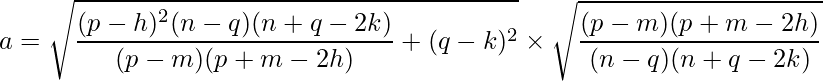
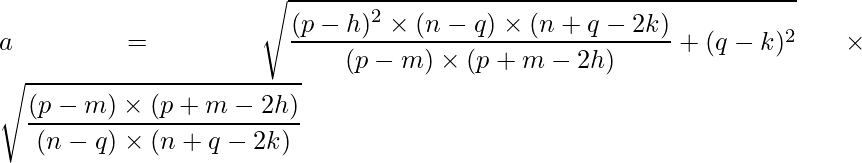
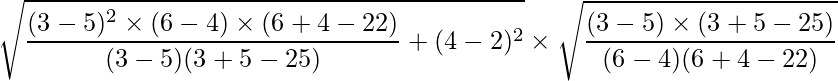
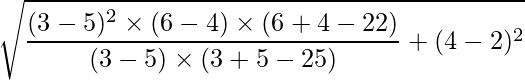
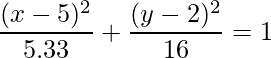
 and (p, q) = (9, 2) and (m, n) = (7, 6) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation
and (p, q) = (9, 2) and (m, n) = (7, 6) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation 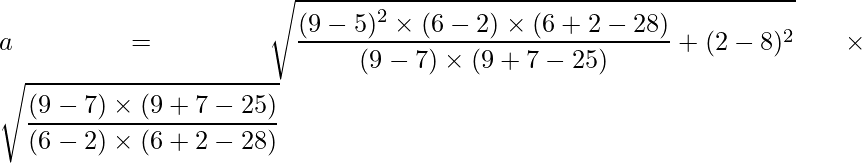
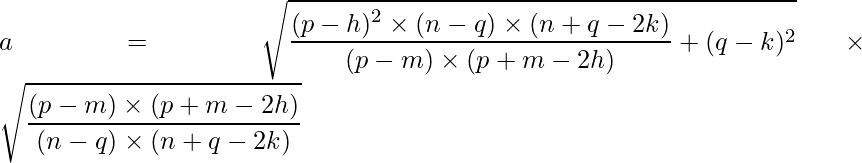
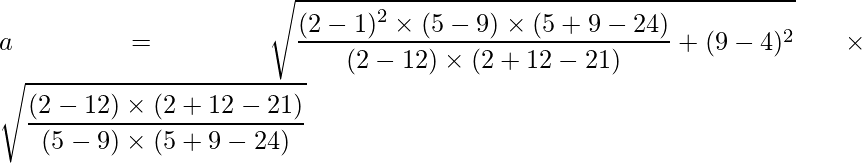
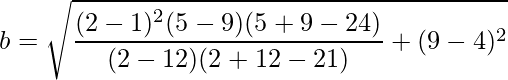
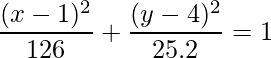
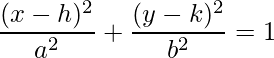
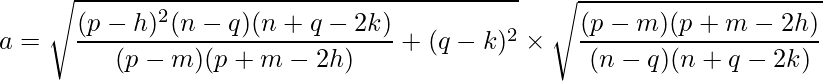
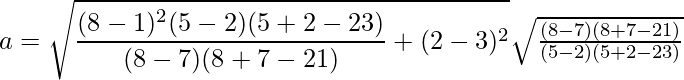

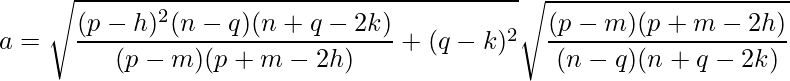
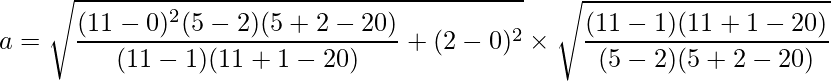
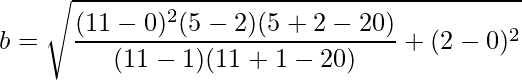






;M_2(3sqrt{1.5}:sqrt{2}))