фокусы которого лежат на оси абсцисс симметрично
относительно начала координат, зная, кроме того,
что:
и 2;
равна 10, а расстояние между фокусами 2c=8;
24, а расстояние между фокусами 2c=10;
его фокусами 2c=6 и эксцентриситет e=3/5.
равна 20, а эксцентриситет e=3/5.
10, а эксцентриситет e=12/13;
его директрисами равно 5 и расстояние между
фокусами 2c=4;
равна 8, а расстояние между директрисами равно 16;
6, а расстояние между директрисами равно 13;
его директрисами равно 32 и e=1/2.
уравнение эллипса, фокусы которого лежат на оси
ординат симметрично начала координат, зная,
кроме того, что:
соответственно 7 и 2;
равна 10, а расстояние между фокусами 2c=8;
его фокусами 2c=24 и эксцентриситет e=12/13.
16, а эксцентриситет e=3/5.
его фокусами 2c=6 и расстояние между директрисами
равно 50/3;
его директрисами равно 32/3 и эксцентриситет e=3/4.
каждого из следующих эллипсов:
;
;
;
;
;
;
;
;
;
.
. Найти его полуоси, фокусы,эксцентриситет, уравнения директрис.
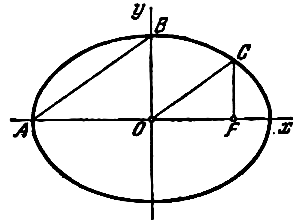
четырехугольника, две вершины которого лежат в
фокусах эллипса
, а две другиесовпадают с концами его малой оси.
. Найти его полуоси, фокусы,эксцентриситет, уравнения директрис.
четырехугольника, две вершины которого лежат в
фокусах эллипса
, две другие лежат сконцами его малой оси.
расстояние от фокуса F(c; 0) эллипса
доодносторонней с этим фокусом директрисы.
циркулем, построить фокусы эллипса
(считая,что изображены оси координат и задана масштабная
единица).
найти точку, абсцисса которых равна–3.
из точек A1(-2; 3), A2(2; -2), A3(2;
-4), A4(-1; 3), A5(-4; -3), A6(3; -1), A7(3;
-2), A8(2; 1), A9(0; 15), A10(0; -16) лежат на эллипсе
, какиевнутри и какие вне его.
линии опеределяются следующими уравнениями.
Изобразить эти линии на чертеже.
;
;
;
.эллипса e=2/3, фокальный радиус точки М эллипса
равен 10. Вычислить расстояние от точки М до
односторонней с этим фокусом директрисы.
эллипса e=2/5, расстояние от точки эллипса до
директрисы равно 20. Вычислить расстояние от
точки М до фокуса, односторонней с этой
директрисой.
; составитьуравнения прямых, на которых лежат фокальные
радиусы точки М1.
459
точка M1(-4; 2,4) лежит
на эллипсе
, определить фокальные радиусы точкиМ1.
эллипса e=1/3, центр его совпадает с началом
координат, один из фокусов (-2; 0). Вычислить
расстояние от точки М1 эллипса с абсциссой, равной 2, до
директрисы, односторонней с данным фокусом.
эллипса e=1/2, центр его совпадает с началом
координат, одна из директрис дана уравнением x=16.
Вычислить расстояние от точки M1
эллипса с абсциссой, равной –4, до
фокуса, одностороннего с данной директрисой.
эллипса
, расстояние которых доправого фокуса равно 14.
эллипса
, расстояние которых долевого фокуса равно 2,5.
проведен перпендикуляр к егобольшой оси. Определить расстояния от точек
пересечения этого перпендикуляра с эллипсом до
фокусов.
уравнения эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если даны:
; 2) эллипсаи его малая полуось b=3;
-2) эллипса и его большая полуось
a=4;
) иМ2(
; 3) эллипса;
; -1) эллипсаи его эксцентриситет e=2/3;
-5/3) эллипса и его эксцентриситет
e=2/3;
12) эллипса и расстояние r1=20
от нее до левого фокуса.
; 2) эллипсаи расстояние между его директрисами, равное 10.
эксцентриситет e эллипса, если:
из фокусов под углом 600;
фокусами виден и вершин малой оси под прямым
углом;
директрисами в три раза больше расстояния между
фокусами;
перпендикуляра, опущенного из центра эллипса на
его директрису, делится вершиной эллипса
пополам.
эллипса проведен перпендикуляр к его большой оси
(см. рис.). Определить, при каком значении
эксцентриситета эллипса отрезки
и 
будутпараллельны.
уравнение эллипса с полуосями a, b и центром C(x0, y0), если
известно, что оси симметрии эллипса параллельны
осям координат.
абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4).
Составить уравнение этого эллипса, зная, что его
оси симметрии параллельны координатным осям.
является центром эллипса, касающегося обеих
координатных осей. Составить уравнение этого
эллипса, зная, что его оси симметрии параллельны
координатным осям.
каждое из следующих уравнений определяет эллипс,
и найти координаты его центра С, полуоси,
эксцентриситет и уравнения директрис:
;
;
.линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
;
;
;
.уравнение эллипса, зная, что:
равна 26 и фокусы суть F1(-10; 0), F2(14;0);
473.2
2 и фокусы суть F1(-1; -1), F2(1;
1);
473.3
эксцентриситет e=
.473.4
расстояние между директрисами равно
.474
эксцентриситет
,фокус F (-4; 1) и уравнение соответствующей
директрисы
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(-4; 1) и уравнение
соответствующей директрисы
.на эллипсе, фокус которого F(-1; -4), а
соответствующая директриса дана уравнением
. Составить уравнение этого эллипса.уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(3; 0) и уравнение
соответствующей директрисы
.-1) лежит на эллипсе, фокус
которого F(1; 0), а соответствующая директриса дана
уравнением
. Составить уравнение этого эллипса.-1) является концом малой оси
эллипса, фокусы которого лежат на прямой
. Составитьуравнение этого эллипса, зная его эксцентриситет
e=
.пересечения прямой
и эллипса 
.пересечения прямой
и эллипса 
.пересечения прямой
и эллипса 
.расположена прямая относительно эллипса:
пересекает ли, касается или проходит вне его,
если прямая и эллипс заданы следующими
уравнениями:
, 
;
, 
;
, 
.каких начениях m прямая
:
;эллипса.
при котором прямая
касается эллипса 
.уравнение касательной к эллипсу
в еготочке M1(x1; y1).
касательные к эллипсу
, проведенныев концах одного и того же диаметра, параллельны.
(Диаметром эллипса называется его хорда,
проходящая через его центр).
уравнения касательных к эллипсу
, параллельныхпрямой
.уравнения касательных к эллипсу
, перпендикулярныхк прямой
.
параллельнопрямой
и вычислить расстояние d между ними.
найти точку М1,ближайшую к прямой
, и вычислить расстояние d от точки М1 доэтой прямой.
проведены касательные к эллипсу
. Составитьих уравнения.
проведены касательные к эллипсу
. Составитьуравнение хорды, соединяющей точки касания.
проведены касательные к эллипсу
. Вычислитьрасстояние d от точки Р до хорды эллипса,
соединяющей точки касания.
через точку А(4; -1) и касается прямой
. Составитьуравнение этого эллипса при условии, что его оси
совпадают с осями координат.
уравнение эллипса, касающегося двух прямых
, 
, приусловии, что его ося совпадают с осями координат.
произведение расстояний от центра эллипса до
точки пересечения любой его касательной с
фокальной осью и до основания перпендикуляра,
опущенного из точки касания на фокульную ось,
если величина постоянная, равная квадрату
большой полуоси эллипса.
произвдение расстояний от фокусов до любой
касательной к эллипсу равно квадрату малой
полуоси.
касаетсяэллипса, фокусы которого находятся в точках F1(-3;
0), F2(3; 0). Составить
уравнение этого эллипса.
уравнение эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
эллипсу
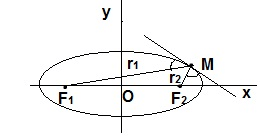
и его малая полуось b=2.прямая, касающаяся эллипса в некоторой точке М,
составляет равные углы с фокальными радиусами F1M, F2M и проходит
вне угла F1MF2.
эллипса
под тупым углом 
к осиOx направлен луч света. Известно, что
. Дойдядо эллипса, луч на него отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
пересечения эллипсов
, 
.эллипсы
, 
(
) пересекаютсяв четырех точках, лежающих на окружности с
центром в начале координат, определить радиус R
этой окружности.
и 
образуют угол 
=300. Опредлитьполуоси эллипса, полученного проектированием на
плоскость
окружности радиуса R=10,лежащей наплоскости
.полуось которого равна 6, является проекцией
окружности радиуса R=12. Опредилть угол
между плоскостями, в которых лежатэллипс и окружность.
круглого цилиндра является окружность радиуса
R=8. Определить полуоси эллипса, полученного в
сечении этого цилиндра плоскостью, наклоненной к
его оси под уголом
=300.круглого цилиндра является окружность радиуса R=
. Определить, под каким углом к осицилиндра нужно его пересечь плоскостью, чтобы в
сечении получить эллипс с большой полуосью a=2.
сжатием (или равномерным растяжением) плоскости
к оси абсцисс называется такое преобразование
точек плоскости, при котором произвольная точка
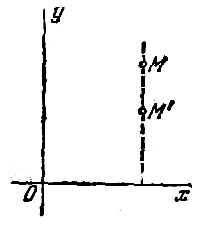
M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что
x’=x, y’=qy, где q>0 – постоянная, называемая
коэффициентом равномерного сжатия. Аналогично
рпи помощи уравнения x’=qx, y’=y определяется
равномерное сжатия плоскости к оси Oy (рис. 2).
Определить, в какую линию преобразуется
окружность
, если коэффициентравномерного сжатия плоскости к оси абсцисс q=4/5.
равномерного сжатия плоскости к оси Oy равен 3/4.
Определить уравнение линии, в которую при таком
сжатии преобразуется эллипс
.линии, в которую преобразуется эллипс
при двух последовательныхравномерных сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ox и Oy равны соответственно 4/3 и
6/7.
коэффициент q равномерного сжатия плоскости к
оси Ox, при котором эллипс
преобразуетсяв эллипс
.коэффициент q равномерного сжатия плоскости к
оси Oy, при котором эллипс
преобразуетсяв эллипс
.коэффициенты q1, q2 двух последовательных равномерных
сжатий плоскости к осям Ox и Oy, при которых
эллипс
преобразуется в окружность 
.Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
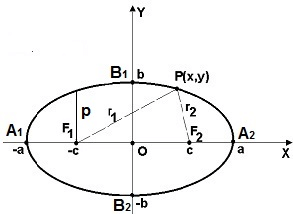
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и — расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно Согласно определению эллипса имеем Из треугольников и по теореме Пифагора найдем
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Раскроем разность квадратов Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение Вновь возведем обе части равенства в квадрат Раскрывая все скобки в правой части уравнения, получим Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим Введем обозначение для разности, стоящей в скобках Уравнение принимает вид Разделив все члены уравнения на получаем каноническое уравнение эллипса: Если то эллипс вытянут вдоль оси Ох, для противоположного неравенства — вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
- т.е. точками пересечения эллипса с осью абсцисс будут точки
- т.е. точками пересечения эллипса с осью ординат будут точки (Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если то параметр а называется большой, а параметр b — малой полуосями эллипса.
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси
Если и эллипс вырождается в окружность. Если и эллипс вырождается в отрезок
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр Зная параметр с, можно вычислить малую полуось эллипса Следовательно, каноническое уравнение заданного эллипса имеет вид:
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса а третья вершина — в центре окружности
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса а малая полуось Так как то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса Итак, Окружность: Выделим полные квадраты по переменным Следовательно, центр окружности находится в точке О(-5; 1).
Построим в декартовой системе координат треугольник Согласно школьной формуле площадь треугольника равна Высота а основание Следовательно, площадь треугольника равна:
Эллипс в высшей математике
где и —заданные положительные числа. Решая его относительно , получим:
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное по абсолютной величине меньше , подкоренное выражение положительно, корень имеет два значения. Каждому значению , удовлетворяющему неравенству соответствуют два значения , равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси . Так же можно убедиться в том, что оно симметрично и относительно оси . Поэтому ограничимся рассмотрением только первой четверти.
При , при . Кроме того, заметим, что если увеличивается, то разность уменьшается; стало быть, точка будет перемещаться от точки вправо вниз и попадет в точку . Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
Полученная линия называется эллипсом. Число является длиной отрезка , число —длиной отрезка . Числа и называются полуосями эллипса. Число эксцентриситетом.
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом (рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось примем прямую пересечения плоскостей, стало быть, ось будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости возьмем окружность радиуса с центром в начале координат, ее уравнение .
Пусть точка лежит на этой окружности, тогда ее координаты удовлетворяют уравнению .
Обозначим проекцию точки на плоскость буквой , а координаты ее—через и . Опустим перпендикуляры из и на ось , это будут отрезки и . Треугольник прямоугольный, в нем , ,, следовательно, . Абсциссы точек и равны, т. е. . Подставим в уравнение значение , тогда cos
а это есть уравнение эллипса с полуосями и .
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей с коэффициентами деформации, равными
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам (х, у, z) с текущими координатами х, у, г, причем
Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в раз, если , и увеличиваются в раз, если и т. д.
Подставляя эти формулы в уравнение (1), будем иметь
где Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Величины называются полуосями эллипсоида; удвоенные величины называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Составьте уравнение эллипса с фокусами на оси ОХ если он проходит через точки (6 ; 4) и (8 ; 3)?
Алгебра | 10 — 11 классы
Составьте уравнение эллипса с фокусами на оси ОХ если он проходит через точки (6 ; 4) и (8 ; 3).
Канонический вид уравнения эллипса с фокусами на оси абсцисс :
x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1.
Пусть 1 / a ^ 2 = t, 1 / b ^ 2 = f.
Из системы уравнений :
f = 1 / b ^ 2 = 1 / 25, откуда b = 5,
t = 1 / a ^ 2 = 1 / 100, откуда а = 10.
Тогда уравнение эллипса запишется в виде
x ^ 2 / 100 + y ^ 2 / 25 = 1.
Составьте уравнение касательной к кривой y = x — 1 / x в точках её пересечения с осью OX?
Составьте уравнение касательной к кривой y = x — 1 / x в точках её пересечения с осью OX.
Составьте линейное уравнение с двумя неизвестными, график которого проходит через точку ( — 1 ; — 2) и начало координат?
Составьте линейное уравнение с двумя неизвестными, график которого проходит через точку ( — 1 ; — 2) и начало координат.
Составьте уравнение касательной к кривой y = x — 1 / x в точках ее пересечения с осью ОХ?
Составьте уравнение касательной к кривой y = x — 1 / x в точках ее пересечения с осью ОХ.
Составить каноническое уравнение эллипса, если даны его вершины (0, 3) и (0, — 3) и расстояние между фокусами, равное 8?
Составить каноническое уравнение эллипса, если даны его вершины (0, 3) и (0, — 3) и расстояние между фокусами, равное 8.
Напишите уравнение прямой, которая : а) проходит через начало координат и точку А(0, 6 ; — 2, 4) ; б) пересекает оси координат в точках В(0 ; 4) и С( — 2, 5 ; 0)?
Напишите уравнение прямой, которая : а) проходит через начало координат и точку А(0, 6 ; — 2, 4) ; б) пересекает оси координат в точках В(0 ; 4) и С( — 2, 5 ; 0).
Построить эллипс если F1, 2 принадлежит оси OX т?
Построить эллипс если F1, 2 принадлежит оси OX т.
М ( — 4 ; корень из 21 ) принадлежит эллипсу Е = 3 / 4.
Прямая проходит через две точки ( — 2 ; 6), (5 ; — 1) ?
Прямая проходит через две точки ( — 2 ; 6), (5 ; — 1) .
Составьте уравнение прямой.
Составьте уравнение прямой, проходящей через точки А( — 1 : — 2) и В (2 : 10)?
Составьте уравнение прямой, проходящей через точки А( — 1 : — 2) и В (2 : 10).
Найдите координаты точки пересечения данной прямой с осью ординат.
‚ М Найти точки пересечения окружности — + — п 4 ‘ с осями координат Составьте уравнение окружность касающейся осей и проходящей через точку К?
‚ М Найти точки пересечения окружности — + — п 4 ‘ с осями координат Составьте уравнение окружность касающейся осей и проходящей через точку К.
Составьте уравнение вида у = кх + в график которого проходит через точки а(4 ; 4) и в( — 2 ; — 5)?
Составьте уравнение вида у = кх + в график которого проходит через точки а(4 ; 4) и в( — 2 ; — 5).
На этой странице сайта, в категории Алгебра размещен ответ на вопрос Составьте уравнение эллипса с фокусами на оси ОХ если он проходит через точки (6 ; 4) и (8 ; 3)?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
http://www.evkova.org/ellips
http://algebra.my-dict.ru/q/4015887_sostavte-uravnenie-ellipsa-s-fokusami-na/
Эллипсом называют плоскую кривую, состоящую из точек, сумма расстояний которых от двух определённых точек плоскости является неизменной, строго заданной величиной, равной суммарной длине двух больших его полуосей (2a). Эти две точки называются фокусами эллипса.
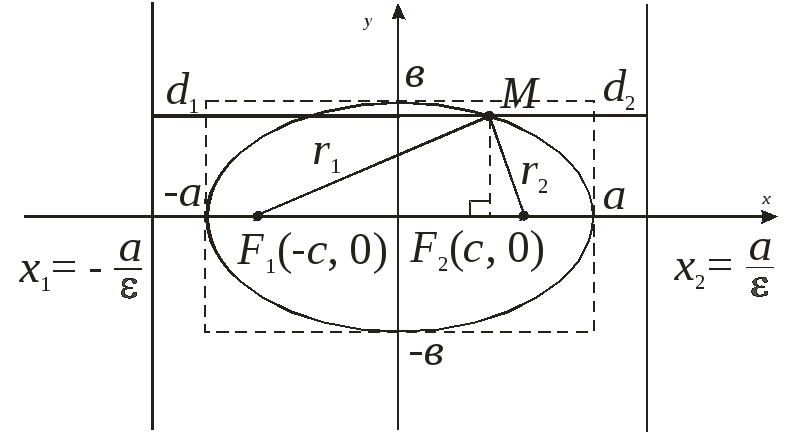
F1 и F2 – фокусы эллипса;
а – большая полуось;
b – малая полуось
с – фокусное расстояние
Теорема
Фокусное расстояние эллипса и его полуоси связаны между собой соотношением [boldsymbol{a^{2}=b^{2}+c^{2}}]
Доказательство:
Когда точка M на линии эллипса находится на его пересечении с вертикальной осью, из теоремы Пифагора выходит, что
r1 + r2 = 2*√(b2 + c2)
Когда точка M пересекает горизонтальную ось
r1 + r2 = а – c + а + c
По определению эллипса r1 + r 2 = const
Это позволяет после приравнивания получить
a² = b² + c²
r1 + r2 = 2а
Что и требовалось доказать.
Уравнение эллипса
Каноническим уравнением эллипса называют уравнение [boldsymbol{1=left(x^{2} / a^{2}right)+left(y^{2} / b^{2}right)}]
Доказательство уравнения:
Введём прямоугольную декартову систему координат.
Сначала докажем, что координаты любой из точек на эллипсе удовлетворяют приведённому каноническому уравнению. Затем покажем, что любое из решений уравнения является координатами точки, лежащей на линии эллипса. Из этого будет следовать удовлетворение каноническому уравнению только тех точек, которые лежат на поверхности эллипса. Опираясь на этот факт и на определение эллипса можно будет однозначно сделать вывод, что написанное нами уравнением является каноническим уравнением или, как ещё говорят, основной формулой эллипса.
- Пусть М(х, у) будет точкой эллипса, т.е. сумму её фокальных радиусов примем равной 2а, т. е. r1 + r2 = 2a.
С помощью формулы расстояния, разделяющего две точки на координатной плоскости, можно легко найти фокальные радиусы точки M.r1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Из этих уравнений получаем √[(x + c)2 + y2] + √[(x — c)2 + y2] = 2a
Если один из корней перенести в правую часть и возвести всё в квадрат, то придём к выражению
(x + c)2 + y2 = 4a2 – 4a√[(x — c)2 + y2] + (x – c)2 + y2После сокращения приходим к 2xc = 4a2 – 4a√[(x-c)2 + y2] – 2xc
После приведения подобных членов, сокращения на 4 и уединения радикала будем иметь
a√[(x-c)2 + y2] = a2 – xcВозведём это выражение в квадрат
a2(x-c)2 + a2 y2 = a4 – 2a2xc + x2c2Если раскрыть скобки и сократить на -2a2 xc, то a2x2 + a2c2 + a2y2 = a4 + x2c2
Отсюда легко получить (a2 – c2)x2 + a2y2 = a2(a2 – c2)
Из этого следует, что b2x2 +a2y2 = a2b2 - Пусть некоторые числа (x, y) полностью удовлетворяют каноническому уравнению
1 = (x2/a2) + (y2/b2)
Пусть нам дана точка M(x,y) на координатной плоскости 0xy
Из канонического уравнения следует, что Y2 = b2(1- x2/a2)
Если это равенство подставить в выражение для фокальных радиусов, которые имеет точка M, то можно получить
r1 = √[(x + c)2 +y2] = √[x2 +2xc + c2 +b2 – b2x2/a2] = √[x2(1 – b2/a2) + 2xc +c2 +b2] =
= √[x2(a2 – b2)/a2 + 2xc + (c2 + b2)] = √[x2 (c2/a2) + 2xc +a2] = √[x(c/a) +a]2 = |a +xε|
т. е. r1 = |a +xε|
Отношение 2с/2a = c/a = ε называется эксцентриситетом эллипса. Оно у него всегда меньше 1.
То же самое просчитываем для r2.
Т. к. x2/a2 больше или равно 1 или x больше или равно большой полуоси (a), то можно сделать вывод о справедливости неравенства a≥|x|> |x|* ε = |xε|
Отсюда явно следует, что a+-|xε|>0 или a+-xε > 0 и r1 = a + xε, r2 = a — xε
Из полученных равенств выходит, что r1 + r2 = 2a, это значит, что точка M однозначно является точкой эллипса. Это нам и нужно было доказать.
Свойства эллипса
- У эллипса имеются две взаимно перпендикулярные оси симметрии.
Доказательство:
Переменные x и y в уравнение эллипса входят лишь во второй степени. Это означает, что если точка M с координатами (x,y) ему принадлежит, то и точки М1 (-x, y) и M2 (x, -y) тоже принадлежат ему. Легко проверить, что указанные координаты удовлетворяют каноническому уравнению эллипса. M1 симметрична по отношению к оси X, а M2 по отношению к оси Y. Получается, что у эллипса есть две взаимно перпендикулярные точки симметрии. - У эллипса есть центр симметрии.
Доказательство:
Если координаты точки М(x,y) будут удовлетворять уравнению эллипса, то и точка
N (–x; –y) ему тоже будет удовлетворять. M и N симметричны по отношению к началу координат. Это как раз и означает, что у эллипса имеется центр симметрии. - Эллипс пересекает каждую из осей в двух точках.
Доказательство:
Возьмём произвольную точку эллипса M(x,y). Расстояние этой точки до фокусов будетr1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Теперь давайте рассмотрим выражение
(x+-c)2 + y2 = x2 +- 2xc + c2+ y2 =
= x2 +- 2xc + a2 – b2 +y2 = x2 +- 2xc+ a2 — b2 + b2(1-x2/a2) =
= (a2 – b2)*x2/a2 +-2xc +a2 = c2*x2/a2+-2xa(c/a) + a2 = (a +c*x/a)2Эксцентриситет эллипса, как сказано ранее, меньше 1. Т. к. |x|≤ a, то a – εx > 0. Поэтому
F1M = a + εx и F2M = a – εx. Напомним, что ε – это эксцентриситет эллипса.
А теперь несколько свойств эллипса без доказательств.
- Эллипс можно получить, сжав окружность.
- Если через эллипс проходят две прямые, то отрезок, концами которого являются середины отрезков созданных при пересечении прямых, обязательно пересекает середину, центр эллипса.
- Угол, созданный касательной к эллипсу и его радиусом, проходящем через фокусы указанной геометрической фигуры, в любых случаях пересекает середину эллипса.
- Уравнение касательной к эллипсу в точке М, имеющей координаты xM и yM
1 = (x*xM)/a2 + (y*yM)/b2 - Эволюта эллипса представляет собой астероиду, растянутую вдоль его малой оси.
- Угол между касательной к эллипсу и одним его фокальным радиусом (r1) имеет ту же величину, что и угол, разделяющий касательную и другой фокальный радиус (r2) фигуры.
Как построить эллипс
Расскажем, как построить эллипс по его большой и малой полуосям и с помощью циркуля.
Построение эллипса по его большой и малой осям
Считается самым простым, не требующим серьёзных навыков.
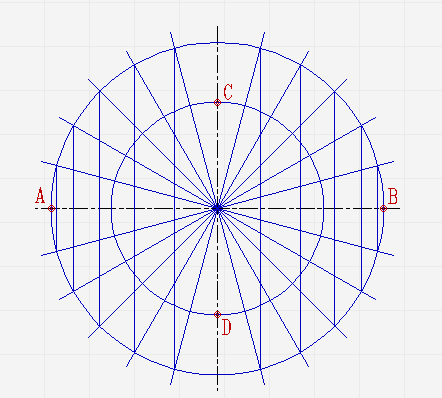
Проведите две перпендикулярные оси;
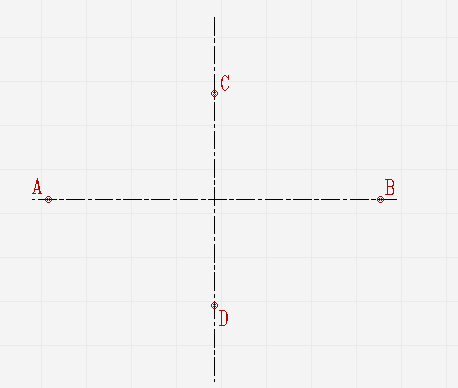
От места пересечения осей на вертикальной отложите верх и вниз отрезки. Они будут составлять малую ось эллипса. На горизонтальной отложите отрезки вправо и влево. Из них будет состоять большая ось;
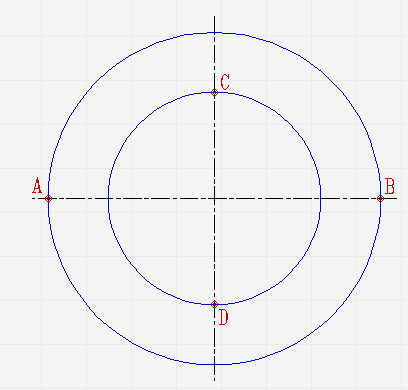
Проведите две концентрические окружности. Одну диаметром AB, диаметром CD;
Проведите ещё диаметры в различных направлениях;
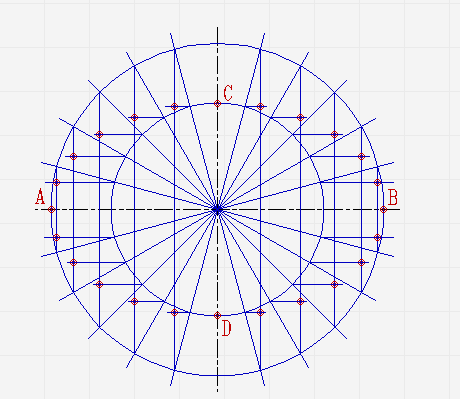
В местах, где лучи соприкасаются с окружностями, проведите линии параллельные малой и большой осям эллипса, пока они не пересекутся в точках, которые принадлежат эллипсу;
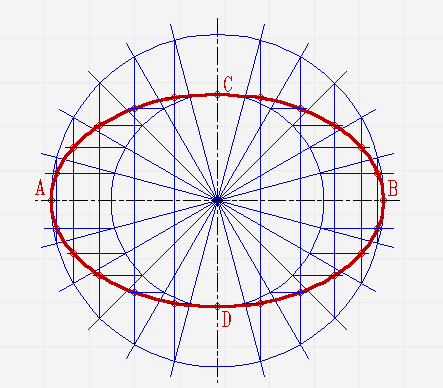
Соедините полученные точки плавной линией.
Нет времени решать самому?
Наши эксперты помогут!
Как построить эллипс с помощью циркуля
Во многом здесь всё аналогично предыдущему способу, поэтому перегружать текст иллюстрациями не будем.
Порядок действий следующий:
- Проведите две перпендикулярные линии. Они будут осями эллипса, а точка их пересечения центром геометрической фигуры;
- Определитесь с величиной большой и малой полуосей, если их значения не заданы в условии задачи;
- Установите раствор циркуля на длину большой полуоси (a). Поместите циркуль в точку O и отметьте на одной из линий две точки, P1 и P2. Установите раствор циркуля на длину малой полуоси. Опять поместите его в точку O и отметьте на другой из линий ещё две точки, обозначьте их как Q1 и Q2. Отрезки P1P2 и Q1Q2 будут большой и малой полуосями будущего эллипса;
- Установите раствор циркуля на величину a. Поместите циркуль в точке Q1 или Q2. После этого обозначьте циркулем на отрезке P1P2 точки F1 и F2. Это будут фокусы фигуры.
- Отметьте на P1P2 любую точку и обозначьте её T. Поставьте в этой точке циркуль и измерьте этим инструментом расстояние до P1. Затем начертите окружность данного радиуса из фокуса F1. После этого нужно сделать ещё одну окружность с радиусом величиной с расстояние от T до P2, но уже с центром из F2;
- Отметьте точки, в которых пересекаются обе окружности. Повторяйте процедуру, описанную в предыдущем пункте с новыми точками, отмечаемыми на отрезке P1P2;
- Соедините точки пересечения окружностей сплошной линией, когда построите их достаточное количество. Так у вас получится построить фигуру эллипс с помощью циркуля.
Примеры решения задач
Задача 1
Эллипс задан уравнением 16x2 + 25y2 = 400. Требуется найти большую и малую полуоси эллипса, координаты его фокусов и эксцентриситет.
Решение:
Разделим полученное уравнение на 400. Этим мы приведём его к виду
(x2/25) + (y2/16) =1. Большая полуось равна 5, корню квадратному из 25, а малая 4, корню квадратному из 16.
Из соотношения a² = b² + c² находим фокусное расстояние. Оно равно
c=+-√(a2 – b2) = +-√(25-16) = +-3, а значит координаты фокусов будут
F1(-3,0) и F2 (3,0). Эксцентриситет ε = с/a = 3/5.
Ответ: a = 5, b = 4, ε = 3/5.
Задача 2
Выяснить, является ли эллипсом линия, заданная как
9x2 + 25y2 – 225 = 0
Преобразуем данное нам уравнение к каноническому виду. Для этого:
Перенесём 225 в правую сторону
9x2 + 25y2 = 225
Поделим обе части этого уравнения на 225
(9x2/225) + (25y2/225) = 1
Сократим дроби и получим
(x2/25) + (y2/9) = 1
Как видим, нам удалось получить каноническое уравнение эллипса в чистом виде, т. е. исходное уравнение представляет собой эллипс, что и требовалось выяснить.
Ответ: 9x2 + 25y2 – 225 = 0 является уравнением эллипса.
Задача 3
Составить каноническое уравнение эллипса если расстояние между фокусами равно 8, а большая ось 10.
Решение:
Если большая ось равняется 10, значит полуось будет 5.
Если фокусное расстояние равно 8, то число c из координат фокусов будет 4.
Далее нужно подставить и вычислить
4 = √(25-b2)
Возведём это уравнение в квадрат
16 = 25 – b2
Перенесём b2 влево, а 16 вправо
b2 = 25 – 16 =9
В результате этих не сложных преобразований и вычислений получим каноническое уравнение
(x2/25) + (y2/9) = 1
Ответ: (x2/25) + (y2/9) = 1.
Задача 4
Получить каноническое уравнение эллипса, если его эксцентриситет равен 12/13, а большая полуось равна 26.
Решение:
Из уравнения эксцентриситета ε = с/a находим, что a = 13, а величина с = 12. Далее нужно вычислить квадрат длины меньшей полуоси
c = √(169 – b2)
Возведём обе части уравнения в квадрат
c2 = 169 – b2
Отсюда
b2 = 169 – 144 = 25
Далее остаётся лишь составить каноническое уравнение
(x2/169) + (y2/25) = 1
Ответ: (x2/169) + (y2/25) = 1
Задача 5
Найти фокусы у эллипса, который задан уравнением (x2/25) + (y2/16) = 1
Решение:
Нам нужно найти число с, которое определяет первые координаты фокусов
c = √(25-16) =3
Фокусы заданного эллипса будут равны
F1(-3,0) и F2(3,0).
Ответ: F1(-3,0) и F2(3,0).
Составьте уравнение эллипса с фокусами на оси ОХ если он проходит через точки (6 ; 4) и (8 ; 3).
На этой странице сайта, в категории Алгебра размещен ответ на вопрос
Составьте уравнение эллипса с фокусами на оси ОХ если он проходит через точки (6 ; 4) и (8 ; 3)?. По уровню сложности вопрос рассчитан на учащихся
10 — 11 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.
Найди верный ответ на вопрос ✅ «Составьте уравнение эллипса с фокусами на оси ОХ если он проходит через точки (6; 4) и (8; 3) …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Составьте уравнение эллипса с фокусами на оси ОХ если он проходит через точки (6; 4) и (8; 3)