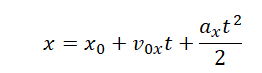Как составить уравнение движения с ускорением - AvtoShod.ru

Ускоре́ние
— производная скорости по времени,
векторная величина, показывающая,
насколько изменяется вектор скорости
точки (тела) при её движении за единицу
времени (т.е. ускорение учитывает не
только изменение величины скорости, но
и её направления). Например, вблизи Земли
падающее на Землю тело, в случае, когда
можно пренебречь сопротивлением воздуха,
увеличивает свою скорость примерно на
9,8 м/с каждую секунду, то есть, его
ускорение равно 9,8 м/с².

Единицей
ускорения служит метр в секунду за
секунду.

Если
вектор

не меняется со временем, движение
называют равноускоренным. При
равноускоренном движении справедливы
формулы:

Частным случаем равноускоренного
движения является случай, когда ускорение
равно нулю в течение всего времени
движения. В этом случае скорость
постоянна, а движение происходит по
прямолинейной траектории (если скорость
тоже равна нулю, то тело покоится),
поэтому такое движение называют
прямолинейным и равномерным.

6. Движение с постоянным ускорением. Единица ускорения.

Единицей
ускорения служит метр в секунду за
секунду.

7. Скорость при движении с постоянным ускорением

Прямолинейное
движение с постоянным ускорением
называют равноускоренным, если модуль
скорости увеличивается со временем,
или равнозамедленным, если он уменьшается.

Примером
ускоренного движения может быть падение
цветочного горшка с балкона невысокого
дома. В начале падения скорость горшка
равна нулю, но за несколько секунд она
успевает вырасти до десятков м/с. Примером
замедленного движения является движение
камня, брошенного вертикально вверх,
скорость которого сначала большая, но
потом постепенно уменьшается до нуля
в верхней точке траектории. Если
пренебречь силой сопротивления воздуха,
то ускорение в обоих этих случаях будет
одинаково и равно ускорению свободного
падения, которое всегда направлено
вертикально вниз, обозначается буквой
g и равно примерно 9,8 м/с2.

Ускорение
свободного падения, g вызвано силой
притяжения Земли. Эта сила ускоряет все
тела, движущиеся по направлению к земле,
и замедляет те, которые движутся от неё.

Чтобы
найти уравнение для скорости при
прямолинейном движении с постоянным
ускорением, будем считать, что в момент
времени t=0 тело имело начальную скорость
v0. Так как ускорение a постоянно, то для
любого момента времени t справедливо
следующее уравнение:

где
v – скорость тела в момент времени t,
откуда после нетрудных преобразований
получаем уравнение
для
скорости
при движении с постоянным ускорением:
v = v0 + at

8. Уравнения движения с постоянным ускорением.

где
v – скорость тела в момент времени t,
откуда после нетрудных преобразований
получаем уравнение для скорости при
движении с постоянным ускорением: v
= v0 + at

Чтобы
вывести уравнение для пути, пройденного
при прямолинейном движении с постоянным
ускорением, построим сначала график
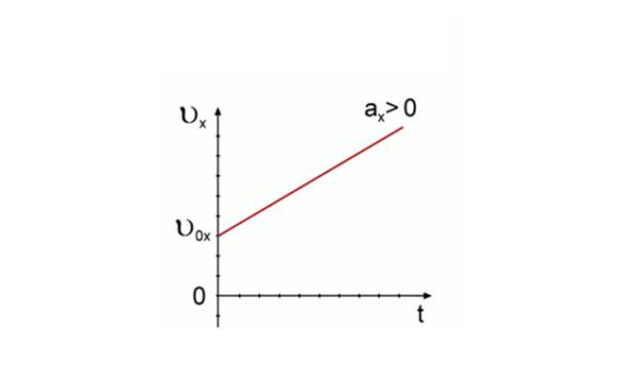
зависимости скорости от времени (5.1).
Для a>0 график этой зависимости изображён
слева на рис.5 (синяя прямая). Как мы
установили в §3, перемещение, совершённое
за время t, можно определить, если
вычислить площадь под кривой зависимости
скорости от времени между моментами
t=0 и t. В нашем случае фигура под кривой,
ограниченная двумя вертикальными
линиями t=0 и t, представляет собой трапецию
OABC, площадь которой S, как известно, равна
произведению полусуммы длин оснований
OA и CB на высоту OC:

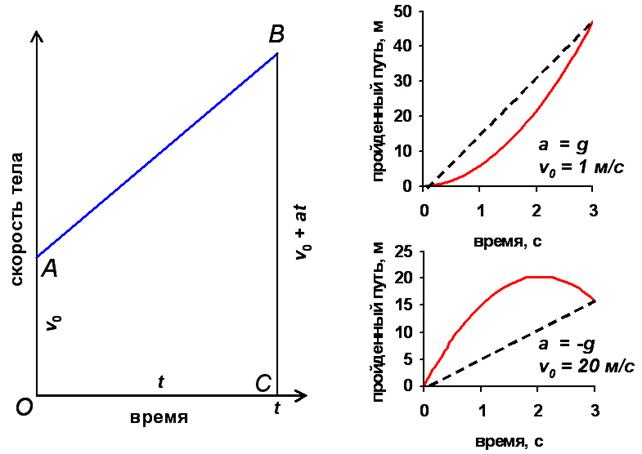
Как
видно на рис.5, OA = v0, CB= v0 + at, а OC = t. Подставляя
эти значения в (5.2), получаем следующее
уравнение для перемещения S, совершённого
за время t при прямолинейном движении
с постоянным ускорением a при начальной
скорости v0 :

Легко
показать, что формула (5.3) справедлива
не только для движения с ускорением
a>0, для которого она была выведена, но
и в тех случаях, когда a<0. На рис.5 справа
красными линиями показаны графики
зависимости S при положительных (верх)
и отрицательных (низ) значениях a,
построенные по формуле (5.3) для различных
величин v0. Видно, что в отличие от
равномерного движения (см. рис. 3), график
зависимости перемещения от времени
является параболой, а не прямой, показанной
для сравнения пунктирной линией.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение и формулы

Уравнение координаты — зависимость координаты тела от времени:

x = x(t)

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с². Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
Построить уравнение вида x₁ = x₂.
Найти время встречи двух тел t_встр.
Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с² без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Построить графики x1(t) и x2(t).
Найти точку пересечения графиков.
Пустить перпендикуляр из этой точки к оси ОХ.
Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с² и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с², достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Задание EF18609

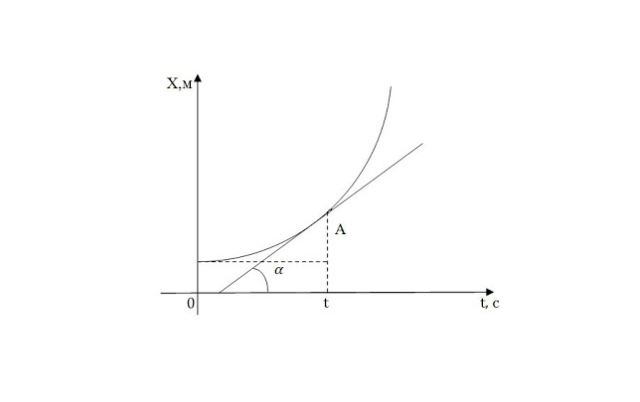
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

Определить характер движения материальной точки.
Записать уравнение координаты материальной точки.
С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение

Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид:

Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)?

Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17682

Мимо остановки по прямой улице с постоянной скоростью проезжает грузовик. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с², и догоняет грузовик на расстоянии 150 м от остановки. Чему равна скорость грузовика?

Алгоритм решения

Записать исходные данные.
Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
Выразить скорость грузовика из уравнения его движения.
Записать уравнение движения мотоциклиста.
Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
Подставить время в формулу скорости грузовика и вычислить ее.

Решение

Исходные данные:

Координата встречи грузовика и мотоциклиста: x = 150 м.
Время запаздывания мотоциклиста: t_запазд = 5 с.
Ускорение, с которым мотоциклист начал движение: a = 3 м/с².

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет вид:

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 14.8k

Источник

Равноускоренное прямолинейное движение. Ускорение

Равноускоренное движение
Ускорение
Уравнение скорости и график скорости при равноускоренном прямолинейном движении
Определение пути и перемещения по графику скорости
Задачи

п.1. Равноускоренное движение

Если тело начинает двигаться из состояния покоя, оно набирает скорость не мгновенно, а в течение некоторого времени. Аналогично происходит при торможении: тело останавливается не сразу, а теряя скорость постепенно.

Движение, во время которого скорость тела за любые равные промежутки времени увеличивается на одну и ту же величину, называют равноускоренным.

Примеры равноускоренного движения:

скатывание велосипеда с горки, скатывание санок с горки;
старт и торможение автомобиля, автобуса, трамвая, поезда;
падение на землю камня, ракеты, метеорита.

Это интересно
Время разгона от 0 до 100 км/ч – одна из основных характеристик современных автомобилей.

п.2. Ускорение

Ускорение – это векторная величина, которая равна отношению изменения скорости тела к интервалу времени, за которое это изменение произошло: $$ overrightarrow{a}=frac{overrightarrow{v}-overrightarrow{v_0}} {t} $$ где (overrightarrow{v_0}) — начальная скорость тела, (overrightarrow{v}) — скорость тела в момент времени (t).

В системе СИ (см. §2 данного справочника) скорость измеряется в метрах в секунду, а время – в секундах. Поэтому:

Единицей ускорения в системе СИ является метр на секунду в квадрате (1 м/с²) – ускорение равноускоренного прямолинейного движения, при котором тело за 1 с увеличивает скорость на 1 м/с.

При описании прямолинейного движения мы переходим от векторов к проекциям на ось ОХ (см. §8 данного справочника).

Назовем проекцией вектора ускорения (overrightarrow{a}) на параллельную ему ось координат OX величину (a_x=pm|overrightarrow{a}|=pm a).
Знак проекции определяется следующим правилом:

если направление вектора (overrightarrow{a}) совпадает с направлением оси OX, то (a_x=agt 0)
если направление вектора (overrightarrow{a}) противоположно направлению оси OX, то (a_x=-alt 0)

При равноускоренном прямолинейном движении проекция ускорения равна: $$ a_x=frac{v_x-v_{0x}}{t} $$ где (v_{0x}) — проекция начальной скорости, (v_x) — проекция скорости в момент времени (t).

п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении

Для проекции скорости на ось ОХ в произвольный момент времени можем записать: $$ v_x(t)=v_{0x}+a_x t $$ Сравним полученное уравнение с уравнением прямой (y(x)=kx+b ) (см. §38 справочника по алгебре для 7 класса).
В уравнении скорости роль углового коэффициента (k) играет проекция ускорения (a_x), а роль свободного члена (b) – начальная скорость (v_{0x}).

В осях (t) и (v) график (v_x(t)=v_{0x}+a_x t) является прямой.
Эта прямая:

возрастает, если (a_xgt 0)
убывает, если (a_xlt 0)
постоянна (параллельна оси (t)), если (a_x=0)

Пример построения графика скорости
1-й участок пути. Пусть автомобиль начал движение из состояния покоя с ускорением 4 м/с². Направим ось ОХ в направлении ускорения и получим уравнение скорости: $$ v_{0x}=0, a_x=4frac{text{м}}{c^2}, v_x(t)=0+4t=4t $$ Через 5 с скорость автомобиля станет равной (v_x(5)=4cdot 5=20) м/с.
2-й участок пути. Пусть автомобиль, набрав эту скорость, проехал с ней без ускорения в течение 10 с. На этом участке уравнение скорости: $$ a_{x}=0, v_x(t)=20frac{text{м}}{c}, 5 cleq tlt 15 c $$ Скорость не меняется, автомобиль движется прямолинейно равномерно.
3-й участок пути. Наконец, на последнем участке пути, автомобиль тормозил с ускорением 5 м/с² до полной остановки. Тогда уравнение скорости на этом участке: $$ v_{0x}=20frac{text{м}}{c}, a_x=5frac{text{м}}{c^2}, v_x(t)=20-5t $$ Проекция ускорения при торможении отрицательна. Скорость станет равна 0 через 4 с после начала торможения, автомобиль остановится.

Опишем полностью движение на всех участках: $$ v_x(t)= begin{cases} 4t, 0leq tlt 5\ 20, 5leq tlt 15\ 20-5t, 15leq tleq 19 end{cases} $$ И построим график:

Участок AB соответствует разгону автомобиля от 0 до 20 м/с, участок BC — равномерному движению со скоростью 20 м/с, участок CD — торможению от 20 м/с до 0.

п.4. Определение пути и перемещения по графику скорости

В §10 данного справочника мы рассматривали неравномерное прямолинейное движение, которое можно разбить на отдельные равномерные участки. Для такого движения путь равен сумме модулей площадей участков, определенных по графику скорости. А перемещение также равно сумме площадей, но уже с учетом знака.
Этот подход можно расширить на любое прямолинейное движение.

Пусть график скорости при прямолинейном движении разбит на (n) участков, площади которых легко определить (треугольники, прямоугольники, трапеции). Тогда:
Весь пройденный путь равен сумме модулей площадей всех участков: $$ s=|s_1|+|s_2|+…+|s_n| $$ Величина перемещения по оси ОХ равна сумме площадей всех участков с учетом знака: $$ triangle x=s_1+s_2+…s_n $$ Конечная координата равна: (x_к=x_0+triangle x)

Пример определения пути и перемещения по графику скорости
Для построенного выше графика скорости автомобиля получаем следующие участки:
1) ΔABE, его площадь равна $$ s_1=frac12 AEcdot BE=frac12cdot 5cdot 20=50 (м) $$ 2) прямоугольник EBCF, его площадь равна $$ s_2=EFcdot BE=10 cdot 20=200 (м) $$ 3) ΔCFD, его площадь равна $$ s_2=frac12 FDcdot GF=frac12cdot 4cdot20=40 (м) $$ Весь пройденный путь: $$ s=s_1+s_2+s_3=50+200+40=290 (м) $$ Скорость автомобиля все время оставалась положительной (направление движения не менялось), поэтому величина перемещения равна пройденному пути: $$ triangle x=s=290 (м) $$

п.5. Задачи

Задача 1. За 1 мин автобус увеличил скорость с 28,8 км/ч до 72 км/ч. Найдите его ускорение, постройте график зависимости скорости от времени.

Дано:
(t=1 мин=60 с)
(v_0=28,8 км/ч=8 м/с)
(v=72 км/ч=20 м/с)
__________________
(a-?)
Как перевести км/ч в м/с – см. §7 данного справочника.

Направим ось ОХ по направлению движения автобуса. Автобус направления движения не меняет, и проекции ускорения и скорости все время положительны и по величине равны значениям величин: $$ a_x=a, v_x=v $$ Поэтому ускорение равно: $$ a=frac{v-v_0}{t} $$ Получаем: $$ a=frac{20-8}{60}=0,2 left(frac{м}{c^2}right) $$ Уравнение зависимости скорости от времени: begin{gather*} v(t)=v_0+at\ v(t)=8+0,2t end{gather*} График:

Ответ: 0,2 м/с²

Задача 2. Поезд двигался прямолинейно равномерно со скоростью 18 км/ч, а в процессе торможения – равноускоренно и остановился через 10 с. Найдите модуль ускорения. Постройте график зависимости скорости от ускорения, найдите пройденный поездом путь за все время торможения.

Дано:
(v_0=18 км/ч=5 м/с)
(v=0)
(t=10 с)
__________________
(a, s-?)
Направим ось ОХ по направлению скорости (v_0). Тогда проекция ускорения: $$ a_x=frac{v-v_0}{t}, a_x=frac{0-5}{10}=-0,5 (м/с^2) $$ Проекция при торможении отрицательна.
Величина (модуль) ускорения: $$ a=|a_x|=0,5 м/c^2 $$ Зависимость скорости от времени: begin{gather*} v(t)=v_0+a_x t\ v(t)=5-0,5t end{gather*} График:

Пройденный путь равен площади треугольника ΔABC: $$ s=frac12 ACcdot BC=frac12cdot 5cdot 10=25 (м) $$ Ответ: 0,5 м/с²; 25 м

Задача 3*. С каким ускорением двигался автомобиль, если его скорость выросла с 36 км/ч до 72 км/ч на пути длиной 600 м? Постройте график зависимости скорости от времени, найдите время движения и путь с помощью графика, проверьте полученное значение пути.

Дано:
(v_0=36 км/ч=10 м/с)
(v=72 км/ч=20 м/с)
(s=600 м)
__________________
(a-?, t-?)
Ускорение равно: (a=frac{v-v_0}{t}). Откуда время равно: (t=frac{v-v_0}{a})
Средняя скорость на всем пути: (v_{cp}=frac{v_0+v}{2})
Весь путь: $$ s=v_{cp}t=frac{v_0+v}{2}cdotfrac{v-v_0}{a}=frac{v^2-v_0^2}{2a} $$ Значит, ускорение равно: $$ a=frac{v^2-v_0^2}{2s} $$ Подставляем: $$ a=frac{20^2-10^2}{2cdot 600}=0,25 left(frac{м}{c^2}right) $$ Уравнение зависимости скорости от времени: begin{gather*} v(t)=v_0+at\ v(t)=10+0,25t end{gather*} График:

Скорость достигает значения (v=20 м/с) в момент времени (t=40 с).
Значит, время движения 40 с.

Путь по графику скорости равен площади четырехугольника ABCD. begin{gather*} S_{ABCD}=S_{ABE}+S_{AECD}=frac12 AEcdot EB+AEcdot AD=frac12cdot 40cdot 10+40cdot 10=200+400=600 (м)\ s=600 м end{gather*} Найденное значение пути совпадает с условием задачи. Все параметры движения найдены верно.
Ответ: 0,25 м/с²; 40 c

Источник

Уравнение равноускоренного движения

4.5

Средняя оценка: 4.5

Всего получено оценок: 335.

Обновлено 4 Августа, 2021

4.5

Средняя оценка: 4.5

Всего получено оценок: 335.

Обновлено 4 Августа, 2021

Одним из достаточно частых движений, изучаемых физикой, является равноускоренное движение. Примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха ещё пренебрежительно мало. Поговорим на эту тему, рассмотрим уравнения равноускоренного движения для координаты и скорости.

Движение с ускорением

Если материальная точка при движении изменяет скорость, то говорят, что она движется с ускорением. Большинство движений вокруг изменяют скорость, а значит, происходят с ускорением.

Если скорость — это быстрота изменения расстояния, то ускорение — это быстрота изменения скорости. Ускорение $overrightarrow a$ равно отношению изменения скорости $overrightarrow v — overrightarrow {v_0} $ ко времени этого изменения $t$:

$$overrightarrow a = {overrightarrow v – overrightarrow {v_0} over t }$$

Рис. 1. Пример равноускоренного движения.

Уравнение скорости равноускоренного движения

Движение, при котором ускорение остаётся постоянным, называется равноускоренным. При этом нет разницы, увеличивается скорость или уменьшается. Из определения ускорения можно получить уравнение скорости при равноускоренном движении:

$$overrightarrow v = overrightarrow {v_0} + overrightarrow a t $$

Можно видеть, что скорость при равноускоренном движении линейно зависит от времени. Следовательно, график скорости представляет собой прямую, пересекающую ось ординат в точке $v_0$, имеющую наклон вверх для положительного ускорения и вниз для отрицательного. Величина наклона тем больше, чем больше модуль ускорения.

Рис. 2. График скорости равноускоренного движения.

Уравнение координаты равноускоренного движения

Уравнение координаты при равноускоренном движении можно получить из графика скорости, учитывая, что координата движения равна площади, ограниченной графиком скорости.

Фигура, ограниченная графиком скорости, представляет собой трапецию, высота которой равна $t$, одно основание равно $v_0$, второе основание равно $v$.

Из геометрии известно, что площадь трапеции равна полусумме оснований, умноженной на высоту. Величину $v$ при этом можно выразить из вышеприведённой формулы. То есть:

$$x={v+v_0over 2}t={2v_0+atover 2}t$$

Переходя к векторной форме и учитывая, что в начальный момент времени координата была равна $overrightarrow {x_0}$, окончательно получаем:

$$overrightarrow x=overrightarrow {x_0}+overrightarrow {v_0} t+ {overrightarrow at^2over 2}$$

Координата при равноускоренном движении имеет квадратичную зависимость от времени, график координаты является параболой.

Рис. 3. График координаты равноускоренного движения.

Что мы узнали?

Равноускоренное движение — это движение, при котором ускорение остаётся постоянным. Уравнение скорости при равноускоренном движении представляет собой прямую зависимость от времени, его график является наклонной прямой. Уравнение координаты равноускоренного движения имеет квадратичную зависимость от времени, его графиком является парабола.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.5

Средняя оценка: 4.5

Всего получено оценок: 335.

А какая ваша оценка?

Источник

Мы с вами изучили равномерное прямолинейное движение, то есть
движение, при котором точка за любые равные промежутки времени совершает
одинаковые перемещения. Но, как мы уже отмечали, при реальном движении тел их
скорости обычно меняются или по модулю, или по направлению, или же одновременно
и по модулю, и по направлению. Например, когда автомобиль трогается с места,
его скорость постепенно возрастает. А при торможении на перекрёстке, наоборот, —
уменьшается.

При вращательном движении скорость любой точки дисков
электрофорной машины изменяется лишь по направлению (конечно же, при условии,
что число оборотов в единицу времени не изменяется).

Наконец, при выстреле из пушки под некоторым углом к
горизонту скорость ядра будет изменяться как по модулю, так и по направлению.

При этом очевидно, что в рассмотренных нами примерах
изменение скорости может происходит как очень быстро, так и достаточно
медленно.

Физическая векторная величина, характеризующая быстроту
изменения скорости, называется ускорением.

Давайте вспомним, как определяется ускорение точки. Для этого
рассмотрим её неравномерное движение вдоль некоторой криволинейной траектории. Пусть
в некоторый момент времени t она
занимает положение М и имеет скорость υ. А спустя некоторый
промежуток времени Δt₁ —
положение М₁ и скорость υ₁.

Найдём изменение скорости точки за это время как
геометрическую разность векторов конечной и начальной скоростей и укажем эту
разность на рисунке:

Если теперь мы с вами разделим вектор изменения скорости на
промежуток времени, в течение которого это изменение произошло, то тем самым получим
так называемый вектор среднего ускорения точки:

Он направлен точно так же, как и вектор изменения скорости.

Но как же нам определить ускорение точки в положении М?
Для этого будем уменьшать рассматриваемые промежутки времени и находить вектор
изменения скорости для каждого случая. Из полученного рисунка видим, что вектор
изменения скорости, а следовательно, и вектор среднего ускорения, уменьшается
по модулю и при этом меняется его направление. В конце концов промежуток времени
станет так мал, что можно будет пренебречь изменением скорости точки за это
время. Следовательно, при стремлении промежутка времени к нулю отношение будет
стремиться к своему некоторому предельному значению.

Физическая векторная величина, равная пределу отношения изменения
скорости к промежутку времени, в течение которого это перемещение произошло,
при стремлении промежутка времени к нулю, называется мгновенным ускорением (или
просто ускорением):

Важно запомнить, что вектор ускорения направлен так же, как и
вектор изменения скорости при стремлении промежутка времени к нулю. И в
общем случае вектор ускорения не совпадает с направлением вектора скорости, а
составляет с ним некоторый угол.

Как мы уже видели, при неравномерном движении по
криволинейной траектории скорость точки непрерывно меняется по модулю и
направлению. Поэтому вектор ускорения часто называют полным ускорением и
представляют в виде суммы двух ускорений:

Первое ускорение называется тангенциальным (или
касательным), так как направлено оно по касательной к траектории движения. Его
модуль характеризует изменение модуля скорости:

Второе ускорение всегда направлено перпендикулярно вектору
мгновенной скорости и поэтому называется нормальным (нормаль — это
перпендикуляр) или центростремительным. Его модуль характеризует
изменение скорости по направлению:

А вектор центростремительного ускорения в любой момент
времени направлен к центру кривизны траектории.

Конечно же движение точки может происходить как с постоянным,
так и с переменным ускорением. Так, если отношение изменения скорости к
промежутку времени в течение которого это изменение произошло одинаково для
любого интервала времени, то говорят, что точка движется с постоянным
ускорением. А движение точки называют равноускоренным движением:

Из формулы видно, что если скорость и промежуток времени
выражены в единицах СИ, то единицей измерения ускорения является метр на
секунду в квадрате (м/с²).

Также из формулы следует, что за единицу ускорения в СИ
принимается ускорение такого равноускоренного движения, при котором за 1 с
скорость точки изменяется на 1 м/с.

Теперь давайте выясним, как зависит скорость точки от времени
при её равноускоренном движении. Итак, пусть в начальный момент времени t₀ скорость точки равнялась ,
а в момент времени t — .

Тогда ускорение точки равно изменению вектора скорости к
промежутку времени, за который это изменение произошло:

Если начальный момент времени принять равным нулю, то из этого
уравнения легко получить формулу для определения скорости точки в любой момент
времени при её равноускоренном движении — уравнение скорости:

Таким образом, чтобы определить скорость точки в произвольный
момент времени, необходимо знать её начальную скорость и ускорение.

На практике при вычислениях скорости мы будем пользоваться
формулами, в которые входят не векторы, а их проекции на соответствующие
координатные оси:

Из записанных формул видно, что при равноускоренном движении
скорость точки линейно зависит от времени. Значит, график скорости представляет
собой прямую линию, наклонённую к оси времени под некоторым углом. При этом чем
больше ускорение точки, тем больший угол с осью времени составляет график
проекции скорости.

Теперь посмотрим на прямую 3. Что можно сказать о движении тела
в этом случае?

Во-первых, очевидно, что за промежуток времени от нуля до t₁ проекция скорости была положительна.

Во-вторых, скорость точки уменьшалась и в момент времени,
равный t₁ она стала равной нулю. Точка
пересечения графика скорости с осью времени называется точкой поворота. В
ней направление скорости меняется на противоположное, после чего тело начинает
двигаться равноускоренно.

Теперь давайте вспомним, что основной задачей механики
является определение положения точки в любой момент времени. Получим уравнения,
которые позволяют это сделать для равноускоренного движения. Для примера
рассмотрим случай, когда проекция начальной скорости и ускорения положительны.
По аналогии со случаем равномерного прямолинейного движения логично
предположить, что проекция перемещения, совершённого телом за время t,
будет равна площади фигуры, ограниченной графиком, осью времени и
перпендикуляром, восставленным к графику из точки t. В данном случае эта
фигура — трапеция.

Для доказательства этого предположения рассмотрим очень малый
промежуток времени Δt внутри
выбранного интервала времени. По аналогии с мгновенной скоростью, если выбранный
промежуток времени достаточно мал, то изменением скорости за это время можно
пренебречь. То есть движение точки можно считать равномерным. Значит, проекция
перемещения за это время будет равна площади этого маленького прямоугольника.
При этом очевидно, что на такие узкие полоски мы можем разбить всю площадь
фигуры под графиком скорости

Тогда, согласно рисунку, проекция перемещения при
равноускоренном движении определяется площадью трапеции. Площадь же трапеции,
как известно из геометрии, равна произведению полусуммы её оснований на высоту.
В нашем случае длина одного из оснований численно равна проекции начальной
скорости точки, второго — проекции скорости через время t.
Высота же трапеции численно равна времени.

Теперь вспомним, что по определению проекция перемещения
численно равна разности конечной и начальной координат точки:

Тогда после небольших математических преобразований получим
формулу для определения координаты точки при её равноускоренном движении:

Важно помнить, что в формулу входят проекции начальной
скорости и ускорения точки. А они могут быть как положительными, так и
отрицательными. Координата начального положения точки также может быть больше
или меньше нуля,

Если движение точки происходит в пространстве, то для
определения оставшихся двух координат используют уравнения, имеющие аналогичной
вид:

Записанные нами формулы называются кинематическими
уравнениями движения точки в координатной форме. Они
применимы для описания как прямолинейного, так и криволинейного движения.

В общем виде кинематические уравнения движения можно записать
с помощью одного векторного уравнения:

Теперь для закрепления материала решим с вами одну небольшую
задачку. Итак, на рисунке представлен график зависимости скорости точки от
времени. Определите, в какой момент времени координата точки станет равной 30
м, если в момент начала наблюдения её координата равнялась –6 м. Определите
скорость точки в этот момент времени.

Источник

6. Движение с постоянным ускорением. Единица ускорения.

7. Скорость при движении с постоянным ускорением

8. Уравнения движения с постоянным ускорением.

Совместное движение двух тел

Равноускоренное прямолинейное движение. Ускорение

п.1. Равноускоренное движение

п.2. Ускорение

п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении

п.4. Определение пути и перемещения по графику скорости

п.5. Задачи

Уравнение равноускоренного движения

Движение с ускорением

Уравнение скорости равноускоренного движения

Уравнение координаты равноускоренного движения

Что мы узнали?

Тест по теме

Оценка доклада

Не пропустите также: