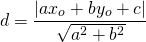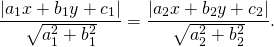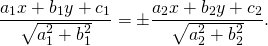Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Расстояние от точки (xo;yo) до прямой ax+by+c=0 определяется по формуле
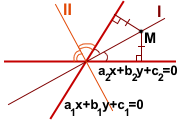
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0, находится от этих прямых на одинаковом расстоянии, то есть
Это равенство можно записать в виде
Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.
Пример.
Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.
Решение:
В формулу уравнения биссектрис подставляем данные прямых:
Ответ: 3x+3y-23=0; 21x-21y-37=0.
П
имеем две прямые:
,
её
вектор нормали
=
и :
,
её
вектор нормали
=
.
Будем предполагать, что векторы
и
всегда располагаются внутри одного из
углов, образуемых пересекающимися
прямыми (векторы
и
–
свободные!).
В общем случае прямые при пересечении
образуют один угол острый, а второй
тупой. Возникает классическая
задача:
найти уравнение биссектрисы тупого и
острого углов.
Существует
несколько способов решения задачи. В
каждом из них на первом шаге устанавливается
факт: векторы
и
располагаются в области тупого угла
или в области острого. На этот вопрос
достаточно просто отвечает скалярное
произведение векторов: а)
∙
> 0 – векторы расположены в области
тупого угла; б)
∙
< 0 – векторы расположены в области
острого угла. Далее рассмотрим наиболее
интересные способы решения поставленной
задачи.
Способ–1.
Пусть векторы
и
располагаются в области тупого угла.
Учтём, что для точек, расположенных
внутри тупого угла с векторами
и
отклонения от прямых
и
положительно: >0,
>0.
Это значит, что для точек биссектрисы
тупого угла выполняется равенство:
или: =
. (
)
Если бы
теперь нужно было построить биссектрису
острого угла, то уравнение нужно записать
в виде: =
–. (
)
Если бы
векторы
и
располагались в области острого угла,
то биссектриса острого угла определялась
бы выражением ,
а биссектриса тупого –
выражением .
Способ–2.
В этом случае примем схему решения
задачи: а) находим точку
пересечения прямых
и ;
б) находим направление биссектрис ;
в) проводим прямую через заданную точку
в заданном направлении.
Для
определения направления биссектрис
построим единичные векторы:
и
,
затем суммы:
=
+
–определяет
направление биссектрисы угла, содержащего
векторы
,
;
=
–
–определяет
направление биссектрисы угла, смежного
первому.
И
угловой коэффициент вектора
,
строим биссектрису угла, содержащего
векторы
,
;
если использовать угловой коэффициент
вектора
,
построим биссектрису смежного угла.
Замечание: на
самом деле, достаточно найти только
один вектор:
для первой биссектрисы он играет
роль направляющего вектора, а для второй
– роль вектора нормали.
Способ–3.
Воспользуемся уравнением пучка прямых:
и вектором
,
который будет играть роль направляющего
или нормального, в зависимости от
конкретного задания.
Интересно рассмотреть
один и тот же пример, решив его сразу
всеми тремя способами: это позволит
сравнить их трудоёмкости!
☺☺
Пример
3–27:
Составить уравнение биссектрисы тупого
угла, образованного прямыми::
;
:
.
Р
Имеем:
=(3,–4)
и
=(12,
5). Вычислим:
∙
=
>0
– векторы расположены в области
тупого угла. Далее рассмотрим решения
поставленной задачи тремя способами.
Способ–1.
Воспользуемся формулой
при условии равенства отклонений
произвольной точки
биссектрисы от
и :
=
,
откуда получаем уравнение биссектрисы
выделенного угла: .
С
В этом случае примем схему решения
задачи: а) находим точку
,
в которой пересекаются прямые
и ;
б) находим направление биссектрис
;
в) проводим прямую через заданную точку
в заданном направлении.
Координаты
точки
находим из системы уравнений:
→
=
.
Для
определения направления искомой
биссектрисы
построим единичные векторы
=
(3,–4)
и
=
(12,5),
затем вектор суммы:
=
–
=–
(3,11)
– нормаль биссектрисы угла, содержащего
векторы
,
.
Примем:
=(3,11).
Тогда уравнение биссектрисы запишем
в виде: 3+11
=0,
или .
Способ–3.
Воспользуемся уравнением пучка :
+
=0,
или в виде:
=0
и направляющим вектором
=(11,–3)
.
Вектору
соответствует угловой коэффициент
=–
.
Тогда:
=
=
=–
.
Получаем уравнение искомой биссектрисы:
.
Ответ:
искомая
биссектриса: .
Замечание: трудоёмкость
рассмотренных способов различна;
одновременное использование разных
способов полезно наблюдением одинакового
окончательного результата.
☻
Соседние файлы в папке ЛА и АГ пособие
- #
- #
- #
- #
- #
- #
Уравнение биссектрисы угла
Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Расстояние от точки (xo;yo) до прямой ax+by+c=0 определяется по формуле
По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0, находится от этих прямых на одинаковом расстоянии, то есть
Это равенство можно записать в виде
Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.
Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.
В формулу уравнения биссектрис подставляем данные прямых:
Составить уравнение биссектрис углов образованных двумя прямыми
Составить уравнение биссектрисы острого угла между прямыми
Решение
Найдем точку пересечения двух прямых
Направляющий вектор первой прямой есть 



Направляющий вектор биссектрисы угла равен сумме нормированных направляющих векторов сторон
Так как точка 
Задание 8
Составить уравнение плоскости, которая проходит через точку 
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9987 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Расстояние от точки (xo;yo) до прямой ax+by+c=0 определяется по формуле

Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0, находится от этих прямых на одинаковом расстоянии, то есть
Это равенство можно записать в виде
Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.
Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.
В формулу уравнения биссектрис подставляем данные прямых:
Что ты хочешь узнать?
Ответ
Проверено экспертом
Даны прямые: 11x-2y+5=0 и 4x+8y-7=0
Уравнения биссектрис углов между прямыми Ax + By + C = 0 и A₁x + B₁y + C₁ = 0:
Знак + или – выбирается в зависимости от того, нужно уравнение биссектрисы острого или тупого углов.
Подставив коэффициенты заданных прямых в приведенную формулу, получим уравнения биссектрис:
В приближённом варианте у ≈ 1,3541х + 1,3772.
Задача 34288 Составить уравнение биссектрисы угла.
Условие
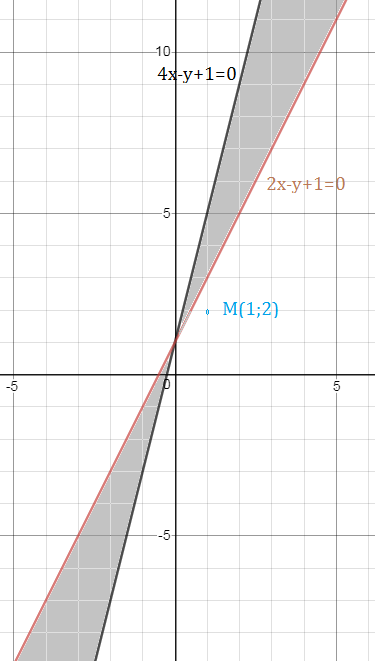
Составить уравнение биссектрисы угла между прямыми l1(4x–y+1=0) и l2(2x–y+1=0) смежного с углом, содержащим точку M(1;2)
Решение
Пусть точка Р(х;у) лежит на биссектрисе угла между прямыми.
Это значит, что расстояние d_(1) это точки до прямой l_(1) равно
расстоянию d_(2) это точки до прямой l_(2)
Прямая 4x–y+1=0 разбивает плоскость хОу на две области:
4x–y+1>0 или 4x–y+1 0 — верно;
Прямая 2x–y+1=0 разбивает плоскость хОу на две области:
2x–y+1>0 или 2x–y+1 0 — верно;
Значит точка M принадлежит области
4x–y+1>0
2x–y+1>0
а смежные области задаются неравенствами противоположных знаков.
Поэтому в (#) знак модуля раскрывается так:
(4x-y+1)/sqrt(4^2+1^2) =- (2x-y+1)/sqrt(2^2+1^2)
Делим на (sqrt(5)+sqrt(17))
((2sqrt(17)+4sqrt(5))/(sqrt(17)+sqrt(5))) * x — y + 1=0
Избавляемся от иррациональности в знаменателе
[b]((7 — sqrt(85))/6)*x — y + 1 = 0[/b]
http://4apple.org/sostavit-uravnenie-bissektris-uglov-obrazovannyh/
http://reshimvse.com/zadacha.php?id=34288
We will learn how to find
the equations of the bisectors of the angles between two straight lines.
Prove that the equation of the bisectors of the angles
between the lines a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0 are given by (frac{a_{1}x + b_{1}y +
c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = ±(frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2}
+ b_{2}^{2}}}).
Let us assume the two given straight lines be PQ and RS whose equations are a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0 respectively, where c(_{1}) and c(_{2}) are of the same symbols.
First we will find the equations of the bisectors of the angles between the lines a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0.
Now, let us
assume that the two straight lines PQ and RS intersect
at T and ∠PTR contains origin O.
Again, let us assume that TU is the bisector of ∠PTR and Z(h, k) is any point on TU. Then the origin O and the point Z are on the same side of both the lines PQ and RS.
Therefore, c(_{1}), and (a(_{1})h + b(_{1})k + c(_{1})) are of the same symbols and c(_{2}) and (a(_{2})h + b(_{2})k + c(_{2})) are also of the same symbols.
Since, we already assumed that c(_{1}), and c(_{2}), are of the same symbols, thus, (a(_{1})h + b(_{1})k + c(_{1})) and (a(_{2})h + b(_{2})k + c(_{2})) shall be of the same symbols.
Therefore, the lengths of the perpendiculars from Z upon PQ and RS are of the same symbols. Now, if ZA ⊥ PQ and ZB ⊥ RS then it implies that ZA = ZB.
⇒ (frac{a_{1}h + b_{1}k + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = (frac{a_{2}h + b_{2}k + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
Therefore, the equation to the locus of Z (h, k) is,
(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})………… (i), which is the equation of the bisector of the angle containing the origin.
Algorithm to find the bisector of the angle containing the origin:
Let the equations of the two lines be a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0.
To find the bisector of the angle containing the origin, we proceed as follows:
Step I: First check whether the constant terms c(_{1}) and c(_{2}) in the given equations of two straight lines are positive or not. Suppose not, then multiply both the sides of the equations by -1 to make the constant term positive.
Step II: Now obtain the bisector corresponding to the positive symbol i.e.
(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = + (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}}), which is the required bisector of the angle containing the origin.
Note:
The bisector of the angle containing the origin means the
bisector of that angle between the two straight lines which contains the origin within it.
Again, ∠QTR does
not contain the origin. Suppose, TV be the bisector of ∠QTR and Z'(α, β) be any point on TV then the origin O and Z’ are on
the same side of the straight line (PQ) but they are on opposite sides
of the straight line RS.
Therefore, c(_{1}) and (a(_{1})α + b(_{1})β + c(_{1})) are of the same symbols but c(_{2}) and (a(_{2})α + b(_{2})β + c(_{2})), are of opposite symbols.
Since, we already assumed that, c(_{1}), and c(_{2}),
are of the same symbols, thus, (a(_{1})α + b(_{1})β + c(_{1})) and (a(_{2})α + b(_{2})β + c(_{2})) shall be of opposite symbols.
Therefore, the lengths of the perpendiculars from Z’ upon PQ and RS are of opposite symbols. Now, if Z’W ⊥ PQ and Z’C ⊥
RS then it readily follows that Z’W = -Z’C
⇒ (frac{a_{1}α +
b_{1}β + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = — (frac{a_{2}α + b_{2}β +
c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
Therefore, the equation to the locus of Z’ (α, β) is
(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} +
b_{1}^{2}}}) = — (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}}) ………… (ii), which is the
equation of the bisector of the angle not containing the origin.
From (i) and (ii) it is seen that the equations of the
bisectors of the angles between the lines a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0 are (frac{a_{1}x +
b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = ±(frac{a_{2}x + b_{2}y +
c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}}).
Note: The bisectors (i) and (ii) are perpendicular to each
other.
Algorithm to find the
bisectors of acute and obtuse angles between two lines:
Let the equations of the two lines be a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0. To separate the bisectors of the obtuse and acute angles
between the lines we proceed as follows:
Step I: First check whether the constant terms c(_{1}) and c(_{2})
in the two equations are positive or not. Suppose not, then multiply both the sides
of the given equations by -1 to make the constant terms positive.
Step II: Determine the symbols of the expression a(_{1})a(_{2})
+ b(_{1})b(_{2}).
Step III: If a(_{1})a(_{2}) + b(_{1})b(_{2}) > 0,
then the bisector corresponding to “ + “ symbol gives the obtuse angle bisector
and the bisector corresponding to “ — “ is the bisector of the acute angle
between the lines i.e.
(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} +
b_{1}^{2}}}) = + (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
and (frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = — (frac{a_{2}x
+ b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
are the bisectors of obtuse and acute angles respectively.
If a(_{1})a(_{2}) + b(_{1})b(_{2}) < 0, then the
bisector corresponding to “ + “ and “ — “ symbol give the acute and obtuse
angle bisectors respectively i.e.
(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} +
b_{1}^{2}}}) = + (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
and (frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = — (frac{a_{2}x
+ b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
are the bisectors of acute and obtuse angles respectively.
Solved examples to find the equations of the bisectors of
the angles between two given straight lines:
1. Find the equations of the bisectors of the angles between
the straight lines 4x — 3y + 4 = 0 and 6x + 8y — 9 = 0.
Solution:
The equations of the bisectors of the angles between 4x — 3y
+ 4 = 0 and 6x + 8y — 9 = 0 are
(frac{4x — 3y + 4}{sqrt{4^2} + (-3)^{2}}) = ± (frac{6x
+ 8y — 9}{sqrt{6^2} + 8^{2}})
⇒ (frac{4x — 3y + 4}{5}) = ±(frac{6x + 8y — 9}{10})
⇒ 40x — 30y + 40 = ±(30x + 40y — 45)
Taking positive sign, we get,
⇒ 40x — 30y + 40 = +(30x + 40y — 45)
⇒ 2x — 14y + 17 = 0
Taking negative sign, we get,
⇒ 40x — 30y + 40 = -(30x + 40y — 45)
⇒ 40x — 30y + 40 = -30x — 40y + 45
⇒ 70x + 10y — 5 = 0
Therefore the equations of the bisectors of the angles
between the straight lines 4x — 3y + 4 = 0 and 6x + 8y — 9 = 0 are 2x — 14y +
17 = 0 and 70x + 10y — 5 = 0.
2. Find the equation of the obtuse angle bisector of lines 4x
— 3y + 10 = 0 and 8y — 6x — 5 = 0.
Solution:
First we make the constant terms positive in the given two
equations.
Making positive terms positive, the two equations becomes
4x — 3y + 10 = 0 and 6x — 8y + 5 = 0
Now, a(_{1})a(_{2}) + b(_{1})b(_{2}) = 4 × 6 + (-3) ×
(-8) = 24 + 24 = 48, which is positive. Hence, “+” symbol gives the obtuse
angle bisector. The obtuse angle bisector is
⇒ (frac{4x — 3y + 10}{sqrt{4^2} + (-3)^{2}}) = + (frac{6x
— 8y + 5}{sqrt{6^2} + (-8)^{2}})
⇒ (frac{4x — 3y + 10}{5}) = +(frac{6x — 8y + 5}{10})
⇒ 40x — 30y + 100 = 30x — 40y — 50
⇒ 10x + 10y + 150 = 0
x + y + 15 = 0, which is the required obtuse angle bisector.
● The Straight Line
- Straight Line
- Slope of a Straight Line
- Slope of a Line through Two Given Points
- Collinearity of Three Points
- Equation of a Line Parallel to x-axis
- Equation of a Line Parallel to y-axis
- Slope-intercept Form
- Point-slope Form
- Straight line in Two-point Form
- Straight Line in Intercept Form
- Straight Line in Normal Form
- General Form into Slope-intercept Form
- General Form into Intercept Form
- General Form into Normal Form
- Point of Intersection of Two Lines
- Concurrency of Three Lines
- Angle between Two Straight Lines
- Condition of Parallelism of Lines
- Equation of a Line Parallel to a Line
- Condition of Perpendicularity of Two Lines
- Equation of a Line Perpendicular to a Line
- Identical Straight Lines
- Position of a Point Relative to a Line
- Distance of a Point from a Straight Line
- Equations of the Bisectors of the Angles between Two Straight Lines
- Bisector of the Angle which Contains the Origin
- Straight Line Formulae
- Problems on Straight Lines
- Word Problems on Straight Lines
- Problems on Slope and Intercept
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Как найти уравнение биссектрисы
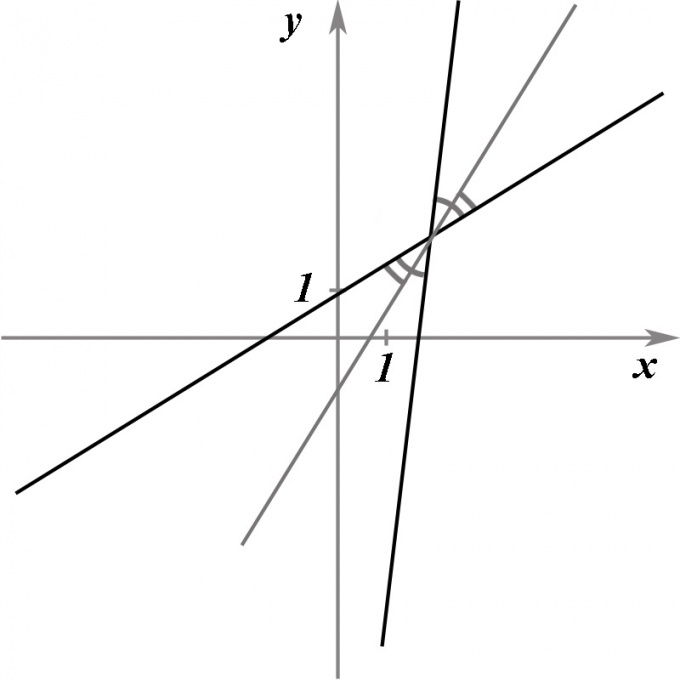
Пусть даны две пересекающиеся прямые, заданные своими уравнениями. Требуется найти уравнение прямой, которая, проходя через точку пересечения этих двух прямых, делила бы точно пополам угол между ними, то есть являлась бы биссектрисой.
Инструкция
Предположим, что прямые заданы своими каноническими уравнениями. Тогда A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0. При этом A1/B1 ≠ A2/B2, иначе прямые параллельны и задача не имеет смысла.
Поскольку очевидно, что две пересекающиеся прямые образуют между собой четыре попарно равных угла, то должны существовать ровно две прямые, удовлетворяющие условию задачи.
Эти прямые будут перпендикулярны друг другу. Доказательство этого утверждения достаточно просто. Сумма четырех углов, образованных пересекающимися прямыми, будет всегда равна 360°. Поскольку углы попарно равны, то эту сумму можно представить в виде:
2a + 2b = 360° или, что очевидно, a + b = 180°.
Поскольку первая из искомых биссектрис делит пополам угол a, а вторая — угол b, то угол между самими биссектрисами всегда равен a/2 + b/2 = (a + b)/2 = 90°.
Биссектриса, по определению, делит угол между прямыми пополам, а значит, для любой точки, лежащей на ней, расстояния до обеих прямых будут одинаковыми.
Если прямая задана каноническим уравнением, то расстояние от нее до некоторой точки (x0, y0), не лежащей на этой прямой:
d = |(Ax0 + By0 + C)/(√(A^2 + B^2))|.
Следовательно, для любой точки, лежащей на искомой биссектрисе:
|(A1*x + B1*y + C1)/√(A1^2 + B1^2)| = |(A2*x + B2*y + C2)/√(A2^2 + B2^2)|.
Из-за того, что в обеих частях равенства стоят знаки модуля, оно описывает сразу обе искомые прямые. Чтобы превратить его в уравнение только одной из биссектрис, нужно раскрыть модуль либо со знаком +, либо со знаком -.
Таким образом, уравнение первой биссектрисы:
(A1*x + B1*y + C1)/√(A1^2 + B1^2) = (A2*x + B2*y + C2)/√(A2^2 + B2^2).
Уравнение второй биссектрисы:
(A1*x + B1*y + C1)/√(A1^2 + B1^2) = -(A2*x + B2*y + C2)/√(A2^2 + B2^2).
Например, пусть заданы прямые, определенные каноническими уравнениями:
2x + y -1 = 0,
x + 4y = 0.
Уравнение их первой биссектрисы получается из равенства:
(2x + y -1)/√(2^2 + 1^2) = (x + 4y + 0)/√(1^2 + 4^2), то есть
(2x + y — 1)/√5 = (x + 4y)/√15.
Раскрывая скобки и переводя уравнение в канонический вид:
(2*√3 — 1)*x + (√3 — 4)*y — √3 = 0.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.