Как построить треугольник с помощью циркуля
Геометрическое построение фигур относится к основным знаниям школьного курса геометрии. Помимо практического применения, здесь имеет значение развитие пространственной логики. Именно поэтому построение треугольника, как простой многоугольной фигуры, с помощью циркуля рассматривается подробно. Циркуль – инструмент не только для построения окружности. Он позволяет также отложить равные отрезки заданной длины. Это и поможет нам с его помощью построить треугольник.

Вам понадобится
- Лист бумаги, циркуль
Инструкция
Возьмите любой листок бумаги. В центре листа поставьте точку. Это будет первая вершина A создаваемого треугольника.

Раскройте циркуль на расстояние, точно соответствующее требуемой стороне создаваемого треугольника. Жестко зафиксируйте ножки циркуля в данном положении.
Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.

В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.
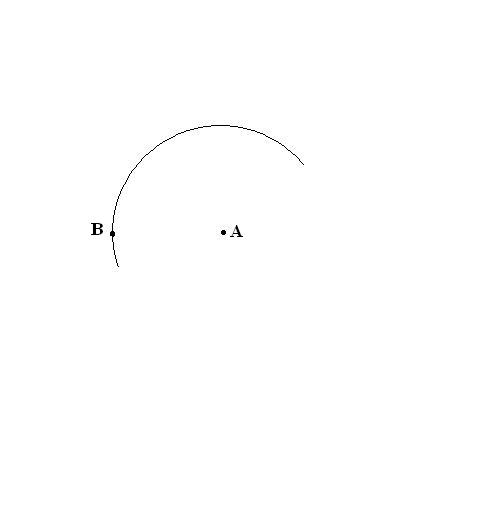
Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.
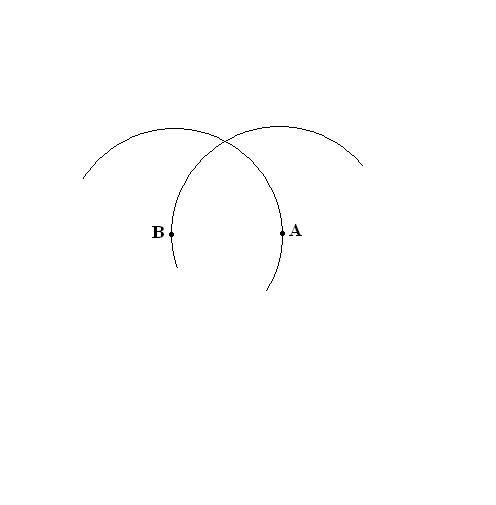
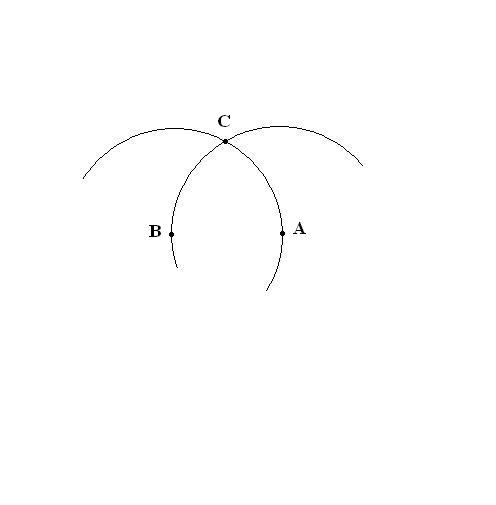
В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.
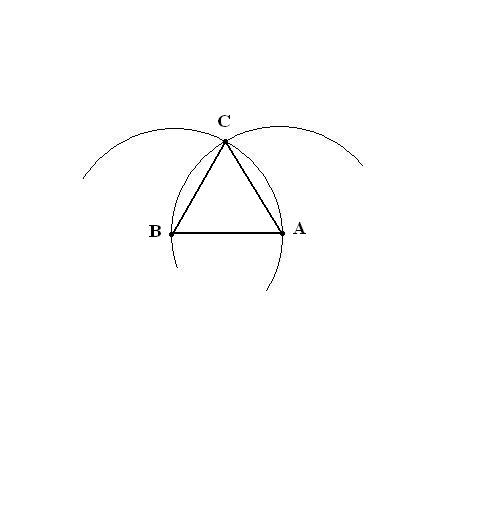
Получив все три вершины, соедините их прямыми линиями с помощью любой ровной поверхности (лучше линейки). Треугольник ABC построен.
Загрузить PDF
Загрузить PDF
В равностороннем треугольнике все стороны и углы равны. Вручную нарисовать идеальный равносторонний треугольник довольно сложно. Но вы можете воспользоваться транспортиром, чтобы точно отложить углы. Также используйте линейку, чтобы проводить абсолютно прямые линии. Эта статья расскажет вам, как нарисовать равносторонний треугольник.
-
1
Проведите прямую линию. На лист бумаги положите линейку и проведите карандашом вдоль длинной стороны линейки. Полученный отрезок является первой стороной равностороннего треугольника, то есть вам нужно нарисовать еще две стороны той же длины, а каждый угол между сторонами должен быть равен 60 градусам. Убедитесь, что на бумаге есть свободное место для построения оставшихся двух сторон.[1]
-
2
При помощи циркуля проведите дугу. В циркуль вставьте карандаш, убедившись, что он заточен. Иглу циркуля поставьте в начальную точку первой стороны треугольника, а затем раздвиньте циркуль так, чтобы кончик карандаша в циркуле касался конечной точки первой стороны треугольника.
-
3
Над первой стороной треугольника проведите дугу. Не меняйте раствор циркуля (расстояние между иглой и кончиком карандаша). При помощи циркуля проведите дугу над первой стороной треугольника, начиная от конечной точки первой стороны треугольника.[2]
-
4
Переставьте циркуль. Не меняя раствора циркуля, поставьте его иглу в конечную точку первой стороны треугольника.
-
5
Над первой стороной треугольника проведите вторую дугу. При помощи циркуля проведите вторую дугу над первой стороной треугольника, начиная от начальной точки первой стороны треугольника. Две дуги пересекутся.
-
6
Отметьте точку пересечения двух дуг. Она должна быть расположена точно над серединой первой стороны треугольника. Теперь соедините начальную точку первой стороны с точкой пересечения дуг, а затем соедините конечную точку первой стороны с точкой пересечения дуг.[3]
-
7
Нарисуйте треугольник. Соедините вышеупомянутые точки при помощи линейки, и вы получите оставшиеся две стороны треугольника. Убедитесь, что линии абсолютно прямые. Нарисовав треугольник, сотрите проведенные вами дуги.[4]
- Скопируйте полученный треугольник на чистый лист бумаги, чтобы работать с готовой фигурой.
- Если вы хотите увеличить или уменьшить треугольник, увеличьте или уменьшите первую сторону треугольника. Чем длиннее стороны треугольника, тем он больше!
Реклама
Если у вас нет циркуля или транспортира, воспользуйтесь любым круглым предметом, чтобы провести дуги. Описанный ниже метод основан на методе с применением циркуля.
-
1
Найдите круглый предмет. Вы можете использовать любой плоский или цилиндрический предмет, например, бутылку, кастрюлю или компакт-диск. Если вам нужно заменить циркуль с определенным раствором круглым предметом, найдите предмет подходящего диаметра. В этом методе каждая сторона равностороннего треугольника будет равна радиусу (половине диаметра) круглого предмета.
- Если в качестве круглого предмета вы используете компакт-диск, то равносторонний треугольник как бы впишется в правый верхний сегмент компакт-диска.
-
2
Нарисуйте первую сторону треугольника. Она должна быть равна радиусу (половине диаметра) выбранного вами круглого предмета. Убедитесь, что проведенная линия абсолютно прямая.
- Если у вас есть линейка, просто измерьте диаметр круглого предмета и проведите отрезок, равный половине диаметра.
- Если у вас нет линейки, положите круглый предмет на бумагу и обведите его карандашом. Уберите круглый предмет – на листе бумаги вы увидите идеальную окружность. Проведите прямую линию, проходящую через центр этой окружности, то есть через точку, равноудаленную от всех точек, лежащих на окружности.
-
3
При помощи круглого предмета проведите дугу. Положите круглый предмет на первую сторону треугольника так, чтобы край предмета совмещался с начальной точкой первой стороны. Во избежание ошибок убедитесь, что первая сторона проходит через центр круглого объекта. Карандашом нарисуйте дугу над первой стороной треугольника, начиная от начальной точки первой стороны.[5]
-
4
Проведите вторую дугу. Положите круглый предмет на первую сторону треугольника так, чтобы край предмета совмещался с конечной точкой первой стороны. Во избежание ошибок убедитесь, что первая сторона проходит через центр круглого объекта. Карандашом нарисуйте вторую дугу над первой стороной треугольника, начиная от конечной точки первой стороны. Дуги пересекутся в точке, лежащей точно над серединой первой стороны треугольника и являющейся вершиной треугольника.
-
5
Нарисуйте треугольник. Для этого соедините начальную точку первой стороны с точкой пересечения дуг, а затем соедините конечную точку первой стороны с точкой пересечения дуг. Вы получите равносторонний треугольник.
Реклама
-
1
Нарисуйте первую сторону. При помощи линейки или прямой стороны транспортира проведите линию определенной длины. Полученный отрезок является первой стороной равностороннего треугольника, то есть две другие стороны будут равны первой стороне.
-
2
При помощи транспортира от начальной точки первой стороны отложите угол, равный 60 градусам. Предполагаемую вторую сторону нарисуйте пунктирной прямой (угол между первой стороной и пунктирной прямой должен быть равен 60 градусам).
-
3
Нарисуйте вторую сторону треугольника. Измерьте первую сторону треугольника, положите линейку на пунктирную прямую, совместите начало линейки с начальной точкой первой стороны и проведите отрезок, равный длине первой стороны треугольника. Этот отрезок является второй стороной треугольника.[6]
-
4
Нарисуйте треугольник. При помощи линейки или прямой стороны транспортира нарисуйте третью сторону треугольника. Для этого соедините конечные точки первой и второй сторон. Вы получите равносторонний треугольник.
Реклама
Советы
- Метод с использованием циркуля является более точным, так как не зависит от аккуратности откладывания углов.
- При проведении дуг не давите на карандаш или циркуль, чтобы иметь возможность стереть их.
- Используйте циркуль с фиксатором, чтобы случайно не изменить раствор циркуля.
Реклама
Предупреждения
- Не повредите поверхность, на которой лежит лист бумаги.
Реклама
Что вам понадобится
- Циркуль (обычный циркуль, используемый вами на уроках геометрии).
- Что-то, что можно поставить под циркуль, чтобы он не скользил.
- Линейка.
- Карандаш (не используйте механические карандаши, потому что они не подходят для циркулей, в которые можно вставить карандаш). Также заточите карандаш.
Об этой статье
Эту страницу просматривали 120 548 раз.
Была ли эта статья полезной?
Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.
Нам понадобится
Фломастер (не обязательно)
Шаг 1 из 8
На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.
Шаг 2 из 8
Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.
При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.
Шаг 3 из 8
Отметьте точки пересечения окружностей.
Шаг 4 из 8
Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.
Шаг 5 из 8
Далее, через центры обеих окружностей нужно провести прямую линию.
Шаг 6 из 8
Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.
Шаг 7 из 8
Соедините все три точки между собой.
Шаг 8 из 8
Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.
Download Article
Download Article
An equilateral triangle has three sides of equal length, connected by three angles of equal width. It can be challenging to draw a perfectly equilateral triangle by hand. However, you can use a circular object to mark out the angles. Make sure to use a ruler to get the lines straight! Continue reading to learn how to draw one.
-
1
Draw a straight line. Lay your ruler on the paper, then trace a pencil along the straight edge. This line segment will form one side of your equilateral triangle, which means that you will need to draw two more lines of exactly the same length, each reaching toward a point at a 60° angle from the first line. Make sure that you have plenty of room to draw all three sides![1]
-
2
Span the segment with your compass. Slide a pencil into your compass, and make sure that it’s sharp! Put the point of your compass at one end of the segment, and set the pencil point at the other.
Advertisement
-
3
Trace a quarter-circle arc. Do not adjust the point of the compass, and do not change the set «width» of the tool from the compass point to the pencil point. Swing the pencil-point of the compass in a quarter-circle up and away from the line segment.[2]
-
4
Switch the compass around. Without changing the width of the compass spread, move the point of the compass to the other end.
-
5
Draw a second arc. Carefully swing the pencil-point of the compass so that the new arc crosses over the first arc that you drew.[3]
-
6
Mark the point where the two arcs cross. This is the apex (the «top» point) of your triangle. It should lie at the exact center of the line segment that you’ve drawn. You can now draw two straight lines leading to this point: one from each end of the «bottom» line segment.[4]
-
7
Finish the triangle. Use a ruler to draw two more straight line segments: the remaining sides of the triangle. Connect each end of the original line segment to the point at which the arcs cross. Make sure that the lines are straight. To finish the job, erase the arcs that you drew so that only the triangle remains![5]
- Consider tracing this triangle onto another page. This way, you can start fresh with a clean shape.
- If you need a bigger or a smaller triangle, repeat the process but adjust the length of the original line segment. The longer the sides, the bigger the triangle!
Advertisement
If you don’t have access to a compass or a protractor, you can use an object with a circular base to trace out an arc instead. This method is essentially the same as using a compass, but you will need to be smart about it!
-
1
Choose your circular object. Use almost any cylindrical object with a circular base, like a bottle or a soup can. Try using a circular roll of tape or a CD. If you are going to substitute the arc of this object for the arc of a compass tracer, you’ll need to choose an object of the right size. In this method, each side of the equilateral triangle will be as long as the radius (half the diameter) of the circular object.
- If you use a CD as your object: imagine an equilateral triangle that fits into the top-right quadrant of a CD.
-
2
Draw the first side. It should be exactly as long as the radius of the circular object – the distance halfway across. Make sure that it is perfectly straight!
- If you have a ruler: simply measure the diameter of the object and draw a line that is half as long.
- If you don’t have a ruler: place the circular object onto a sheet of paper, then carefully trace the circumference with your pencil. Remove the object, and you should have a perfect circle. Use a straight edge to draw a line across the exact center of the circle: the point that is completely equidistant from any point around the circumference of the circle.
-
3
Use the circular object to trace an arc. Place the object over the line segment, with the edge of the circle resting at one end of the line. For accuracy, make sure that the line cleaves through the exact center of the circle. Use your pencil to trace an arc: roughly one-quarter of the way around the perimeter of the circle.[6]
-
4
Trace another arc. Now, shift the circular object so that the edge touches the other end of the line segment. Make sure that the line segment runs through the exact center of the circle. Draw another quarter-arc that crosses the first arc at a point directly above the line segment. This point is the apex of your triangle.
-
5
Complete the triangle. Draw the remaining sides of the triangle: two more straight lines will connect the apex with the two open ends of the line segment. Now, you should have a perfectly equilateral triangle!
Advertisement
-
1
Draw the first side. Use a ruler or the straight edge of your protractor to trace a straight line segment of an appropriate length. This line segment will become the first side of your triangle, and each of the other sides will be just as long – so make sure that it’s the right size![7]
-
2
Use a protractor to measure a 60° angle at one end.[8]
-
3
Trace the second side. Measure out a new line segment that is equal in length to the first. Start it at one end of the original line segment, where you measured the 60° angle. Start from the vertex (the point) of the angle, and trace the straight edge of the protractor until you reach the next «point.»[9]
-
4
Finish the triangle. Use the straight edge of your protractor to trace out the final side of the triangle. Connect the point at the end of the second line segment to the unattached end of the first line segment. You should now have an equilateral triangle.
Advertisement
Add New Question
-
Question
How would I draw an equilateral triangle with three lines in it forming six right angles?
Assuming you know the length of each of the three given lines (and all three lines are of equal length), this is not a difficult construction. First draw any line, then draw a line segment perpendicular to the first line. On that line segment, measure off the given line length. At the end of the line segment, use a protractor to form 30° angles on either side of the line segment. Extend the new lines to intersect the first line you drew. This will complete an equilateral triangle. (Each of the other two given lines will bisect one of the other angles and be perpendicular to the opposite side.)
-
Question
How do I construct a trapezoid?
Draw two parallel lines. Draw a third line intersecting the first two lines. Draw a fourth line also intersecting the first two lines, but not intersecting the third line between the two lines and not parallel to the third line.
-
Question
How do I construct an equilateral triangle inscribed in a circle?
The easiest way is to use a protractor to draw three 120° angles around the center of the circle, and then connect the three points on the circle where the three angles intersect the circumference. That will result in an inscribed equilateral triangle.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Use a compass that has a lock to ensure that you don’t unintentionally change the spread of the compass.
-
Don’t make the compass lines dark; you want them to be thin so you can easily erase them later.
-
The compass method is usually more precise as it does not rely on the correct measurement of angles.
Thanks for submitting a tip for review!
Advertisement
-
Don’t mark the surface beneath the paper.
Advertisement
Things You’ll Need
- A pair of compasses (the type used for mathematical constructions, not the North/South type)
- Something to put under the compass so the point doesn’t slip
- A ruler
- A pencil (try not to use mechanical pencils, they may not fit into the pencil holder on the compass). Also make sure it is sharp, not blunt.
References
About This Article
Article SummaryX
To draw an equilateral triangle, start by laying a ruler on a piece of paper and drawing a straight line. Next, insert a compass at an end of the line you’ve just drawn and put a pencil at the other. Trace a quarter circle with the pencil end of the compass moving upwards, then switch the ends of the compass around. To form the apex, draw a second arc with the pencil so it crosses over the first arc. Finish by drawing 2 straight lines up to the apex for the triangle’s sides and erasing the arcs so only the triangle can be seen. For tips on how to draw an equilateral triangle using a protractor, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 459,923 times.
Reader Success Stories
-
«It helped me sort out how to build my towers using spaghetti in my class experiment. Using different methods, I…» more
Did this article help you?
Как начертить равносторонний треугольник
Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.
На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.
Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.
При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.
Отметьте точки пересечения окружностей.
Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.
Далее, через центры обеих окружностей нужно провести прямую линию.
Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.
Соедините все три точки между собой.
Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.
Построение с помощью циркуля и линейки — описание, алгоритмы и задачи
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Построение отрезка, равного данному
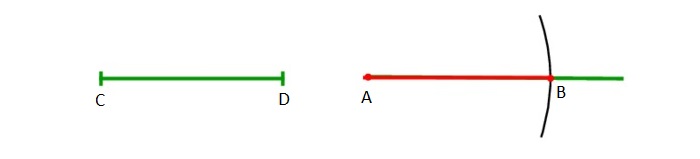
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
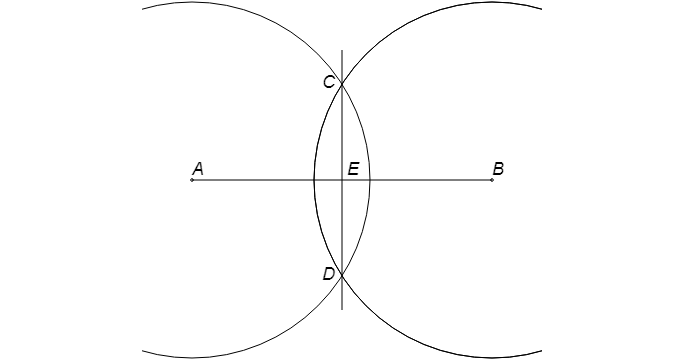
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
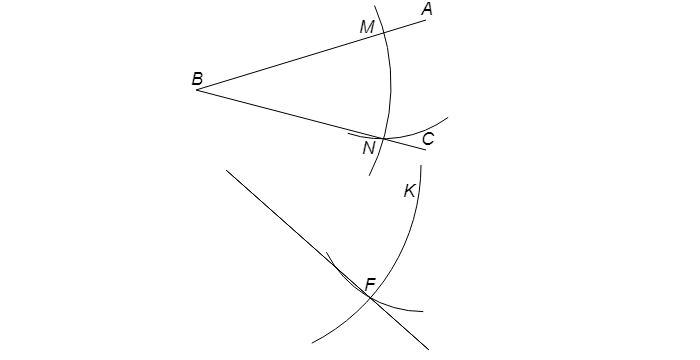
Имеется угол ABC.
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
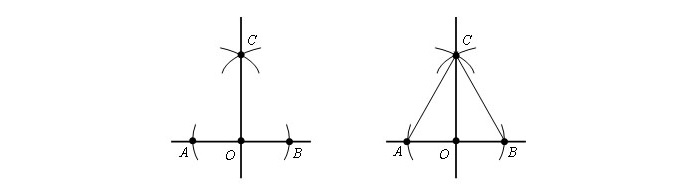
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
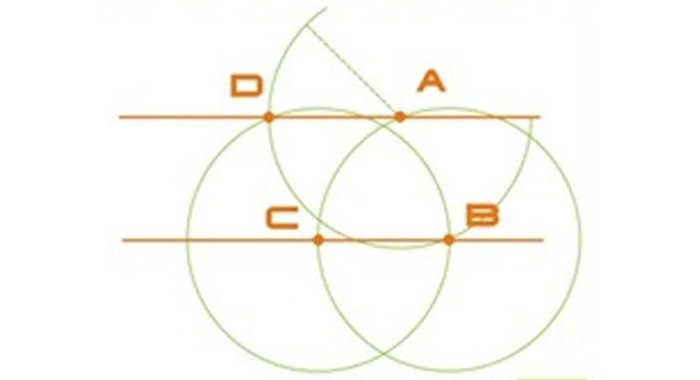
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
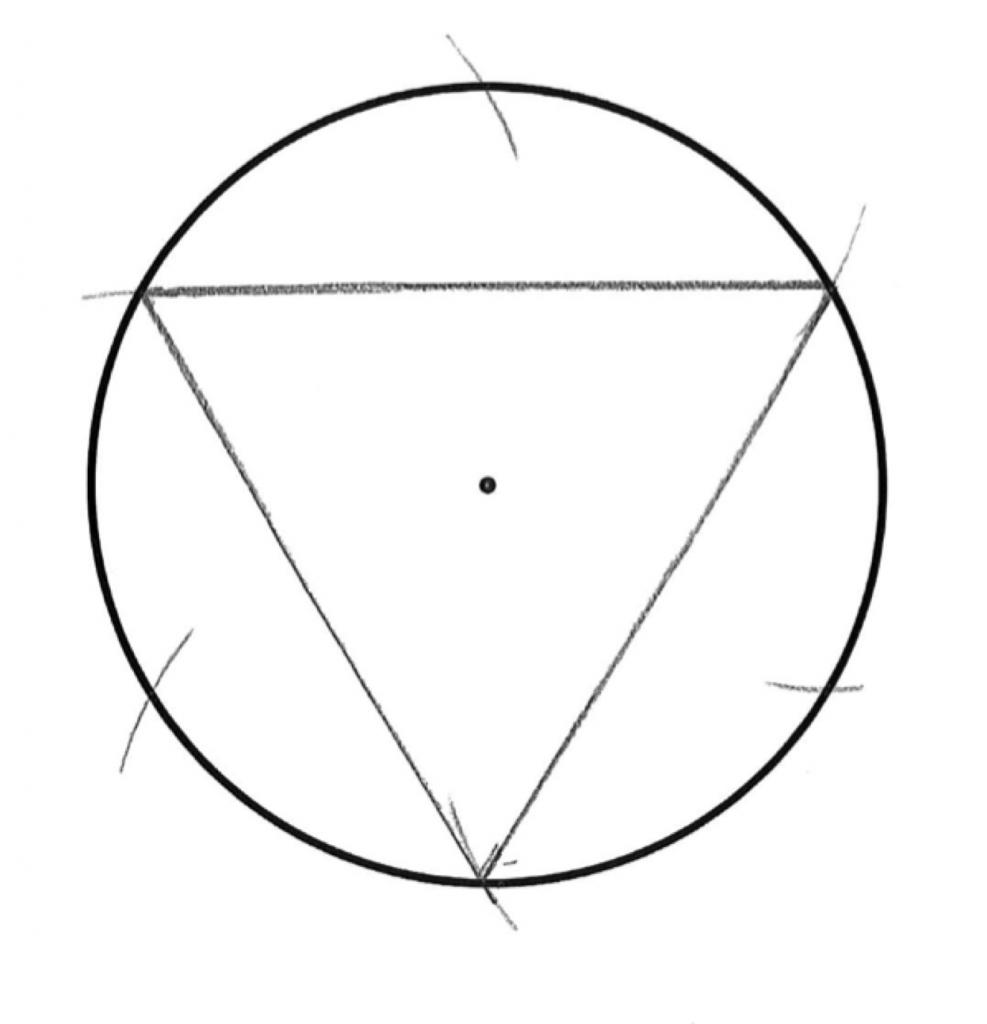
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
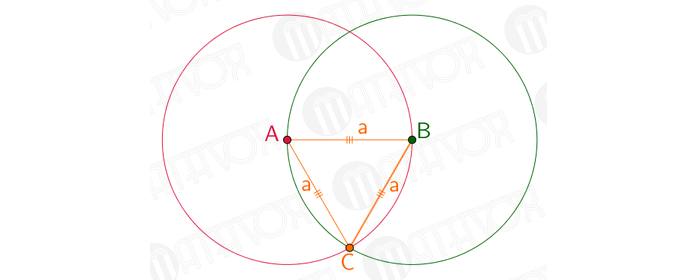
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
Вариант 1
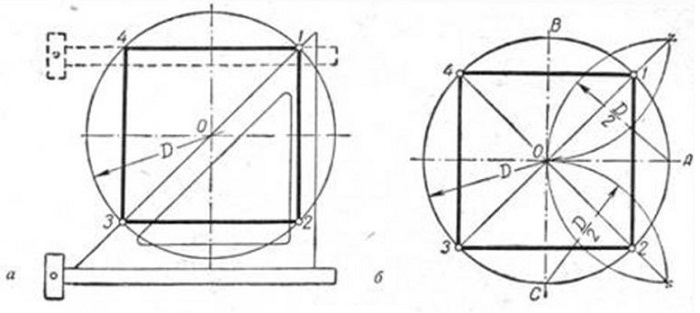
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
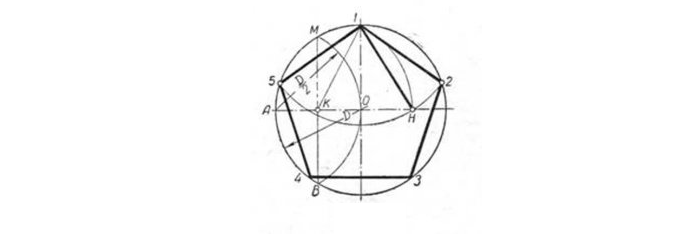
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
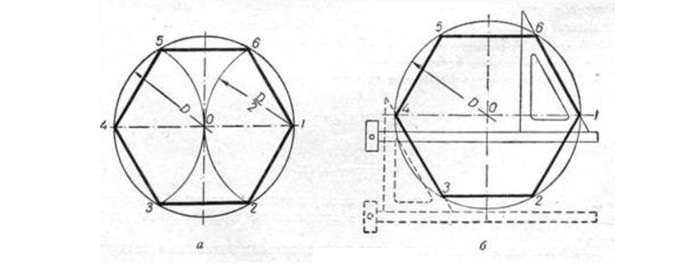
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.
Как нарисовать треугольник: этапы выполнения задания
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
- Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
http://nauka.club/matematika/geometriya/postroenie-s-pomoshchyu-tsirkulya-i-lineyki.html
http://fb.ru/article/403321/kak-narisovat-treugolnik-etapyi-vyipolneniya-zadaniya