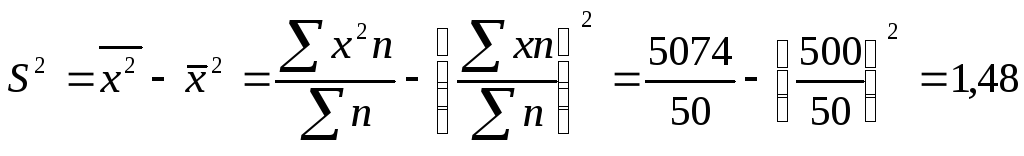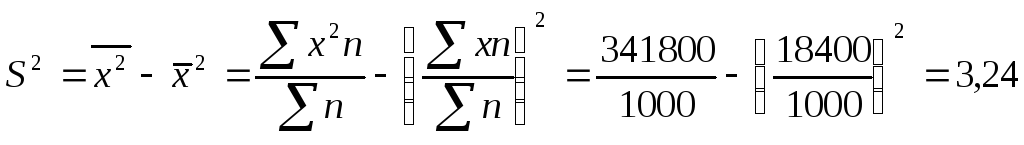Изучая математическую статистику в 7-м классе,
важно наглядно представить учащимися образец
для решения практических задач. Именно для этого
мною был разработан данный справочный материал.
1.Представление данных.
1.1. Таблицы
Смета расходов на покупку спортивного
инвентаря.
| № | Наименование | Ед. измерения | Количество | Цена (едруб) | Стоимость (руб) |
| 1 | Мяч футбольный | Шт. | 30 | 1000 | |
| 2 | Мяч волейбольный | Шт. | 15 | 800 | 12000 |
| 3 | Ракетка | Шт. | 24 | 250 | 6000 |
| 4 | Воланы | коробка | 10 | 300 | 3000 |
| ИТОГО: | 51000 |
Таблицы предназначены для упорядочивания
большого количества данных. Часто в таблицы
заносят результаты вычислений, измерений.
1.2. Диаграммы.
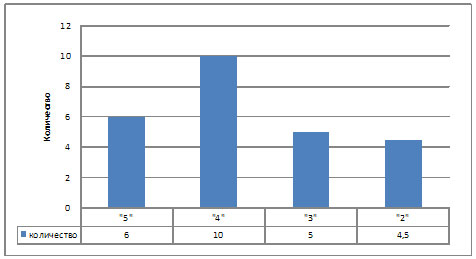
За контрольную работу по математике
школьники получили 6 оценок “отлично”, 10 оценок
“хорошо”, 5 оценок “ удовлетворительно” и 3
оценки “не удовлетворительно”.
Столбиковая диаграмма.
Построим столбиковую диаграмму по
этим данным.
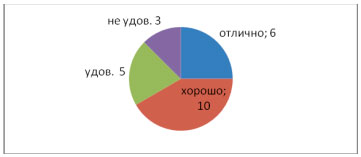
Круговая диаграмма.
Построим круговую диаграмму по этим
данным.
Для построения этой диаграммы мы:
- Разделили 360° на общее число учащихся (24)
- Затем последовательно умножаем 15° на
количество учащихся, получивших ту или иную
оценку. - Затем круг делим на полученные сектора,
подписываем данные.
360°24=15° (такому углу соответствует
оценка одного учащегося)
15°6=90° —
сектор образованный этим углом соответствует
учащимся с оценкой “5”
15°10=150°
— сектор образованный этим углом соответствует
учащимся с оценкой “4”
15°5=75° —
сектор образованный этим углом соответствует
учащимся с оценкой “3”
15°3=45° —
сектор образованный этим углом соответствует
учащимся с оценкой “2”
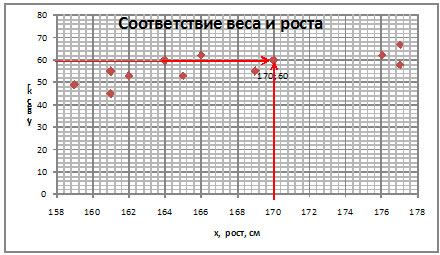
Диаграмма рассеивания.
Для выявления связи между величинами
применяются диаграммы рассеивания.
В таблице приведены данные о весе и
росте 12 девушек.
|
Рост, см |
165 |
177 |
161 |
162 |
170 |
176 |
177 |
164 |
166 |
161 |
169 |
159 |
Х |
|
Вес, кг |
53 |
67 |
45 |
53 |
60 |
62 |
58 |
60 |
62 |
55 |
55 |
49 |
У |
Для построения этой диаграммы нужно в
системе координат поставить точки, абсциссы
которых – рост, а ординаты – вес.
- Описательная статистика
2.1. Среднее значение
Определение: Средним арифметическим
нескольких чисел называется число, равное
отношение суммы этих чисел к их количеству.
Среднее арифметическое набора чисел х1,х2,х3,х4,х5
принято обозначать . Например, среднее арифметическое
пяти чисел запишется так:
Здесь в числителе дроби — сумма данных пяти
чисел, а в знаменателе – их количество – 5.
Найти среднюю оценку учащегося по
математике, если за истекший период он получил: 3,
4, 4, 5, 3, 2, 4, 3.
Запишем дробь и вычислим ее значение:
2.2. Медиана
Определение: Число, разделяющее набор
чисел на две части, равные по численности, так что
с одной стороны от этого числа все значения
больше медианы, а с другой – меньше.
Метод вычисления медианы: Чтобы найти
медиану набора чисел нужно:
- Записать числа в порядке возрастания.
- Если в полученном наборе нечетное количество
членов, то медианой служит число стоящее
посередине. - Если в полученном наборе четное количество
членов, то медианой набора – есть полусумма двух
чисел, расположенных посередине.
Найти медиану набора чисел: 9,3, 1, 5, 7.
Запишем числа в порядке возрастания.
1, 3, 5, 7, 9.
Здесь медиана набора число, стоящее
посередине – 5.
Найти медиану набора чисел: 9,3, 1, 5, 7,8
Запишем числа в порядке возрастания.
Выберем два центральных числа: 5 и 7. Найдем их
полусумму: (5+7):2=6. То есть медиана
данного набора есть число-6.
2.3. Наибольшее и наименьшее значение и размах.
Найти наибольшее, наименьшее значение и
размах для ряда чисел:
12,7,25,3,19,15.
Очевидно, что наибольшим значением данного
ряда является число 25, тогда как наименьшим число
– 3. Найдем размах данного ряда.
Определение: Разность между наибольшим и
наименьшим числом называется размахом набора
чисел.
Размах показывает насколько велико
рассеивание в числовом наборе. Итак, размах
данного набора равен разности 25 и 3, т.е. 22.
2.4. Отклонение.
Определение: Отклонением данного
значения от среднего арифметического значения
данного набора является разность между этим
числом и средним арифметическим. Соответственно
если некоторое значение меньше среднего, то его
отклонение отрицательно, если больше среднего –
его отклонение положительно. Так же необходимо
помнить, что сумма всех отклонений ряда чисел от
среднего арифметического этих чисел равна нулю.
Составить таблицу отклонений от
среднего арифметического для набора чисел:
2,4,5,7,10.
Вычислим среднее арифметическое этих чисел:
Составим таблицу отклонений.
| Число | Отклонение от среднего арифметического |
| 2 | 2-5,6= -3,6 |
| 4 | 4-5,6= -1,6 |
| 5 | 5-5,6= -0,6 |
| 7 | 7-5,6=1,4 |
| 10 | 10-5,6=4,4 |
2.5. Дисперсия.
Определение: Среднее арифметическое
квадратов отклонений от среднего значения
называется дисперсией набора чисел. Дисперсию
обозначают S2.
В таблице представлены средние
месячные температуры, в градусах. Вычислите
дисперсию температуры за приведенный период.
| Месяцы | Январь | Февраль | Март | Апрель | Май |
| Средняя температура | -12 | -7 | 0 | 9 | 16 |
Решение:
- Вычислим среднюю температуру за 5 месецев.
- .Составим таблицу отклонений и их квадратов.
- Найдем среднее арифметическое для квадратов
отклонений от среднего значения
Итак, средняя температура составила 6
градусов.
| Число (температура) | Отклонение от среднего | Квадрат отклонения |
| -12 | -12-6=-18 | (-18)2=324 |
| -7 | -13 | 169 |
| 0 | -6 | 36 |
| 9 | 3 | 9 |
| 16 | 10 | 100 |
( последний столбец таблицы)
Итак, дисперсия средних температур за 5 месяцев
составила 127,6. Ответ: S2=127,6
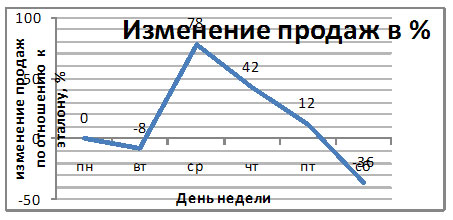
Составление таблицы изменений в процентах.
В таблице представлено количество
продаваемых за неделю шоколадок в школьном
буфете. Составьте таблицу изменения продаж по
отношению к понедельнику в процентах.
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество |
50 |
46 |
89 |
71 |
44 |
32 |
Число проданных в понедельник шоколадок
составляет 100% — эталон.
Вычислим, сколько составляет 1% эталона.
1% =50:100=0,5.
Вычислим, сколько процентов эталона составляет
количество проданных шоколадок в другие дни
недели.
Вторник – 46. Какой процент составляет 46 от 50.
46:0,5=92
Среда -89. 89 : 0,5= 178
Четверг – 71. 71 :0,5=142
Пятница – 44 44:0,5=88
Суббота -32 32 :0,5 =64
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество проданных |
50 |
46 |
89 |
71 |
44 |
32 |
|
% от эталона |
100 |
92 |
178 |
142 |
88 |
64 |
|
Изменение продаж в % |
0 |
-8 |
78 |
42 |
-12 |
-36 |
Алгебра 7 класс. Что такое отклонение? например: 2,7,3,5,11,15
Дисперсией числового ряда называется среднее арифметическое квадратов отклонений от среднего арифметического.
Пусть есть некий ряд (значения некоторой случайной величины — скажем, возраст детей в семье): 2,7,3,5,11,15.
1) находим среднее арифметическое: (2+7+3+5+11+15) / 6= 7,17
2) находим среднее арифметическое квадратов отклонений:
(2-7,17)^2+(7-7,17)^2+(3-7,17)^2+(5-7,17)^2+(11-7,17)^2+(15-7,17)^2/6=
Дисперсия характеризует разброс — чем больше дисперсия, тем сильнее «разбросан» (варьируется) признак относительно центрального значения.
Как посчитать среднее значение, квадратическое отклонение и погрешность
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 24 человек(а).
Количество просмотров этой статьи: 62 795.
После сбора данных их нужно проанализировать. Обычно нужно найти среднее значение, квадратичное отклонение и погрешность. Мы расскажем вам, как это сделать.
- Например, 5 школьникам был предложен письменный тест. Их результаты (в баллах по 100 бальной системе): 12, 55, 74, 79 и 90 баллов.
- Среднее значение (μ) = Σ/N, где Σ сумма всех числовых значений, а N количество значений.
- Для вышеуказанного примера это квадратный корень из [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Обратите внимание, что если это выборочное среднеквадратическое отклонение, то делить нужно на N-1, где N количество значений.)
- Если в нашем примере 5 школьников, а всего в классе 50 школьников, и среднее отклонение, посчитанное для 50 школьников равно 17 (σ = 21), средняя погрешность = 17/кв. корень(5) = 7.6.
Метод вычисления отклонений каждого значения от среднего арифметического
Для вычисления отклонений всех чисел выполним следующие действия:
. Находим среднее арифметическое;
2. Для вычисления отклонение из данного набора чисел вычитаем среднее арифметическое.
Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.
Среднее арифметическое находится по формуле


Найти отклонений всех чисел от среднего арифметического.
Сумма чисел в массиве (2):
Вычисление отклонения (3):
Блок схема 2 — Вычисление отклонений каждого значения от среднего арифметического
Описание методов создания, уничтожения и синхронизации потоков, примененных в программе
Создание потоков
Для создания многопоточных приложений в C++Builder реализован абстрактный класс TThread.- абстрактный класс, который допускает создание отдельных потоков выполняющихся в приложении.
Создайте потомка класса TThread, чтобы представить выполняемый поток в многопоточном приложении.
Каждый новый экземпляр потомка TThread — новый поток выполнения.
Множество экземпляров, полученные от класса TThread, делает C++Builder многопоточным приложением.
__fastcall TMyThread:: TMyThread (bool CreateSuspended)
// B метод объекта Execute (), вставьте код, который должен выполняться, когда поток выполняется.
void __fastcall TMyThread:: Execute ()
// — — Place thread code here — —
Для получения безопасного доступа куправлению свойствами и методами VCL-объектов в потоке предусмотрен метод Synchronize ()
ResetEvent (FMain->g_BusyEvent [1]); // запрещаем переформирование массива(FMain->g_BusyEvent [0]); // запрещаем переформирование массива
>++;(Terminated) break; // прекратить извне поток
Synchronize (&Mon); // блокирует одновременный доступ к компоненту нескольких потоков
SetEvent (FMain->g_BusyEvent [0]); // разрешаем параллельную обработку(FMain->g_BusyEvent [1]); // разрешаем параллельную обработку
Синхронизация потоков
Синхронизации потоков основывается на использовании событий (event). Объект типа событие может принимать одно из двух состояний: активное или пассивное. Когда событие находится в активном состоянии, его видят многие потоки одновременно. В результате такой объект можно использовать для управления работой сразу многих потоков. В библиотеке VCL события представлены классом TEvent.
Метод CreatEvents (): Создает объект класса TEvent, представляющий объект события.
Метод ResetEvent (): Переводит объект события в пассивное состояние.
Метод SetEvent (): Переводит объект события в активное состояние.
WaitForSingleObject (): Заставляет ждать, пока другой поток или процесс не пошлют сигнал об активизации объекта событие.
Завершение потоков
Потоки могут быть запущены и остановлены сколько угодно раз в процессе их выполнения. Для временной остановки запущенного потока можно обратиться к методу потока suspend. Для продолжения выполнения приостановленного потока вызовите метод потока Resume. Вы можете использовать вложенные вызовы вышеперечисленных методов, т.к. метод Suspend увеличивает внутренний счетчик потока, a Resume уменьшает. Поток не будет выполняться до тех пор, пока счетчик не обратиться в ноль, т.е., если вы вызвали пять раз метод Suspend, а затем четыре раза Resume, вам понадобится еще один (пятый) вызов метода Resume для продолжения выполнения потока.
Выполнение потока автоматически завершается после завершения функции Execute () или закрытии приложения.
Чтобы занятая потоком память освобождалась при завершении потока надо установить FreeOnTerminate=false.
Расчет среднего абсолютного отклонения
На чтение 6 мин. Просмотров 1.3k. Опубликовано 27.07.2021
Статистические данные позволяют измерить разброс или разброс. Хотя чаще всего используются диапазон и стандартное отклонение, есть и другие способы количественной оценки дисперсии. Мы посмотрим, как рассчитать среднее абсолютное отклонение для набора данных.
Содержание
- Определение
- Варианты
- Пример: Среднее абсолютное отклонение относительно среднего
- Пример: Среднее абсолютное отклонение от среднего
- Пример: среднее абсолютное отклонение относительно медианы
- Пример: Среднее абсолютное отклонение от медианы
- Быстрые факты
- Распространенное использование
Определение
Начнем с определения среднего абсолютного отклонения, которое также называется средним абсолютным отклонением. Формула, отображаемая в этой статье, является формальным определением среднего абсолютного отклонения. Возможно, имеет смысл рассматривать эту формулу как процесс или серию шагов, которые мы можем использовать для получения нашей статистики.
- Мы начинаем со среднего значения или измерения центра набора данных, которое мы обозначим m.
- Затем мы находим, насколько каждый из значения данных отклоняются от m. Это означает, что мы берем разницу между каждым из значений данных и m.
- После этого мы берем абсолютное значение каждого отличия от предыдущего шага. Другими словами, мы отбрасываем любые отрицательные знаки для любых различий. Причина в том, что есть положительные и отрицательные отклонения от m. Если мы не найдем способ устранить отрицательные знаки, все отклонения нейтрализуют друг друга, если мы сложим их вместе.
- Теперь мы сложим все эти абсолютные значений.
- Наконец, мы делим эту сумму на n , которое представляет собой общее количество значений данных. Результат – среднее абсолютное отклонение.
Варианты
Существует несколько вариантов описанного выше процесса. Обратите внимание, что мы не указали точно, что такое m . Причина этого в том, что мы можем использовать различные статистические данные для m. Обычно это центр нашего набора данных, поэтому можно использовать любое из измерений центральной тенденции.
Наиболее распространенными статистическими измерениями центра набора данных являются среднее значение, медиана и мода. Таким образом, любой из них может использоваться как m при вычислении среднего абсолютного отклонения. Вот почему принято относиться к среднему абсолютному отклонению относительно среднего или среднему абсолютному отклонению от медианы. Мы увидим несколько примеров этого.
Пример: Среднее абсолютное отклонение относительно среднего
Предположим, что мы начнем со следующего набор данных:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
Среднее значение этого набора данных равно 5. Следующая таблица организует нашу работу по вычислению среднего абсолютного отклонения от среднего..
| Значение данных | Отклонение от среднего | Абсолютное значение отклонения |
| 1 | 1-5 = -4 | | -4 | = 4 |
| 2 | 2 – 5 = -3 | | -3 | = 3 |
| 2 | 2 – 5 = -3 | | -3 | = 3 |
| 3 | 3-5 = -2 | | -2 | = 2 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 9 | 9 – 5 = 4 | | 4 | = 4 |
| Сумма абсолютных отклонений: | 24 |
Теперь разделим эту сумму на 10, поскольку всего имеется десять значений данных. Среднее абсолютное отклонение от среднего составляет 24/10 = 2,4.
Пример: Среднее абсолютное отклонение от среднего
Теперь мы начинаем с другого набора данных:
1, 1, 4, 5, 5, 5, 5, 7, 7, 10.
Как и в предыдущем наборе данных, среднее значение этого набора данных равно 5.
| Значение данных | Отклонение от среднего | Абсолютное значение отклонения |
| 1 | 1-5 = -4 | | -4 | = 4 |
| 1 | 1-5 = -4 | | -4 | = 4 |
| 4 | 4-5 = -1 | | -1 | = 1 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 10 | 10 – 5 = 5 | | 5 | = 5 |
| Сумма абсолютных отклонений: | 18 |
Таким образом, среднее абсолютное отклонение от среднего составляет 18/10 = 1,8. Сравним этот результат с первым примером. Хотя среднее значение было одинаковым для каждого из этих примеров, данные в первом примере были более разбросанными. Из этих двух примеров видно, что среднее абсолютное отклонение от первого примера больше, чем среднее абсолютное отклонение от второго примера. Чем больше среднее абсолютное отклонение, тем больше разброс наших данных.
Пример: среднее абсолютное отклонение относительно медианы
Начните с того же набора данных, что и в первом примере:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
Медиана набора данных равна 6. В следующей таблице мы показываем детали расчета среднего абсолютного отклонения от медианы.
| Значение данных | Отклонение от медианы | Абсолютное значение отклонения |
| 1 | 1-6 = -5 | | -5 | = 5 |
| 2 | 2-6 = -4 | | -4 | = 4 |
| 2 | 2-6 = -4 | | -4 | = 4 |
| 3 | 3-6 = -3 | | -3 | = 3 |
| 5 | 5-6 = -1 | | -1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 9 | 9 – 6 = 3 | | 3 | = 3 |
| Сумма абсолютных отклонений: | 24 |
Снова делим сумму на 10 и получить среднее среднее отклонение от медианы как 24/10 = 2,4.
Пример: Среднее абсолютное отклонение от медианы
Начните с того же набора данных, что и раньше:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
На этот раз мы обнаруживаем, что режим этого набора данных равен 7. В следующей таблице мы показываем детали вычисления среднего абсолютного отклонения для режима.
| Данные | Отклонение от режима | Абсолютное значение отклонения |
| 1 | 1-7 = -6 | | -5 | = 6 |
| 2 | 2-7 = -5 | | -5 | = 5 |
| 2 | 2-7 = -5 | | -5 | = 5 |
| 3 | 3-7 = -4 | | -4 | = 4 |
| 5 | 5-7 = -2 | | -2 | = 2 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 9 | 9-7 = 2 | | 2 | = 2 |
| Сумма абсолютных отклонений: | 22 |
Делим сумму абсолютных отклонений и видим, что у нас есть среднее абсолютное отклонение о режиме 22/10 = 2.2.
Быстрые факты
Есть несколько основных свойств, касающихся средних абсолютных отклонений
- Среднее абсолютное отклонение от медианы всегда меньше или равно среднему абсолютному отклонению около значение.
- Стандартное отклонение больше или равно среднему абсолютному отклонению относительно среднего.
- Среднее абсолютное отклонение иногда сокращается до MAD. К сожалению, это может быть неоднозначным, поскольку MAD может альтернативно относиться к среднему абсолютному отклонению.
- Среднее абсолютное отклонение для нормального распределения примерно в 0,8 раза превышает размер стандартного отклонения.
Распространенное использование
Среднее абсолютное отклонение имеет несколько применений. Первое применение состоит в том, что эту статистику можно использовать для обучения некоторым идеям, лежащим в основе стандартного отклонения. Среднее абсолютное отклонение относительно среднего намного легче вычислить, чем стандартное отклонение. Это не требует, чтобы мы возводили отклонения в квадрат, и нам не нужно находить квадратный корень в конце нашего расчета. Кроме того, среднее абсолютное отклонение более интуитивно связано с разбросом набора данных, чем стандартное отклонение. Вот почему иногда сначала изучают среднее абсолютное отклонение, прежде чем вводить стандартное отклонение.
Некоторые зашли так далеко, что утверждают, что стандартное отклонение должно быть заменено средним абсолютным отклонением. Хотя стандартное отклонение важно для научных и математических приложений, оно не так интуитивно понятно, как среднее абсолютное отклонение. Для повседневных приложений среднее абсолютное отклонение – более ощутимый способ измерить разброс данных.
-
Различия между стандартными отклонениями для совокупности и выборки
-
Как рассчитать образец стандарта Отклонение
-
Эмпирическая взаимосвязь между средним, медианным и модой
-
Разница между средним и медианным значением и Режим
-
Что такое диапазон в статистике?
-
Когда стандартное отклонение равно нулю?
-
Разница между описательной и выводимой статистикой
-
Как определяются выбросы в статистике?
-
-
Как рассчитать стандарт населения Отклонение
-
Что такое первый и третий квартили?
-
Расчет Коэффициент корреляции
-
Пример доверительного интервала для дисперсии совокупности
-
Что такое моменты в статистике?
-
Дисперсия и стандартное отклонение
-
Ярлык формулы суммы квадратов
Содержание
- 1 Математическая теория
- 2 Практическое воплощение в Excel
- 3 Что измеряет стандартное отклонение?
- 4 Как рассчитать стандартное отклонение?
- 5 Функции расчета стандартного отклонения в Excel
- 5.1 Метод 1 Подготовка данных
- 5.2 Метод 2 Таблица данных
- 5.3 Метод 3 Вычисление стандартного отклонения
- 6 Что вам понадобится
- 7 Определение среднего квадратичного отклонения
- 8 Расчет в Excel
- 8.1 Способ 1: мастер функций
- 8.2 Способ 2: вкладка «Формулы»
- 8.3 Способ 3: ручной ввод формулы
- 8.4 Помогла ли вам эта статья?

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.
В Excel используются несколько вариантов этой функции отклонения:
- Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
- Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
- Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
- Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.
Математическая теория
Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.
Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!
Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: Описать формулу возможно так: среднеквадратическое отклонение будет измеряться в тех же единицах что и измерения случайной величины и применяется при вычислении стандартной среднеарифметической ошибки, когда производятся построения доверительных интервалов, при проверке гипотез на статистику или же при анализе линейной взаимосвязи между независимыми величинами. Функцию определяют, как квадратный корень из дисперсии независимых величин.
Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: 
Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.
Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:
=СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:
- Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.
Теперь создадим файл примера и на его основе рассмотрим работу этой функции. 
Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). 


=ЕСЛИ(H4
Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.
Что измеряет стандартное отклонение?
Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.
Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.
В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.
В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.
Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.
Как рассчитать стандартное отклонение?
Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.
Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.
Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.
Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.
Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.
Функции расчета стандартного отклонения в Excel
В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.
Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.
Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.
Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.
Метод 1 Подготовка данных
-
Соберите данные, которые вы хотите использовать в вашей таблице Excel.
-
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
- Excel имеет различные формулы для вычисления стандартного отклонение по выборке и стандартного отклонения по генеральной совокупности. Имейте это в виду, когда вы будете вводить формулу.
Метод 2 Таблица данных
-
Откройте программу Microsoft Excel.
- Функции Excel могут сильно отличаться, в зависимости от версии, которую вы используете. Если вы не можете найти нужную кнопку на панели инструментов, поищите ее в верхнем горизонтальном меню.
-
Составьте таблицу ваших данных.
В большинстве случаев, вы начнете с ячейки A1.
- Введите заголовки в верхних ячейках столбцов.
- Введите название или дату в первых ячейках каждой строки. Введите соответствующие данные в ячейках справа.
-
Сохраните документ Excel, чтобы избежать потери данных.
Метод 3 Вычисление стандартного отклонения
- Поставьте курсор в ячейку ниже последнего введенного значения.
- Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. Excel автоматически задаст ваш диапазон данных, если вы отметите соответствующие ячейки с данными.
-
Введите знак равенства. Помните, что формула должна вводиться без пробелов.
- Наберите «СТАНДОТКЛОН».
Это формула Excel для стандартного отклонения. При использовании этой формулы Excel будет автоматически вычислять среднее значение и стандартное отклонение.
- Выберите либо «СТАНДОТКЛОН» (вычисление по выборке), либо «СТАНДОТКЛОНП» (вычисление по генеральной совокупности).
- Укажите диапазон данных.
- В Excel диапазоны данных указываются в следующем виде: (C2:C15). Вся формула будет выглядеть как:»=СТАНДОТКЛОН(C2:C15)».
- Нажмите кнопку «Enter «.
Стандартное отклонение отобразится в ячейке.
- Вы можете также использовать функцию Excel для выбора формулы стандартного отклонения. Нажмите на «Вставить функцию» в строке формул. Затем выберите «Статистические » и выберите «СТАНДОТКЛОН». Введите свой диапазон данных в открывшемся окне. Нажмите «OK».
Что вам понадобится
- Microsoft Excel
- Данные
- Таблица данных
- Формула для вычисления стандартного отклонения
- Диапазон данных
Информация о статье
Эту страницу просматривали 67 780 раза.
Была ли эта статья полезной?
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Расчет дисперсии и среднего квадратического отклонения по индивидуальным данным и в рядах распределения.
Основными
обобщающими показателями вариации в
статистике являются дисперсии и среднее
квадратическое отклонение.
Дисперсия
— это средняя арифметическая квадратов
отклонений каждого значения признака
от общей средней. Дисперсия обычно
называется средним квадратом отклонений
и обозначается
.
В зависимости от исходных данных
дисперсия может вычисляться по средней
арифметической простой или взвешенной:
—дисперсия
невзвешенная (простая);
—дисперсия
взвешенная.
Среднее
квадратическое отклонение представляет
собой корень квадратный из дисперсии
и обозначается S:
—среднее
квадратическое отклонение невзвешенное;
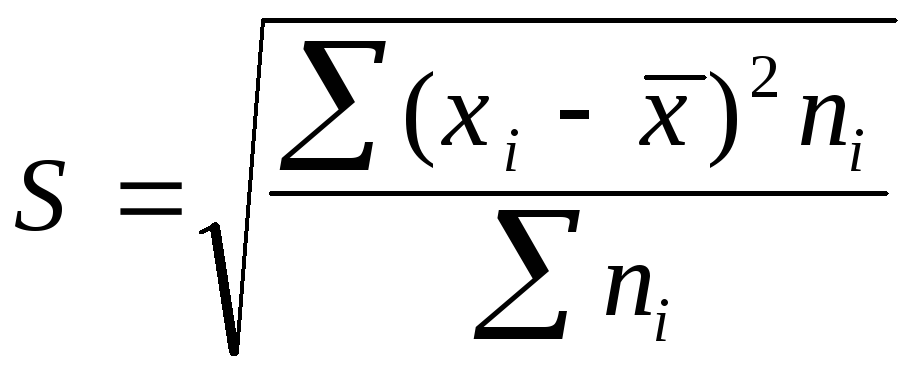
квадратическое отклонение взвешенное.
Среднее
квадратическое отклонение
— это обобщающая характеристика абсолютных
размеров вариации признака в совокупности.
Выражается оно в тех же единицах
измерения, что и признак (в метрах,
тоннах, процентах, гектарах и т.д.).
Среднее
квадратическое отклонение является
мерилом надежности средней. Чем меньше
среднее квадратическое отклонение, тем
лучше средняя арифметическая отражает
собой всю представляемую совокупность.
Вычислению
среднего квадратического отклонения
предшествует расчет дисперсии.
Порядок
расчета дисперсии взвешенную:
1)
определяют среднюю арифметическую
взвешенную
;
2)
определяются отклонения вариант от
средней
;
3)
возводят в квадрат отклонение каждой
варианты от средней
;
4)
умножают квадраты отклонений на веса
(частоты)
;
5)
суммируют полученные произведения
;
6)
Полученную сумму делят на сумму весов
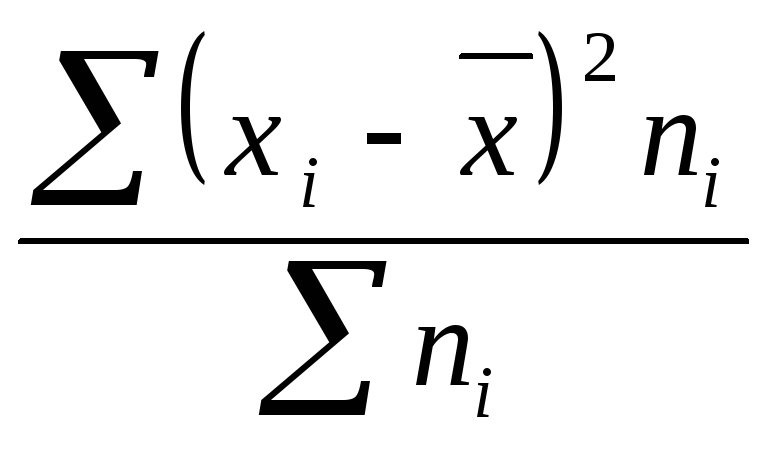
Пример
3.
Таблица
6.3.
|
Произведено ( |
Число |
|
|
|
|
|
8 |
7 |
56 |
-2 |
4 |
28 |
|
9 |
10 |
90 |
-1 |
1 |
10 |
|
10 |
15 |
150 |
0 |
0 |
0 |
|
11 |
12 |
132 |
1 |
1 |
12 |
|
12 |
6 |
72 |
2 |
4 |
24 |
|
ИТОГО |
50 |
500 |
74 |
Исчислим
среднюю арифметическую взвешенную:
шт.
Значения
отклонений от средней и их квадратов
представлены в таблице 6.3. Определим
дисперсию:
=1,48
Среднее
квадратическое отклонение будет равно:
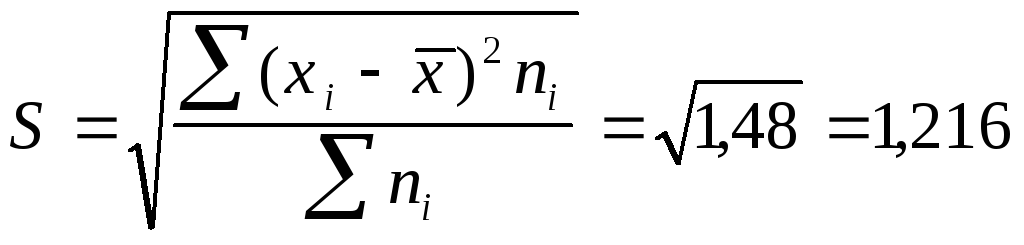
Если
исходные данные представлены в виде
интервального ряда распределения, то
сначала надо определить дискретное
значение признака, а далее применить
тот же метод, что изложен выше.
Пример
4.
Покажем
расчет дисперсии для интервального
ряда на данных о распределении посевной
площади колхоза по урожайности пшеницы:
Таблица
6.4
|
Урожайность |
Посевная |
|
|
|
|
|
|
14 |
100 |
15 |
1500 |
-3,4 |
11,56 |
1156 |
|
16 |
300 |
17 |
5100 |
-1,4 |
1,96 |
588 |
|
18 |
400 |
19 |
7600 |
0,6 |
0,36 |
144 |
|
20 |
200 |
21 |
4200 |
2,6 |
6,76 |
1352 |
|
ИТОГО |
1000 |
18400 |
3240 |
Средняя
арифметическая равна:
ц с
1га.
Исчислим
дисперсию:
Расчет дисперсии по формуле по индивидуальным данным и в рядах распределения.
Техника
вычисления дисперсии сложна, а при
больших значениях вариант и частот
может быть громоздкой. Расчеты можно
упростить, используя свойства дисперсии.
Свойства
дисперсии.
-
Уменьшение
или увеличение весов (частот) варьирующего
признака в определенное число раз
дисперсии не изменяет. -
Уменьшение
или увеличение каждого значения признака
на одну и ту же постоянную величину А
дисперсии не изменяет. -
Уменьшение
или увеличение каждого значения признака
в какое-то число раз к соответственно
уменьшает или увеличивает дисперсию
в
раз, а среднее квадратическое отклонение
— в к раз. -
Дисперсия
признака относительно произвольной
величины всегда больше дисперсии
относительно средней арифметической
на квадрат разности между средней и
произвольной величиной:
.
Если А равна нулю, то приходим к
следующему равенству:
,
т.е. дисперсия признака равна разности
между средним квадратом значений
признака и квадратом средней.
Каждое
свойство при расчете дисперсии может
быть применено самостоятельно или в
сочетании с другими.
Порядок
расчета дисперсии простой:
1)
определяют среднюю арифметическую
;
2)
возводят в квадрат среднюю арифметическую;
3)
возводят в квадрат каждую варианту ряда
;
4)
находим сумму квадратов вариант
;
5)
делят сумму квадратов вариант на их
число, т.е. определяют средний квадрат
;
6)
определяют разность между средним
квадратом признака и квадратом средней
.
Пример
5.
Имеются
следующие данные о производительности
труда рабочих:
Таблица
6.4
|
Табельный |
Произведено |
|
|
1 |
8 |
64 |
|
2 |
9 |
81 |
|
3 |
10 |
100 |
|
4 |
11 |
121 |
|
5 |
12 |
144 |
|
ИТОГО |
50 |
510 |
Произведем
следующие расчеты:
шт.
Пример
6.
Определить
дисперсию в дискретном ряду распределения,
используя табл. 6.5.
Таблица
6.5.
|
Произведено |
Число |
|
|
|
|
8 |
7 |
56 |
64 |
448 |
|
9 |
10 |
90 |
81 |
810 |
|
10 |
15 |
150 |
100 |
1500 |
|
11 |
12 |
132 |
121 |
1452 |
|
12 |
6 |
72 |
144 |
864 |
|
ИТОГО |
50 |
500 |
510 |
5074 |
Получим
тот же результат, что в табл. 6.3.
Рассмотрим
расчет дисперсии в интервальном ряду
распределения.
Порядок
расчета дисперсии взвешенной (по формуле
):
-
определяют
среднюю арифметическую
;
-
возводят
в квадрат полученную среднюю
;
-
возводят
в квадрат каждую варианту ряда
;
-
умножают
квадраты вариант на частоты
;
-
суммируют
полученные произведения
;
-
делят
полученную сумму на сумму весов и
получают средний квадрат признака
;
-
определяют
разность между средним значением
квадратов и квадратом средней
арифметической, т.е. дисперсию
.
Пример
7.
Имеются
следующие данные о распределении
посевной площади колхоза по урожайности
пшеницы:
Таблица
6.6
|
Урожайность |
Посевная |
|
|
|
|
|
14 |
100 |
15 |
1500 |
225 |
22500 |
|
16 |
300 |
17 |
5100 |
289 |
36700 |
|
18 |
400 |
19 |
7600 |
361 |
144400 |
|
20 |
200 |
21 |
4200 |
441 |
88200 |
|
ИТОГО |
1000 |
18400 |
341200 |
В
подобных примерах прежде всего
определяется дискретное значение
признака в каждом интервале, а затем
применяется метод расчета, указанный
выше:
Средняя
величина отражает тенденцию развития,
т.е. действие главных причин. Среднее
квадратическое отклонение измеряет
силу воздействия прочих факторов.
Соседние файлы в папке statistica
- #
- #
- #
- #
- #
- #
- #
- #
- #

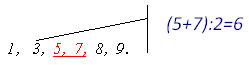































 Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
 Откройте программу Microsoft Excel.
Откройте программу Microsoft Excel.
 Составьте таблицу ваших данных.
Составьте таблицу ваших данных.