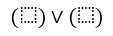Логические выражения и таблица истинности
Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
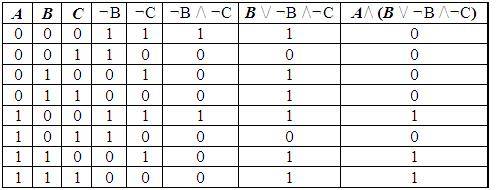
Пример 1. Для формулы A/ (B / ¬B /¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
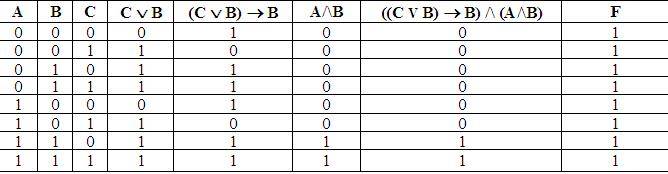
Пример 2. Определите истинность логического выражения F(А, В) = (А/ В)/(¬А/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А/ В; 2) ¬А; 3) ¬В; 4) ¬А/¬В; 5) (А/ В)/(¬А/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
|
А |
В |
А/ В |
¬А |
¬В |
¬А/¬В |
F |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A/ B) / ¬С
- В данной функции три логические переменные – А, В, С
- количество строк таблицы = 23 =8
- В формуле 3 логические операции.
- Расставляем порядок действий
1) А/ В; 2) ¬С; 3) (AVB) / ¬С .
- количество столбцов таблицы = 3 + 3 = 6
|
А |
В |
С |
A/B |
¬С |
(A/B) / ¬С |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Пример 4. Определите истинность формулы: F = ((С /В) => В) / (А / В) => В.
Построим таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
Какое выражение соответствует F?
1) ¬X/¬Y/Z 2) ¬X/¬Y/Z 3) X/Y/¬Z 4) X/Y/Z
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
|
X |
Y |
Z |
F |
¬X |
¬Y |
¬Z |
¬X/¬Y/Z |
¬X/¬Y/Z |
X/Y/¬Z |
X/Y/Z |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
Очевидно, что значения заданной функции F совпадают со значениями выражения X/Y/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/¬Y/Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X/¬Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X/Y/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X/Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
Сегодня мы постараемся объяснить, как составить таблицу истинности для логического выражения. Обратите внимание на то, что булева алгебра встречается, по меньшей мере, в трех заданиях единого государственного экзамена. Если вы прочитаете данную статью, то, наверняка, получите больше баллов на экзамене по информатике.
Операции
Перед тем как составлять таблицу истинности, предлагаем познакомиться с операциями булевой алгебры.
Начнем наше знакомство с функцией отрицания. Ее также называют инверсией. Приведем такой пример: выражение «я сегодня иду в кино». Применяем к нему инверсию, в результате имеем: «я сегодня НЕ иду в кино».
Теперь поговорим о функциях умножения и сложения, в булевой алгебре они имеют названия – конъюнкция и дизъюнкция соответственно. Предположим, нам говорят: «ты пойдешь в кино, если выучишь уроки и вынесешь мусор». В данном предложении союз «И» выполняет функцию конъюнкции, а «ЕСЛИ» – дизъюнкции.
Логическое следствие – это еще одна сложная операция логики, которая содержит в себе два выражения: условие и следствие. Если интерпретировать на русский язык, то предложение строится примерно следующим образом: «если я успею выучить литературу, то пойду в кино». Часть предложения до запятой – условие, а после запятой – следствие.
Теперь коротко о функции эквивалентности или равнозначности. Провести параллель с русским языком в данном случае довольно сложно. Для равнозначности стоит запомнить, что если два входных выражения являются либо ложными, либо истинными, то результат положительный, то есть равен единице.
Алгоритм
Сейчас мы поговорим о том, как составить таблицу истинности по информатике, а точнее, обсудим алгоритм наших действий.
Для составления таблицы, в первую очередь необходимо определиться с количеством ячеек, столбцов и строк. Будем все делать поэтапно.
- Определяем количество строк. Для этого необходимо подсчитать, сколько переменных входит в состав выражения, и возвести двойку в это число. Например, как составить таблицу истинности, а точнее узнать количество строк для выражения с тремя переменными? Два возводим в третью степень и получаем восемь. Без учета шапки, нам понадобится восемь строк.
- Для того чтобы определить количество столбцов, нам необходимо подсчитать и пронумеровать операции в данном выражении. Например, в выражении неА*С+В всего три операции. Первая – отрицание, вторая – умножение, третья – сложение. Значит для заполнения значений операций нам нужно три колонки. Но, стоит учитывать и то, что наше выражение состоит из трех переменных, а нам необходимо заполнить их возможные комбинации, добавляем еще три колонки. Итого получается 6.
- Далее переходим к перечислению возможных комбинаций переменных и заполнению таблицы. Обязательно учитывайте приоритет операций.
Первый пример (три переменных)
Предлагаем вам решить следующую задачу: вычислите, сколько комбинаций удовлетворяют условию F=1 выражения: (неА+В)*неС+А. А сейчас о том, как составить таблицу истинности для решения задачи. Прибегаем к помощи составленного алгоритма действий.
- Количество строк=9 (восемь комбинаций переменных + одна строчка – шапка таблицы).
- Приоритет функций: 1- инверсия, 2 – сложение в скобках, 3 – инверсия С, 4 – умножение, 5 – сложение.
- Количество столбцов = 8.
- Составление таблицы и заполнение.
|
Выражение А |
Выражение В |
Выражение С |
Операция №1 |
Операция №2 |
Операция №3 |
Операция №4 |
Операция №5 |
|
— |
— |
— |
+ |
+ |
+ |
+ |
И |
|
— |
— |
+ |
+ |
+ |
— |
— |
Л |
|
— |
+ |
— |
+ |
+ |
+ |
+ |
И |
|
— |
+ |
+ |
+ |
+ |
— |
— |
Л |
|
+ |
— |
— |
— |
— |
+ |
— |
И |
|
+ |
— |
+ |
— |
— |
— |
— |
И |
|
+ |
+ |
— |
— |
— |
+ |
— |
И |
|
+ |
+ |
+ |
— |
— |
— |
— |
И |
- Нахождение ответа на вопрос.
- Запись ответа. Ответ:6. Обратите внимание на то, что в условии задания спрашивается сколько комбинаций удовлетворяют, но не просится их перечислять.
Второй пример (4 переменных)
Предлагаем вам рассмотреть вопрос: как составить таблицу истинности для формулы: А*В*неС+D? Какое количество комбинаций соответствует: F=0.
Действуем по тому же алгоритму. Количество строк в нашем случае увеличивается до 17, а столбцов – до 8. Приоритет операций:
- А*В;
- неС;
- перемножение результатов первой и второй операции;
- сложение результат третьей операции и значения переменной D.
Предлагаем вам самостоятельно попробовать составить и заполнить таблицу, а затем свериться с результатами в данном разделе статьи.
|
Переменная А |
Переменная В |
Переменная С |
Переменная D |
Умножение (1) |
Инверсия (2) |
Умножение (3) |
Сложение (4) |
|
— |
— |
— |
— |
— |
+ |
— |
— |
|
— |
— |
— |
+ |
— |
+ |
— |
+ |
|
— |
— |
+ |
— |
— |
— |
— |
— |
|
— |
— |
+ |
+ |
— |
— |
— |
+ |
|
— |
+ |
— |
— |
— |
+ |
— |
— |
|
— |
+ |
— |
+ |
— |
+ |
— |
+ |
|
— |
+ |
+ |
— |
— |
— |
— |
— |
|
— |
+ |
+ |
+ |
— |
— |
— |
+ |
|
+ |
— |
— |
— |
— |
+ |
— |
— |
|
+ |
— |
— |
+ |
— |
+ |
— |
+ |
|
+ |
— |
+ |
— |
— |
— |
— |
— |
|
+ |
— |
+ |
+ |
— |
— |
— |
+ |
|
+ |
+ |
— |
— |
+ |
+ |
+ |
+ |
|
+ |
+ |
— |
+ |
+ |
+ |
+ |
+ |
|
+ |
+ |
+ |
— |
+ |
— |
— |
— |
|
+ |
+ |
+ |
+ |
+ |
— |
— |
+ |
Из полученной таблицы мы делаем вывод: данному условию удовлетворяет 7 различных комбинаций переменных.
Построение таблиц истинности
Екатерина Андреевна Гапонько
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Определение 2
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Определение 3
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
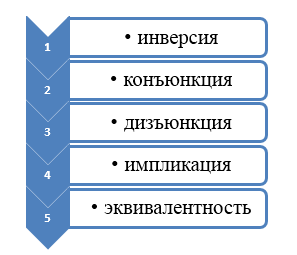
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Рисунок 1.
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
-
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
-
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
-
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
«Построение таблиц истинности» 👇
Рисунок 2.
Пример 1
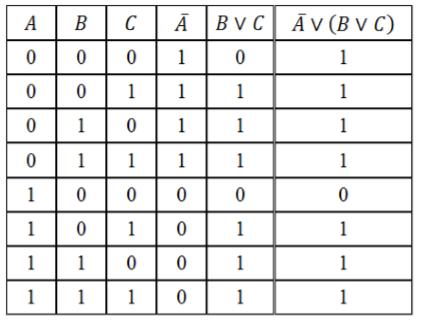
Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- инверсия ($bar{A}$);
- дизъюнкция, т.к. она находится в скобках ($B vee C$);
-
дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.
Кол-во столбцов = $3 + 3=6$.
-
Заполним таблицу, учитывая таблицы истинности логических операций.
Рисунок 3.
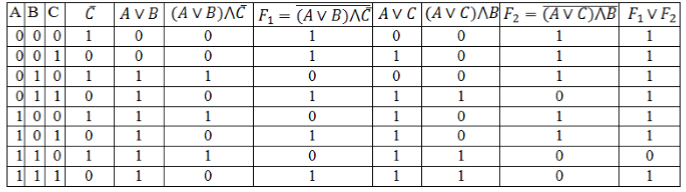
Пример 2
По данному логическому выражению построить таблицу истинности:
[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($bar{C}$);
- дизъюнкция, т.к. она находится в скобках ($A vee B$);
- конъюнкция ($(Avee B)bigwedge overline{C}$);
- отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
- дизъюнкция ($A vee C$);
- конъюнкция ($(Avee C)bigwedge B$);
- отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);
-
дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).
Кол-во столбцов = $3 + 8 = 11$.
-
Заполним таблицу, учитывая таблицу истинности логических операций.
Рисунок 4.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
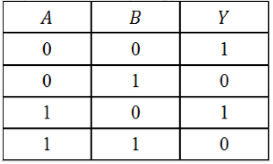
Пример 3
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
Рисунок 5.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Рисунок 6.
- Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
- В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 12.04.2016
Инфоурок
›
Информатика
›Презентации›Построение таблиц истинности для сложных высказываний.
Построение таблиц истинности для сложных высказываний.
Скачать материал

Скачать материал


- Сейчас обучается 83 человека из 36 регионов


- Сейчас обучается 46 человек из 24 регионов


- Сейчас обучается 39 человек из 27 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ ДЛЯ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ. Подготовила учитель информатики высшей категории Габриэль Татьяна Васильевна
-
2 слайд
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ Сложные высказывания можно записывать в виде формул. Для этого простые логические высказывания нужно обозначить как логические переменные буквами и связать их с помощью знаков логических операций. Такие формулы называются логическими выражениями. Например:
-
3 слайд
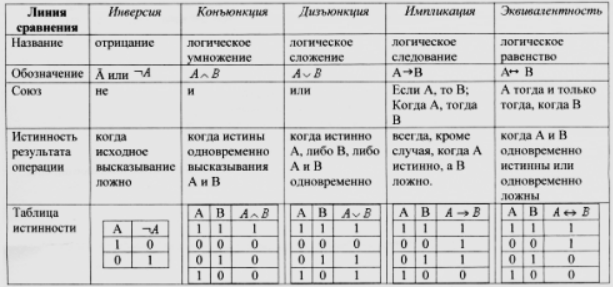
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ Чтобы определить значение логического выражения необходимо подставить значения логических переменных в выражение и выполнить логические операции. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: 1. инверсия; 2. конъюнкция; 3. дизъюнкция; 4. импликация и эквивалентность. Для изменения указанного порядка выполнения логических операций используются круглые скобки.
-
4 слайд
ТАБЛИЦЫ ИСТИННОСТИ Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет истинность или ложность логического выражения при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
-
5 слайд
АЛГОРИТМ ПОСТРОЕНИЯ ТАБЛИЦЫ ИСТИННОСТИ 1) записать выражение и определить порядок выполнения операций 2) определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (определяется по формулеQ=2n + 1, где n — количество входных переменных) 3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций) 4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных. 5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности
-
6 слайд
Например, построим таблицу истинности для логической функции: Количество входных переменных в заданном выражении равно трем (A,B,C). Значит, количество входных наборов, а значит и строк Q=23=8. Количество столбцов равно 6 (3 переменные + 3 операции). Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов и (B V C), а также искомого окончательного значения сложного арифметического выражения
-
-
8 слайд
ABCB V C 000 001 010 011 100 101 110 111
-
9 слайд
ABCB V C 000100 001111 010111 011111 100000 101010 110010 111010
-
10 слайд
Задание. Постройте таблицу истинности для данного логического выражения: Количество входных переменных в заданном выражении равно двум (A,B,). Значит, количество входных наборов, а значит и строк Q=22 =4 + 1 =5, а количество столбцов равно 2 + 4 = 6 АBАVB¬A¬АVB 00 01 10 11
-
11 слайд
Проверка АВ 000110 011111 101000 111011
Краткое описание документа:
Презентация к уроку информатики и ИКТ на тему: «Построение таблиц истинности для сложных высказываний» в 10 профильном классе. Презентация может быть использована для объяснения новой темы. Программа профильного курса рассчитана на 280 часов по 4 часа в неделю. Используется учебник Н. Д. Угриновича, глава: «Основы логики и логические основы компьютера» и программа дистанционного курса по информатике и ИКТ(http://elearning.edu54.ru/Курс рассчитан на 280 учебных часов, включает в себя 18 дистанционных модулей).
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 063 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 15.05.2014
- 1394
- 3
- 15.05.2014
- 4183
- 155
- 15.05.2014
- 1951
- 48
- 15.05.2014
- 981
- 0
Рейтинг:
5 из 5
- 15.05.2014
- 3562
- 17
- 15.05.2014
- 1240
- 0
- 14.05.2014
- 736
- 16
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
-
Настоящий материал опубликован пользователем Габриэль Татьяна Васильевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 10 месяцев
- Подписчики: 0
- Всего просмотров: 4738
-
Всего материалов:
4
Файлы
Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….
13
4.1.Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание
«(2·2=5 или 2·2=4) и (2·2≠5 или 2·2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0), В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме: «(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
14
4.2.Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
1) необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В нашем случае логическая функция 
2)необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
3)необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
4)необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
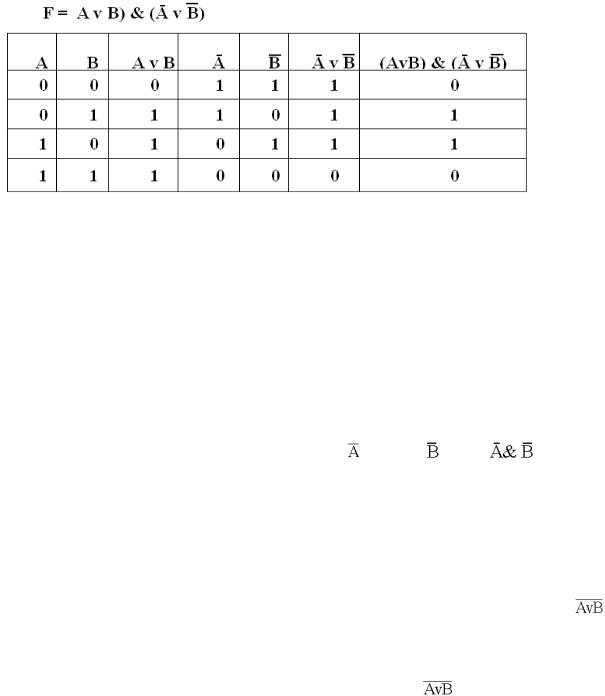
15
Таблица 8 – Таблица истинности логической функции
4.3.Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов-
падают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения 

ца 9).
Таблица 9 – Таблица истинности логического выражения
|
А |
В |
|||
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
Теперь построим таблицу истинности логического выражения (таблица 10).
Таблица 10 – Таблица истинности логического выражения
|
А |
В |
А v В |
|
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:

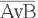
16
5. Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений
|
переменных всего четыре: |
|||
|
(0, 0), |
(0, 1), |
(1, 0), |
(1, 1). |
Если формула содержит три переменные, то возможных наборов значений
|
переменных восемь: |
|||||||
|
(0, 0, 0), |
(0, 0, 1), |
(0, 1, 0), |
(0, 1, 1), |
(1, 0, 0), |
(1, 0, 1), |
(1, 1, 0), |
(1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
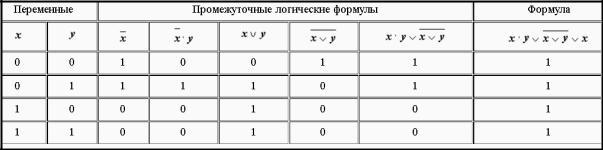
Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере-
менные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:
Таблица 11 – Таблица истинности для формулы с переменными Х и У
Пример 2
Cоставить таблицу истинности сложного логического выражения: D = неA & (B+C).
А, В, С – три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С) количество столбцов (таблица 12):
1)А,
2)В,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #