Как составить судоку для детей

Была ли эта статья полезной?

Мы часто встречаем в газетах и журналах в разделе «Досуг» головоломку судоку. Это игра с цифрами, которые в определенном порядке необходимо разместить в квадрате с ячейками. Судоку — не только развивающее логику, но и расслабляющее занятие — недаром фанаты игры советуют «решать не торопясь и получая удовольствие от процесса».

Многие считают родиной головоломки судоку Японию — из-за названия, соединенного из двух японских слов: Su (число) и doku (единственное). Но это не совсем верно. Имя Sudoku игра получила только в 1985-м году — к тому времени она была уже известна в Америке, но называлась «Место Числа» («Number Plaсe»). Хотя справедливости ради можно заметить, что популярность логическая игра получила именно под японским именем.

С историей ее появления нет полной ясности. Прообразом современной игры можно считать и древнекитайский «Магический квадрат», и «Латинский квадрат», изобретенный в ХVIII веке швейцарцем Эйлером.

Суть игры судоку

В классическом варианте судоку — это квадрат со стороной в 9 ячеек, в каждую из них нужно вписать цифры от 1 до 9 так, чтобы они не повторялись ни по горизонтали, ни по вертикали, ни в маленьких квадратиках 3х3, из которых состоит большой квадрат.

Некоторые из чисел уже поставлены — это подсказки (или ключи), от которых нужно отталкиваться при решении судоку.

В зависимости от количества и местоположения этих ключей судоку может менять уровень сложности: от простого, где место каждой цифры однозначно, до сложного, в котором приходится просчитывать варианты подстановки чисел на несколько ходов вперед.

Но судоку для детей можно и упростить. Например, уменьшить квадрат и количество цифр, которые необходимо расставлять.

Важно помнить: любая судоку имеет единственное правильное решение.

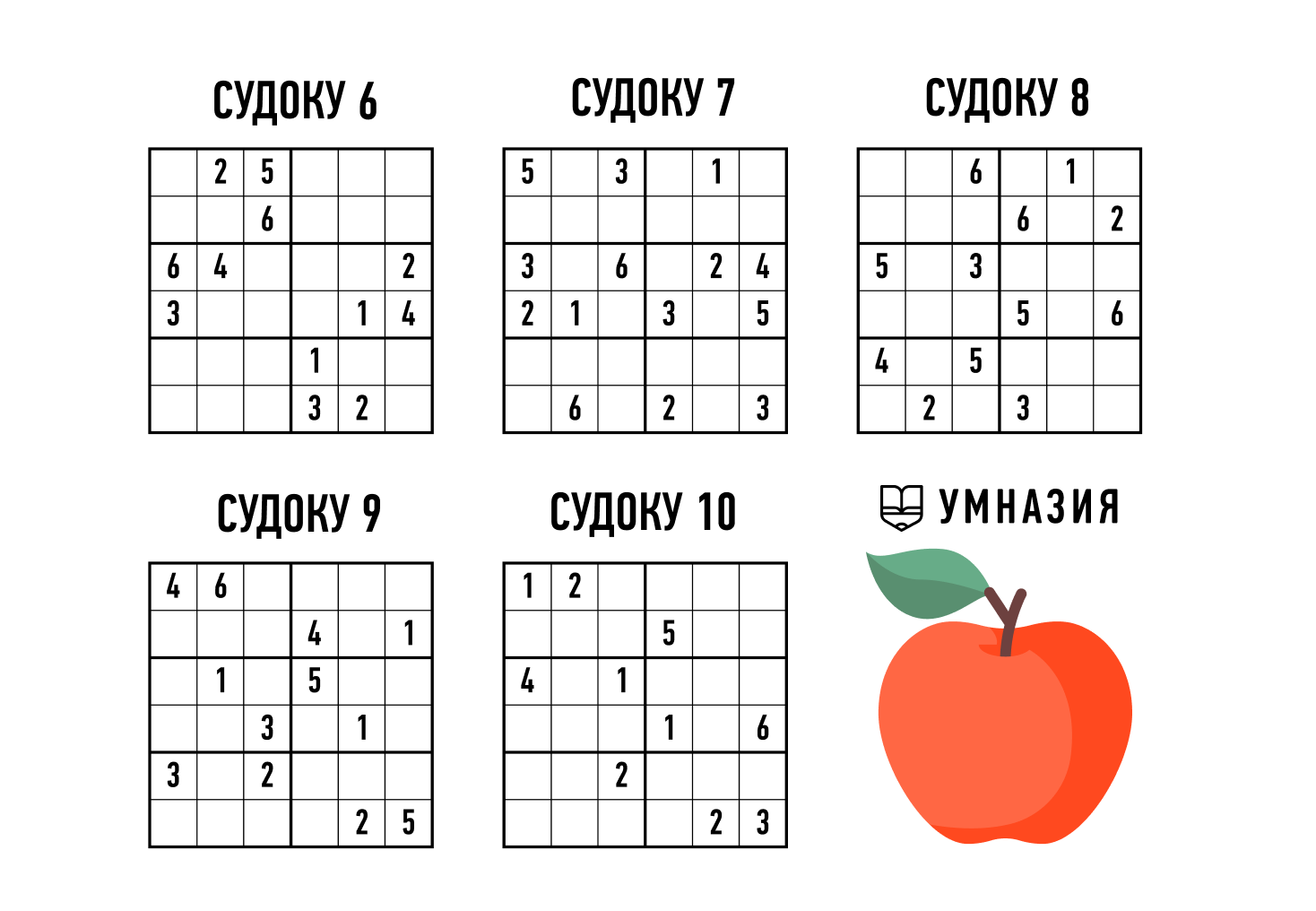
Судоку для детей

Не стоит думать, что маленьким детям будет неинтересно решать судоку. Конечно, сразу предлагать классический вариант с большим полем и цифрами не стоит. Но судоку с полем 3х3 или 4х4 и картинками вместо цифр — почему нет?

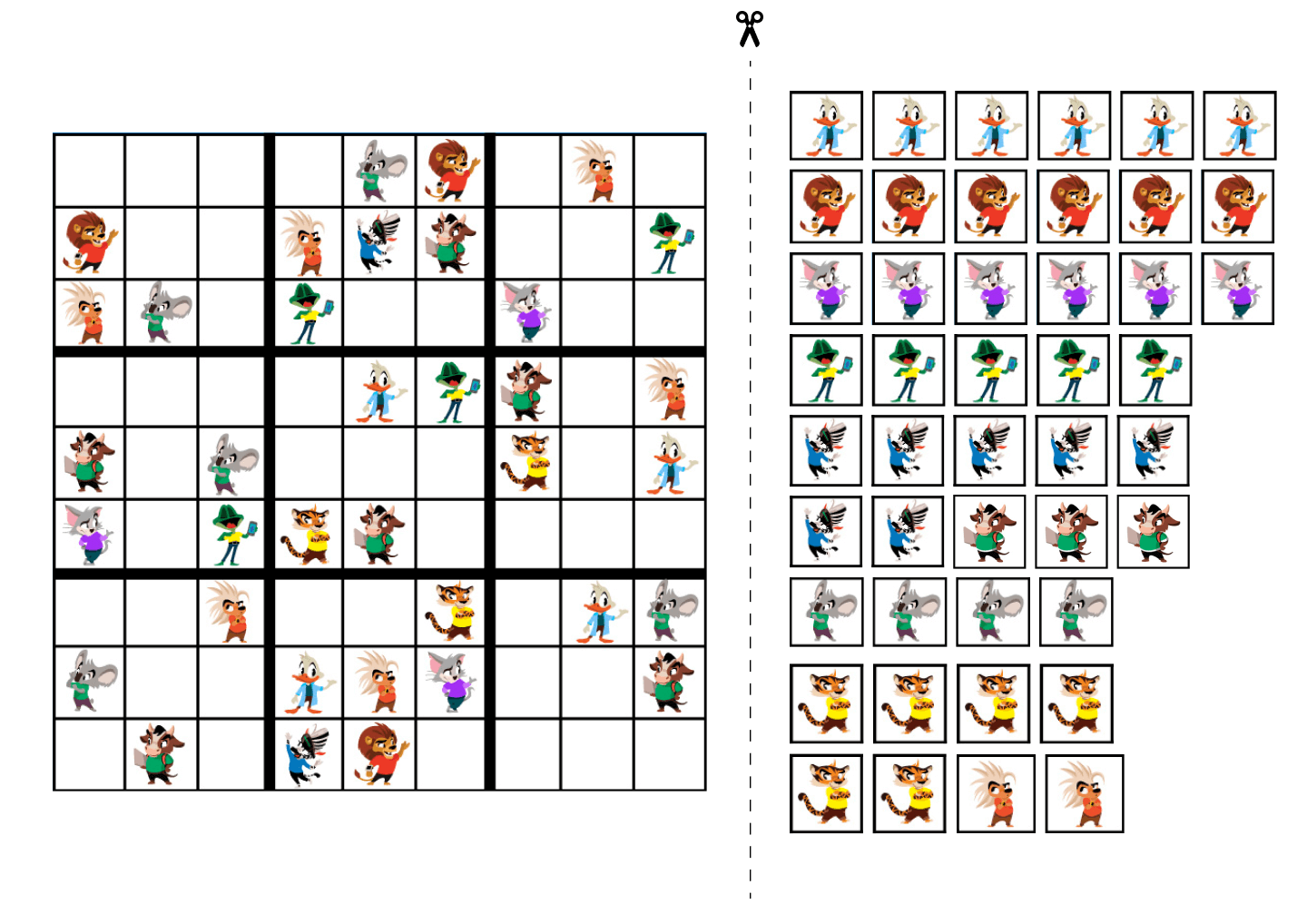
Можно распечатать поле для судоку и отдельно картинки. Тогда задание превратится в своеобразный пазл — с той только разницей, что ребенку нужно будет подумать перед тем, как поставить картинку в нужное место.

Игра вполне может увлечь вашего малыша, а польза от нее будет обязательно.

В чем польза судоку для детей?

Как и любая логическая игра, судоку направлено в первую очередь на развитие логики. Чтобы правильно поставить цифру/картинку, ребенок должен проанализировать все поле судоку, а это совсем непросто, особенно без навыка.

При решении судоку развивается внимание и усидчивость. Одной из особенностей этой игры является необходимость сконцентрироваться на задании — без этого неизбежны ошибки.

И, наконец, судоку — одна из немногих логических игр, в которой результат можно оценить визуально: правильно решенная головоломка приносит не только моральное, но и эстетическое удовлетворение, ощущение «правильности» и упорядоченности. Такие маленькие победы очень важны для малышей.

Необходимо отметить, что, несмотря на огромное количество судоку (в том числе и детских), представленных в онлайн-вариантах на различных платформах и гаджетах, первые судоку ребенок должен решить «на бумажке». Для этого задание необходимо скачать и распечатать.

Пример решения детского судоку

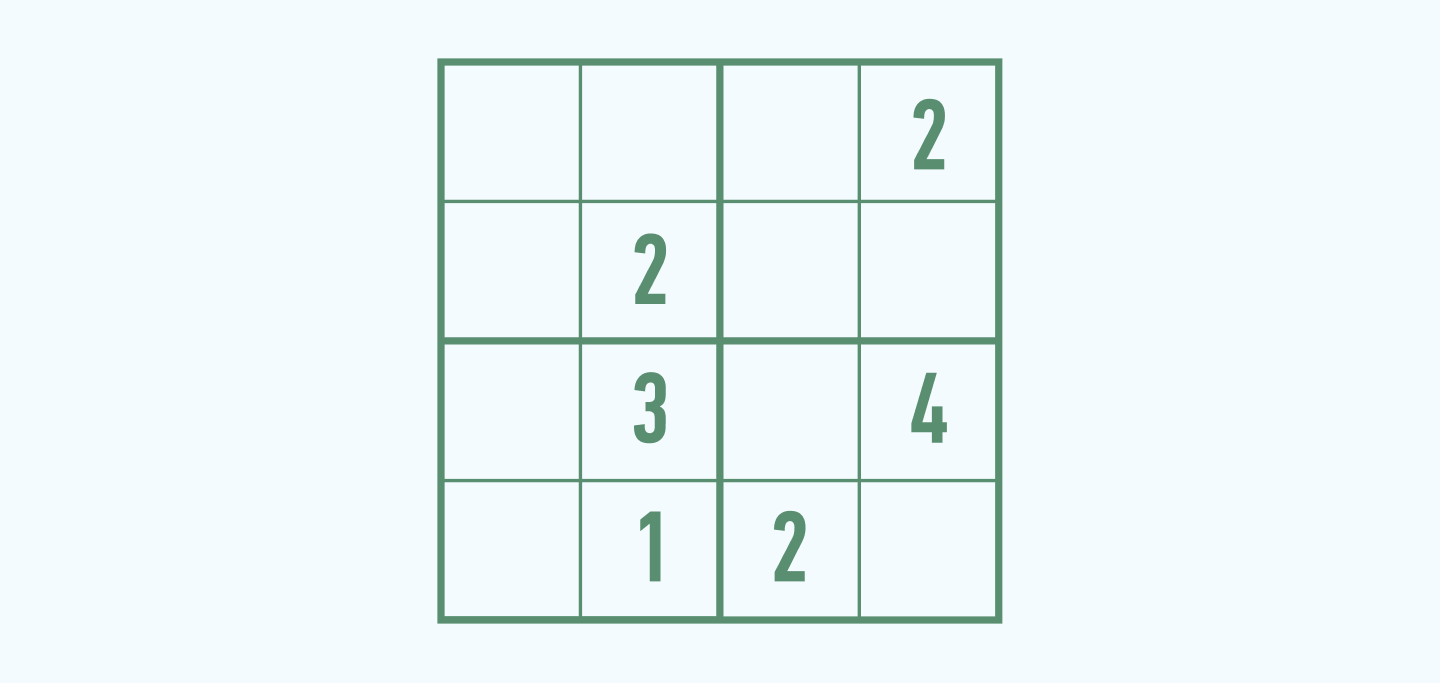
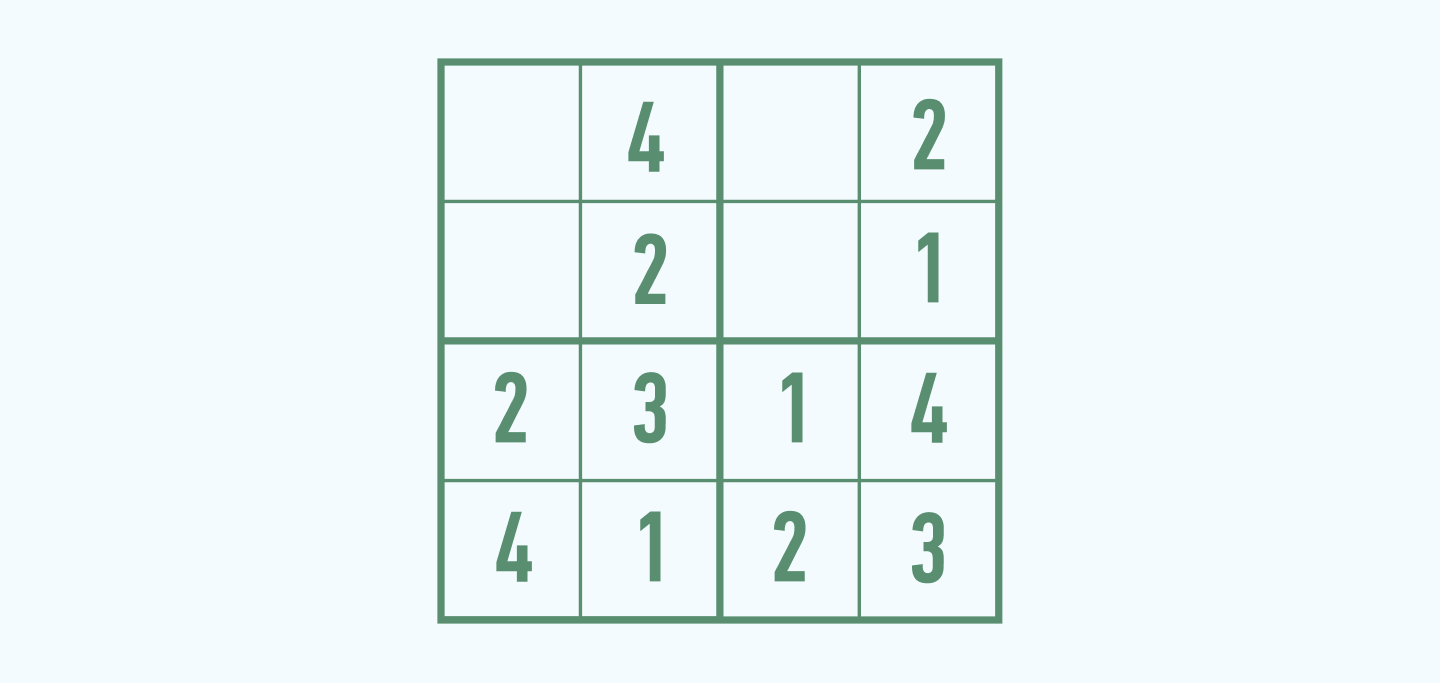
Простой вариант для ребенка — судоку 4х4. Цифры в ячейках нужно расставить так, чтобы они не повторялись в линиях по горизонтали, по вертикали и в маленьких квадратах 2 на 2 (таких квадратов в данном случае четыре).

Начинать решение лучше с того маленького блока, столбца или строки, где больше заполненных ячеек. Например, во второй вертикальной строке уже стоят три цифры из четырех — 1, 2 и 3. Нам останется добавить только цифру 4.

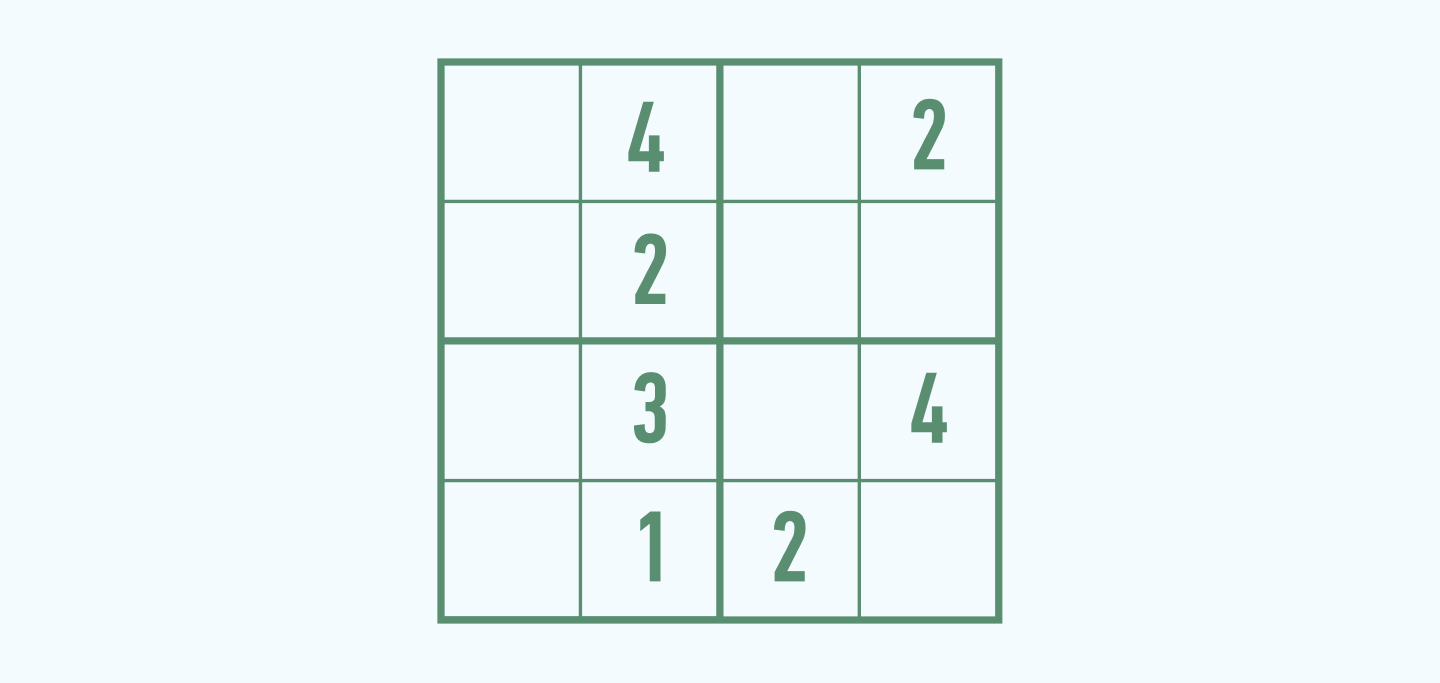
Теперь обратимся к нижнему левому квадрату. В нем уже есть цифры 3 и 1. Нам осталось найти место для двойки и четверки. В верхнюю клеточку этого квадрата мы не сможем поставить цифру 4, так как она уже есть в данной строке; а в нижнюю ячейку не можем поставить 2, потому что двойка уже присутствует в нижней строке. Таким образом, в верхнюю ячейку нужно поставить 2, а в нижнюю — 4.

Теперь мы можем с легкостью заполнить недостающими цифрами — 1 и 3 — две нижние строки.

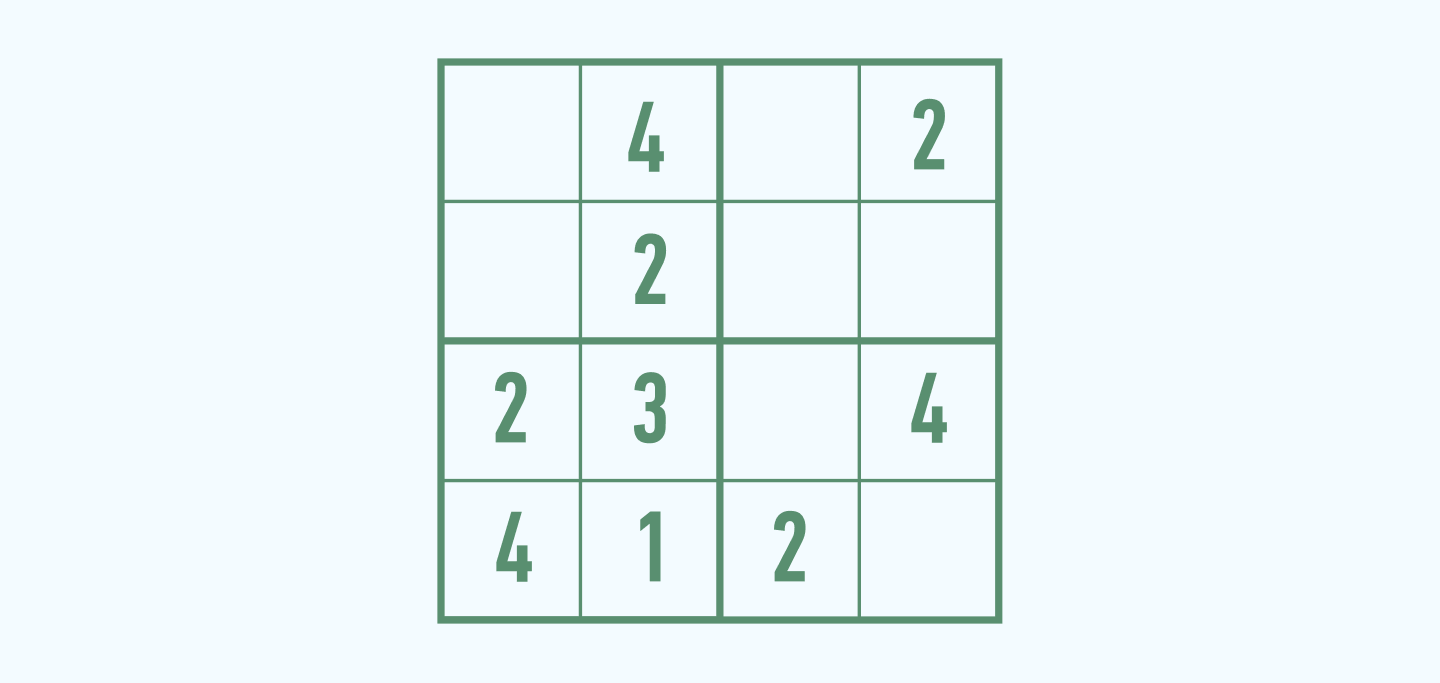
В крайнем правом столбце осталась незаполненной одна ячейка — смело ставим в нее единицу.

Обратимся к левому верхнему блоку. В нем недостает цифр 1 и 3. Тройку можно поставить в любую из ячеек, а вот единицу — только в верхнюю, так как она уже присутствует во второй строке сверху. Соответственно, в верхнюю ячейку ставим 1, а в нижнюю — 3.

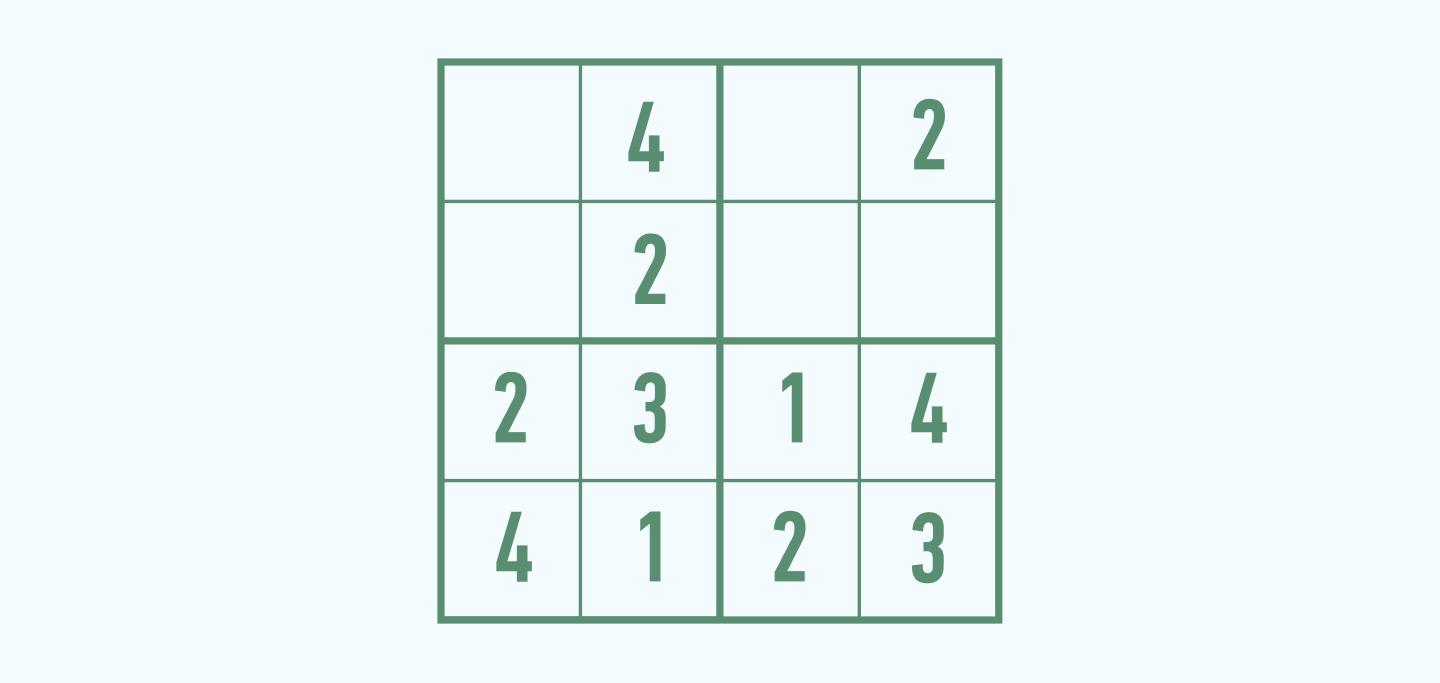
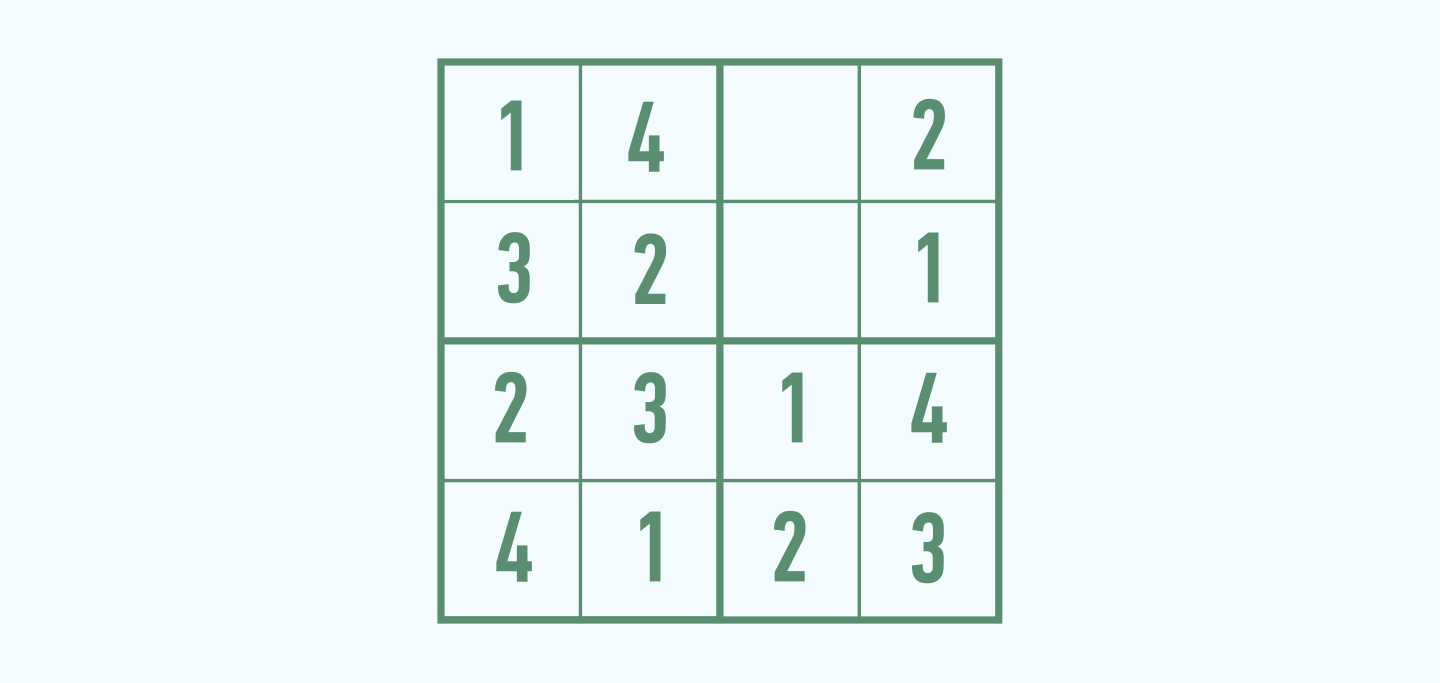
Теперь нетрудно догадаться, какие цифры нужно подставить в оставшиеся ячейки.

Проверяем, чтобы не было повторений ни в одной из горизонталей и вертикалей. Все правильно? Судоку решено!

Первое судоку, конечно, взрослый должен решить вместе с ребенком. Но — обязательно проговаривая вслух ход рассуждений и привлекая ребенка к обсуждению: «Какой цифры здесь не хватает? Может быть, поставим сюда тройку? А, нет, здесь уже есть тройка» — и так далее.

Важно понять алгоритм действий: выбираем объект (вертикаль, горизонталь или блок), в котором минимум неизвестных и пытаемся заполнить в нем клетки. Не обязательно все сразу — в сложных судоку так точно не получится. И потом — как в кроссворде: после подстановки новой цифры проверяем, что дают эти новые знания для дальнейшего решения.

Детские судоку в картинках

Так как судоку свойства чисел никак не используются, для детей цифры можно заменить картинками. Есть даже довольно милый вариант, когда клетки судоку нужно не заполнять символами, а раскрашивать в разные цвета. И задание, и решенная головоломка выглядят в этом случае очень нарядно.

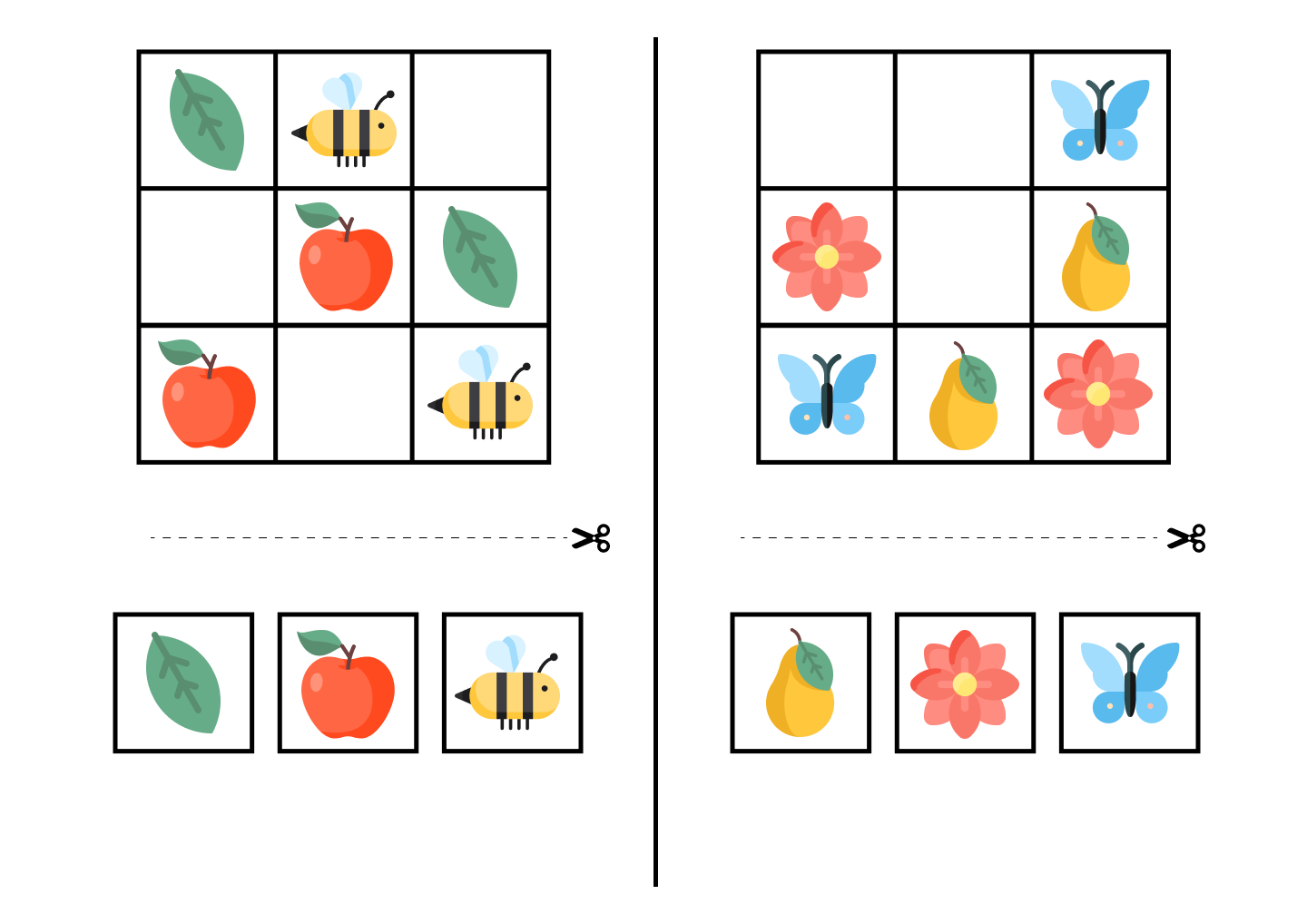
Судоку 3 на 3 для детей

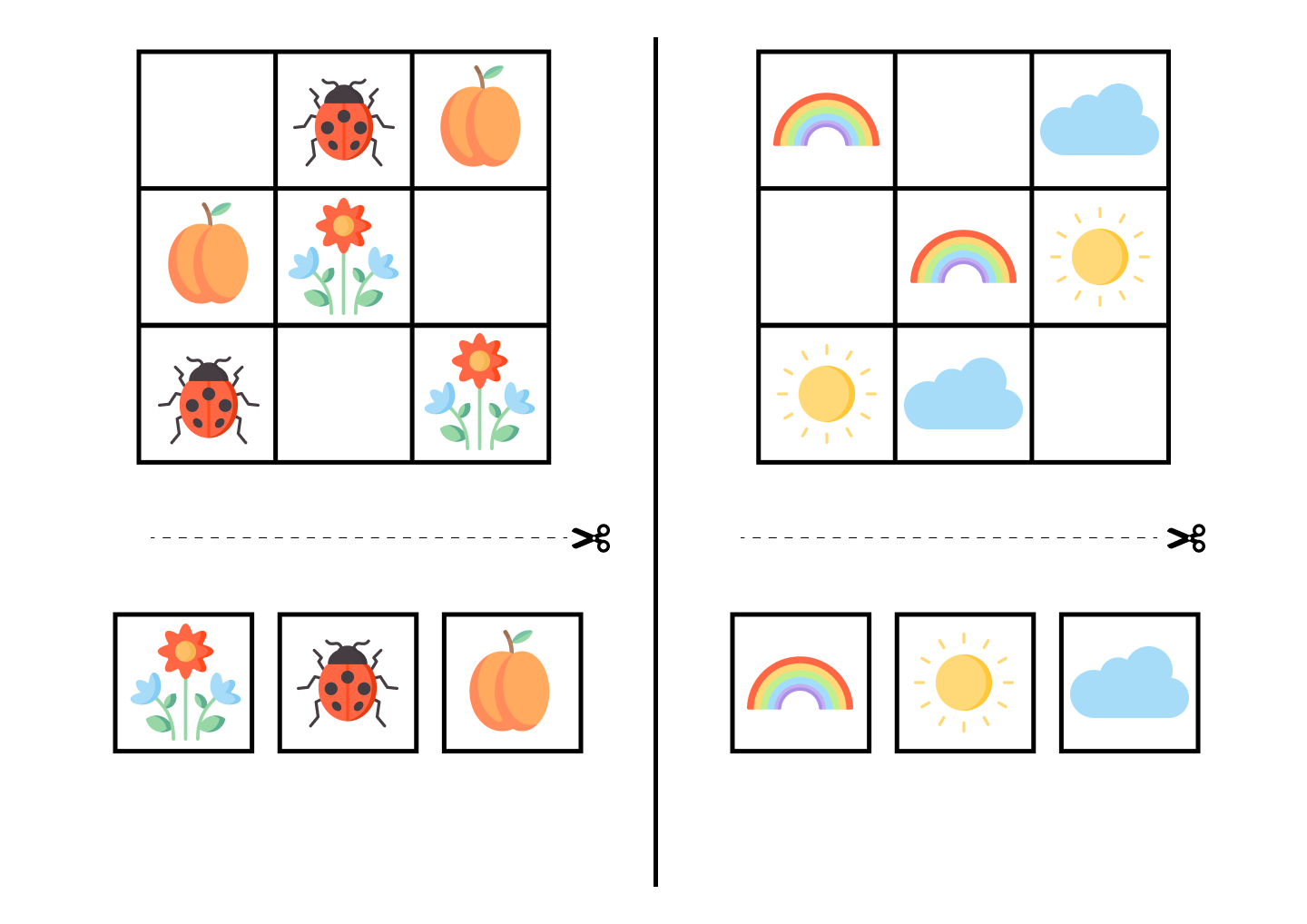
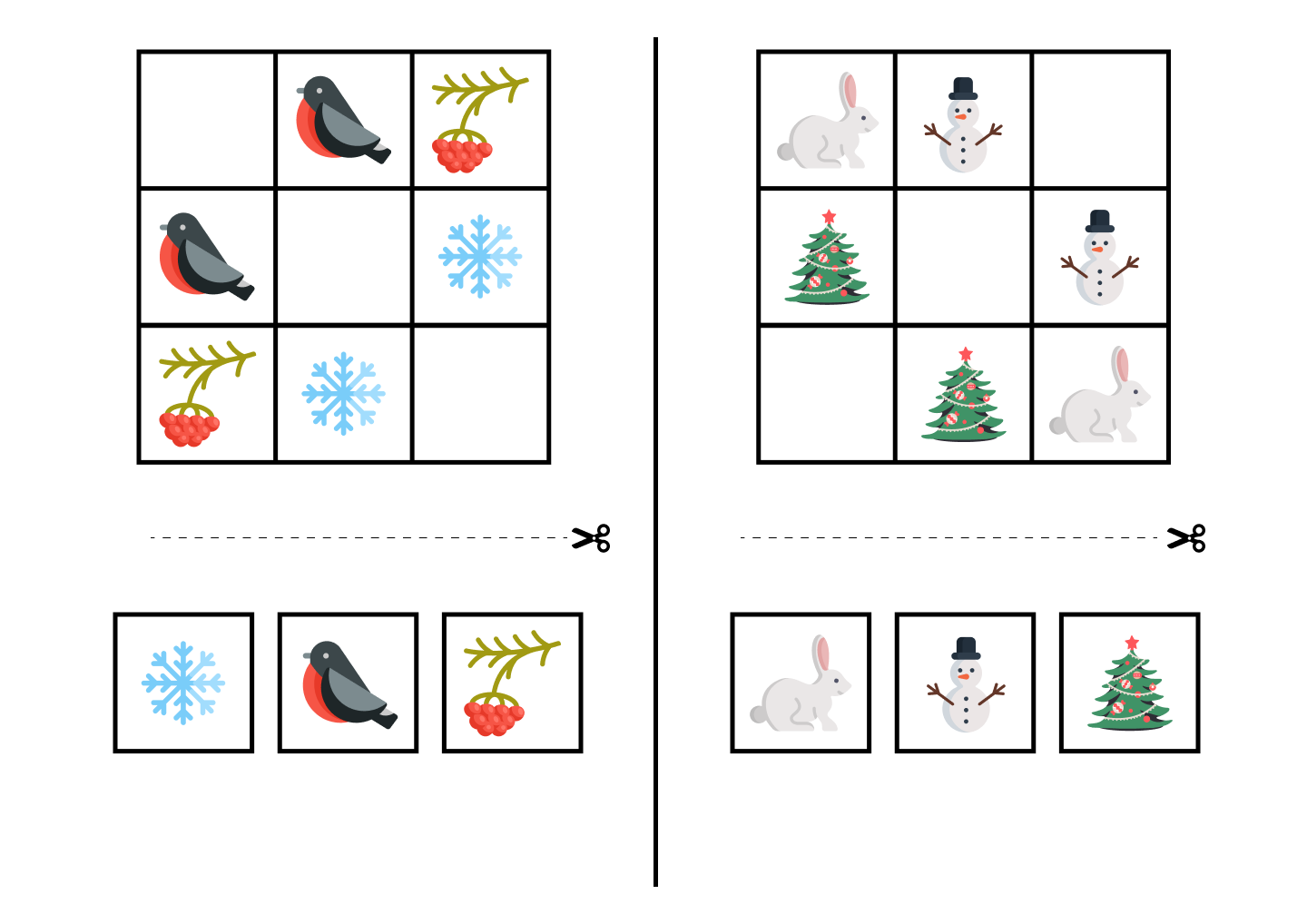
Самым маленьким даже судоку 4х4 могут оказаться не по силам. Начинать нужно с самого простого — 3х3 с картинками.

Распечатайте и вырежьте судоку и отдельно картинки. Их нужно расставлять таким образом, чтобы не было повторений по вертикали и горизонтали.

Эти примеры решаются очень просто: находите линию, на которой 2 ячейки заполнены — и ставите единственную картинку, которая отсутствует. Теперь уже на другой линии 2 заполненные ячейки — и так далее.

Эти судоку легко решать не только потому, что здесь мало ячеек, но и из-за отсутствия блоков — здесь нужно смотреть только на вертикали и горизонтали.

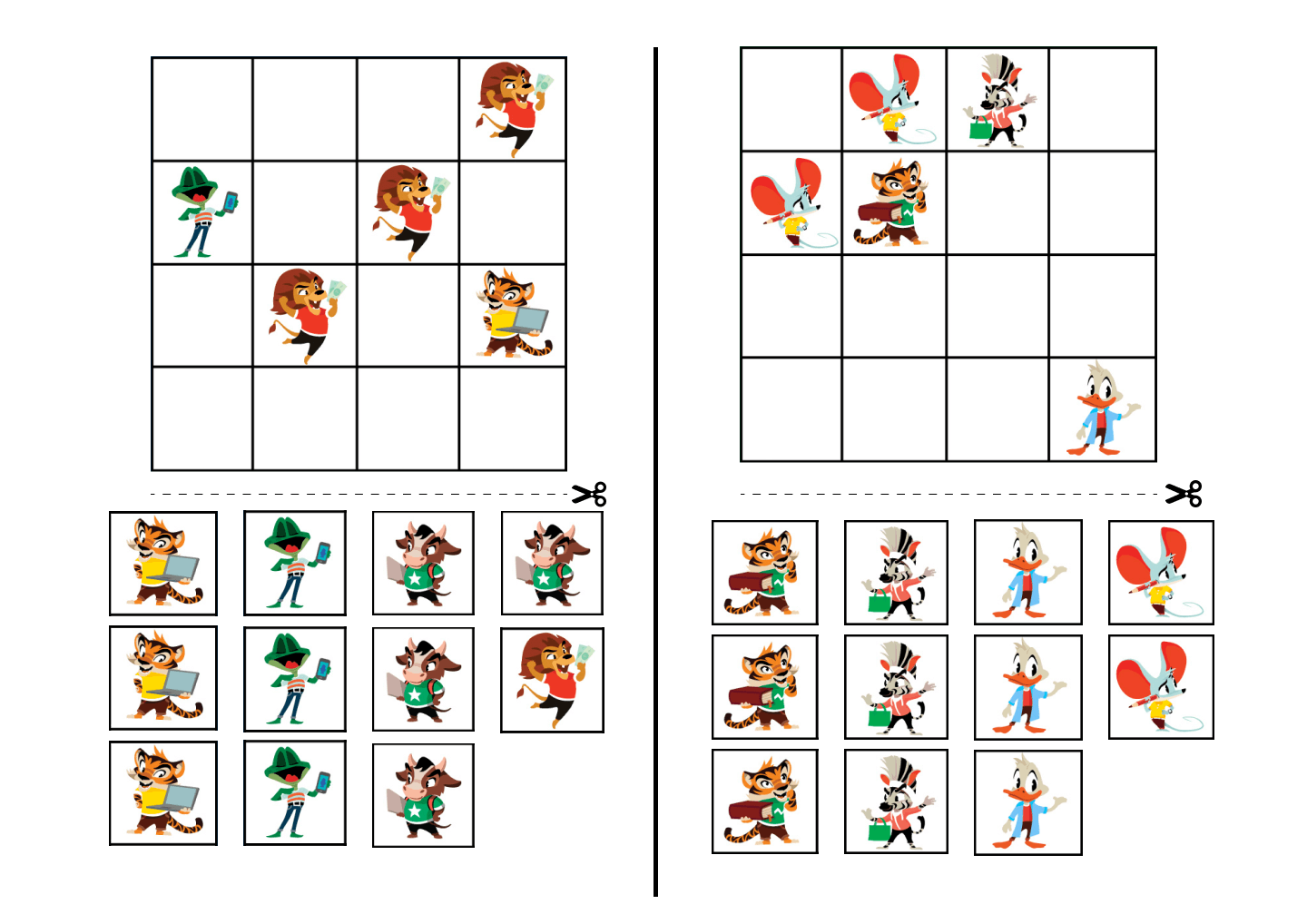
Судоку 4 на 4 для детей

Судоку 4х4 решаются чуть сложнее — повторений не должно быть в вертикальных и горизонтальных строках, а также в маленьких блоках 2 на 2.

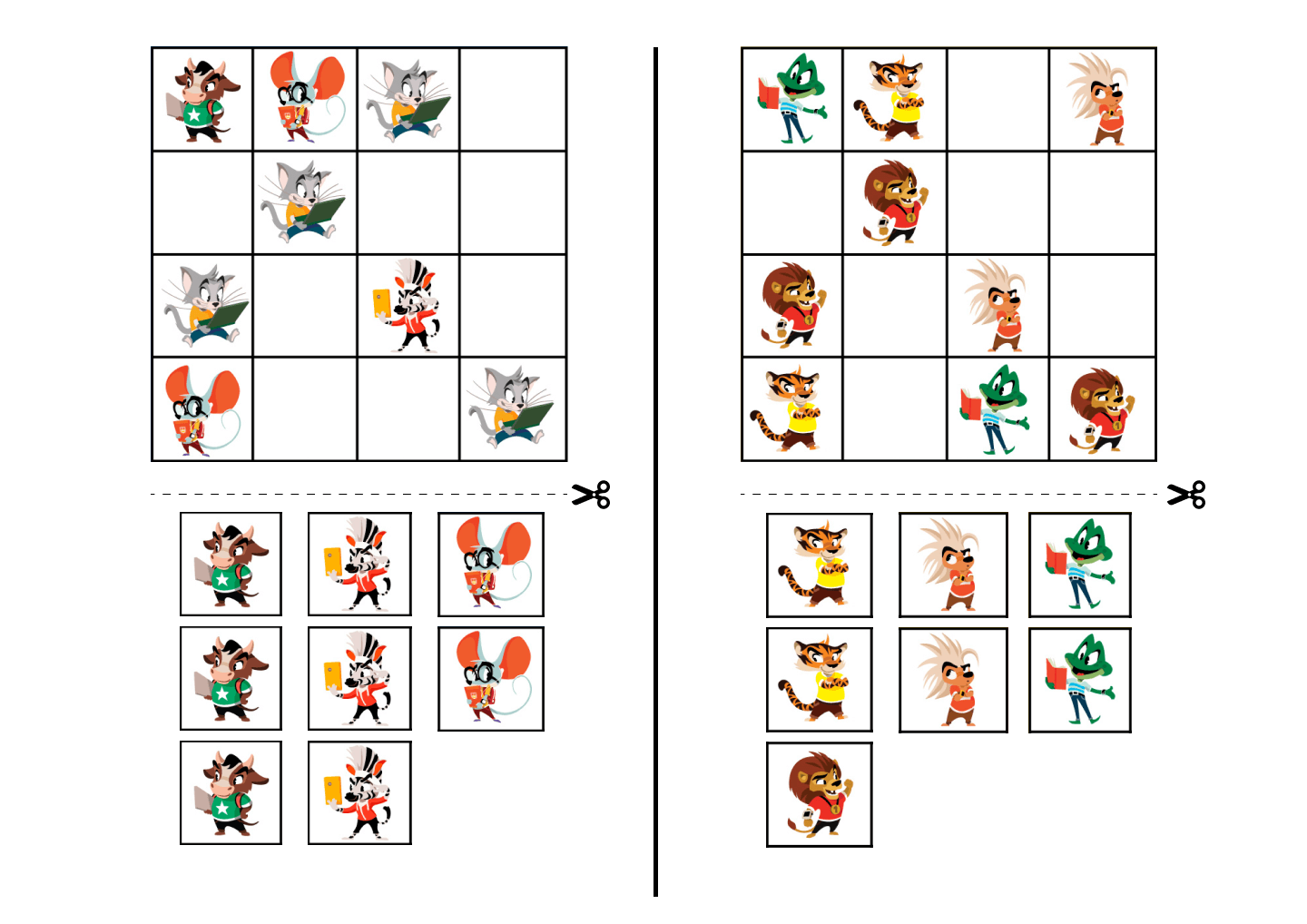
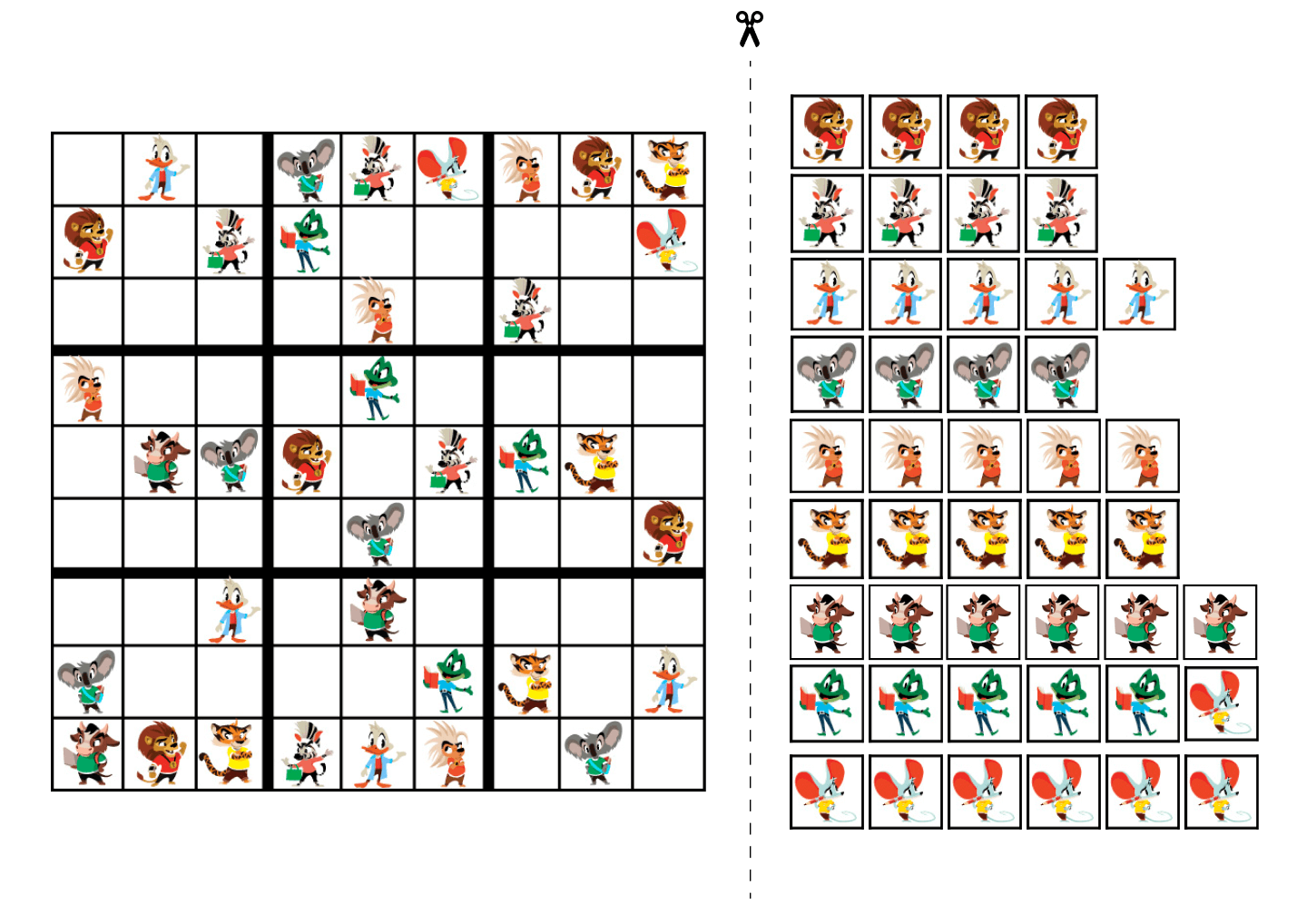
Судоку 9 на 9 для детей

Этот вариант судоку сложнее предыдущих и потребует от ребенка больше внимания и усидчивости.

Детские судоку с цифрами

После того, как ребенок поймет алгоритм решения судоку, ему будет безразлично, чем заполнять ячейки — картинками или цифрами. Картинки, конечно, ярче и интереснее — но надолго застревать на этом этапе не стоит. Можно объяснить, что судоку с картинками — это «для малышей», а «взрослые люди» решают задания с цифрами. Возможно, ребенок сам захочет перейти на новый уровень.

Судоку для детей 6-7 лет

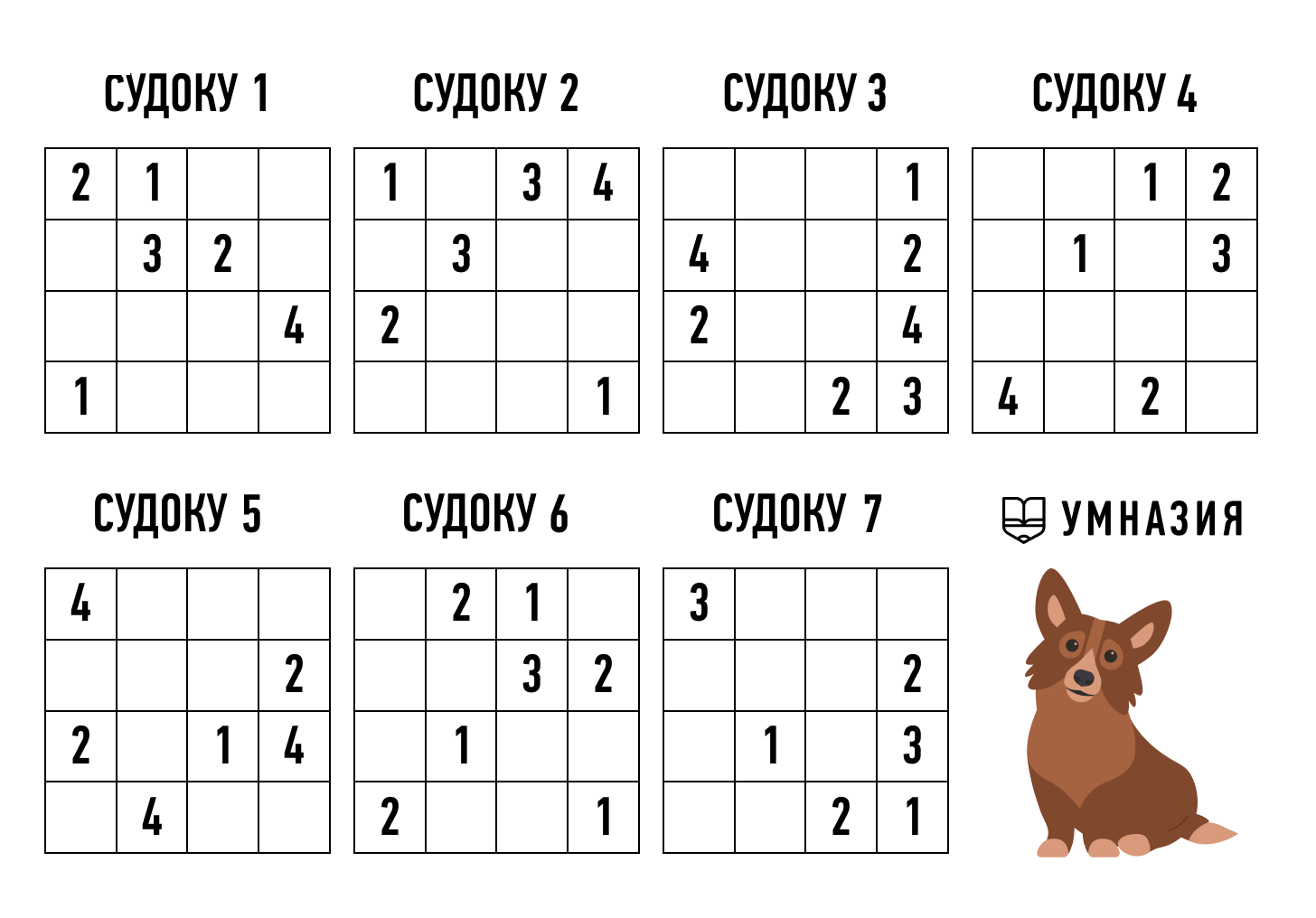
Дошкольникам не составит труда решить судоку 4х4. Алгоритм решения не отличается от такового в предыдущих случаях — нужно только помнить, что цифры от 1 до 4 не должны повторяться ни по горизонтали и вертикали, ни в блоках (маленьких квадратах, выделенных жирной чертой).

Скачайте и распечатайте судоку — не слишком мелко, чтобы ребенку было удобно вписывать цифры.

Судоку для детей 8-9 лет

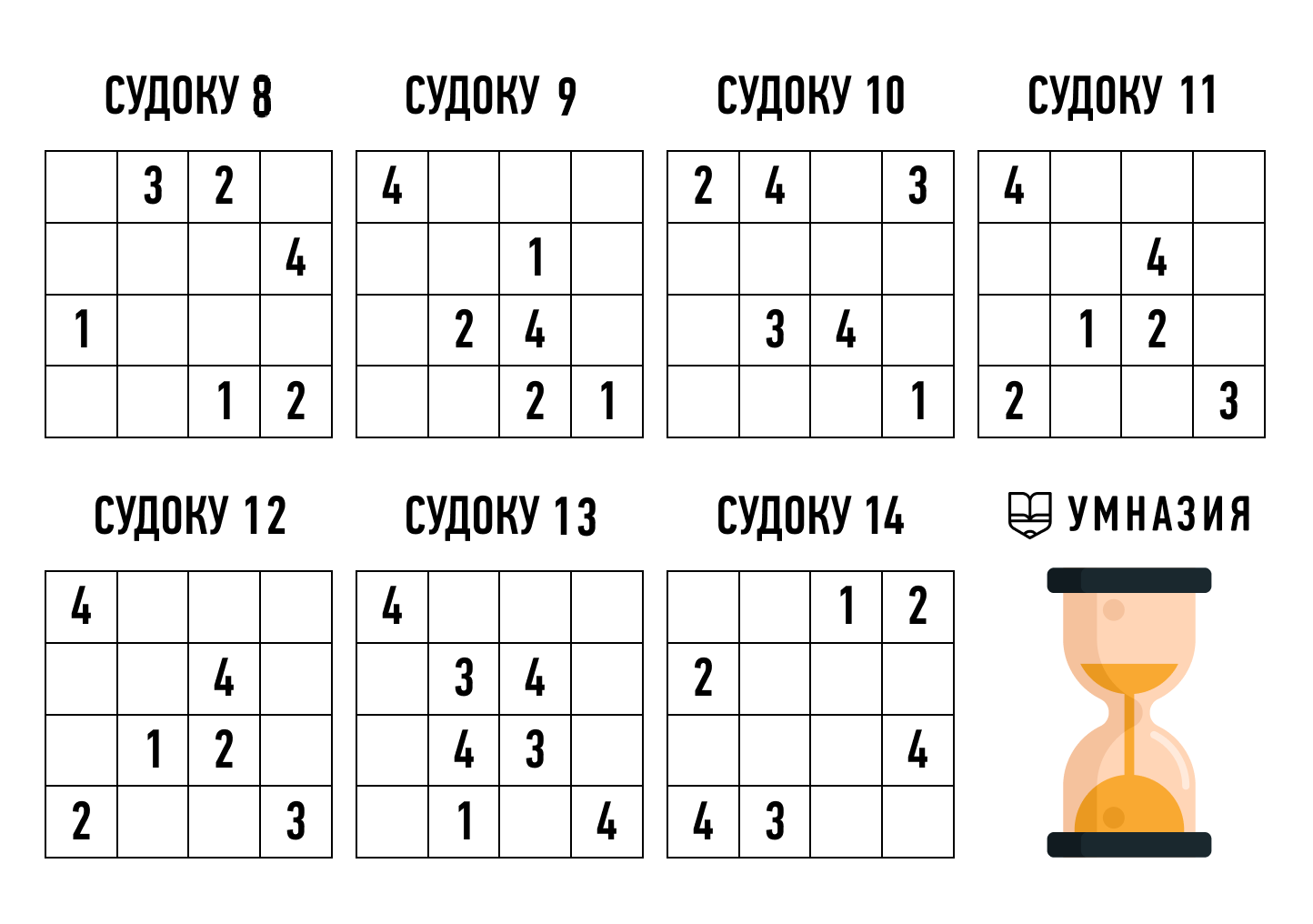
Для школьников задачу можно усложнить: детское судоку 6х6 состоит из блоков, которые представляют собой не квадрат, а прямоугольник 2х3. Вид немного непривычный, но принцип решения тот же самый.

Для удобства на начальном этапе (после скачивания и распечатки задания) отдельные блоки можно вручную раскрашивать в разные цвета, чтобы четко очертить границы.

Такие судоку полезны тем, что позволяют понять: форма блока может быть любой, главное, чтобы не повторялись символы внутри него. Это подготовит к решению «судоку-фигур», в которых блоки имеют не квадратную, а произвольную форму многоугольника. При этом правило «не повторяться по горизонтали и вертикали» должно выполняться.

Судоку для детей 10-11 лет

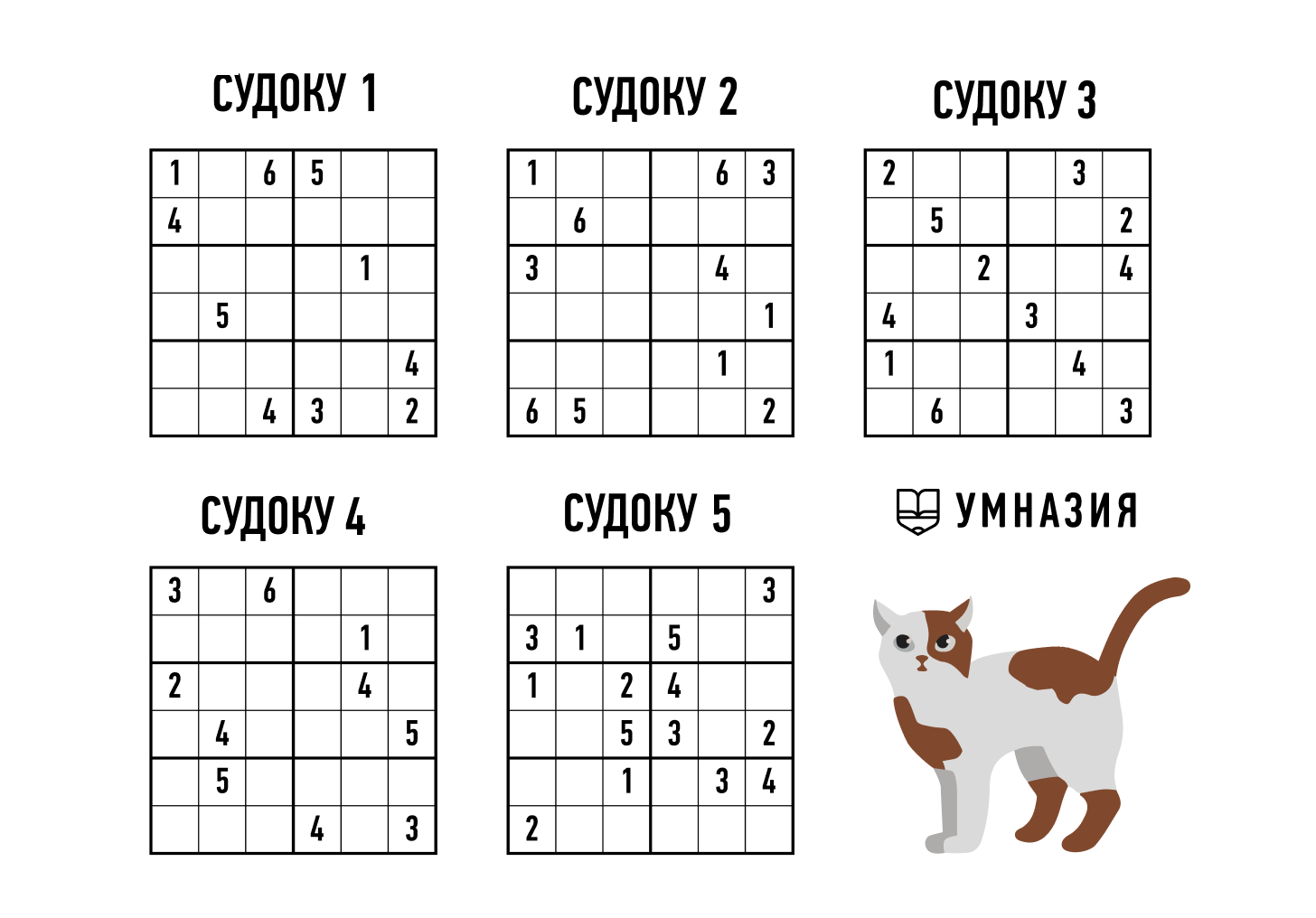
Дети в этом возрасте в состоянии справиться с полноценным вариантом cудоку — 9х9. Именно этот вариант считается классическим: 81 ячейка в квадрате 9х9; 9 более мелких квадратов 3х3. Цифры от 1 до 9 расставляются таким образом, чтобы в квадратах, по горизонтали и по вертикали все цифры были разными во всех столбцах и строках.

Судоку такого размера кажутся большими и сложными, но это не всегда так. В зависимости от количества чисел, которые уже проставлены по условию, они могут быть и очень простыми, если пустых клеток в них немного, и заполнение их очевидно. В то же время бывают и невероятно сложные cудоку 9х9. Для их решения существует много «хитростей» и «стратегий», но для детских cудоку они не нужны.

Алгоритм генерации судоку

Доброго времени суток!

Думаю, головоломка Судоку не нуждается в представлении. Многие из нас проводят за её решением достаточно много времени. Например, когда нужно убить время в дороге или просто поворочать мозги, чтобы не сохли. На хабре есть довольно много постов о решении головоломки. Но когда человек решает с десяток, а может и сотню головоломок, то найдётся пытливый ум, который задаст себе вопрос «А как же получается таблица Судоку, имеющая единственное решение? И как можно описать алгоритм для сетки 9×9?».

Приведённый алгоритм является вполне логичным. Но моей задачей было описание и реализация. Обо всём этом написано под катом.

Шаг 1. Взять за основу базовую сетку

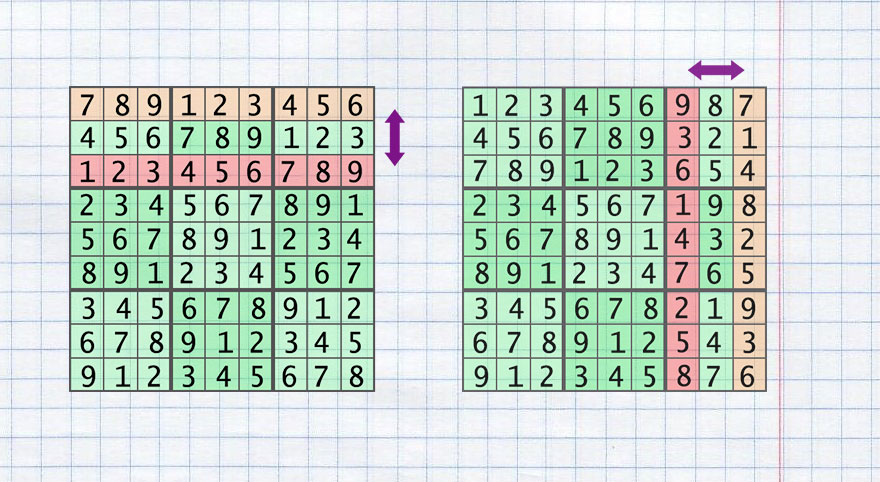
Сетка должна подчинятся правилам Судоку. Размещаем в первую строку 1 2… 8 9, в строках ниже смещаем на 3 позиции влево, т.е. 4 5… 2 3 и 7 8… 5 6.
Далее переходя в следующий район по вертикали смещаем на 1 позицию влево предыдущий район.

В итоге должна получиться вот такая сетка, её я и назову базовой:

Для реализации создадим класс grid. Заполним его в соответствии с Шагом 1, в котором table — список значений таблицы, метод show — просто наглядный вывод таблицы.

class grid:
	def __init__(self,n = 3):
		"""Generation of the base table"""
		self.n = n
		self.table = [[((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)]
		print "The base table is ready!"

	def __del__(self):
		pass
	
	def show(self):
		for i in range(self.n*self.n):
			print self.table[i]

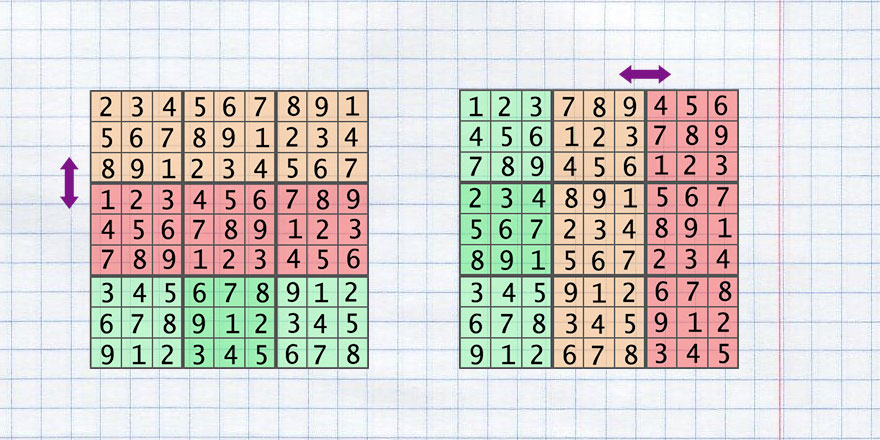
Шаг 2. Перетасовать сетку

Есть несколько видов перестановок, выполнив которые таблица Судоку останется в допустимом состоянии.
К ним относятся:

• Транспонирование всей таблицы — столбцы становятся строками и наоборот (transposing)

• Обмен двух строк в пределах одного района (swap_rows_small)
• Обмен двух столбцов в пределах одного района (swap_colums_small)

• Обмен двух районов по горизонтали (swap_rows_area)
• Обмен двух районов по вертикали (swap_colums_area)

Для каждой из перестановок напишем метод:

transposing

	def transposing(self):
		""" Transposing the whole grid """
		self.table = map(list, zip(*self.table))

swap_rows_small

	def swap_rows_small(self):
		""" Swap the two rows """
		area = random.randrange(0,self.n,1)
		line1 = random.randrange(0,self.n,1)
		#получение случайного района и случайной строки
		N1 = area*self.n + line1
		#номер 1 строки для обмена

		line2 = random.randrange(0,self.n,1)
		while (line1 == line2):
			line2 = random.randrange(0,self.n,1)

		N2 = area*self.n + line2
		#номер 2 строки для обмена

		self.table[N1],self.table[N2] = self.table[N2], self.table[N1]

swap_colums_small

Для обмена столбцов можно поменять строки у транспонированной таблицы:

	def swap_colums_small(self):
		grid.transposing(self)
		grid.swap_rows_small(self)
		grid.transposing(self)

swap_rows_area

	def swap_rows_area(self):
		""" Swap the two area horizon """
		area1 = random.randrange(0,self.n,1)
		#получение случайного района

		area2 = random.randrange(0,self.n,1)
		while (area1 == area2):
			area2 = random.randrange(0,self.n,1)

		for i in range(0, self.n):
			N1, N2 = area1*self.n + i, area2*self.n + i
			self.table[N1], self.table[N2] = self.table[N2], self.table[N1]

swap_colums_area

	def swap_colums_small(self):
		grid.transposing(self)
		grid.swap_rows_area(self)
		grid.transposing(self)

Может быть есть ещё более сложные преобразования, но, думаю, можно ограничиться этими. Этот каркас инвариантен своей структуре, такие перестановки есть почти тоже самое, что и действия над матрицами относительно определителя или вращение Кубика Рубика.

Теперь, для того чтобы получить случайную комбинацию, достаточно запустить в случайном порядке функции перемешивания. Так и поступим, amt — количество перемешиваний:

	def mix(self,amt = 10):
		mix_func = ['self.transposing()', 
					'self.swap_rows_small()', 
					'self.swap_colums_small()', 
					'self.swap_rows_area()', 
					'self.swap_colums_area()']
		for i in xrange(1, amt):
			id_func = random.randrange(0,len(mix_func),1)
			eval(mix_func[id_func])

base
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[4, 5, 6, 7, 8, 9, 1, 2, 3]
[7, 8, 9, 1, 2, 3, 4, 5, 6]
[2, 3, 4, 5, 6, 7, 8, 9, 1]
[5, 6, 7, 8, 9, 1, 2, 3, 4]
[8, 9, 1, 2, 3, 4, 5, 6, 7]
[3, 4, 5, 6, 7, 8, 9, 1, 2]
[6, 7, 8, 9, 1, 2, 3, 4, 5]
[9, 1, 2, 3, 4, 5, 6, 7, 8]

swap_colums_area
[7, 8, 9, 4, 5, 6, 1, 2, 3]
[1, 2, 3, 7, 8, 9, 4, 5, 6]
[4, 5, 6, 1, 2, 3, 7, 8, 9]
[8, 9, 1, 5, 6, 7, 2, 3, 4]
[2, 3, 4, 8, 9, 1, 5, 6, 7]
[5, 6, 7, 2, 3, 4, 8, 9, 1]
[9, 1, 2, 6, 7, 8, 3, 4, 5]
[3, 4, 5, 9, 1, 2, 6, 7, 8]
[6, 7, 8, 3, 4, 5, 9, 1, 2]

swap_colums_small
[7, 8, 9, 4, 5, 6, 2, 1, 3]
[1, 2, 3, 7, 8, 9, 5, 4, 6]
[4, 5, 6, 1, 2, 3, 8, 7, 9]
[8, 9, 1, 5, 6, 7, 3, 2, 4]
[2, 3, 4, 8, 9, 1, 6, 5, 7]
[5, 6, 7, 2, 3, 4, 9, 8, 1]
[9, 1, 2, 6, 7, 8, 4, 3, 5]
[3, 4, 5, 9, 1, 2, 7, 6, 8]
[6, 7, 8, 3, 4, 5, 1, 9, 2]

swap_colums_small
[7, 8, 9, 4, 5, 6, 1, 2, 3]
[1, 2, 3, 7, 8, 9, 4, 5, 6]
[4, 5, 6, 1, 2, 3, 7, 8, 9]
[8, 9, 1, 5, 6, 7, 2, 3, 4]
[2, 3, 4, 8, 9, 1, 5, 6, 7]
[5, 6, 7, 2, 3, 4, 8, 9, 1]
[9, 1, 2, 6, 7, 8, 3, 4, 5]
[3, 4, 5, 9, 1, 2, 6, 7, 8]
[6, 7, 8, 3, 4, 5, 9, 1, 2]

transposing
[7, 1, 4, 8, 2, 5, 9, 3, 6]
[8, 2, 5, 9, 3, 6, 1, 4, 7]
[9, 3, 6, 1, 4, 7, 2, 5, 8]
[4, 7, 1, 5, 8, 2, 6, 9, 3]
[5, 8, 2, 6, 9, 3, 7, 1, 4]
[6, 9, 3, 7, 1, 4, 8, 2, 5]
[1, 4, 7, 2, 5, 8, 3, 6, 9]
[2, 5, 8, 3, 6, 9, 4, 7, 1]
[3, 6, 9, 4, 7, 1, 5, 8, 2]

swap_colums_small
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[6, 9, 3, 7, 1, 4, 5, 2, 8]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[3, 6, 9, 4, 7, 1, 2, 8, 5]

swap_rows_small
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[6, 9, 3, 7, 1, 4, 5, 2, 8]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[3, 6, 9, 4, 7, 1, 2, 8, 5]

swap_rows_small
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[6, 9, 3, 7, 1, 4, 5, 2, 8]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[3, 6, 9, 4, 7, 1, 2, 8, 5]

swap_rows_area
[7, 1, 4, 8, 2, 5, 6, 3, 9]
[8, 2, 5, 9, 3, 6, 7, 4, 1]
[9, 3, 6, 1, 4, 7, 8, 5, 2]
[2, 5, 8, 3, 6, 9, 1, 7, 4]
[1, 4, 7, 2, 5, 8, 9, 6, 3]
[3, 6, 9, 4, 7, 1, 2, 8, 5]
[5, 8, 2, 6, 9, 3, 4, 1, 7]
[4, 7, 1, 5, 8, 2, 3, 9, 6]
[6, 9, 3, 7, 1, 4, 5, 2, 8]

swap_colums_small
[7, 1, 4, 8, 2, 5, 6, 9, 3]
[8, 2, 5, 9, 3, 6, 7, 1, 4]
[9, 3, 6, 1, 4, 7, 8, 2, 5]
[2, 5, 8, 3, 6, 9, 1, 4, 7]
[1, 4, 7, 2, 5, 8, 9, 3, 6]
[3, 6, 9, 4, 7, 1, 2, 5, 8]
[5, 8, 2, 6, 9, 3, 4, 7, 1]
[4, 7, 1, 5, 8, 2, 3, 6, 9]
[6, 9, 3, 7, 1, 4, 5, 8, 2]

Шаг 3. Удаление клеток

После полученного решения нам необходимо получить задачу (именно в такой последовательности мы можем гарантировать однозначность решения). И это самая сложная часть. Какое количество можно убрать, чтобы гарантировать однозначность решения? Это один из важных факторов, от которого зависит сложность Судоку. Всего в Судоку 81 клетка, обычно считают лёгким когда на поле есть 30-35 «подсказок», средним — 25-30, и сложным — 20-25. Это данные большого набора реальных примеров. Нет никаких законов для сложности. Можно сделать 30-клеточный неразрешимый вариант и 22 клеточный «лёгкий».

• Случайный подход — можно попробовать выкинуть 50-60 клеток наугад, но где вероятность что Судоку можно будет решить? Например, если заполнены 3 строки ( = 27 клеток)
• Случайно с простым ограничением — для примера можно взять некое число N в качестве предела, так что N строк и столбцов могут быть пустыми. Принимая N = 0 — для лёгких уровней, N=1 — средний, N=2 — сложный

Итак, приступим к вычёркиванию ячеек (все варианты равнозначны, поэтому у нас 81 ячейка, которую можно вычеркнуть, поэтому проверим все перебором):

1. Выбрать случайную ячейку N
2. Отметить N просмотренной
3. Удалить N
4. Посчитать решения. Если оно не единственное, то вернуть N обратно

На выходе получится самая сложная из возможных вариантов Судоку для данного перемешивания. Переменная difficult оценивает сложность — количество оставшихся элементов.

flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)]
iterator = 0
difficult = example.n ** 4 #Первоначально все элементы на месте

while iterator < example.n ** 4:
	i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # Выбираем случайную ячейку
	if flook[i][j] == 0:	#Если её не смотрели
		iterator += 1
		flook[i][j] = 1 	#Посмотрим

		temp = example.table[i][j]	#Сохраним элемент на случай если без него нет решения или их слишком много
		example.table[i][j] = 0
		difficult -= 1 #Усложняем, если убрали элемент

		table_solution = []
		for copy_i in range(0, example.n*example.n):
			table_solution.append(example.table[copy_i][:]) #Скопируем в отдельный список

		i_solution = 0
		for solution in solver.solve_sudoku((example.n, example.n), table_solution):
			i_solution += 1 #Считаем количество решений

		if i_solution != 1: #Если решение не одинственное -- вернуть всё обратно
			example.table[i][j] = temp
			difficult += 1  #Облегчаем

example.show()
print "difficult = ",difficult

# coding=utf-8
import random
import solver

class grid:
	def __init__(self,n = 3):
		""" Generation of the base table """
		self.n = n
		self.table = [[ ((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)]
		print "The base table is ready!"

	def __del__(self):
		pass
	
	def show(self):
		for i in range(self.n*self.n):
			print self.table[i]

	def transposing(self):
		""" Transposing the whole grid """
		self.table = map(list, zip(*self.table))

	def swap_rows_small(self):
		""" Swap the two rows """
		area = random.randrange(0,self.n,1)
		line1 = random.randrange(0,self.n,1)
		#получение случайного района и случайной строки
		N1 = area*self.n + line1
		#номер 1 строки для обмена

		line2 = random.randrange(0,self.n,1)
		#случайная строка, но не та же самая
		while (line1 == line2):
			line2 = random.randrange(0,self.n,1)

		N2 = area*self.n + line2
		#номер 2 строки для обмена

		self.table[N1],self.table[N2] = self.table[N2], self.table[N1]


	def swap_colums_small(self):
		grid.transposing(self)
		grid.swap_rows_small(self)
		grid.transposing(self)


	def swap_rows_area(self):
		""" Swap the two area horizon """
		area1 = random.randrange(0,self.n,1)
		#получение случайного района

		area2 = random.randrange(0,self.n,1)
		#ещё район, но не такой же самый
		while (area1 == area2):
			area2 = random.randrange(0,self.n,1)

		for i in range(0, self.n):
			N1, N2 = area1*self.n + i, area2*self.n + i
			self.table[N1], self.table[N2] = self.table[N2], self.table[N1]


	def swap_colums_area(self):
		grid.transposing(self)
		grid.swap_rows_area(self)
		grid.transposing(self)
	
	def mix(self,amt = 10):
		mix_func = ['self.transposing()', 
					'self.swap_rows_small()', 
					'self.swap_colums_small()', 
					'self.swap_rows_area()', 
					'self.swap_colums_area()']
		for i in xrange(1, amt):
			id_func = random.randrange(0,len(mix_func),1)
			eval(mix_func[id_func])

example = grid()
example.mix()

flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)]
iterator = 0
difficult = example.n ** 4 #Первоначально все элементы на месте

example.show() 
print "---------------------------"

while iterator < example.n ** 4:
	i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # Выбираем случайную ячейку
	if flook[i][j] == 0:	#Если её не смотрели
		iterator += 1
		flook[i][j] = 1 	#Посмотрим

		temp = example.table[i][j]	#Сохраним элемент на случай если без него нет решения или их слишком много
		example.table[i][j] = 0
		difficult -= 1 #Усложняем если убрали элемент

		table_solution = []
		for copy_i in range(0, example.n*example.n):
			table_solution.append(example.table[copy_i][:]) #Скопируем в отдельный список

		i_solution = 0
		for solution in solver.solve_sudoku((example.n, example.n), table_solution):
			i_solution += 1 #Считаем количество решений

		if i_solution != 1: #Если решение не одинственное вернуть всё обратно
			example.table[i][j] = temp
			difficult += 1 # Облегчаем

example.show()
print "difficult = ",difficult

#!/usr/bin/env python3

# Author: Ali Assaf <ali.assaf.mail@gmail.com>
# Copyright: (C) 2010 Ali Assaf
# License: GNU General Public License <http://www.gnu.org/licenses/>

from itertools import product

def solve_sudoku(size, grid):
    """ An efficient Sudoku solver using Algorithm X.

    >>> grid = [
    ...     [5, 3, 0, 0, 7, 0, 0, 0, 0],
    ...     [6, 0, 0, 1, 9, 5, 0, 0, 0],
    ...     [0, 9, 8, 0, 0, 0, 0, 6, 0],
    ...     [8, 0, 0, 0, 6, 0, 0, 0, 3],
    ...     [4, 0, 0, 8, 0, 3, 0, 0, 1],
    ...     [7, 0, 0, 0, 2, 0, 0, 0, 6],
    ...     [0, 6, 0, 0, 0, 0, 2, 8, 0],
    ...     [0, 0, 0, 4, 1, 9, 0, 0, 5],
    ...     [0, 0, 0, 0, 8, 0, 0, 7, 9]]
    >>> for solution in solve_sudoku((3, 3), grid):
    ...     print(*solution, sep='\n')
    [5, 3, 4, 6, 7, 8, 9, 1, 2]
    [6, 7, 2, 1, 9, 5, 3, 4, 8]
    [1, 9, 8, 3, 4, 2, 5, 6, 7]
    [8, 5, 9, 7, 6, 1, 4, 2, 3]
    [4, 2, 6, 8, 5, 3, 7, 9, 1]
    [7, 1, 3, 9, 2, 4, 8, 5, 6]
    [9, 6, 1, 5, 3, 7, 2, 8, 4]
    [2, 8, 7, 4, 1, 9, 6, 3, 5]
    [3, 4, 5, 2, 8, 6, 1, 7, 9]
    """
    R, C = size
    N = R * C
    X = ([("rc", rc) for rc in product(range(N), range(N))] +
         [("rn", rn) for rn in product(range(N), range(1, N + 1))] +
         [("cn", cn) for cn in product(range(N), range(1, N + 1))] +
         [("bn", bn) for bn in product(range(N), range(1, N + 1))])
    Y = dict()
    for r, c, n in product(range(N), range(N), range(1, N + 1)):
        b = (r // R) * R + (c // C) # Box number
        Y[(r, c, n)] = [
            ("rc", (r, c)),
            ("rn", (r, n)),
            ("cn", (c, n)),
            ("bn", (b, n))]
    X, Y = exact_cover(X, Y)
    for i, row in enumerate(grid):
        for j, n in enumerate(row):
            if n:
                select(X, Y, (i, j, n))
    for solution in solve(X, Y, []):
        for (r, c, n) in solution:
            grid[r][c] = n
        yield grid

def exact_cover(X, Y):
    X = {j: set() for j in X}
    for i, row in Y.items():
        for j in row:
            X[j].add(i)
    return X, Y

def solve(X, Y, solution):
    if not X:
        yield list(solution)
    else:
        c = min(X, key=lambda c: len(X[c]))
        for r in list(X[c]):
            solution.append(r)
            cols = select(X, Y, r)
            for s in solve(X, Y, solution):
                yield s
            deselect(X, Y, r, cols)
            solution.pop()

def select(X, Y, r):
    cols = []
    for j in Y[r]:
        for i in X[j]:
            for k in Y[i]:
                if k != j:
                    X[k].remove(i)
        cols.append(X.pop(j))
    return cols

def deselect(X, Y, r, cols):
    for j in reversed(Y[r]):
        X[j] = cols.pop()
        for i in X[j]:
            for k in Y[i]:
                if k != j:
                    X[k].add(i)

if __name__ == "__main__":
    import doctest
    doctest.testmod()

The base table is ready!
[5, 4, 6, 8, 7, 9, 2, 1, 3]
[8, 7, 9, 2, 1, 3, 5, 4, 6]
[2, 1, 3, 5, 4, 6, 8, 7, 9]
[6, 5, 7, 9, 8, 1, 3, 2, 4]
[9, 8, 1, 3, 2, 4, 6, 5, 7]
[3, 2, 4, 6, 5, 7, 9, 8, 1]
[7, 6, 8, 1, 9, 2, 4, 3, 5]
[1, 9, 2, 4, 3, 5, 7, 6, 8]
[4, 3, 5, 7, 6, 8, 1, 9, 2]
---------------------------
[0, 0, 6, 0, 0, 0, 0, 0, 0]
[8, 7, 0, 0, 1, 0, 0, 0, 6]
[0, 0, 0, 5, 4, 0, 0, 0, 9]
[6, 0, 0, 0, 8, 1, 3, 0, 4]
[0, 0, 0, 3, 0, 0, 0, 5, 0]
[0, 0, 0, 0, 0, 7, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 9, 0, 4, 0, 0, 0, 0, 8]
[0, 0, 5, 0, 6, 0, 1, 0, 0]
difficult =  22

Скачать в zip

Я уверен, что есть и более сложные подходы в построении таблицы Судоку. Моя цель была достигнута, получился рабочий алгоритм. Теперь мне не нужно искать новые выпуски, я могу их генерировать
В принципе, здесь был приведён частный случай Судоку 9х9. Но нет ограничений для использования его на 16х16 и 25х25.

• Для проверки решения применялся Алгоритм Х и его реализация для Судоку
• Решение Судоку на всех языках http://rosettacode.org/wiki/Sudoku

Если у кого есть лучшие предложения — не стесняйтесь оставить комментарий.
Спасибо за внимание.

Мастер-класс по изготовлению дидактической игры судоку

На прошлом занятии мы с вами, уважаемые читатели, начали подготовку к освоению головоломки судоку — популярной игры для людей самого разного возраста. Напомним, что цель этой головоломки — заполнить цифрами клетки игрового поля таким образом, чтобы они не повторялись в определённых местах — блоках

Одно из самых важных качеств игрока судоку — умение видеть и помнить, каких конкретно цифр не хватает в рассматриваемом блоке. Это умение можно постепенно тренировать, чем мы с вами и займёмся на этом занятии. Как и прежде, для того, чтобы придать занятию более привлекательный вид, мы рассмотрим другую подобную головоломку, в которой вместо цифр используются разноцветные клетки.

Итак, имеется игровое поле размером 4×4 клетки, которые нужно закрасить одним из четырёх заданных цветов таким образом, чтобы в каждом блоке — строке, столбце и больших диагоналях — не было клеток одинакового цвета. Часть клеток, задающая алгоритм последующего решения головоломки, уже закрашена (рис. 1).

Таким образом, наша игровая задача состоит в том, чтобы закрасить остальные клетки. Как это сделать правильно, без ошибок, ведь эти клетки закрашиваются однозначным образом, поэтому попытки закрашивания наугад очень часто приводят к неудачам? Для этого нужно выбирать такие ходы, в которых мы абсолютно уверены. Давайте поучимся их находить.

Первый такой ход очевиден: на одной диагонали уже имеются три заполненные клетки, осталось заполнить последнюю — «В3». А так как в одном блоке (строке, столбце или диагонали) не может быть одинаковых цветов, то определяем её цвет: синий (рис. 2).

Как же играть дальше? Для этого нужно выбрать блок с наибольшим числом закрашенных клеток. Таких блоков у нас два: четвёртая строка и столбец «А». Выбираем любой из них, допустим, четвёртую строку.

В ней имеются две клетки: синяя и жёлтая, следовательно, не хватает красной и зелёной. Куда же поставить, например, красную? Можно бы и на поле «Б4», и на поле «В4», однако один из этих вариантов будет неправильным, ведь квадрат заполняется единственным способом. Поэтому давайте проанализируем каждый из этих двух возможных ходов внимательнее.

Допустим, мы закрасим красным цветом клетку «Б4». Тогда последнюю оставшуюся свободную клетку этого блока «В4» мы должны будем закрасить зелёным цветом. Этот вариант можем считать приемлемым, допустимым (рис. 3).

Рассмотрим теперь другой вариант, когда красным цветом мы закрасим клетку «В4». В этом случае оставшуюся в блоке последнюю клетку «Б4» нам придётся закрашивать зелёным цветом (рис. 4), а это будет нарушением правил заполнения квадрата, так как в столбце «Б» окажутся две клетки зелёного цвета. Следовательно, второй вариант недопустим, и нижнюю строку мы должны заполнять только по первому варианту (рис. 3).

Далее аналогично заполняем квадрат, придерживаясь правила: выбираем блок с наибольшим количеством закрашенных клеток и находим варианты, когда заполнение свободных клеток в нём не приводит к повторению цветов в любом из остальных блоков. Допустим, мы выбираем столбец «А». Здесь не хватает двух цветов: жёлтого и зелёного. Жёлтым цветом нельзя заполнять клетку «А3», так как в этом случае придётся закрашивать в зелёный цвет клетку «А2», а это недопустимо (подумайте, почему). Следовательно, мы можем раскрасить жёлтым цветом клетку «А2» и зелёным — «А3» (рис. 5).

Далее поступаем аналогичным образом. Выберем, к примеру, третью строку и закрасим её недостающими цветами: красным и жёлтым (это очень легко, сделайте самостоятельно), затем столбец «Б» — и закрасим единственную свободную клетку в синий цвет. Получим то, что изображено на рис. 6.

Как же действовать дальше? Можно поступать так же, как мы поступали и раньше (выбирать незаполненный блок и заполнять оставшиеся в нём две клетки), а можно просто выбирать любой из четырёх цветов и смотреть, какую клетку из оставшихся пустых можно им закрасить, не нарушая правила: в каждом блоке должны быть клетки только разных цветов. Попробуйте завершить заполнение квадрата последним способом.

Итак, алгоритм решения рассмотренной головоломки следующий: ищем блок с наибольшим числом закрашенных клеток и заполняем оставшиеся таким образом, чтобы в любом из остальных блоков одинаковые цвета не повторялись. И очень важно при этом, выбирая ход, учитывать его последствия, обращая внимание, не приведут ли дальнейшие ходы для выбранного блока к нарушению правил игры. А это как раз то, чему мы стремимся научить своих детей: предвидеть результаты своих действий, отвечать за свои поступки.

Ниже приводятся примеры других вариантов этой головоломки. При решении головоломки на рис. 7, заполняя столбец «В», необходимо избегать повторения цветов в блоках, состоящих из больших диагоналей. Более сложный вариант представлен на рис. 8. Здесь нельзя изначально выделить блоки с наибольшим количеством закрашенных клеток, однако заполнение больших диагоналей не представляет особого труда, главное — следить за тем, чтобы одинаковые цвета во всех блоках не повторялись.

Попробуйте решить эти головоломки самостоятельно, а затем составьте подобные упражнения для своих детей, начиная с варианта, представленного на рис. 1. При этом совсем не обязательно придерживаться такого же расположения закрашенных клеток, как это было использовано на нашем занятии. Множество подобных упражнений под названием «Заполни квадрат» представлено на сайте детских компьютерных игр «Логозаврия: умные игры для умных детей, родителей, учителей» (www.logozavr.ru) в разделах для детей от 6 до 12 лет.

Составление подобных головоломок и организация их решения очень просты: достаточно только иметь бумагу и авторучку (карандаш), а цвета можно обозначать буквами: «К» — красный, «Ж» — жёлтый, «З» — зелёный, «С» — синий. Поэтому их можно разгадывать, используя излишки свободного времени, в самых различных местах.

Успехов! Играйте с нами, играйте как мы, играйте лучше нас!

Виктор Варченко,

доцент кафедры педагогики и образовательных технологий

Балтийского федерального университета имени Иммануила Канта