Download Article
Download Article
Drawing a syntax tree may feel like a confusing and daunting prospect at first glance, but once you understand what you’re doing it becomes much easier to handle. This guide will demonstrate how to create a syntax diagram of a simple English sentence with transitive core verb, negation, and auxiliary and modal verbs.
-
1
Decide on your medium. There are several ways to create a syntax tree, from various types of software to even just pen and paper. While there are advantages and disadvantages to either side, the more important thing is picking whichever you are more comfortable using.
-
2
Write out and analyze your sentence. On a separate piece of paper, write out the sentence you will be creating a syntax tree of. This will be used as a reference throughout the project. After you have it written down, look over and analyze it. Identify any noun phrases, verbs, and prepositional or adverbial phrases in the sentence.
Advertisement
-
3
Determine which features will be checked, if any. There are far too many possible features to check than is practical, so most trees instead focus on whatever features are most relevant to what the tree maker is trying to examine. By ignoring features that are irrelevant, you can save time and effort doing something that you don’t need to do.
Advertisement
-
1
Identify the verb phrase. Begin by identifying which part of the sentence contains the main verb. This will be the starting point from which you can work your way up the tree. The verb phrase essentially serves as the core action of the sentence, and it usually done by the subject.
-
2
Construct the VP verb phrase. This will contain the verb and its object, but not the subject. Begin by creating a node labeled VP. Create two child nodes beneath it labeled V and DP. The V node will contain the verb, while the DP node will contain the object. Create two child nodes of the DP labeled D and NP.
- This DP is called a «determiner phrase», and consists of a determiner (e.g. «the», «a», «that» or «this») and a following noun phrase. The determiner will be placed under D, and the noun phrase under NP.
- If the noun phrase is a name, the D node should still be placed on the tree. However, its contents should be treated as null.
-
3
Begin to build up the vP verb phrase. This is distinct from the capital VP verb phrase and when complete it will contain the verb and as its subject and objects, as well as most prepositional or adverbial phrases.
- Begin by creating a new node over the VP labeled v’. Next, draw a child of that new node to the left of the VP and label it v, then perform a move operation from the V node to the new v node.
-
4
Continue to expand on the vP verb phrase. If there are any prepositional or adverbial phrases to include, this is where they will be added. If there are none, skip this step. Create a new v’ node over the one you created last step, and create a new child node labeled PP to the right.
- Create two children of this new node labeled P to the left and DP to the right. Write down the preposition under P and the fill out the newly-created determiner phrase.
- Repeat this step as many times as you have prepositional phrases, starting from the highest v’ each time.
- Create two children of this new node labeled P to the left and DP to the right. Write down the preposition under P and the fill out the newly-created determiner phrase.
-
5
Complete the vP verb phrase. After any prepositional phrases have been added to the tree, create a new node over the highest v’ and label it vP. Then, as a child of this new vP node, create another DP node structure beneath. This will be the subject of the verb. The vP verb phrase should be complete.
Advertisement
-
1
Identify any modal or auxiliary verbs. These are verbs that modify the main verb in some way.
- Common modals include examples such as «may», «can», «shall», and «will», or their past tense forms «might», «could», «shall», and «would».
- Auxiliary verbs are used in conjunction with participle forms on affected verbs to construct passive phrases or complex tenses.
- The past participle of most verbs is identical to their standard past tense, though some verbs instead end with —en: «froze» becomes «frozen» or «broke» becomes «broken«.
- The present participle is formed by suffixing the present tense of a verb with —ing: «freeze» becomes «freezing» or «break» becomes «breaking«.
- The Progressive Phrase pairs the auxiliary verb «to be» with the present participle of the modified verb, e.g. «is jumping». The Perfective Phrase pairs the auxiliary verb «to have» with the past participle of the modified verb, e.g. «have jumped». The Passive Phrase pairs the auxiliary verb «to be» with the past participle of the modified verb, e.g. «is jumped».
- Multiple auxiliary verbs can be used in the same sentence, and if this occurs then the lower node will be inflected to the participle used by the auxiliary closest above it. The order of priorities from highest to lowest is the Perfective Phrase, followed by the Progressive Phrase, and lastly the Passive Phrase, e.g. «have been being told».
-
2
Add modals and auxiliary verbs above vP. Going from the bottom up, begin with the passive phrase, followed by the Progressive, the Perfective, and finally the Modal Phrase. If any of these are not present in your sentence, skip it and move onto the next phrase that is.
- Beginning with the passive phrase, create a new node above vP and label it PassP. Then, create a new node beneath that and label it Pass. Under the Pass node, enter the word «be», inflected as appropriate.
- Repeat the process for the rest of the auxiliaries, using ProgP and Prog for the Progressive Phrase, PerfP and Perf for the Perfective Phrase, and ModalP and Modal for the Modal Phrase.
-
3
Add negation. If your sentence contains negation, add a new node over the highest model or auxiliary node and label it NegP, then create a new child node and label it Neg. Under the new Neg node, write «not».
- If your sentence does not contain negation, skip this step.
-
4
Begin construction of the Tense Phrase. Above either NegP (if present), the highest modal or auxiliary phrase, or vP (if none of the above are present), create a new node and label it T’. Then, create a child of this new node labeled T. This node will contain the tense of the sentence.
-
5
Perform a move operation to move the highest verb to the T position. If there is no negation, the impact on the sentence may not be immediately visible. However, if the sentence does contain negation, the highest auxiliary or modal will be moved before NegP.
- If there is negation in the sentence but there are no modals or auxiliaries to move, the closest verb will be the main verb from vP. However, English does allow the vP verb to be moved before NegP. Instead, insert the word «do» under the T node in its place.
-
6
Complete the Tense Phrase. Above T’, create a new node labeled TP. Create a new child DP node structure beneath the new TP node. Perform a move operation to move the subject DP from vP to this new DP node. The tree should now be complete, if you picked this kind of simple sentence to graph.
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
About This Article
Thanks to all authors for creating a page that has been read 844 times.
Did this article help you?
Дерево синтаксического разбора¶
Закончив с реализацией дерева как структуры данных, рассмотрим примеры его применения при решении некоторых реальных задач. Этот раздел будет посвящён деревьям синтаксического разбора. Они могут использоваться для представления таких конструкций реального мира, как предложения естественного языка или математические выражения.
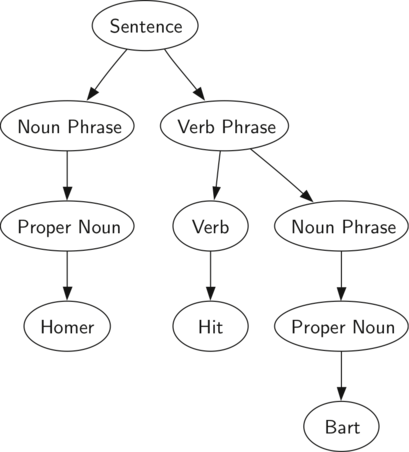
Рисунок 1: Дерево синтаксического разбора простого предложения
На рисунке 1 изображена иерархическая структура простого предложения. Такое представление позволяет нам работать с его отдельными частями, используя поддеревья.
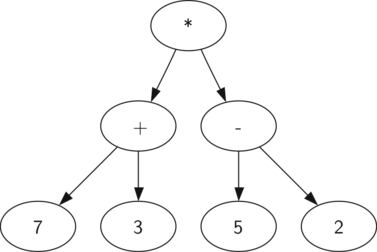
Рисунок 2: Дерево синтаксического разбора выражения (((7+3)*(5-2)))
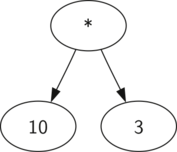
Также в виде дерева синтаксического разбора можно представить математическое выражение наподобие (((7 + 3) * (5 — 2))) (см. рисунок 2). Мы уже рассматривали выражения с полной расстановкой скобок: исходя из этого, что можно сказать о данном примере? Нам известно, что умножение имеет более высокий приоритет, чем сложение и вычитание. Однако, благодаря скобкам мы знаем, что здесь сначала нужно вычислить сумму и разность. Иерархия дерева помогает лучше понять порядок вычисления выражения в целом. Перед тем, как найти стоящее на самом верху произведение, требуется произвести сложение и вычитание в поддеревьях. Первая операция — левое поддерево — даст 10, вторая — правое поддерево — 3. Используя свойство иерархической структуры, мы можем просто заменить каждое из поддеревьев на узел, содержащий найденный ответ. Эта процедура даст упрощённое дерево, показанное на рисунке 3.
Рисунок 3: Упрощённое дерево синтаксического разбора для (((7+3)*(5-2)))
До конца этого раздела мы собираемся как следует протестировать деревья синтаксического разбора. Точнее, будет рассмотрено:
- Как построить дерево разбора для математического выражения с полной расстановкой скобок.
- Как вычислить выражение, хранящееся в дереве разбора.
- Как записать оригинальное математическое выражение из дерева разбора.
Первый шаг при постороении дерева синтаксического разбора — это разбить строку выражения на список токенов. Их насчитывается четыре вида: левая скобка, правая скобка, оператор и операнд. Мы знаем, что прочитанная левая скобка всегда означает начало нового выражения и, следовательно, необходимо создать связанное с ним поддерево. И наоборот, считывание правой скобки сигнализирует о завершении выражения. Так же известно, что операнды будут листьями и потомками своих операторов. Наконец, мы знаем, что каждый оператор имеет обоих своих потомков.
Используя сказанную выше информацию, определим следующие правила:
- Если считан токен ‘(‘ — добавляем новый узел, как левого потомка текущего, и спускаемся к нему вниз.
- Если считанный один из элементов списка [‘+’,’-‘,’/’,’*’], то устанавливаем корневое значение текущего узла равным оператору из этого токена. Добавляем новый узел на место правого потомка текущего и спускаемся вниз по правому поддереву.
- Если считанный токен — число, то устанавливаем корневое значение равным этой величине и возвращаемся к родителю.
- Если считан токен ‘)’, то перемещаемся к родителю текущего узла.
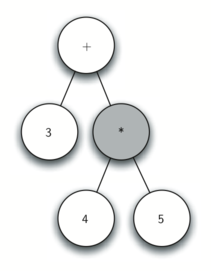
Перед тем, как писать код на Python, давайте рассмотрим в живую приведённые выше правила. Мы будем работать с выражением ((3 + (4 * 5))) и разобьём его следующим образом: [‘(‘, ‘3’, ‘+’, ‘(‘, ‘4’, ‘*’, ‘5’ ,’)’,’)’]. Начинать будем с дерева разбора, содержащего пустой корневой узел. Рисунок 4 демонстрирует его структуру и содержимое по мере вычисления каждого нового токена.

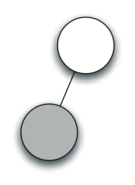
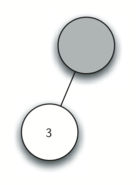
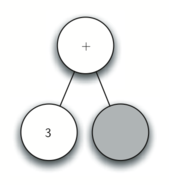
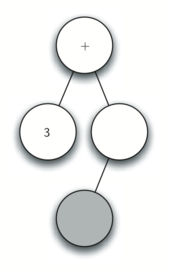
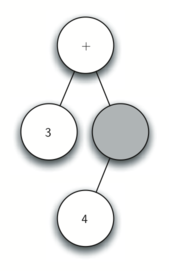
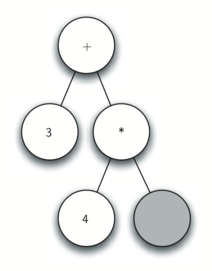
Рисунок 4: Трассировка постороения дерева разбора.
Используя этот рисунок, пройдём по примеру шаг за шагом.
а) Создаём пустое дерево.
б) Читаем ( в качестве первого токена. По правилу 1 создаём новый узел, как левого потомка корня. Делаем его текущим.
в) Считываем следующий токен — 3. По правилу 3 устанавливаем значение текущего узла в 3 и перемещаемся обратно к его родителю.
г) Следующим считываем +. По правилу 2 устанавливаем корневое значение текущего узла в + и добавляем ему правого потомка. Этот новый узел становится текущим.
д) Считываем (. По правилу 1 создаём для текущего узла левого потомка. Этот новый узел становится текущим.
е) Считываем 4. По правилу 3 устанавливаем значение текущего узла равным 4. Делаем текущим родителя 4.
ж) Считываем следующий токен — *. По правилу 2 устанавливаем корневое значение текущего узла равным * и создаём его правого потомка. Он становится текущим.
з) Считываем 5. По правилу 3 устанавливаем корневое значение текущего узла в 5, после чего текущим становится его родитель.
и) Считываем ). По правилу 4 делаем текущим узлом родителя *.
к) Наконец, считываем последний токен — ). По правилу 4 мы должны сделать текущим родителя +. Но такого узла не существует, следовательно, мы закончили.
Из примера выше очевидна необходимость отслеживать не только текущий узел, но и его предка. Интерфейс дерева предоставляет нам способы получить потомков заданного узла — с помощью методов getLeftChild и getRightChild, — но как отследить родителя? Простым решением для этого станет использование стека в процессе прохода по дереву. Перед тем, как спуститься к потомку узла, проследний мы кладём в стек. Когда же надо будет вернуть родителя текущего узла, мы вытолкнем из стека нужный элемент.
Используя описанные выше правила совместно с операциями из Stack и BinaryTree, мы готовы написать на Python функцию для создания дерева синтаксического разбора. Код её представлен в ActiveCode 1.
Постороение дерева синтаксического разбора (parsebuild)
Четыре правила для постороения дерева разбора закодированы в первых четырёх if-ах 11, 15, 19 и 24 строк ActiveCode 1. В каждом случае вы видите код, воплощающий одно из описанных выше правил с помощью нескольких вызовов методов классов BinaryTree или Stack. Единственная ошибка, на которую в этой функции происходит проверка, — ветка else, вызывающая исключение ValueError, если мы получаем токен, который не можем рапознать.
Итак, дерево синтаксического разбора построено, но что с ним теперь делать? В качестве первого примера, напишем функцию, вычисляющую дерево разбора и возвращающую числовой результат. Для этого будем использовать иерархическу природу дерева. Посмотрите ещё раз на рисунок 2. Напоминаем: оригинальное дерево можно заменять упрощённым, показанным на рисунке 3. Это предполагает возможность написать алгоритм, вычисляющий дерево разбора с помощью рекурсивного вычисления каждого из его поддеревьев.
Как мы уже делали для рекурсивных алгоритмов в прошлом, написание функции начнём с выявления базового случая. Естественным базовым случаем для рекурсивных алгоритмов, работающих с деревьями, является проверка узла на лист. В дереве разбора такими узлами всегда будут операнды. Поскольку объекты, подобные целым или действительным числам, не требуют дальнейшей интерпретации, функция evaluate может просто возвращать значение, сохранённое в листе дерева. Рекурсивный шаг, продвигающий функцию к базовому случаю, будет вызывать evaluate для правого и левого потомков текущего узла. Так мы эффективно спустимся по дереву до его листьев.
Чтобы собрать вместе результаты двух рекурсивных вызовов, мы просто применим к ним сохранённый в родительском узле оператор. В примере на рисунке 3 мы видим, что два потомка корневого узла вычисляются в 10 и 3. Применение к ним оператора умножения даст окончательный результат, равный 30.
Код рекурсивной функции evaluate показан в листинге 1. Сначала мы получаем ссылки на правого и левого потомков текущего узла. Если оба они вычисляются в None, значит этот узел — лист. Это проверяется в строке 7. Если же узел не листовой, то ищем в нём оператор и применяем его к результатам рекурсивных вычислений левого и правого потомков.
Для реализации арифметики мы используем словарь с ключами ‘+’, ‘-‘, ‘*’ и ‘/’. Хранимые в нём значения — функции из модуля операторов Python. Этот модуль предоставляет в наше распоряжение множество часто употребляемых операторов в виде функций. Когда мы ищем в словаре оператор, извлекается связанный с ним объект. А поскольку это функция, то мы можем вызвать её обычным способом function(param1, param2). Таким образом, поиск opers[‘+’](2,2) эквивалентен operator.add(2,2).
Листинг 1
def evaluate(parseTree): opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv} leftC = parseTree.getLeftChild() rightC = parseTree.getRightChild() if leftC and rightC: fn = opers[parseTree.getRootVal()] return fn(evaluate(leftC),evaluate(rightC)) else: return parseTree.getRootVal() |
Наконец, проследим работу функции evaluate на дереве синтаксического разбора, которое изображено на рисунке 4. В первом вызове evaluate мы передаём ей корень всего дерева в качестве параметра parseTree. Затем получаем ссылки на левого и правого потомков, чтобы убедиться в их существовании. В строке 9 идёт следующий рекурсивный вызов. Мы начинаем с поиска оператора в корне дерева, которым в данном случае является +. Он отображается как вызов функции operator.add, принимающей два параметра. Традиционно для вызова функции первым, что сделает Python, станет вычисление переданных в функцию параметров. В нашем случае оба они — рекурсивные вызовы evaluate. Вычисляя слева направо, сначала выполнится левый рекурсивный вызов, куда передано левое поддерево. Мы обнаружим, что этот узел не имеет потомков, следовательно, является листом. Поэтому хранящееся в нём значение просто вернётся, как результат вычисления. В данном случае это будет целое число 3.
К настоящему моменту у нас есть один параметр, вычисленный для верхнего вызова operator.add. Но мы ещё не закончили. Продолжая вычислять параметры слева направо, сделаем рекурсивный вызов для правого поддерева корня. Обнаружив, что у него есть и правый, и левый потомки, ищем оператор, хранящийся в узле, (‘*’) и вызываем для него функцию, передавая в неё левого и правого потомков в качестве параметров. В этой точке вычисления оба рекурсивных вызова вернут листья — целые 4 и 5, соответственно. Имея их, вернём результат operator.mul(4,5). Теперь у нас есть все операнды для верхнего оператора +, и остаётся просто вызвать operator.add(3,20). Результат вычисления дерева для выражения ((3 + (4 * 5))) равен 23.
Время на прочтение
11 мин
Количество просмотров 38K
Что такое PLY?
PLY — это аббревиатура из первых букв выражения: Python Lex-Yacc.
Фактически, это порт утилит lex и yacc на python в красивой обертке.
Работать с ply очень просто и порог входа для начала использования практически нулевой.
Написан он на чистом питоне и представляет из себя LALR(1) парсер, но кому это интересно?
Я по натуре практик (как и большинсво из вас) поэтому пошли в бой!
Что будем делать?
На сайте есть пример написания очередного калькулятора, поэтому повторяться не будем. А сделаем что-то навроде парсера очень очень узкого подмножества PHP 
Наша задача в конце статьи построить синтаксическое дерево для такого примера:
<?php
$val = 5;
$result = substr( "foobar", 2*(7-$val) );
echo "это наш результат: $result";
Пример очень маленький и взят с потолка. Но чтобы построить дерево кода нужно много и походу мы задействуем такой механизм PLY как state.
Lex
Lex — это штука, которая разбивает текст на базовые элементы языка. Ну или группирует текст в базовые элементы. Как-то так.
Что мы здесь видим, кроме бесполезного кода? Видим токены (базовые элементы):
PHP_START — ‘<?php’
PHP_VAR — ‘$result’
PHP_EQUAL — ‘=’
PHP_NAME — ‘substr’
PHP_OPEN — ‘(‘
PHP_STRING — «foobar», ‘это наш результат: $result’
PHP_NUM — ‘2’, ‘7’
PHP_CLOSE — ‘)’
PHP_ECHO — «echo»
PHP_COLON — ‘;’
PHP_COMA — ‘,’
PHP_PLUSMINUS — ‘-‘
PHP_DIVMUL — ‘*’
Для разбора текста на токены в PLY имеется ply.lex. И работает он с регулярными выражениями.
А еще он очень придирчивый к тому что мы пишем в коде. Он требует обязательного присутствия массива с именем tokens.
Для каждого элемента этого массива мы обязаны иметь в коде регулярку или функцию с именем t_ЭЛЕМЕНТ.
Почему он такой придирчивый? Потому что он не работает напрямую во время выполнения программы, а выполняется лишь единожды при первом запуске программы и создает файл lextab.py, в котором описаны таблицы переходов и регулярки. При следующем запуске программы он проверяет наличие этого файла и в случае его присутствия уже не пытается строить таблицы заново, а использует сгенерированные.
Назад к коду.
Если бы синтаксис PHP ограничивался тринадцатью выше перечисленными токенами, то мы бы написали следующее:
# coding=utf8
import ply.lex as lex
# без этой штуки ничего не сынтерпретируется, потому что этот массив шарится между лексером и парсером и кроме того используется внутренне библиотекой
tokens = (
'PHPSTART', 'PHPVAR', 'PHPEQUAL', 'PHPFUNC',
'PHPSTRING', 'PHPECHO', 'PHPCOLON', 'PHPCOMA',
'PHPOPEN', 'PHPCLOSE', 'PHPNUM', 'PLUSMINUS', 'DIVMUL'
)
# определим регулярку для абстрактного идетификатора
ident = r'[a-z]w*'
# для каждого токена из массива мы должны написать его определение вида t_ИМЯТОКЕНА = регулярка
t_PHPSTART = r'<?php'
t_PHPVAR = r'$'+ident # очень удобно, правда?
t_PHPEQUAL = r'='
t_PHPFUNC = ident
t_PHPSTRING = r'"(\.|[^"])*"'
t_PHPECHO = r'echo'
t_PHPCOLON = r';'
t_PHPCOMA = r','
t_PHPOPEN = r'('
t_PHPCLOSE = r')'
t_PHPNUM = r'd+'
t_PLUSMINUS = r'+|-'
t_DIVMUL = r'/|*'
# здесь мы игнорируем незначащие символы. Нам ведь все равно, написано $var=$value или $var = $value
t_ignore = ' rntf'
# а здесь мы обрабатываем ошибки. Кстати заметьте формат названия функции
def t_error(t):
print "Illegal character '%s'" % t.value[0]
t.lexer.skip(1)
lexer = lex.lex(reflags=re.UNICODE | re.DOTALL)
data = '''
<?php
$result = substr("foobar", "bar");
echo $result;
'''
lexer.input(data)
while True:
tok = lexer.token() # читаем следующий токен
if not tok: break # закончились печеньки
print tok
В комментарих к коду я примерно описал что у нас там творится. Замечу лишь, что вместо регулярок, определяющих токен, можно писать функции в которых будут эти же регулярки, но кроме этого можно будет туда вписать что-то еще свое. Например:
def t_PHPVAR(t):
r'$[a-zA-Z]w*'
print 'Урра, мы распарсили переменную ' + t.value # value - это то что нашлось регуляркой
return t
Кстати вывод примера, что написан выше будет таким:
LexToken(PHPSTART,'<?php',1,1)
LexToken(PHPVAR,'$val',1,7)
LexToken(PHPEQUAL,'=',1,12)
LexToken(PHPNUM,'5',1,14)
LexToken(PHPCOLON,';',1,15)
LexToken(PHPVAR,'$result',1,17)
LexToken(PHPEQUAL,'=',1,25)
LexToken(PHPFUNC,'substr',1,27)
LexToken(PHPOPEN,'(',1,33)
LexToken(PHPSTRING,'"foobar"',1,35)
LexToken(PHPCOMA,',',1,43)
LexToken(PHPNUM,'2',1,45)
LexToken(DIVMUL,'*',1,46)
LexToken(PHPOPEN,'(',1,47)
LexToken(PHPNUM,'7',1,48)
LexToken(PLUSMINUS,'-',1,49)
LexToken(PHPVAR,'$val',1,50)
LexToken(PHPCLOSE,')',1,54)
LexToken(PHPCLOSE,')',1,56)
LexToken(PHPCOLON,';',1,57)
LexToken(PHPFUNC,'echo',1,59)
LexToken(PHPSTRING,'"xd1x8dxd1x82xd0xbe xd0xbdxd0xb0xd1x88 xd1x80xd0xb5xd0xb7xd1x83xd0xbbxd1x8cxd1x82xd0xb0xd1x82: $result"',1,64)
LexToken(PHPCOLON,';',1,107)
Числа в конце — это номер строки и номер символа. Как видите, номер строки не изменяется. Его нужно менять самим. Как? При проходе токена с переходом на новую строку. Для этого уберем символ новой строки из игнорируемых токенов и добавим новую функцию t_newline:
t_ignore = ' rtf'
def t_newline(t):
r'n+'
t.lexer.lineno += len(t.value)
Вот теперь у нас все работает:
LexToken(PHPSTART,'<?php',2,1)
LexToken(PHPVAR,'$val',3,7)
LexToken(PHPEQUAL,'=',3,12)
LexToken(PHPNUM,'5',3,14)
LexToken(PHPCOLON,';',3,15)
LexToken(PHPVAR,'$result',4,17)
LexToken(PHPEQUAL,'=',4,25)
LexToken(PHPFUNC,'substr',4,27)
LexToken(PHPOPEN,'(',4,33)
LexToken(PHPSTRING,'"foobar"',4,35)
LexToken(PHPCOMA,',',4,43)
LexToken(PHPNUM,'2',4,45)
LexToken(DIVMUL,'*',4,46)
LexToken(PHPOPEN,'(',4,47)
LexToken(PHPNUM,'7',4,48)
LexToken(PLUSMINUS,'-',4,49)
LexToken(PHPVAR,'$val',4,50)
LexToken(PHPCLOSE,')',4,54)
LexToken(PHPCLOSE,')',4,56)
LexToken(PHPCOLON,';',4,57)
LexToken(PHPFUNC,'echo',5,59)
LexToken(PHPSTRING,'"xd1x8dxd1x82xd0xbe xd0xbdxd0xb0xd1x88 xd1x80xd0xb5xd0xb7xd1x83xd0xbbxd1x8cxd1x82xd0xb0xd1x82: $result"',5,64)
LexToken(PHPCOLON,';',5,107)
Работает, но не полностью. Наша строка «это наш результат: $result» возвращается лексером как есть. А как парсить её будем? Создавать отдельный лексер? Неа. В PLY (да и в сишном lex) есть поддержка такой штуки как state. State — это переключалка на другой тип токенов. Вот это мы и будем использовать.
State
Итак, для того чтобы создать новый state нам нужно его предварительно объявить:
states = (
('string','exclusive'),
)
‘string’ — это название нового состояния, а exclusive — это тип. Вообще, может быть два типа состояний: exclusive и inclusive. Exclusive — общих токенов не видно (общие, это те которые мы писали до этого, они по умолчанию находятся в состоянии INITIAL). Inclusive — видны общие токены и в текущем состоянии мы просто добавляем к ним дополнительные.
В случае нашей строки нам не нужны другие токены, так как внутри у нас там все по другому. Впрочем парочку мы позаимствуем. Нам нужен токен PHPVAR, потому что переменная у нас выглядит одинаково и снаружи и внутри строки, и нужен будет еще один токен, который вы увидите походу ниже.
Чтобы сделать токен общим мы должны присвоить ему префикс ANY_, ну а чтобы сделать токен видимым только для какого-то определенного состояния — <состояние>_. Ниже приведены измененные токены.
# для каждого токена из массива мы должны написать его определение вида t_ИМЯТОКЕНА = регулярка
t_PHPSTART = r'<?php'
t_ANY_PHPVAR = r'$'+ident # очень удобно, правда?
t_PHPEQUAL = r'='
t_PHPFUNC = ident
t_PHPECHO = r'echo'
t_PHPCOLON = r';'
t_PHPCOMA = r','
t_PHPOPEN = r'('
t_PHPCLOSE = r')'
t_PHPNUM = r'd+'
t_PLUSMINUS = r'+|-'
t_DIVMUL = r'/|*'
# изменили токен PHPSTRING и сделали из него функцию, добавили его во все состояния
def t_ANY_PHPSTRING(t): # нужен в обоих состояниях, потому что двойные кавычки матчатся и там и там.
r'"'
if t.lexer.current_state() == 'string':
t.lexer.begin('INITIAL') # переходим в начальное состояние
else:
t.lexer.begin('string') # парсим строку
return t
t_string_STR = r'(\.|[^$"])+' # парсим пока не дойдем до переменной или до кавычки, попутно игнорируем экранки
# говорим что ничего не будем игнорировать
t_string_ignore = '' # это кстати обязательная переменная, без неё нельзя создать новый state
# ну и куда же мы без обработки ошибок
def t_string_error(t):
print "Illegal character '%s'" % t.value[0]
t.lexer.skip(1)
Кстати, заметили это: LexToken(PHPFUNC,’echo’,5,59)?
PLY перед построением таблицы сортирует регулярные выражения по возрастанию и в процессе парсинга побеждает длиннейшее. Вот поэтому echo и не парсится как PHPECHO. Как это обойти? Легко. Просто изменим тип возвращаемого токена в функции.
Вот так:
@TOKEN(ident)
def t_PHPFUNC(t):
if t.value.lower() == 'echo':
t.type = 'PHPECHO'
return t
Теперь echo возвращается как нужно. Кстати о декораторе TOKEN: вместо того, чтобы писать регулярку в начале тела функции, можно просто поместить её в переменную и применить к функции как декоратор. Что мы и сделали.
Вот. Теперь вроде все. Да не все.
Неплохо бы игнорировать комментарии.
Что же, добавим еще одну маленькую функцию в лексер:
def t_comment(t):
r'(/*(.|n)*?*/)|(//.*)'
pass
Полный исходный код лексера (lexer.py)
# coding=utf8
import ply.lex as lex
from ply.lex import TOKEN
import re
states = (
('string','exclusive'),
)
# без этой штуки ничего не съинтерпретируется, потому что этот массив шарится между лексером и парсером и кроме того используется внутренне библиотекой
tokens = (
'PHPSTART', 'PHPVAR', 'PHPEQUAL', 'PHPFUNC',
'PHPSTRING', 'PHPECHO', 'PHPCOLON', 'PHPCOMA',
'PHPOPEN', 'PHPCLOSE', 'PHPNUM', 'PLUSMINUS', 'DIVMUL',
'STR'
)
# определим регулярку для абстрактного идетификатора
ident = r'[a-z]w*'
# для каждого токена из массива мы должны написать его определение вида t_ИМЯТОКЕНА = регулярка
t_PHPSTART = r'<?php'
t_ANY_PHPVAR = r'$'+ident # очень удобно, правда?
t_PHPEQUAL = r'='
t_PHPCOLON = r';'
t_PHPCOMA = r','
t_PHPOPEN = r'('
t_PHPCLOSE = r')'
t_PHPNUM = r'd+'
t_PLUSMINUS = r'+|-'
t_DIVMUL = r'/|*'
@TOKEN(ident)
def t_PHPFUNC(t):
if t.value.lower() == 'echo':
t.type = 'PHPECHO'
return t
# игнорируем комментарии
def t_comment(t):
r'(/*(.|n)*?*/)|(//.*)'
pass
# изменили токен PHPSTRING и сделали из него функцию, добавили его во все состояния
def t_ANY_PHPSTRING(t): # нужен в обоих состояниях, потому что двойные кавычки матчатся и там и там.
r'"'
if t.lexer.current_state() == 'string':
t.lexer.begin('INITIAL') # переходим в начальное состояние
else:
t.lexer.begin('string') # парсим строку
return t
t_string_STR = r'(\.|[^$"])+' # парсим пока не дойдем до переменной или до кавычки, попутно игнорируем экранки
# говорим что ничего не будем игнорировать
t_string_ignore = '' # это кстати обязательная переменная, без неё нельзя создать новый state
# ну и куда же мы без обработки ошибок
def t_string_error(t):
print "Illegal character '%s'" % t.value[0]
t.lexer.skip(1)
# здесь мы игнорируем незначащие символы. Нам ведь все равно, написано $var=$value или $var = $value
t_ignore = ' rtf'
def t_newline(t):
r'n+'
t.lexer.lineno += len(t.value)
# а здесь мы обрабатываем ошибки. Кстати заметьте формат названия функции
def t_error(t):
print "Illegal character '%s'" % t.value[0]
t.lexer.skip(1)
lexer = lex.lex(reflags=re.UNICODE | re.DOTALL | re.IGNORECASE)
if __name__=="__main__":
data = '''
<?php
$val = 5;
$result = substr( "foobar", 2*(7-$val) );
echo "это наш результат: $result";
'''
lexer.input(data)
while True:
tok = lexer.token() # читаем следующий токен
if not tok: break # закончились печеньки
print tok
Вот теперь переходим к парсеру (parser.py).
Yacc
Yacc — это штука (парсер), в которую мы передаем токены и описываем правила их соединения (грамматику). Походу работы этой программы мы можем создать абстрактное дерево или же сразу выполнять программу (как это сделано в примере с калькулятором на сайте).
В PLY для описания грамматики существует класс ply.yacc.
Описывать граматику в ply очень просто и это доставляет даже некоторое наслаждение. Для описания у нас снова существуют специальные функции p_имяфункции, где в doc-строках мы и описываем эту самую грамматику.
Давайте попробуем написать очень простую грамматику для нашего абстрактного примера с php:
php -> [PHPSTART phpbody]? phpbody -> [phpline phpcolons]* phpcolons -> [ PHPCOLON ]+ phpline -> assign | func | [PHPECHO args] assign -> PHPVAR PHPEQUAL expr expr -> [fact | expr PLUSMINUS fact] fact -> [term | fact DIVMUL term] term -> [arg | PHPOPEN expr PHPCLOSE] func -> PHPFUNC PHPOPEN args PHPCLOSE args -> [ expr [PHPCOMA expr]* ]? arg -> string | phpvar | PHPNUM | func string -> PHPSTRING str PHPSTRING str -> [STR | str phpvar]? phpvar -> PHPVAR
Текста написано уже много, и рассказывать еще можно очень долго. Но для понимания основ ply.yacc достаточно разобрать один пример. А дальше я уже выложу исходник парсера.
Итак, выдранный кусок из парсера:
def p_str(p):
'''str :
| STR
| str phpvar'''
if len(p) == 1:
p[0] = Node('str', [''])
elif len(p) == 2:
p[0] = Node('str', [p[1]])
else:
p[0] = p[1].add_parts([p[2]])
По порядку. Парсинг начинается с первой сверху функции с шаблоном p_<функция>. Т.е. у меня например первой в исходнике стоит p_php, поэтому парсер начнет работу именно с неё (сверху вниз). Парсер работает с правилами в doc-строках, и после их матчинга возвращает управление в функцию с правилами и при этом передает переменную p. В переменной p хранится результат парсинга. Причем после обработки мы должны засунуть наши результаты в p[0]. Элементы, начиная с p[1], это правая часть наших правил — отматченные токены и правила.
'''str :
| STR
| str phpvar'''
По сути правило выше — это скомбинированное (слитое) правило. ‘|’ как несложно догадаться — это ИЛИ, ну или различные варианты токена.
Между двоеточием и левой/правой частью обязателен пробел. Так любит ply. Если правая часть может быть пустой, то после двоеточия ничего не пишем. Токены должны быть написаны большими буквами, а правила маленькими, без префикса p_. Т.е. в примере выше использовались правила p_str и p_phpvar.
Например, если мы имеем «» (пустую строку), то в p у нас будет только одно значение — p[0], причем оно не определно и мы должны его заполнить.
Если у нас строка «привет $vasya пупкин», то эта функция выполнится три раза. Первый раз для значения STR, и мы вернем это значение обратно в p[0], второй раз для $vasya, и добавим это к предыдущему значению (p[1] будет содержать ноду, которую мы вернули в p[0] на прошлой итерации), а третий раз добавим на выход «пупкин». Наверное я сумбурно описал, но это надо просто потрогать. Открыть среду исполнения и поиграться 
Кстати, иногда более удобен вариант с разделенными вариантами (тафтология, простите):
def p_str_empty(p):
'''str :'''
p[0] = Node('str', [''])
def p_str_raw(p):
'''str : STR'''
p[0] = Node('str', [p[1]])
def p_str_var(p):
'''str : str phpvar'''
p[0] = p[1].add_parts([p[2]])
Он абсолютно идентичен предыдущему варианту кода. Просто фломастеры другие. Функции имеют разные названия (потому что разделять их надо в питоне), но префиксы идентичные (str), что и заставляет ply группировать их вместе как варианты одного правила.
Для удобства построения дерева я использовал такой простенький и эффективный класс:
class Node:
def parts_str(self):
st = []
for part in self.parts:
st.append( str( part ) )
return "n".join(st)
def __repr__(self):
return self.type + ":nt" + self.parts_str().replace("n", "nt")
def add_parts(self, parts):
self.parts += parts
return self
def __init__(self, type, parts):
self.type = type
self.parts = parts
Он одновременно и хранит все нужное, и структурирует вывод, что чень удобно при отладке.
Полный код парсера
# coding=utf8
from lexer import tokens
import ply.yacc as yacc
class Node:
def parts_str(self):
st = []
for part in self.parts:
st.append( str( part ) )
return "n".join(st)
def __repr__(self):
return self.type + ":nt" + self.parts_str().replace("n", "nt")
def add_parts(self, parts):
self.parts += parts
return self
def __init__(self, type, parts):
self.type = type
self.parts = parts
def p_php(p):
'''php :
| PHPSTART phpbody'''
if len(p) == 1:
p[0] = None
else:
p[0] = p[2]
def p_phpbody(p):
'''phpbody :
| phpbody phpline phpcolons'''
if len(p) > 1:
if p[1] is None:
p[1] = Node('body', [])
p[0] = p[1].add_parts([p[2]])
else:
p[0] = Node('body', [])
def p_phpcolons(p):
'''phpcolons : PHPCOLON
| phpcolons PHPCOLON'''
def p_phpline(p):
'''phpline : assign
| func
| PHPECHO args'''
if len(p) == 2:
p[0] = p[1]
else:
p[0] = Node('echo', [p[2]])
def p_assign(p):
'''assign : PHPVAR PHPEQUAL expr'''
p[0] = Node('assign', [p[1], p[3]])
def p_expr(p):
'''expr : fact
| expr PLUSMINUS fact'''
if len(p) == 2:
p[0] = p[1]
else:
p[0] = Node(p[2], [p[1], p[3]])
def p_fact(p):
'''fact : term
| fact DIVMUL term'''
if len(p) == 2:
p[0] = p[1]
else:
p[0] = Node(p[2], [p[1], p[3]])
def p_term(p):
'''term : arg
| PHPOPEN expr PHPCLOSE'''
if len(p) == 2:
p[0] = p[1]
else:
p[0] = p[2]
def p_func(p):
'''func : PHPFUNC PHPOPEN args PHPCLOSE'''
p[0] = Node('func', [p[1], p[3]])
def p_args(p):
'''args :
| expr
| args PHPCOMA expr'''
if len(p) == 1:
p[0] = Node('args', [])
elif len(p) == 2:
p[0] = Node('args', [p[1]])
else:
p[0] = p[1].add_parts([p[3]])
def p_arg(p):
'''arg : string
| phpvar
| PHPNUM
| func'''
p[0] = Node('arg', [p[1]])
def p_phpvar(p):
'''phpvar : PHPVAR'''
p[0] = Node('var', [p[1]])
def p_string(p):
'''string : PHPSTRING str PHPSTRING'''
p[0] = p[2]
def p_str(p):
'''str :
| STR
| str phpvar'''
if len(p) == 1:
p[0] = Node('str', [''])
elif len(p) == 2:
p[0] = Node('str', [p[1]])
else:
p[0] = p[1].add_parts([p[2]])
def p_error(p):
print 'Unexpected token:', p
parser = yacc.yacc()
def build_tree(code):
return parser.parse(code)
Основной файлик, откуда вызываем все
# coding=utf8
from parser import build_tree
data = '''
<?php
$val = 5;
$result = substr( "foobar", 2*(7-$val) ); /* comment */
echo "это наш результат: ", $result;
'''
result = build_tree(data)
print result
Вывод синтаксического дерева
line: assign: $val arg: 5 assign: $result arg: func: substr args: arg: str: foobar *: arg: 2 -: arg: 7 arg: var: $val echo: args: arg: str: это наш результат: arg: var: $result
Заключение
Если есть какие-то замечания или пожелания, с удовольствием допишу/изменю пост.
Код статьи здесь
Ну и если интересно с чего я вдруг про ply решил написать — pyfox. Делаю потихонечьку обработку css на python. Вернее парсер css написан, но вот прогулка по dom еще полностью не реализована (не все псевдоселекторы работают). Сейчас конкретно проблема с nth-child. Не на уровне css а на уровне эффективного матчинга — в dom нету такого свойства как номер среди соседей, а считать предыдущих соседей не хочется. Видимо придется HTMLParser кастомизировать. Может кто решит присоединитсья ко мне? Всех welcome 
Дерево разбора
может рассматриваться как графическое
представление порождения, из которого
удалена информация о порядке замещения
не терминалов.
Каждый внутренний
узел дерева представляет применение
продукции.
Внутренний узел
дерева помечен нетерминалом А из
заголовка соответствующей продукции,
а дочерние узлы слева направо символами
из тела продукции, использованные в
порождении для замены А.
Например,
дерево для разбора – (id+id):
E
/
—
E
/
|
(
E )
/
|
E
+ E
|
|
id
id
Листья
дерева разбора не терминальными или
терминальными и будучи прочитаны слева
на право, образуют сентенциальную
форму
называемую кроной или границей дерева.
Для
того что бы увидеть связь между
порождениями и деревьями разбора
рассмотрим произвольное приведение.
α1
→ α2
→ … →
αn
Где альфа 1
отдельный не терминал А.
Для
каждой сентенциальной формы альфа 1
можно построить дерево разбора, кроной
которого является альфа 1 этот процесс
представляет собой индукцию по i.
Пример,
последовательность деревьев разбора:
1)
Порождение E
=> -E
E
-> E
/
—
E
Для моделирования
этого шага корню Е в начало дерева
добавляют два дочерних узла помеченных
«-» и «Е».
2)
– E
=> — (E)
добавляют 3 дочерних узла, помеченных
(, Е, ) к листу Е для получения дерева с
кроной – (Е).
E
/
—
E
/
|
(
E
)
Продолжая построение
описываемым способом получается
полноценное дерево разбора.
E
-> E
-> E
/
/ /
—
E
— E
— E
/
| / | / |
(
E
) ( E
) ( E
)
/
| / | / |
E
+ E
E
+ E
E
+ E
|
| |
id
id
id
Т.к.
дерево разбора игнорирует порядок, в
котором производилось замещение символов
в сентенциальной
форме, между порождениями и деревьями
возникает соотношение «многих к одному».
Каждое дерево
связано с единственным левым и единственным
правым порождением.
17. Нисходящий синтаксический анализ
Можно
рассмотреть как поиск левого порождения
входящей строки. Рассмотрим
последовательность построений деревьев
разбора для входящей строки (id+id)*id,
представляющий собой нисходящий
синтаксический анализ, построенный в
соответствии с грамматикой:
E
-> TE’
E’
-> +TE’|e
T
->FT’
T’
-> *FT’|e
F
-> (E)|id
Эта
последовательность деревьев соответствует
левому порождению входящей строки. На
каждом шаге нисходящего синтаксического
анализа ключеваой проблемой является
определение продукции, применимой для
нетерминалов, например А. Когда А
продукция выбрана, остальные части
процесса синтаксического анализа
состоят из проверки соответвствий
терминальных символов в теле продукции
входящей строки. В рассмотренном примере
строится дерево с двумя узлами,
помеченными E’,
в первом (в прямом) порядке обхода узла
Е’ выбирается продукция
E’
-> +TE’,
во втором E’
-> e.
Синтаксический анализатор может выбрать
нужную E’
продукцию, рассматривающую очередной
входящий символ. Класс Грамматик для
которых можно построить синтаксический
анализатор, просматривающий k-символов
во входящем потоке называется классом
LL(k).
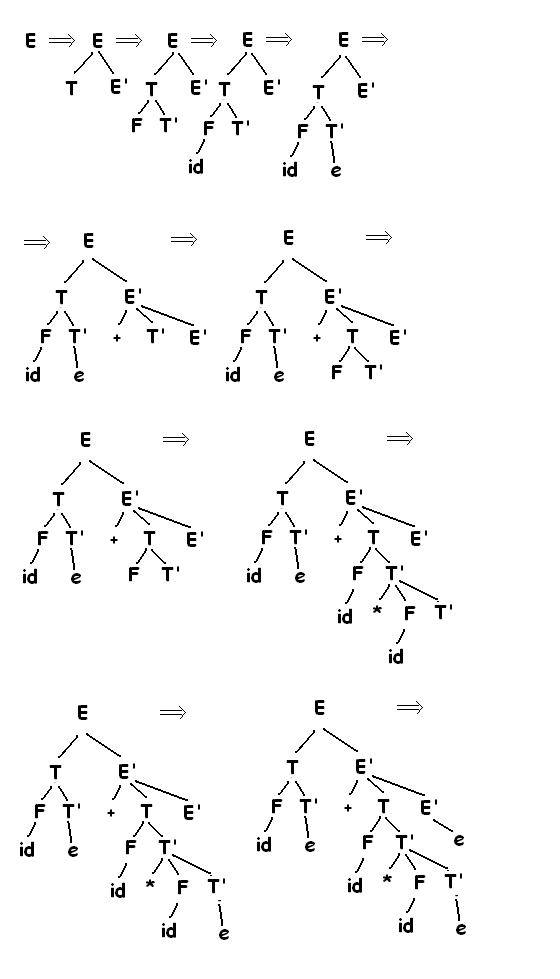
Метод
рекурсивного спуска
Программа
синтаксического анализатора методом
рекурсивного спуска состоит из набора
процедур по одной для каждого нетерминала.
Работа программы начинается с вызова
процедуры для стартового символа и
успешно заканчивается в случае
сканирования всей входящей строки.
Типичная
процедура для нетерминала низходящего
анализатора
Void
A() {
-
Выбираем
А-продукцию А->X1X2…Xk
For(от
1 до k)
{
If
(Xi-нетерминал)
Вызов процедуры Xi();
else
if(Xi
равно текущему входному символу a)
Переход
к следующему входному символу
else
(Обнаружена ошибка)
}}
Этот
псевдокод недетерминирован т.к. он
начинается с выбором А-продукции не
указанным способом.
Рекурсивный
способ в общем случае может потребовать
выполнения возврата т.е. повторения
сканирования входного потока. При
анализе синтаксической конструкции
языка программирования
возврат требуется редко. В ситуациях ,
наподобие, синтаксического анализа
естественного языка возврат не слишком
эффективен и предпочтительней являются
табличные методы. Чтобы разрешить
возврат код в примере должен быть
модифицирован:
-
Невозможно
выбрать единую А-продукцию в строке
(1), поэтому требуется испытывать каждую
из нескольких продукций в некотором
порядке. -
Ошибка
в строке (*) не является окончательной
и предполагает возворат к строке (1) и
испытание другой А-продукции.
Объявлять
о найденной во входной строке ошибке
можно только в том случае, если больше
не имеется непроверенных А-продукций.
Пример:
Рассмотрим
Грамматику:
S
-> cAd
A
-> ab|a
Чтобы
построить дерево разбора для входной
строки ω-cod
начинают с дерева, состоящего из
единичного узла с меткой S
и указателя входного потока, указывающего
на С или первый символ ω.
S
имеет единичную продукцию, поэтому ее
используют для разворачивания и получения
дерева.
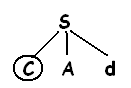
Соответствует
первому символу входного потока ω,
поэтому указатель входного потока
перемещается к а-второму символу ω и
рассматривается следующий лист,
помеченный А.
Затем
разворачивается А с использованием
альтернативы А -> ab
и получаем таким образом дерево,
показанное на рис.
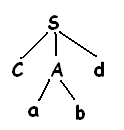
Имеется
совпадение второго входного символа
а, поэтому выполняется переход к третьему
символу d
и сравнивают его с очередным листком
b.
Т.к. b
не соответствует d,
то сообщается об ошибке и происходит
возврат к А.
Чтобы
выяснить нет ли альтернативной продукции,
которая не была проверена до этого
времени, вернувшись к а необходимо
отбросить указатель входного потока
так, чтобы он указывал на позицию 2, в
которой указатель находится, когда
впервые столкнулся с а. Это означает
что процедура для а должна хранить
указатель на входной поток в локальной
переменной.
Вторая
альтернатива для а дает дерево разбора:
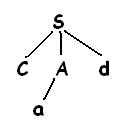
Лист
а соответствует второму символу ω, а
лист d
– третьему символу. Т.к. построено дерево
разбора для входящей строки ω, то алгоритм
завершает работу и сообщает об успешном
выполнении синтаксического анализа и
построении дерева разбора. Левосторонняя
грамматика может привести синтаксический
анализатор, работающий методом
рекурсивного спуска к бесконечному
циклу, т.е. когда пытаются проверить
нетерминал а, то в конечном счете можно
найти этот же нетерминал а и перейти к
попытке развернуть а, так и не взяв ни
одного символа из входного потока.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В задаче демонстрируются понятие синтаксической структуры и явление синтаксической омонимии.
Синтаксическая структура предложения — это система связей между синтаксическими единицами, то есть словами или группами слов.
Графически синтаксическую структуру удобно представлять в виде синтаксических деревьев, где синтаксические единицы изображаются в виде точек (узлов), а связи — в виде дуг (для отражения ненаправленных связей) или стрелок (для отражения направленных связей), соединяющих эти узлы. Схемы в нашей задаче фактически и являются синтаксическими деревьями. Связи в синтаксических деревьях из задачи направленные, они изображаются стрелками; такие деревья называются деревьями зависимостей (или подчинения). В синтаксическом дереве существует единственный узел, в который не входит ни одна стрелка (этот узел иногда называют вершиной, потому что, когда изображается дерево предложения, этот узел всегда расположен на самом верху, а иногда корнем, потому что с него начинается, «вырастает» все дерево). В каждый узел, кроме вершины, входит ровно одна стрелка.
Синтаксические деревья в этой задаче не представляют сложности для лингвиста, но могут оказаться не такими простыми для неспециалистов, поскольку в традиционной грамматике (а в школе изучается именно она) принято рассматривать в качестве вершины предложения скорее подлежащее, чем сказуемое, и не упорядочивать по тесноте связи зависимые от сказуемого члены предложения. Более распространенный в современной лингвистике способ представления синтаксической структуры предложен французским лингвистом Люсьеном Теньером: в вершине находится сказуемое, а от него непосредственно или опосредованно зависят все остальные члены предложения, причем важна теснота связей: наиболее тесной считается связь сказуемого с подлежащим, затем с дополнениями, наименее тесна связь сказуемого с обстоятельствами.
Предложение Теньер назвал «драмой в миниатюре», в центре которой находится действие с его участниками. Вершиной предложения является глагол–сказуемое ― предикат, все остальные синтаксические единицы, входящие в предложение, подчиняются ему непосредственно или опосредованно. В непосредственном подчинении оказываются актанты, то есть «действователи» (аналоги дополнений, к актантам причисляется и подлежащее), и сирконстанты (аналоги обстоятельств). Актанты упорядочены по тесноте (I, II, III), первый актант часто оказывается подлежащим.
Стоит добавить, что аналогичные идеи высказывались в языкознании и раньше. Так, в 70–80 гг. XIX века русский лингвист Дмитревский образно определил предложение как «драму мысли», в которой сказуемое, являющееся единственным главным членом предложения, воплощает собой действие драмы, «дополнения» (субстантивные члены, в число которых Дмитревский включал и подлежащее) напоминают действующих лиц сцены, а обстоятельства рисуют обстановку. Но это был лишь кратковременный эпизод в истории науки, в те времена и вплоть до середины XX века господствовала традиционная грамматика.
Более сложные деревья (например, такие) можно увидеть в Синтаксическом корпусе русского языка.
Каждому смыслу предложения соответствует ровно одна синтаксическая структура (и одно синтаксическое дерево). Если предложению можно приписать более одной синтаксической структуры, мы сталкиваемся с синтаксической омонимией. Два наиболее распространенных типа синтаксической омонимии, отображаемых в деревьях подчинения, — это стрелочная и разметочная омонимия (в соответствии с классификацией типов синтаксической омонимии А. В. Гладкого; см. Гладкий А. В. Синтаксические структуры естественного языка в автоматизированных системах общения. Глава 7. Синтаксическая омонимия. М., 1985. С. 110–126).
1. Со стрелочной омонимией мы сталкиваемся тогда, когда для зависимого слова можно найти разных «хозяев», то есть при разном понимании фразы стрелки к зависимому слову идут от разных узлов. Стрелочная омонимия представлена в задаче во фразах 3 и 6:
3. …возвратился из командировки в Новосибирск: возвратился → в Новосибирск (схема е) или из командировки → в Новосибирск (схема в).
6. Работа по-новому всколыхнула…: Работа → по-новому или по-новому ← всколыхнула.
2. Омонимия может возникнуть и за счёт различной интерпретации связи.
Так, для разных смыслов предложения 4 годятся схемы б и д. Это связано с тем, что в предложении именные группы слева и справа от сказуемого можно интерпретировать и как подлежащее, и как прямое дополнение. Такой тип омонимии иногда называют типом «мать любит дочь». Это разновидность разметочной омонимии: обычно в дереве стрелки, обозначающие связи, размечаются, то есть на них подписывается тип связи. В нашей задаче вместо разметки используется относительное расположение стрелок. Та же разновидность разметочной омонимии представлена в предложении 5 (см. схемы в и г).
Кроме чисто синтаксической омонимии в задаче представлена и лексико-синтаксическая омонимия, которая возникает не только из-за разных потенциальных «хозяев» и различной интерпретации связей, но и из-за лексической омонимии (см. также задачу «Ели на опушке»). Так, в предложении 1 словосочетание знакомые студентки омонимично не только из-за омонимии формы студентки (им. мн. или род. ед.), но и из-за лексической омонимии: знакомые — прилагательное или существительное. В предложении 5, кроме указанных в предыдущем абзаце двух смыслов, представляющих собой случай чисто синтаксической омонимии, есть и третий смысл (схема д), возникающий за счёт добавления лексической омонимии: простой может быть и существительным, и прилагательным.
Задача использовалась на ХХI Традиционной лингвистической олимпиаде (1991 г.).