Перед
расчетом переходного режима электрической
системы на
основе ее принципиальной схемы составляют
расчетную схему, которая
отличается от принципиальной тем, что
на ней в однолинейном
изображении показываются только те
элементы, по которым
возможно протекание аварийных токов
или их составляющих. При наличии в
расчетной схеме трансформаторов
целесообразно
имеющиеся в ней магнитно-связанные цепи
представить одной
эквивалентной электрически связанной
цепью. Схема замещения
сложной электрической системы является
соединением схем
замещения отдельных ее элементов (см.
таблицу на с. 55). В ней
элементы соединены так же, как на
расчетной схеме.
После
составления схемы замещения рассчитываются
ее параметры
в именованных или относительных единицах,
затем полученные
значения приводятся к основной ступени
напряжения.
3.2.1. Система относительных единиц
Выражение
электрических величин в относительных
единицах широко
применяется в теории электрических
машин. Это обусловлено тем, что
представление любой величины не в
именованных, а относительных
единицах существенно упрощает
теоретические выкладки и придает
результатам расчета большую наглядность.
Под относительным
значением какой-либо величины следует
понимать ее отношение к другой одноименной
величине, принятой за базисную.
Следовательно, перед тем как представить
какие-либо
величины
в относительных единицах, надо выбрать
базисные единицы.
За
базисный ток и базисное линейное
напряжение примем некоторые
произвольные величины I6,
Uб.
Тогда базисная мощность трехфазной
цепи будет определяться формулой
а базисное
сопротивление — формулой
Отсюда
вытекает, что только две базисные
величины могут быть выбраны произвольно,
а остальные являются связанными.
Следовательно,
параметры электрической системы в
относительных базисных
единицах будут вычисляться по формулам
U*б
= U/U6, (3.1)
I*б
= I/Iб, (3.2)
S*
б
= S/S
б, (3.3)
Z
*б
= Z/Z
б. (3.4)
Здесь
U,
I,
S,
Z
— параметры
в именованных единицах (В, А, ВА, Ом);
индексы означают следующее: * — величина
выражена в относительных
единицах; б — величина приведена к
базисным условиям.
Относительное
сопротивление можно определить иначе:
Z
*б
= Z/Z
б=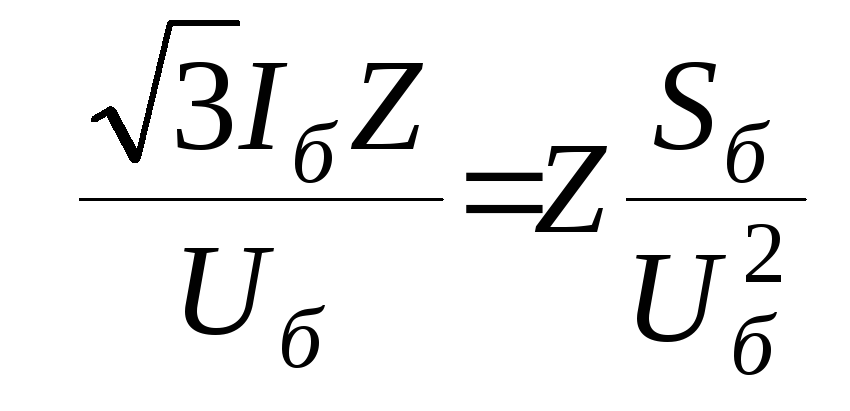
Частным
случаем относительных базисных единиц
являются относительные
номинальные единицы, когда за базисные
приняты номинальные
единицы какого-либо элемента — UHOM,
IHOM,
SHOM.
В
относительных
номинальных единицах выражаются
параметры генераторов,
двигателей, трансформаторов, реакторов.
В этом случае
пересчет к базисным условиям производится
следующим
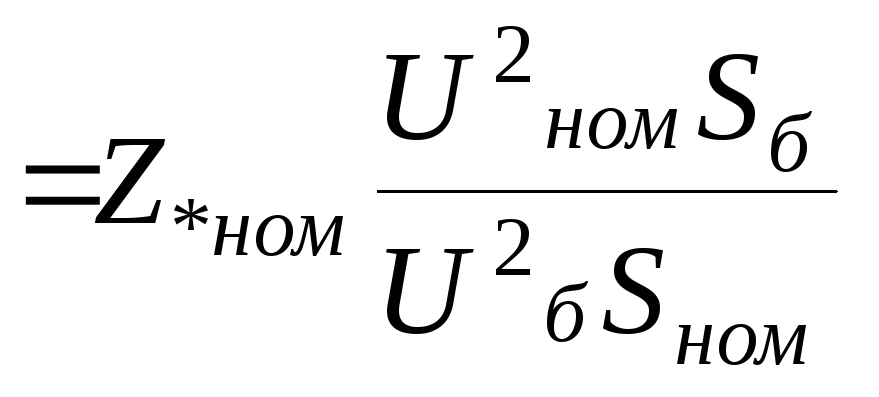
3.2.2.
Приведение
параметров схемы к
основной ступени напряжения
При
наличии в расчетной схеме трансформаторов
возникает необходимость
приведения сопротивлений и ЭДС схемы,
находящихся
на разных ступенях трансформации, к
одной ступени, принятой
за основную. Приведение базируется на
известной теории
трансформатора, дающей для приведенных
параметров следующие
соотношения:
Ē=
(k1k2…kn)E, (3.7)
Ū
=(k1k2…kn)U, (3.8)
(3.9)
=(k1k2…kn)2Z.
Здесь
под коэффициентом трансформации k
трансформатора
или
автотрансформатора понимается отношение
междуфазного напряжения холостого хода
его обмотки, обращенной в сторону
основной ступени напряжения, к аналогичному
напряжению его обмотки,
находящейся ближе к ступени, элементы
которой подлежат
приведению.
Приведение
в именованных единицах. Все
сопротивления элементов
схемы в этом случае должны быть выражены
в омах. Для
элементов, сопротивления которых
приведены в относительных
номинальных единицах (генераторов,
трансформаторов и др.), выражения
сопротивлений будут следующими:
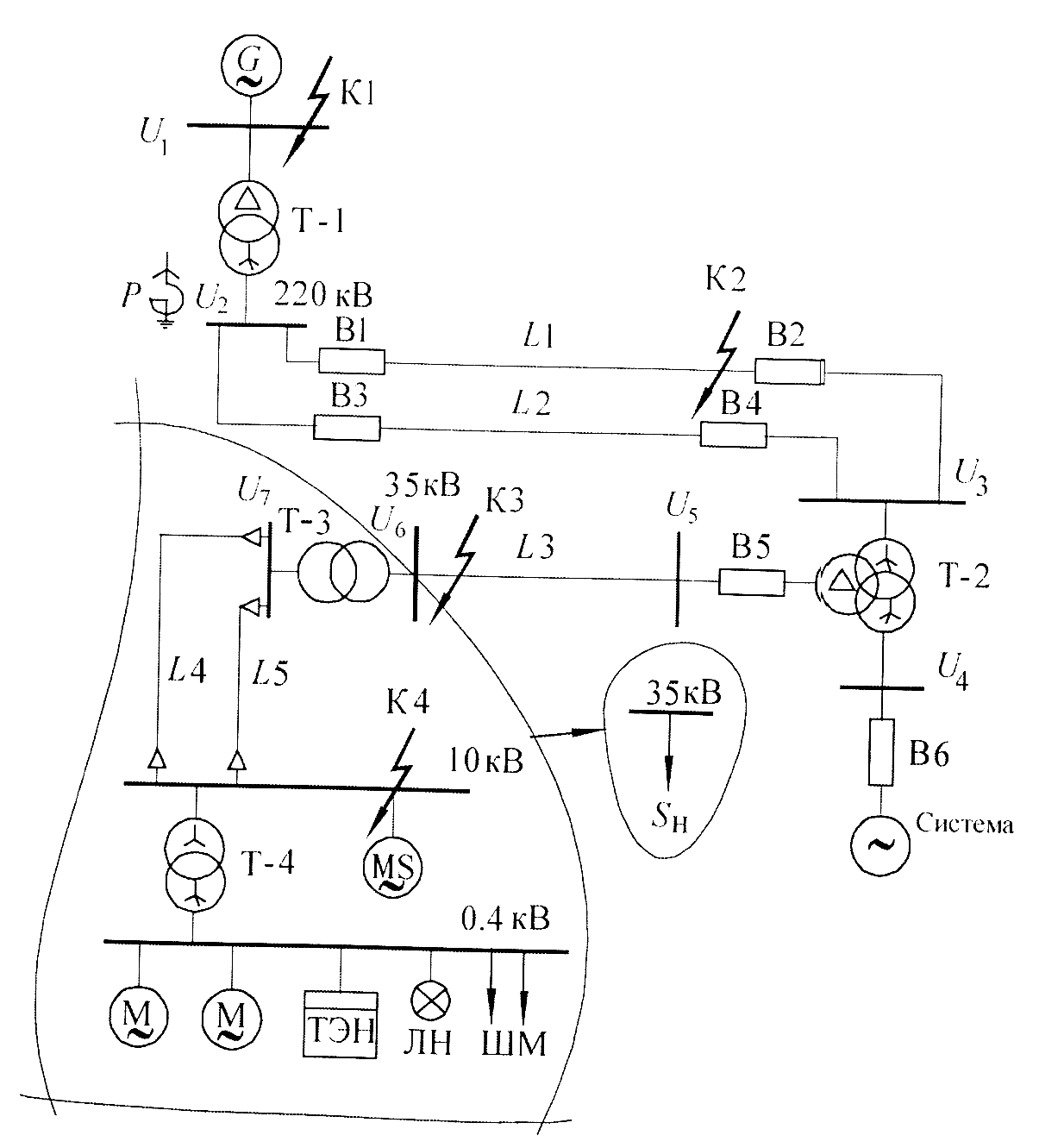
Сопротивления
некоторых элементов схемы ЭС, показанной
на рис. 3.2 (за основную принята ступень
220 кВ), определяются так: генератора
G
линии
L4
(3.10)
трансформатора
Т-4

Токи
и напряжения, рассчитываемые в схеме,
элементы которой
приведены указанным образом, реальны
только для ее основной
ступени. Истинные токи и напряжения на
других ступенях схемы
находятся пересчетом по выражениям
(3.8) и (3.9). Приведение
в относительных базисных единицах.
Выражения
для сопротивлений некоторых элементов
схемы (приведенных к
ступени 220 кВ), показанной на рис. 3.2, в
относительных базисных
единицах имеют вид:
генератора
G
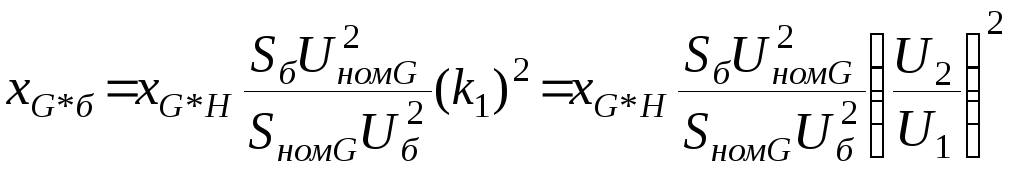
линии
L4
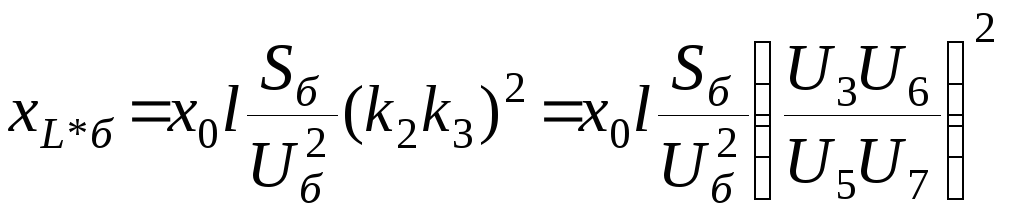
трансформатора
Т-4
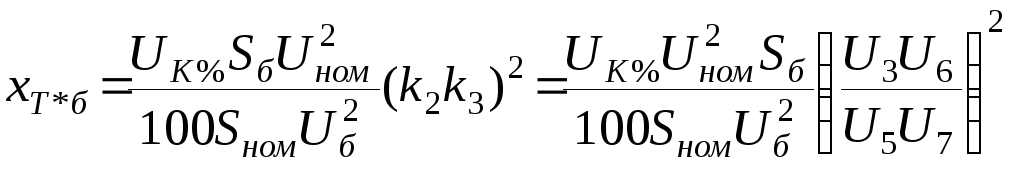
Введем
коэффициенты трансформации из формул
(3.12) –(3.14) в базисное напряжение.
Полученные выражения имеют тот же
вид, что и (3.6):
где
Uб2=
Uб1(1/k1)
Uб3=
Uб1(1/k1k2)
(3-15)
и
представляют собой базисные напряжения
на той ступени, где находится
приводимое сопротивление. Следовательно,
для расчета параметров
схемы в относительных базисных единицах
необходимо
выбрать базисные единицы для одной из
ступеней схемы, а затем
по
формулам
(3.15) определить базисные напряжения для
других
ступеней. При этом базисные токи на
каждой ступени рассчитываются следующим
образом:
Затем
в относительных базисных единицах
рассчитываются все величины
по выражениям (3.1) — (3.6), причем в каждом
из указанных
выражений под Uб,
Iб,
z6
следует понимать базисные параметры
той ступени трансформации, на которой
находятся подлежащие
приведению величины.
В
рассмотренном приведении участвуют
действительные коэффициенты
трансформации, заданные в качестве
исходных величин. «Такое
приведение называется точным. В
практических расчетах применяется
приближенное приведение, позволяющее
упростить выражения, уменьшить объем
вычислений. Приближенное приведение
заключается в том, |что
для каждой ступени трансформации
устанавливают среднее
номинальное
напряжение Ucp
из
следующей шкалы напряжений:
515, 340, 230, 154, 115, 37,
24, 20, 18, 15.75, 13.8, 10.5, 6.3, 3.15, 0.69, 0.4, 0.23, 0.127 кВ.
При
этом принимается, что номинальные
напряжения всех элементов, кроме
реакторов, находящихся на одной ступени,
одинаковы
и равны £/ср.
Коэффициент трансформации каждого
трансформатора
в этом случае равен отношению Ucp.B
/
Ucp.H(средненоминальных
напряжений высшей и низшей обмоток).
Коэффициент трансформации
каскада трансформаторов будет определяться
как отношение
средненоминальных напряжений крайних
ступеней, что упрощает
приведение.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Схемы замещения выполняют в однолинейном изображении; при этом удобно сопротивления и э. д. с. отмечать порядковыми номерами и указывать их численные значения.
При расчете в именованных единицах сопротивления всех элементов приводят к одной ступени напряжения.
Для каждой ступени напряжения приняты следующие значения средних номинальных междуфазных напряжений Uсp (кВ): 515; 340; 230; 154; 115; 37; 24; 20; 18; 15,75; 13,8; 10,5; 6,3; 3,15.
В практических расчетах возможно приближенное приведение сопротивлений по средним коэффициентам трансформации, равным отношению средних номинальных напряжений Uсp соответствующих ступеней.
Сопротивление всех элементов схемы замещения можно выражать в относительных единицах при выбранных базисных условиях или в омах. При расчете в относительных единицах базисная мощность может быть взята произвольной (например, 100 или 1 000 MBА). Базисное напряжение
для каждой ступени напряжения обычно принимается равным Uсp. Базисный ток и базисное сопротивление определяют по выражениям
Сопротивления в относительных единицах при базисных условиях определяют следующим образом.
Если сопротивление, включенное на ступени Uсp, задано:
а) в относительных единицах при Sн и
(генераторы, трансформаторы), то
б) в процентах при
и
(реакторы), то
в) в омах х (воздушные линии, кабели) на единицу длины, то при длине l
Примечания:
1. В указанных формулах следует принимать Ucp и той ступени, на которой находится данный элемент.
2. Сопротивления элементов, выраженные в относительных единицах при базисных условиях, дают схему замещения, приведенную по средним коэффициентам трансформации к одной (и притом любой из указанных в расчетной схеме) ступени напряжения.
Электродвижущая сила источников питания в относительных единицах выражается через
где Е — междуфазная э. д. с. источника, кВ; — фазная э. д. с. источника, кВ; Uсp — среднее междуфазное номинальное напряжение той ступени, где находится данный источник, кВ;
— то же, но фазное напряжение, кВ.
При расчете в именованных единицах сопротивления всех элементов выражаются в омах и должны быть приведены к какой-либо одной ступени напряжения (например, к ) по формуле
где — сопротивление в омах, приведенное к ступени
;
— сопротивление в омах, заданное на ступени
.
Соответственно приведение э. д. с, известных на других ступенях напряжения, выполняется по формуле
где — фазная э. д. с. в киловольтах, приведенная к ступени
; En — междуфазная э. д. с. в киловольтах, заданная на ступени
.
Дополнительные условия для составления схемы замещения определяются видом к. з.
Составленную схему замещения путем соответствующих преобразований приводят к простейшему виду для определения результирующей э. д. с. и результирующего сопротивления
относительно точки к. з.
Основные формулы преобразования схем и нахождения токораспределения приведены в табл. 38-1.
Для приведения к простейшему виду схемы замещения с несколькими источниками производят замену отдельных генерирующих ветвей результируюс э. д. с. и сопротивлениями
(рис. 38-10, а) одной эквивалентной генерирующей ветвью (рис. 38-10,6), э. д. с. и сопротивление которой определяются следующими выражениями:
где — проводимости ветвей.
При двух генерирующих ветвях в узле
По найденным результирующей э. д. с. и результирующему сопротивлению
определяют периодическую слагающую тока в месте к. з.
После этого, постепенно развертывая схему, можно найти токи и напряжения в отдельных ветвях и точках исходной схемы.
Рис. 38-10. Замена нескольких генерирующих ветвей одной эквивалентной.
Таблица 38-1
На чтение 11 мин Просмотров 8 Опубликовано 10 апреля 2023 Обновлено 10 апреля 2023
Содержание
- Схемы замещения электрических сетей
- Схема замещения линии электропередачи
- Содержание
- Общие положения
- Воздушная линия электропередачи
- Кабельная линия электропередачи
- Схема замещения с сосредоточенными параметрами
Схемы замещения электрических сетей
Электрические сети состоят из множества элементов, электрически соединённых между собой. Это генераторы электростанций, повышающие и понижающие трансформаторы, ЛЭП, компенсирующие устройства.
При проектировании и эксплуатации электрических сетей требуются решение и анализ их режимов работы на основе математических моделей, составленных для схем замещения.
Расчётные схемы электрических сетей состоят из П-образных схем замещения ЛЭП и Г-образных схем замещения трансформаторов.
П-образная схема замещения трёхфазной ЛЭП состоит из трёх продольных ветвей с сосредоточенными R и Х фаз линии и поперечных ветвей, содержащих ёмкостные связи между фазами и нейтралью. Нейтраль всегда имеется в моделях электрических сетей, даже если в сети физически не существует такой точки. Ёмкостные связи в схеме замещения ЛЭП разделены пополам и сосредоточены по концам схемы.
Поскольку в симметричной схеме параметры фаз одинаковые, удобно пользоваться так называемым однолинейным представлением схем замещения с изображением только одной фазы (рис. 12).
Рис. 12. Однолинейная П-образная схема замещения
трёхфазной ЛЭП
Для ВЛ низкого напряжения и КЛ схема замещения упрощается за счёт исключения ёмкостной проводимости или одного из сопротивлений R1 , Х1.
О схемах замещения трансформаторов подробно рассказывается в разделе 2.
Схемы замещения батарей статических конденсаторов (БСК) и реакторов очень просты, так как в них малы потери на нагрев и они моделируются только ёмкостью или индуктивностью соответственно.
Важно отметить, что элементы схем замещения типа R, Х, G и В (сопротивления и проводимости) даются для одной фазы, так как схемы, если это не оговаривается специально, считаются симметричными. Однако элементы типа отбора мощности (потери холостого хода и на корону) даются для всей трёхфазной системы.
Нагрузки, заданные в виде сопротивлений или проводимостей, также задаются для одной фазы, но как отбор мощности – для трёх фаз.
3.2. Пример составления схемы замещения
электрической сети
Составим схему замещения электрической сети для принципиальной схемы (рис. 13).
Рис. 13. Принципиальная схема сети
Полная схема замещения включает в себя все элементы сети: каждую цепь линии, каждый трансформатор и т.п. (рис. 14). Эквивалентная схема замещения более простая, чем полная схема: в ней преобразованы в одну параллельные ветви (как продольные, так и поперечные) и там, где это возможно, объединены в одну последовательные ветви (рис. 15). При параллельном сложении схем замещения трёхобмоточных трансформаторов (в виде двух трёхлучевых звёзд) предполагается, что потенциалы нулевых точек одинаковы и эти точки можно совместить.
Рис. 14. Полная схема замещения сети (сопротивления в Ом, проводимости в мкСм, мощности в МВА, коэффициенты
трансформации в о.е.)
Схема замещения БСК мощностью 10 МВАр представлена в виде ёмкости со значением ёмкостной проводимости в мкСм.
Рис. 15. Эквивалентная схема замещения сети
(сопротивления в Ом, проводимости в мкСм, мощности в МВА, коэффициенты трансформации в о.е.)
Расчётные схемы содержат те же данные, что и схемы замещения, но для удобства подготовки и чтения схем в них не прорисовываются отдельные элементы, а все ветви представляются сплошными линиями с указанием элементов трансформации, а для поперечных ветвей изображается вид элемента (рис. 16).
В отличие от схемы замещения в расчётной схеме ёмкостная проводимость ЛЭП даётся в целом для линии, а ветки холостого хода трансформаторов и отводы активной мощности на корону в ЛЭП указываются в прилегающих узлах как мощности нагрузок.
Рис. 16. Расчётная схема сети (сопротивление в Ом,
мощности в МВА, коэффициенты трансформации в о.е.)
Задайтесь несложной схемой электрической сети (4-5 узлов), для которой составьте полную и эквивалентную схемы замещения, на которых представьте численные значения параметров и нагрузок. Все узловые точки пронумеровать. В подрисуночной надписи к схемам указать единицы измерения.
Источник
Схема замещения линии электропередачи
Схема замещения линии электропередачи — это представление линии электропередачи в виде математической модели для исследования различных режимов работы электрической сети.
Содержание
Общие положения
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил, их сечением и частотой электрического тока. Для большинства расчётных задач зависимостью активного сопротивления провода от частоты переменного тока пренебрегают, вследствие низкой частоты тока в электрической сети (в России 50 Гц). Эта зависимость обусловлена наличием скин эффекта.
Активное сопротивление проводников электрического тока изменяется при их нагреве или охлаждении. При этом температура проводников изменяется при изменении величины протекающего электрического тока (более подробно можно ознакомиться здесь). Вследствие этого величины удельных активных сопротивлений являются переменными величинами, и определение их по справочным таблицам позволяет получить лишь приближённую оценку их величины. Зачастую этого приближения вполне достаточно, так как оно лежит в пределах точности задания других параметров электрической сети.
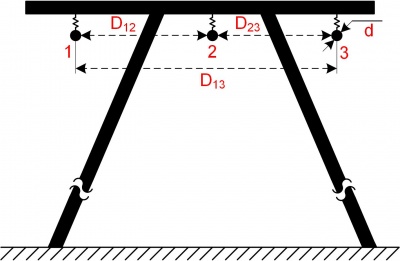
Магнитное поле, возникающее вокруг и внутри проводников, определяет их индуктивное сопротивление. Электродвижущая сила (э.д.с.), соответствующая индуктивному сопротивлению наводится в каждом проводнике линии электропередачи от проводов всех фаз. Поэтому её величина, а следовательно, и величина пропорционального её индуктивного сопротивления зависят от взаимного расположения проводов. Если это расположение обеспечивает одинаковое потокосцепление каждого провода, то наводимые в проводах э.д.с. становятся равными, а индуктивные сопротивления фазных проводов линии электропередачи одинаковыми. Такое равенство имеет место при расположении фазных проводов по вершинам равностороннего треугольника.
Индуктивные сопротивления фазных проводов линии электропередачи, у которой провода расположены горизонтально, по всей длине, отличаются друг от друга. Чтобы избежать появления нежелательной нессиметрии фазных значений сопротивлений, а следовательно токов и напряжений, применяют транспозицию проводов.
В большинстве случаев можно принять, что активное и реактивное сопротивление, активная и ёмкостная проводимости равномерно распределены по всей её длине. Для линий электропередач небольшой длины (при частоте 50 Гц границей можно считать длину 300 км) распределёность параметров можно не учитывать и можно использовать более простое представление в виде схемы замещения с сосредоточенными параметрами. Обычно в расчётах режимов работы энергосистем применяется П-образная схема замещения линии электропередач с сосредоточенными параметрами.
Воздушная линия электропередачи
Расчеты параметров приведены для одной цепи ЛЭП.
Величина активного сопротивления воздушной линии электропередачи влияет на нагрев проводов, при протекании по ним электрического тока. Для сталеалюминиевых проводов, являющихся наиболее часто используемыми для воздушных ЛЭП, активное сопротивление определяется главным образом алюминиевой частью. Это обусловлено эффектом вытеснения переменного тока к поверхности проводника (скин-эфффект). Активное сопротивление в первую очередь зависит от материала, из которого изготовлен проводник, его длины и сечения. При расчётах режимов работы энергосистемы активное сопротивление принято измерять в [Ом]:
[math]displaystyle R = rho frac, [/math]
где [math]displaystyle rho[/math] — удельное активное сопротивление проводника [ [math]displaystyle frac <text<Ом>cdot text<мм>^2><text<км>> [/math] ]; [math]L[/math] — длина проводника [км]; [math]F[/math] — площадь поперечного сечения проводника [ [math]displaystyle text<мм>^2 [/math] ].
Для сталеалюминиевых проводов (обозначение марки провода — АС), выполненных в виде стального многопроволочного сердечника и многопроволочной алюминиевой оболочки, из-за поверхностного эффекта и разницы в удельных сопротивлениях стали и алюминия практически весь ток протекает по алюминиевым проводникам. Если учесть также, что ток протекает по отдельным проводникам, навитым вокруг сердечника и имеющим длину на 3—4 % больше длины провода, то расчётное удельное сопротивление сталеалюминиевого провода, отнесенное к единице его длины, составит [math]displaystyle rho = 31,5 frac <text<Ом>cdot text<мм>^2><text<км>>[/math] .
Обычно в справочных материалах приводится удельное (погонное) сопротивление линии электропередачи [math]displaystyle R_0[/math] [Ом/км] для стандартных сечений, тогда результирующее сопротивление одного провода определяется как,
[math]displaystyle R = R_0 cdot L. [/math]
Справочные значения приводятся для температуры окружающей среды 20°С. Активное сопротивление зависит от температуры, но при расчётах эта зависимость учитывается не всегда.
Индуктивное сопротивление воздушной ЛЭП определяется индуктивностью фаз ЛЭП по отношению к земле и взаимоиндукцией между фазами и, следовательно, зависит от взаимного расположения фаз, расстояния между фазами и диаметра провода.
Для устранения разницы в величине индуктивного сопротивления фаз (крайних и средней) производится транспозиция проводов.
Расположение проводов воздушной линии электропередачи на опоре может быть горизонтальным или треугольным.
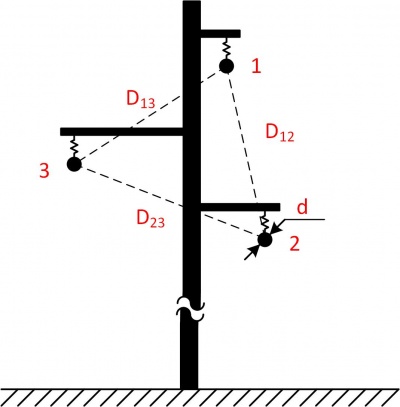
Удельное индуктивное сопротивление фазы одноцепной транспонированной линии подсчитывается с учётом взаимоиндукции фаз по соотношению:
где [math]displaystyle D_text<ср>[/math] — среднегеометрическое расстояние между фазами [м]; [math]displaystyle r_<text<э>>[/math] — эквивалентный радиус фазы, если нет расщепления то [math]displaystyle r_<text<э>>=r[/math] [м]; [math]r[/math] — радиус провода фазы [м]; [math]m[/math] — число проводов в фазе, если нет расщепления то [math]displaystyle m=1[/math] [шт.];
где [math]displaystyle a_i[/math] — расстояние между первым и [math]displaystyle i[/math] -м проводом в фазе [м]; [math]displaystyle r = frac<2>[/math] — радиус фазного проводника.
| Класс напряжения, кВ | 35 | 110 | 150 | 220 | 330 | 500 | 750 |
|---|---|---|---|---|---|---|---|
| Среднее геометрическое расстояние, м | 3,5 | 5,0 | 6,5 | 8,0 | 11,0 | 14,0 | 19,5 |
Усреднённые среднегеометрические расстояния между фазными проводниками воздушных ЛЭП [1]
Удельная активная проводимость воздушной линии (характеризующая потери на корону крайне малый ток утечки через изоляторы) определяется по соотношению:
Эквивалентная активная проводимость определяется следующим образом:
[math]displaystyle G = G_0 cdot L. [/math]
Для воздушных линий погонные потери активной мощности на корону существенно зависят от погодных условий и напряжения, поэтому активная погонная проводимость является переменным и нелинейным параметром. В большинстве случаев более целесообразно непосредственно учитывать для линии электропередачи в виде дополнительной нагрузки по концам линии (узлы 1 и 2) [math]displaystyle P_1=P_2=frac<Delta P_<к.0>><2>[/math] или в виде активной проводимости на землю [math]displaystyle frac <2>[/math] .
Коронирование проводов приводит:
- к снижению КПД передачи электрической энергии;
- к усиленному окислению поверхности проводов;
- к появлению радиопомех.
Ёмкостная проводимость линии определяется токами смещения за счёт электростатического поля линии (между фазами и по отношению к земле). Эта проводимость создает так называемый зарядный, или ёмкостный, ток, вектор которого опережает на 90° вектор напряжения линии. Величина удельной ёмкостной проводимости
Эквивалентная ёмкостная проводимость:
[math]displaystyle B = B_0 cdot L. [/math]
Ёмкостная проводимость воздушных линий электропередачи слабо зависит от конструктивных особенностей ЛЭП и имеет значение от [math]2,55 cdot 10^<-6>[/math] до [math]2,80 cdot 10^<-6>[/math] [См/км] для ВЛ 110—220 кВ и от [math]displaystyle 3,4 cdot 10^<-6>[/math] до [math]displaystyle 4,2 cdot 10^<-6>[/math] [См/км] для ВЛ 330—750 кВ. Значения удельных проводимостей приводятся в справочной литературе [1] .
Кабельная линия электропередачи
Кабельные линии электропередач в расчётах представляют такой же П-образной схемой замещения, что и воздушные линии. Удельные продольные активные и реактивные сопротивления определяются по справочным таблицам так же как и для воздушных линий.
Особенностью кабельных линий электропередач является близкое расположение фаз (по сравнению с воздушными линиями), что приводит к снижению удельного индуктивного сопротивления и увеличению удельной ёмкостной проводимости.
Для кабельных линий электропередачи напряжением 110 кВ и выше необходимо учитывать потери в изоляции кабеля. Они определяются по формуле:
[math] G = B cdot operatorname delta. [/math]
Параметр [math]operatorname delta[/math] называется тангенс диэлектрчиеских потерь и определяется по данным завода изготовителя кабеля. Обычно находится в пределах от 0,003 до 0,006.
Схема замещения с сосредоточенными параметрами
При расчёте режима работы электрической сети воздушная трехфазная линия переменного тока напряжением до 500 кВ и длиной до 300 км может быть представлена схемой замещения с сосредоточенными параметрами П-образного вида. В случае превышения длины линии электропередачи 300 км необходимо изменить схему замещения одним из трёх способов:
- Разделить её на сегменты длиной менее 300 км.
- Представить линию волновыми параметрами.
- При длинах от 300 до 500 км можно использовать поправочные коэффициенты, значение которых при малых длинах близко к единице:
- [math]displaystyle K_R = 1 — frac<3>X_0 B_0 [/math] ;
- [math]displaystyle K_X = 1 — frac<6>X_0 B_0 (1 — frac) [/math] ;
- [math]displaystyle K_C = frac<3 + k_r><2(1+K_R)>[/math] .
В зависимости от класснапряжения воздушной ЛЭП можно использовать различные схемы замещения:
- 220 кВ и выше. Полная схема замещения с активным и ёмкостным шунтом.
- от 35 кВ до 220 кВ. Сокращённая схема замещения только с ёмкостным шунтом.
- до 35 кВ. Схема замещения без шунтов.
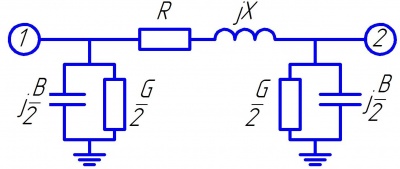
Для расчёта режимов электрической сети, как правило, используется П-образная схема замещения сети, параметры схемы замещения вычисляются для одной фазы. При расчётах режима удобно схемы замещения представлять в виде, представленном на рисунке.
Полное продольное сопротивление и проводимости (шунты узлов 1 и 2) схемы замещения имеют вид
[math]displaystyle Z = R +jX; [/math] [math]displaystyle Y_1 = Y_2 = frac<2>+jfrac<2>. [/math]
Зачастую при расчётах установившихся режимов активная проводимость ЛЭП не учитывается, так как принятые меры борьбы с короной достаточно эффективны и, следовательно, потери на корону достаточно малы. Для воздушных линий классом напряжения менее 220 кВ потери на коронирование можно не учитывать, так как это существенно не скажется на полученной оценке параметров установившегося режима.
В случае исследования режимов воздушных линий напряжением менее 35 кВ можно не учитывать также ёмкостные шунты. В этом случае, схема замещения будет содержать только продольное сопротивление [math]Z[/math] .
Источник



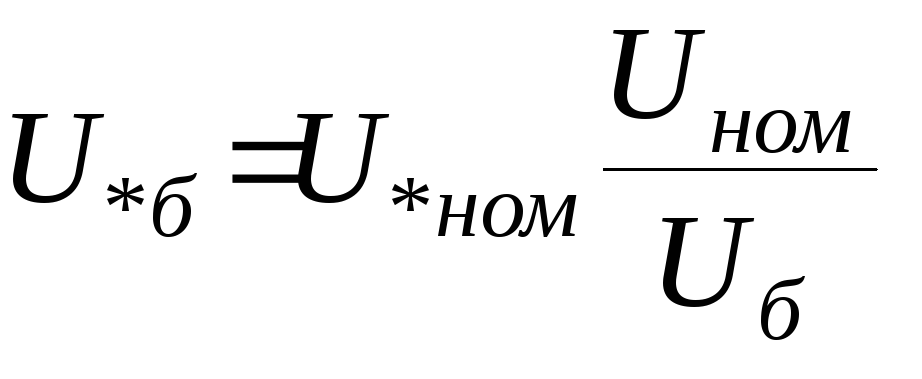
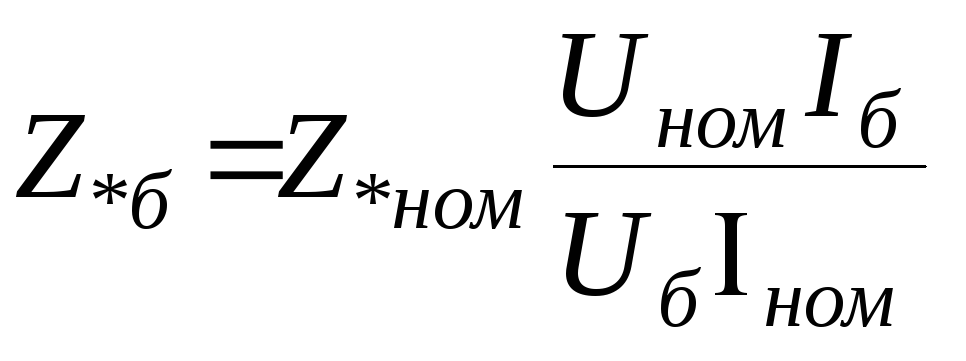
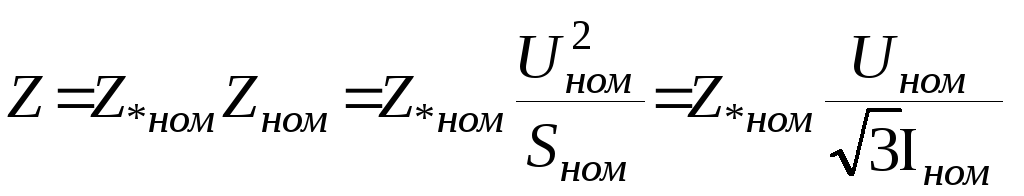
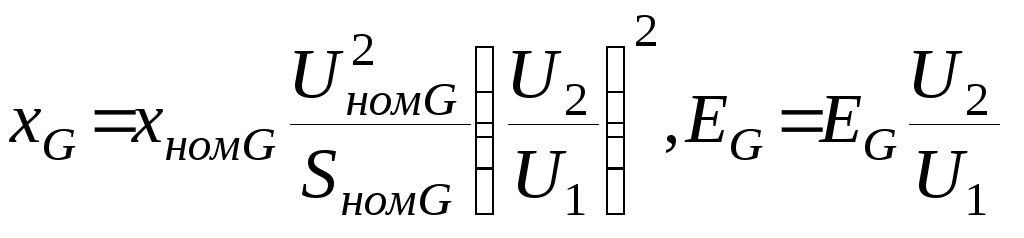
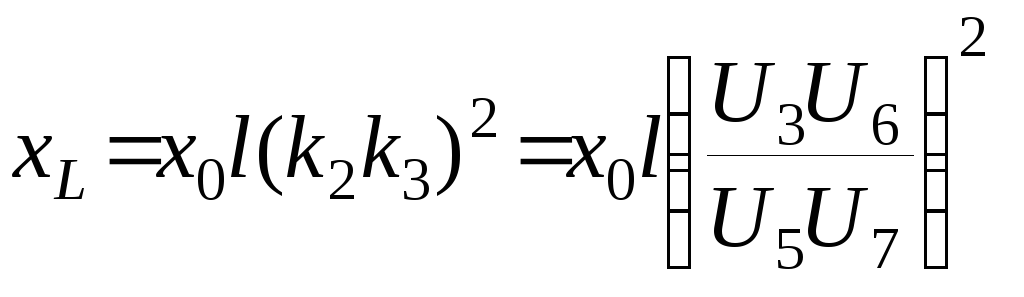

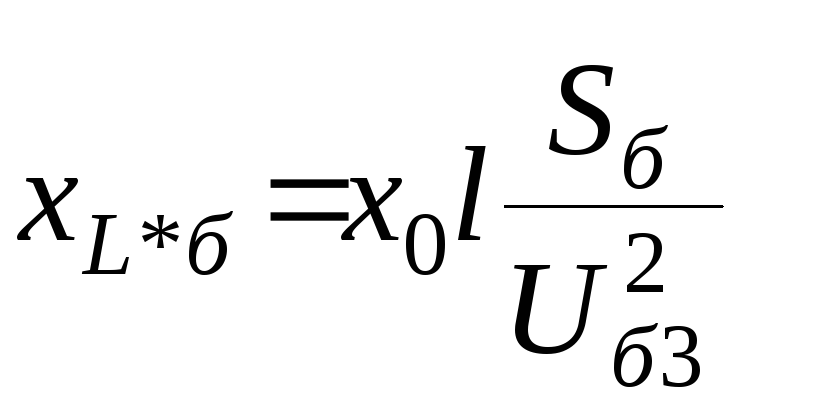
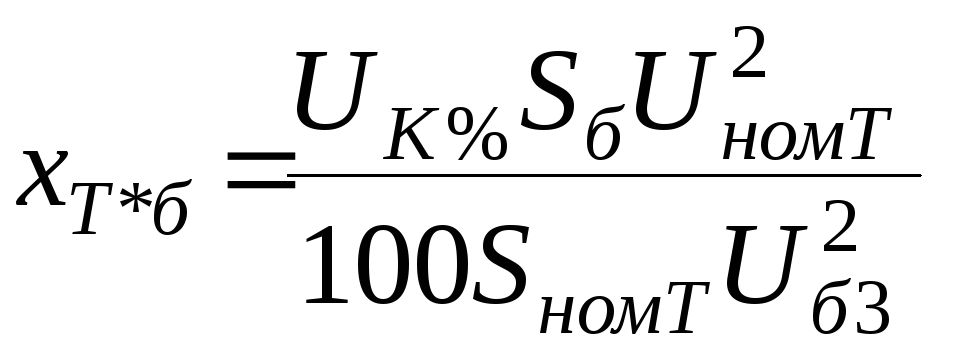
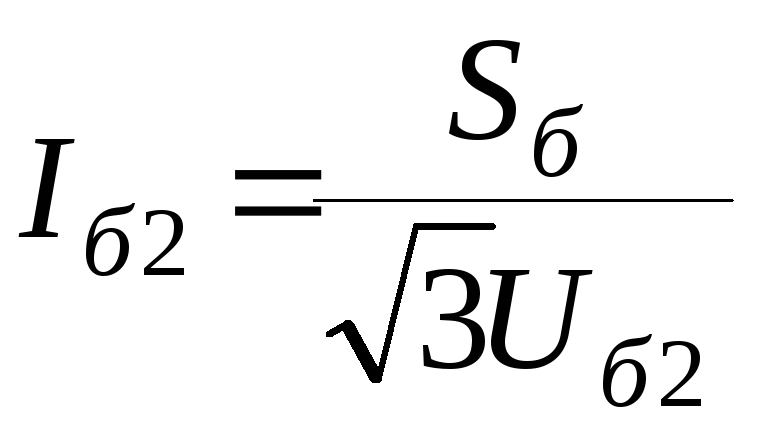
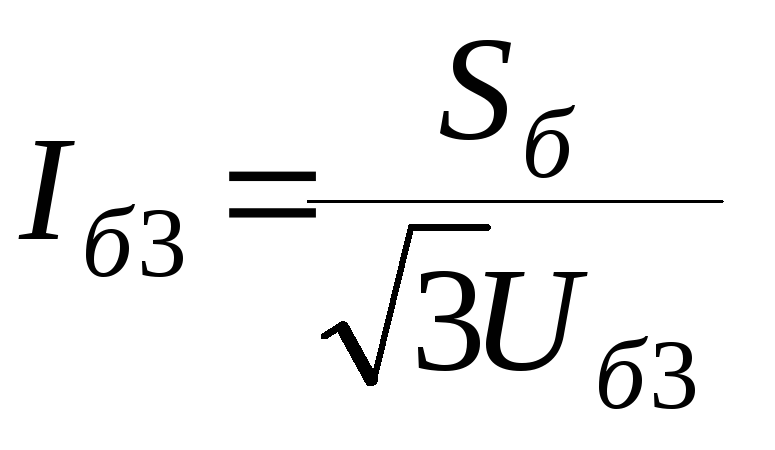













.jpg/400px-%D0%A1%D1%85%D0%B5%D0%BC%D0%B0_%D0%B7%D0%B0%D0%BC%D0%B5%D1%89%D0%B5%D0%BD%D0%B8%D1%8F_%D0%9B%D0%AD%D0%9F_(%D1%82%D0%BE%D0%BB%D1%8C%D0%BA%D0%BE_%D1%91%D0%BC%D0%BA%D0%BE%D1%81%D1%82%D1%8C).jpg)
.jpg/400px-%D0%A1%D1%85%D0%B5%D0%BC%D0%B0_%D0%B7%D0%B0%D0%BC%D0%B5%D1%89%D0%B5%D0%BD%D0%B8%D1%8F_%D0%9B%D0%AD%D0%9F_(%D0%B1%D0%B5%D0%B7_%D1%88%D1%83%D0%BD%D1%82%D0%BE%D0%B2).jpg)