I этап: Анализ задачи
Назначение этапа:
– понять в целом ситуацию, описанную в задаче;
– выделить условия и требования;
– назвать известные и искомые объекты, выделить все отношения (зависимости) между ними.
Анализ задачи всегда направлен на её требование, т.е. на вопрос текстовой задачи.
Приёмы анализа содержания задачи:
- задать специальные вопросы и ответить на них:
Ø можно ли сразу ответить на вопрос задачи?
Ø что требуется найти в задаче?
Ø что означают те или иные слова в тексте?
Ø что в задаче неизвестно?
«По дороге в одном и том же направлении идут два мальчика. Вначале расстояние между ними было 2 км, но так как скорость идущего впереди мальчика 4 км/ч, а скорость второго 5 км/ч, то второй нагоняет первого. С начала движения до того, как второй мальчик догонит первого, между ними бегает собака со скоростью 8 км/ч. От идущего позади мальчика она бежит к идущему впереди, добежав, возвращается обратно и так бегает до тех пор, пока мальчики не окажутся рядом. Какое расстояние пробежит за всё это время собака?»
- перефразировка текста задачи:
замена данного в задаче описания некоторой ситуации другим, сохраняющим все отношения, связи, качественные характеристики, но более явно их выражающим.
Это достигается в результате
– отбрасывания несущественной, излишней информации;
– замены описания некоторых понятий соответствующими терминами и, наоборот, замены некоторых терминов описанием содержания соответствующих понятий;
– преобразования текста задачи в форму, удобную для поиска плана решения.
Особенно эффективно использование данного приёма в сочетании с разбиением текста задачи на смысловые части.
Результатом перефразировки должно быть выделение основных ситуаций.
Переформулируем рассмотренную задачу:
Первая часть: «скорость одного мальчика 4 км/ч, а скорость догоняющего его второго мальчика 5 км/ч»
Вторая часть: «расстояние, на которое мальчики сблизились, 2 км.»
Третья часть: «время движения мальчиков – это время, в течение которого второй мальчик догонит первого, т.е. в течение которого второй мальчик пройдёт на 2 км больше, чем первый»
Четвёртая часть: «скорость, с которой бежит собака, 8 км/ч. Время движения собаки равно времени движения мальчиков до встречи»
Требование: «определить расстояние, которое пробежала собака»
- построение вспомогательной модели задачи:
| объекты | скорость | время | расстояние |
| 1-й м. 2-й м. собака | 4 км/ч 5 км/ч 8 км/ч |  ? ч. ? ч. одинаковое ? ч. ? ч. ? ч. одинаковое ? ч. |
? км. ? км., на 2 км. больше 1-го м. ? км. |
Ø схематический чертёж


После построения вспомогательной модели необходимо проверить:
1)все ли объекты задачи показаны на модели;
2)все ли отношения между объектами отражены;
3)все ли числовые данные приведены;
4)есть ли вопрос (требование) и правильно ли он указывает искомое?
3.4. Приёмы поиска плана решения задачи и его выполнение.
II этап: Поиск и составление плана решения задачи
Назначение этапа:
– установить связь между данными и исходными объектами;
– наметить последовательность действий.
Приёмы поиска плана решения задачи:
- разбор задачи по текступроводится в виде цепочки рассуждений, которая может начинаться как от данных задачи, так и от её вопросов.
Ø при разборе задачи от данных к вопросу нужно выделить в тексте задачи два данных и на основе знания связи между ними (такие знания должны быть получены при выполнении первого этапа решения) определить, какое неизвестное может быть найдено по этим данным и с помощью какого арифметического действия. Считая это неизвестное данным, надо вновь выделить два взаимосвязанных данных, определить неизвестное, которое может быть найдено по ним, а также соответствующее арифметическое действие и т.д. пока не будет выяснено действие, выполнение которого приводит к получению искомого.
Проведём такой разбор по тексту задачи:
«На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?»
| 1) | известно | 6 ч. по 56 км/ч |
| можно узнать | расстояние, которое поехал турист за 6 ч. | 6 · 56 = 336 (км) |
| 2) | известно | 336 км. в 4 раза меньше оставшегося |
| можно узнать | расстояние, которое осталось проехать | 336 · 4 = 1344 (км) |
| 3) | известно | 336 км. и 1344 км. |
| можно узнать | весь путь | 336 + 1344 = 1680 (км) |
Ø при разборе задачи от вопроса к данным нужно обратить внимание на вопрос задачи и установить (на основе информации, полученной при анализе текста задачи), что достаточно узнать для ответа на вопрос задачи. Для чего нужно обратиться к условиям и выяснить, есть ли для этого необходимые данные. Если таких данных нет или есть только одно данное, то установить, что нужно знать, чтобы найти недостающее данное (недостающие данные), и т.д. Потом составляется план решения задачи. Рассуждения при этом проводятся в обратном порядке.
- разбор задачи по вспомогательной моделиможет быть проведён по-разному, – в результате получаются различные арифметические способы её решения.

Источник
Применение анализа и синтеза при решении геометрических задач
«Все наше достоинство заключено в мысли. Не пространство и не время, которых мы не можем заполнить, возвышают нас, а именно она, наша мысль. Будем же учиться хорошо мыслить» (Блез Паскаль).
Когда голодный и оборванный человек попросил рыбака накормить его, рыбак мог бы накормить, но в этом случае он бы утолил голод человека один раз. Рыбак взял человека с собой на рыбалку и научил быть сытым всю жизнь.
В обучении умению решать задачи у нас происходит обратное. Наиболее распространённый метод обучения решению задач основан на принципе «делай как я». Исторически сложилась такая методика, когда учитель демонстрирует на примерах способы решения так называемых типовых задач, а учащиеся по образцу решают аналогичные. Все обучение направлено на выработку практических навыков выполнения типовых видов задач и упражнений. Происходит простое натаскивание, как рыбак накормил бы голодного человека один раз.
Если выпускник школы скоро забудет способы решения многочисленных видов математических, физических, химических и иных школьных задач, то это не очень большая беда. Но если у него не выработано общего разумного подхода к любой житейской, технической или научной задаче, если он не овладел способностью к правильному рациональному поиску способа решения таких задач, то вот это большая беда. Именно это является одной из причин, что выпускники наших школ неэффективно работают, что отражается на нашей экономике и жизни. Ведь работа в любой области, повседневная жизнь человека состоит из последовательной постановки и решения самых различных задач, а поэтому школа должна научить их рационально решать эти задачи.
Таким образом, ведущим системообразующим фактором в обучении выступает, прежде всего технология обучения. Исследователи подчёркивают примат метода над предметом изучения, считая, что для развития мышления важно не столько то, чему учат, сколько то, как учат. Ведь обучение математике сводится не столько к запоминанию теорем, их доказательству, сколько к овладению методами познания. Существенной характеристикой учебной задачи является овладение обобщённым способом решения конкретно-практических задач. Поставить перед школьниками учебную задачу – значит ввести их в ситуацию, требующую ориентации на общий способ её разрешения.
Н.И. Лобачевский отмечал: «В математике важнее всего способ преподавания». Роль учителя должна состоять в вооружении учащихся технологией деятельности и соответствующими способами работы. Если долго решать задачи одного типа, представления учащихся пребывают в фазе необобщённых элементарных знаний, при решении общим методом в поле зрения ученика находятся связи между различными понятиями, а это есть главное условие оформления знаний. При отдельном изучении различных типов задач время затрачивается больше. Целенаправленное обучение приёмам мыслительной деятельности нисколько не замедляет усвоения программного материала. Наоборот, этот процесс всё более и более ускоряется по мере овладения этими приёмами, т.е. по мере развития мышления учащихся.
Ещё великий французский математик и философ Рене Декарт (1596-1650) в своё время имел намерения разработать универсальный метод решения задач. Однако его «Правила для направления ума» остались неоконченными. «Когда мне приходилось, будучи молодым человеком, слышать о каких-либо искусных умозаключениях, я пытался воспроизвести их самостоятельно, не читая автора. Постепенно я стал замечать, что пользуюсь при этом определёнными правилами», — писал он. Гальперин П.Я. отмечал, что на развитие учащихся оказывает действие определённый тип учения, который «характеризуется усвоением, прежде всего общего метода анализа явлений изучаемой области».
Решение любой математической задачи состоит из отдельных шагов. Решить математическую задачу – значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, свойств, формул), применяя которые к условиям задачи или к их следствиям (промежуточные результаты решения), получаем то, что требуется найти в задаче – ответ. Математическое доказательство – тоже цепочка логических следствий из аксиом, определений, ранее доказанных теорем до требуемого заключения. Таким образом, при доказательстве теорем мы сводим её к ранее доказанным теоремам, а те в свою очередь ещё к другим. Каждый шаг доказательства состоит из трёх частей:
1 – предложение, на основе которого производится этот шаг доказательства (аксиомы, определения, теоремы);
2 – логическое рассуждение на основе аксиом, определений, ранее доказанных теорем;
3 – логический вывод из этого рассуждения.
Таким образом, любая задача элементарной геометрии является, по существу теоремой, а её решение – доказательством, скромной математической победой.
Формировать культуру решения задач и доказательства теорем можно через построение общей схематической модели решения, т.е. алгоритма. «Самое трудное в решении любой задачи – планирование своих действий. Если есть алгоритм, значит, есть программа действий, а потому трудности носят чаще всего технический, а не принципиальный характер», — писал А.Мордкович.
Алгоритм – это система операций, применяемая по строго определенной схеме, правилам, которая после последовательного их выполнения приводит к решению поставленной задачи.
Мы недооцениваем способности детей к прогнозированию, составлению моделей деятельности, планированию. А они обнаруживаются в раннем возрасте: трёх-четырёхлетние дети планируют свои игры без взрослых. А в школе эти способности не развиваются – за них всё решают учителя и взрослые. Необходимо учить детей выделять главные моменты в своих действиях; намечать последовательность выполнения работы; выбирать способы и приёмы, которыми рациональнее пользоваться.
Алгоритм необходимо составлять вместе с учащимися. И хотя время затрачивается больше, это оправдывается более высоким развивающим эффектом. Развивается мыслительная деятельность учащихся через напряжение умственных сил, способности их к прогнозированию. Школьники учатся самостоятельно продумывать и составлять план деятельности, переносить его на новый материал, совершенствовать. Ведомый учителем ученик становится ведущим на уроке.
Алгоритм анализа условия и решения задачи мы с учащимися составили в виде памятки:
- Прочитать задачу.
- Выделить условие и вопрос.
- Сделать по условию чертёж.
- Отметить на чертеже данные и искомые величины. Проанализировать данные, выявить связи между ними и все возможные расположения фигур.
- Подумать, что надо знать, чтобы ответить на вопрос задачи. Записать формулу для искомой величины (формула может быть выведена из теоремы, из условия задачи, из треугольника на чертеже, из частных методов решения элементарных задач).
- Неизвестные величины в этой формуле подчеркнуть.
- Записать выражения (формулы) для нахождения этих подчёркнутых величин (или выведенные из теорем, или из условия задачи, или из треугольника на чертеже, или из частных методов решения элементарных задач).
- А теперь можно ответить на вопрос задачи? (действия по контролю). Продолжать до тех пор, пока можно будет ответить на вопрос задачи.
- Подставить найденные подчеркнутые величины в формулу для искомой величины. Вычислить.
- Записать ответ.
Поиск и конструирование методов решения вырабатывает дисциплинированное мышление в процессе решения, прививает эстетический взгляд на решение задачи, предполагает оценку решения не только с точки зрения её безупречной логической правильности, но и красоты и изящества.
До тех пор, пока какой-либо частный факт не соотнесён с общей структурой, он быстро забывается, т.е. знание общей структуры способствует сохранению материала в памяти. А. В. Гончаров писал, что перегрузка памяти учащихся вызывается отсутствием обобщающих линий и чрезмерной раздробленностью содержания. Вместо бездумного решения большого количества задач полезнее решать меньше, но при этом само решение должно содержать глубокое изучение этих задач, сущности их решения, выявление общих методов и приёмов, используемых в этом решении.
Отвечая на вопросы памятки при решении задач, учащиеся составили алгоритм решения геометрической задачи в виде блок схемы (Приложение 1).
Основным содержанием этого этапа стало моделирование. Деятельность учащихся имеет теоретический, исследовательский характер, приобретает опыт творческого мышления.
Данный алгоритм составили не сразу, в несколько этапов. Сначала более простой, а с появлением задач другого содержания дополняли его. Детям необходимо понять, что любое дело в жизни совершенствуется.
Самостоятельное составление алгоритма учащимися развивает:
- способность к формализации математического материала (отделение формы от содержания), абстрагированию конкретных количественных отношений;
- способность обобщать математический материал, вычленять главное, отвлекаясь от несущественного;
- способность к оперированию числовой и знаковой символикой;
- способность к последовательному, правильно расчленённому логическому рассуждению;
- способность сокращать процесс рассуждения, мыслить свернутыми структурами;
- способность к переключению от одной умственной операции к другой (гибкость мышления);
- способность к пространственным представлениям;
- развивает устную и письменную речь.
Восприятие объектов облегчается, если они расположены в определённой строго продуманной системе, требующей минимальных усилий со стороны наших органов чувств. Восприятие объектов, расположенных хаотически, осуществляется неохотно и требует значительных волевых усилий. Оформлять запись решения задачи также интересно. И не так это просто – выбрать наиболее удобный способ оформления решения. Сам выбор удобного способа оформления решения является интересной задачей. Часто процесс решения задачи зависит от удачно выбранного способа записи решения.
В алгоритме использовался аналитический способ решения задач. Анализ может выступать в двух формах:
- Когда в рассуждениях двигаются от искомых к данным задачи;
- Когда целое расчленяют на части.
Пример аналитического оформления решения задачи (Приложение 2).
Синтез тоже может выступать в двух формах:
- Когда в рассуждениях двигаются от данных задачи к искомому;
- Когда элементы объединяют в целое.
Пример синтетического оформления решения задачи (Приложение 3).
Аналитико-синтетический метод существует в виде восходящего и нисходящего анализа. Нисходящий анализ применяется реже. В нашем случае его можно применить на отдельном шаге решения сложной задачи. Это анализ в форме рассуждения от искомого к данным.
| Общая схема нисходящего анализа | Дополнительные указания |
| Пусть требуется доказать некоторое утверждение А. Предполагаем, что оно верно и пытаемся получить из него верное следствие. При этом возможно несколько случаев: |
1 – Получено неверное следствие. Значит предположение о справедливости А ошибочно. Решение задачи закончено
2 – Получено верное следствие. В этом случае следует обязательно проверить обратимость рассуждения:
- если все рассуждения обратимы, то А верно;
- если среди рассуждений есть необратимые, то приходится применять другие методы поиска решения задачи
3 – Если верное следствие получить не удаётся, то также приходится перейти к другим методам 1. Уменьшить число параметров.
3. Использовать все данные задачи.
Можно, изменив условие, сформулировать и доказать соответствующее верное утверждение, т.е. решить другую задачу.
Такая проверка обязательна, т.к. из неверного утверждения 
Примеры необратимых рассуждений:
Пример решения задач нисходящим анализом (Приложение 4).
Основной способ решения задач – восходящий анализ.
Пусть требуется доказать утверждение А. Подбираем такое утверждение В, из которого следует А; затем отыскиваем утверждение С, из которого следует В; …до тех пор, пока найдём путь решения.
Аналитико-синтетический метод – метод попеременного движения с двух сторон:
- сначала разворачивается заключение задачи (искомая величина);
- потом разворачивается условие задачи;
- получение цепочки выводов от условия и заключения.
Основным способом он является потому, что разбор и решение задач восходящим анализом проводят ещё в начальных классах при решении составных задач (3–4-е классы).
Пример доказательства восходящим анализом (Приложение 5).
Особенности метода:
- не требуется обратимости рассуждений (только при доказательстве, при решении задач обратимость имеет место), т.к. возможность обратного перехода проверяется на каждом шаге поиска решения;
- учащиеся должны хорошо усвоить фразу: «Чтобы доказать… достаточно доказать…». Термин «достаточно» подходит больше, чем «надо», поскольку можно подобрать несколько различных утверждений, для каждого из которых искомое является следствием;
- в общей схеме восходящего анализа не разъясняется, как получить утверждение, из которого следует искомое, такое утверждение подыскивается, исходя из конкретных условий задач.
«В поиске решения важную роль играет отбор нужных выводов из условия и достаточных по отношению к заключению совокупностей свойств. Это творческий процесс, научить этому невозможно, остается «учить плавать, бросая в воду». (М. Волович).
Работа над более кратким, рациональным оформлением задачи продолжается. Такая форма записи неудобна тем, что заполняет всю площадь листа. Но полное развёрнутое решение необходимо для формирования умения решать задачи. Приём разбиения решения на шаги облегчает усвоение метода решения. Шохор-Троцкий С.И. в книге по методике арифметики указывал, что свертывание процесса рассуждения зависит от натренированности в решении задач. На первых этапах овладения задачей она выполнялась посредством развёрнутого процесса, на поздних – сокращённого. Но для способных учащихся это условие не является обязательным. Способных отличает ярко выраженная тенденция к быстрому и радикальному свертыванию процесса рассуждения и соответствующих математических действий. Восприятие математических задач способными приобретает свернутый вид. Аналитико-синтетическая ориентировочная деятельность способных настолько «свернута» и максимально ограничена во времени, что в некоторых случаях создаётся впечатление – она имеет характер одноактного одномоментного видения математического материала. Способные при восприятии задач сразу видят её «скелет», очищенный от всех конкретных значений. У них наблюдается обобщённое формализованное восприятие математического материала (быстрое схватывание формальной структуры задачи), когда числовые данные, конкретное содержание «выпадает» и остаются чистые соотношения между показателями, характеризирующие принадлежность задачи к определенному типу.
Видно, что общая блок-схема сохраняется и при аналитико-синтетическом методе решения задачи (Приложение 6).
И Гальперин П.Я. отмечал, что мыслительные операции можно целенаправленно формировать путём постепенного перехода от развёрнутых внешних действий, заранее запрограммированных и выполняемых в заданной последовательности, ко всё более свернутым умственным действиям.
Свёртывание начинается после того, как ученик обобщит способ решения. Обобщение и свертывание происходит по разному у детей, отличающихся своими способностями. У способных обобщение наступает сразу, «с места». Средние обобщают после многократных упражнений. Неспособные обобщают с большим трудом и после длительного решения однотипных задач.
Сокращённая, обобщённая форма записи решения задачи сохраняет информацию, не загружая мозг избыточной информацией и позволяет дольше и легче использовать её.
Сокращенная форма записи решения.
Далее полезно познакомить учащихся с аналитико-синтетическим способом решения задач. На самом деле этот способ скрыто присутствовал в нашем методе, но теперь он должен приобрести теоретическое обоснование.
К 7–8-у классу в психике учащихся уже преобладает анализ.
«Анализ решения экспериментальных задач учениками показал, что учащимся свойственна аналитико-синтетическая обработка математического материала, носящая характер аналитико-синтетического осмысливания материала», — писал В. А. Крутецкий, [2].
Уже найденное известное решение задачи обычно излагают синтетическим методом, а чтобы найти способ решения, пользуются анализом. Синтез позволяет изложить известное решение задачи быстро и чётко. Однако ученику трудно понять, как было найдено решение, как бы он сам мог догадаться решить задачу. Анализ требует большей затраты учебного времени, но зато позволяет показать ученику, как найти решение, как можно самому догадаться её решить. Если использовать систематически анализ, у учащихся формируются навыки поиска решения задач. Анализ в чистом виде вообще не применяется. Если ученик пользовался им при поиске решения задачи, то только до тех пор, пока в его сознании не возникнет идея решения. При решении задач синтезом в сознании человека проводится и анализ, но часто настолько быстро, подсознательно, что ему кажется, будто он сразу увидел решение, не прибегая к анализу. Чем более сложной является задача, тем в более отчётливой форме он сможет проследить элементы анализа в своих рассуждениях.
Анализ и синтез соответствуют психическим процессам дедукции и индукции.
- Индукция — форма умозаключения от единичных фактов к общим положениям.
- Дедукция — вывод от общего к частному.
Индукция и дедукция — различная последовательность во времени анализа и синтеза. При индуктивной обработке информации анализ предшествует синтезу, при дедуктивной – синтез-анализу. Интегративная аналитико-синтетическая деятельность присуща обоим полушариям мозга, но в каждом она характеризуется специфической последовательностью анализа и синтеза. Индукция преимущественно связана с функционированием левого полушария, а дедукция – правого. Обработка идёт параллельно-последовательно по двум каналам, что обеспечивает её быстроту и надёжность. Таким образом более или менее стабильно устанавливается межполушарная асимметрия. Оба полушария работают теперь главным образом параллельно, постоянно обмениваясь информацией. Левое полушарие при этом как бы обладает законодательной властью, а правое — исполнительной. Левое вырабатывает цели, а правое реализует их достижение.
Можно надеяться, что относительно равномерное применение индуктивных и дедуктивных методов обучения привело бы к большей продуктивности в освоении знаний. Учитель становится человеком, впрямую формирующим функции мозга.
Пример аналитико-синтетического способа решения задачи (Приложение 
На каждом этапе (шаге) решения задачи обсуждается план решения, рассматривается несколько вариантов решения, выбирается рациональный. Решаются так называемые элементарные задачи по отношению к данной неэлементарной задаче. Данная неэлементарная на некотором этапе обучения сама может стать элементом решения более сложных задач.
Промежуточный мыслительный процесс, протекающий в сознании учащегося между двумя этапами решения, помогает устанавливать связи между ними, углублять понимание и активизировать мыслительную деятельность. Состоит из:
- вспоминания, применения по ходу ознакомления с материалом определений, теорем, законов, различных правил, в том числе мнемонических, которые как раз и предназначены для лучшего запоминания тех или иных фактов;
- созерцания, представления наглядных образцов (моделей, графиков, рисунков, диаграмм);
- любой деятельности с образами;
- оперирования знаками и символами (введение стрелок и других обозначений, подчёркивание записей…);
- любых рассуждений, действий, углубляющих понимание.
Если промежуточные элементарные задачи громоздки, или дети забыли их решение, лучше вспомнить их решение в устном счёте, подготовив заранее детей к решению более сложной задачи.
Аналитико-синтетический метод можно применять и при решении задач и упражнений по другим предметам: по алгебре, физике, химии.
Литература
- Груденев Я. И. Совершенствование методики работы учителя математики. – М,: Педагогика, 1992г.
- Крутецкий В. А. Психология математических способностей школьников. – М,: Просвещение, 1985 г.
- Мордкович А. В. Семинар для молодых учителей. «Математика» – приложение к газете «Первое сентября», №1-30. – 1993 г.
Источник
Инфоурок
›
Алгебра
›Другие методич. материалы›Схема анализа решения текстовой задачи.
Схема анализа решения текстовой задачи.
-
Настоящий материал опубликован пользователем Коряковцева Нина Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 5 лет и 4 месяца
- Подписчики: 78
- Всего просмотров: 1187835
-
Всего материалов:
519
Как решаются задачи по математике через схему анализа и обратные задачи.
Начну с того ,что методика обучения математике-это наука и искусство .На сегодняшний день считается ,что предметом методики обучения математики является методическая система ,включающая в себя цели ,содержание, методы, средства и формы обучения.
Использование задач в школе рассматриваются в двух разделах:
-обучение математики через задачи,
-обучению решению задач.
В широком понимании задача –это цель ,в узком-это задание на нахождение какого либо результата, когда сами действия, необходимы для какого либо результата не указаны, но в условии задана часть необходимых сведений, нужных для выполнения задания.
Структура задач:
1.требование(заключение)
2.Условие(или некоторое утверждение)
3.отсутствие действий.
Структура задач может быть разных видов(условие-требование;требование-условие;условие-требование-условие)
Чтобы научиться решать задачи имеются алгоритм лишь для решения определенного типа задач. При решении нетиповых задач требуется творческий подход.
Решение любой задачи можно разделить на несколько этапов.
1.понимание постановки и усвоения условия
2.поиск решения, составления плана
3.осуществление плана ,или решения
4.проверка
Приведем пример задачи.
Коля и Петя ехали на велосипеде из города в лагерь разными дорогами. Коля ехал по дороге, которая была короче на 9 км, но со скоростью на 3 км/ч меньше ,чем Петя; Петя ехал 3ч со скоростью 18 км/ч. Кто из мальчиков раньше приехал в лагерь?
Перед тем как решать задачу необходимо вспомнить формулы которые потребуются если это необходимо. Далее записываем условие. Есть различные формы записи условия задачи.
1.в виде таблицы.
|
имя |
скорость |
расстояние |
время |
|
Петя |
18 км/ч |
? |
3ч |
|
Коля |
На 3 км/ч меньше |
На 9 км короче |
? |
2.в виде схемы

Скорость Коли- на 3км/ч менбше,чем


Время Пети – 3 ч
Время Коли — ?
Кто раньше приехал в лагерь-?
А можно решить задачу с помощью схемы анализа и схемы синтеза.
Анализ и синтез –два метода научного познания.
Анализ-в переводе с греческого означает «расчленение, разложение» -это путь мышления от заключения к условию, от искомого к данным, от следствия к основанию, от сложного к простому.
Синтез— в переводе с греческого означает «соединение, составление» -это путь мышления от простого к сложному, от условия к заключению, от данных к искомому.
Схема анализа
1.Сперва ставим главный вопрос в задаче (ребята должны это понимать)
2.Можно ли сразу ответить на вопрос задачи?(нет неизвестно, сколько времени был в пути Коля)
3.Что нужно знать ,чтобы определить сколько времени был в пути Коля?(Достаточно знать длину его дороги и скорость ,с которой он ехал. Но неизвестно ни то ,ни другое)
4.Что нужно знать ,чтобы определить скорость Коли?(скорость Пети и на сколько Коля ехал медленнее, чем Петя. Известно то и другое)
5.Что нужно знать ,чтобы определить длину дороги Коли?(достаточно знать длину дороги Пети и на сколько дорога Коли отличается от дороги Пети)
6.Что нужно знать ,чтобы найти длину дороги Пети?(скорость Пети и время, которое затратил он. Известно и то и другое)
Кто раньше приехал в лагерь? ?
Время Коли ?
Время Пети 3 ч

Скорость Коли ?
Длина дороги Коли ?

На сколько отличается на 9 км
дорога Коли короче
Скорость Пети 18
км/ч
Длина дороги Пети ?
На сколько на 3 км/ч
Отличается меньше
скорость
Время Пети 3ч
Скорость Пети 18км/ч
После того как составили таблицу составляем план решения с конца.
План решения:
Находим последовательно
1.длину дороги Пети
2.длину дороги Коли
3.Скорость Коли
4.Время Коли
5.Сравниваем время.
Далее решение и оформление.
Схема синтеза составляется для самого решения и уже решения начинаются с верху.
Схема синтеза.(вопросно-ответной форме)
На сколько на 3км/ч отличается меньше
скорость
Скорость 18
Пети км/ч
Время 3ч
Пети
Скорость 18км/ч
Пети
На сколько отличается на 9км
дорога Коли короче
Скорость Коли
Длина дороги Пети
Длина дороги Коли
время Пети
время Коли
Кто раньше приехал в лагерь?
Решение:
1.Какова длина дороги Пети?
2.Какова длина дороги Коли?
3.Какова скорость Коли?
4.Сколько времени Коля был в пути?
Ответ: Коля и Петя приехали в лагерь одновременно.
Есть другие способы оформления решения. Так же можно решить задачу с помощью уравнения. В данном примере можно составить обратную задачу. Обратные задачи можно задавать как домашнее задание , чтобы дети сами составили обратные задачи.
Обратные задачи:
Задача 1.
Коля и Петя ехали на велосипедах из города в лагерь. Они прибыли туда одновременно ,хотя ехали разными дорогами. Дорога Коли была на 9 км короче. Петя ехал 3 ч со скоростью 18 км/ч. На сколько километров в час медленнее ехал Коля?
Задача 2.
Коля и Петя ехали на велосипедах в лагерь разными дорогами, но прибыли туда одновременно. Петя ехал со скоростью 18 км/ч в течении 3 ч. Коля ехал медленнее на 3 км/ч. На сколько километров отличалась дорога Коли?
Так же можно и доказывать теоремы по геометрии если ребята привыкнут составлять схемы и правильно задавать вопросы .
После того как ребята научатся решать задачи с помощью синтеза и анализа им будет легче в геометрии. В геометрии все теоремы можно доказать с помощью синтеза и анализа.
Сущность синтетического метода состоит в отыскании таких необходимых условий ,вытекающих из совокупности данных, переход к искомых очевиден.
Приведем пример.(синтетического метода)
Теорема: если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Дано: АВСD-четырехугольник,
АВ=СD,
АD=ВС.
Доказать:АВСD- параллелограмм.
Доказательство:
1.Из условий известно,что АВСD-четырехугольник,АВ=СD,АD=ВС.
Проведем в четырехугольнике диагональ АС, получим и ∆ АВС.
Отсюда необходимостью следует:
2 ∆ АВС = ∆ СDА
⇓
.
3.
⇓
4. АВ║ СD , ВС║ АD ⇒ АВСD — параллелограмм .
От условия теоремы пришли к заключению.
Далее рассмотрим аналитическим методом доказательство является заключение теоремы. Используя известные ранее предложения, преобразуют заключение теоремы до тех пор ,пока в качестве логического следствия не появится условие теоремы.
Рассмотрим на этой же теореме.
Аналитический метод
Теорема: если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Дано: АВСD-четырехугольник,
АВ=СD,
АD=ВС.
Доказать:АВСD- параллелограмм.
Доказательство:
Чтобы доказать, что АВСD- параллелограмм,
достаточно
1. АD║ ВС и АВ║СD
достаточно
Иметь равные накрест лежащие углы при пересечении двух прямых третьей( требуется дополнительное построение : проведение диагонали АС)
достаточно
2.
достаточно
3. ∆ АВС = ∆ СDА
достаточно
4. АD = ВС и АD = СD (это известно из условия).
Теорема доказана.
Таким образом метод анализ и синтеза облегчит ребятам при решении задач. А дальше как я и говорила в геометрии. Этод метод можно использовать даже в начальной школе.
«СИСТЕМА РАБОТЫ НАД ТЕКСТОВОЙ АРИФМЕТИЧЕСКОЙ ЗАДАЧЕЙ
В НАЧАЛЬНОЙ ШКОЛЕ. Виды анализа задачи».
с.Новоандреевка, 2017г.
«Ребёнок не должен получать готовых знаний, должен напрягать свой ум и волю, должен чувствовать себя соавтором в решении возникающих проблем». (В. В. Давыдов)
1 Теоретические аспекты опыта
Обучение детей самостоятельному анализу решения простых и составных задач волнует каждого учителя. Ключ к решению задачи — это прежде всего пошаговый анализ действий, которые необходимо выполнить для того, чтобы ответить на главный вопрос задачи.
Во время анализа устанавливается зависимость между данными и искомыми значениями величин.
Основные традиционные приёмы анализа задачи – это разбор от вопроса к числовым данным (анализ) и от числовых данных к вопросу ( синтез). Анализ – логический прием, состоящий в расчленении исследуемого объекта на составные элементы и исследовании каждого из них в отдельности. Он может использоваться многократно. Разбор задачи от вопроса к данным — это суждение, которое состоит в том, чтобы подобрать два числовых значения одной или разных величин таким образом, чтобы дать ответ на вопрос задачи. Одно из значений или оба могут быть неизвестными. Для их нахождения подбираются два других, и так продолжается процесс подбора, пока не приходим к известным числовым значениям величин. В результате такого разбора учащиеся устанавливают зависимость между числовыми значениями величин, расчленяют ее на простые задачи и составляют план ее решения
При аналитическом способе решения задачи выясняется, что нужно предварительно узнать, чтобы ответить на вопрос задачи. Чтобы помочь детям вести рассуждения аналитическим способом, можно использовать прием, называемый “деревом рассуждений”. Суть его состоит в том, что по ходу рассуждений строится схема, которая помогает увидеть, какие простые задачи следует выделить и каким будет план решения данной составной задачи.
Синтез – логическая операция установления связи между составными частями исследуемого объекта и изучения его как единого целого. Исследуемый объект называется в требовании задачи, а его элементы описываются в условии. Разбор задачи от числовых данных состоит в том, что к двум числовым данным подбирается вопрос, затем к следующим двум данным, одно из которых может быть результатом первого действия, подбирается следующий вопрос. И этот процесс продолжается, пока не будет получен ответ на вопрос задачи
Синтетический способ характеризуется тем, что основным вопросом при поиске решения задачи является вопрос о том, что можно найти по двум или нескольким известным в тексте задачи числовым значениям. По вновь полученным числовым значениям и другим известным в задаче данным вновь ищется ответ на вопрос, что можно узнать по этим значениям. И так до ответа на вопрос составной задачи. Иными словами, суть этого способа состоит в вычленении простой задачи из предложенной составной и решении ее.
Аналитико-синтетический метод. Значительно чаще, используется на практике, чем аналитический и синтетический методы. Он сочетает элементы и анализа и синтеза. Так при решении сложной задачи она с помощью синтеза разбивается на ряд более простых задач, а затем при помощи синтеза происходит соединение решений этих задач в единое целое. Обучение учащихся начальных классов рассмотренным методам поиска решения задач сводится к обучению их правильному формулированию вопросов, соответствующих аналитическому или синтетическому методу. При разборе задачи нового вида учитель должен в каждом отдельном случае поставить детям вопросы так, чтобы навести их на правильный или осознанный выбор арифметических действий.
2. Обратимся к практике.
Анализ задачи аналитическим способом. Будем идти от вопроса к данным.
ЗАДАЧА.
Лида нарисовала 4 домика, а Вова на 3 домика больше. Сколько домиков нарисовали дети ?
Составляем дерево рассуждения с пояснением:
Чтобы ответить на вопрос задачи необходимо знать 2 величины: сколько домиков нарисовала Лида и сколько нарисовал Вова. Сколько нарисовала Лида нам известно-4, а сколько нарисовал Вова неизвестно, но сказано что на 3 домика больше, вспомню на 3 больше значит столько же и еще з, поэтому к 4 прибавлю 3 , теперь зная величину сколько прочитал Вова и сколько прочитала Лида я отвечу на вопрос задачи.
АНАЛИЗ ЗАДАЧИ СИНТЕТИЧЕСКИМ СПОСОБОМ .
Начинаем от числовых данных.
Задача
В двух пачках 160 тетрадей, причем в одной из них на 20 тетрадей больше, чем в другой.
Сколько тетрадей в каждой пачке?

160т.

Составляем дерево рассуждения, сопровождая пояснением:
В задаче нам известны 2 величины : 160-сколько тетрадей в двух пачках и 20 на столько во второй больше, зная эти величины, найду третью: сколько тетрадей в двух пачках, если количество их равное, для этого 160 – 20, теперь мне известна величина сколько тетрадей в пачках при их равном количестве и величина 2 – сколько пачек тетрадей , разделим эти величины и узнаем сколько тетрадей в одной пачке при равном количестве тетрадей. Мы ответили лишь на один вопрос задачи : сколько тетрадей в одной пачке, чтобы узнать количество тетрадей во второй пачке прибавим 20 т.к. сказано,что во второй пачке на 20 тетрадей больше.
Таким образом, рассуждение можно строить двумя способами:
от вопроса задачи к числовым данным;
от числовых данных идти к вопросу;
Нужно помнить, что введение понятия «СОСТАВНАЯ ЗАДАЧА» вводится тогда, когда научились решать все виды простых задач.
Разбор составной задачи заканчивается составлением дерева рассуждения –
это объяснение того, что узнаем, выполнив то или иное действие, и указание по порядку арифметических действий.
Нужно обратить внимание и на то, что полный анализ задачи, решаемой в 4-5 действий , является многословным, забирает много времени. Здесь целесообразно использовать схему неполного анализа , при котором в условие задачи записываются не только числа, но и выражения, это
во-первых укорачивает условие задачи, а во-вторых,делает более прозрачный путь к её решению.
Рассмотрим задачу:
Птицефабрика должна отправить в магазины 6000 яиц. Она уже отправила 10 ящиков по 350 яиц и 4 ящика по 150 яиц. Сколько яиц осталось отправить в магазины?

(150 х 4) яиц 6000 яиц
Осталось — ?
При этом рассуждаем: если было 10 ящиков по 350 яиц в каждом, то яиц было 350 × 10. Отправила также 4 ящика по 150 яиц, это составляет (150×4) яиц.
Выполняя анализ от вопроса, учащиеся рассуждают примерно так:
«Чтобы ответить на вопрос задачи, надо знать две величины : сколько всего яиц надо отправить (6 000 яиц) и сколько яиц птицефабрика уже отправила. Чтобы узнать, сколько яиц фабрика отправила, надо знать, сколько она отправила в первый и во второй раз. В первом вопросе узнаем, сколько птицефабрика отправила яиц в 10 ящиках, во втором – сколько она отправила яиц в 4 ящиках, в третьем – сколько она отправила всего яиц и в четвертом – сколько яиц осталось отправить».
Схемы полного (рис.1) и неполного (рис.2) анализа наглядно показывают преимущество и недостатки каждого из них.
?
?
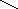
350 Х10
150:4
?
6000
4
150
10
350
?
6000000
?
?
После анализа учащиеся самостоятельно записывают решение в форме математического выражения или по отдельным действиям. Для учащихся, которые затрудняются , ведется более подробный анализ.
Вывод
Такая работа, которая проводится в системе, способствует развитию учебной мотивации, большинству детей помогает видеть взаимосвязь между величинами, овладевать разными способами решения задач, т.е. способствует формированию математической компетентности.
Исследовательская деятельность помогает разнообразить деятельность детей на уроке, поддерживает интерес к математике и, главное, помогает им овладеть умением решать задачи. Конечно, подобный вид работы, требует больших затрат времени. Однако время, потраченное на них, окупается умением решать задачи не только на уровне государственных стандартов, но и нестандартные задачи. А самое главное у детей появляется желание решать задачи.
Вспомним старую притчу о том, как один мудрец бедняков накормил.
— Пришёл мудрец к бедным и сказал: «Я вижу, вы голодны. Давайте я дам вам рыбу, чтобы вы утолили голод». Но время прошло, и люди опять проголодались.
Притча гласит: «Не надо давать рыбу, следует научить ловить её»
Не надо давать готовый путь к решению, надо побуждать учащихся к действию, учить их анализировать, рассуждать и находить путь решения самостоятельно.
Литература:
-
Аргинская И.И., Дмитриева Н.Я.Обучаем по системе Л.В. Занкова: 2кл.: Кн. Для учителя. – М.: Просвещение, 1993. – 160с.
-
Занков Л.В. Беседы с учителями. (Вопросы обучения в начальных классах.) М., Просвещение, 1970. — 200с.
-
Иванов Д.А., Митрофанов К. Г., Соколова О.В. Компетентностный подход в образовании. Проблемы, понятия, инструментарий. М.: изд-во Академии повышения квалификации и проф. переподготовки работников образования.- 2006г.
-
Лысенкова. С. Н.. Когда легко учиться: из опыта работы учителя начальных классов школы №587 Москвы.- 2-е изд.М.: Педагогика, 1985 – 176с.(пед. поиск: опыт, проблемы, находки)
-
Мамыкина М. Ю. Работа над задачей в системе Л. В. Занкова. Начальная школа
№ 4.2003г.
-
Матвеева Н.А.. Различные арифметические способы решения задач. Начальная школа №3.2001г.
-
Математика. 1-4 классы: обучение решению текстовых задач/ авт.-сост. И.Л. Кустова. – Волгоград: Учитель, 2009. – 103с.
-
Новиков А.Учебный процесс в логике исторических типов организационной культуры. Народное образование №1, 2008г.с.163
-
Петерсон Л.Г., Кубышева М.А., Мазурина С.Е., Зайцева И.В. Что значит «уметь учиться». – М.: АПК и ППРО, УМЦ «Школа 2000…», 2008. – 80с.
-
Узорова, Нефёдова. 500 задач с пояснением, пошаговым решением и правильным оформлением. 1класс. АСТ.: Астрель. Москва.2004г.
-
Фадеева. Схемы записи задач. Начальная школа №4.2003г.
-
Фонин С.Н.. Моделирование, как важное средство обучения решению задач. Начальная школа. №3.1990г.
-
Шульга Р.П. Решение задач разными способами – средство повышения интереса к математике. Начальная школа №12. 1990г.
-
Ф.Семья. Совершенствование работы над составными задачами. Начальная школа №5.1991г.
Содержание
- Способ разбора задачи аналитический синтетический с 2 мя или 3 мя
- Статья на тему «Разбор составных задач» (3-4 класс)
- Дистанционное обучение как современный формат преподавания
- Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО
- Скоростное чтение
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
- Доклад на тему: «СИСТЕМА РАБОТЫ НАД ТЕКСТОВОЙ АРИФМЕТИЧЕСКОЙ ЗАДАЧЕЙ В НАЧАЛЬНОЙ ШКОЛЕ. Виды анализа задачи».
- Содержимое разработки
Способ разбора задачи аналитический синтетический с 2 мя или 3 мя
На основе аналитического и синтетического методов решения задач при работе над поиском решения задачи применяются два основных способа разбора задачи: аналитический (анализ) и синтетический (синтез). Однако на практике чаще употребляют аналитическо-синтетический разбор задачи.
Под анализом подразумевают способ рассуждений от общего к частному (анализировать – разбивать на составляющие), таким образом при разборе текста задачи от вопроса к данным применяется аналитический способ.
Под синтезом подразумевают способ рассуждений от частного к общему (синтезировать – получать из частей). В задачах это разбор от данных к вопросу, однако, назвать этот метод чисто синтетическим нельзя, т.к. прежде, чем получать метод разбора от данных к вопросу, эти данные нужно предварительно вычленить из задачи, т.е. проанализировать условие задачи.
Непосредственно сам разбор задачи представляет собой цепочку рассуждений, основанных на анализе и синтезе. Организуя разбор задачи вместе с детьми, учитель должен продумать систему специально подобранных вопросов, при помощи которых организуется выбор решения задачи. Эти вопросы не должны быть наводящими, должны вести к самостоятельному выбору решения. Разбор составной задачи заканчивается составлением плана решения. Если вы разбираете задачу с одновременным составлением схемы разбора, то план решения прослеживается прямо по схеме.
Проиллюстрируем различные способы разбора задач на примере следующей задачи: «За день туристы преодолели 100 км. 84 км они проехали автобусом, а остальной путь прошли пешком за 4 часа. Сколько километров туристы проходили за 1 час?» [Б3, №716].
В результате анализа содержания задачи появляется ее краткая запись в виде чертежа:
Направление рассуждений будет следующим:
1) Разбор от вопроса к данным.
Что спрашивается в задаче? (Сколько км туристы проходили за 1 час?) Что нужно знать, чтобы ответить на этот вопрос? (Путь, который прошли туристы и время, которое они затратили на этот путь). Можно ли сразу узнать, сколько км туристы проходили за 1 час? (Нельзя, т.к. мы не знаем путь, который они прошли). Можно ли сразу узнать путь, пройденный пешком? (Можно). Почему вы думаете, что можно? (Так как мы знаем общий путь и путь, пройденный пешком). Далее осуществляется наметка плана решения.
Источник
Статья на тему «Разбор составных задач» (3-4 класс)
Способы разбора составных задач.
Решить составную задачу-значит разложить её на простые задачи так , чтобы последняя простая задача давала ответ на вопрос всей задачи .
Существует три способа разбора задачи :
Аналитический способ разбора это такой ход рассуждения , когда рассуждаем от вопроса задачи к числовым данным.
Различают полный аналитический способ разбора и неполный. Полный аналитический способ—это такой способ, когда на вопрос учителя ученик называет две величины , известны они или неизвестны. При неполном анализе ученик называет только одну, неизвестную, величину.
Задача. В одной коробке 6 карандашей, а в другой на 2 карандаша меньше .Сколько карандашей в двух коробках вместе?
Образец полного анализа:
В. Что нужно знать для того, чтобы найти сколько карандашей в 2 коробках вместе?
О. Надо знать, сколько карандашей в первой и во второй коробках.
В. Известно, сколько карандашей в первой коробке?
В. А известно, сколько во второй коробке?
О. Нет, неизвестно.
В. А что нужно знать для того, чтобы найти, сколько карандашей во второй коробке?
О. Надо знать, сколько карандашей в первой коробке и на сколько карандашей меньше во второй, чем в первой.
В. Известно, сколько в первой?
В. А на сколько меньше, известно?
Составляем план решения задачи:
Сколько карандашей во второй коробке?
Сколько карандашей в двух коробках?
Образец неполного аналитического разбора:
В. Можем ли мы сразу найти, сколько карандашей в двух коробках?
В. Почему не можем?
О. Потому что мы не знаем, сколько карандашей во второй коробке.
В. А можем найти, сколько карандашей во второй коробке?
Составляем план решения задачи:
Сколько карандашей во второй коробке?
Сколько карандашей в двух коробках?
Синтетический способ разбора задачи — это такой ход рассуждения, когда мы рассуждаем от числовых данных к вопросу задачи.
Задача: На одном поле колхозники собрали 9 000кг пшеницы, а на втором на 1 320кг пшеницы меньше. После того как часть пшеницы увезли на элеватор, на первом поле осталось 2 360кг, а на втором 1 320кг. На сколько кг пшеницы больше отвезли с одного поля, чем с другого?
В. Нам известно, что с первого поля собрали 9 000кг и осталось ещё 2 360 кг. Что с этими данными можем найти?
О. Сколько отвезли.
В. Нам известно, что с первого поля собрали 9 000 кг и ещё известно, со второго поля собрали на 1 320 кг меньше. Что можно найти?
О. Сколько собрали с другого поля.
В. Известно, сколько собрали со второго поля и сколько осталось на втором поле. Что можно найти?
О. Сколько отвезли.
В. Известно, сколько отвезли с первого поля и сколько со второго. Что можем найти?
О. На сколько больше отвезли с одного поля, чем с другого. Составляем план решения задачи:
Сколько пшеницы кг пшеницы отвезли с первого поля?
Сколько собрали со второго поля?
Сколько отвезли со второго поля?
На сколько больше отвезли с одного поля, чем со второго?
Аналитико — синтетический способ разбора — это объединение анали- тического и синтетического способов разбора.
Задача: Две девочки купили 8 м ленты по одинаковой цене. Одна из них уплатила 15 рублей, а другая 9 рублей. Сколько метров ленты купила каждая девочка?
Образец аналитико — синтетического разбора:
В. Что надо знать для того, чтобы найти, сколько метров в первом куске?
О. Стоимость и цену.
В. Известна стоимость?
О. Цена неизвестна.
В. Что известно про цену?
В. Что такое 8 м?
О. Столько метров ленты было в двух кусках вместе.
В. Если бы мы знали, сколько стоят 2 куска, что бы мы могли найти?
О. Можно найти цену.
В. Можем теперь найти общую стоимость?
В. А можем найти количество метров ленты в первом куске?
Составляем план решения задачи:
Какова общая стоимость 2 кусков ленты?
Сколько метров ленты в первом куске?
Сколько во втором?
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 798 человек из 78 регионов
Курс повышения квалификации
Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО
- Сейчас обучается 308 человек из 59 регионов
Курс повышения квалификации
Скоростное чтение
- Сейчас обучается 618 человек из 78 регионов
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-517735
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Якутии школьников отправили на дистанционку из-за морозов
Время чтения: 1 минута
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
На базе колледжей создадут программы профориентации
Время чтения: 2 минуты
ЕСПЧ запретил учителям оскорблять учеников
Время чтения: 3 минуты
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
Доклад на тему: «СИСТЕМА РАБОТЫ НАД ТЕКСТОВОЙ АРИФМЕТИЧЕСКОЙ ЗАДАЧЕЙ В НАЧАЛЬНОЙ ШКОЛЕ. Виды анализа задачи».
Система работы над задачей- значима для учащихся начальных классов.Как правильно анализировать данные задачи и вести разбор? Какие пути решения должны четко представлять учащиеся., алгоритм рассуждения при решении задачи и помощь в построении данного алгоритма.
Содержимое разработки
«СИСТЕМА РАБОТЫ НАД ТЕКСТОВОЙ АРИФМЕТИЧЕСКОЙ ЗАДАЧЕЙ
В НАЧАЛЬНОЙ ШКОЛЕ. Виды анализа задачи».
«Ребёнок не должен получать готовых знаний, должен напрягать свой ум и волю, должен чувствовать себя соавтором в решении возникающих проблем». (В. В. Давыдов)
1 Теоретические аспекты опыта
Обучение детей самостоятельному анализу решения простых и составных задач волнует каждого учителя. Ключ к решению задачи — это прежде всего пошаговый анализ действий, которые необходимо выполнить для того, чтобы ответить на главный вопрос задачи.
Во время анализа устанавливается зависимость между данными и искомыми значениями величин.
Основные традиционные приёмы анализа задачи – это разбор от вопроса к числовым данным (анализ) и от числовых данных к вопросу ( синтез). Анализ – логический прием, состоящий в расчленении исследуемого объекта на составные элементы и исследовании каждого из них в отдельности. Он может использоваться многократно. Разбор задачи от вопроса к данным — это суждение, которое состоит в том, чтобы подобрать два числовых значения одной или разных величин таким образом, чтобы дать ответ на вопрос задачи. Одно из значений или оба могут быть неизвестными. Для их нахождения подбираются два других, и так продолжается процесс подбора, пока не приходим к известным числовым значениям величин. В результате такого разбора учащиеся устанавливают зависимость между числовыми значениями величин, расчленяют ее на простые задачи и составляют план ее решения
При аналитическом способе решения задачи выясняется, что нужно предварительно узнать, чтобы ответить на вопрос задачи. Чтобы помочь детям вести рассуждения аналитическим способом, можно использовать прием, называемый “деревом рассуждений”. Суть его состоит в том, что по ходу рассуждений строится схема, которая помогает увидеть, какие простые задачи следует выделить и каким будет план решения данной составной задачи.
Синтез – логическая операция установления связи между составными частями исследуемого объекта и изучения его как единого целого. Исследуемый объект называется в требовании задачи, а его элементы описываются в условии. Разбор задачи от числовых данных состоит в том, что к двум числовым данным подбирается вопрос, затем к следующим двум данным, одно из которых может быть результатом первого действия, подбирается следующий вопрос. И этот процесс продолжается, пока не будет получен ответ на вопрос задачи
Синтетический способ характеризуется тем, что основным вопросом при поиске решения задачи является вопрос о том, что можно найти по двум или нескольким известным в тексте задачи числовым значениям. По вновь полученным числовым значениям и другим известным в задаче данным вновь ищется ответ на вопрос, что можно узнать по этим значениям. И так до ответа на вопрос составной задачи. Иными словами, суть этого способа состоит в вычленении простой задачи из предложенной составной и решении ее.
Аналитико-синтетический метод. Значительно чаще, используется на практике, чем аналитический и синтетический методы. Он сочетает элементы и анализа и синтеза. Так при решении сложной задачи она с помощью синтеза разбивается на ряд более простых задач, а затем при помощи синтеза происходит соединение решений этих задач в единое целое. Обучение учащихся начальных классов рассмотренным методам поиска решения задач сводится к обучению их правильному формулированию вопросов, соответствующих аналитическому или синтетическому методу. При разборе задачи нового вида учитель должен в каждом отдельном случае поставить детям вопросы так, чтобы навести их на правильный или осознанный выбор арифметических действий.
2. Обратимся к практике.
Анализ задачи аналитическим способом. Будем идти от вопроса к данным.
ЗАДАЧА.
Лида нарисовала 4 домика, а Вова на 3 домика больше. Сколько домиков нарисовали дети ?
Составляем дерево рассуждения с пояснением:
Чтобы ответить на вопрос задачи необходимо знать 2 величины: сколько домиков нарисовала Лида и сколько нарисовал Вова. Сколько нарисовала Лида нам известно-4, а сколько нарисовал Вова неизвестно, но сказано что на 3 домика больше, вспомню на 3 больше значит столько же и еще з, поэтому к 4 прибавлю 3 , теперь зная величину сколько прочитал Вова и сколько прочитала Лида я отвечу на вопрос задачи.
АНАЛИЗ ЗАДАЧИ СИНТЕТИЧЕСКИМ СПОСОБОМ .
Начинаем от числовых данных.
В двух пачках 160 тетрадей, причем в одной из них на 20 тетрадей больше, чем в другой.
Сколько тетрадей в каждой пачке?


Составляем дерево рассуждения, сопровождая пояснением:
В задаче нам известны 2 величины : 160-сколько тетрадей в двух пачках и 20 на столько во второй больше, зная эти величины, найду третью: сколько тетрадей в двух пачках, если количество их равное, для этого 160 – 20, теперь мне известна величина сколько тетрадей в пачках при их равном количестве и величина 2 – сколько пачек тетрадей , разделим эти величины и узнаем сколько тетрадей в одной пачке при равном количестве тетрадей. Мы ответили лишь на один вопрос задачи : сколько тетрадей в одной пачке, чтобы узнать количество тетрадей во второй пачке прибавим 20 т.к. сказано,что во второй пачке на 20 тетрадей больше.
Таким образом, рассуждение можно строить двумя способами:
от вопроса задачи к числовым данным;
от числовых данных идти к вопросу;
Нужно помнить, что введение понятия «СОСТАВНАЯ ЗАДАЧА» вводится тогда, когда научились решать все виды простых задач.
Разбор составной задачи заканчивается составлением дерева рассуждения –
это объяснение того, что узнаем, выполнив то или иное действие, и указание по порядку арифметических действий.
Нужно обратить внимание и на то, что полный анализ задачи, решаемой в 4-5 действий , является многословным, забирает много времени. Здесь целесообразно использовать схему неполного анализа , при котором в условие задачи записываются не только числа, но и выражения, это
во-первых укорачивает условие задачи, а во-вторых,делает более прозрачный путь к её решению.
Птицефабрика должна отправить в магазины 6000 яиц. Она уже отправила 10 ящиков по 350 яиц и 4 ящика по 150 яиц. Сколько яиц осталось отправить в магазины?

(150 х 4) яиц 6000 яиц
При этом рассуждаем: если было 10 ящиков по 350 яиц в каждом, то яиц было 350 × 10. Отправила также 4 ящика по 150 яиц, это составляет (150×4) яиц.
Выполняя анализ от вопроса, учащиеся рассуждают примерно так:
«Чтобы ответить на вопрос задачи, надо знать две величины : сколько всего яиц надо отправить (6 000 яиц) и сколько яиц птицефабрика уже отправила. Чтобы узнать, сколько яиц фабрика отправила, надо знать, сколько она отправила в первый и во второй раз. В первом вопросе узнаем, сколько птицефабрика отправила яиц в 10 ящиках, во втором – сколько она отправила яиц в 4 ящиках, в третьем – сколько она отправила всего яиц и в четвертом – сколько яиц осталось отправить».
Схемы полного (рис.1) и неполного (рис.2) анализа наглядно показывают преимущество и недостатки каждого из них.
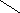
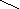
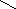
После анализа учащиеся самостоятельно записывают решение в форме математического выражения или по отдельным действиям. Для учащихся, которые затрудняются , ведется более подробный анализ.
Такая работа, которая проводится в системе, способствует развитию учебной мотивации, большинству детей помогает видеть взаимосвязь между величинами, овладевать разными способами решения задач, т.е. способствует формированию математической компетентности.
Исследовательская деятельность помогает разнообразить деятельность детей на уроке, поддерживает интерес к математике и, главное, помогает им овладеть умением решать задачи. Конечно, подобный вид работы, требует больших затрат времени. Однако время, потраченное на них, окупается умением решать задачи не только на уровне государственных стандартов, но и нестандартные задачи. А самое главное у детей появляется желание решать задачи.
Вспомним старую притчу о том, как один мудрец бедняков накормил.
— Пришёл мудрец к бедным и сказал: «Я вижу, вы голодны. Давайте я дам вам рыбу, чтобы вы утолили голод». Но время прошло, и люди опять проголодались.
Притча гласит: «Не надо давать рыбу, следует научить ловить её»
Не надо давать готовый путь к решению, надо побуждать учащихся к действию, учить их анализировать, рассуждать и находить путь решения самостоятельно.
Аргинская И.И., Дмитриева Н.Я.Обучаем по системе Л.В. Занкова: 2кл.: Кн. Для учителя. – М.: Просвещение, 1993. – 160с.
Занков Л.В. Беседы с учителями. (Вопросы обучения в начальных классах.) М., Просвещение, 1970. — 200с.
Иванов Д.А., Митрофанов К. Г., Соколова О.В. Компетентностный подход в образовании. Проблемы, понятия, инструментарий. М.: изд-во Академии повышения квалификации и проф. переподготовки работников образования.- 2006г.
Лысенкова. С. Н.. Когда легко учиться: из опыта работы учителя начальных классов школы №587 Москвы.- 2-е изд.М.: Педагогика, 1985 – 176с.(пед. поиск: опыт, проблемы, находки)
Мамыкина М. Ю. Работа над задачей в системе Л. В. Занкова. Начальная школа
Матвеева Н.А.. Различные арифметические способы решения задач. Начальная школа №3.2001г.
Математика. 1-4 классы: обучение решению текстовых задач/ авт.-сост. И.Л. Кустова. – Волгоград: Учитель, 2009. – 103с.
Новиков А.Учебный процесс в логике исторических типов организационной культуры. Народное образование №1, 2008г.с.163
Петерсон Л.Г., Кубышева М.А., Мазурина С.Е., Зайцева И.В. Что значит «уметь учиться». – М.: АПК и ППРО, УМЦ «Школа 2000…», 2008. – 80с.
Узорова, Нефёдова. 500 задач с пояснением, пошаговым решением и правильным оформлением. 1класс. АСТ.: Астрель. Москва.2004г.
Фадеева. Схемы записи задач. Начальная школа №4.2003г.
Фонин С.Н.. Моделирование, как важное средство обучения решению задач. Начальная школа. №3.1990г.
Шульга Р.П. Решение задач разными способами – средство повышения интереса к математике. Начальная школа №12. 1990г.
Ф.Семья. Совершенствование работы над составными задачами. Начальная школа №5.1991г.
Источник