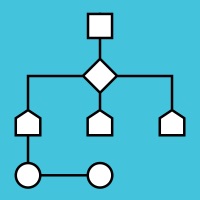
Как составить сетевой график по ресурсам

Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.

В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.

Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.

Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.

Виды сетевых графиков

Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).

На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).

Рассмотрим второй вариант графика и алгоритм его построения подробнее.

Алгоритм построения сетевого графика

Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.

Шаг 1. Определить основную цель проекта

Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.

Шаг 2. Выявить ограничения

Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.

Шаг 3. Определить состав работ

Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.

Шаг 4. Оценить длительность работ

Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.

Шаг 5. Определить последовательность работ

Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.

Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.

Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.

Шаг 6. Указать связи между работами

Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.

Шаг 7. Определить раннее начало и раннее окончание

Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.

Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.

Шаг 8. Определить поздние начало и окончание

Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Шаг 9. Определить временной резерв

Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Шаг 10. Выявить критический путь

Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.

Пример построения сетевого графика

Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.

Шаг 1. Определить основную цель проекта

Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.

В этом случае целью нашего небольшого проекта будет —  сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.

Шаг 2. Выявить ограничения

Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.

Шаг 3. Определить состав работ

Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:

  • Нам нужен дизайн-проект новой комнаты;
  • Нам надо закупить материалы для ремонта;
  • Надо составить смету ремонта;
  • Надо выполнить сам ремонт;
  • И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.

Отобразим эти работы в виде блоков:

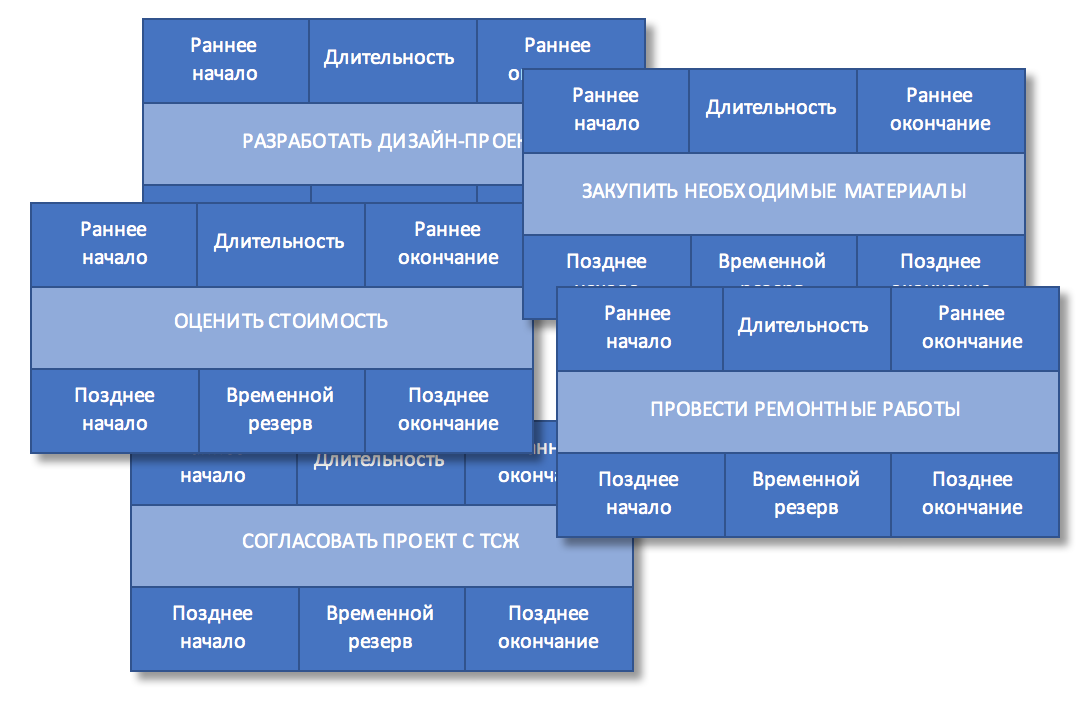
Состав работ

Рисунок 1. Состав работ

Шаг 4. Оценить длительность работ

Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Длительность работ

Рисунок 2. Длительность работ

Шаг 5. Определить последовательность работ

Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Последовательность работ

Рисунок 3. Последовательность работ

Шаг 6. Указать связи между работами

Укажем стрелками связи между работами.

Связи между работами

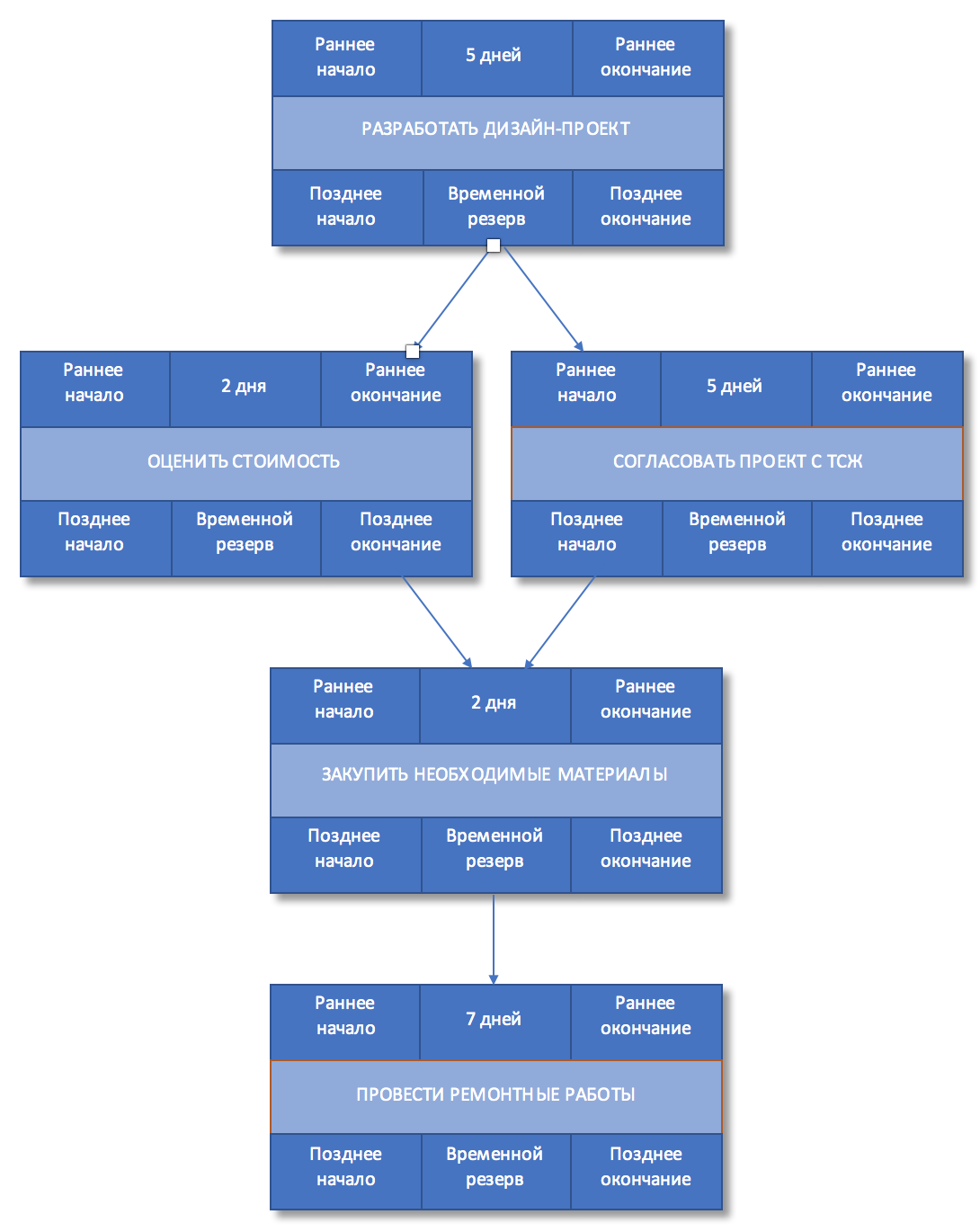
Рисунок 4. Связи между работами

Шаг 7. Определить раннее начало и раннее окончание

Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.

Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.

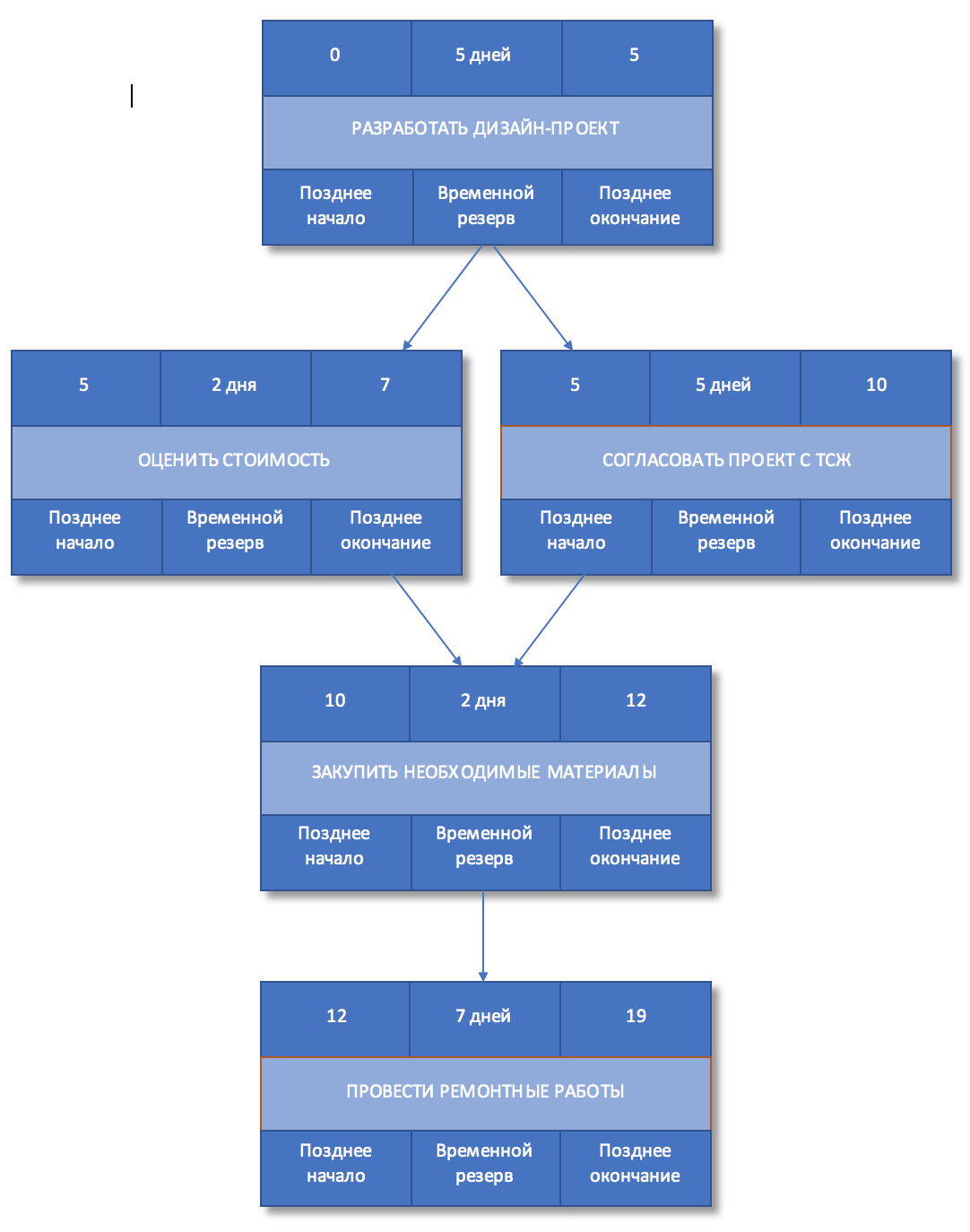
Раннее начало и окончание работ

Рисунок 5. Раннее начало и окончание работ

Шаг 8. Определить поздние начало и окончание

Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

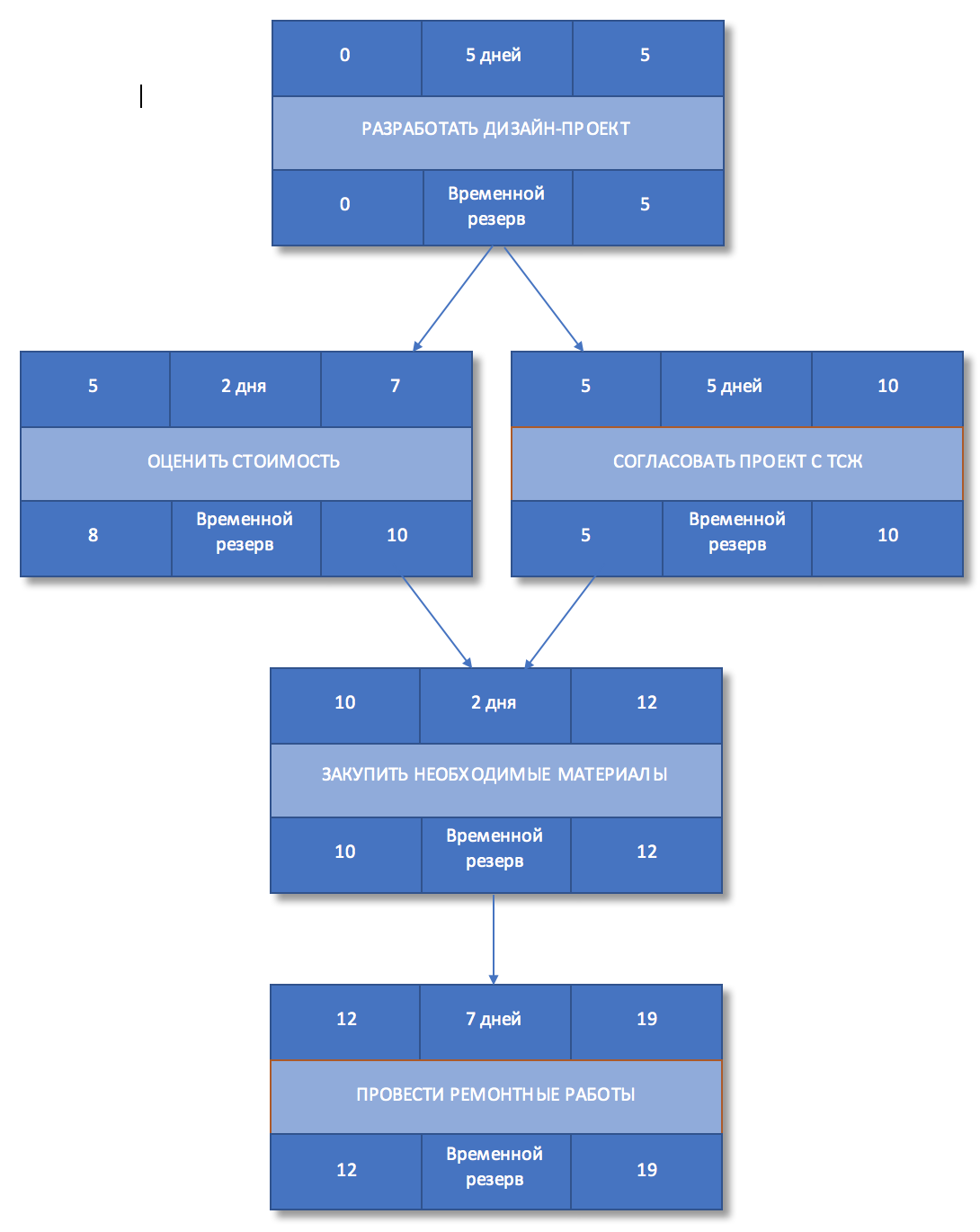
Позднее начало и окончание работ

Рисунок 6. Позднее начало и окончание работ

Шаг 9. Определить временной резерв

Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

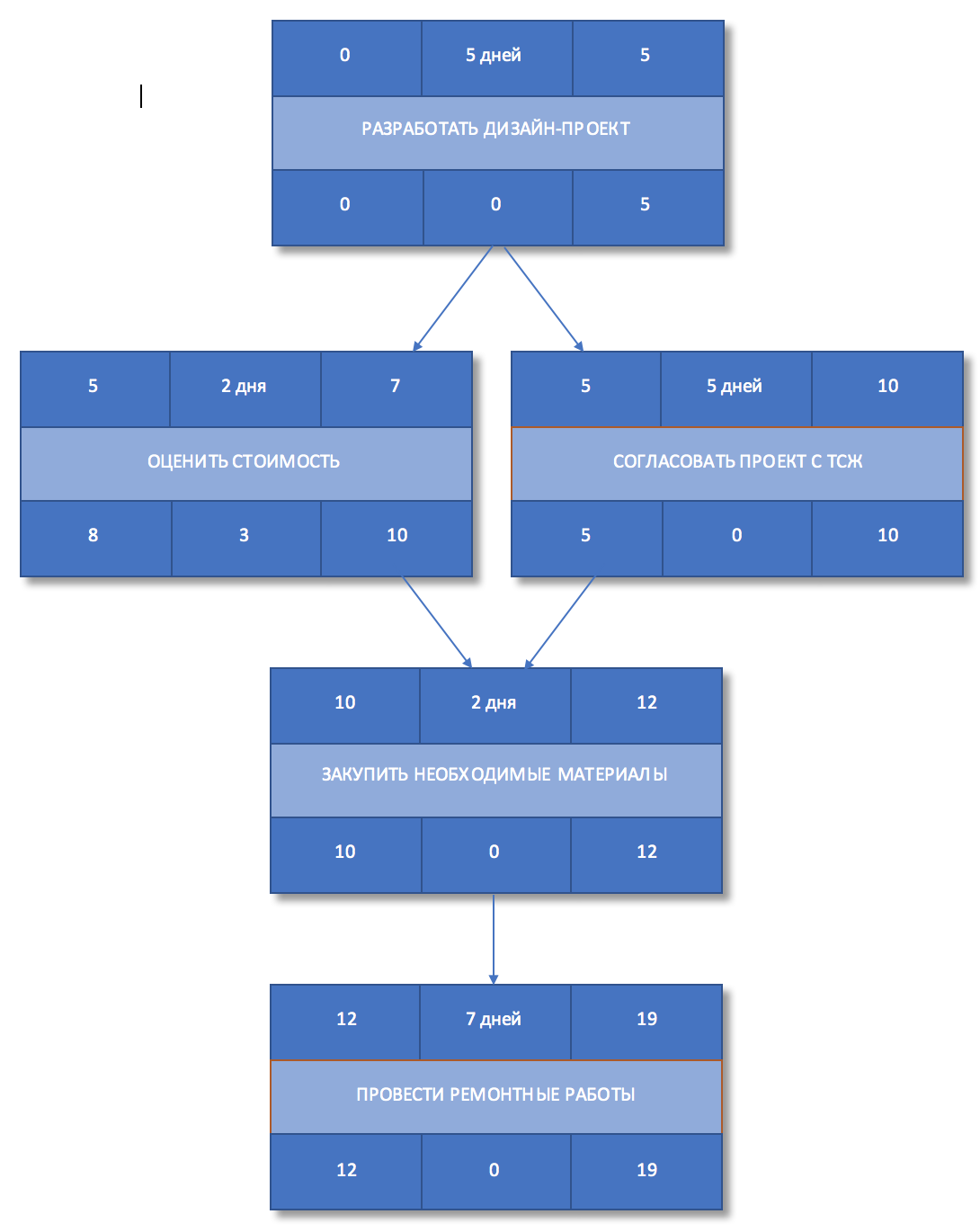
Временной резерв

Рисунок 7. Временной резерв

Шаг 10. Выявить критический путь

Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.

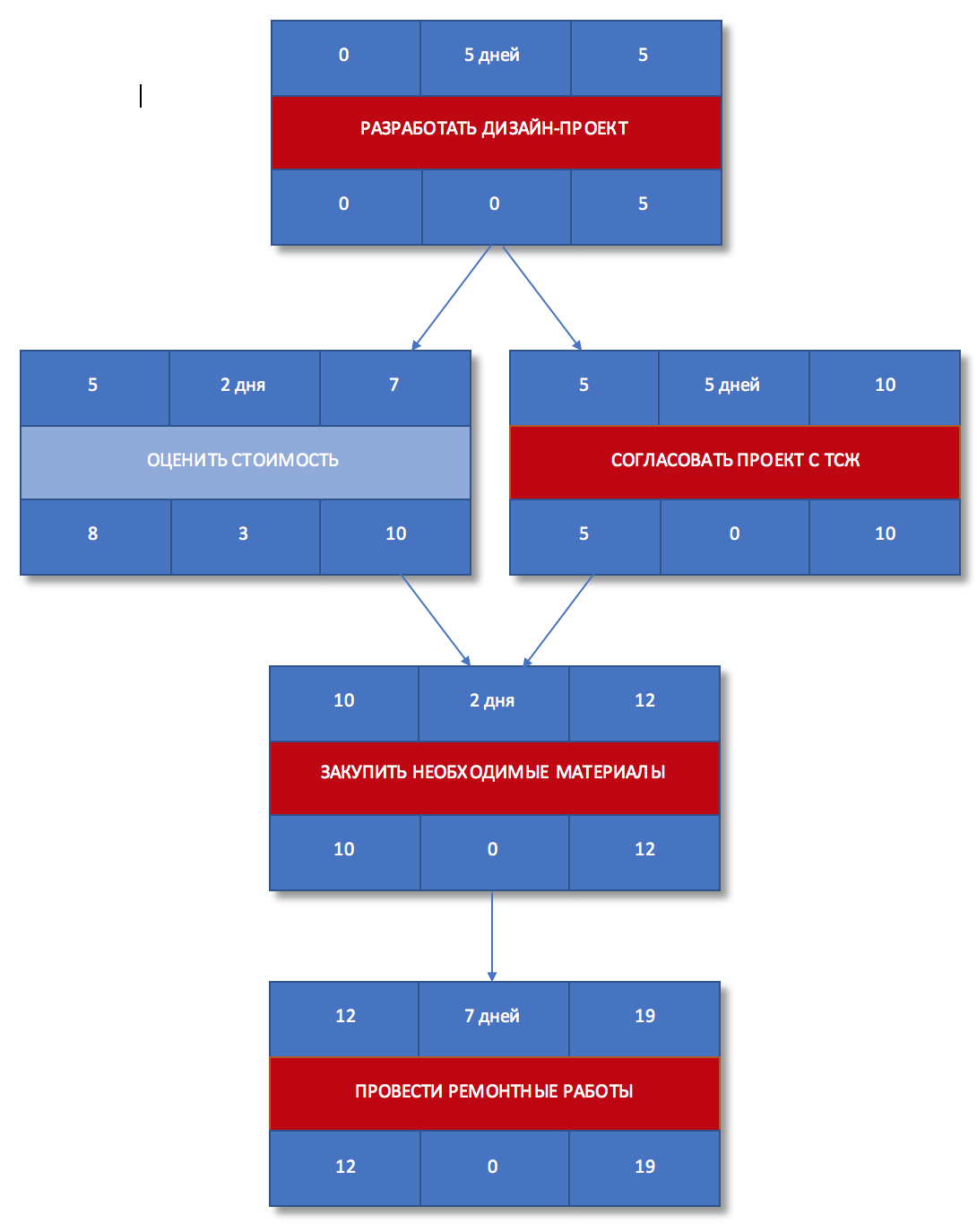
Критический путь

Рисунок 8. Критический путь

Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.

Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.

Просмотры: 138 634

Источник

Анализ сетевого графика

С помощью данной программы можно онлайн определить параметры сетевого графика (рассчитать сроки свершения событий, резервы времени и критический путь), найти коэффициенты напряженности. Оптимизация сетевого графика проводится по следующим критериям: число исполнителей, резервы-затраты, сокращение сроков (см. вкладку Параметры сетевого графика).

Сетевой график можно нарисовать, а также задать в виде матрицы или таблицы (меню Действия).

  • Ввод данных
  • Параметры сетевого графика
  • Решение
  • Видеоинструкция
  • Оформление Word

Нумерация вершин с №1

Выберите нужный тип вершины и нажмите левой кнопкой мыши на графическом полотне

Размеры графического полотна

Ширина
Высота

Созданный сетевой график можно сохранить в форматах docx и png (меню Действия).

Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).

Для сформированного графа можно выполнить следующие действия:

Здесь будет показано решение

Инструкция к сервису

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0, для этого нужно снять отметку с пункта Нумерация вершин с №1.

1234
1103015

Нумерация вершин с 0

0123
1103015



Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить.

Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции.

Построенный граф можно сохранить в формате docx или png.

Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.

Основные определения

Ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг, называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в направлении достижения результата при осуществлении комплекса работ.

Наиболее распространен способ представления моделируемого комплекса работ в понятиях работ и событий.

Понятие «работа» имеет следующие значения:

  • «действительная работа» – процесс, требующий затрат времени и ресурсов;
  • «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.

Работа на графике изображается стрелкой, над которой указывается затрачиваемое на нее время. Длина стрелки и ее ориентация на графике не имеют значения. Желательно только выдерживать направление стрелок так, чтобы начальное событие для работы (обозначается i) располагалось слева в сетевом графике, а конечное (обозначается j) — справа. Для отображения фиктивных работ используют пунктирные стрелки, над которыми время не указывается или проставляется ноль.

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 1. Каждая операция в сети представляется одной и только одной дугой (стрелкой). Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой.

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:

а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?

б) Какие операции должны непосредственно следовать после завершения данной операции?

в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

  • в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
  • В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
  • в сети не должно быть замкнутых контуров (рис.1);
  • Любые два события должны быть непосредственно связаны не более чем одной работой.
  • В сети рекомендуется иметь одно исходное и одно завершающее событие.
  • Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка

завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Методы оптимизации сетевого графика

Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.

После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.

Для возможности оптимизации сетевой модели, все исходные данные вводятся в виде таблицы (Операции/Добавить в виде таблицы).

  • Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч
  • Оптимизация сетевой модели по критерию «время – стоимость» (время — затраты). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j). Иначе, заполняются столбцы tопт (Нормальный режим), Минимальное время работ, tmin (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc.

Графики привязки (а) и загрузки (b) до оптимизации

1,261,311,452,532,613,684,644,725,866,817,83 1122 3194175 6 7 8189 10 11 12 13 141315 16 17 181019 20 21 22423 24 25 26127

Графики привязки (а) и загрузки (b) после оптимизации

1,261,311,452,532,613,684,644,725,866,817,83 1122 3114145 6 7158 9 10 111812 13 14 151016 17 18419 20 21 221023 24 25 26727

Диаграмма Ганта

1,241,331,452,5112,6143,64,6174,75,8196,8277,825

Чтобы построить диаграмму Ганта по графику работ, необходимо выделить пункт Строить диаграмму Ганта. Также можно создать график на основе введенных данных. Для этого следует указать количество работ (мероприятий) и даты их проведения.

Количество работ

Примеры сетевых моделей

Рассмотрим варианты сетевых графиков из кулинарной области на примере варки борща из курицы.

а) Варка в обычной посуде

12345
11030157

Работы:

1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.

1,3: варить курицу, 30 мин.

2,3: положить капусту и варить 10 мин.

3,4: положить 1/2 свеклы, морковь и картофель. Варить 15 мин.

4,5: доложить остатки свеклы, лук, зелень. Варить 7 мин.

б) Варка в посуде с эффектом русской печи (трехслойное дно, крышка без отверстий)

12345
1010203060

Работы:

1,2: чистка овощей (капуста, морковь, картофель, свекла, лук), 10 мин.

1,4: варить курицу в обычной посуде, 30 мин.

2,3: положить овощи в спецпосуду, добавить 3 ложки воды, нагреть до T=70 C и выключить, 10 мин.

3,4: приготовление овощей в собственном соку, 20 мин.

4,5: добавить к курице приготовленные овощи. Настаивается 60 мин.

Список литературы

  1. Мушик Э., Мюллер П. Методы принятия технических решений. Пер. с нем. –М.: Мир, 1990.
  2. Таха Х. Введение в исследование операций. В 2-х книгах. Кн. 2. Пер. с англ. –М.: мир, 1985.
  3. Управление в системах РАВ: Учебник. –Л.: Воениздат, 1980.

Текст

РазмерЦвет

Линия

ТолщинаЦвет

пунктирная — — — —
Размеры в px и фон

wh

Текст (вес)

РазмерЦвет

Линия

ТолщинаЦвет

пунктирная — — —
концевой маркер →

Тип

Число строк

Минимальное время работ, tmin

Максимальное время работ, tmax

Количество исполнителей, чел., Ч

Коэффициент затрат на ускорение работ, руб./сут., h(i,j)

Нормальная стоимость, Cн

Срочная стоимость, Cc

По умолчанию минимальное количество заполняемых столбцов равно трем: i, j, tопт. Чтобы иметь возможность ввести и другие данные, выделите соответствующий пункт.

В каждой строке укажите вершины в формате:v1-v2:n, например
1-2:4
1-3:8
2-4:12
4-1:6

Выберите номер критического пути.

Источник

Моделирование сетевого графика проекта

Моделирование сетевого графика проекта

Султанов Искандер Анварович

Свежие публикации автора:

Содержание

  • 1 Глоссарий разработки сетевого графика
  • 2 Базовый алгоритм и виды связей сетевого графика
  • 3 Методы расчета длительности операций
  • 4 Методы оптимизации сетевого графика

Менеджер проекта, занимаясь его планированием, должен помнить о проектном треугольнике ограничений: «продолжительность» – «стоимость» – «содержание». Ресурсные и стоимостные ограничения предопределяют качество расписания проекта. Сетевое планирование, хотя и является достаточно рутинным инструментом календарной проработки, тем не менее, позволяет лучшим образом выполнить оптимизацию плана в отношении ресурсов и сроков. Сетевой график, построенный по методу «вершина – работа», предоставляет все возможности применения прикладных методов оптимизации.

Глоссарий разработки сетевого графика

Построение сетевого графика методологически основано на общей концепции СПУ (системы планирования и управления) проектов. Ключевые аспекты данной методологии были рассмотрены в статье на тему сетевого планирования проекта. В настоящем материале мы развиваем начатое осмысление теоретических и прикладных вопросов сетевого моделирования. В первую очередь, нас интересует разработка сетевой диаграммы вида «вершина – работа» в контексте ее составления, оптимизации и корректировки. Логика сетевого планирования достаточно проста, математически метод не сложен.

Тем не менее, на практике применить полноценно эту модель удается не всегда. Возникают затруднения, во многом определяемые психологией участников, не готовых объективно рассчитать сроки исполнения сформулированных задач. Данный метод дает более слабый результат в условиях перегруженности ответственных ресурсов по проектным задачам. Сетевые графики хорошо работают в проектах, где ответственные исполнители заняты только на одном проекте, например, в строительстве. Ниже показана модель процесса календарного планирования, которая служит направляющим ориентиром в работе со средством планирования «сетевой график».

разработка календарного плана

Схема разработки календарного плана проекта

Введем основные понятия, которые понадобятся для составления сетевой модели проекта и ее оптимизации:

  • отношение предшествования – это характеристика связи последующей работы в отношении предшествующей;
  • путь – это непрерывная последовательность операций (работ) в сетевом графике;
  • предшествующий путь – участок полного пути от исходного до рассматриваемого события;
  • последующий путь – участок полного пути от рассматриваемого события до любого следующего;
  • критический путь – это полный путь, характеризуемый нулевым резервом;
  • критическая работа – действие, для которого полный резерв имеет нулевое значение;
  • предкритическая работа – операция, для которой менеджер проекта установил число предельного значения полного резерва;
  • резерв пути – разница между временной длительностью проекта и длиной пути на графике;
  • веха – работа с нулевой продолжительностью, обозначает важное, значимое событие в проекте;
  • минимальное время от начала проекта до начала выполнения операции без нарушения отношения предшествования называется ранним сроком начала работы;
  • максимальное время с начала проекта до начала выполнения операции, которое позволяет проекту закончиться вовремя без нарушения отношения предшествования, называется поздним сроком начала работы;
  • минимальное время, которое требуется для выполнения всех работ без нарушения отношения предшествования, называется ранним окончанием проекта;
  • возобновляемый ресурс предполагает ограничение в использовании его на каждом шаге планируемого периода;
  • невозобновляемый ресурс предполагает ограничение в использовании его на всем периоде реализации проекта.

Базовый алгоритм и виды связей сетевого графика

Сетевой график позволяет увидеть структуру работ, представить все этапы и взаимосвязи с требуемой степенью детализации. На его основе производится разработка обоснованного плана мероприятий с учетом более эффективного использования ресурсов по заданным критериям. Диаграмма позволяет производить поливариантный анализ альтернативных решений для улучшения календарного плана с использованием компьютерных технологий. Вспомним основные правила построения сетевой модели метода «вершина – работа».

  1. Элементы сетевого графика включают работы и зависимости (связи) между ними. События на графике не отражаются за исключением вех, представляющих собой основные наиболее важные события, изображаемых в форме «ромбиков», работ с нулевой продолжительностью.
  2. Работа представляет собой неделимый элемент процесса, требующий времени и других ресурсов для выполнения, изображается в виде прямоугольника, вытянутого по горизонтали. Исходя из этого правила, длина прямоугольника может свидетельствовать о продолжительности операции.
  3. Разработка графика начинается с размещения на нем исходной работы в крайней левой точке и завершается включением в него конечной операции, закрывающей проект. Календарно начальный момент исходного действия обозначает старт проекта.
  4. Зависимости (связи) между работами оформляются стрелками, направленными слева направо под разными углами наклона. На основе данного правила связи между операциями определяются одной из форм отношений зависимости.
  5. Сетевой график имеет только одну работу, в которую входят зависимости, но не выходит ни одна, и одну работу, не имеющей ни одной входящей зависимости.
  6. Сетевой график не может иметь циклов, т.е. зависимости не должны связывать работы по кругу.

вид сетевого графика

Вид сетевого графика метода «вершина – работа»

Сетевой график строится по следующему алгоритму составления.

  1. На диаграмме размещается начальная работа проекта, не имеющая предшественников.
  2. Расположение операции, непосредственно следующей за работой, связанной с ней отношением предшествования, на графике левее предыдущей. Отображение связи предшествования.
  3. Переход к пункту 2 до тех пор, пока не закончатся работы, имеющие предшественников.

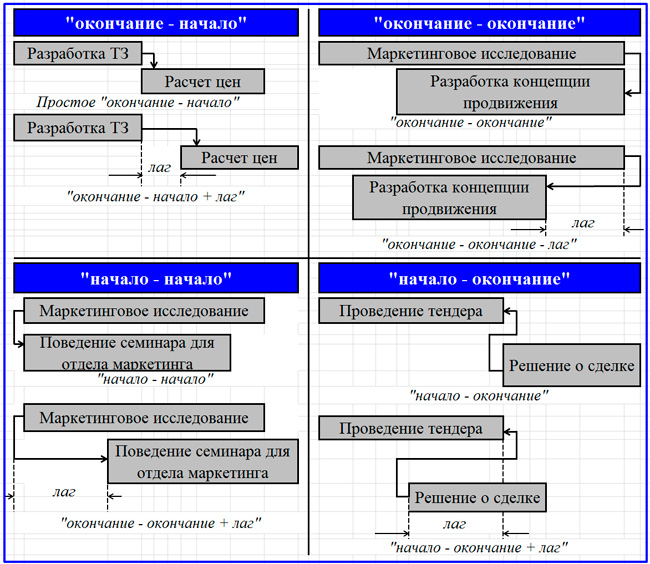
Разработка сетевой диаграммы производится с учетом возможных связей между работами. Основные виды отношений предшествования используются в четырех вариантах связей и в двух дополнительных их разновидностях. Далее на схеме представлены варианты связи следующей по идентификационному номеру работы к предыдущей или, наоборот, последующей. Основные или базовые виды предшествования связаны с перестановками слов «начало» и «окончание»:

  • «окончание – начало» (простой вид отношения предшествования);
  • «окончание – окончание»;
  • «начало – начало»;
  • «начало – окончание».

примеры вариантов отношений

Примеры вариантов отношений предшествования

Методы расчета длительности операций

Для обеспечения построения, анализа и управления расписанием проекта необходимо рассчитать следующие параметры сетевого графика: стоимость, задействованные ресурсы и продолжительность работ. Требуемые ресурсы нужно рассчитать до определения продолжительности операций, так как их длительность во времени, как правило, зависит от состава задействованного ресурсного обеспечения. Кроме того, важно понимать, насколько ресурсы календарно доступны, что, в свою очередь, влияет на сроки работ и их продолжительность. Очевидно, что ключевым параметром выступает именно длительность операций. Для ее оценки используется ряд специальных методов, краткая характеристика которых приведена в табличной форме далее.

методы оценки длительности операции

Основные методы оценки длительности операций

В случае отсутствия статистических данных по аналогичным операциям и невозможности применить экономико-математические методы расчета часто используют экспертные оценки. У данного метода есть серьезное достоинство – его простота, при условии, что удалось привлечь опытных и объективных экспертов. Но этого достичь бывает нелегко, позиции экспертов по вопросам продолжительности могут оказаться противоположными. Тем не менее, такое положение вещей вполне допустимо при использовании средневзвешенных оценок квалифицированных экспертных мнений.

В разнообразных проектах присутствуют идентичные по природе работы. Например, подготовка устава проекта, разработка ТЗ, проведение тендера по структуре и трудоемкости мало чем отличаются друг от друга. Это свойство используется для оценки длительности по аналогам. В некоторых случаях информацию о параметрах аналогичных работ вполне допустимо использовать для планирования расписания. Для этого схожесть типа и содержания операций должны быть подвергнуты экспертизе.

Параметрическая оценка длительности тесно сопряжена с нормативным подходом. Данный подход задействует такие параметры, в частности, как производительность (объем производства в единицу времени) или выработка. Например, чтобы выполнить монтаж I-го уровня сложности оборудования «А» требуется, допустим, 100 нормо-часов труда специалистов высшей квалификационной категории. Подобного рода мероприятия называют еще работами фиксированного объема, потому что продолжительность их связана с числом выделяемых ресурсов и может быть оценена как объем работ, деленный на количество человеческих ресурсов.

Помимо варианта фиксированного объема отдельно выделяется случай фиксированной продолжительности работы. Примерами таких работ являются действия, связанные с режимом дежурства на объекте, обслуживания оборудования и т.д. Продолжительность в подобных случаях обусловлена длительностью работы обслуживаемого объекта. Для параметрического метода, как мы видим, важно найти параметр, от которого зависит продолжительность операции и причинно-следственные связи, на основе которых возможно определить зависимости параметра от других значений.

Методы оптимизации сетевого графика

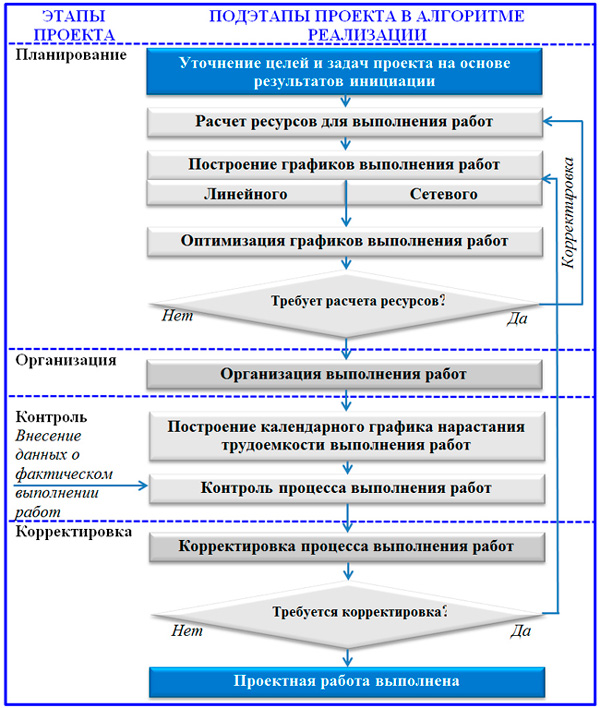
Сетевой график проектной реализации связан с содержанием уникальной задачи, параметрами времени и пространства, в которых выполняется проект. Данной деятельности присущи все традиционные функции управления без исключения. С этой точки зрения процесс можно разделить на этапы, в которых весомую долю занимает планирование. Далее вашему вниманию представляется упрощенная блок-схема функциональных этапов управления проектом.

блок-схема управления проектом

Функционально-процессная блок-схема управления проектом

На текущий момент нас интересует оптимизация сетевого графика как подэтап процесса планирования проектной задачи. Это связано с тем, что после сбора информации о работах и ограничениях разработка визуальной модели в форме сетевой диаграммы подразумевает дальнейшее ее улучшение с использованием методов расчета расписания. Основных методов два: метод критического пути (сокращенно МКП) и анализ расписания по методу PERT.

При использовании МКП производится последовательный расчет наиболее ранних и самых поздних сроков работ по проекту. Далее устанавливается размер полного резерва, при этом критическими работами считаются действия, имеющие нулевой полный резерв. Наконец, рассчитываются временные резервы для выполнения операций, и в качестве самого длинного пути сети выбирается критический путь. Критических путей может быть несколько. Оптимизация сетевого графика методом критического пути применяется для следующих моделей диаграммы:

  • для моделей с дискретным и непрерывным временем;
  • для моделей с простым отношением предшествования;
  • в сетях с обобщенными связями.

Метод оценки и анализа программ (PERT) служит вторым методом, по которому проводится оптимизация сетевого графика. Его основные отличия от МКП основаны на допущении, что длительность работ носит случайный характер, и для целей оценки и анализа сроков следует учитывать неопределенность временного параметра работ проекта. Также делается допущение о независимости всех случайных величин продолжительности критического пути. Для этих целей на основе метода математической статистики и теории вероятности используется β-распределение и оценка параметров распределения с трех экспертных позиций: оптимистичной, пессимистичной и наиболее вероятной.

Корректировка сетевого графика и сокращение общей продолжительности проекта входят в состав ключевых задач проект-менеджера. МКП дает возможность рассчитать оптимальные сроки выполнения проекта, но не позволяет найти инструменты для более действенного сокращения его продолжительности. В этом отношении метод критического пути не обладает достаточной гибкостью. Метод PERT также не лишен недостатков. Во-первых, он нацеливает в основном на оптимистический вариант оценки, во-вторых, PERT в меньшей степени применим к небольшим проектным задачам.

Для эффективной корректировки лучше всего подходят такие современные методы, как метод критической цепи и методы сжатия. Им мы намерены уделить внимание в отдельной статье. Все названные модели и методы являются предметной зоной компетенций PM, владея которыми, менеджеру проще демонстрировать свою эффективность, достигая результата проекта в условиях временных и ресурсных ограничений.

Источник

  1. . Математические метода сетевого планирования и управления. Календарное планирование ресурсов в управлении проектами

1.1 Построение сетевых графиков

Существуют несколько
общих правил построения сетевых графиков:

  1. в
    сетевых графиках не должно быть
    «тупиков», т.е. событий, из которых не
    выходит ни одна работа (за исключением
    завершающего события);

  2. в
    сетевых графиках не должно быть и
    событий (кроме исходного), которым не
    предшествует хотя бы одна работа;

  3. при
    построении сетевых графиков нельзя
    допускать, чтобы два смежных события
    были связаны двумя или большим количеством
    работ. Эта ошибка приводит к путанице
    из-за того, что две различные работы
    будут иметь одно и то же обозначение.
    Чтобы избежать этого, рекомендуется
    ввести дополнительное событие и связать
    его с последующим зависимостью или
    фиктивной работой;

  4. в
    сети не должно быть замкнутых циклов,
    т.е. цепей, соединяющих некоторые события
    с ними же самими;

  5. кроме
    того, если какие-либо сложные работы
    могут быть начаты до полного окончания
    непосредственно предшествующей им
    работы, то последняя изображается как
    ряд последовательно выполняемых работ,
    каждая из которых завершается определенным
    событием;

  6. если
    для выполнения одной из работ необходимо
    получение результатов всех работ,
    входящих в предшествующее для нее
    событие, а для другой работы достаточно
    получить результат только одной или
    нескольких из этих работ, то должно
    быть дополнительно введено новое
    событие, отражающее результаты только
    этих последних работ, а также фиктивная
    работа, связывающая новое событие с
    прежним.

Пример 1.
Пусть для выполнения работы D
необходимо предварительно выполнить
работы A,
B,
С, а для E,
выходящей из общего для них события
(4), предварительным условием является
выполнение работы С.

В этом случае
нельзя изображать взаимную связь и
зависимость работ так, как показано на
рис. 1.1, потому что при таком изображении
получается, что начало работы E
зависит от выполнения все трех
предшествующих A,
B,
C,
а это не соответствует условиям
разработки. Здесь следует ввести в сеть
дополнительное событие (3’) и холостую
связь (фиктивную работу) (C’)
(рис. 1.2).

Рис. 1.1

Рис. 1.2

    1. Определение
      продолжительности работ

После составления
сетевого графа необходимо определить
продолжительность каждой работы. Как
известно, длительность их выполнения
тесно связана с использованием ресурсов.
Увеличение ресурсов, как правило, ведет
к сокращению продолжительности.

Продолжительность
ведения работ оценивают наиболее
компетентные специалисты-эксперты,
ответственные исполнители с использованием
нормативно-справочной базы и с учетом
имеющихся трудовых, финансовых и
материальных ресурсов. При оценке
параметров сетевого графика на начальной
стадии устанавливаются только
продолжительности работ, а не сроки их
выполнения. При этом оценки работ следует
рассматривать независимо от оценок
предшествующих и последующих работ.

Для выяснения
продолжительности работ в зависимости
от характера и условий производства
могут быть использованы следующие
способы.

    1. В
      ситуациях, имеющих массовый характер,
      т.е. продолжительность работ, часто
      встречавших ранее в аналогичных
      условиях, временные оценки делаются
      по достигнутой производительности
      труда, исходя из объема работы, количества
      смен, численности исполнителей в смену;

    2. Продолжительности
      работ, для которых на предприятии
      имеются нормы времени, показываются
      по нормам;

    3. В
      единичным производстве продолжительность
      работ устанавливается методом экспертных
      оценок, при котором опрашиваются
      опытные специалисты и ответственные
      исполнители;

    4. Если
      с привлечением экспертов оценку
      получить невозможно и нет нормативов,
      то продолжительность может быть
      выяснена на основе вероятностных
      оценок.

Широкое применение
получила система трех и двух вероятностных
оценок времени. В системе с тремя оценками
от ответственного исполнителя получают
минимальную (),
максимальную ()
и наиболее вероятную оценки времени.

Минимальное
(оптимистическая
оценка) — это
необходимое для выполнения работы время
при наиболее благоприятном стечении
обстоятельств.

Максимальное
(пессимистическая
оценка) –
это время, необходимое для выполнения
работы при наиболее неблагоприятном
стечении обстоятельств (за исключением
аварий и стихийных бедствий).

Наиболее вероятная
оценка –
возможное время выполнения данной
работы при отсутствии неожиданных
трудностей.

Оценки
,ислужат исходными для расчета ожидаемого
времени ()
выполнения работы. Величина—
математическое ожидание случайной
величины продолжительности выполнения
работы.

Для более полной
характеристики
используется понятие дисперсии. Дисперсия
– это мера неопределенности, рассеивания
случайной величины вокруг ее математического
ожидания. Очевидно, от значений дисперсий
отдельных работ зависит неопределенность
срока окончания всего проекта в целом.

В системе СПУ
предполагается, что

(1.1)

При этом можно
показать, что

(1.2)

Формулы (1.1) и (1.2)
служат для оценки продолжительности
работ.

    1. Определение
      полных путей и критического пути

Путь сетевого
графика, имеющий начало в исходном
событии, а конец в завершающем, именуется
полным. В каждом сетевом графике имеется
несколько путей, продолжительность
каждого из них определяется суммой
продолжительностей составляющих их
работ.

Среди полных путей
сетевого графика особое значение имеет
наиболее продолжительный из них —
критический.
В графике их может быть несколько. Пути,
отличные от критического имеют резервы
времени. Любая работа, лежащая на
некритическом пути, в случае задержки
выполнения может оказаться критической.

Важную роль в
сетевом графике играют пути, близкие
по продолжительности к критическим, —
подкритические. Их продолжительность
отличается от продолжительности
критического на величину, не превосходящую
заданной. К своевременному выполнению
работ подкритического пути должны
приниматься необходимые меры, чтобы
избежать появления на сетевом графике
нового критического пути. Критический
путь имеет исключительно важное значение,
а его продолжительность считается
главным параметром графика.

Пример 2.

Найти критический
путь для сети проекта, показанной на
рис. 1.3.

Рис. 1.3

Найдем
все полные пути и их продолжительности:

1
путь — 1-2-4, его продолжительность 10+7=17

2
путь – 1-2-3-4, 10+0+9=19

3
путь – 1-3-4, 12+9=21

Полный
путь максимальной длины – это критический
путь.

,

    1. Расчет
      временных параметров и резервов времени
      событий

Расчет
основных временных
параметров производится
по соответствующим формулам. Существует
множество методов расчета. Рассмотрим
метод динамического программирования.

Ранним
сроком
свершения событияназывается са­мый
ранний момент времени, к которому
завершаются все предшествующие этому
событию работы. Счет времени будем вести
от момента наступления начального
события. Для удоб­ства расчетов,
полагаем, что ранний срок свершения
исходного (1-го) события
равен нулю (т.е.

).
Ранний срок любого последующего события
(-го)
определяется продолжительнос­тью
самого длительного из предшествующих
путей. Отсюда, для определения ранних
сроков свершения событий имеем рекурентное
соотношение:

,

где
— максимально предшествующий путь.

Ранний срок
свершения события – минимально возможный
срок наступления этого события

Поздним
сроком
свершения события i
является са­мый
поздний момент времени, после которого
остается ровно столько времени, сколько
необходимо для завершения всех работ,
следующих за этим событием. Каждое
событие должно совершаться в такой
срок, чтобы осталось достаточно времени
для выполнения работ, следующих за этим
событием. Таким путем будет тот
последующий, который имеет максимальную
продолжительность .
Самый поздний из допустимых сроков
свершения события в сумме с продолжительностью
выполнения последующих работ должен
не превышать длины критического пути.
Отсюда,

,

т.е.
поздний срок свершения события вычисляется
как разность между продолжительностью
критического пути и продолжительностью
максимального из последующих за событием
путей.

Очевидно,
для событий, лежащих на критическом
пути, время раннего свершения события

равно
времени позднего свершения этого события
,
т.е..
Зная ранние и поздние сроки свершения
событий сетевого графика, легко выяснить
резерв времени каждого из них. Разница
между наиболее ранним из возможных
сроков называетсярезервом времениэтого события, т.е.

.

Резерв
времени события
показывает максимально допустимое
время, на которое можно отодвинуть
моментего свершения, не вызывая увеличения
критического пути. События критического
пути резерва времени не имеют. Учитывая,
чтоесть продолжительность пути максимальной
длины, проходящего через событие, получим

.

Отсюда
резерв времени любого события
равен полному резерву времени максимального
пути, проходящего через это событие.

    1. Расчет
      временных параметров и резервов времени
      работ

Зная
сроки свершения событий, можно определить
времен­ные параметры работ. Ранний
срок начала работы (i,
j)
равен раннему сроку
свершения события (i):

.

Ранний срок начала
работы – это минимальный срок, к которому
данная работа должна быть начата.

Ранний
срок окончания работы равен
сумме раннего срока свершения начального
события работы и ее продолжительности:

или
.

Ранний
срок окончания работы – это минимальный
срок, к которому работа может быть
закончена.

Поздний
срок окончания работы совпадает
с поздним сро­ком свершения ее конечного
события:

Поздний срок
окончания работы – предельный срок, к
которому работа должна быть закончена.

Поздний
срок начала работы равен
разности между поздним сроком свершения
ее конечного события и продолжительностью:

Поздний срок начала
работы – предельный срок, к которому
должна быть начата работа, чтобы не
увеличился общий срок выполнения работы.

или
.

Так
как сроки выполнения работ находятся
в границах, определяемых
и,
то они могут иметь
разного вида резервы времени. Полный
ре­зерв времени работы- это
максимально возможный запас времени,
на который можно отсрочить начало работы
или уве­личить продолжительность ее
выполнения при условии, что конечное
для данной работы событие наступит не
позднее своего позднего
срока:

или
.

Все некритические
работы имеют полный резерв времени
отличный от нуля. Полный резерв показывает,
насколько можно увеличить длительность
работы или отсрочить ее начало, чтобы
не увеличился срок выполнения работы

Сво­бодный
резерв времени — это
запас времени, которым можно располагать
при выполнении данной работы при условии,
что начальное и конечное ее событие
наступят в свои ранние сро­ки:

.

Свободный резерв
присущ только данной работе, и его
использование никак не повлияет на
вы­полнение последующих работ. Только
отдельные работы про­екта обладают
свободным резервом времени. Свободный
резерв показывает, насколько можно
увеличить продолжительность работы
или отсрочить ее начало, не нарушая
ранних сроков последующих работ.

    1. Оптимизация
      сетевых графиков

После разработки
сетевого графика и расчета параметров
его нужно оптимизировать. Обычно под
оптимизацией понимается всякое улучшение
комплекса работ с учетом сроков их
выполнения и рационального использования
различных ресурсов. В практических
целях различают оптимизацию по критерию
времени, стоимости и по ресурсам.

      1. Оптимизация
        проекта по времени

Пусть задан срок
выполнения проекта
,
а расчетное.
В этом случае оптимизация комплекса
работ сводится к сокращению продолжительности
критического пути, которое может быть
осуществлено либо за счет перераспределения
внутренних резервов, либо за счет
привлечения дополнительных средств.

Рассмотрим две
постановки задачи оптимизации проекта
по времени с использованием дополнительных
средств.

Задача 1 заключается
в определении величины дополнительных
вложений
в отдельные работы проекта с тем, чтобы
общий срок его выполнения не превышал
заданной величины,
а суммарный расход дополнительных
средств был минимальным.

Пусть задан сетевой
график выполнения проекта. Продолжительность
каждой работы равна
.
Известно, что вложение дополнительных
средствв работусокращает время ее выполнения до,
причем,
где—
технологические коэффициенты использования
дополнительных средств. Но сокращение
продолжительности работы не беспредельно,
для каждой работы существует минимально
возможное время ее выполнения.
Требуется определить количество
дополнительных средств,
которые необходимо вложить в работы,
а также время началаи окончаниявыполнения этих работ, чтобы проект был
выполнен в срок,
а суммарные дополнительные затраты
были минимальными.

Задача 2 заключается
в сокращении срока выполнения проекта
на сколько это возможно за счет вложения
суммы дополнительных средств, не
превышающей В. Время выполнения каждой
работы должно быть не меньше минимально
возможного времени
.
Необходимо определить время началаи окончаниякаждой работы и величину дополнительных
средств,
которые нужно выделить на ускорение
выполнения работы.

      1. Оптимизация
        проекта по стоимости

Под стоимостью
выполнения работы будем подразумевать
лишь прямые затраты. Пусть для каждой
работы имеются следующие данные:
— минимальная продолжительность (срочный
режим выполнения), которой соответствует
наибольшие затраты —и нормальная (наибольшая) продолжительность
—,
которой соответствует наименьшие
затраты —.
Предположим, что затраты на выполнение
отдельных работ находятся в обратной
зависимости от продолжительности их
выполнения. Коэффициентпоказывает, насколько увеличится
стоимость работы,
при уменьшении ее продолжительности
на единицу времени:

Его называют
коэффициентом
дополнительных затрат (КДЗ).

Рассмотрим две
постановки задачи оптимизации проекта
по стоимости при нефиксированной и
нефиксированной величине критического
пути.

1. Оптимизация
стоимости проекта при нефиксированной
величине критического пути. Пусть задан
сетевой график проекта и известны
продолжительность каждой работы и
стоимость ее выполнения в нормальном
и срочномрежиме работы. Если все работы выполняются
в нормальном режиме, то критический
срок будет наибольшим, а стоимость
выполнения проекта – наименьшей.
Необходимо сократить критический срок
до некоторого минимально возможного
значения при наименьшем возрастании
стоимости выполнения проекта.

  1. Минимизация
    стоимости проекта при фиксированной
    его продолжительности. Пусть задан
    сетевой график проекта. Известны
    продолжительности выполнения работ и
    их стоимость в срочном режиме
    .
    Для них определены критическое времяи стоимость выполнения проекта.
    Стоимость при этом является максимальной.
    Предполагается, что коэффициенты
    дополнительных затратдля каждой работы известны. Ставится
    задача минимизации стоимости проекта
    при фиксированном срокевыполнения проекта за счет увеличения
    времени выполнения отдельных работ.
    Критическое времяможет быть меньше заданного срокаили равно ему. Если,
    то оптимизация возможна только за счет
    резервов некритических работ, если,
    то за счет всех работ проекта. После
    оптимизации все работы будут критическими,
    так и как их продолжительности будут
    достигать наибольших возможных значений.
    Ни одно событие, ни одна работа не будут
    иметь резерва. Такой план можно назватьбезрезервным.
    Ранние и поздние сроки свершения событий
    здесь совпадают, а времена начала и
    окончания работ совпадают со сроками
    свершения событий.

      1. Оптимизация
        проекта по ресурсам

Задача оптимального
распределения ресурсов является одной
из важнейших задач планирования.
Предложений по проекту больше, чем
ресурсов. Необходима система приоритетов,
которая поможет выбрать проекты,
наилучшим образом содействующие целям
организации, в рамках имеющихся ресурсов.

Виды ограничений
на количество ресурсов:

Люди

Люди являются
наиболее очевидным ресурсом проекта.
Людские ресурсы обычно классифицируются
по их рабочему профилю – например,
программист, инженер-механик, сварщик,
контроллер, заведующий отделом сбыта,
инспектор. В редких случаях некоторые
умения взаимозаменяемы, но при этом,
как правило, теряется производительность.
Наличие многих квалификаций усложняет
составление календарного плана проекта.

Материалы

Задержка в выполнении
многих проектов часто объясняется
нехваткой материалов. Если известно,
что может возникнуть недостаток наличия
материалов это может сказаться на
проекте, они должны быть включены в
сетевой план проекта, и должен быть
составлен график. Например, доставка и
установка нефтяной буровой вышки в
Сибири должна произойти в очень короткий
срок – в течение одного летнего месяца.
Любая задержка в доставке будет означать
отставание в один год – дорогостоящая
задержка. Другим примером может быть
обновление покрытия и замена некоторых
конструкций моста Золотые ворота в
Сан-Франциско. Работа по проекту была
ограничена с 00 часов до 5.00 утра, и за
каждую минуту работы после 5 утра
налагался штраф в $1000. Составление
графика доставки и замены конструкций
в течение этих 5 часов было чрезвычайно
важным для управления проектом.
Планирование материалов важно и при
разработке продуктов, когда несвоевременное
поступление товара на рынок может
привести к потере доли на рынке.

Под оптимальным
распределением ресурсов понимается
такое размещение работ во времени,
которое при заданной интенсивности
потребления ресурсов обеспечило бы
выполнение всего комплекса работ в
минимальный срок. На практике получили
широкое применение эвристические приемы
распределения ресурсов. Их сущность
состоит в следующем:

  1. Для каждой работы
    определяется ее ранние и поздние сроки
    начала и окончания и полные резервы
    времени.

  2. Строится сетевой
    график в календарной шкале времени по
    ранним срокам начала и окончания работ.
    По эпюре ресурса выясняется интенсивность
    его потребления для каждого интервала
    времени. Если для каждого интервала
    интенсивность не превышает наличного
    количества ресурса, то распределение
    считается удовлетворительным. Если же
    существуют интервалы, для которых
    интенсивность превышает наличное
    количество ресурса, то график подлежит
    корректировке.

  3. Для корректировки
    работы нумеруются в порядке возрастания
    их полных резервов времени
    .
    При равных значениях— в порядке убывания их интенсивности.
    При равных же интенсивностях работы
    выбираются из интервала в произвольной
    последовательности. Начатые в предыдущих
    интервалах работы считаются
    первостепенными. Включение новых в
    порядке шкалы приоритетов происходит
    только в том случае, если для этого
    имеются ресурсы.

  4. Для ускорения
    корректировки выполнения работ
    устанавливаем монотонно возрастающую
    последовательность их ранних начал и
    окончаний путем проектирования на ось
    времени t.
    Пусть это будет последовательность
    ,
    где—
    крайняя левая проекция (очевидно,),—
    следующая запроекция,
    и т.д.,— крайняя правая проекция.

Шкала приоритетов
по возрастанию
или по убыванию интенсивности применяется
последовательно для каждого из промежутков,и промежуткасуммарная интенсивность потребления
ресурса не превышает наличного его
объема, то переходят к следующему
промежутку. Если же превышает, то
последующие работы сдвигаются вправо
на промежуток. Затем процесс начинается
сначала, пока не

проанализированы
все промежутки
,и т.д. и не зафиксированы новые начала
работ.

Постановка
задачи.

Пусть на промышленном
предприятии составлен сетевой график
выполнения учетно-плановых работ (рис.
5). На его дугах, исходя из трудоемкости
выполнения каждой работы, проставлены
их продолжительность и необходимое
число исполнителей. Известно, что в
распоряжении руководителей проектировочных
работ имеется 30 человек. Требуется
распределить трудовые ресурсы по
времени, т.е. определить сроки начала и
окончания работ так, чтобы с имеющимися
трудовыми ресурсами обследовать комплекс
работ в минимальный срок. Исследовать
возможности выполнения работ в срок,
равный критическому пути для графика.

Рис. 1.4

Таблица 1.1

1
– 2

1

10

1
– 3

5

20

2
– 3

3

10

2
– 4

2

8

3
– 4

6

19

3
– 5

5

11

4
– 5

0

0

4
– 6

5

18

5
– 6

3

16

Этап
1

Найдем
все полные пути и их продолжительности:

1
путь 1 – 2 – 4 – 6, его продолжительность
1 + 2 + 5 = 8

2
путь 1 – 2 – 4 – 5 – 6, его продолжительность
1 + 2 + 0 + 3 = 6

3
путь 1 – 2 – 3 – 4 – 6, его продолжительность
1 + 3 + 6 + 5 = 15

4
путь 1 – 2 – 3 – 4 – 5 – 6, его продолжительность
13

5
путь 1 – 2 – 3 – 5 – 6, его продолжительность
12

6
путь 1 – 3 – 4 – 6, его продолжительность
16

7
путь 1 – 3 – 4 – 5 – 6, его продолжительность
14

8
путь 1 – 3 – 5 – 6, его продолжительность
13

,

Этап
2

Для каждого события
определим ранний и поздний срок свершения
события. Ранний срок свершения события
– максимальный из путей, предшествующий
этому событию.

Для события 1 —
,
для события 2 —,
для события 3 —,
для события 4 —(1
+ 2, 1 + 3 + 6, 5 + 6), для события 5 —(1
+ 2 + 0, 1 + 3 + 5, 1 + 3 + 6 + 0, 5 + 6 + 0) = 11, для события
6 – 16.

Поздний срок
свершения события равен разности
критического пути и максимального из
путей, следующих за данным событием.

Для события 1 —
,
для события 2 —,
для события 3 —,
для события 4 —,
для события 5 —,
для события 6 —.

Резерв времени
события равен разности раннего и позднего
срока свершения события:

R(1)
= 0 – 0 = 0, R(2) = 2 – 1 =1, R(3) = 5 – 5 = 0, R(4) = 11 –
11 = 0, R(5) = 13-11= 2, R(6) = 16 – 16.

Этап
3

Определяем ранние
и поздние сроки начала и окончания
работ:

  1. ранний
    срок начала работ

,

,
,,,,,,,.

  1. ранний
    срок окончания работ

,

,,,

,

,

,

,

.

  1. поздний
    срок начала работ

,

,

,

,

,

,

,

,

.

  1. поздний
    срок окончания работ

,
,,,,,,,.

  1. полный
    резерв времени работ

,

,

,

,

,
,

,
,

.

Для
оптимизации проекта по ресурсам
составляем диаграммы по ранним срокам
начала и окончания работ (график Ганта)
(рис. 1.5). Проектируем на ось t
ранние
сроки начала и окончания работ. Получим
промежутки
(0;
1),
(1;
3),(3;
4),(4;
5),(5;
10),(10;
11),(11;
14),(14;
16).

Шаг
1.
Рассмотрим промежуток
(0;
1). Над ними расположены работы (1; 2) и
ресурсы (1; 3). Так как сумма ресурсов для
их выполнения 10+20=30 не превышает наличных
ресурсов в 30 человек, то оставляем их в
первоначальном положении.

Шаг
2.
Анализируется промежуток
(1;
3), над ними – работы (1; 3), (2; 3), (2; 4). Их
сумма 20+10+8=38 больше наличного ресурса
в 30 единиц. Устанавливаем порядок работ.
В первую очередь выполняются начатые
в промежутке,
т.е. (1; 3). Ее интенсивность.
Оставшиеся (2; 3) и (2; 4) упорядочим согласно
возрастанию их полных резервов времени.
Имеем:,.
Следовательно, в моментначинаем выполнять работу (2; 3). Так как,
то начало (2; 4) сдвигаем к моменту.

Шаг
3.
Сдвинув (2; 4) к моменту
,
замечаем, что в промежуткеинтенсивность потребленияпревышает наличный ресурс в 30 единиц.
Так как (1; 3) и (2; 3) начаты в предыдущих
промежутках, то (2; 4) сдвигаем до момента.

Шаг
4.
В промежутке
(4;
5) имеем.
Следовательно, после выполнения операций
четвертого шага корректировки получим
линейный график (рис. 1.6).

Шаг
5.
В промежутке
(5;
6) интенсивность потребления превышает
наличный ресурс.
Так как (2; 4) выполнялась в предыдущем
промежутке, то выполнению в начале
промежуткаподлежат работы (3; 4) и (3; 5). Их резервы
времени равны:,.
В моментследует начать работу (3; 4). Начало (3; 5)
сдвигаем к моменту.
Получим линейный график (рис. 1.7).

Шаг
6.
В промежутке (6; 11) линейного графика
(рис. 1.7) интенсивность потребления равна
наличному ресурсу. Времена начала этих
работ оставляем без изменения.

Шаг
7.
В промежутке (11, 14) интенсивность
потребления (18+16=34) превышает ресурс.
Так как
,,
то следует сделать сдвиг (5; 6) до момента.
Однако это приведет к удлинению общей
продолжительности реализации работ до
величины 16+3=19. Можно поступить иначе.
Работа (5; 6) имеет резерв времени 2 дня.
Увеличим ее продолжительность с 3 до 4
дней, сократив количество человек,
занятых ежедневно на этом участке, до
12 (3*16=4*12). В результате получим окончательный
линейный график (рис. 1.8). Здесь интенсивность
использования трудовых ресурсов
приведена в соответствие с ограничениями
на ресурсы без удлинения критического
пути.

Рис. 1.5

Рис. 1.6

Рис. 1.7

Рис. 1.8

Источник

2.2. Практическое занятие по структурному планированию

Целью занятия является получение навыков составления сетевых графиков, расчета раннего и позднего времени начала работ, нахождения критического пути.

Форма занятия – практическое занятие с использованием рабочей тетради.

Продолжительность – два академических часа.

2.2.1. Пример составления и расчета сетевого графика

Предположим, что мы составляем проект Внедрение бухгалтерской системы для небольшой бухгалтерии, содержащей порядка 10 рабочих мест.

Этап 1. Составление перечня работ

В результате анализа выделяем перечень работ по проекту и оцениваем их длительность в днях. Результаты заносим в табл.2.4.

Таблица
2.4.

№ Название работы Длительность
1 Начало проекта —
2 Выбор системы 15
3 Приобретение программного обеспечения 7
4 Составление проекта сети 7
5 Приобретение компьютеров и сетевого оборудования 15
6 Обучение администратора и программиста 30
7 Монтаж локальной сети 20
8 Установка ПО на компьютеры 5
9 Установка сетевого ПО, настройка сети 25
10 Ввод начальных данных в информационную базу 40
11 Обучение персонала 30
12 Передача в эксплуатацию 5
13 Конец проекта —

Этап 2. Определение взаимосвязей между работами

Для каждой работы из табл.2.4 требуется установить номера тех работ, до окончания которых она не может быть начата. Результат заносится в табл.2.5.

Таблица
2.5.

№ Название работы Предшественники
1 Начало проекта —
2 Выбор системы 1
3 Приобретение программного обеспечения 2
4 Составление проекта сети 2
5 Приобретение компьютеров и сетевого оборудования 2
6 Обучение администратора и программиста 4
7 Монтаж локальной сети 4; 5
8 Установка ПО на компьютеры 3; 5
9 Установка сетевого ПО, настройка сети 6; 7; 8
10 Ввод начальных данных в информационную базу 9
11 Обучение персонала 9
12 Передача в эксплуатацию 10; 11
13 Конец проекта —

Этап 3. Составление сетевого графика работ

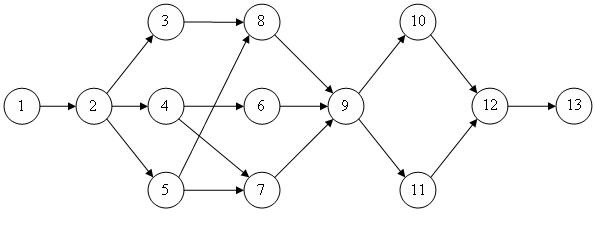
Каждая из работ табл.2.5 на сетевом графике обозначается кружком, в который заносится ее номер. Кружки соединяются стрелками. Стрелка соответствует одному из чисел столбца Предшественники и соединяет работу-предшественник с работой-последователем. Результат изображен на рис.2.9.

Сетевой график проекта внедрения бухгалтерской системы

Рис.
2.9.
 Сетевой график проекта внедрения бухгалтерской системы

Этап 4. Вычисление раннего времени начала работ

В соответствии со схемой, приведенной на рис.2.2 вычисляем раннее время начала работ с учетом их длительностей из табл.2.4 и связей, задаваемых сетевым графиком на рис.2.9. Вычисления начинаются с первой и заканчиваются последней работой проекта. Последовательность вычислений приведена в табл.2.6. Результат показывает, что длительность проекта равна 122 дня.

Таблица
2.6.

№ Раннее время начала Длитель-ность
1 — — — — 0
2 1 0 0 0+0 0
3 2 0 15 0+15 15
4 2 0 15 0+15 15
5 2 0 15 0+15 15
6 4 15 7 15+7 22
7

4

5

15

15

7

15

Max(15 + 7;

15 + 15)

 30
8

3

5

15

15

7

15

Max(15 + 7;

15 + 15)

 30
9

6

7

8

22

30

30

30

20

5

Max(22+30;

30+20;

30+5)

 52
10 9 52 25 52+25 77
11 9 52 25 52+25 77
12

10

11

77

77

40

30

Max(77+40;

77+30)

 117
13 12 117 5 117+5 122

Этап 5. Вычисление позднего времени начала работ

Используя длительности работ и сетевой график, вычисляем позднее время начала работ. Вычисления начинаются с последней работы проекта, ведутся в обратном порядке и заканчиваются первой работой. Результаты вычислений приведены в табл.2.7.

Таблица
2.7.

№ Позднее время начала
13 — — — — 122
12 13 122 5 122-5 117
11 12 117 30 117-30 87
10 12 117 40 117-40 77
9

10

11

77

87

 25

Min(77-25;

87-25)

 52
8 9 52 5 52-5 47
7 9 52 20 52-20 32
6 9 52 30 52-30 22
5

7

8

32

47

 15

Min(32-15;

47-15)

 17
4

6

7

22

32

 7

Min(22-7;

32-7)

 15
3 8 47 7 47-7 40
2

3

4

5

40

15

17

 15

Min(40-15;

15-15;

17-15

 0
1 2 0 0 0-0 0

Этап 6. Вычисление резерва времени работ

Резерв времени равен разнице между поздним и ранним временем начала работ. Занесем в табл.2.8 и значения и разность (резерв).

Таблица
2.8.

Работа № Раннее время начала Позднее время начала Резерв времени
1 0 0 0
2 0 0 0
3 15 40 25
4 15 15 0
5 15 17 2
6 22 22 0
7 30 32 2
8 30 47 17
9 52 52 0
10 77 77 0
11 77 87 10
12 117 122 5
13 122 122 0

Этап 7. Нахождение критического пути

Критический путь состоит из работ с нулевым резервом времени. В табл.2.9 они выделены заливкой. Обозначим на сетевом графике критический путь пунктирными стрелками. Результат приведен на pис.2.10.

Критический путь проекта внедрения информационной системы

Рис.
2.10.
Критический путь проекта внедрения информационной системы

2.2.2. Задания для самостоятельного выполнения

Задание 1

Вычислить критический путь по сетевому графику, изображенному на рис.2.9 со значениями длительностей работ, приведенными в табл.2.9.

Таблица
2.9.

1 2 3 4 5 6 7 8 9 10 11 12 13
1 — 60 25 15 30 20 15 70 30 90 20 5 —
2 — 30 15 20 25 30 45 45 25 60 40 7 —
3 — 44 22 17 34 28 23 64 26 78 32 9 —
4 — 24 17 18 26 19 31 69 33 82 15 3 —
5 — 36 24 19 25 12 18 55 24 80 22 4 —
6 — 57 32 24 18 28 21 59 24 35 27 6 —
7 — 29 18 14 37 16 44 38 29 51 22 8 —
8 — 37 20 17 18 21 16 40 27 28 30 7 —
9 — 18 19 31 30 35 29 38 21 43 19 4 —
10 — 21 27 14 34 22 35 30 27 12 40 6 —

Задание 2

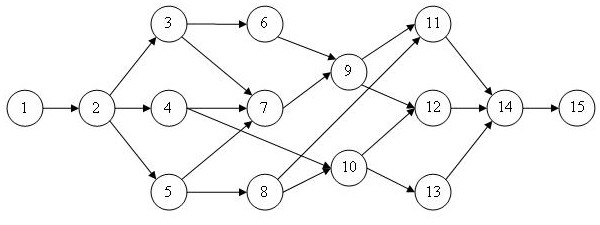
Последовательность работ проекта описывается сетевым графиком, изображенным на рис.2.11. Найти критический путь при условии, что длительности работ заданы одним из вариантов в табл.2.10.

Сетевой график для задания 2

Рис.
2.11.
 Сетевой график для задания 2

Таблица
2.10.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 — 4 7 8 6 4 6 5 3 7 5 4 3 2 —
2 — 7 10 8 9 7 5 6 5 3 4 3 5 5 —
3 — 3 6 4 7 5 4 5 4 6 3 6 7 4 —
4 — 2 2 3 2 4 4 5 4 3 3 4 5 7 —
5 — 7 6 5 4 4 5 6 7 5 5 8 6 3 —
6 — 5 7 6 7 8 9 8 9 9 7 6 6 5 —
7 — 4 4 5 6 6 5 4 5 5 7 6 8 5 —
8 — 7 5 4 3 3 4 5 4 4 2 3 2 2 —
9 — 2 3 4 5 7 3 5 6 4 6 8 7 4 —
10 — 4 7 3 2 7 5 4 7 2 4 7 10 6 —

Задание 3

Для проекта Ремонт квартиры выполнить следующие действия:

  1. самостоятельно составить перечень работ (не менее 15);
  2. самостоятельно оценить длительность этих работ;
  3. самостоятельно определить последовательность выполнения работ;
  4. построить сетевой график;
  5. выполнить расчет раннего и позднего времени начала работ, найти критический путь.
Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как исправить аутизм
  • Как найти пожарную часть
  • Как найти в айфоне стикеры избранные
  • Цель существования человека как найти
  • Физика как найти время в физике формулы

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии