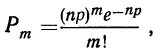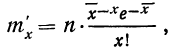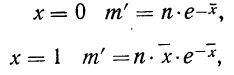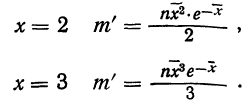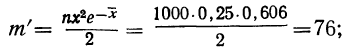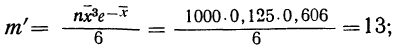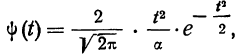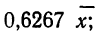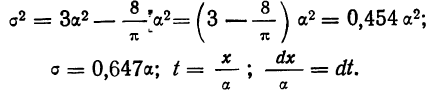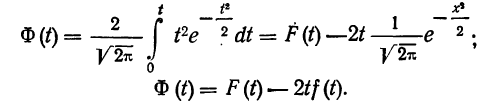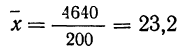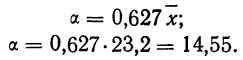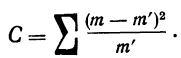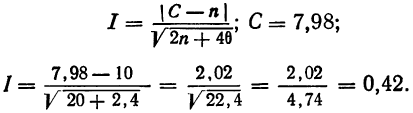ПРИНЦИПЫ РАЗДЕЛЕНИЯ ЗАТРАТ ДЛЯ ОПРЕДЕЛЕНИЯ СЕБЕСТОИМОСТИ
Затратами являются ресурсы, потребленные предприятием для производства и реализации продукции, работ, услуг. Это все отрицательные денежные потоки, связанные с операционной (основной) деятельностью компании.
Многие ошибочно под затратами и расходами понимают одно и то же. Отличие между ними в том, что расходы — это только часть затрат, понесенная предприятием в связи с получением доходов.
Если затраты не принесли компании дохода, они не включаются в расходы. Затрат у компании всегда будет больше, чем расходов.
Данный подход отражается в учете производственных затрат предприятия следующим образом:
Пока понесенные производственные затраты не принесли дохода, их отражают в бухгалтерском учете и отчетности в составе активов компании как затраты незавершенного производства (НЗП) или как готовую продукцию (на складе).
Все расходы компании за определенный период образуют полную себестоимость произведенной и реализованной продукции, которая отражается в Отчете о финансовых результатах как себестоимость продаж по строке 2120.
Определение (калькулирование) себестоимости каждого вида произведенной предприятием продукции (работ, услуг) является ключевой задачей управленческого учета любого предприятия, так как определение себестоимости продаж:
• позволяет рассчитать операционную прибыль компании за определенный период;
• требуется для оценки остатков незавершенного производства и готовой продукции (на складе);
• используется при формировании ценовой и ассортиментной политики предприятия;
• является базой для снижения и оптимизации затрат по каждому виду произведенной продукции и по предприятию в целом.
Система учета затрат и калькулирования себестоимости произведенной продукции индивидуальна для каждого предприятия, так как зависит от выбора объектов учета затрат (аналитических срезов), в соответствии с которыми затраты группируют для целей планирования (бюджетирования), учета, анализа и оптимизации.
Аналитические срезы учета затрат формируют по:
• местам возникновения затрат;
• носителям затрат.
К СВЕДЕНИЮ
Место возникновения затрат — это структурное подразделение предприятия, в котором происходит первоначальное потребление ресурсов (цех, участок, отдел и т. д.). Носители затрат — виды производимой продукции (работ, услуг).
ОСНОВНЫЕ ГРУППИРОВКИ ЗАТРАТ
Затраты являются самым сложным участком планирования, учета, анализа и оптимизации деятельности предприятия. Чтобы упростить эти процессы, затраты классифицируют на разные виды. Рассмотрим основные группировки затрат.
Прямые и косвенные затраты
Затраты группируют на прямые и косвенные в зависимости от способа их включения в себестоимость продукции (работ, услуг). На основе данной классификации формируют управленческий План счетов (синтетические счета, субсчета и аналитики).
Прямыми являются затраты, которые прямо связаны с производством и реализацией конкретного вида продукции (партии продукции), выполненными работами или оказанными услугами. К прямым затратам относятся:
• материальные затраты, то есть сырье и материалы, использованные при производстве продукции;
• затраты на производственный персонал при сдельной форме оплаты труда.
ОБРАТИТЕ ВНИМАНИЕ!
Если компания производит один вид продукции, все производственные затраты будут полностью считаться прямыми.
- являются затраты, которые нельзя прямо соотнести с определенным видом производимой продукции (работ, услуг). При калькулировании себестоимости продукции косвенные затраты сначала учитывают на отдельных счетах, затем собранные по итогам месяца затраты распределяют по видам произведенной продукции (работам, услугам) согласно принятой на предприятии методике.
Косвенные затраты всегда связаны одновременно с производством и реализацией нескольких видов продукции. Их либо невозможно прямо соотнести с конкретным видом продукции, либо это можно сделать, но нецелесообразно в связи с малыми величинами данных затрат и неэкономичностью отдельного их учета.
Примеры производственных косвенных затрат:
• вспомогательные материалы и комплектующие изделия;
• оплата труда производственного персонала (компенсационные и социальные выплаты);
• оплата труда вспомогательного производственного персонала (ремонтников, наладчиков и др.);
• расходы на ремонт и содержание общепроизводственного оборудования, производственных зданий и сооружений.
Затраты на продукт и затраты периода
Затратами на продукт признаются затраты, образующие его производственную себестоимость, поэтому их называют еще производственными.
Производственную себестоимость определяют, так как по ней в бухгалтерском балансе учитывается и отражается готовая продукция, которая не была реализована (то есть готовая продукция на складе и остатки незавершенного производства).
К затратам на продукт относят:
• сырье и основные материалы;
• полную оплату труда и страховые взносы персонала, занятого в производстве конкретных видов продукции;
• амортизацию зданий и оборудования, задействованных в производстве конкретных видов продукции;
• затраты на обслуживание и управление вспомогательных производств (отражают на счете 23 «Вспомогательные производства» бухгалтерского учета);
• общепроизводственные затраты на обслуживание и управление основного производства (отражают на счете 25 «Общепроизводственные расходы»).
Затратами на продукт являются все прямые затраты предприятия, а также часть косвенных затрат, к которым относятся расходы вспомогательных производств и общепроизводственные затраты.
Затратами периода признаются затраты, которые не относятся к конкретным видам продукта и зависят не от объемов производства, а от временного периода, поэтому их называют еще периодическими.
К затратам периода относятся:
• коммерческие затраты, учитываемые на счете 44 «Коммерческие расходы» бухгалтерского учета и связанные с реализацией и поставкой продукции (работ, услуг);
• управленческие затраты (счет 26 «Общехозяйственные расходы» бухгалтерского учета), то есть все затраты на административное управление предприятия в целом.
К затратам периода относятся только косвенные расходы, которые не включаются в производственную себестоимость продукции и не учитываются в стоимости готовой продукции на складе и остатках НЗП.
Группировка производственных и периодических затрат показана на рис. 1.
Основываясь на делении затрат на производственные и периодические, калькулирование производственной и полной себестоимости готовой продукции можно осуществлять по следующему алгоритму.
Согласно приведенному алгоритму коммерческие и управленческие затраты никогда не относятся на стоимость готовой продукции на складе и остатки незавершенного производства. Модель формирования производственной и полной себестоимости продукции (работ, услуг) по описанному алгоритму отражена на рис. 2.
Представленный алгоритм формирования себестоимости продукции отвечает требованиям Международных стандартов финансовой отчетности, однако он не единственно возможный с точки зрения отечественных стандартов РСБУ.
Так, по другому возможному варианту общехозяйственные (управленческие) расходы, учитываемые на счет 26, могут не сразу списываться на счет 90, а распределяться по видам продукции аналогично общепроизводственным затратам (например, пропорционально предусмотренному учетной политикой показателю или с помощью заранее определенных коэффициентов).
В этом случае производственная себестоимость будет делиться на два вида:
- сокращенную производственную себестоимость (без учета управленческих затрат);
- полную производственную себестоимость (с учетом управленческих затрат).
Постоянные и переменные затраты
В зависимости от того, как затраты зависят от объема производства и реализации продукции, то есть от деловой активности предприятия, они группируются на постоянные и переменные.
Переменные расходы имеют строгую зависимость от динамики изменения объема выпуска продукции. С ростом объемов производства переменные расходы увеличиваются. Когда объемы производства уменьшаются, эти расходы снижаются. Данная зависимость может быть строго пропорциональной (линейной) или нелинейной.
Переменные затраты делятся на:
• производственные (сырье и материалы, сдельная заработная плата производственного персонала и др.);
• непроизводственные (комиссионная оплата труда коммерческого персонала, затраты на транспортировку, логистику и др.).
Постоянные затраты не изменяются вместе с динамикой объемов производства, то есть остаются постоянными при любом уровне деловой активности предприятия. К ним можно отнести амортизационные отчисления зданий и сооружений, оплату труда административного персонала и др.
Среди постоянных затрат необходимо выделять условно-постоянные или полупостоянные затраты, которые возрастают при увеличении объемов производства продукции скачкообразно (ступенчато).
При достижении максимальной загрузки оборудования дальнейший рост производства продукции возможен, например, путем приобретения новых производственных фондов.
В связи с этим изменится амортизация основных средств. Однако данное увеличение произойдет не постепенно, а ступенчато, то есть только после ввода основных средств в эксплуатацию.
Необходимо также выделять смешанные затраты, которые одновременно относятся и к переменным, и к постоянным. Например, оплата труда производственного персонала: сдельная часть будет относиться к переменным затратам, а компенсационная и социальная части — к постоянным.
Группировки затрат на прямые и косвенные, переменные и постоянные имеют разные критерии и цели. Отождествление прямых затрат с переменными или постоянных с косвенными является существенной ошибкой. Например, лизинговые платежи за оборудование, используемое для производства определенного вида продукции, будут относиться к прямым производственным затратам и в то же время к постоянным расходам.
Деление затрат на прямые и косвенные необходимо в первую очередь для правильного калькулирования себестоимости производимой и реализуемой продукции, отражения ее в финансовой и управленческой отчетности.
Деление затрат на переменные и постоянные служит для проведения маржинального анализа и ранжирования различных сегментов бизнеса по уровню прибыльности.
МЕТОДЫ РАСПРЕДЕЛЕНИЯ КОСВЕННЫХ ЗАТРАТ
Определение (калькулирование) производственной себестоимости предполагает исчисление всей совокупности затрат на выпуск продукции одного вида. С этой целью прямые затраты соотносятся с конкретными видами продукции, а косвенные распределяются между ними согласно принятым на предприятии правилам.
Распределение косвенных расходов по видам продукции (носителям затрат) — процесс более сложный и менее точный, чем отнесение на себестоимость прямых затрат. Чем крупнее предприятие, тем сложнее корректно распределить косвенные затраты, так как с ростом бизнеса увеличивается перечень видов выпускаемой продукции (работ, услуг) и косвенных расходов.
Для повышения точности калькулирования себестоимости продукции необходимо более тщательно разделять затраты на прямые и косвенные, стремясь снизить перечень косвенных затрат. Так, коммерческие затраты являются косвенными. Однако если затраты были осуществлены для продвижения конкретных видов товаров, то эти расходы нужно признавать прямыми и прямо относить на себестоимость соответствующих товаров.
Косвенные затраты традиционно учитывают по местам их возникновения, то есть по структурным подразделениям предприятия, где они были понесены. Такой учет необходим не только для контроля затрат и калькулирования себестоимости, но и для оценки эффективности деятельности подразделений компании и оптимизации этих затрат.
При этом главной проблемой учета и распределения косвенных затрат административно-управленческих подразделений являются расходы на услуги, которые предоставляют подразделения друг другу в рамках самой компании (так называемые взаимные услуги).
ЭТО ВАЖНО
Если доля взаимных услуг в компании высокая, то при распределении косвенных затрат по объектам калькулирования расходы на эти услуги нужно учитывать путем применения специально рассчитанных коэффициентов или двухступенчатой процедуры распределения.
Практика калькулирования себестоимости продукции разнообразна, так как существуют различные методы распределения производственных, коммерческих и управленческих косвенных затрат по отдельным видам продукции.
Выбор конкретного способа распределения затрат в первую очередь зависит от:
- характера производственного процесса (моно- или многопродуктовое производство);
- специфики производственного учета и системы управления затратами на предприятии.
Для монопроизводственных предприятий наиболее подходящим способом является перенесение прямых затрат на себестоимость конкретного вида продукции путем прямого расчета или суммирования. Косвенные затраты распределяют в данном случае пропорционально выбранной базе.
В многопродуктовых (комплексных) производствах чаще всего применяют коэффициентный способ и способ пропорционального распределения косвенных затрат. В этом случае даже отдельные прямые расходы распределяются между видами продукции по принятым коэффициентам или пропорционально выбранной базе.
Если специфика производственного процесса позволяет принять один из производимых продуктов за основной, а остальные считать побочными, то используется способ исключения затрат. В этом случае стоимость затрат на побочные продукты по принятым в компании измерителям вычитается из величины общих прямых расходов.
В результате разница между общей суммой затрат и стоимостью побочной продукции считается себестоимостью основного вида продукта. Косвенные затраты при этом распределяют пропорционально выбранной базе.
При распределении косвенных затрат ключевым вопросом является выбор базы распределения. Для более корректного распределения целесообразно за базу принимать показатель, который больше учитывает специфику предприятия.
Так, для компаний с высоким уровнем материальных затрат лучшей базой распределения будут прямые затраты на сырье и материалы, для торговых предприятий — выручка от реализации соответствующих видов товаров.
Если у предприятия много направлений деятельности, то лучше всего применять специально рассчитанные коэффициенты.
ПРИМЕРЫ РАСПРЕДЕЛЕНИЯ ЗАТРАТ И КАЛЬКУЛИРОВАНИЯ СЕБЕСТОИМОСТИ ПРОДУКЦИИ
Одноступенчатое распределение затрат
Мебельное предприятие ООО «Мебельдрев» выпускает шесть видов продуктов. Всю продукцию производят на базе одного вида сырья в едином технологическом процессе комплексного производства.
Прямые материальные затраты (сырье и материалы) относятся непосредственно на себестоимость конкретного вида продукции в размере фактически израсходованных затрат и определяются путем их суммирования за отчетный период.
Помимо основного сырья в качестве материальных затрат используют вспомогательные материалы, которые собирают на отдельном счете и по итогам отчетного периода распределяют по видам продукции по принятым на предприятии коэффициентам.
Производственный персонал принимает участие в производстве всех видов продукции, поэтому затраты на оплату его труда, включая начисленные страховые взносы, учитывают на отдельном счете и по итогам отчетного периода распределяют по видам продукции пропорционально принятой базе распределения (прямым материальным затратам).
Производственное оборудование используется комплексно для производства всех видов продукции, поэтому затраты на его амортизацию по итогам отчетного периода также распределяют по видам продукции пропорционально принятой базе распределения (прямым материальным затратам).
Общепроизводственные расходы, являясь косвенными производственными затратами, собирают на отдельном счете учета и по итогам отчетного периода распределяют по видам продукции пропорционально базе распределения.
К общепроизводственным расходам предприятия относятся затраты на:
• электроэнергию и топливо;
• водоснабжение и тепловую энергию;
• проведение ремонтных работ основных производственных фондов;
• заработную плату и страховые взносы мастеров и начальников производственных участков и цехов;
• амортизацию транспортного оборудования;
• вывоз твердых бытовых отходов.
Общепроизводственные расходы относят на конкретный вид продукции пропорционально всем производственным затратам (основное и вспомогательное сырье и материалы, оплата труда и страховые взносы производственного персонала, амортизация основных производственных фондов).
Коммерческие и управленческие (общехозяйственные) расходы в течение отчетного периода собирают на отдельных счетах учета и по итогам отчетного периода распределяют по видам продукции пропорционально базе распределения (производственной себестоимости).
Правила распределения затрат, применяемые на предприятии «Мебельдрев», представлены в табл. 1.
Данные о фактических производственных прямых и косвенных затратах предприятия за отчетный период (месяц) представлены в табл. 2.
Учитывая методы распределения затрат (см. табл. 1), на основе данных табл. 2 рассчитаем производственную и полную себестоимость каждого вида продукции, выпущенной предприятием «Мебельдрев» в отчетном периоде (табл. 3).
Уточним расчет показателей табл. 3 на примере продукта 1.
1. Сырье и материалы (прямые материальные затраты). Так как применяемый на предприятии метод учета сырья и материалов — суммирование затрат по фактической их величине, то данные переносятся из табл. 2 (для продукта 1 — показатель 1.1 = 5 541 990 руб.).
2. Вспомогательные материалы (косвенные материальные затраты) = 4 880 010 руб. × 0,25 = 1 220 003 руб.
3. Оплата труда и страховые взносы производственного персонала = (5 541 990 руб. / 19 553 490 руб.) × 10 220 440 руб. = 2 896 750 руб.
4. Амортизация основных производственных фондов = (5 541 990 руб. / 19 553 490 руб.) × 2 880 180 руб. = 816 321 руб.
5. Общепроизводственные расходы (косвенные затраты) = (5 541 990 руб. + 1 220 003 руб. + 2 896 750 руб. + 816 321 руб.) / (19 553 490 руб. + 4 880 010 руб. + 10 220 440 руб. + 2 880 180 руб.) × 14 990 110 руб. = 4 183 457 руб.
6. Производственная себестоимость = 5 541 990 руб. + 1 220 003 руб. + 2 896 750 руб. + 816 321 руб. + 4 183 457 руб. = 14 658 520 руб.
7. Коммерческие расходы (косвенные затраты) = 14 658 520 руб. / 52 524 230 руб. × 2 880 450 руб. = 803 879 руб.
8. Управленческие (общехозяйственные) расходы (косвенные затраты) = 14 658 520 руб. / 52 524 230 руб. × 15 330 550 руб. = 4 278 467 руб.
9. Полная себестоимость = 14 658 520 руб. + 803 879 руб. + 4 278 467 руб. = 19 740 867 руб.
В результате расчетов определили производственную и полную себестоимость партии каждого вида продукции, выпущенной предприятием «Мебельдрев» за отчетный период, то есть совокупные затраты каждого вида продукции.
Чтобы определить себестоимость единицы изделия, то есть удельные затраты, необходимо учесть в расчетах объем (количество) произведенной предприятием продукции. Расчет производственной и полной себестоимости единицы продукции представлен в табл. 4.
В результате распределения затрат и калькулирования себестоимости рассчитана производственная и полная себестоимость единицы каждого вида продукции предприятия в отчетном периоде методом одноступенчатого распределения затрат.
Двухступенчатое распределение косвенных затрат
Рассмотрим пример распределения косвенных расходов в страховой компании «Стравита». Компания предоставляет услуги страхования по трем продуктам (договоры страхования А, Б и В) и состоит из пяти структурных подразделений (первые три отдела относятся к основным, два последних — к обслуживающим):
• коммерческий отдел реализации договоров страхования (КО);
• отдел страховых выплат (ОСВ);
• отдел перестрахования (ОП);
• информационно-аналитический отдел (ИАО);
• отдел обслуживания (ОО).
Первая ступень распределения косвенных расходов
Первая ступень распределения предполагает разделение всех косвенных затрат по структурным подразделениям компании и проводится в два этапа.
Этап 1. Постатейное и прямое распределение косвенных затрат по местам их возникновения. Расходы, которые можно идентифицировать с конкретным отделом, относят на соответствующие подразделения. Затраты, относящиеся ко всему предприятию, учитывают как общехозяйственные (управленческие) расходы.
Все косвенные затраты компании «Стравита», разделенные по местам их возникновения, представлены в табл. 5.
Этап 2. Распределение общехозяйственных (управленческих) затрат по структурным подразделениям пропорционально выбранным базам распределения:
• аренда офисных помещений — площадь офисных помещений;
• амортизация основных средств — остаточная стоимость оборудования;
• электроэнергия и отопление — площадь офисных помещений;
• заработная плата и страховые взносы управленческого персонала — численность персонала подразделений.
Данные по выбранным базам распределения представлены в табл. 6. Распределение общехозяйственных расходов между структурными подразделениями компании «Стравита» — в табл. 7.
Уточним расчет показателей табл. 7 на примере коммерческого отдела (КО):
Амортизация основных средств = 4020 тыс. руб. / 15 800 тыс. руб. × 4330 тыс. руб. = 1102 тыс. руб.
Аренда офисных помещений = 150 м2 / 550 м2 × 8500 тыс. руб. = 2318 тыс. руб.
Электроэнергия и отопление = 150 м2 / 550 м2 × 840 тыс. руб. = 229 тыс. руб.
Заработная плата управленческого персонала = 45 чел. / 125 чел. × 8420 тыс. руб. = 3031 тыс. руб.
Страховые взносы управленческого персонала = 45 чел. / 125 чел. × 2526 тыс. руб. = 909 тыс. руб.
В результате на первой ступени были получены данные о сумме всех косвенных затрат за отчетный период в разрезе каждого структурного подразделения компании «Стравита».
Вторая ступень распределения косвенных расходов
Вторая ступень распределения предполагает определение ставок распределения косвенных затрат на конкретные виды продуктов (услуг), закрепленных за основными подразделениями компании, и проводится в два этапа.
Этап 1. Перераспределение всех косвенных расходов, приходящихся на обслуживающие подразделения компании, на основные ее отделы пропорционально следующим базам:
• затраты информационно-аналитического отдела — по времени предоставления услуг другим подразделениям (ч);
• затраты обслуживающего отдела — по количеству заявок на обслуживание (шт.).
Данные по выбранным базам распределения представлены в табл. 8. Распределение расходов обслуживающих подразделений страховой компании между ее основными подразделениями — в табл. 9.
Уточним расчет показателей табл. 9 на примере коммерческого отдела (КО):
1. Общие затраты подразделений = 4158 тыс. руб. + 7590 тыс. руб. = 11 748 тыс. руб.
2. Перераспределение затрат информационно-аналитического отдела (ИАО) = 50 ч / (140 ч – 10 ч) × 5769 тыс. руб. = 2219 тыс. руб.
3. Перераспределение затрат обслуживающего отдела (ОО) = 25 шт. / (75 шт. – 5 шт.) × 4258 тыс. руб. = 1521 тыс. руб.
4. Общие затраты подразделений после перераспределения = 11 748 тыс. руб. + 2219 тыс. руб. + 1521 тыс. руб. = 15 487 тыс. руб.
Рассмотренный способ перераспределения расходов обслуживающих подразделений, называемый прямым методом, — это один из возможных вариантов. Существуют и другие методы (например, пошаговый или метод учета взаимных услуг).
Достоинства прямого метода:
• простота;
• минимально необходимый набор данных (снижает трудозатраты на его осуществление).
Несмотря на эти достоинства прямого метода другие методы дают более точные результаты, так как учитывают фактор оказания взаимных услуг подразделений. Правда, они требуют большего количества данных, что усложняет систему управленческого учета компании.
В результате перераспределения все косвенные затраты компании «Стравита» за отчетный период были распределены на три основных подразделения, реализующих продукты (услуги) организации (табл. 10).
Этап 2. Расчет ставки распределения косвенных расходов на страховые продукты, закрепленные за основными подразделениями, и полной их себестоимости.
Для определения ставки распределения косвенных расходов в качестве базы распределения был выбран показатель количества отработанных часов в разрезе основных подразделений компании.
Расчет ставок распределения и полной себестоимости страховых продуктов представлен в табл. 11.
Уточним расчет показателей табл. 11 на примере коммерческого отдела (КО):
1. Количество отработанных часов (23 раб. дня) = численность персонала (табл. 6) × количество рабочих дней в отчетном периоде × 8 ч = 45 чел. × 23 раб. дня × 8 ч = 8280 ч.
2. Ставка распределения косвенных затрат на 1 ч труда = сумма косвенных расходов подразделения (табл. 10) / количество отработанных часов × 1000 = 15 487 тыс. руб. / 8280 ч × 1000 = 1870 руб.
3. Фактические трудозатраты по видам страховых продуктов — по данным управленческого учета за отчетный период.
4. Себестоимость договора страхования А = ставка распределения косвенных затрат на 1 ч труда × фактические трудозатраты по договору страхования А = 1870 руб. × 0,75 ч = 1403 руб.
Полная себестоимость страховых продуктов составит:
• договор страхования А: 1403 руб. + 570 руб. + 816 руб. = 2789 руб.;
• договор страхования Б: 281 руб. + 1140 руб. + 1749 руб. = 3170 руб.;
• договор страхования В: 935 руб. + 1710 руб. + 1166 руб. = 3812 руб.
Как видим, расчет полной себестоимости продукции (работ, услуг) зависит от специфики бизнеса. В рассмотренном примере у страховой компании нет прямых затрат, все затраты являются косвенными и требуют распределения, по итогам которого формируется полная себестоимость продуктов.
ЗАКЛЮЧЕНИЕ
Распределение косвенных затрат по видам продукции — более сложный и менее точный процесс, чем отнесение на себестоимость прямых затрат. Чем крупнее компания, тем сложнее корректно распределить косвенные расходы.
Чтобы повысить точность калькулирования себестоимости продукции (работ, услуг), необходимо:
• более тщательно разделять затраты на прямые и косвенные путем снижения перечня косвенных затрат;
• построить системы бухгалтерского (управленческого) учета (счетов, субсчетов и аналитик), учитывающие понесенные затраты в различных срезах, включая взаимные услуги структурных подразделений;
• правильно выбрать базу распределения затрат (за базу принимается показатель, который больше учитывает специфику бизнеса).
Повышение точности распределения косвенных затрат и калькулирования себестоимости продукции усложняет учетный процесс и удорожает его. В связи с этим каждому предприятию необходимо найти свой оптимальный баланс между точностью и стоимостью затрат на к
Статья опубликована в журнале «Планово-экономический отдел» № 5, 2022.
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
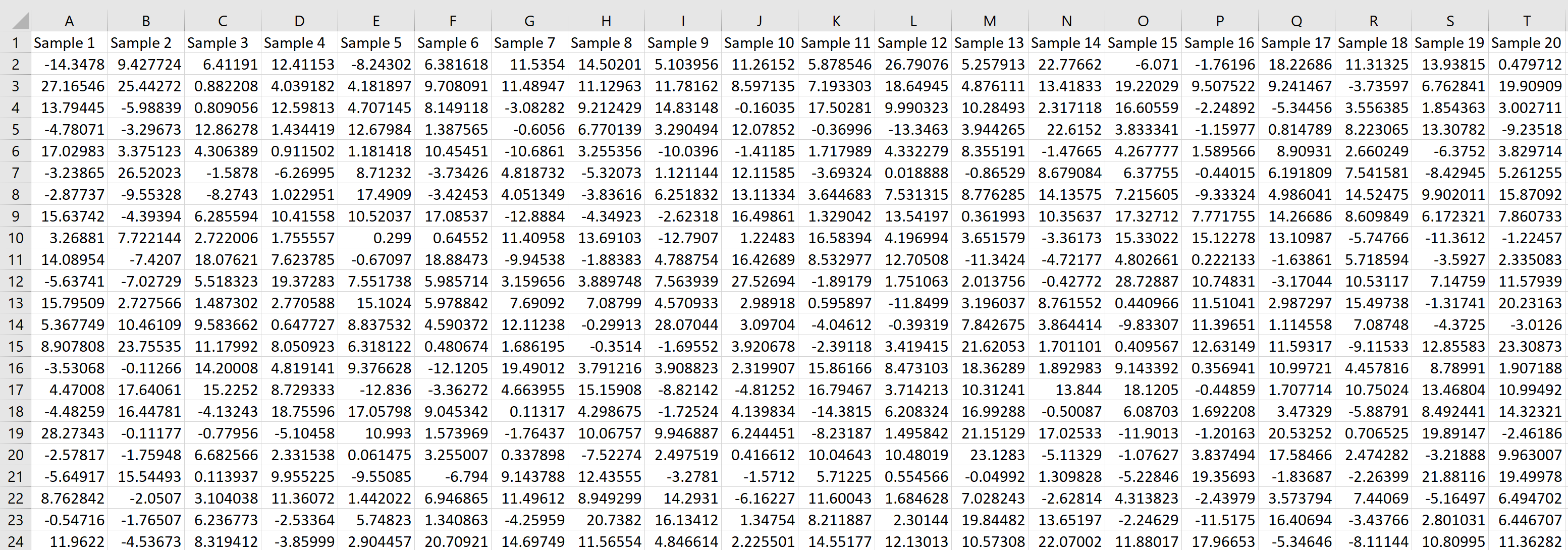
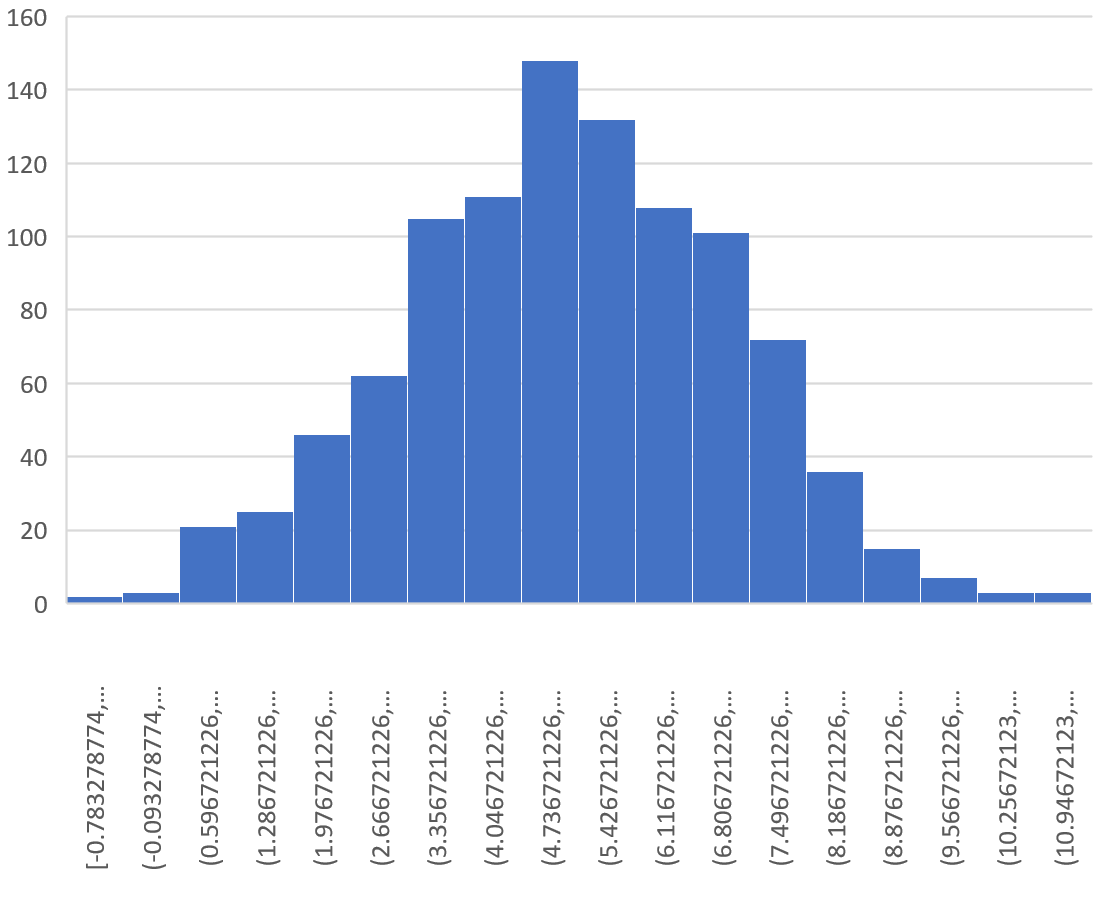
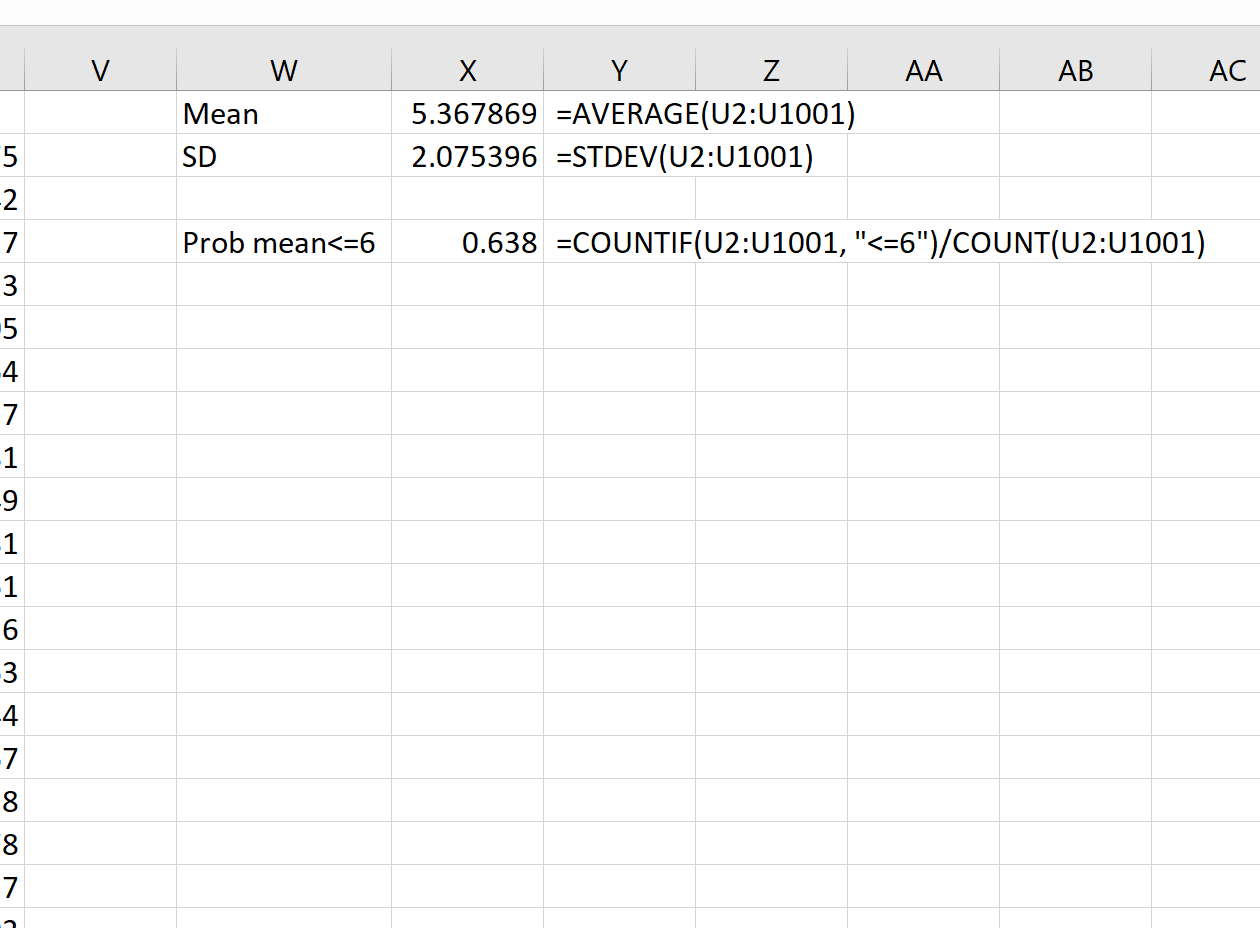
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях:
Предприятие, производящее ту или иную продукцию, вкладывает в это определенные средства. Важным понятием в образовании прибыли и рентабельности деятельности предприятия является себестоимость продукции. Средства, которые вкладываются в общую организацию производства, управление им, обслуживание и т.п., составляют значительную часть формируемой себестоимости.
Рассмотрим, что входит в состав общехозяйственных расходов (ОПР), каких разновидностей они могут быть, как производить их учет, на основе чего происходит списание. Основные нюансы, касающиеся общехозяйственных расходов на производстве, проанализируем в этой статье.
Общепроизводственные расходы в Плане счетов бухгалтерского учета финансово-хозяйственной деятельности организаций.
Что такое общепроизводственные расходы
Производство продукции предусматривает прямые траты (на сырье, оборудование, оплату наемного труда и т.п.), а также косвенные расходы. Помимо затрат непосредственно на изготовление продукции, средства нужно потратить на саму организацию этого процесса, им нужно непрерывно управлять, регулировать его, причем на всех производственных уровнях (руководство бригадой, цехом, отделением, участком, линией и т.п.).
Средства, затрачиваемые на организацию процесса производства и управление им во всех структурных подразделениях организации, считают общепроизводственными расходами. Ранее этот вид трат носил наименование «цеховые расходы».
ВАЖНАЯ ИНФОРМАЦИЯ! Национальная система бухучета в современной ситуации постепенно приводится к международным рыночным стандартам. С этим связан и пересмотр механизмов формирования ОПР в отечественном бухгалтерском учете. В данной статье мы рассматриваем только актуальные на сегодня положения.
Состав общепроизводственных расходов
Расходы, которые Правила бухгалтерского учета в п. 15 относят к общепроизводственным, включают в себя такие траты, входящие в конечном итоге в себестоимость продукции, как:
- Средства на управление производством:
- зарплата, премии, матпомощь и другие выплаты руководителям структурных подразделений;
- медицинская страховка управленческого аппарата;
- средства, выделяемые на мероприятия социального характера, которые осуществляются для руководства;
- командировочные для производственного и руководящего персонала;
- оплата проводимых для сотрудников тренингов, семинаров и т.п.;
- разные траты, такие как закупка канцелярских принадлежностей, выписывание методической литературы, оплата почтовых услуг, интернета и др.
- Расходы на основные средства и необоротные активы (их использование и/или содержание):
- непосредственные затраты на эксплуатацию активов (стоимость вспомогательных средств типа смазки, оплата труда вспомогательных рабочих, затраты на топливо, электричество и другие виды энергии для производства, коммунальные услуги и другие траты на помещение);
- арендная плата, если необоротные активы взяты в лизинг;
- затраты на охранные услуги – сторожевую и противопожарную безопасность (зарплата и страховка собственного персонала или траты на сторонних наемных специалистов);
- затраты на восстановление необоротных активов (ремонт зданий, оборудования, транспорта, в том числе и суммы, затраченные на запчасти и материалы и на сами услуги);
- траты на ремонт арендуемых активов (по договоренности с собственником).
- Амортизация общепроизводственных основных фондов и нематериальных активов (по разным структурным подразделениям).
- Обслуживающие затраты:
- зарплата персоналу, обслуживающему производственный процесс;
- социальные и иные выплаты;
- средства, затраченные на контроль над процессом производства, его качеством.
- Прогрессивные расходы – затраты на модернизацию и улучшение процесса производства:
- оплата труда соответствующего персонала (непосредственно занятого разработками, модернизацией, повышением эффективности и т.п.);
- затраты на опытные образцы, модели, пробы, испытания и др.;
- оплата консультаций, экспертиз, сторонних исследований и др. подобных процедур;
- иные траты, целью которых является улучшение производства.
- Затраты на охрану труда работников:
- деньги на сигнализацию;
- средства для устройства и поддержания в работоспособном состоянии защитных конструкций, ограждений, люков и т.п.;
- содержание вспомогательного оборудования, если таковое предусмотрено трудовым договором – раздевалок, шкафчиков для хранения личных вещей и одежды, душевых, прачечных, сушилок, дезинфекционной комнаты и т.п.;
- финансы на спецодежду, обувь и средства индивидуальной и групповой защиты;
- покупка лечебного питания или средств для профилактики заболеваний (если профессия предусматривает их выдачу);
- затраты на медосмотры персонала;
- другие расходы на охрану труда.
- Расходы на сбрежение окружающей среды:
- затраты на очистные сооружения;
- средства на утилизацию опасных отходов;
- другие природоохранные траты.
- Обязательные государственные платежи:
- налоги (на землю, на транспорт, коммунальный);
- сборы (за загрязнение среды, использование природных ресурсов).
- Прочие ОПР:
- затраты на перемещение грузов внутри производства;
- недостачи, потери, убыль, выясненные в результате инвентаризации;
- оплата простоев;
- другие траты, которые нельзя внести в иные категории, кроме ОПР.
Виды общепроизводственных расходов
Общепроизводственные затраты можно разделить на:
- переменные – те траты, которые могут изменяться в зависимости от динамики объемов производства, экономии ресурсов, модернизационных технологий и т.п.;
- постоянные – те, на которые не влияет динамика производства (в основном это затраты на бухгалтерию и управление).
ОБРАТИТЕ ВНИМАНИЕ! Это условное деление, и в некоторых случаях расходы могут переходить из одной группы в другую. Предприятие вправе самостоятельно определять перечень тех и других затрат, фиксируя это в учетной политике.
Учет общепроизводственных расходов
Учитывать ОПР нужно отдельно по каждому структурному подразделению. Для этого необходимо сначала осуществить распределение.
Распределение ОПР
Для корректного учета нужно четко представлять, какая сумма приходится на каждый вид продукции, а также работ или услуг. Для этого необходимо:
- отделить списываемую на себестоимость сумму ОПР от нераспределенной;
- разделить постоянные и переменные ОПР между всеми объектами учета.
Для распределения постоянных ОПР нужно выполнить следующие процедуры:
- выбрать единицу измерения – базу распределения;
- установить норму для обычной деятельности предприятия (обычно планируется на несколько лет);
- исходя из запланированной нормы, вычислить плановое количество ОПР;
- разделить это количество на выбранную единицу (так получится ожидаемая сумма ОПР при нормальной работе производства).
Нормативное значение постоянных ОПР на выбранную базовую единицу рассчитывают по такой формуле:
NОПРconst = ОПРнорм. / Бнорм.
где:
- NОПРconst – норма постоянных общехозяйственных расходов;
- ОПРнорм. – показатель ОПР при нормальных мощностях;
- Бнорм. – показатель распределительной базы при нормальных мощностях.
Далее необходимо сравнить фактический показатель с установленным нормативом. Для расчета общей суммы фактических распределенных ОПР удобно применить следующую формулу:
∑ОПРconst = NОПРconst х Бфакт.
где:
- ∑ОПРconst – сумма распределенных постоянных общепроизводственных расходов;
- Бфакт. – база распределения постоянных ОПР при фактических мощностях.
ОБРАТИТЕ ВНИМАНИЕ! Если сложить распределенные и нераспределенные постоянные ОПР, в сумме должна получиться их фактическая величина. Если получилось меньше рассчитанной нормы, в себестоимость закладывают фактический показатель, а не вычисленный норматив. Если расчет превысил фактические показатели, то в себестоимость войдет рассчитанная норма, то есть только часть постоянных ОПР.
Результат распределения отражается в специальной ведомости.
Коэффициент распределения
Он необходим для того, чтобы корректно рассчитать стоимость выпускаемой продукции. Для него нужно знать сумму косвенных расходов и выбранного показателя базы распределения. Вычисляется по такой формуле:
Краспр. = (∑ОПР / Б) х 100%
где:
- Краспр. – коэффициент распределения;
- ∑ОПР – сумма косвенных расходов;
- Б – показатель выбранной базы.
Так, если ОПР составляют 100 000 руб., а в качестве базы выбрана зарплата, которая в данном случае равна 10 200 руб., то коэффициент распределения будет 100 000 / 10 200 х 100 = 98%. Такой показатель значит, что при формировании цены на готовую продукцию нужно учитывать, что зарплата рабочих, занятых изготовлением каждой единицы, практически равна себестоимости самого изделия.
Пример
Во время отчетного периода мебельный цех выпускал тумбочки и комоды. Затраты на выпуск включают в себя:
- расходы на материал – 25 500 руб. (15 000 руб. на комоды и 10 500 руб. на табуретки);
- вознаграждение за труд работникам цеха – 12 000 руб. (по 6 тыс. руб. за изготовление каждого вида продукции);
- другие прямые расходы – 16 200 руб. (9 200 руб. на комоды и 7 000 руб. на табуретки);
- ОПР, подлежащие распределению – 80 000 руб.
Сумма составляет 133 700 руб.
Предприятие само решает, по какой именно базе распределить эти средства. Если выбраны материальные затраты, норматив составит 133 700 / 25 500 = 5,2. Если же выбрать базой траты на оплату труда, норматив будет 133 700 / 12 000 = 11,1.
Чтобы рассчитать сумму ОПР, включаемую в себестоимость каждого вида продукции, можно действовать двумя способами в зависимости от выбранной базы. ОПР в составе себестоимости вычисляется умножением вычисленного норматива на фактическую величину базы.
Если учитывать материальные затраты, то доля ОПР в себестоимости 5,2 х 15 000 = 78 000 — по комодам и 5,2 х 10 500 = 54 600 — по табуреткам. Соответственно, производственная себестоимость составит сумму этих величин с зарплатой и прочими прямыми расходами: по комодам — 78 000 + 9200 + 6 000 = 93 200 руб., по табуреткам — 54 600 + 7000 + 6000 = 67 600 руб.
Если за базу принять расходы на оплату труда, вычислять придется так же, но с другими показателями. ОПР в себестоимости комодов будет составлять 11,1 х 6 000 = 66 600 руб., как и табуреток. Производственная себестоимость – сумма материальных расходов, вычисленной плановой величины и прочих прямых расходов – для комодов будет 66 600 + 15 000 + 9 200 = 90 800 руб., а для табуреток 66 600 + 10 500 + 7 000 = 84 100 руб.
Как видим, себестоимость изделий может значительно отличаться в зависимости от установленной базы распределения ОПР.
Как правильно выбрать базу распределения
Поскольку от корректности выбора показателя базовой единицы в конечном итоге зависит себестоимость, нужно подходить к этому вопросу взвешенно. Если базу назначить неправильно, это может исказить суммы ОПР по отдельным отраслям деятельности или видам изделий. На выбор базы могут оказывать влияние следующие факторы:
- отражение связи между причинами накладных расходов и самими расходами;
- динамика базовых единиц, которая напрямую изменяет сумму накладных расходов.
Такой базой могут служить, в зависимости от особенностей отрасли:
- количество выпускаемой продукции (в штуках, килограммах, метрах, литрах и т.п.);
- прямые расходы на производство;
- материальные затраты;
- машино-часы;
- человеко-часы;
- объем производства в показателях стоимости;
- расходы на эксплуатацию оборудования (если есть такая калькуляционная статья) и др.
Амортизационные отчисления на средства ОПР
Обычно вычисляют годовую амортизацию, хотя и начисляют ее ежемесячно: нужно определить сумму расходов, потраченных на восстановление всех основных средств производства и управленческого аппарата. Для ее вычисления правомерно применение следующей формулы:
∑А = (∑ПС х NА ) / 100
где:
- ∑А – сумма амортизации;
- ∑ПС – первоначальная стоимость активов;
- NА – норма по амортизации.
Бухгалтерский учет и списание ОПР
Общепроизводственные расходы отражают на счете 25 «ОПР», по кредиту в зависимости от конкретного вида расходов. Когда истекает расчетный месяц, остаток на этом счете списывается по дебету:
- 20 «Основное производство»;
- 23 «Вспомогательные производства»;
- 29 «Обслуживающие производства и хозяйства».
Проводки при этом будут следующими:
- дебет 25, кредит 10 – списание стоимости материалов и запчастей для обслуживания и ремонта;
- дебет 25, кредит 02, 05 – начисление амортизации по нематериальным активам и ОС;
- дебет 25, кредит 70 – начисление заработной платы общепроизводственным работникам;
- дебет 25, кредит 69 – отчисления во внебюджетные фонды;
- дебет 25, кредит 60, 76 – списание расходов на содержание помещений;
- дебет 20, кредит 25 – списание ОПР на деятельность основного производства;
- дебет 23, кредит 25 – списание ОПР на деятельность вспомогательных производств;
- дебет 29, кредит 25 – списание ОПР на деятельность обслуживающего производства.
Как отразить в учете распределение общепроизводственных расходов между отдельными видами продукции?
Обязанности бухгалтера касательно общепроизводственных расходов
Производя бухучет по ОПР, бухгалтерия должна выполнять такие операции:
- вовремя корректно учитывать косвенные расходы;
- правильно отражать их в учетных документах;
- включать сумму общепроизводственных расходов в фактическую себестоимость единицы продукции;
- контролировать косвенные затраты – способствовать эффективному и бережному использованию материалов, энергии, других ресурсов;
- анализировать состав и уровень ОПР в каждом расчетном периоде;
- разрабатывать планы и рекомендации по уменьшению ОПР;
- составлять сметы на обслуживание управленческого аппарата и производственного оборудования;
- следить за соблюдением этих смет.
В отчетном периоде заработная плата работников производственного цеха составила 120 000 рублей, отчисления в виде страховых взносов — 37 500 рублей, затраты на электроэнергию и другие коммунальные платежи — 190 000 рублей, амортизация производственного здания — 33 500 рублей. Какие проводки сформировать в бухучете по результатам отчетного периода?
Посмотреть ответ
Налоговый учет общепроизводственных расходов
Налоговый учет ОПР зависит от системы налогообложения, применяемой на производстве:
- Общая налоговая система. Бизнесмен платит обычный налог на прибыль в размере 20%, а вычисляя прибыль, нужно из доходов вычесть расходы, в которые входят и общепроизводственные.
- «Упрощенка». Предпринимателям- «упрощенцам» нужно учитывать ОПР, если они платят налог на прибыль. Если при УСН платится налог на доход, то, естественно, общепроизводственные траты в налоговую базу не войдут.
Налоговые особенности учета общепроизводственных расходов.
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
- число попаданий при п выстрелах, если известна вероятность попадания при 1 выстреле. Число попаданий может быть 0, 1, 2….. n;
- число появлений герба при n бросаниях монеты.
Примеры непрерывных случайных переменных:
- ошибка измерения;
- дальность полета снаряда.
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
Закон распределения имеет чаще всего табличную -форму изложения. В этом случае перечисляются все возможные значения случайной переменной и соответствующие им вероятности:
Такая таблица называется также рядом распределения случайной переменной.
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х<х, зависит от текущей переменной х и является функцией от х. Эта функция носит название функции распределения случайной переменной X.
F(x) = P(X
Функция распределения является одной из форм выражения закона распределения. Она является универсальной характеристикой случайной переменной и может существовать для прерывных и непрерывных случайных переменных.
Функция распределения F(x) называется также интегральной функцией распределения, или интегральным законом распределения.
Основные свойства функции распределения могут быть сформулированы так:
- F(x) всегда неотрицательная функция, т. е.
- Так как вероятность не может быть больше единицы, то
- Ввиду того что F(x) является неубывающей функцией, то при
- Предельное значение функции распределения при х=
равно нулю, а при х=
равно единице.
Если случайная переменная X дискретна и задана рядом распределения, то для нахождения F(x) для каждого х необходимо найти сумму вероятностей значений X, которые лежат до точки х.
Графическое изображение функции распределения представляет собой некоторую неубывающую кривую, значения которой начинаются с 0 и доходят до 1.
В случае дискретной случайной переменной величины вероятность F(x) увеличивается скачками всякий раз, когда х при своем изменении проходит через одно из возможных значений 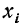
В случае непрерывной случайной переменной величины функция F(x) при графическом изображении дает плавную, монотонно возрастающую кривую следующего вида (см. график 3).
Обычно функция распределения непрерывной случайной переменной представляет собой функцию, непрерывную во всех точках. Эта функция является также дифференцируемой функцией. График функции распределения такой случайной переменной является плавной кривой и имеет касательную в любой ее точке.
Плотность распределения
Если для непрерывной случайной переменной X с функцией распределения F(x) вычислять вероятность попадания ее на участок от х до х+ 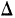
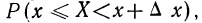
Если величину 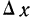
т. е. производной от функции распределения, которая характеризует плотность, с которой распределяются значения случайной переменной в данной точке. Эта функция называется плотностью распределения и часто обозначается f(x). Ее называют также дифференциальной функцией распределения, или дифференциальным законом распределения.
Таким образом, функция плотности распределения f(x) является производной интегральной функции распределения F(x).
Вероятность того, что случайная переменная X примет значение, лежащее в границах от а до 6, равна определенному интегралу в тех же пределах от плотности вероятности, или:
Кривая, изображающая плотность распределения случайной переменной, называется кривой распределения (дифференциальной).
Построим кривую некоторой заданной функции плотности вероятности и найдем участок, ограниченный абсциссами а и b. Площадь, ограниченная соответствующими ординатами кривой распределения самой кривой и осью абсцисс, и отобразит вероятность того, что случайная переменная будет находиться в данных пределах (см. график 4).
Плотность распределения является одной из форм закона распределения, но существует только для непрерывных случайных величин.
Основные свойства плотности распределения могут быть сформулированы так:
1. Плотность распределения есть функция, не могущая принимать отрицательных значений, т. е.
Отсюда в геометрическом изображении плотности распределения (в кривой распределения) не может быть точек, лежащих ниже оси абсцисс.
2.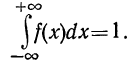
Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона и нормальное распределение.
Биномиальное распределение
Если производится n независимых испытаний, в каждом из которых вероятность появления данного события А есть величина постоянная, равная р, и, следовательно, вероятность непоявления события А также постоянна и равна q=1—р, то число появлений события А во всех n испытаниях представляет собой случайную переменную. Вероятность того, что событие А появится в n испытаниях m раз, равна:
т. е. m+1, члену разложения бинома 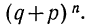
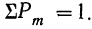
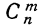
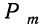
Ввиду того что вероятности 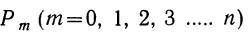
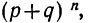
График биномиального распределения, на котором по оси абсцисс откладываются числа наступлений события, а по оси ординат — вероятности этих чисел, представляет собой ломаную линию. Форма графика зависит от значений р, q и n.
Если р и q одинаковы, то график распределения симметричен. Если же р и q неодинаковы, то график распределения будет скошенным.
Одна из частот на графике имеет максимальное значение. Это наиболее вероятная частота. Ее значение можно определить приближенно, аналитически как произведение nр.
Найдем вероятности числа наступления события А при 20 испытаниях при p = 0,1 и р = 0,4 и построим график их распределений (см. график 5). Найдем вероятности частот при n = 20 для p = 0,1 и р=0,4.
График показывает, что приближение р к 0,5 вносит в распределение большую симметрию. Оказывается также, что при увеличении n распределение становится симметричным и для
Биномиальное распределение имеет широкое распространение в практической деятельности людей. Например, продолжительное наблюдение за качеством выпускаемой заводом продукции показало, что p-я часть ее является браком. Иначе говоря, мы выражаем через р вероятность для любого изделия оказаться бракованным. Биномиальное распределение показывает вероятность того, что в партии, содержащей n изделий, окажется m бракованных, где m = 0, 1, 2, 3 … n.
Предположим, имеется 100 изделий из партии изделий, в ко торой доля брака равна 0,05. Вероятность того, что из этих из делий окажется 10 бракованных, равна:
Закон биномиального распределения называется также схемой Бернулли. .
Нормальное распределение
Расчет вероятностей по формуле биномиального распределения при больших n очень громоздок. При этом значении m прерывны, и нет возможности аналитически отыскать их сумму в некоторых границах. Лаплас нашел закон распределения, являющийся предельным законом при неограниченном возрастании числа испытаний n и называемый законом нормального распределения.
Плотность вероятности нормального распределения выражается при этом формулой:
где t представляет собой нормированное отклонение частоты т от наиболее вероятной частоты nр, т. е. 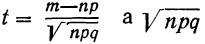
Максимальная ордината кривой соответствует точке m=nр, т. е. математическому ожиданию случайной переменной m; величина этой ординаты равна 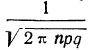
Для практического нахождения вероятностей используют таблицу значений f(t).
Эмпирические и теоретические распределения
В примерах распределений, приведенных в разделе I, мы пользовались данными, почерпнутыми из наблюдений.
Поэтому всякий наблюденный ряд распределения назовем эмпирическим, а график, изображающий распределение
частот этого ряда, — эмпирической кривой распределения. Эмпирические кривые распределения могут быть представлены полигоном и гистограммой. При этом изображение в виде полигона применяется для рядов с прерывными значениями признака, а гистограмма— для рядов с непрерывными значениями признака.
Наблюдая многочисленные ряды распределения, математики стремятся описать эти распределения путем анализа образования величины признака, пытаются построить теоретическое распределение, исходя из данных об эмпирическом распределении.
Мы уже видели на примере распределения случайной переменной, что распределение ее задается законом распределения. Закон распределения, заданный в виде функции распределения, позволяет математически описать ряды распределения некоторых совокупностей.
Теоретическим законом распределения многих совокупностей, наблюдаемых на практике, является нормальное распределение. Иначе говоря, многие эмпирические подчинены закону нормального распределения, функция плотности вероятности которого приведена в предыдущем параграфе.
Чтобы эту формулу применять для нахождения теоретических данных по некоторому эмпирическому ряду, необходимо вероятностные характеристики заменить данными эмпирического ряда. При этой замене величина стандартизованного отклонения t будет представлять собой 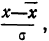
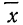
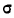
Следовательно, нормальное распределение ряда распределения зависит от величин средней арифметической и его среднего квадратического отклонения.
Свойства кривой нормального распределения
Дифференциальный закон нормального распределения, заданный функцией:
имеет ряд свойств. Полагая 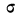
Рассмотрим ее свойства.
- Кривая нормального распределения имеет ветви, удаленные в бесконечность, причем кривая асимптотически приближается к оси Ot.
- Функция является четной: t(—t) = f(t). Следовательно, кривая нормального распределения симметрична относительно оси Оу.
- Функция имеет максимум при t = 0. Величина этого максимума равна
Следовательно, модального значения кривая
достигает при t = 0, а так как 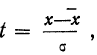
Наибольшую частоту кривая будет иметь при значении х, равном среднему арифметическому из отдельных вариантов. Средняя арифметическая является центром группирования частот ряда.
4. При t=±1 функция имеет точки перегиба. Это означает, что кривая имеет точки перегиба при отклонениях от центра
группирования 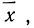
5. Сумма частостей, лежащих в пределах от а до b, равна определенному интегралу в тех же пределах от функции f(t), т. е.
Если учесть действительную величину среднего квадратического отклонения, то окажется, что при больших величинах о значение f(t) мало, при малых, наоборот, велико. Отсюда изменяется и форма кривой распределения. При больших 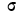
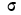
На графике 7 показаны 3 кривые нормального распределения (I, II, III) при 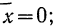
Зная общие свойства кривой нормального распределения, рассмотрим те условия, которые приводят к образованию кривых данного типа.
Формирование нормального распределения
Закон нормального распределения является наиболее распространенным законом не только потому, что он наиболее часто встречается, но и потому, что он является предельным законом распределения, к которому приближается ряд других законов распределения.
Нормальное распределение образуется в том случае, когда действует большое число независимых (или слабо зависимых), случайных причин. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Основное условие формирования нормального распределения состоит в том, чтобы все случайные величины, действующие вместе, играли в общей сумме примерно одинаковую роль. Если одна из случайных ошибок окажется по своему влиянию резко превалирующей над другими, то закон распределения будет обусловлен действием этой величины.
Если есть основания рассматривать изучаемую величину как сумму многих независимых слагаемых, то при соблюдении указанного выше условия ее распределение будет нормальным, независимо от характера распределения слагаемых.
Нормальное распределение встречается часто в биологических явлениях, отклонениях размеров изделий от их среднего размера, погрешностях измерения и т. д.
Если взять распределение людей по номеру носимой ими обуви, то это распределение будет нормальным. Но это правило применимо только в том случае, когда численность совокупности велика и сама совокупность однородна.
Из того факта, что нормальное распределение встречается нередко в разных областях, не следует, что всякий признак распределяется нормально. Наряду с нормальным распределением существуют другие различные распределения.
Но все же умение выявить нормальное распределение в некоторой эмпирической совокупности является важным условием для ряда практических расчетов и действий. Зная, что эмпирическое распределение является нормальным, можно определить оптимальные размеры предприятий, размеры резервов и т. д.
Важным условием определения характера данной эмпирической кривой является построение на основе эмпирических данных теоретического нормального распределения.
Построение кривой нормального распределения
Первый способ. Для того чтобы построить кривую нормального распределения, пользуются следующей егo формулой:
где N — число проведенных испытаний, равное сумме частот эмпирического распределения
k — величина интервала дробления эмпирического ряда распределения;
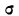
t—нормированное отклонение, т. е.
Величина 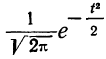
Для нахождения значений теоретических частот (см. пример 1) сначала необходимо найти среднюю арифметическую эмпирического ряда распределения, т. е. 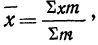
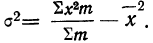
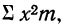
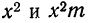
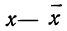
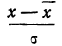
Найденная при умножении величина и составляет теоретическую частоту каждого варианта, записанного в строке (графа 9). Ввиду того что частоты могут быть только целыми числами, округляем их до целых и получим теоретические частоты, которые будем обозначать 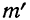
Пример 1.
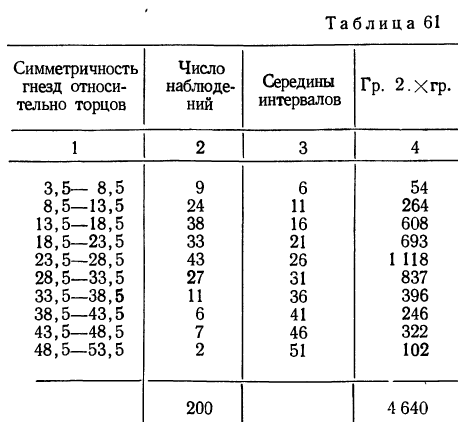
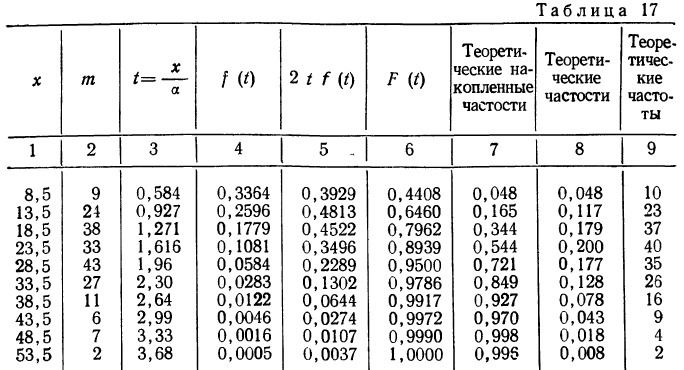
В таблице 3 приведено эмпирическое распределение веса 500 спиралей и расчет частот нормального распределения. (Вес спиралей х дан в миллиграммах.)
Из таблицы находим:
Строим график эмпирических и теоретических данных. На графике 8 сплошной линией дано изображение эмпирического распределения, а пунктирной — построенного на его основе теоретического распределения.
Пример 2.
В таблице 4 дается эмпирическое распределение ПО замеров межцентрового расстояния при шевинговании зубцов динамомашины 110412 и расчет теоретических частот.
Исчислим:
Построим графики эмпирического и теоретического распределений (см. график 9).
Оба эмпирических распределения хорошо воспроизводятся теоретическим нормальным распределением.
Второй способ построения кривой нормального распределения основан на применении функции стандартизованного нормального распределения, в котором 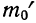
За начало отсчета признака при этом способе построения берется его средняя арифметическая. Ей соответствует наибольшая ордината.
Вычисление ординат производится по формуле:
где N — число наблюдений;
k — величина интервала эмпирического распределения.
Так как значение наибольшей ординаты получается при
t = 0, когда 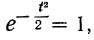
Придавая t последовательно значения 0,5; 1,0; 1,5; 2,0, т. е. сначала меньшие, а потом увеличивающиеся, находим в таблице стандартизованного нормального распределения для данных t соответствующие 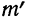
Например, при t = 0,5 величина стандартизованного нормального распределения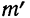
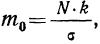
Пример 3.
Взяты результаты измерения 100 отклонений шага резьбы х от всей длины резьбы. Получен следующий ряд распределения, для которого по общим правилам производится расчет средней и дисперсии.
Отсюда;
Рассчитаем наибольшую ординату:
так как величина 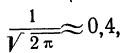
Взяв значение t = 0,5 по таблице стандартизованного нормального распределения, находим 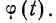
Для данного примера будем иметь:
Полученный результат наносим на график, а для сравнения наносим на график и результаты непосредственных измерений отклонений (см. график 10).
Как видно из графика, теоретическая кривая довольно близко воспроизводит полигон эмпирического распределения.
Пример 4.
Даны результаты измерений отклонений шага резьбы (х) в микронах на 1 витке от среднего значения. Приводятся эти данные с соответствующими расчетами:
Теоретические частоты (ординаты) рассчитываются так же, как и в предыдущем примере. Сначала находится величина наибольшей частоты:
затем другие частоты:
Эмпирические и теоретические частоты наносим на график (см. график 11) и убеждаемся, что эмпирическое распределение довольно близко воспроизводится теоретическим распределением.
Третий способ построения кривой нормального распределения (или вычисления теоретических частот) по имеющимся эмпирическим данным основан на применении функции:
которая дает площадь нормальной кривой, заключенной между —t и +t.
Вообще говоря, можно находить площадь нормальной кривой, заключенную между любыми точками 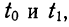
применяя функцию F(t). Искомая площадь будет представлять собой 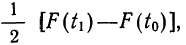
Пример 5.
Получены результаты 208 измерений межцентровых расстояний при шевинговании зубцов шестерни динамо-машины (см. табл. 7). Вычислим нужные параметры и теоретические частоты и построим графики эмпирического и теоретического распределений.
Колонки 1, 2, 3, 4 и 5 необходимы для расчетов 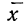
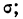
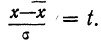
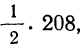
Чтобы получить теоретическую частоту для каждого интервала, достаточно из верхней строки (в 8-й колонке) вычесть число той же колонки, стоящее строкой ниже.
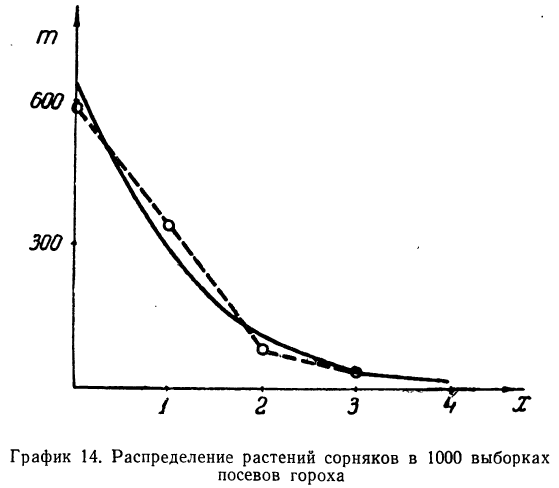
На графике 12 показано, что теоретическое распределение достаточно точно отражает эмпирически полученный материал, только наблюдается некоторое смещение теоретической кривой вправо, что, очевидно, вызвано большим удельным весом правого конца эмпирического распределения.
Пример 6.
Дается ряд распределения ударной вязкости в 240 испытаниях. Приведем этот ряд распределения и построим для него теоретическое распределение (см. график 13).
Критерии согласия
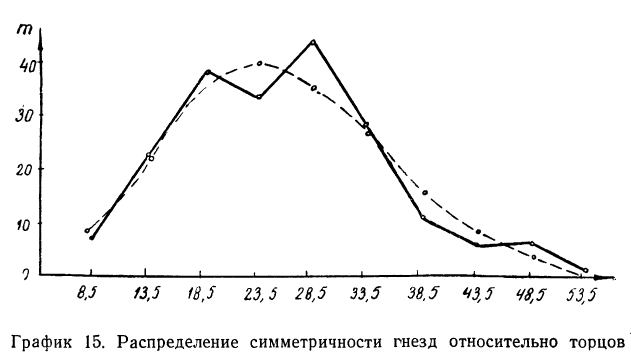
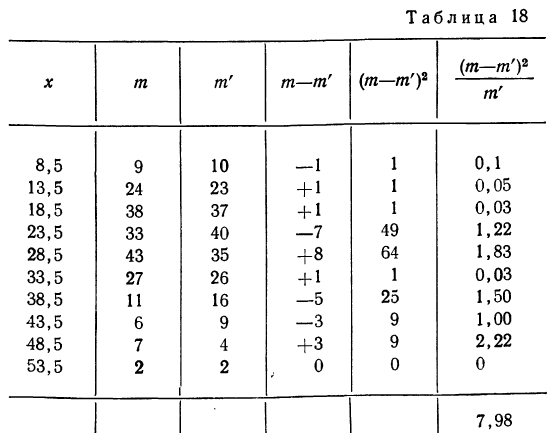
Определение близости эмпирических распределений к теоретическому нормальному распределению по графику может быть недостаточно точным, субъективным и по-разному оценивать расхождения между ними. Поэтому математики выработали ряд объективных оценок для того, чтобы определить, является ли данное эмпирическое распределение нормальным. Такие оценки называются критериями согласия. Критерии согласия были предложены разными учеными, занимавшимися этим вопросом. Рассмотрим критерии согласия Пирсона, Романовского, Колмогорова и Ястремского.
Критерий согласия Пирсона основан на определении величины 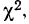
где m — эмпирические частоты;
m’ — теоретические частоты.
Для оценки того, насколько данное эмпирическое распределение воспроизводится нормальным распределением, исчисляют по распределению Пирсона вероятности достижения 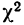
Значения 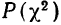
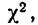
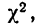
Пересечение данного столбца с соответствующей строкой дает искомую вероятность
При вероятностях, значительно отличающихся от нуля, расхождение между теоретическими и эмпирическими частотами можно считать случайным.
Проф. В. И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину
Он предложил вычислять отношение:
где k — число степеней свободы.
Если указанное отношение имеет абсолютное значение, меньшее трех, то предлагается расхождение между теоретическим и эмпирическим распределениями считать несущественным; если же это отношение больше трех, то расхождение существенно. Несущественность расхождения (когда величина отношения Романовского меньше трех) говорит о возможности принять за закон данного эмпирического распределения нормальное распределение.
По данным примера 2 рассчитаем величину
Пример 7.
Вычисление 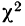
Из таблицы 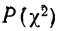
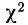
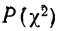
Находим отношение Романовского:
Это отношение значительно меньше трех, поэтому расхождение между теоретическими и эмпирическими частотами можно считать несущественными, и, таким образом, теоретическое распределение достаточно хорошо воспроизводит эмпирическое.
Пример 8.
Вычислим критерий 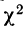
По таблице находим вероятность 
Отношение Романовского
также значительно меньше трех, поэтому теоретическое воспро* изведение эмпирического ряда достаточно удовлетворительное.
Критерий 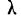
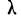
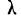
где D — максимальная граница разности: 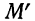
Приведем таблицу значений 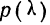
Если найденному значению 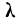
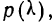
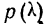
Рассмотрим применение этого критерия на двух примерах.
Пример 9.
В таблице вероятностей 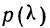
Эта большая вероятность указывает на то, что расхождение между наблюдением и теоретическим распределением вполне могло быть случайным.
Пример 10.
Величина вероятности 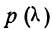
Критерий Б. С. Ястремского. В общем виде критерий Ястремского можно записать следующим неравенством:
где
Для числа групп, меньших 20, 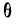
Значение I, меньшее 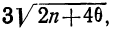
При значениях I, больших 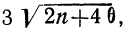
Пример 11.
Определим величину I и оценим эмпирическое распределение 500 спиралей (m) по сравнению с соответствующим нормальным (m’).
что говорит о нормальном распределении исследуемой совокупности.
Элементарные приемы определения «нормальности» распределения. Для определения элементарными способами близости данного опытного распределения к нормальному прибегают к числам Вестергарда и к сравнению средней арифметической, моды и медианы.
Числами Вестергарда являются: 0,3; 0,7; 1,1; 3. Для пользования ими определяют сначала основные характеристики — среднюю арифметическую 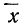
Для того чтобы данное эмпирическое распределение было подчинено закону нормального распределения, необходимо, чтобы распределение удовлетворяло следующим условиям:
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
было расположено
всей совокупности;
- в промежутках от —3 до +3 было расположено 0,998 всей совокупности.
Для приводимого распределения 500 спиралей по весу (пример 1) все эти условия соблюдаются, что говорит о подчинении данного распределения закону нормального распределения.
К элементарным приемам определения «нормальности» следует отнести применение графического метода, особенно удобное с помощью полулогарифмической сетки Турбина. На сетке накопленные эмпирические частоты при нормальном их распределении дают прямую линию. Всякое отклонение от прямой свидетельствует об отклонении эмпирического распределения от «нормального».
Распределение Пуассона
Вероятности частот событий, редко встречающихся при некотором числе испытаний, находят по формуле:
где m — частота данного события;
n — число испытаний;
р — вероятность события при одном испытании;
е= 2,71828.
Это выражение носит название закона распределения Пуассона.
Подставим вместо nр среднее число фактически наблюдавшихся случаев в эмпирическом материале. Теоретические ординаты кривой распределения по закону Пуассона m’ найдем по формуле:
где х — переменное значение числа раз;
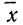
n — число наблюдений.
При
Пример 12.
Наблюдалось следующее распределение растений сорняков в 1000 выборках посевов гороха. Результаты эксперимента записаны в следующей таблице:
Определим по закону Пуассона теоретические частоты разного числа растений сорняков. Для этого предварительно исчислим среднее число растений сорняков в одной выборке:
Из таблицы находим
Определим теоретическое число выборок, в которых число растений сорняков будет равно 0:
то же:
для числа растений сорняков, равного 1:
для числа растений сорняков, равного 2:
для числа растений сорняков, равного 3:
для числа растений сорняков более 3:
Графическое сопоставление обоих распределений говорит о соответствии между эмпирическим и теоретическим распределениями.
Распределение Максвелла
В технике часто встречается распределение по закону Максвелла. Это — распределение существенно положительных величин. Например, эмпирическое распределение эксцентриситетов биений теоретически воспроизводится распределением Максвелла.
Дифференциальный закон распределения Максвелла выражается следующей формулой:
где 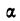
Интегральный закон распределения выразится тогда:
Пример 13.
Заимствуем из книги А. М. Длина таблицу распределения симметричности гнезд относительно торцов в круглых плашках (в 0,01 мм) и проведем дополнительные расчеты.
Из этой таблицы легко определим среднюю симметричность:
и параметр рассеяния:
Формула интегрального распределения по закону Максвелла позволяет найти накопленные, а затем теоретические частости и частоты.
Изобразим на графике 15 данные эмпирического и теоретического рядов распределения.
Определим близость их по критерию согласия Ястремского. Для этого приведем в табл. 18 расчет величины С:
По критерию Ястремского находим
Величина I значительно меньше 3. Следовательно, данное эм лирическое распределение хорошо согласуется с законом распределения Максвелла.
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
- Элементы теории ошибок
- Статистические оценки
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд
17 авг. 2022 г.
читать 3 мин
Выборочное распределение — это вероятностное распределение определенной статистики , основанное на множестве случайных выборок из одной совокупности .
В этом руководстве объясняется, как выполнить следующие действия с выборочными распределениями в Excel:
- Сгенерируйте выборочное распределение.
- Визуализируйте распределение выборки.
- Рассчитайте среднее значение и стандартное отклонение выборочного распределения.
- Рассчитайте вероятности относительно выборочного распределения.
Создание выборочного распределения в Excel
Предположим, мы хотим сгенерировать выборочное распределение, состоящее из 1000 выборок, в каждой из которых размер выборки равен 20 и происходит от нормального распределения со средним значением 5,3 и стандартным отклонением 9 .
Мы можем легко сделать это, введя следующую формулу в ячейку A2 нашего рабочего листа:
= NORM.INV ( RAND (), 5.3, 9)
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и перетащить формулу на 20 ячеек вправо и на 1000 ячеек вниз:
Каждая строка представляет выборку размера 20, в которой каждое значение получено из нормального распределения со средним значением 5,3 и стандартным отклонением 9.
Найдите среднее значение и стандартное отклонение
Чтобы найти среднее значение и стандартное отклонение этого выборочного распределения средних значений выборки, мы можем сначала найти среднее значение каждой выборки, введя следующую формулу в ячейку U2 нашего рабочего листа:
= AVERAGE (A2:T2)
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и дважды щелкнуть, чтобы скопировать эту формулу в каждую другую ячейку в столбце U:
Мы видим, что первая выборка имела среднее значение 7,563684, вторая выборка имела среднее значение 10,97299 и так далее.
Затем мы можем использовать следующие формулы для расчета среднего значения и стандартного отклонения среднего значения выборки:
Теоретически среднее значение выборочного распределения должно быть 5,3. Мы видим, что фактическое среднее значение выборки в этом примере равно 5,367869 , что близко к 5,3.
И теоретически стандартное отклонение выборочного распределения должно быть равно s/√n, что будет равно 9/√20 = 2,012. Мы видим, что фактическое стандартное отклонение выборочного распределения составляет 2,075396 , что близко к 2,012.
Визуализируйте распределение выборки
Мы также можем создать простую гистограмму для визуализации выборочного распределения выборочных средних.
Для этого просто выделите все средние значения выборки в столбце U, щелкните вкладку « Вставка », затем выберите параметр « Гистограмма » в разделе « Диаграммы ».
В результате получается следующая гистограмма:
Мы видим, что распределение выборки имеет форму колокола с пиком около значения 5.
Однако из хвостов распределения мы можем видеть, что некоторые выборки имели средние значения больше 10, а некоторые — меньше 0.
Рассчитать вероятности
Мы также можем рассчитать вероятность получения определенного значения среднего значения выборки на основе среднего значения совокупности, стандартного отклонения совокупности и размера выборки.
Например, мы можем использовать следующую формулу, чтобы найти вероятность того, что среднее значение выборки меньше или равно 6, учитывая, что среднее значение генеральной совокупности равно 5,3, стандартное отклонение генеральной совокупности равно 9 и размер выборки равен:
= COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)
Мы видим, что вероятность того, что среднее значение выборки меньше или равно 6, составляет 0,638.
Это очень близко к вероятности, рассчитанной Калькулятором распределения выборки :
Дополнительные ресурсы
Введение в выборочные распределения
Калькулятор распределения выборки
Введение в центральную предельную теорему

_2022-49%20(%D0%A1%D1%85%D0%B5%D0%BC%D0%B0).jpg)
_2022-51%20(%D0%A0%D0%B8%D1%81%D1%83%D0%BD%D0%BE%D0%BA1).jpg)
_2022-52%20(%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC).jpg)
_2022-52%20(%D0%A0%D0%B8%D1%81%D1%83%D0%BD%D0%BE%D0%BA).jpg)
_2022-55%20(%D0%A1%D1%85%D0%B5%D0%BC%D0%B0).jpg)
_2022-57%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B01).jpg)
_2022-57%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B02).jpg)
_2022-58%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B03).jpg)
_2022-59%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B04).jpg)
_2022-60%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B05).jpg)
_2022-60%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B06).jpg)
_2022-61%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B07).jpg)
_2022-62%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B08).jpg)
_2022-62%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B09)_1.jpg)
_2022-63%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B010).jpg)
_2022-63%20(%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B011).jpg)
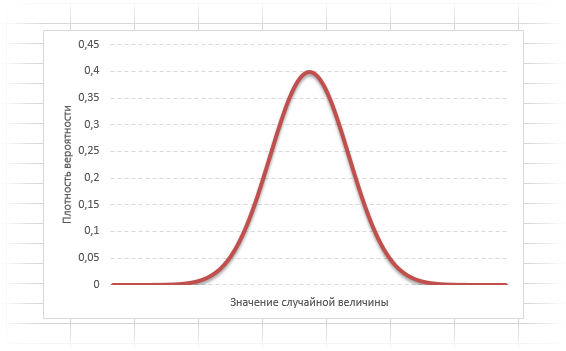
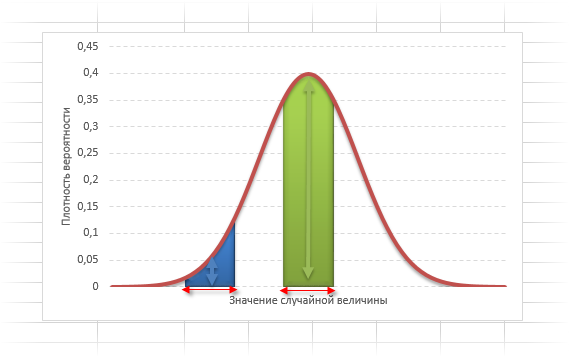
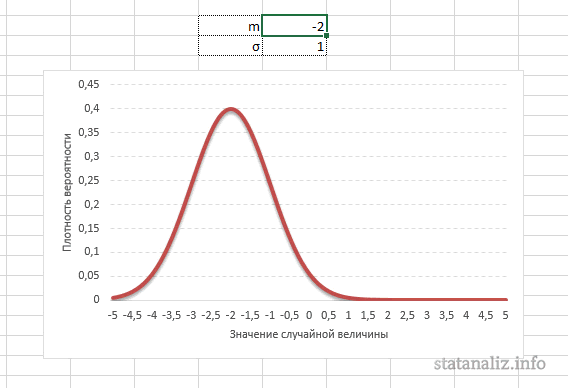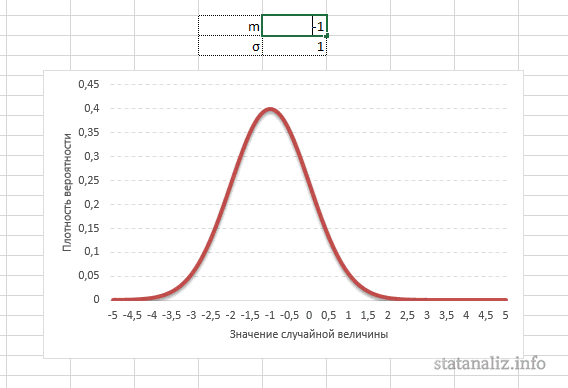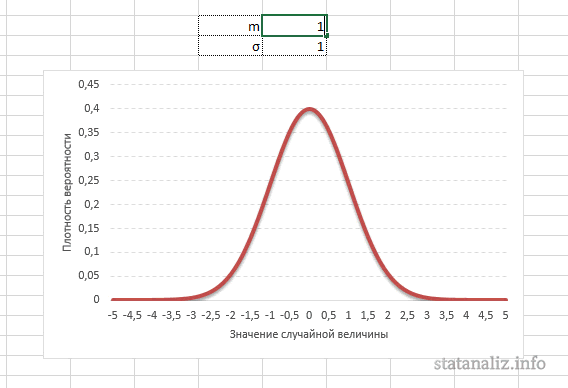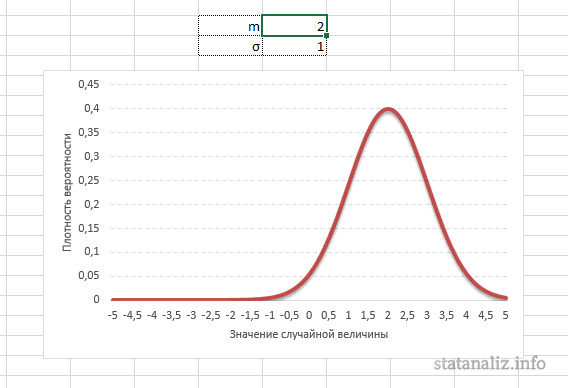
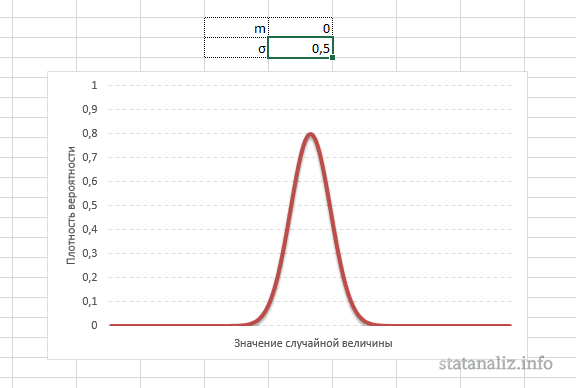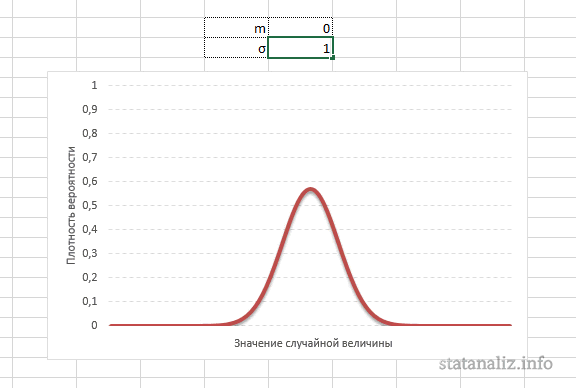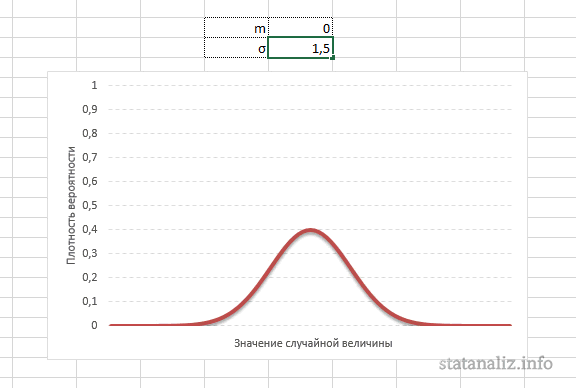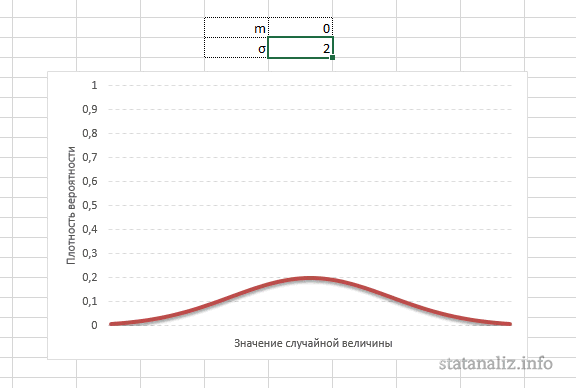
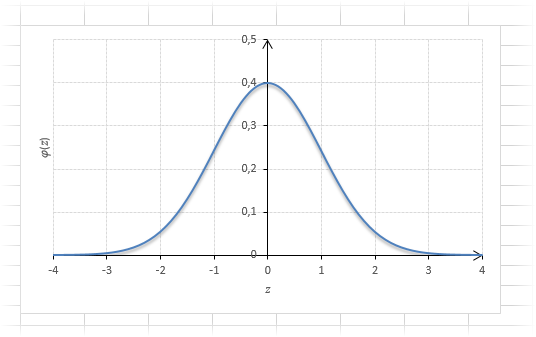
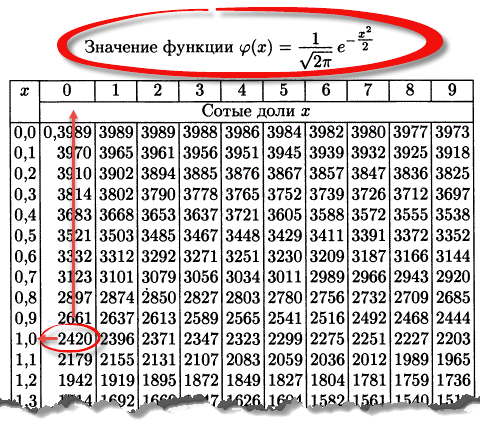
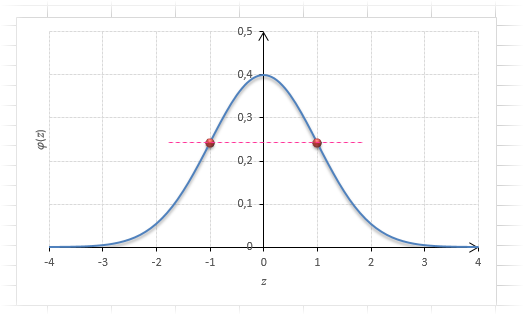
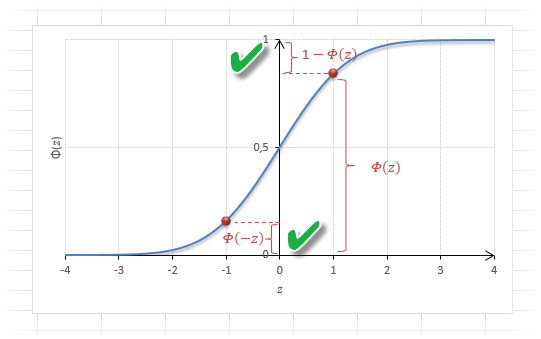
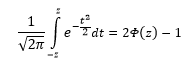
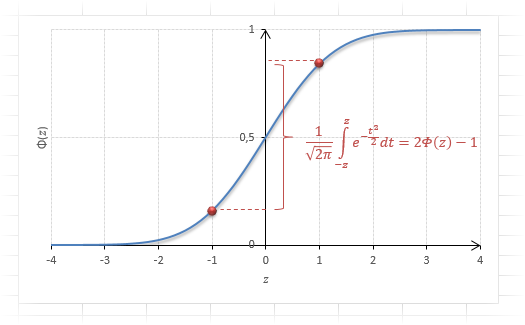
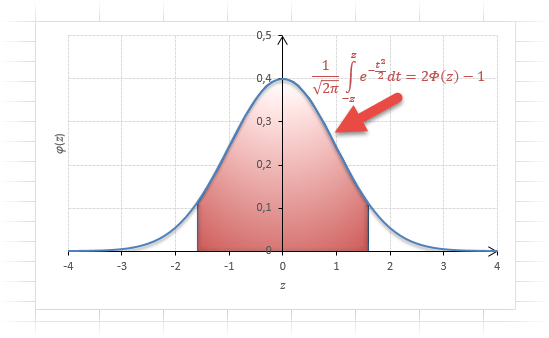
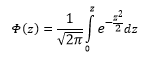
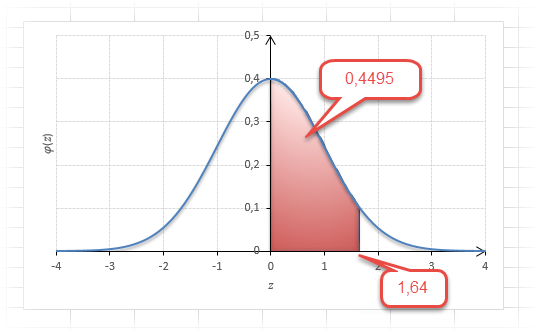
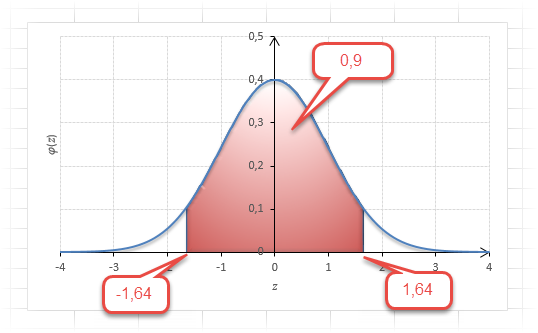
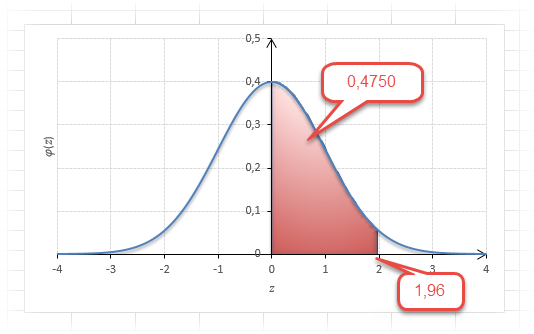
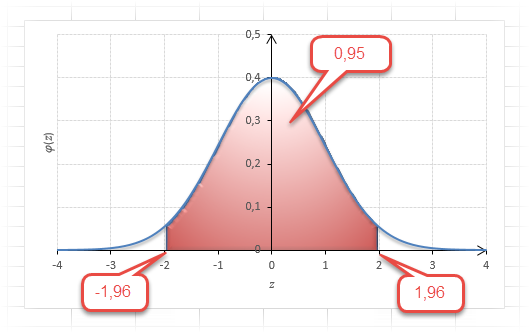
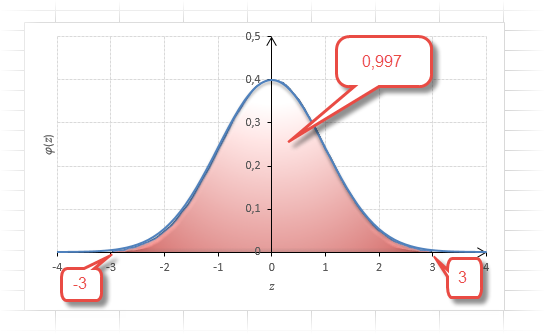
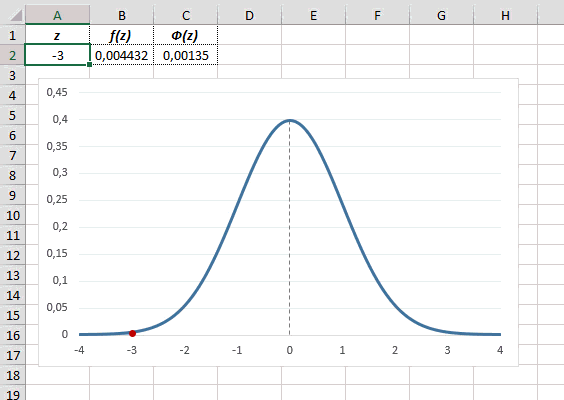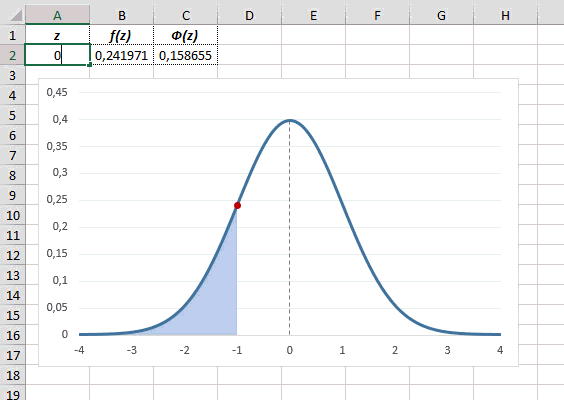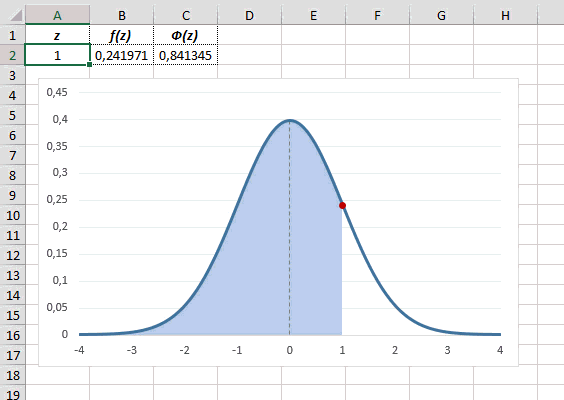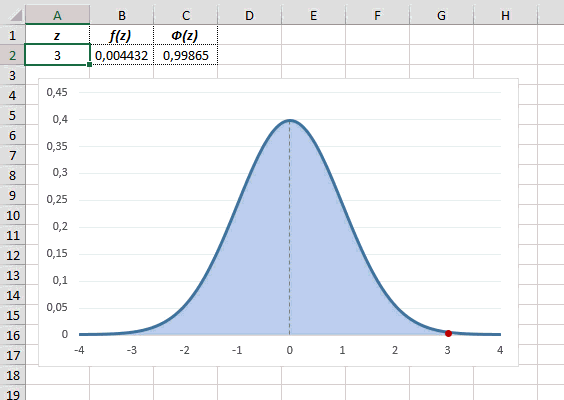
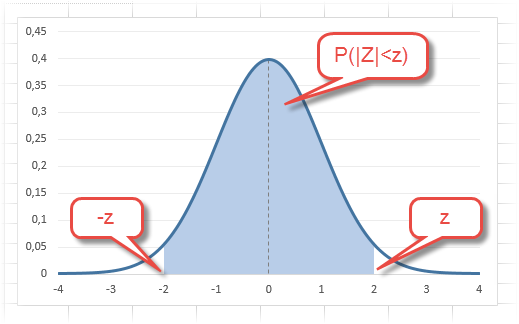
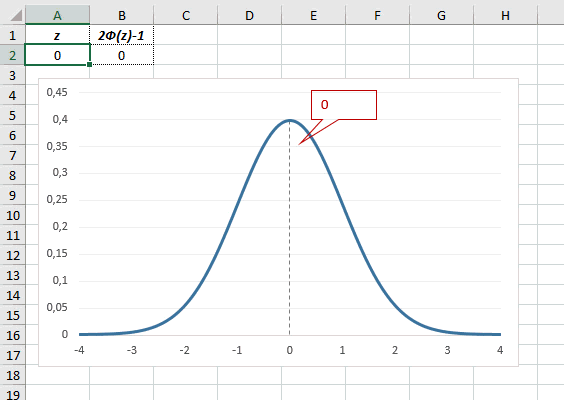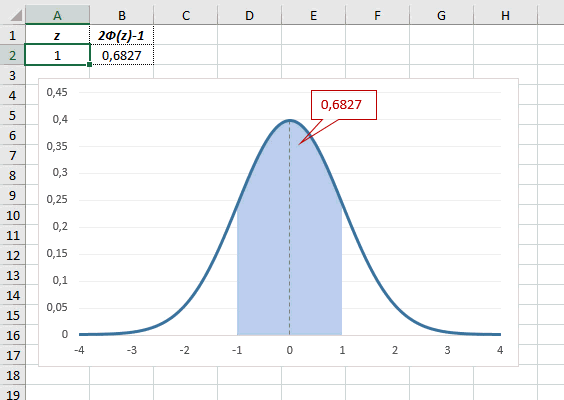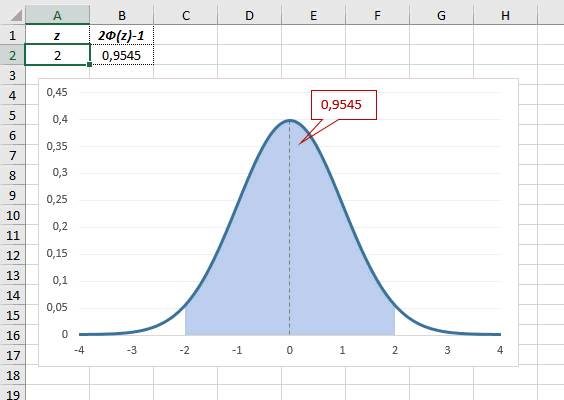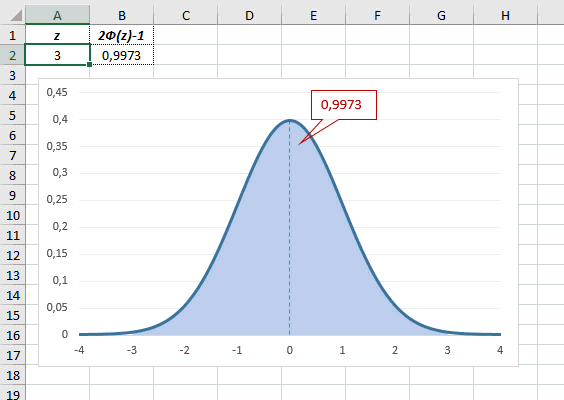
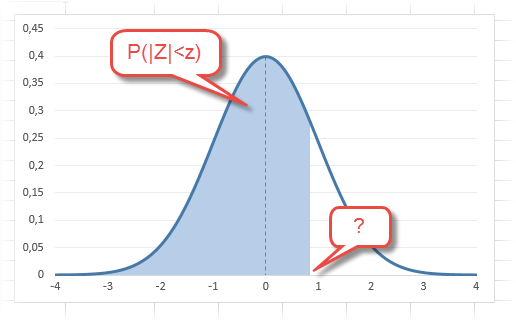
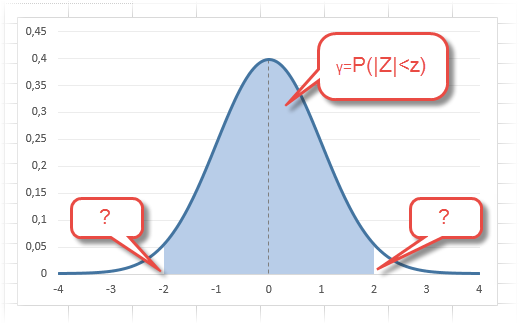
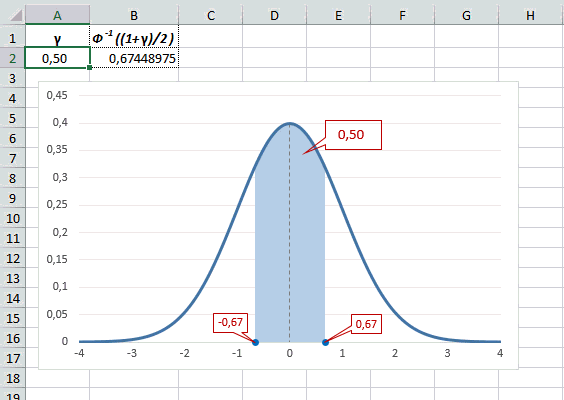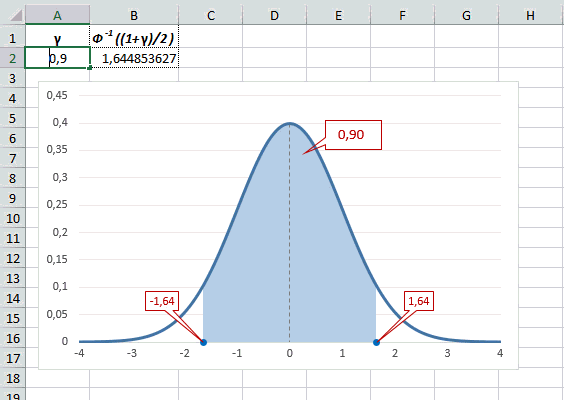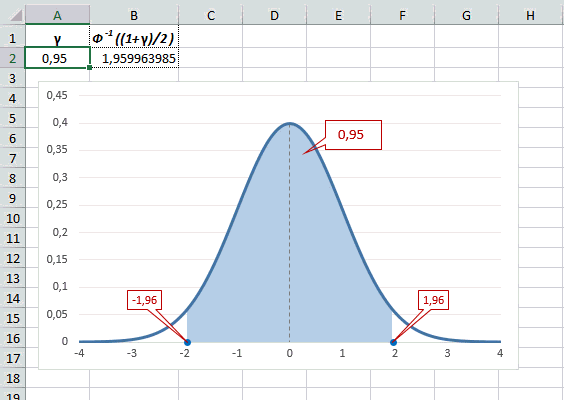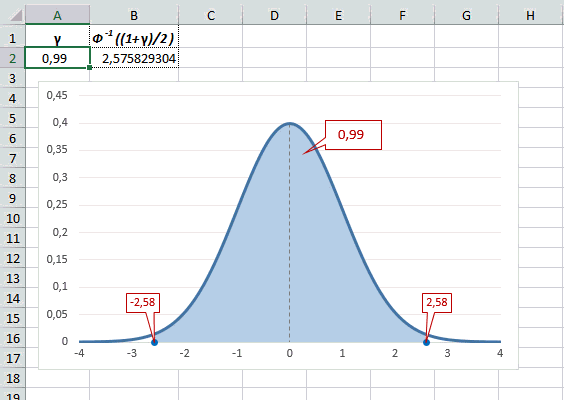
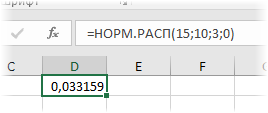
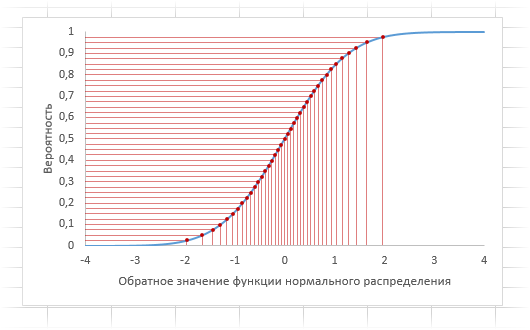
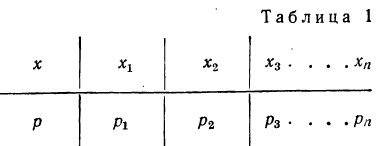
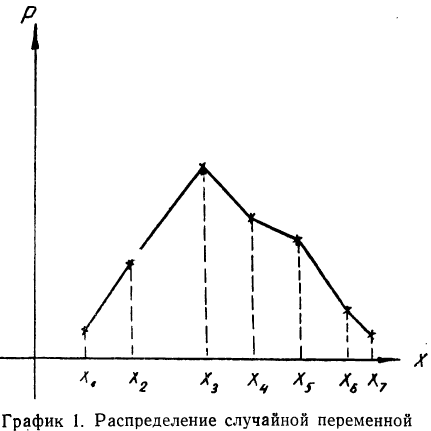
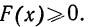
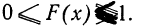
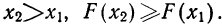
 равно нулю, а при х=
равно нулю, а при х= равно единице.
равно единице.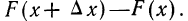
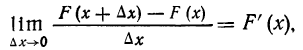
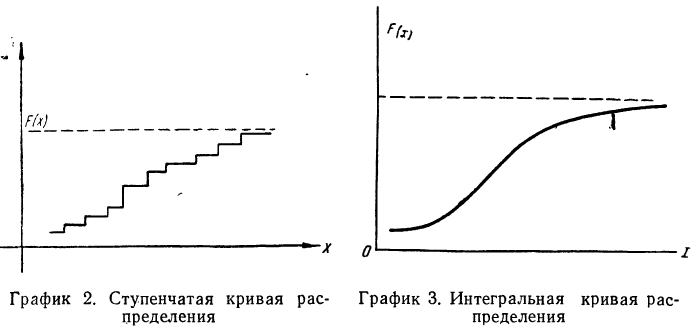
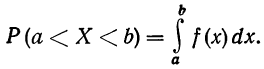
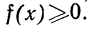
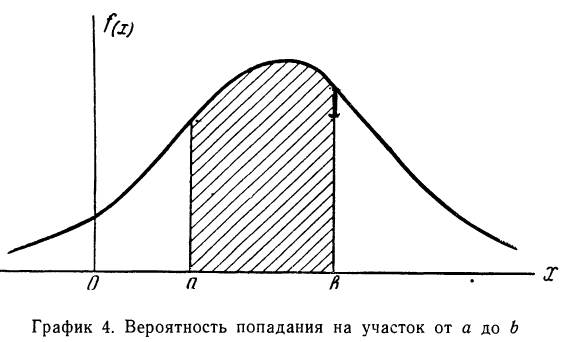
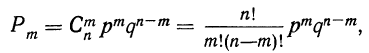
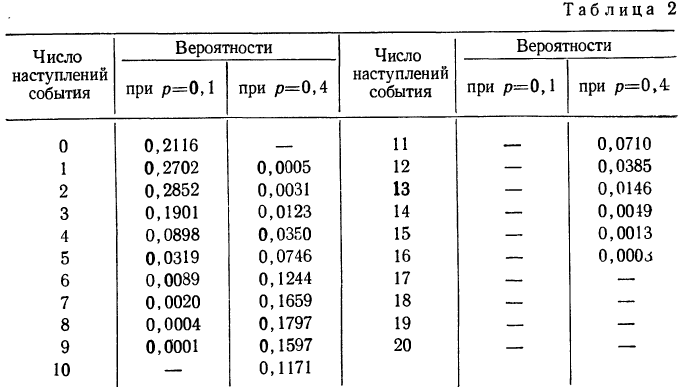
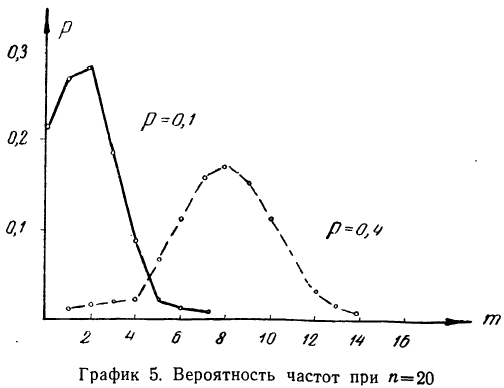
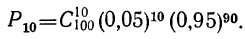
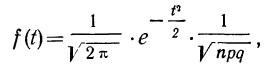
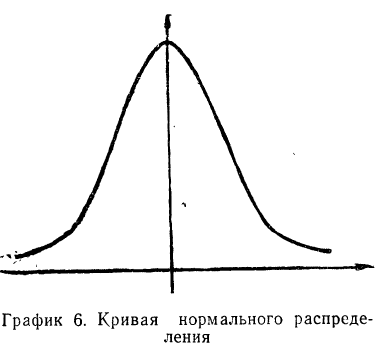
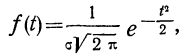
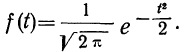
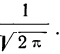
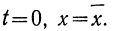
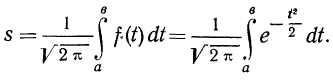
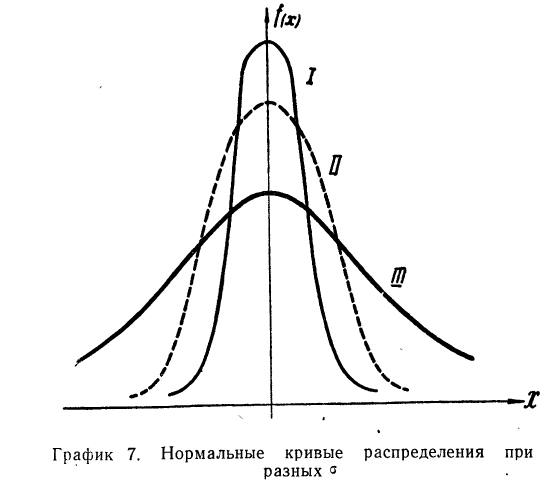
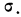
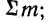
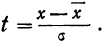
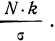
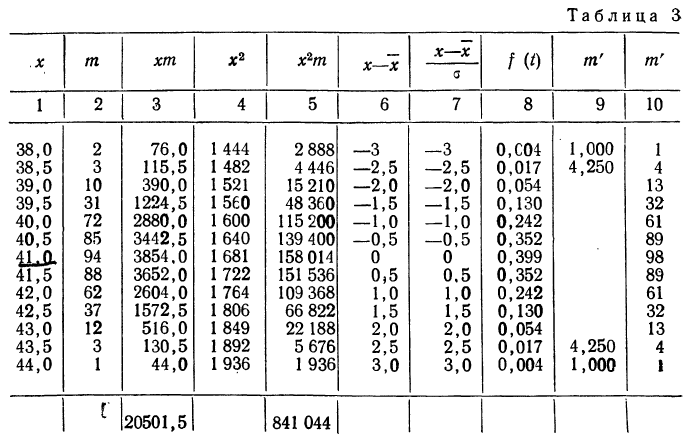
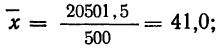
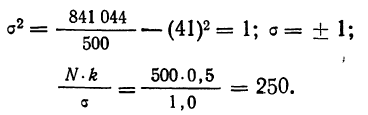
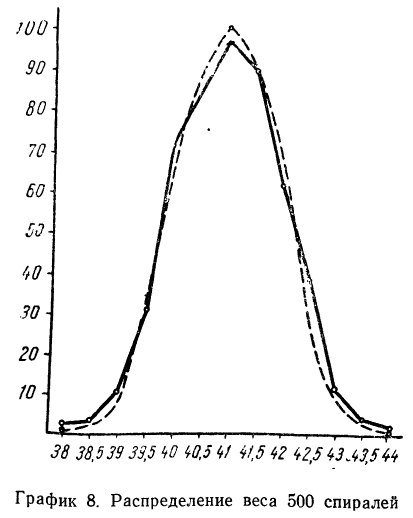
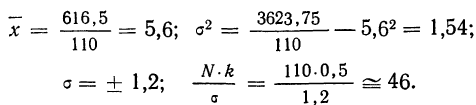
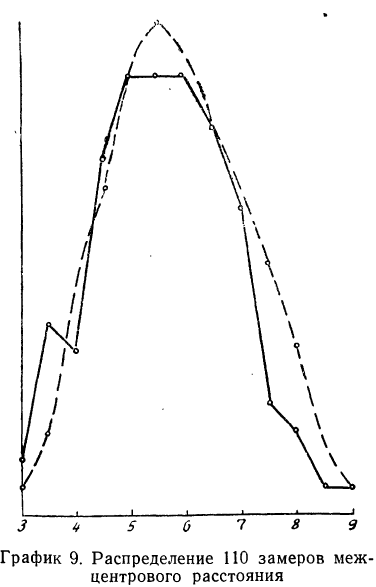
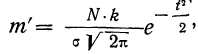
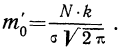
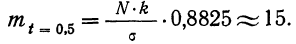
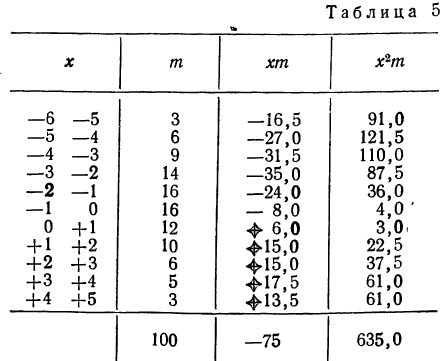
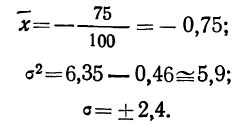
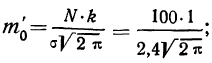
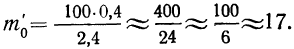
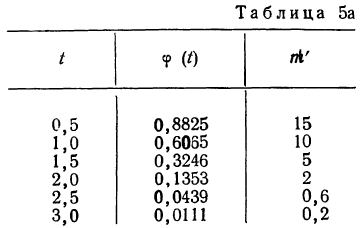
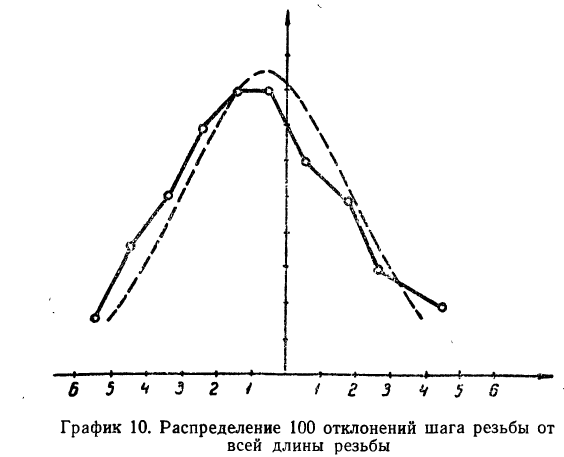

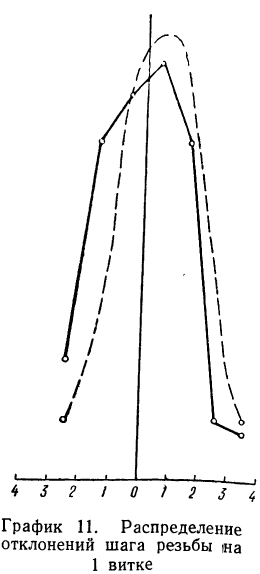
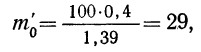
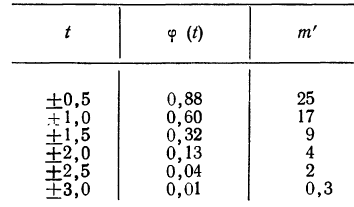
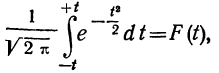
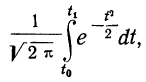
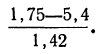
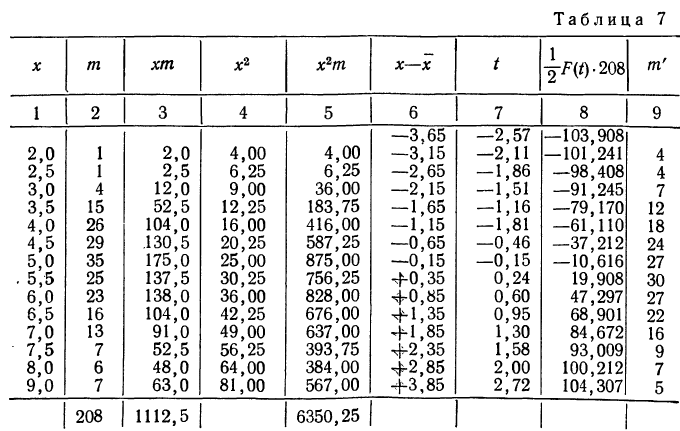
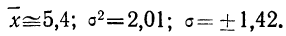
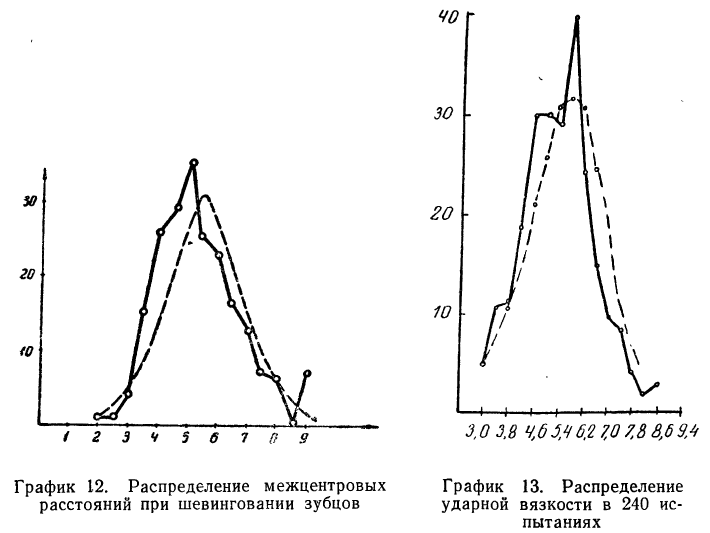
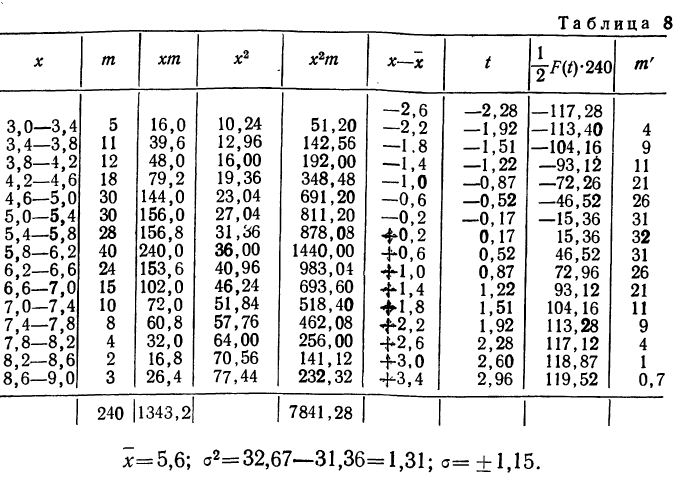
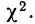
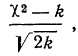
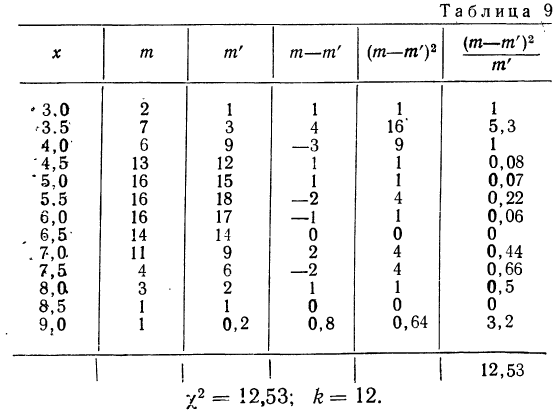
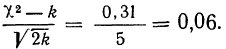
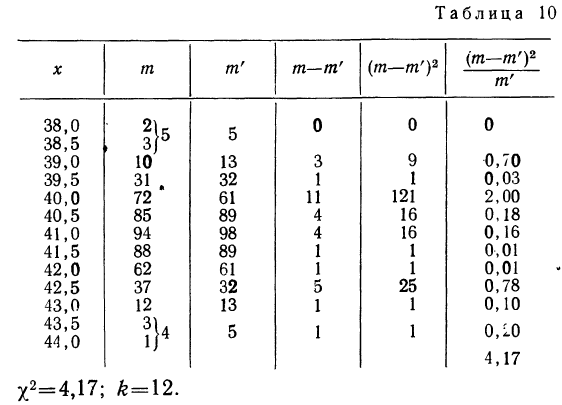
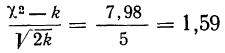
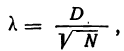
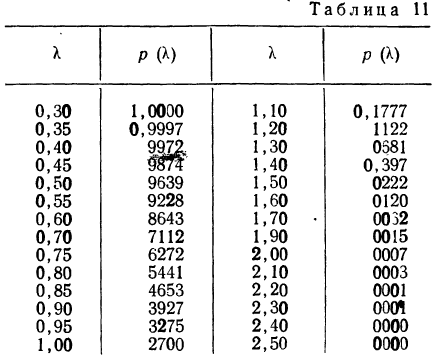
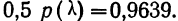
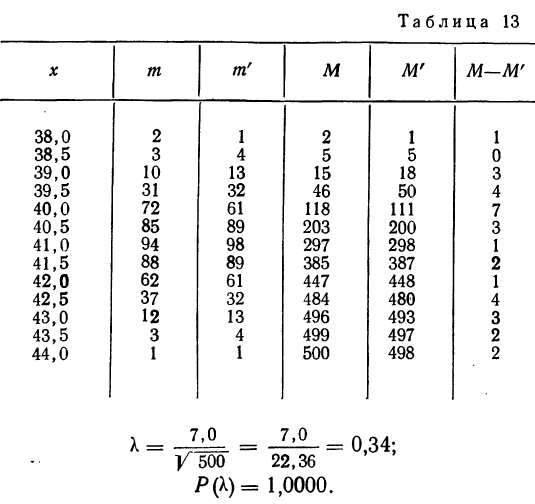
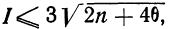
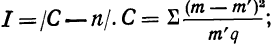
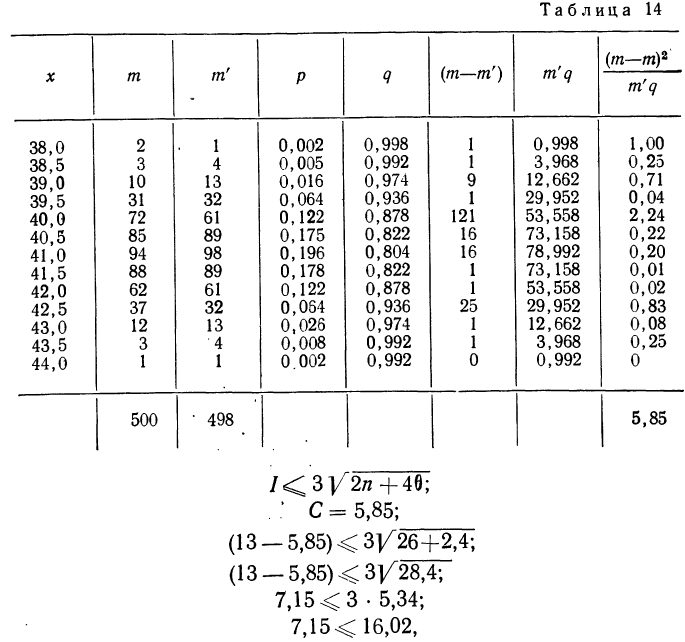
 была расположена
была расположена  часть всей совокупности;
часть всей совокупности;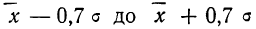 была расположена
была расположена  часть всей совокупности;
часть всей совокупности;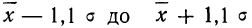 было расположено
было расположено  всей совокупности;
всей совокупности;