Сумма и произведение элементов массива
Просмотров 10.7к. Обновлено 15 октября 2021
Заполнить массив вещественных чисел вводом с клавиатуры. Посчитать сумму и произведение элементов массива. Вывести на экран сам массив, полученные сумму и произведение его элементов.
- Присвоить переменной, в которой будет храниться сумма, значение 0, а переменной для произведения — значение 1.
- В цикле увеличивая индекс массива от начала до конца
- считывать с клавиатуры число и записывать его в текущую ячейку массива,
- увеличивать переменную с суммой на введенное число.
- умножать переменную с произведением на введенное число.
- В цикле увеличивая индекс массива от начала до конца вывести все элементы массива.
- Вывести сумму и произведение.
Pascal
сумма элементов массива паскаль
const N = 10;
var
a: array[1..N] of real;
sum, mult: real;
i: integer;
begin
sum := 0;
mult := 1;
for i:=1 to N do begin
read(a[i]);
sum := sum + a[i];
mult := mult * a[i];
end;
for i:=1 to N do write(a[i]:5:2);
writeln;
writeln(sum:5:2);
writeln(mult:5:2);
end.
4.3 2.3 4.5 3.3 8.3 1.2 8.3 9.1 2.3 3.6
4.30 2.30 4.50 3.30 8.30 1.20 8.30 9.10 2.30 3.60
47.20
914812.11
Язык Си
#include
#define N 10main() {
float a[10], sum, mult;
int i;
sum = 0;
mult = 1;
for (i=0; i < 10; i++) {
scanf("%f", &a[i]);
sum += a[i];
mult *= a[i];
}
for (i=0; i < 10; i++) {
printf("%.2f ", a[i]);
}
printf("n%.2fn", sum);
printf("%.2fn", mult);
}
Python
сумма элементов массива python (питон)
a = [0]*10
s = 0
m = 1
for i in range(10):
a[i] = float(input())
s += a[i]
m *= a[i]
print(a)
print(s)
print('%.4f'%m)
КуМир
алг сумма элементов
нач
цел N=10
вещ таб a[1:N]
вещ sum, mult
цел i
sum := 0
mult := 1
нц для i от 1 до N
ввод a[i]
sum := sum + a[i]
mult := mult * a[i]
кц
нц для i от 1 до N
вывод a[i], " "
кц
вывод нс, sum, нс
вывод mult
кон
Basic-256
dim a(10)
sum = 0
mult = 1
for i=0 to 9
input a[i]
sum = sum + a[i]
mult = mult * a[i]
next ifor i=0 to 9
print a[i] + " ";
next i
print sum
print mult
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
142 |
S+=X[i];
cout<<«S=»<<S<<«n»;
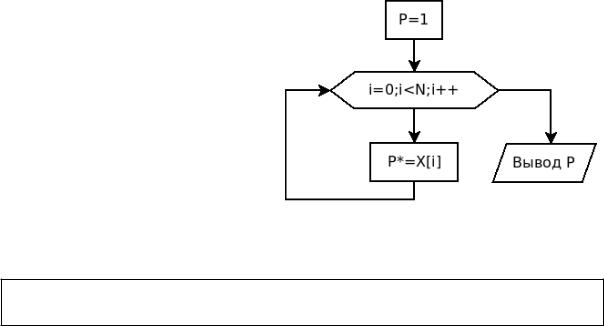
Дан массив X, состоящий из N элементов. Найти произведение элементов этого массива. Решение этой задачи сводится к тому, что значение переменной Р, в которую предварительно была записана единица, последовательно умножается на значение i–го элемента массива. Блок-схема алгоритма приведена на рис. 5.5.
Соответствующий фрагмент
программы будет иметь вид:
for (P=1,i=0;i<N;i++) P*=X[i]; cout<<«P=»<<P<<«n»;
Рисунок 5.5. Вычисление произведения элементов массива
ЗАДАЧА 5.1. Задан массив целых чисел. Найти сумму простых чисел и произведение отрицательных элементов массива.
Алгоритм решения задачи состоит из следующих этапов.
1.Вводим массив X[N].
2.Для вычисления суммы в переменную S записываем значение 0, для вычисления произведения в переменную P записываем 1.
3.В цикле (i изменяется от 0 до N-1 с шагом 1) перебираем все элементы массива X, если очередной элемент массива является простым числом, добавляем его к сумме, а если очередной элемент массива отрицателен, то умножаем его на P.
4.Выводим на экран значение суммы и произведения.
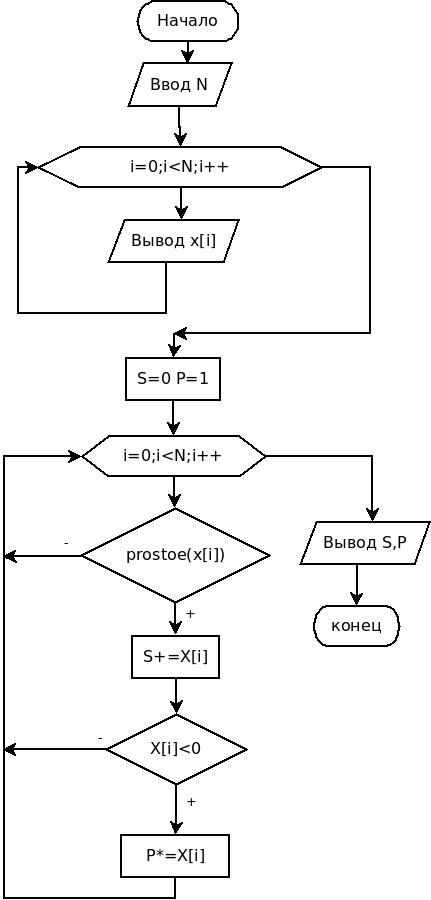
Блок-схема решения задачи представлена на рис. 5.6. Для решения задачи нам понадобится хорошо уже известная функция проверки является ли число простым.
Текст программы с подробными комментариями приведён далее.
#include <iostream> using namespace std; //Текст функции prostoe. bool prostoe (int N)
{int i; bool pr;
if (N<2) pr=false; else
for(pr=true,i=2;i<=N/2;i++) if (N%i==0)
{pr=false;
break;
}
return pr;
}
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
143 |
Рисунок 5.6. Блок—схема алгоритма решения задачи 5.1
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
144 |
int main()
{
int *X,i,N,S,P;
//Ввод размерности массива. cout<<«Введите размер массива «;cin>>N;
//Выделение памяти для хранения динамического массива. X=new int [N];
//Ввод массива X. cout<<«Ведите массив Хn»; for(i=0;i<N;i++)
{
cout<<«X(«<<i<<«)=»;cin>>X[i];}
//В цикле перебираем все элементы массива for(P=1,S=i=0;i<N;i++)
{
//Если очередной элемент массива – простое число, //добавляем его к сумме.
if (prostoe(X[i])) S+=X[i];
//Если очередной элемент массива отрицателен, //умножаем его на P.
if (X[i]<0) P*=X[i];
}
//Вывод S и P на экран.
cout << «S=» <<S<<«tP=»<<P<< endl; //Освобождение занимаемой массивом X памяти. delete [] X;
return 0;
}
Результаты работы программы представлены ниже.
Введите размер массива 10 Ведите массив Х
X(0)=-7
X(1)=-9
X(2)=5
X(3)=7
X(4)=2
X(5)=4
X(6)=6
X(7)=8
X(8)=10
X(9)=12 S=14 P=63
5.3.4 Поиск максимального элемента в массиве и его номера
Дан массив X, состоящий из n элементов. Найти максимальный элемент массива и номер, под которым он хранится в массиве.
Алгоритм решения задачи следующий. Пусть в переменной с именем Max хранится значение максимального элемента массива, а в переменной с именем Nmax – его номер. Предположим, что нулевой элемент массива является максимальным и
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
145 |
запишем его в переменную Max, а в Nmax – его номер (то есть ноль). Затем все
элементы, начиная с первого, сравниваем в цикле с максимальным. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Max, а в переменную Nmax – текущее значение индекса i. Процесс определения
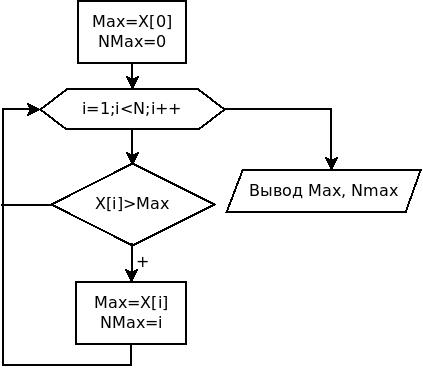
максимального элемента в массиве приведен в таблице 5.3 и изображен при помощи блок-схемы на рис. 5.7.
Таблица 5.3. Определение максимального элемента и его номера в массиве
|
Номера элементов |
0 |
1 |
2 |
3 |
4 |
5 |
|
Исходный массив |
4 |
7 |
3 |
8 |
9 |
2 |
|
Значение переменной Max |
4 |
7 |
7 |
8 |
9 |
9 |
|
Значение переменной Nmax |
1 |
2 |
2 |
4 |
5 |
5 |
Рисунок 5.7. Поиск максимального элемента и его номера в массиве
Соответствующий фрагмент программы имеет вид: for (Max=X[0],Nmax=i=0;i<n;i++)
if (Max<X[i])
{
Max=X[i]; Nmax=i;
}
cout<<«Max=»<<Max<<«n»;
cout<<«Nmax=»<<Nmax<<«n»;
При поиске максимального элемента, можно найти его номер, а потом по номеру извлечь значение максимального элемента из массива. Текст программы
иллюстрирующий этот вариант алгоритма приведён далее.
#include <iostream> using namespace std;

|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
146 |
int main()
{float *X; int i,N,nom;
//Ввод размерности динамического массива
cout<<«Введите размер массива «;cin>>N;
|
X=new float[N]; |
//Выделения памяти для хранения |
|
//динамического массива X. |
//Ввод динамического массива Х. cout<<«Введите элементы массива Хn»; for(i=0;i<N;i++)
cin>>X[i];
//В переменной nom будем хранить номер максимального //элемента. Предположим, что максимальным элементом, //является элемент с номером 0.
nom=0;
for(i=1;i<N;i++)
//Если очередной элемент больше X[nom], значит nom не //является номером максимального элемента, элемент с //номером i больше элемента X[nom], поэтому //переписываем число i в переменную nom.
if (X[i]>X[nom]) nom=i;
cout << «Максимальный элемент=»<<X[nom]; cout << «, его номер=» << nom<< endl;
return 0;
}
Совет. Алгоритм поиска минимального элемента в массиве будет отличаться от приведенного выше лишь тем, что в условном блоке и, соответственно, в конструкции if текста программы знак поменяется с < на >.
ЗАДАЧА 5.2. Найти минимальное простое число в целочисленном массиве X[N].
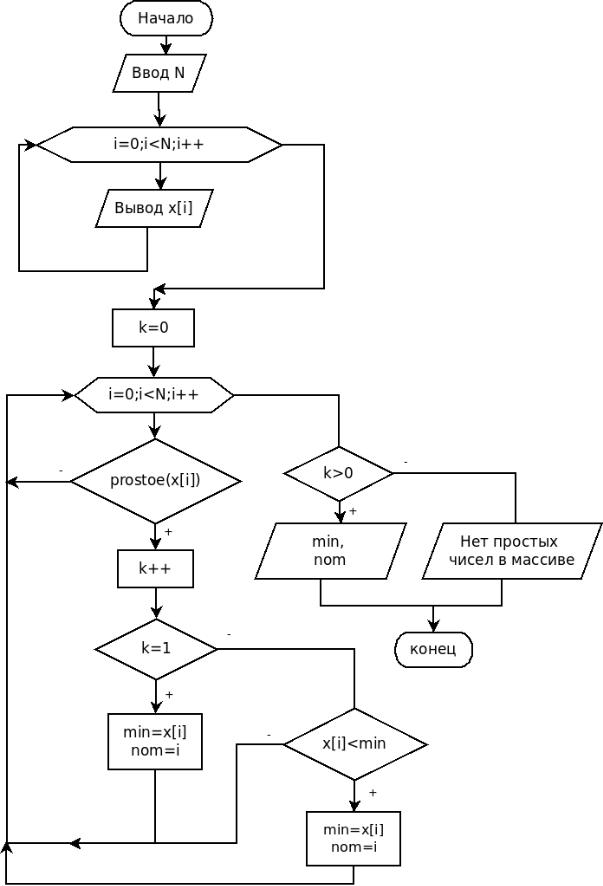
Эта задача относится к классу задач поиска минимума (максимума) среди элементов, удовлетворяющих условию. Подобные задачи рассматривались в примерах обработку последовательности чисел. Блок-схема приведена на рис. 5.8.
Необходимо первое простое число объявить минимумом, а затем все последующие простые элементы массива сравнивать с минимумом. В цикле будем последовательно проверять, является ли элемент массива простым числом (функция prostoe). Если X[i] является простым числом, то количество простых чисел k
увеличиваем на 1, далее, проверяем, если k равено 1, то этот элемент объявляем
минимальным, иначе сравниваем его с минимальным .
Текст программы:
#include <iostream> using namespace std; bool prostoe (int N)
{int i; bool pr; if (N<2) pr=false; else
for(pr=true,i=2;i<=N/2;i++) if (N%i==0)
{pr=false; break; } return pr;
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
147 |
}
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
148 |
Рисунок 5.8. Блок—схема рещения задачи 5.2

|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
149 |
int main(int argc, char **argv)
{
int i,k,n,nom,min,*x;
//Ввод количества элементов в массиве. cout<<«n=»; cin>>n;
//Выделяем память для динамического массива x. x=new int [n];
//Ввод элементов массива. cout<<«Введите элементы массива X»; for(i=0;i<n;i++)
cin>>x[i];
//С помощью цикла по переменной i, перебираем все элементы //в массиве x, k — количество простых чисел в массиве.
for(i=k=0;i<n;i++)
//Проеверяем, является ли очередной элемент массива //простым числом. Если x[i] — простое число.
if (prostoe(x[i]))
{
//Увеличиваем счётчик количества простых чисел в массиве. k++;
//Если текущий элемент является первым простым числом в //массиве, объявляем его минимумом, а его номер сохраняем //в перемнной nom.
if (k==1) {min=x[i];nom=i;} else
//Все последующие простые числа в массиве сравниваем с
//минимальным простым числом. Если текущее число меньше
//min, перезаписываем его
//в переменную min, а его номер — в переменную nom. if (x[i]<min) {min=x[i];nom=i;}
}
//Если в массиве были простые числа, выводим значение и //номер минимального простого числа.
if (k>0) cout<<«min=»<<min<<«tnom=»<<nom<<endl;
//Иначе выводим сообщение о том, что в массиве нет простых //чисел.
else cout<<«Нет простых чисел в массиве»<<endl; return 0;
}
Аналогично можно написать программу для задачи поиска минимума (максимума) среди элементов, удовлетворяющих какому-либо условию (минимум среди положительных элементов, среди чётных и т.д.).
ЗАДАЧА 5.3. Найти k минимальных чисел в массиве вещественных чисел.
Перед решением этой довольно сложно задачи рассмотрим более простую задачу. Найти два наименьших элемента в массиве.
Фактически надо найти номера (nmin1, nmin2) двух наименьших элементов массива. На первом этапе надо найти номер минимального (nmin1) элемента массива. На втором этапе надо искать минимальный элемент, при условии, что его номер не
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
150 |
равен nmin1. Вторая часть очень похожа на предыдущую задачу (минимум среди элементов, удовлетворяющих условию, в этом случае условие имеет вид i!=nmin).
Текст программы с комментариями приведен далее.
#include <iostream> using namespace std;
int main(int argc, char **argv)
{
int kvo,i,n,nmin1,nmin2; double *X; cout<<«n=»;cin>>n;
X=new double [n];
cout<<«Введите элементы массива Хn»; for(i=0;i<n;i++)
cin>>X[i];
//Стандартный алгоритм поиска номера первого минимального //элемента (nmin1).
for(nmin1=0,i=1;i<n;i++)
if (X[i]<X[nmin1]) nmin1=i;
//Второй этап — поиск номера минимального элемента, //среди элементов, номер которых не совпадает nmin1. //kvo — количество таких элементов.
for(kvo=i=0;i<n;i++)
//Если номер текущего элемента не совпадает с nmin1, if (i!=nmin1)
{
//увеличиваем количество таких элементов на 1. kvo++;
//Номер первого элемента, индекс которого не равен nmin1, //объявляем номером второго минимального элемента.
if (kvo==1) nmin2=i; else
//очередной элемент индекс которого не равен nmin1 //сравниваем с минимальным, если он меньше, номер // перезаписываем в переменную nmin2.
if (X[i]<X[nmin2]) nmin2=i;}
//Вывод двух минимальных элементов и их индексов. cout<<«nmin1=»<<nmin1<<«tmin1=»<<X[nmin1]<<endl; cout<<«nmin2=»<<nmin2<<«tmin2=»<<X[nmin2]<<endl; return 0;
}
По образу и подобию можно написать задачу поиска трёх минимальных элементов в массиве. Первые два этапа (поиск номеров двух минимальных элементов в массиве) будут полным повторением кода, приведенного на листинге выше. На третьем этапе нужен цикл, в котором будем искать номер минимального элемента, при условии, что его номер не равен nmin1 и nmin2. Авторы настоятельно рекомендуют читателям
самостоятельно написать подобную программу. Аналогично можно написать программу поиска четырёх минимальных элементов. Однако при этом усложняется и увеличивается код программы. К тому же, рассмотренный прием не позволит решить задачу в общем случае (найти k минимумов).
Для поиска k минимумов в массиве можно поступить следующим образом. Будем

|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
151 |
формировать массив nmin, в котором будут храниться номера минимальных элементов массива x. Для его формирования организуем цикл по переменной j от 0 до k—1. При каждом вхождении в цикл в массиве nmin будет j-1 элементов и мы будем искать j-й минимум (формировать j-й элемент массива). Алгоритм формирования j-го элемента состоит в следующем: необходимо найти номер минимального элемента в массиве x, исключая номера, которые уже хранятся в массиве nmin. Внутри цикла по j необходимо выполнить такие действия. Для каждого элемента массива x (цикл по переменной i) проверить содержится ли номер в массиве nmin, если не содержится, то количество (переменная kvo) таких элементов увеличить на 1. Далее, если kvo равно 1, то это первый элемент, который не содержится в массиве nmin, его номер объявляем номером минимального элемента массива (nmin_temp=i;). Если kvo>1, сравниваем текущий элемент x[i] с минимальным
(if (x[i]<X[nmin_temp]) nmin_temp=i;).
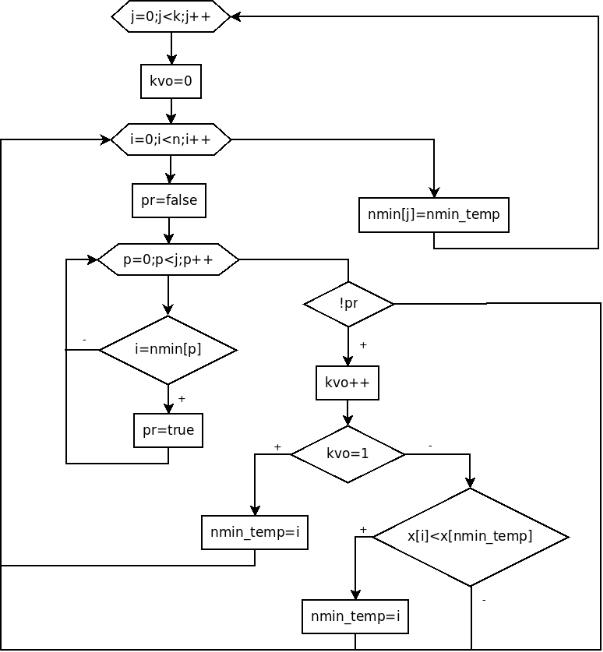
Блок-схема алгоритма поиска k минимальных элементов массива представлена на
рис. 5.934. Далее приведён текст программы с комментариями.
#include <iostream> using namespace std;
int main(int argc, char **argv)
{int p,j,i,n,*nmin,k,kvo,nmin_temp; bool pr;
double *x; cout<<«n=»;cin>>n; x=new double [n];
cout<<«Введите элементы массива Хn»; for(i=0;i<n;i++)
cin>>x[i];
cout<<«Введите количество минимумовn»;cin>>k;
nmin=new int[k];
//Цикл по переменной j для поиска номера j+1 минимального //элемента
for(j=0;j<k;j++)
{
kvo=0;
//Перебираем все элементы массива. for(i=0;i<n;i++)
{
//Цикл по переменной p проверяет содержится ли номер i в // массиве nmin.
pr=false;
for(p=0;p<j;p++)
if (i==nmin[p]) pr=true;
//Если не содержится, то количество элементов увеличить на // 1.
if (!pr)
{
kvo++;
34 В блок-схеме отсутствует ввод данных и вывод результатов.
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
152 |
Рисунок 5.9. Блок—схема алгоритма поиска k минимальных элементов в
массиве x.
//Если kvo=1, то найден первый элемент, который не
//содержится в массиве nmin, его номер объявляем номером
//минимального элемента массива
if (kvo==1) nmin_temp=i; else
//Если kvo>1, сравниваем текущий элемент x[i] с // минимальным.
if (x[i]<x[nmin_temp]) nmin_temp=i;
}
}
//Номер очередного минимального элемента записываем в // массив nmin.
nmin[j]=nmin_temp;
|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
153 |
}
//Вывод номеров и значений k минимальных элементов // массива.
for(j=0;j<k;j++)
cout<<«nmin1=»<<nmin[j]<<«tmin1=»<<x[nmin[j]]<<endl; return 0;
}
Проверку содержится ли число i в массиве nmin, можно оформить в виде функ-
ции, тогда программа будет иметь вид:
#include <iostream> using namespace std;
//Функция проверяет содержится ли число i в массиве x из n //элементов. Функция возвращает true, если содержится //false, если не содержится.
bool proverka(int i, int *x, int n)
{
bool pr; int p; pr=false;
for(p=0;p<n;p++)
if (i==x[p]) pr=true; return pr;
}
int main(int argc, char **argv)
{
int j,i,n,*nmin,k,kvo,nmin_temp;
double *x; cout<<«n=»;cin>>n; x=new double [n];
cout<<«Введите элементы массива Хn»; for(i=0;i<n;i++)
cin>>x[i];
cout<<«Введите количество минимумовn»;cin>>k; nmin=new int[k];
//Цикл по переменной j для поиска номера j+1 минимального // элемента
for(j=0;j<k;j++)
{
kvo=0;
//Перебираем все элементы массива. for(i=0;i<n;i++)
{
//Вызов функции proverka, чтобы проверить содержится ли число i
//в массиве nmin из j элементов if (!proverka(i,nmin,j))
{
kvo++;
if (kvo==1) nmin_temp=i; else

|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
154 |
if (x[i]<x[nmin_temp]) nmin_temp=i;
}
}
nmin[j]=nmin_temp;
}
//Вывод номеров и значений k минимальных элементов // массива.
for(j=0;j<k;j++)
cout<<«nmin1=»<<nmin[j]<<«tmin1=»<<x[nmin[j]]<<endl; return 0;
}
Авторы настоятельно рекомендуют читателю разобраться со всеми версиями решения задачи 5.3.
ЗАДАЧА 5.4. Поменять местами максимальный и минимальный элементы в массиве X.
Алгоритм решения задачи можно разбить на следующие этапы.
1.Ввод массива.
2.Поиск номеров максимального (nmax) и минимального (nmin) элементов массива.
3.Обмен элементов местами (рис. 2.1) с помощью временной (буферной) переменная temp:
temp=X[nmax];X[nmax]=X[nmin]; X[nmin]=temp;
Текст программы с комментариями:
#include <iostream> using namespace std;
int main(int argc, char **argv)
{int i,N,nmax,nmin; float temp; cout<<«N=»;cin>>N; float X[N];
cout<<«Введите элементы массива Хn»; for(i=0;i<N;i++)
cin>>X[i];
//Поиск номеров максимального и минимального элементов //массива.
for(nmax=nmin=0,i=1;i<N;i++)
{
if (X[i]<X[nmin]) nmin=i; if (X[i]>X[nmax]) nmax=i;
}
//Обмен максимального и минимального элементов местами. temp=X[nmax];X[nmax]=X[nmin]; X[nmin]=temp;
//Вывод преобразованного массива. cout<<«Преобразованный массив Хn»; for(i=0;i<N;i++)
cout<<X[i]<<» «; cout<<endl; return 0;
}
ЗАДАЧА 5.5. Найти среднее геометрическое среди простых чисел,

|
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++. |
155 |
расположенных между максимальным и минимальным элементами массива.
Среднее геометрическое k элементов (SG) можно вычислить по формуле SG=√k P , P – произведение k элементов. При решении этой задачи необходимо найти произведение и количество простых чисел, расположенных между максимальным и
минимальным элементами.
Алгоритм решения задачи состоит из следующих этапов:
1.Ввод массива.
2.Поиск номеров максимального (nmax) и минимального (nmin) элементов массива.
3.В цикле перебираем все элементы массива, расположенные между максимальным и минимальным элементами. Если текущий элемент является простым числом, то необходимо увеличить количество простых чисел на 1, и умножить P на значение элемента массива.
|
4. Вычислить |
k |
|
SG=√P . |
|
|
При решении |
этой задачи следуем учитывать, что неизвестно какой элемент |
расположен раньше максимальный или минимальный.
Текст программы с комментариями приведён далее.
#include <iostream> #include <math.h> using namespace std; bool prostoe (int N)
{
int i; bool pr;
if (N<2) pr=false; else
for(pr=true,i=2;i<=N/2;i++) if (N%i==0)
{
pr=false;
break;
}
return pr;
}
int main(int argc, char **argv)
{int i,k,n,nmax,nmin, p, *x;
//Ввод количества элементов в массиве. cout<<«n=»; cin>>n;
//Выделяем память для динамического массива x. x=new int [n];
//Ввод элементов массива. cout<<«Введите элементы массива X»; for(i=0;i<n;i++)
cin>>x[i];
//Поиск номеров максимального и минимального элементов в //массиве.
for(nmax=nmin=i=0;i<n;i++)
{
if (x[i]<x[nmin]) nmin=i;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
We are given an array, and we have to calculate the product of an array using both iterative and recursive methods.
Examples:
Input : array[] = {1, 2, 3, 4, 5, 6}
Output : 720
Here, product of elements = 1*2*3*4*5*6 = 720Input : array[] = {1, 3, 5, 7, 9}
Output : 945
Iterative Method: We initialize result as 1. We traverse array from left to right and multiply elements with results.
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
int multiply(int array[], int n)
{
int pro = 1;
for (int i = 0; i < n; i++)
pro = pro * array[i];
return pro;
}
int main()
{
int array[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(array) / sizeof(array[0]);
cout << multiply(array, n);
return 0;
}
Java
import java.io.*;
public class GFG
{
static int arr[] = {1, 2, 3, 4, 5, 6};
static int multiply()
{
int pro = 1;
for (int i = 0; i < arr.length; i++)
pro = pro * arr[i];
return pro;
}
public static void main(String[] args)
{
System.out.println(multiply());
}
}
Python3
def multiply( array , n ):
pro = 1
for i in range(n):
pro = pro * array[i]
return pro
array = [1, 2, 3, 4, 5, 6]
n = len(array)
print(multiply(array, n))
C#
using System;
class GFG
{
static int []arr = {1, 2, 3, 4, 5, 6};
static int multiply()
{
int pro = 1;
for (int i = 0; i < arr.Length; i++)
pro = pro * arr[i];
return pro;
}
public static void Main()
{
Console.Write(multiply());
}
}
PHP
<?php
function multiply($arr, $n)
{
$pro = 1;
for ($i = 0; $i < $n; $i++)
$pro = $pro * $arr[$i];
return $pro;
}
$arr = array(1, 2, 3, 4, 5, 6);
$n = sizeof($arr) / sizeof($arr[0]);
echo multiply($arr, $n);
return 0;
?>
Javascript
<script>
var arr = [ 1, 2, 3, 4, 5, 6 ];
function multiply() {
var pro = 1;
for (i = 0; i < arr.length; i++)
pro = pro * arr[i];
return pro;
}
document.write(multiply());
</script>
Time Complexity: O(n)
Auxiliary Space: O(1)
Recursive Method:
C++
#include<iostream>
using namespace std;
int multiply(int a[], int n)
{
if (n == 0)
return(a[n]);
else
return (a[n] * multiply(a, n - 1));
}
int main()
{
int array[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(array) / sizeof(array[0]);
cout << multiply(array, n - 1)
<< endl;
return 0;
}
Java
import java.io.*;
public class GFG
{
static int arr[] = {1, 2, 3, 4, 5, 6};
static int multiply(int a[], int n)
{
if (n == 0)
return(a[n]);
else
return (a[n] * multiply(a, n - 1));
}
public static void main(String[] args)
{
System.out.println(multiply(arr,
arr.length - 1));
}
}
Python3
def multiply( a , n ):
if n == 0:
return(a[n])
else:
return (a[n] * multiply(a, n - 1))
array = [1, 2, 3, 4, 5, 6]
n = len(array)
print(multiply(array, n - 1))
C#
using System;
class GFG
{
static int []arr = {1, 2, 3, 4, 5, 6};
static int multiply(int []a, int n)
{
if (n == 0)
return(a[n]);
else
return (a[n] * multiply(a, n - 1));
}
public static void Main()
{
Console.Write(multiply(arr,
arr.Length - 1));
}
}
PHP
<?php
function multiply( $a, $n)
{
if ($n == 0)
return($a[$n]);
else
return ($a[$n] *
multiply($a, $n - 1));
}
$array = array(1, 2, 3, 4, 5, 6);
$n = count($array);
echo multiply($array, $n - 1)
?>
Javascript
<script>
var arr = [ 1, 2, 3, 4, 5, 6 ];
function multiply(a , n) {
if (n == 0)
return (a[n]);
else
return (a[n] * multiply(a, n - 1));
}
document.write(multiply(arr,
arr.length - 1));
</script>
Time Complexity: O(n)
Auxiliary Space: O(n)
Using Library functions:
C++
#include <iostream>
#include <numeric>
using namespace std;
int multiply(int array[], int n)
{
int pro = 1;
return accumulate(array, array + n, pro,
multiplies<int>());
}
int main()
{
int array[] = { 1, 2, 3, 4, 5, 6 };
int n = sizeof(array) / sizeof(array[0]);
cout << multiply(array, n);
return 0;
}
Java
import java.util.Arrays;
import java.util.function.IntBinaryOperator;
public class GFG {
public static int multiply(int[] array)
{
int pro = 1;
return Arrays.stream(array).reduce(
pro, new IntBinaryOperator() {
@Override
public int applyAsInt(int left, int right)
{
return left * right;
}
});
}
public static void main(String[] args)
{
int[] array = { 1, 2, 3, 4, 5, 6 };
int n = array.length;
System.out.println(multiply(array));
}
}
Python3
from functools import reduce
def multiply(array, n):
return reduce((lambda x, y: x * y), array)
array = [1, 2, 3, 4, 5, 6]
n = len(array)
print(multiply(array, n))
C#
using System;
using System.Linq;
public class GFG {
static int Multiply(int[] array, int n)
{
int pro = 1;
return array.Aggregate(pro, (current, t) =
> current * t);
}
static public void Main(string[] args)
{
int[] array = { 1, 2, 3, 4, 5, 6 };
int n = array.Length;
Console.WriteLine(Multiply(array, n));
}
}
Javascript
<script>
function multiply(array) {
let pro = 1;
return array.reduce((acc, cur) => acc * cur, pro);
}
let array = [1, 2, 3, 4, 5, 6];
let n = array.length;
console.log(multiply(array));
</script>
Time Complexity: O(n)
Auxiliary Space: O(1)
This article is contributed by Rishabh Jain. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Last Updated :
01 Mar, 2023
Like Article
Save Article
Такая задача часто встречается, если вы начали изучение программирования и уже дошли до работы с массивами.
Давайте разберемся с ней. Если вам необходимо найсти сумму или произведение элементов массива, или даже и то и другое, то нам понадобится для этого всего лишь один цикл.
Мы с напишем программу, которая выведет сам массив, сумму элементов массива, а также произведение элементов массива. Напишем ее на C++.
Прежде чем написать, давайте немного разберем сам алгоритм, обозначим шаги, которые необходимо будет сделать.
Первое — создадим сам массив, создадим начальную переменную для хранения суммы и начальную переменную для хранения произведения элементов массива.
Второе — с помощью цикла берем каждый элемент с первого до последнего. Элемент прибавляем его к переменной, котроая хранит сумму и записываем в переменную, которая хранит сумму (тавталогия?). Аналогичное проделываем и с переменной, которая хранит произведение.
Третье — выводим массив и выводим значения переменных, которые хранят сумму и произведение элементов массива.
Давайте теперь уже напишем программу, которая найдет сумму и произведение элементов массива на C++
#include
using namespace std;
int main()
{
/* Заполним массив значениями */
int n = 6;
int mass[n] = {5, 3, 2, 9, 3, 8};
/* Создадим переменные для хранения суммы и произведения */
int sumValue = 0; // Сумма
int proValue = 1; // Произведение (по умолчанию 1)
cout << endl << "Массив = ";
/* Проходим по всем элементам массива */
for (int i = 0; i < n; ++i) {
// Вынесем текущий элемент в переменную
int currentElementValue = mass[i];
// Сразу выведем его
cout << currentElementValue << " ";
// Пересчитываем сумму элементов массива с текущим значением
sumValue = sumValue + currentElementValue;
// Пересчитываем произведение элементов массива с текущим значением
// Если бы по умолчанию proValue был не 1, а 0, то так сделать нельзя было бы
// т.к. был бы всегда 0 при умножениях.
proValue = proValue * currentElementValue;
}
cout << endl << "Сумма элементов массива = " << sumValue;
cout << endl << "Произведение элементов массива = " << proValue;
return 0;
}
Компилируем и запускаем. Видим следующий вывод программы.
Проверяем на калькуляторе — все работает как нужно.
Ну какая же это константа? Вернее, константа — только в том смысле, что size не будет изменяться, но во время компиляции эта константа неизвестна.
const int size = a;
Соответственно, это тоже неверно — в С++ размер массива должен быть известен во время компиляции:
int arr[size];
mul надо инициализировать — вы начинаете множить мусор. Да и в int результат вряд ли поместится без переполнения.
Так что…
int n;
cin >> n;
int * arr = new int[n];
for (int i = 0; i < n; i++)
cin >> arr[i];
double mul = 1;
for (int i = 0; i < n; i++)
mul *= arr[i];
cout << mul;
Только вот смотрите — можно два цикла объединить в один, так?
double mul = 1;
for (int i = 0; i < n; i++)
{
cin >> arr[i];
mul *= arr[i];
}
Но тогда встает вопрос — а зачем нам вообще массив? и мы получаем (еще и одну переменную экономим…)
int main()
{
int n;
cin >> n;
double mul = 1;
for (int i = n; i > 0; i--)
{
cin >> n;
mul *= n;
}
cout << mul;
}

