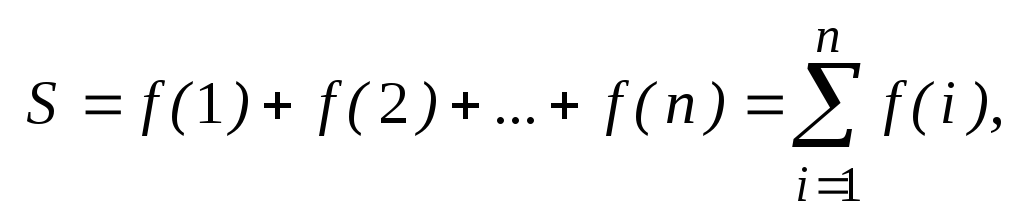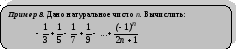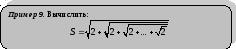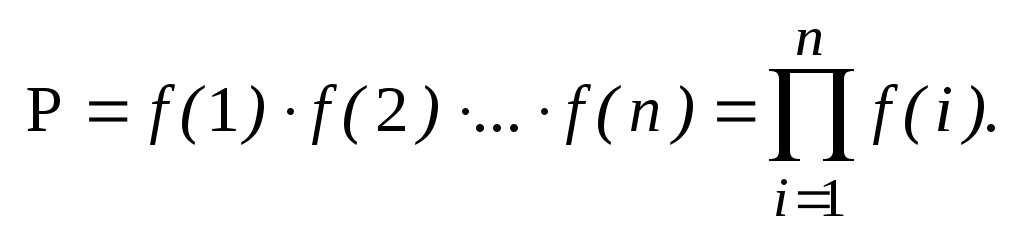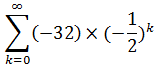Как составить программу расчета конечной суммы - AvtoShod.ru

Урок 2. Вычисление конечных сумм и произведений

Цель урока:

Предметная: Сформировать представление учащихся о методах вычисления конечных сумм и произведений с помощью цикла с параметром.
Общеобразовательная: Развивать умение осваивать новый материал, умение логически мыслить, применять полученные знания на практике.

Ход урока:

1.Организационный момент. (4 мин)

Приветствие класса
Проверка домашнего задания
Объявление нового раздела и темы урока

2. Изучение нового материала: рассмотрение принципов вычисления конечных сумм с использованием цикла с параметром (10 мин)

Учащиеся читают теорию (текст спроецирован на экран или интерактивную доску либо находится в файле, имеющемся на каждом компьютере):

Вычисление конечной суммы сводится к нахождению суммы некоторого количества слагаемых

S = формула = f (1) + f (2) + …+ f (n),

где i – номер слагаемого, f (i) – слагаемое с номером i.

Вычисление суммы ряда организуется в виде циклического процесса, когда при каждом прохождении цикла номер слагаемого увеличивается на единицу, а сумма – на величину i-го слагаемого, равного f (i). Т. о., s_i = s_i-1 + f (i), где s_i и s_i-1 – суммы первых i и i − 1 слагаемых соответственно. Процесс повторяется до тех пор, пока не будут просуммированы все n слагаемых.

Учащимся предлагается ответить на вопросы:

1) Какая величина будет параметром цикла при вычислении конечной суммы? (номер слагаемого i)

2) Чему равны начальное и конечное значения параметра цикла? (начальное значение – 1, конечное значение – n)

3) Сколько раз необходимо повторить цикл? (n раз).

3. Рассмотрение конкретных примеров (10 мин).

Пример. Составить программу вычисления суммы

формула.
Формула суммирования должна быть записана в программе следующим образом:

S := S + f (i)

Это означает, что к предыдущему значению суммы добавляется i-е слагаемое и вычисленное значение присваивается той же переменной S (старое значение S при этом стирается). Если начальное значение S приравнять нулю, то после первого выполнения цикла значение S будет равно значению первого слагаемого: S = 0 + f (1).

Программа решения задачи будет иметь вид:

PROGRAM Summa;

CONST n : integer = 50;

VAR x, S : real;

i : integer;

BEGIN

readln (x);

S := 0.;

FOR i := 1 TO n DO

S := S + (cos ( (2 * i + 1) * x) ) / (2 * i + 1);

writeln (‘S = ‘, S);

END.

(Вопрос для учащихся:

что нерационально в этой программе?

Ответ:

Дважды вычисляется величина 2 * i + 1, и поэтому программа тратит лишнее время.

Для исправления этой ошибки следует ввести дополнительную переменную, например, k, и присвоить этой переменной значение 2i + 1. Исправленная программа имеет вид:

PROGRAM Summa;

CONST n : integer = 50;

VAR x, S : real;

i, k : integer;

BEGIN

readln (x);

S := 0.;

FOR i := 1 TO n DO

BEGIN

k := 2 * i + 1;

S := S + cos (k * x) / k;

END;

writeln (‘S = ‘, S);

END.

Примечания.

1. Оператор присвоения начального значения суммы S := 0. расположен до начала цикла, т. к. это присваивание необходимо сделать только один раз, до начала вычисления суммы.

2. Поскольку результат вычислений – одно число (окончательное значение суммы, вычисленное в цикле), то оператор вывода стоит после цикла и выполняется один раз.

4. Практическая работа: Составление программы вычисления конечной суммы (15 мин)

Учащиеся самостоятельно составляют программу вычисления суммыформула

Программа имеет вид:

PROGRAM Summa1;

CONST n : integer = 20;

VAR k : integer;

a, x, S : real;

BEGIN

readln (a, x);

S := 0.;

FOR k := 0 TO 20 DO

S := S + (a / x) * (2 * (k – 1));

writeln (‘S = ‘, s);

END.

5. Подведение итогов урока. Закрепление пройденного на уроке. (4 мин)

Учащимся предлагается ответить на контрольные вопросы:

1) По какой формуле вычисляется конечная сумма?

2) Чему равно начальное значение суммы?

3) Что прибавляется к сумме при очередном прохождении цикла?

4) Попробуйте догадаться, каким образом следует вычислять конечное произведение вида

P = формула = f (1) • f (2) • … • f (n) ?

6. Домашнее задание. (2 мин)

Составить программу вычисления произведения P = формула . Числa n и x вводится с клавиатуры.

Программа должна иметь вид:

PROGRAM Proizv;

VAR i, j, n : integer;

P, x : real;

BEGIN

readln (n, x);

P := 1.;

FOR i := 1 TO n DO

BEGIN

j := 2 * i;

P := P * ( (cos (j + 1) ) / (sin (j — 1)));

END;

writeln (‘P = ‘, P);

END.

на главную

Источник

Вычисление
конечной суммы сводится к нахождению
суммы заданного количества слагаемых:

где
i
– номер слагаемого; f(i)
– слагаемое
с номером i.

Вычисление
конечной суммы организуется в виде
циклического алгоритма, когда при каждом
прохождении цикла номер слагаемого i
увеличивается на единицу, а сумма
изменяется на величину i-го
слагаемого f(i),
т. е. используется следующее рекуррентное
соотношение:

где
– суммы слагаемыхi
и i–1
соответственно.

Цикл
повторяется до тех пор, пока не будут
просуммированы все n
слагаемых. Для того чтобы начальное
значение суммы не исказило результат,
она предварительно должна быть обнулена
(S₀=0).
Вывод результата осуществляется после
окончания работы цикла.

Рассмотрим
в качестве примеров несколько задач.

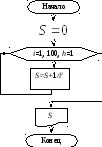
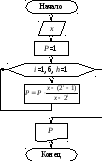
Алгоритм
решения задачи:

Программа:

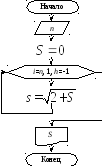
CLS

S
= 0

FOR
i = 1 TO 100

S
= S + 1 / i ^ 2

NEXT
i

PRINT
«S=»;
S

END

Результаты
работы программы:

S=
1.634984

Программа:

CLS

INPUT
«n=»; n

S
= 0

FOR
i = 1 TO n

S
= S + (-1) ^ i / (2 * i + 1)

NEXT
i

PRINT
«S=»; S

END

Алгоритм
решения задачи:

Результаты
работы программы:

n=?
5

S=-.2559885

Программа:

CLS

INPUT
«n=»;
n

s
= 0

FOR
i = n TO 1 STEP -1

s
= SQR(2 + s)

NEXT
i

PRINT
«S=»; s

END

Алгоритм
решения задачи:

Результаты
работы программы:

n=?
10

S=
1.999998

2.3. Вычисление конечного произведения

Вычисление
конечного произведения представляет
собой процесс нахождения произведения
заданного количества сомножителей по
формуле:

Как
и суммирование вычисление произведения
организуется с помощью циклического
процесса по рекуррентному соотношению:

где
P_i
и P_i_-1
– произведения сомножителей i
и i–1
соответственно, причем i
изменяется от 1 до
n. В отличие
от суммирования начальное значение
произведения Р₀
должно быть равно единице.

Рассмотрим
в качестве примеров несколько задач.

Алгоритм
решения задачи:

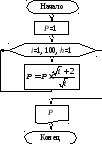
Программа:

CLS

P
= 1

FOR
i = 1 TO 100

P
= P * (SQR(i) + 2) / SQR(i)

NEXT
i

PRINT
«P=»; P

END

Результаты
работы программы:

P=
1.379896E+13

Программа:

CLS

INPUT
«x=»; x

P
= 1

FOR
i = 1 TO 6

P
= P * (x — (2 ^ i — 1)) / (x — 2 ^ i)

NEXT
i

PRINT
«P=»; P

END

Алгоритм
решения задачи:

Результаты
работы программы:

x=?
0.1

P=
.274885

Программа:

CLS

INPUT
«n,x=»; n, x

P1
= 1

P2
= 1

S
= 0

FOR
i = 1 TO n

P1
= P1 * i

P2
= P2 * x

S
= S + P2 / P1

NEXT
i

PRINT
«S=»; S

END

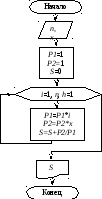
Алгоритм
решения задачи:

Результаты
работы программы:

n,x=?
10,2

S=
6.388995

2.4. Вложенные циклы

Допускается
вкладывать циклы FOR…NEXT,
то есть помещать цикл FOR…NEXT
внутри другого цикла FOR…NEXT.
Существуют две конструкции вложенных
циклов

Особенности
вложенных циклов:

счетчикам
необходимо давать разные имена,
оператор
NEXT
для внутреннего цикла должен предшествовать
оператору NEXT
для внешнего цикла.
Оператор
NEXT
K,J,I
эквивалентен операторам NEXT
K:
NEXT
J:
NEXT I

FOR
I = 1 TO n

.
. . . .

FOR
J = 1 TO m

.
. . . .

FOR
K = 1 TO

.
. . . . .

NEXT
K,J,I

Программа:

CLS

INPUT
«vvod
x=»;
x

P
= 1

pi
= 3.14

FOR
i = 1 TO 4

S
= 0

FOR
j = 1 TO 5

S
= S + (x * SIN(i * pi / 180) + 2 ^ j)

NEXT
j

P
= P * S

NEXT
i

PRINT
«P=»;
P

END

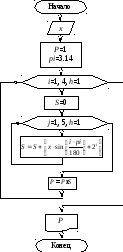
Алгоритм
решения задачи:

Результаты
работы программы:

vvod
x=?
0.2

P=
1.481793E+07

vvod
x=? 1.5

P=
1.50903E+07

vvod
x=? 3.4

P=
1.549465E+07

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#

25.09.2019180.65 Кб14, 21,22,23,24,25,26,27,28,29,30.docx
#
#
#
#
#
#
#
#
#

Источник

В этом уроке мы расскажем как вычислить сумму бесконечного сходящегося ряда (последовательности) с определенной точностью. Будет рассмотрена соответствующая программа, написанная на языке программирования Си. В конце статьи можно скачать исходник этой программы для Visual Studio.

Сходящийся ряд — это числовая последовательность элементов множества X, имеющая предел в этом множестве.

Сходящийся ряд

Рассмотрим задачу вычисления суммы сходящегося ряда с определенной точностью на примере. Пусть дан ряд:

Вычисление суммы ряда с определенной точностью ε означает, что сумма ряда вычисляется до тех пор, пока модуль разности между текущим и предыдущим членом последовательности больше ε. В виде формулы это утверждение можно записать так: |a_n — a_n-1| > ε, то есть пока это выражение истинно, вычисления продолжаются.

Сначала напишем на языке Си функцию, которая будет вычислять и возвращать значение k-го члена ряда по переданному в нее значению k.

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

res — это переменная вещественного типа повышенной точности double, в которую будет записан результат вычисления k-го члена ряда. Это же значение и будет возвращаться функцией.

Выражение res *= (double)powf(-0.5, k); эквивалентно выражению res = res * (double)powf(-0.5, k);

Оператор powf — это оператор возведения числа в степень. В нашем случае он вычисляет: -0.5^k.

Функцию f можно записать короче:

double f(int k)

{

return —32.0 * powf(—0.5, k);

}

Теперь перейдем к функции main. Для начала считаем с консоли число e — это и будет заданная точность вычислений ε.

float e;

printf(«e = «);

scanf_s(«%f», &e);

Объявим переменные, в которых будут хранится: значение предыдущего, значение текущего члена ряда, сумма ряда и номер текущего члена ряда (число k) соответственно.

double previous, current;

double sum = 0;

int k = 0;

Отдельно вычислим первый член ряда (потом он станет «предыдущим»), чтобы затем перейти к вычислениям в цикле.

current = f(k);

sum += current;

k++;

Запись выражения sum += current; эквивалентна записи: sum = sum + current;

Теперь перейдем к вычислениям в цикле. Условием выхода из цикла будет ложность выражения: |a_n — a_n-1| > ε.

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

Сумма посчитана. Осталось вывести результат вычислений в консоль.

printf(«sum = %fn», sum);

В итоге код программы с необходимыми подключенными библиотеками будет выглядеть следующим образом:

#include <stdio.h>

#include <math.h>

#include <conio.h>

double f(int k)

{

double res;

res = —32.0;

res *= (double)powf(—0.5, k);

return res;

}

int main()

{

float e;

printf(«e = «);

scanf_s(«%f», &e);

double previous, current;

double sum = 0;

int k = 0;

current = f(k);

sum += current;

k++;

{

previous = current;

current = f(k);

sum += current;

k++;

} while (abs(current — previous) > e);

printf(«sum = %fn», sum);

_getch();

return 0;

}

Оператор _getch(); в строке 34 нужен для того, чтобы консоль не закрывалась сразу по завершении исполнения программы.

Демонстрация работы программы для нашего ряда представлена на скриншоте ниже. Точность вычислений составляет: ε = 0.01.

Скачать исходник

Источник

Раздел:
Задачи /
Простейшие /

Программа вычисления суммы

Основы программирования
Каждый профессионал когда-то был чайником. Наверняка вам знакомо состояние, когда “не знаешь как начать думать, чтобы до такого додуматься”. Наверняка вы сталкивались с ситуацией, когда вы просто не знаете, с чего начать.
Эта книга ориентирована как раз на таких людей, кто хотел бы стать программистом, но совершенно не знает, как начать этот путь.
Подробнее…

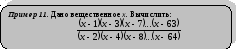
Условие задачи 2.4

Задача 2.4
Написать программу для вычисления суммы по формуле:

S = (1*2) / (3*4) + (3*4) / (5*6) + … + (85*86) / (87*88)

Хотя в учебнике, из которого я взял эту задачу, она помечена звёздочкой
(что означает средний уровень сложности), особых затруднений её решение не должно
вызвать даже у новичка, если, конечно, он знает, что такое циклы.

Итак, как вы уже догадались, составить программу вычисления суммы по заданной выше формуле можно, используя цикл.

Алгоритм будет несложным. Мы используем четыре переменных для работы с множителями и одну переменную (Sum) для вычисления суммы:

Сначала мы определяем первый множитель (n1) и присваиваем ему значение 1.
Затем в цикле:

Увеличиваем значения остальных множителей (n2, n3, n4) таким образом, чтобы в первой итерации n2, n3 и n4 были равны соответственно 2, 3 и 4. А последующих итерациях они также будут зависеть от значения первого множителя n1.
Вычисляем выражение (n1 * n2) / (n3 * n4) и прибавляем его к значению переменной Sum.

В итоге после завершения цикла будет вычислена нужная нам сумма.

Ниже приведены решения на Паскале и
С++.

Решение задачи 2.4 на Паскале

program summa;

const
  MAX_NUM = 85;

//****************************************************************
// ГЛОБАЛЬНЫЕ ПЕРЕМЕННЫЕ
//****************************************************************
var
  n1, n2, n3, n4  : Integer;
  Sum             : Single;

//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
begin
  Sum := 0;
  n1 := 1;
  while n1 <= MAX_NUM do
    begin
      n2 := n1 + 1;
      n3 := n2 + 1;
      n4 := n3 + 1;
      Sum := Sum + (n1 * n2) / (n3 * n4);
      Inc(n1, 2);
    end;
  WriteLn('Summa = ', Sum:0:4);
  WriteLn('The end. Press ENTER...');
  ReadLn;
end.

Решение задачи 2.4 на С++

#include 
#include 

using namespace std;

const int MAX_NUM = 85;  

//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
int main(int argc, char *argv[])
{
  int n1, n2, n3, n4;
  float Sum;
  
  Sum = 0;
  n1 = 1;
  while (n1 <= MAX_NUM)
  {
    n2 = n1 + 1;
    n3 = n2 + 1;
    n4 = n3 + 1;
    Sum = Sum + float(n1 * n2) / float(n3 * n4);
    n1 = n1 + 2;
  }
  cout << "Summa = " << Sum << endl;  
  
  system("PAUSE");
  return EXIT_SUCCESS;
}

ВАЖНО!
Обратите внимание на строку в примере на С++, которая выделена красным цветом.
Результат выражений (n1 * n2) и (n3 * n4) мы явно преобразуем к типу float.
Если этого не сделать, то деление первого выражения на второе вернёт ноль,
так как n1…n4 — это целочисленные переменные. Поэтому нам надо либо объявлять
n1…n4 как float, либо явно преобразовывать их в тип float. Вот такой вот
С++ заморочистый язык.

Как стать программистом 2.0

Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки…
Подробнее…

Помощь в технических вопросах

Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации.
Подробнее…

Источник

Цель работы
Постановка задания (задача №1)
- Варианты заданий
- Образец выполнения (вариант №1)
  - Условие задания
  - Решение задачи с использованием макроса на VBA
  - Решение задачи с использованием функции на VBA
  - Результаты работы программы
Постановка задания (задача №2)
- Варианты заданий
- Образец выполнения (вариант №1)
  - Условие задания
  - Решение задачи с использованием макросов на VBA
  - Результаты работы программы

ВНИМАНИЕ	Для получения программы своего варианта пишите на наш электронный адрес proglabs@mail.ru
💡 Время нашего ответа обычно составляет не более 10 минут.

Цель работы

Приобретение навыков написания программ на VBA с использованием циклических алгоритмов.

Постановка задания (задача №1)

Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):

Написать программу вычисления суммы (произведения) конечного числа элементов ряда с использованием цикла с параметром.

Варианты заданий

№	Сумма (произведение) ряда
1	$S_n = sumlimits_{n = 1}^{50} frac{cos(nx) + sin(nx)}{n + 1}$, $x$ вводится пользователем с клавиатуры
2	$P_n = prodlimits_{n = 1}^{10} frac{n cdot sin(n + 2)}{n^2 + 2}$
3	$S_n = sumlimits_{n = 1}^{25} frac{n^3 + 5n^2 — 7n + 14 + 2cos(n)}{n^5 + 2n^3 — 4n + 11}$
4	$P_n = prodlimits_{n = 1}^{20} frac{n^4 + 10n^3 — 8n^2 + 15n — 2n + 7}{3n^5 + 2n^3 — n + 17}$
5	$S_n = sumlimits_{n = 1}^{50} frac{sin(nx) — cos(nx)}{n^3 + 4n + 5}$, $x$ вводится пользователем с клавиатуры
6	$P_n = prodlimits_{n = 1}^{10} frac{a + n}{cos(a^n) cdot n}$, $a$ вводится пользователем с клавиатуры
7	$S_n = sumlimits_{n = 1}^{100} frac{a cdot sin(a^n)}{n + a}$, $a$ вводится пользователем с клавиатуры
8	$P_n = prodlimits_{n = 1}^{10} frac{n^x}{n^{x + 1} + 5n}$, $x$ вводится пользователем с клавиатуры
9	$S_n = sumlimits_{n = 1}^{50} frac{n cdot sin(n)}{n cdot sin(n) + 5n + 4}$
10	$P_n = prodlimits_{n = 1}^{5} frac{cosfrac{1}{n} + n}{cosfrac{1}{n} + n + n^2}$

Образец выполнения (вариант №1)

Условие задания

$S_n = sumlimits_{n = 1}^{50} frac{cos(nx) + sin(nx)}{n + 1}$,

$x$ вводится пользователем с клавиатуры

Решение задачи с использованием макроса на VBA

‘ процедура (запускается при помощи макроса), вычисляющая конечную сумму ряда

Sub Sum()

‘ раздел объявления переменны

Dim x As Double ‘ значение, вводимое пользователем в ячейку A2

Dim S As Double ‘ рассчитываемая сумма конечного ряда

Dim n As Integer ‘ счетчик цикла с параметром

Dim current As Double ‘ значение текущего слагаемого ряда

‘ производим очистку от прошлых выводов

Worksheets(«Task1»).Cells(2, «B»).ClearContents

S = 0 ‘ перед накоплением суммы необходимое стартовое обнуление

‘ считываем значение переменной х, введенное пользователем в ячейку А2

x = Worksheets(«Task1»).Cells(2, 1)

‘ в цикле от 1 до 50 вычисляем очередной член ряда и добавляем к результирующей сумме

For n = 1 To 50 Step 1

‘ получаем значение текущего члена ряда конечной суммы

current = (Cos(n * x) + Sin(n * x)) / (n + 1)

‘ добавляем значение текущего члена к итоговой сумме

S = S + current

Next n ‘ конец цикла со счетчиком

‘ выводим значение рассчитанной суммы в ячейку B2

Worksheets(«Task1»).Cells(2, 2) = S

End Sub

Решение задачи с использованием функции на VBA

‘ функция (выбираемая пользователем вручную), вычисляющая конечную сумму ряда

‘ x — входной параметр, значение которого вводит пользователь с клавиатуры в ячейку А2

Function GetSum(x As Double) As Double

‘ раздел объявления переменны

Dim S As Double ‘ рассчитываемая сумма конечного ряда

Dim n As Integer ‘ счетчик цикла с параметром

Dim current As Double ‘ значение текущего слагаемого ряда

‘ производим очистку от прошлых выводов

Worksheets(«Task1»).Cells(2, «B»).ClearContents

S = 0 ‘ перед накоплением суммы необходимое стартовое обнуление

‘ в цикле от 1 до 50 вычисляем очередной член ряда и добавляем к результирующей сумме

For n = 1 To 50 Step 1

‘ получаем значение текущего члена ряда конечной суммы

current = (Cos(n * x) + Sin(n * x)) / (n + 1)

‘ добавляем значение текущего члена к итоговой сумме

S = S + current

Next n ‘ конец цикла со счетчиком

GetSum = S ‘ возвращаем результат из функции

End Function

Результаты работы программы

Поскольку интерфейс программы одинаков, то приведем обобщенные результаты.

➡ Важно понимать, что для одного и того же значения переменной $x$, как макрос, так и функция получит одинаковый результат.

Тестирование через макрос

Тестирование через функцию

ВНИМАНИЕ	Для получения макроса или функции своего варианта пишите на наш электронный адрес proglabs@mail.ru
💡 Время нашего ответа обычно составляет не более 10 минут.

Постановка задания (задача №2)

К задаче своего варианта необходимо написать пять программ, используя циклы с предусловием и постусловием.

Варианты заданий

№	Условие
1	Вычислить произведение вводимых пользователем с клавиатуры чисел, если числа считываются до тех пор, пока не будет введена единица.
2	Вычислять и выводить в ячейки рабочего листа кубы вводимых пользователем с клавиатуры чисел до тех пор, пока не будет введено $3$.
3	Вычислять и выводить в ячейки рабочего листа члены арифметической прогрессии до тех пор, пока очередной член прогрессии не окажется большим $50$. Первый член арифметической прогрессии равен $2$, разность равна $5$.
4	Вычислять и выводить в ячейки рабочего листа члены геометрической прогрессии до тех пор, пока очередной член прогрессии не окажется большим $250$. Первый член геометрической прогрессии равен $3$, знаменатель равен $4$.
5	Общий член последовательности задан формулой: $a_n = frac{n^2}{5}$. Вычислить сумму $n$ первых членов последовательности, меньших $75$.
6	Общий член последовательности задан формулой: $a_n = frac{5n}{n^2 + 1}$. Вычислить сумму $n$ первых членов последовательности, больших $1$.
7	Общий член последовательности задан формулой: $a_n = frac{n}{5} + 2n + 1$. Суммировать первые $n$ членов последовательности, до тех пор, пока сумма не окажется большей $100$. Вывести значение суммы и последнего $n$-го члена последовательности.
8	Общий член последовательности задан формулой: $a_n = frac{n}{3} + n + 4$. Вычислять произведение первых $n$ членов последовательности до тех пор, пока произведение не окажется большим $1000$. Вывести значение произведения и последнего $n$-го члена последовательности.
9	Первый член арифметической прогрессии равен $-50$, разность равна $7$. Вывести на в ячейки рабочего листа все члены данной арифметической прогрессии, меньшие нуля.
10	Первый член арифметической прогрессии равен $90$, разность равна $-8$. Вычислить сумму всех положительных членов данной арифметической прогрессии.

Образец выполнения (вариант №1)

Условие задания

Вычислить произведение вводимых пользователем с клавиатуры чисел, если числа считываются до тех пор, пока не будет введена единица.

Решение задачи с использованием макросов на VBA

Всего было закодировано $5$ различных макросов для всех видов циклов с пред- и постусловием.

‘ решение задачи с использование цикла While-Wend

Sub While_Wend()

‘ раздел объявления переменных

Dim x As Integer ‘ значение, вводимое пользователем с клавиатуры

Dim P As Long ‘ накапливаемое произведение вводимых чисел

P = 1 ‘ при расчете произведения следует присвоить изначально результату 1

‘ запрашиваем 1ое число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

‘ пока пользователь не введет число, равное единице, продолжаем вычисления

‘ цикл выполняется, пока условие в заголовке цикла является ИСТИННЫМ

While (x <> 1)

P = P * x

‘ запрашиваем очередное число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

Wend

‘ выводим накопленное произведение в соот-щую ячейку листа Excel

Worksheets(«Task2»).Cells(5, «B») = P

End Sub

‘ решение задачи с использование цикла Do While-Loop

Sub Do_While_Loop()

‘ раздел объявления переменных

Dim x As Integer ‘ значение, вводимое пользователем с клавиатуры

Dim P As Long ‘ накапливаемое произведение вводимых чисел

P = 1 ‘ при расчете произведения следует присвоить изначально результату 1

‘ запрашиваем 1ое число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

‘ пока пользователь не введет число, равное единице, продолжаем вычисления

‘ цикл выполняется, пока условие в заголовке цикла является ИСТИННЫМ

Do While (x <> 1)

P = P * x

‘ запрашиваем очередное число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

Loop

‘ выводим накопленное произведение в соот-щую ячейку листа Excel

Worksheets(«Task2»).Cells(6, «B») = P

End Sub

‘ решение задачи с использование цикла Do Until-Loop

Sub Do_Until_Loop()

‘ раздел объявления переменных

Dim x As Integer ‘ значение, вводимое пользователем с клавиатуры

Dim P As Long ‘ накапливаемое произведение вводимых чисел

P = 1 ‘ при расчете произведения следует присвоить изначально результату 1

‘ запрашиваем 1ое число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

‘ пока пользователь не введет число, равное единице, продолжаем вычисления

‘ цикл выполняется, пока условие в заголовке цикла является ЛОЖНЫМ

Do Until (x = 1)

P = P * x

‘ запрашиваем очередное число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

Loop

‘ выводим накопленное произведение в соот-щую ячейку листа Excel

Worksheets(«Task2»).Cells(7, «B») = P

End Sub

‘ решение задачи с использование цикла Do-Loop While

Sub Do_Loop_While()

‘ раздел объявления переменных

Dim x As Integer ‘ значение, вводимое пользователем с клавиатуры

Dim P As Long ‘ накапливаемое произведение вводимых чисел

P = 1 ‘ при расчете произведения следует присвоить изначально результату 1

‘ пока пользователь не введет число, равное единице, продолжаем вычисления

‘ цикл выполняется, пока условие в заголовке цикла является ИСТИННЫМ

‘ запрашиваем очередное число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

‘ если введенное число не равно 1, то пересчитываем произведение

If (x <> 1) Then

‘ пересчитываем произведение

P = P * x

End If

Loop While (x <> 1)

‘ выводим накопленное произведение в соот-щую ячейку листа Excel

Worksheets(«Task2»).Cells(8, «B») = P

End Sub

‘ решение задачи с использование цикла Do-Loop Until

Sub Do_Loop_Until()

‘ раздел объявления переменных

Dim x As Integer ‘ значение, вводимое пользователем с клавиатуры

Dim P As Long ‘ накапливаемое произведение вводимых чисел

P = 1 ‘ при расчете произведения следует присвоить изначально результату 1

‘ пока пользователь не введет число, равное единице, продолжаем вычисления

‘ цикл выполняется, пока условие в заголовке цикла является ЛОЖНЫМ

‘ запрашиваем очередное число от пользователя

x = InputBox(«Введите число х: «, «Сообщение для пользователя»)

‘ если введенное число не равно 1, то пересчитываем произведение

If (x <> 1) Then

‘ пересчитываем произведение

P = P * x

End If

Loop Until (x = 1)

‘ выводим накопленное произведение в соот-щую ячейку листа Excel

Worksheets(«Task2»).Cells(9, «B») = P

End Sub

Результаты работы программы

Программа имеет следующий интерфейс:

Для тестирования задачи необходимо последовательно запустить каждый из созданных нами ранее $5$ макросов:

Покажем результаты работы программы только при запуске макроса «While — Wend», так как результаты для других макросов будут абсолютно аналогичными.

Будем последовательно вводить следующие числа: $2$, $5$, $4$, $3$, $1$. При вводе числа $1$ программа прекратит свое исполнение и отобразит результат в соответствующей ячейке.

Каким должен быть ответ? Наша цель — найти произведение введенных чисел, то есть ответ будет равен — $2 cdot 5 cdot 4 cdot 3 = 120$.

В конечном итоге, после последовательного запуска всех макросов, в ячейки электронной таблицы будет выведен следующий результат:

💡 Делаем вывод, что все макросы отработали успешно и все заданные циклы с пред- и постусловием отработали корректно.

ВНИМАНИЕ	Для получения $5$ процедур своего варианта пишите на наш электронный адрес proglabs@mail.ru
💡 Время нашего ответа обычно составляет не более 10 минут.

Источник

Урок 2. Вычисление конечных сумм и произведений

Цель урока:

Ход урока:

1.Организационный момент. (4 мин)

2. Изучение нового материала: рассмотрение принципов вычисления конечных сумм с использованием цикла с параметром (10 мин)

3. Рассмотрение конкретных примеров (10 мин).

Примечания.

4. Практическая работа: Составление программы вычисления конечной суммы (15 мин)

5. Подведение итогов урока. Закрепление пройденного на уроке. (4 мин)

6. Домашнее задание. (2 мин)

2.3. Вычисление конечного произведения

2.4. Вложенные циклы

Программа вычисления суммы

Условие задачи 2.4

Цель работы

Постановка задания (задача №1)

Варианты заданий

Образец выполнения (вариант №1)

Условие задания

Решение задачи с использованием макроса на VBA

Решение задачи с использованием функции на VBA

Результаты работы программы

Постановка задания (задача №2)

Варианты заданий

Образец выполнения (вариант №1)

Условие задания

Решение задачи с использованием макросов на VBA

Результаты работы программы

Не пропустите также: