Уравнение вида a⋅x2 + b⋅x + c = 0 — квадратное уравнение.
a, b, c — действительные числа, a ≠ 0.
Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.
D = b2 — 4⋅a⋅c;
- если D < 0, то квадратное уравнение не имеет корней;
- если D = 0, то уравнение имеет один действительный корень(иногда говорят, что корней два, но они одинаковые):
- x1 = x2 = -b / (2⋅a);
- если D > 0, то уравнение имеет два действительных корня:
- x1 = (-b + √D) / (2⋅a);
- x2 = (-b + √D) / (2⋅a).
Программа для решения квадратного уравнения на языке программирования Паскаль
{$CODEPAGE UTF8}
program QuadraticEquation;
var
a, b, c, x1, x2, discriminant : real;
begin
{ввыод данных}
write('a = ');
readln(a);
write('b = ');
readln(b);
write('c = ');
readln(c);
{дискриминант}
discriminant := sqr(b) - 4 * a * c;
if discriminant < 0 then
writeln('Квадратное уравнение не имеет корней')
else
begin
if discriminant = 0 then
begin
{квадратное уравнение имеет два одинаковых корня}
x1 := -b / (2 * a);
x2 := x1;
end
else
begin
{уравнение имеет два разных корня}
x1 := (-b + sqrt(discriminant)) / (2 * a);
x2 := (-b - sqrt(discriminant)) / (2 * a);
end;
{вывод корней уравнения}
writeln('x1 = ', x1:8:3);
writeln('x2 = ', x2:8:3);
end;
writeln('Press Enter to Exit...');
readln;
end.
Функция sqr языка Pascal используется для возведения числа в квадрат.
Функция sqrt используется для получения квадратного корня числа.
В программе используется форматированный вывод вещественных чисел. variable:8:3 — означает, что для вывода переменной предусмотрено 8 символов, 5 из них под целую часть и 3 под дробную.
Смотрите также:
Перейти к содержанию
Решить квадратное уравнение
Просмотров 12.6к. Обновлено 15 октября 2021
Найти корни квадратного уравнения и вывести их на экран, если они есть. Если корней нет, то вывести сообщение об этом. Конкретное квадратное уравнение определяется коэффициентами a, b, c, которые вводит пользователь.
Квадратное уравнение имеет вид ax2 + bx + c = 0. Коэффициенты a, b и c — это конкретные числа, а x надо найти, решив уравнение.
- Вычислить дискриминант по формуле d = b2 — 4ac.
- Если дискриминант больше нуля, то вычислить два корня уравнения:
x1 = (-b+√d) / 2a
x2 = (-b-√d) / 2a - Если дискриминант равен нулю, то вычислить только один корень (второй будет равен ему).
- Если дискриминант отрицателен, то вывести сообщение, что корней нет.
Pascal
квадратное уравнение паскаль
var
a,b,c,d,x1,x2: real;
begin
write('a='); readln(a);
write('b='); readln(b);
write('c='); readln(c);
d := b*b - 4*a*c;
if d > 0 then begin
x1 := (-b + sqrt(d)) / (2*a);
x2 := (-b - sqrt(d)) / (2*a);
writeln('x1=',x1:3:2,'; x2=',x2:3:2);
end
else
if d = 0 then begin
x1 := (-b) / (2*a);
writeln('x=',x1:5:2);
end
else
writeln('Корней нет');
end.
a=7
b=1
c=-6
x1=0.86; x2=-1.00
Язык Си
#include < stdio.h>
#include < math.h>main() {
float a,b,c,d,x1,x2;
printf("a="); scanf("%f",&a);
printf("b="); scanf("%f",&b);
printf("c="); scanf("%f",&c);
d = b*b - 4*a*c;
if (d>0) {
x1 = (-b + sqrt(d)) / (2*a);
x2 = (-b - sqrt(d)) / (2*a);
printf("x1=%.2f; x2=%.2f", x1, x2);
}
else
if (d = 0) {
x1 = -b / (2*a);
printf("x1=%.2f; x2=%.2f", x1, x2);
}
else printf("Корней нет.");
printf("n");
}
a=-20
b=8
c=1.5
x1=-0.14; x2=0.54
Ключ -lm при компиляции gcc.
Python
python квадратное уравнение
print("Введите коэффициенты для квадратного уравнения (ax^2 + bx + c = 0):")
a = float(input("a = "))
b = float(input("b = "))
c = float(input("c = "))discr = b**2 - 4 * a * c;
print("Дискриминант D = %.2f" % discr)
if discr > 0:
import math
x1 = (-b + math.sqrt(discr)) / (2 * a)
x2 = (-b - math.sqrt(discr)) / (2 * a)
print("x1 = %.2f nx2 = %.2f" % (x1, x2))
elif discr == 0:
x = -b / (2 * a)
print("x = %.2f" % x)
else:
print("Корней нет")
КуМир
алг квадратное уравнение
нач
вещ a, b, c, D, x1, x2
ввод a
ввод b
ввод c
D := b**2 - 4*a*c
вывод "D = ", D, нс
если D > 0 то
x1 := (-b + sqrt(D)) / (2 * a)
x2 := (-b - sqrt(D)) / (2 * a)
вывод "x1 = ", x1, нс
вывод "x2 = ", x2, нс
иначе
если D = 0 то
x1 := -b / (2 * a)
вывод "x = ", x1, нс
иначе
вывод "корней нет", нс
все
все
кон
Basic-256
input "a = ", a
input "b = ", b
input "c = ", c
d = b^2 - 4*a*cdecimal 3
if d > 0 then
x1 = (-b + sqrt(d)) / (2*a)
x2 = (-b - sqrt(d)) / (2*a)
print "x1 = " + x1 + ", x2 = " + x2
else
if d = 0 then
x = -b / (2*a)
print "x = " + x
else
print "Корней нет"
endif
endif
Команда decimal указывает сколько знаков после запятой следует выводить.
Программирование на Паскале. Тема: «Решение квадратного уравнения с использованием конструкции IF–THEN–ELSE»
Цели урока:
Оборудование:
До сих пор мы с вами говорили о каких-то отвлечённых задачах из области математики. Сегодня мы поговорим о конкретной задаче, которая встречается у вас почти на каждом уроке. Это решение квадратного уравнения. Я хочу, чтобы вы на примере этой задачи поняли, что программирование — это не просто прихоть учителя, это действительно раздел информатики, который может нам помочь, например, в решении конкретных математических задач. Нужно только уметь разбираться в этом.
2. Математическое решение
Давайте вспомним, что понимают под квадратным уравнением?
Что из себя представляют числа a,b,c и как их называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b 2 -4ac) (Приложение 3)
Как мы решаем далее квадратное уравнение? (сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D 0, то два корня)
Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного уравнения сведу к условию D
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Найти дискриминант D=b 2 — 4ac.
Сравнить его с нулём
D=b 2 -4ac=10 2 -4*3*3=100 — 36 =64
Х1=
X2 =
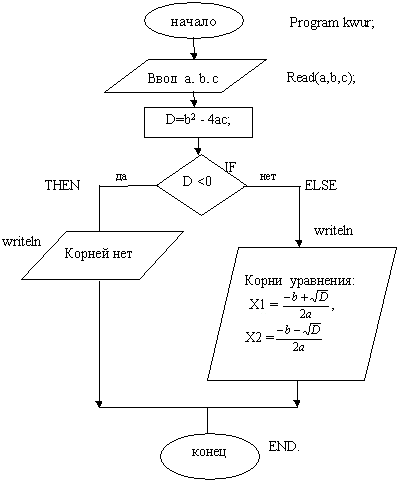
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Подпишем основные элементы блок — схемы применительно к языку программирования.
4. Составление программы по блок — схеме.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Var a,b,c,d,x1,x1: real;
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
Запуск программы — ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
1,5х 2 -0,6х — 4,8 = 0
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
1. За простое воспроизведение (набор программы) без проверки оценка «3»
2. За проверку работы программы на примерах, представленных учителем оценка «4»
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка «5»
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | 0 |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
1) Напишите программу проверки пароля. Пусть пароль — некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет — сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами — Циклическими.
На сегодня наш урок закончен. До свидания.
Литература:
Решение квадратного уравнения
Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.
a, b, c — действительные числа, a ≠ 0.
Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.
- если D 0, то уравнение имеет два действительных корня:
- x1 = (-b + √D) / (2⋅a);
- x2 = (-b + √D) / (2⋅a).
Программа для решения квадратного уравнения на языке программирования Паскаль
Функция sqr языка Pascal используется для возведения числа в квадрат.
Функция sqrt используется для получения квадратного корня числа.
В программе используется форматированный вывод вещественных чисел. variable:8:3 — означает, что для вывода переменной предусмотрено 8 символов, 5 из них под целую часть и 3 под дробную.
Исходник программы Паскаль, которая находит корни квадратного уравнения по заданным коэффициентам
Добрый день. Сегодня я хочу поделиться программой, написанной на языке программирования Паскаль, а именно исходник программы, которая находит корни квадратного уравнения.
Итак, задача звучит следующим образом:
«Составьте программу вычисления корней квадратного уравнения по данным значениям его коэффициентов«.
Решение задачи на языке паскаль довольно простое. Вначале необходимо считать данные (значения коэффициентов) в три переменные a,b,c. Затем нужно посчитать дискриминант, после проверить больше или меньше нуля или равно ему значение дискриминанта. В зависимости от значения дискриминанта считать значение корней или вывести сообщение о том, что корней нет.
Исходный код программы нахождения корней:
Скачать исходник: koren2.pas
http://programm.top/pascal/programm/quadratic-equation/
http://zedpost.ru/ishodnik-programmi-paskal-kotoraya-nahodit-korni-kvadratnogo-uravneniya-po-zadannim-koefficientam-.html
Уравнение вида a⋅x2 + b⋅x + c = 0 — квадратное уравнение.
a, b, c — действительные числа, a ≠ 0.
Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.
D = b2 — 4⋅a⋅c;
- если D < 0, то квадратное уравнение не имеет корней;
- если D = 0, то уравнение имеет один действительный корень(иногда говорят, что корней два, но они одинаковые):
- x1 = x2 = -b / (2⋅a);
- если D > 0, то уравнение имеет два действительных корня:
- x1 = (-b + √D) / (2⋅a);
- x2 = (-b + √D) / (2⋅a).
program QuadraticEquation;
var
a, b, c, x1, x2, discriminant : real;
begin
{ввыод данных}
write('a = ');
readln(a);
write('b = ');
readln(b);
write('c = ');
readln(c);
{дискриминант}
discriminant := sqr(b) - 4 * a * c;
if discriminant < 0 then
writeln('Квадратное уравнение не имеет корней')
else
begin
if discriminant = 0 then
begin
{квадратное уравнение имеет два одинаковых корня}
x1 := -b / (2 * a);
x2 := x1;
end
else
begin
{уравнение имеет два разных корня}
x1 := (-b + sqrt(discriminant)) / (2 * a);
x2 := (-b - sqrt(discriminant)) / (2 * a);
end;
{вывод корней уравнения}
writeln('x1 = ', x1:8:3);
writeln('x2 = ', x2:8:3);
end;
writeln('Press Enter to Exit...');
readln;
end.
Вариант № 2
{ Пример 1.5. Решить квадратное уравнение ax^2 + bx + c = 0.
Система тестов
╔═════╦═══════════════╦══════════════╦══════════════════════════════╗
║Номер║ Проверяемый ║ Коэффициенты ║ ║
║теста║ случай ╟───┬────┬─────╢ Результаты ║
║ ║ ║ a │ b │ c ║ ║
╠═════╬═══════════════╬═══╪════╪═════╬══════════════════════════════╣
║ 1 ║ d>0 ║ 1 │ 1 │ -2 ║ x1 = 1, x2 = -2 ║
╟─────╫───────────────╫───┼────┼─────╫──────────────────────────────╢
║ 2 ║ d=0 ║ 1 │ 2 │ 1 ║ Корни равны: x1= -1, x2= -1 ║
╟─────╫───────────────╫───┼────┼─────╫──────────────────────────────╢
║ 3 ║ d<0 ║ 2 │ 1 │ 2 ║ Действительных корней нет ║
╟─────╫───────────────╫───┼────┼─────╫──────────────────────────────╢
║ 4 ║ a=0, b=0, c=0 ║ 0 │ 0 │ 0 ║ Все коэффициенты равны нулю,║
║ ║ ║ │ │ ║ х - любое число ║
╟─────╫───────────────╫───┼────┼─────╫──────────────────────────────╢
║ 5 ║ a=0, b=0,c<>0 ║ 0 │ 0 │ 2 ║ Неправильное уравнение ║
╟─────╫───────────────╫───┼────┼─────╫──────────────────────────────╢
║ 6 ║ a=0, b<>0 ║ 0 │ 2 │ 1 ║ Линейное уравнение. Один ║
║ ║ ║ │ │ ║ корень: х= -0,5 ║
╟─────╫───────────────╫───┼────┼─────╫──────────────────────────────╢
║ 7 ║a<>0, b<>0, c=0║ 2 │ 1 │ 0 ║ x1 = 0, x2 = - 0,5 ║
╚═════╩═══════════════╩═══╧════╧═════╩══════════════════════════════╝
}
Program QuadraticEquation;
Uses Crt; { подключение библиотеки Crt }
Var a, b, c : Real; { a, b, c - коэффициенты уравнения}
Discr : Real; { Discr - дискриминант }
x1, x2 : Real; { x1, x2 - корни }
Test, NTest : Integer; { Ntest - количество тестов }
BEGIN
ClrScr;
Write('Введите количество тестов : ');
ReadLn(NTest);
For Test := 1 to NTest do { цикл по всем тестам задачи }
begin
Write('Тест ', Test, '. Введите коэффициенты a, b, c : ');
ReadLn(a, b, c);
If (a=0) and (b=0) and (c=0)
then begin Write('Все коэффициенты равны нулю.');
WriteLn('x - любое число ')
end
else
If (a=0) and (b<>0)
then WriteLn('Линейное уравнение. Oдин корень: x =', (-c/b):6:2)
else
If (a=0) and (b=0) and (c<>0)
then WriteLn('Неправильное уравнение.')
else
begin
Discr := b*b - 4*a*c;
If Discr > 0
then begin
x1:=(-b + Sqrt(Discr)) / (2*a);
x2:=(-b - Sqrt(Discr)) / (2*a);
WriteLn('x1=' , x1:6:2 , '; x2=' , x2:6:2)
end
else
If Discr = 0
then
begin
x1 := -b/(2*a);
WriteLn('Корни равны: x1=', x1:6:2, ' x2=', x1:6:2)
end
else WriteLn('Действительных корней нет.');
end;
WriteLn
end;
ReadLn
END.
Цели урока:
- Повторить с учащимися правила решения
квадратных уравнений - Вспомнить алгоритмическую конструкцию IF-THEN-ELSE
- Составить блок-схему программы и саму программу
на языке Pascal - Проверить работоспособность программы на
конкретных примерах - Расширить представления учащихся о применении
языка Pascal - Воспитать у учащихся чувство аккуратности,
внимательности, ответственности - Научить учащихся самостоятельно находить свои
ошибки в программах
Оборудование:
- Таблички с формулами
- Плакат с блок-схемой алгоритма КВУР
- Листочки с индивидуальными заданиями
- Система программирования «Turbo Pascal 7.0»
ХОД УРОКА
1. Введение.
До сих пор мы с вами говорили о каких-то
отвлечённых задачах из области математики.
Сегодня мы поговорим о конкретной задаче,
которая встречается у вас почти на каждом уроке.
Это решение квадратного уравнения. Я хочу, чтобы
вы на примере этой задачи поняли, что
программирование — это не просто прихоть
учителя, это действительно раздел информатики,
который может нам помочь, например, в решении
конкретных математических задач. Нужно только
уметь разбираться в этом.
2. Математическое решение
Давайте вспомним, что понимают под квадратным
уравнением?
Вопросы:
Что из себя представляют числа a,b,c и как их
называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b2-4ac)
(Приложение 3)
Как мы решаем далее квадратное уравнение?
(сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D <0, то нет корней, если D=0, то один корень,
если D>0, то два корня)
Как найти корни квадратного уравнения? Найдите
формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного
уравнения сведу к условию D0, то что я получу в случае D=0?
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax2+bx+c=0.
Мы должны решить его, т.е. найти такие значения
х, при которых правая часть уравнения =0. Мы знаем,
что для этого нам надо:
Найти дискриминант D=b2 — 4ac.
Сравнить его с нулём
Если D<0 , то «корней нет» иначе два корня х1 и
х2.
Х1 = , Х2=
Пример: (вызываем ученика)
3х2-10х+3=0
D=b2-4ac=102-4*3*3=100 — 36 =64
D>0, два корня
Х1=,
X2 =
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить
блок-схему алгоритма в тетради. Кто справится
первым, прошу к доске.
Подпишем основные элементы блок — схемы
применительно к языку программирования.
4. Составление программы по блок — схеме.
Теперь, пользуясь нашими записями, составим
программу и покажем её учителю. Тот, кто до конца
урока составит только программу, не проверив её
на компьютере, получит три, тот, кто наберёт
программу на компьютере, но не проверит её на
примерах, получит три. Тот, кто выполнит всё
задание, получит пять.
А я раздам вам домашнее задание.
Ответ:
Program kwur;
Uses CRT;
Var a,b,c,d,x1,x1: real;
Begin
Clrscr;
Write(‘введите коэффициенты уравнения a,b,c’);
readln(a,b,c);
D:=b*b-4*a*c;
If d>=0 then
Begin
X1:=(-b+sqrt(d))/(2*a); x2:=(-b-sqrt(d))/(2*a);
Writeln(‘x1=’,x1′ x2=’,x2)
END;
Else writeln(‘действительных корней нет’)
End.
5. Практическая работа (Приложение
1).
1. Составить и набрать программу КВУР на
компьютере.
Подсказка:
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать
ALT+ENTER.
Запуск программы — ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и
показать учителю их решения (если нет такой
возможности, то занести их в маршрутный лист (Приложение 4)
3х2 -10х +1=0
0,5х2+2х — 4=0
4х2 + х — 6=0
2х2 + 3х +8=0
х2 +4 =0
5х2 -8х = 0
1,5х2-0,6х — 4,8 = 0
-2х2+4х — 8 = 0
9х2+4х -7 = 0
0,1х2— 9 = 0
3. Переделайте программу КВУР таким образом,
чтобы в ней учитывался случай, когда D=0 и
уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
Оценивание:
1. За простое воспроизведение (набор программы)
без проверки оценка «3»
2. За проверку работы программы на примерах,
представленных учителем оценка «4»
3. За решение всех заданий и дополнительное
изменение программы для случая D=0, оценка «5»
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
Ответы:
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | 0 |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с
точностью до 2-х знаков после запятой.
6. Домашнее задание: (Приложение 2)
1) Напишите программу проверки пароля. Пусть
пароль — некоторое число, зафиксированное в
программе. Программа печатает приглашение
«введите пароль» и вводит число. Если введённое
число совпадает с фиксированным паролем, то
программа выводит приветствие, если нет —
сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали
конкретные задачи из математики, применяя свои
умения по программированию. Вы получили
следующие оценки за свои знания. (Перечисление
оценок) На следующем уроке нам предстоит
познакомиться с новыми алгоритмами —
Циклическими.
На сегодня наш урок закончен. До свидания.
Литература:
- И. Семакин, Л. Залогова «Информатика. Базовый
курс. 9 класс», М., БИНОМ, 2005г. - А.А. Чернов «Конспекты уроков информатики в 9-11
классах», Волгоград: Учитель, 2006г. - Л.И. Белоусова, С.А. Веприк «Сборник задач по
курсу информатики», М., «Экзамен», 2007.