Преподаватель который помогает студентам и школьникам в учёбе.
Проекция вектора на ось в физике — формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
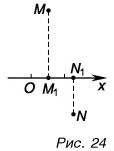
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
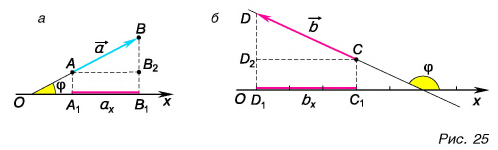
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 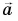
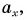
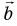
Проекция 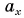
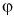
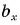
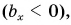
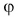
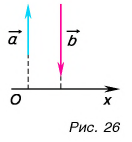
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 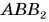
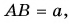
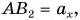
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
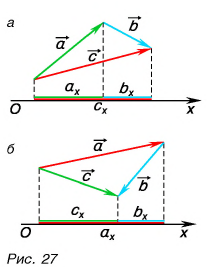
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 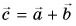
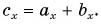
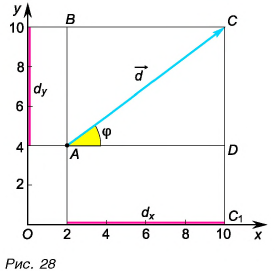
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 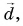
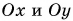
Модуль вектора 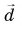
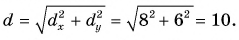
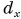
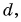
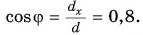
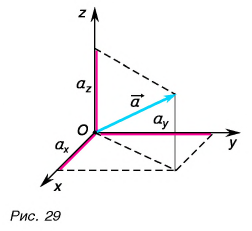
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 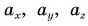
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
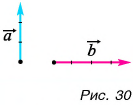
Пример №1
1. Определите сумму и разность взаимно перпендикулярных векторов 
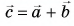
Решение
Сумму векторов 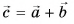
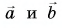
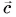
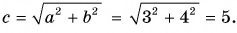
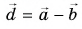
Модуль вектора 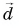
Ответ:
- Заказать решение задач по физике
Пример №2
Выразите вектор 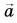
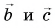
Решение
По правилу треугольника находим: 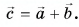
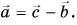
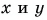
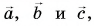
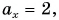
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
Проекция вектора на ось. Проекция вектора на вектор
Навигация по странице:
- Определение проекции вектора на ось
- Определение проекции вектора на вектор
- Формула вычисления проекции вектора на вектор
- Примеры задач на проекцию вектора
- плоские задачи
- пространственные задачи
Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются проекциями точек A и B на ось l. (рис. 1).
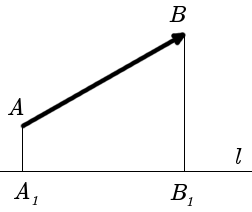 |
| рис. 1 |
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
|b| = √32 + 42 = √9 + 16 = √25 = 5
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 11 | = 2.2 |
| |b| | 5 |
Ответ: Пр ba = 2.2.
Примеры вычисления проекции вектора для пространственных задачи
Пример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 12 | = 2 |
| |b| | 6 |
Ответ: Пр ba = 2.
В математике существуют два определения:
1) геометрическая проекция вектора — вектор;
2) проекция вектора на ось — число.
Геометрическая проекция вектора — это вектор, который можно получить, если провести перпендикуляры от концов вектора до выбранной оси. Проекция начала вектора соответствует началу геометрической проекции, а проекция конца вектора соответствует концу геометрической проекции.
Ваш браузер не поддерживает HTML5 видео
Для вектора
v→
геометрическая проекция на оси (t) — это вектор
vt→
.
Для вектора
n→
геометрическая проекция на оси (y) — это вектор
ny→
.
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
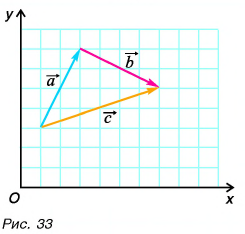
ax=4bx=−3
Если длина вектора
a→
равна
a→
и
α
— это острый угол, созданный вектором и осью (x), то скалярная проекция вектора вычисляется по формуле:
ax=a→⋅cosα
.
Знак проекции вектора выбирается в зависимости от направления оси.
На рисунке видно, что эту формулу можно получить из соотношения в прямоугольном треугольнике:
.
Обрати внимание!
Если вектор и ось проекций параллельны, то скалярная проекция на этой оси — число, которое равно длине вектора, если направления вектора и оси совпадают, или число, противоположное длине вектора, если направления вектора и оси — противоположные.
Если вектор и ось проекций перпендикулярны, то проекция вектора на этой оси равна (0).
at=3bt=−5ct=0dt=0
Прямая
с заданной на ней точкой и единичным
базисным вектором
называетсяосью.
Ортогональной
проекцией
точки A
на ось называется точка пересечения
оси с перпендикулярной к ней плоскостью,
проходящей через точку А.
Пусть
в пространстве задана направленная
прямая l.
Проекцией точки М
на ось l
называется основание
перпендикуляра
,
опущенного из точкиМ
на ось. Если точка М
лежит на оси l,
то проекция точки М
на ось совпадает с М
(рис. IV.4).
Рис.
IV.4
Пусть
– произвольный вектор.Проекцией
вектора
на осьl
называется координата вектора
относительно единичного вектора
оси, гдеА1
и В1
– проекции точек A
и B
на ось l,
то есть если
,
то число
называется проекцией вектора
на осьl,
в направлении
.
Обозначение для проекции:.
Из правил сложения
векторов и умножения вектора на число,
заданных своими координатами, следует,
что:
,
где
.
Легко
показать, что
,
где
– угол между векторами
и
,
отсчитываемый по правилам тригонометрии:
от векторапротив часовой стрелки до вектора
.
Следует
помнить: проекция
вектора на ось положительна (отрицательна),
если вектор образует с осью острый
(тупой) угол, и равна нулю, если этот угол
прямой.
Действия над
векторами, заданными проекциями,
выполняются аналогично действиям над
матрицей-строкой (матрицей-столбцом).
Рассмотрим
3-х мерное линейное пространство L
и
(рис.IV.5).
Введем декартову систему координат
Oxyz.
Представим вектор
в виде линейной комбинации базисных
векторов,
,
:
.
(IV.1)
Проекцией
вектора
на осьOx
называется величина направленного
отрезка
и записывается
.
Так
как, по определению,
,
то если
– угол между осью Ox
и вектором
,
то
.
(IV.2)
Аналогично
определяются проекции вектора
на другие оси.
Рис.
IV.5.
Сопоставляя
(IV.1)
и (IV.2)
и учитывая, что проекция есть направленный
отрезок (если
,
то),
то
,
,
.
Заметим,
что
,
получаем
,
,
.
(IV.3)
,
,
называются направляющими косинусами.
Возводя в квадрат и складывая, получим
,
то есть сумма
квадратов направляемых косинусов равна
1:
.
(IV.4)
Пусть
углы вектора
с осями Ox,
Оу,
Оz
соответственно равны ,
,
.
По свойству проекции вектора на ось
имеем:
,
,
.
или, что то же
самое:
,
,
.
(IV.5)
Числа
,
,
называются направляющими косинусами
вектора
().
Линейные свойства проекции вектора на ось
Пусть
дана ось Ox
и векторы
и
:
,
.
Тогда, как следует
из свойств сложения векторов, имеем
1)
;
2)
,
.
Отсюда,
как следует из (IV.2),
получаем
a)
;
b)
.
Координаты вектора
Найдем
координаты вектора
,
если известны координаты точек
и
.
Имеем:
.
Следовательно,
координаты
вектора равны разностям соответствующих
координат его конца и начала.
Зададим
в пространстве декартову систему
координат Oxyz
и вектор
,
где координаты точек
,
.
Проекция
вектора
на ось Ox
(рис. IV.6)
определяется
.
(IV.6)
Рис.
IV.6.
Тригонометрическая
формула (IV.6)
устанавливает связь между геометрическим
образом отрезка и его проекцией на ось
Ox,
которая в алгебраической форме имеет
вид
.
(IV.7)
Знак
правой части в (IV.7)
определяется
,
для
.
Таким образом,
,
(IV.8
а)
,
(IV.8
б)
.
(IV.8
в)
Для
нахождения длины отрезка
воспользуемся теоремой Пифагора, получим
.
(IV.9)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проекция вектора на ось
Определение и формула проекции вектора на ось

Под осью понимается прямая, для которой указано направление.
Чтобы построить проекцию вектора на ось
, нужно из точек
и
(начало и конец вектора
соответственно) опустить перпендикуляры на направленную прямую
, основания этих перпендикуляров будут началом и концом искомой проекции (рис. 1).
Числовой характеристикой проекции вектора на ось
является числовая проекция
этого вектора на данную ось – число, которое равно произведению длины данного вектора на косинус угла между этим вектором и вектором, определяющим направление оси.
Если направление оси определяется вектором , то числовая проекция вектора
на эту ось обозначается как
, причем
Примеры нахождения проекции вектора на ось
Из определения скалярного произведения двух векторов и
:
получаем, что
В результате формула (1) принимает вид:
То есть числовой проекцией вектора на ось, направление которой совпадает с направлением вектора
, есть отношение скалярного произведения векторов
и
к модулю вектора
:
| Понравился сайт? Расскажи друзьям! | |



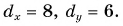
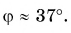
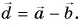

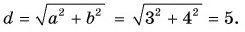
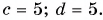

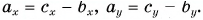
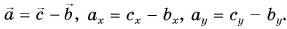







![Rendered by QuickLaTeX.com [cos left(mathop{bar{a},; bar{b}}limits^{wedge } right)=frac{left(bar{a},; bar{b}right)}{left|bar{a}right|cdot left|bar{b}right|} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9da8cdc572664cef99c631ca9dfb5383_l3.png)
![Rendered by QuickLaTeX.com [{Pi text{p}}_{bar{b}} bar{a}=left|bar{a}right|cdot frac{left(bar{a},; bar{b}right)}{left|bar{a}right|cdot left|bar{b}right|} =frac{left(bar{a},; bar{b}right)}{left|bar{b}right|} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d1b6993adfac670fd5d2502fbb5bafb2_l3.png)
![Rendered by QuickLaTeX.com [{Pi text{p}}_{bar{b}} bar{a}=frac{left(bar{a},; bar{b}right)}{left|bar{b}right|} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-86442d66cfafef044cc11e06dcf15f5f_l3.png)