Получить доход как можно больше, рискуя при этом как можно меньше – мечта каждого инвестора. Над возможностью реализации этой «голубой мечты» ломают головы не только миллионы участников фондового рынка, но и крупнейшие ученые, в том числе лауреаты Нобелевской премии. К примеру, американцы Г. Бринсон, Л. Рэндольф Худ и Г. Бибауэр провели фундаментальное исследование «Детерминанты эффективности портфеля» и установили, что не выбор времени для покупки, а распределение активов в портфеле определяет 75,5% — 98,6% доходности.

Правильному подбору инвестиционного портфеля посвящены портфельные теории, которых на сегодняшний день насчитываются десятки. Чем позже по времени создана теория, тем, как правило, более сложную математику она применяет и требует все большего объема вычислений. Однако, каждая из теорий имеет определенные допущения, применима для ограниченного числа случаев и инструментов. А вот «идеальной» теории на все случаи жизни пока никто не придумал.
При всем многообразии любая портфельная теория базируется на основных идеях и понятиях, изложенных в статье «Выбор портфеля», которую опубликовал в 1952 г. скромный аспирант Гарри Марковиц. Впоследствии положения этой статьи им были развиты в опубликованной в 1959 г. монографии. Освоив основные идеи Марковица, каждый инвестор сможет проще разобраться в любой портфельной теории, лучше понять основы формирования инвестиционных портфелей и уяснить, что многие рекомендации по инвестированию, которые даются, так сказать, в «готовом виде», на самом деле являются итогом серьезных научных изысканий.
В данной статье мы решили обратиться к «первоистокам» и изложить следующие основные моменты:
-
Суть теории Марковица.
-
Алгоритм расчета портфеля по Марковицу.
-
Ограничения портфельной теории Марковица, ее развитие Шарпом, Тейнором, Сортино.
-
Критика портфельных теорий.
-
Составление портфеля в сервисе Fin-plan Radar.
Суть теории Марковица
Со словом инвестиции постоянно используются понятия «доход» и «риск». А утверждение «чем выше доход, тем больше риск» стало аксиомой. Мы об этом всегда говорим на наших вебинарах. Применимо к конкретным видам финансовых инструментов мы изложили действие данной аксиомы в нашей статье «Концепция риск-доходность».
Но, что такое доход? Казалось бы, элементарный вопрос: из цены продажи вычитаешь цену покупки – вот и доход. А как определить доход, когда акцию мы еще не продали, да и цена покупки неизвестна, т.к. точка входа пока под вопросом?
А риск? Ясно, это нечто страшное и ужасное, но как его определить? Утверждения, что риск – это нежелательное явление для инвестора, вряд ли нас устроят. Как реально измерить риск, установить, где он больше, а где меньше – вот что требует инвестор от теоретиков.
Исторической заслугой Марковица является придание будущей доходности и риску математического выражения. На основе его работ стало возможным посчитать и будущую доходность, и риск.
В своей статье Марковиц формирование портфеля разбивает на 2 этапа:
-
Анализ исторических данных. Здесь на основе существующих котировок ценных бумаг определяется будущая доходность и риск по каждой акции.
-
Окончательное формирование портфеля — в портфель отбираются бумаги с лучшей доходностью и меньшим риском.
Затем проводится оптимизация портфеля по принципу:
-
лучшая доходность при заданном, т.е. допустимом для нас, риске;
-
минимальный риск при заданной, т.е. устраивающей нас доходности.
Будущая доходность является случайной величиной, точное значение которой не известно. Существует лишь вероятность того, что случайная величина примет то или иное значение. Наиболее вероятное значение случайной величины называется ее математическим ожиданием. Его Марковиц и определил в качестве будущего дохода.
Проиллюстрируем это на примере депозитарных расписок TCS Group Holding PLC:
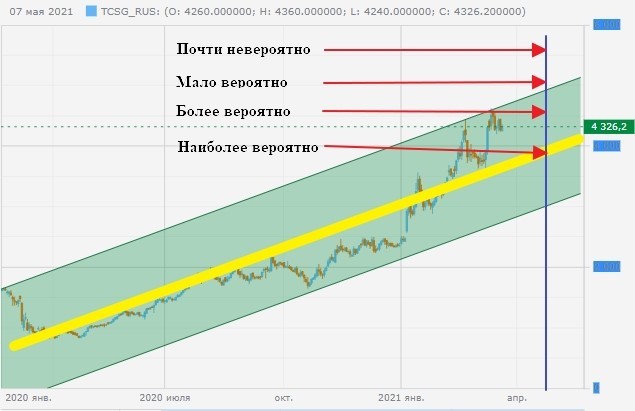
Котировки акций движутся в рамках восходящего ценового канала. Желтой линией условно обозначено математическое ожидание будущей цены акций (а, следовательно, и их потенциальной доходности). Стрелками указаны вероятные значения цены акций в конкретный момент времени, отмеченный синей линией. Математическое ожидание вычислить достаточно сложно. Но приемлемую точность дает расчет его величины на основе средних значений доходности акций за определенный период.
Риск Марковиц определил как дисперсию, т.е. разброс цен на акцию. Иными словами, чем выше разброс котировок, т.е. волатильность акции – тем больше риск инвестора.
Обратим внимание на котировки, например, Магнита:
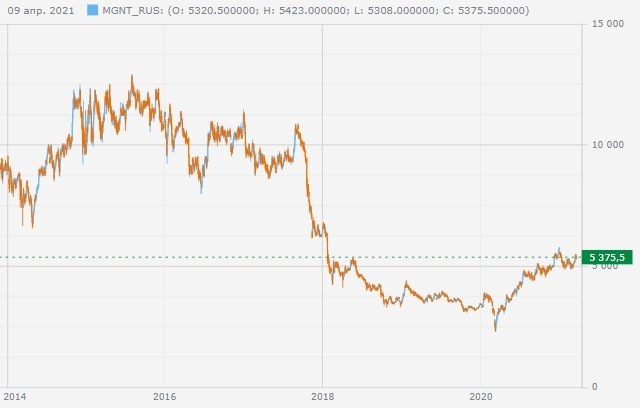
В период с 2014 г. по настоящее время разброс цен составлял от максимума в 2015 г. 12 309 руб. до минимума в марте 2020 г. 2 501 руб. за акцию, т.е. разница практически в 5 раз.
Сравним с графиком Магнитогорского металлургического комбината за тот же период.
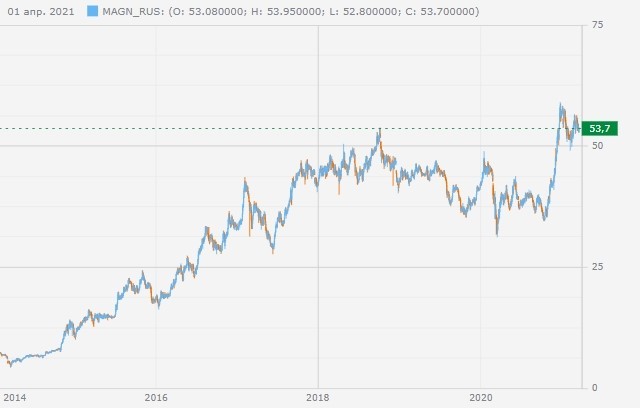
Цена акций тоже изменилась значительно — от 5,5 до 55 руб. Но график существенно менее «рваный», чем у Магнита. В период до 2017 г. акции уверенно росли с относительно небольшими просадками. Наибольшее падение было с 53,7 руб. в самом начале октября 2018 г. до 33,7 руб. на 19 марта 2020 г. в пик ковидного кризиса, т. е. в 1,6 раза.
Определение численного значения дисперсии, т.е. риска также является сложной математической задачей. Но вполне точное значение дает использование стандартного (среднеквадратичного) отклонения доходностей за определенный период.
Итак, подытожим:
-
Будущая доходность акции – это ее математическое ожидание, которое примерно равно среднему значению доходности акций за определенный период.
-
Риск – это волатильность акции, которая измеряется ее дисперсией, примерно равной стандартному (среднеквадратичному) отклонению доходностей за тот же период.
Таким образом, Марковиц первым определил подход к численному выражению будущей доходности и риска на основе математических вычислений. Тем самым инвестиции на бирже были выведены из области догадок, предположений, средне потолочных прогнозов в сферу конкретных расчетов.
Расчеты, последующие выводы и инвестиционные решения – мы сторонники именно такого подхода. Это наиболее рациональный путь в сравнении с действиями, основанными на эмоциях. Об этом прекрасно известно участникам наших вебинаров.
Определив будущую доходность и риск по каждой акции, можно переходить к составлению портфеля. Доходность портфеля в целом посчитать очень просто. Это сумма доходностей включенных в портфель акций («Как посчитать доходность»).
С рисками дело обстоит сложнее. Дело в том, что в экономике все субъекты (фирмы, организации, предприятия) и объекты (изделия, сырье и т.д.) взаимосвязаны. Растут цены на нефть – растут и акции нефтяных компаний, но падают акции компаний транспортных. В кризис неплохо чувствуют себя акции нециклических компаний и падают акции циклических, зато растут цены на золото и акции компаний его добывающих, и т.д. и т.п. Естественно речь идет только об общих тенденциях. В конкретных случаях приведенные зависимости могут и нарушаться.
Допустим, кто-то предпочитает инвестиции в нефть и вложился в нефтяные фьючерсы и акции нефтедобытчиков. Риски по этим инструментам будут усиливать друг друга. Конечно, при росте цен можно получить как бы «двойной» доход, но при падении – «двойной» убыток.
А кто-то сторонник отраслевой диверсификации, и кроме акций нефтяников приобретет акции транспортников. Доход все равно будет равным сумме доходов по каждому инструменту, а вот общий риск уменьшится за счет частичной взаимной компенсации рисков по каждой акции в отдельности. Примеры мы приводили в статье «Как хеджировать риски».
С учетом этой всеобщей взаимосвязи Марковиц ввел в расчет риска портфеля функции корреляции и ковариации рисков отдельных акций. В этом состоит его вторая революционная идея. До Марковица считалось, что для «правильного» портфеля достаточно подобрать наиболее доходные акции, а можно ограничиться вообще одной, но «самой, самой хорошей». Марковиц не на пальцах, а путем конкретных математических расчетов доказал неверность подобного подхода: да в этом случае можно получить неплохой доход, но, при этом, инвестор принимает на себя и непомерный риск. Достаточно взглянуть на график котировок Магнита, акции которого до начала 2016 г. росли весьма неплохо, но впоследствии обесценились в 5 раз.
Корреляция показывает степень взаимозависимости котировок ценных бумаг.Если между двумя акциями она равна 1, то котировки полностью взаимозависимы и на графике движутся параллельно друг другу: провал у одной бумаги соответствует точно такому же провалу у другой. Соответственно отклонения их доходности, т.е. риски, будут складываться. Если же корреляция равна -1, то котировки полностью противоположны: каждое падение одной бумаги сопровождается ростом другой, и наоборот. Общий риск портфеля из двух бумаг при этом уменьшается. Если корреляция равна 0, то котировки бумаг, а, следовательно, и риски абсолютно независимы.
Величины корреляции 1, -1 и 0 являются крайними и очень маловероятными. Реально корреляция принимает значения в диапазонах от 1 до 0 и от 0 до -1.
Для удобства расчетов обычно используется не корреляция, а ковариация, которая представляет собою меру корреляции.
С введением в расчет риска корреляции и ковариации Марковиц доказал необходимость широкой диверсификации портфеля. Причем такой диверсификации, которая является не простым набором доходных акций, а ценных бумаг компаний различных отраслей, обладающих желательно отрицательной корреляцией. Только в таком случае появляется возможность снизить риск портфеля.
После того, как портфель подобран следующий шаг состоит в его оптимизации. И здесь появляются доли акций в портфеле. Согласно расчетам Марковица изменяя эти доли можно получить массу портфелей с одинаковой доходностью, но только один из них обеспечит минимальный риск. И, наоборот, имеется такая же масса портфелей с равным риском, но только один из них обеспечит наибольшую доходность.
Смысл процедуры оптимизации состоит в том, чтобы перебирая все возможные сочетания долей акций найти портфель:
-
с минимальным риском, имеющий нужный нам уровень доходности;
-
либо с приемлемым для нас риском и наибольшей доходностью.
Оптимизация только одного портфеля требует очень большого объема вычислительных работ, который периодически необходимо возобновлять для учета изменений ситуации на рынке. Не случайно на работы Марковица более 30 лет мало кто обращал внимание. Только появление компьютерной техники решительно изменило ситуацию, а Марковиц в 1990 г. был удостоен Нобелевской премии.
Выполнить эту работу вполне возможно в Excel. Но это очень трудозатратно! Сейчас существует много программ, которые позволяют в несколько кликов провести оптимизацию портфеля. К примеру, сервис Fin-Plan RADAR. О формировании портфеля в нем мы расскажем в последнем разделе статьи.
Алгоритм расчета портфеля по Марковицу
Алгоритм расчета состоит из следующих шагов.
Шаг 1. Выбираем заинтересовавшие нас акции. Выгружаем в Exel их котировки за период согласно Марковицу не менее трех лет.
Шаг 2. Рассчитываем фактические доходности за каждый месяц. Затем определяем доходность каждой акции как среднее значение ежемесячных доходностей. Полученный результат и дает нам ожидаемую доходность на будущее.
Затем рассчитываем риск для каждой акции по формуле стандартного отклонения для каждого столбца. В результате получаем все исходные данные для определения доходности, риска и оптимизации портфеля.
Шаг 3.Составляем Таблицу ковариации. Для этого необходимо вычислить ковариацию доходностей для каждой из входящих в портфель пар акций.
Шаг 4. Приступаем к расчету риска и доходности портфеля в целом для произвольно взятых долей.
Для определения общей доходности портфеля находим общую сумму доходностей всех акций, взятых в соответствии с их долями. Риск портфеля согласно Марковицу рассчитываем путем двойного перемножения долей на каждое значение таблицы ковариации и извлечения из результата квадратного корня.
Шаг 5. Оптимизации портфеля. Вначале зафиксируем приемлемую для нас доходность портфеля и найдем доли акций, которые обеспечивают минимальный риск. Затем зафиксируем приемлемый для нас риск и будем искать максимальную доходность. Для этого будет перебирать все возможные варианты значений долей каждой акции в пределах установленных нами допустимых значений.
Даже без детального изложения расчетов понятно, что оптимизация по Марковицу только одного портфеля требует значительного времени на проведение вычислений и подразумевает совершенное владение Excel – ем, и большие затраты сил и времени. Это зачастую инвестор не может себе позволить!
Ограничения портфельной теории Марковица, ее развитие Шарпом, Тейнором, Сортино
В публикациях о теории Марковица часто говорится о ее многих недостатках. Но термин «недостаток» не вполне справедлив. Да, действительно, Марковиц не учитывал облигации, фьючерсы, опционы, дивиденды, торговлю с плечом, рассматривал только растущие акции. Но цель, все это учесть Марковиц и не ставил. Он сделал именно то, что сделал – рассмотрел портфель длительное время растущих акций.
Дело в том, что любая теория имеет ограниченную сферу применения. Поэтому лучше говорить не о ее недостатках, а об ограничениях.
К настоящему времени разработаны портфельные теории, которые рассматривают комбинации акций и облигаций, учитывают дивиденды, торговлю с плечом и т.п. Но они используют настолько сложный математический аппарат и требуют такого огромного объема вычислений, которые непосильны обычному инвестору, вооруженному Exel-ем. Поэтому на практике из этих теорий применяются только основные выводы и некие частные моменты, например, в виде коэффициентов, с помощью которых можно давать оценку риска и потенциальной доходности портфеля.
В теорию Марковица существенные дополнения внес У. Шарп. Во-первых, в общем риске акции он выделил несистематический, т.е. присущий только данной бумаге, и систематический риск – риск рынка в целом. Подробнее о рисках и как с ними бороться рассказано в статье Риски инвестирования и способы их минимизации. Во-вторых, вместо вычисления взаимозависимости между акциями, как у Марковица, Шарп предложил определять корреляцию конкретной акции и рынка в целом. Для оценки движения рынка на практике используются рыночные индексы. Взаимосвязь устанавливается путем расчета коэффициента β, который определяется как отношение ковариации доходностей акции и рынка к квадрату стандартного отклонения рынка. Такой подход значительно упростил расчет доходности и риска портфеля.
И, наконец, Шарп определил, как сравнить портфели, которые обладают разными рисками и доходностями. Делается это путем вычисления коэффициента Шарпа. Коэффициент Шарпа показывает, какой доход сверх безрискового получит инвестор на единицу риска. Чем выше этот коэффициент, тем выгоднее портфель. Если коэффициент отрицателен, значит, доходность портфеля ниже безрисковой и проще инвестировать в безрисковый актив. В качестве доходности безрискового актива могут выбираться ключевая ставка Центрального банка, ставки по депозитам в очень надежном банке, доходность государственных облигаций со сроком погашения примерно равным сроку инвестирования.
Д. Трейнор предложил в формуле Шарпа заменить риск портфеля коэффициентом β. Смысл заключается в том, что несистематический риск инвестор может устранить путем диверсификации портфеля. Поэтому целесообразно оценивать портфель только в отношении систематического риска, который β и отражает. Недостаток коэффициента Шарпа состоит в том, что стандартное отклонение доходности портфеля искажает реальный риск инвестора. Оно растет при любом усилении волатильности цен на акцию, как в положительную, так и в отрицательную сторону. Но риск для инвестора несут только отрицательные отклонения.
Поэтому Ф. Сортино предложил в формуле Шарпа учитывать только падение котировок, заменив их общее стандартное отклонение стандартным отклонением убытков. Он же рекомендовал вместо доходности безрискового актива включить в формулу MAR (minimum acceptable return) – минимально приемлемый для инвестора уровень доходности. Коэффициент Сортино – по своей сути показывает, за счет чего по портфелю была получена сверхнормативная доходность. За счет качественных инвестиционных идей или же за счет принятия излишнего риска по портфелю.
Коэффициенты Шарпа, Тейнора и Сортино наиболее часто применяются при сравнении и оценке портфелей.
Критика портфельных теорий
Все портфельные теории, как и все теории технического анализа, основаны на исторических данных о курсах акций. То есть, доходность и риск на будущее прогнозируются на основе их значений в прошлом. Но кто сказал, что доходность будет обязательно равна математическому ожиданию? Напротив, сами же теории утверждают, что это только наиболее вероятный результат. Существует, пусть и меньшая, вероятность того, что доходность окажется существенно выше или ниже математического ожидания. А как быть с будущей доходностью в преддверии или в условиях экономического кризиса или надувания рыночных «пузырей»? Ведь портфельные теории, ориентируя всех инвесторов только на растущие акции, прямо провоцируют такие «пузыри».
Значит, все наши старания по оптимизации портфеля могут оказаться бесполезными.
Марковиц сам сознавал ограниченность исторического подхода и в статье упоминал, что результаты его расчетов доходности и риска имеет смысл корректировать на основе экспертных заключений. Но как подобрать заслуживающих доверия экспертов и как встроить их оценки в разработанные формулы – Марковиц не указал. И чем могут помочь любые эксперты при наступлении в принципе непредсказуемых событий, т.н. «черных лебедей», которые могут до основания потрясти фондовый рынок? Ярким примером такого «черного лебедя» является нынешняя пандемия.
Еще одно ограничение заключается в том, что рекомендации по отбору акций в портфель довольно расплывчаты. По-сути их две: растущие акции и их диверсификация по отраслям. Но если взять не российский, а, допустим, американский рынок, где в каждой отрасли найдется десяток, а то и десятки растущих акций, то какую конкретно из них выбирать?
Построение портфельных теорий только на базе исторического анализа стало основанием для критики со стороны многих ученых и практиков. Последовательным противником выступает, например, У. Баффет, взгляды которого сформировались под влиянием книги «Разумный инвестор» Бенджамина Грэма. Ни Грэм, ни Баффет не отрицают важности исторического анализа котировок акций. Но Баффет уточняет, что если этот анализ использовать для прогноза на краткий временной интервал, то возможность предсказания курса акции равна вероятности выпадения «орла» или «решки». А вот если горизонт инвестиций расширить до нескольких лет, то получим вполне приемлемые результаты.
Расхождение возникает в определении риска. Вслед за Марковицем все портфельные теории оценивают степень риска волатильностью ценных бумаг. Баффет же указывает, что действительный риск инвестора состоит в неверной оценке реальной стоимости компании и ее будущей прибыльности, а также во влиянии внешних для фондового рынка и мало предсказуемых факторов: войн, катастроф, природных катаклизмов, решений правительств, налогов, инфляции и т.п.
Грэм подчеркивал, что принцип «покупай, пока дешево, когда все продают, продавай, когда дорого, когда все покупают», работает далеко не всегда. На рынке бывают периоды затяжного роста или падения. Поэтому можно очень долго ожидать момента для покупки, теряя деньги за счет инфляции, либо распродать все акции, а потом покупать их по более высоким ценам. Разумному инвестору не так уж важно само по себе отслеживание рынка и не стоит уповать на прогнозирование его динамики. Главное, по мнению Грэма, заключается в том, чтобы покупать акции компаний с высоким «запасом надежности» и продавать их не при любом повышении цен, а только в случае, когда запас надежности начинает иссякать. В этом случае принцип «покупай дешево, продавай дорого» начинает прекрасно работать. Кейсы по акциям, у которых в свое время иссяк запас надежности и потенциал роста, с необходимыми пояснениями доступны у нас на сайте «Инвестиционные кейсы от компании Fin-plan».
«Запас надежности» определяется разницей между ценой акций и их истинной стоимостью, которая определяется путем фундаментального анализа финансовой отчетности. «Запас надежности» складывается из следующего:
-
Отношение долга компании к ее активам. Чем оно ниже, тем лучше.
-
Способность компании генерировать прибыль, высокая рентабельность ее бизнеса. Причем значение имеет не только высокая прибыль и рентабельность в предшествующие периоды, но и уверенность в их росте на будущее.
-
Недооцененность акций рынком, что выражается в низких значениях коэффициентов P/E (цена/прибыль) и P/B (цена/активы).
Акции с высоким «запасом надежности» мы обычно называем «фундаментально хорошими» акциями.
Грэм, как и Марковиц настаивает на диверсификации портфеля, но рекомендует обязательно включать в него облигации. Это является дополнительным способом снижения риска, особенно от факторов внешних по отношению к фондовому рынку. Дело в том, что облигации приносят стабильный доход, который компенсирует просадки акций.
Таким образом, критики не столько отвергают портфельные теории, сколько дополняют их критериями отбора инструментов для создания наименее рискованных портфелей. В частности, рекомендация по подбору фундаментально хороших акций снимает ограничение теории Марковица по включению в портфель исключительно растущих бумаг.
Составление портфеля в сервисе Fin-plan Radar
Для того, чтобы произвести формирование портфеля по изложенной в статье теории Марковица, необходимо произвести большое кол-во расчетов. Посмотрите, какой алгоритм действий вытекает из уже изложенного материала. Вначале надо подобрать фундаментально хорошие акции. Для этого отыскать и проанализировать финансовую отчетность за несколько лет в идеале по всем эмитентам, акции которых обращаются на рынке. На этой основе определить справедливую стоимость компаний, сравнить ее с рыночной стоимостью, рассчитать все коэффициенты, характеризующие оценку акций рынком, и выбрать недооцененные.
Затем следует «изучить внутреннюю кухню» и на основе стратегий развития компаний-эмитентов, если они есть, характеристик конкурентных преимуществ, анализа рынков сбыта, объемов будущих капиталовложений и.т.д. и т.п. спрогнозировать способность генерировать прибыль и денежные потоки в будущем. Подобрав таким способом фундаментально хорошие акции, составить несколько портфелей, используя принцип межотраслевой диверсификации. Провести оптимизацию каждого портфеля по схеме, рассмотренной во втором разделе, или иной подобной схеме, предлагаемой более сложными теориями. Наконец, сравнить портфели между собою путем расчетов по каждому из них коэффициентов (Шарпа, Трейнора, Сортино).
Но это еще не все! Для снижения риска следует подобрать и добавить в портфель облигации, определиться с их удельным весом в портфеле с учетом приемлемого риска. Только после выполнения всего перечисленного можно считать, да и то приближенно, что составленный портфель является надежным, т.е. обладает заданным критериям риска и доходности. Почему приближенно? Да потому, что с каждым выходом новой финансовой отчетности, с каждым существенным изменением на рынке все исходные показатели изменяются, и расчеты требуется возобновлять.
Проведение всех огромных вычислений в большинстве случаев доступно только крупным инвестиционным компаниям с большим штатом сотрудников.
На что же тогда уповать? Отслеживать котировки, пытаясь предсказать движение цен, иными словами, играть в «орел» – «решку»? Или выстраивать графики скользящих средних, искать разворотные фигуры, определять ценовые каналы, линии Боллинджера и т.п.? Но это тоже требует больших временных затрат и по мысли Грэма более присуще спекулянту, а не инвестору. Или охотиться за прогнозами, которые появляются ежедневно, изменяются часто и нередко противоречат друг другу?
Иными словами, большинство инвесторов предпочитают идти по легкому пути — инвестировать «наугад», руководствуясь интуицией, какими-то предположениями, слухами, домыслами и т.п., а не конкретными расчетами. Что и приводит, нередко, к печальным последствиям.
С учетом этой ситуации в помощь инвесторам созданы специальные сервисы. Один из них — сервис Fin-plan Radar. Подробно с его возможностями и описанием, как им пользоваться, можно познакомиться в статье Fin-plan Radar: возможности сервиса.
В Fin-plan Radar собрана подробная база данных по всем компаниям России и США, российским акциям и акциям США, российским облигациям, ETF, которые обращаются на отечественных площадках.
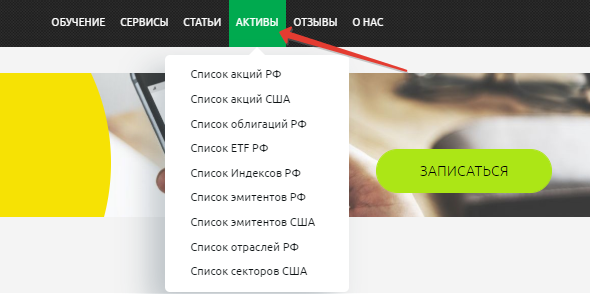
По каждому эмитенту и финансовому инструменту собрана актуальная база данных: финансовые показатели, биржевые показатели, расчетные коэффициенты и мультипликаторы.
По акциям уже в готовом виде есть все необходимое для оценки «запаса надежности» и принятия решения о включении ее в портфель: риск (Просад), вероятная будущая доходность (Target), мера корреляции с рынком (β – бета).
Причем все эти параметры даются в режиме реального времени: котировки обновляются ежедневно, а экономические данные сразу же после выхода отчетности за очередной квартал.
Конечно, сами по себе риск, доходность, корреляция с рынком, прогноз бизнеса по отдельной акции еще ничего не говорят. Выбор акции невозможно свести к одному какому-либо критерию. Это всегда набор критериев и поиск некого компромисса между рисками и доходностью. Поэтому для полной оценки акции стоит смотреть на комплекс показателей: фундаментальные показатели, мультипликаторы, их динамика и т.д.
По всем инструментам российских бирж в распоряжении инвестора в сервисе есть обширный набор фильтров и готовых стратегий, которые позволяют значительно сократить время на поиск подходящих инструментов для последующего сравнительного анализа.
Покажем, как в несколько шагов с помощью сервиса Fin-plan Radar можно сформировать портфель. Для выбора активов и формирования портфеля воспользуемся готовыми стратегиями.
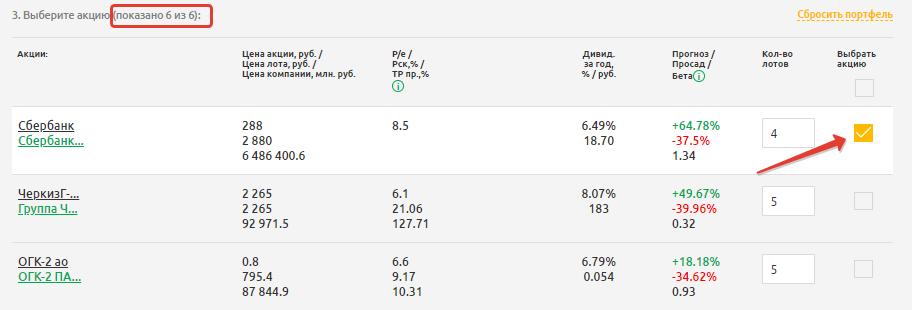
Шаг 1. Для выбора акций РФ используем стратегию «Купить сейчас», которая позволяет отобрать бумаги на основании сочетания критериев фундаментального и технического анализа. То есть это акции, имеющие в своей основе фундаментальные источники роста, и одновременно по ним сейчас с точки зрения технического анализа имеются актуальные точки входа.

Из полученного перечня в 6 акций выбираем акции Сбербанка-ао.
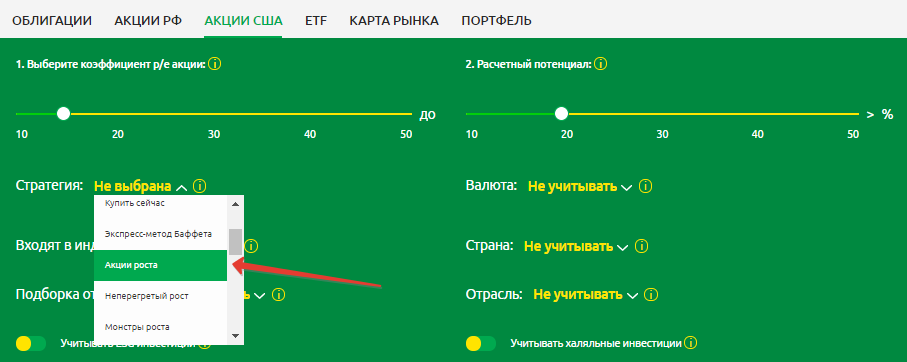
Шаг 2. Для выбора акций США используем стратегию «Акции роста». Этот фильтр позволяет отобрать акции компаний, которые растут кратно, как по выручке, так и по прибыли.
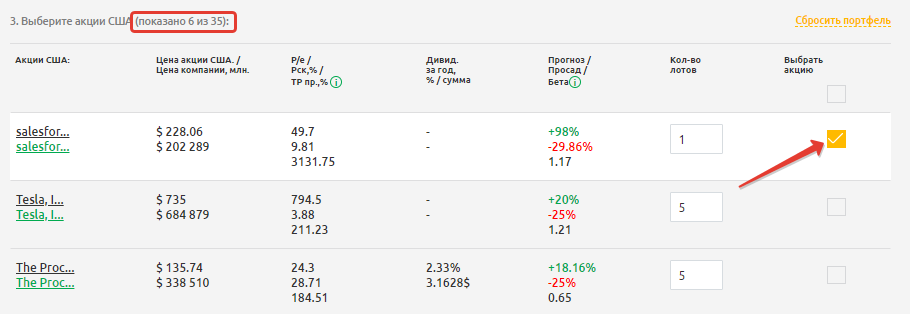
Из списка 35 предложенных бумаг выбираем акции salesforce.com, inc, которую мы определили ранее в список «Лучшие акции США 2021».
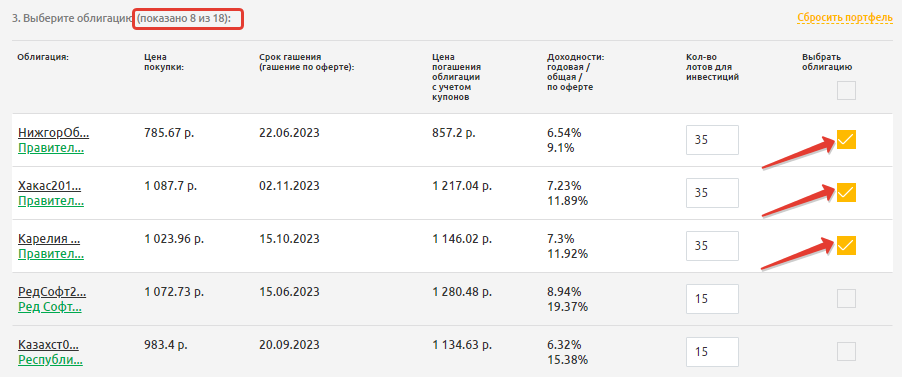
Шаг 3. Для компенсации риска по акциям добавим в портфель облигации, используя стратегию «Топ по показателям (2-3 года)». В этой стратегии – как надежные государственные и муниципальные бумаги, так и корпоративные облигации компаний с качественным финансовым состоянием.

Из предложенного списка в 18 бумаг пойдем по консервативному пути и выберем 3 муниципальных выпуска:
ИТОГ! Получим следующий портфель с долевым соотношением акций РФ/акций США/облигаций 8,8%/13,3%/77,9% соответственно.
Все основные показатели портфеля рассчитываются автоматически: риски, потенциал, коэффициенты.
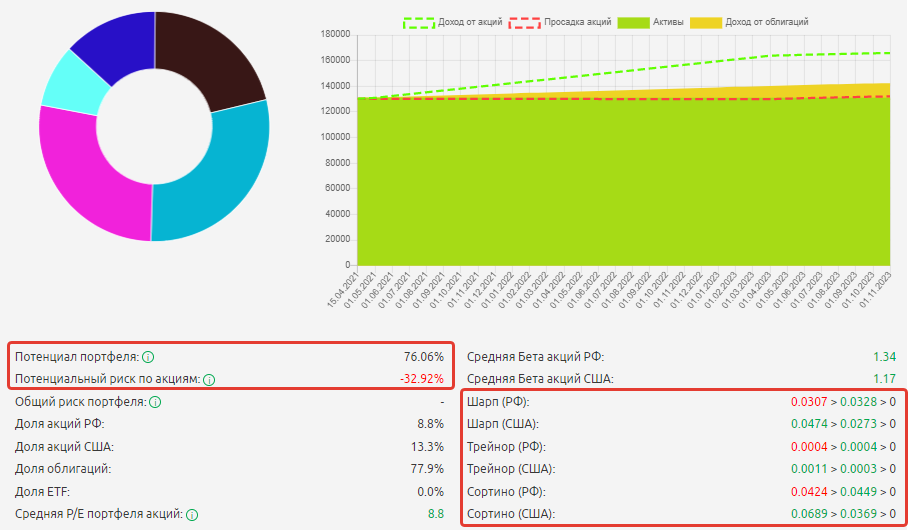
Потенциальная доходность портфеля составляет 76,06%, а его общий риск сводится к 0.
Коэффициенты Шарпа, Тейнора и Сортино по акциям США значительно лучше контрольных показателей. Но акции Сбербанка при желании можно заменить на другие активы. При этом все показатели по портфелю пересчитаются автоматически. Задача инвестора сводится только к аналитике и принятию инвестиционного решения.
Ограничение ответственности: Указанная в посте аналитика ценных бумаг не является персональной инвестиционной рекомендацией. Прежде, чем совершать торговые сделки, всегда проводите собственный анализ.
Вывод
Теория Марковица имела революционное значение для фондового рынка, создав основу для формирования и оптимизации инвестиционных портфелей на основе строгих математических расчетов.
Введение понятия и функции корреляции курсов акций показало, что портфель является не простой набором ценных бумаг, а целостным, внутренне взаимосвязанным объектом, который при правильном подборе инструментов позволяет снизить риск инвестирования.
Теория Марковица, как и любая иная теория, имеет свои ограничения, которые последовательно преодолевались в работах последователей и оппонентов. В частности, были разработаны коэффициенты для сравнения портфелей с различным риском и доходностью, а также критерии отбора акций в портфель на основе фундаментального анализа.
Общий недостаток всех портфельных теорий заключается в том, что они требуют сбора огромного фактического материала и выполнения колоссального объема математических расчетов. Это превращает «инвестирование по науке» в задачу, непосильную для рядового инвестора.
В помощь инвесторам разработан сервис Fin-plan Radar, который на основе постоянно обновляющейся базы экономических и биржевых данных обеспечивает автоматический расчет рыночных мультипликаторов и коэффициентов, необходимых для подбора наиболее доходных акций с минимально возможным риском. С помощью массы фильтров и готовых стратегий сервис помогает инвестору отобрать именно его интересующие акции, провести его хеджирование, ребалансировку и оптимизацию с автоматическим пересчетом потенциальной доходности, риска и коэффициентов, характеризующих качество портфеля.
Нашими методиками отбора надежных и качественных активов мы делимся на открытых мастер-классах. Вы можете записаться на очередной открытый урок по ссылке.
Удачных Вам инвестиций!
Если эта статья была Вам полезна, поделитесь ей или оставьте комментарий в специальном поле под статьей.
Хоть теория и современная, первому ее упоминанию уже 70 лет.
Современную теорию портфеля — Modern Portfolio Theory, MPT — впервые сформулировал Гарри Марковиц в статье «Выбор портфеля», опубликованной в Журнале финансов 1952 года. Она заключается в диверсификации с помощью слабо коррелирующих между собой активов — то есть портфель нужно составлять из активов, которые в одной ситуации ведут себя по-разному.
Теория использует математический процесс, который описывает влияние балансировки долей активов на отношение риска к доходности портфеля. Сейчас принципы MPT используют для оптимизации инвестиционных стратегий и частные инвесторы, и крупные институциональные игроки, включая хедж-фонды.
В основе MPT лежит тезис о том, что риск и доходность взаимосвязаны. Это означает, что желание инвестора получить более высокую доходность непременно повышает уровень риска, а между двумя портфелями с одинаковой ожидаемой доходностью рационально выбирать менее рискованный вариант.
Под риском в теории понимается волатильность портфеля — то есть то, насколько изменчива его цена. Математически волатильность выражается через статистический показатель, который называется стандартным отклонением. Пример его расчета я приводил в статье про всепогодную стратегию.
MPT утверждает, что для каждого уровня риска есть соответствующая комбинация активов, которая максимизирует доход, — такой портфель называется оптимальным. Другая идея MPT заключается в том, что за счет диверсификации по различным классам активов можно сгладить волатильность портфеля. Таким образом, мы либо максимизируем доход при заданном уровне риска, либо минимизируем риск при целевой доходности.
Рассмотрим, как это работает.
Что такое эффективная граница
На диаграмме ниже представлена так называемая эффективная граница для портфелей, составленных из акций и среднесрочных казначейских облигаций в разных пропорциях.
Оптимальные портфели расположены на фиолетовой линии. Варианты выше нее недостижимы: не существует портфелей с таким отношением доходности к риску. А портфели ниже линии неэффективны: они либо дают доходность ниже ожидаемой, либо подразумевают больший риск.
Если мы сравним портфель из акций и облигаций в пропорции 25/75, он будет предпочтительнее портфеля, состоящего на 100% из облигаций. Первый подвержен меньшему риску за счет эффекта диверсификации, а его прибыль выше за счет доли акций.
Для более высокой доходности инвестору нужно увеличивать долю акций, но риски при этом тоже возрастают. В среднем стандартное отклонение для портфеля, состоящего целиком из акций, то есть S&P 500, достигает 17%. С таким уровнем риска вероятны периодические просадки в 20—30%, а иногда и больше. Недавняя история это подтверждает: в марте 2020 года S&P 500 показал −35% по отношению к своему предыдущему максимуму.
Оптимизация портфеля означает поиск компромисса между риском и прибылью. Поэтому инвестору важно заранее определиться с желаемой доходностью и комфортным для себя уровнем риска. Повторюсь, что речь здесь идет про волатильность, с которой готов мириться инвестор. Этот риск не означает полной потери актива, но может включать ее, например если компания обанкротится. Но диверсификация портфеля обычно снимает этот вопрос.
Как работает балансирование долей в портфеле
За счет балансирования пропорций активов мы можем увеличить ожидаемую доходность портфеля. Общая доходность будет представлять собой средневзвешенное значение доходности по каждому рассматриваемому активу.
Предположим, у инвестора портфель на 10 000 $, состоящий из акций и облигаций в пропорции 20/80. Значит, в абсолютном выражении на акции приходится 2000 $, а на облигации — 8000 $. При этом предположим, что ожидаемая доходность акций составит 10%, а облигаций — 5%.
На основе этих данных можно посчитать общую ожидаемую доходность портфеля:
8000 / 10 000 × 5% + 2000 / 10 000 × 10% = 4% + 2% = 6%
Если инвестору нужна более высокая доходность, скажем 7,5%, ему придется увеличить долю акций. Для такой потенциальной доходности соотношение инструментов в портфеле должно быть 50/50:
5000 / 10 000 × 5% + 5000 / 10 000 × 10% = 2,5% + 5% = 7,5%
Еще балансировать доли активов можно для минимизации рисков. Рассмотрим, как это работает.
Одна из метрик, отражающая чувствительность портфеля к системному риску рынка, — коэффициент «бета». Он показывает уязвимость портфеля к глобальным рыночным событиям, на которые инвестор никак не может повлиять.
Что за коэффициент «бета»
Коэффициент «бета» — это статистический параметр, который характеризует направление и амплитуду движения актива относительно широкого рынка. Под последним обычно понимают индекс S&P 500, который покрывает 80% капитализации американского рынка и служит индикатором состояния экономики США.
«Бету» могут рассчитывать как для отдельной акции, так и для портфеля в целом.
Для расчета сравнивают поведение актива с бенчмарком на определенном отрезке времени. Например, Московская биржа ежедневно предоставляет калькуляцию значений коэффициента «бета» для российских эмитентов по итогам 30 торговых сессий. Формула расчета коэффициента довольно сложная, поэтому здесь ее рассматривать не будем.
Проанализируем значения.
0 < «бета» < 1 — актив движется однонаправленно с S&P 500, но колеблется не так сильно — риск меньше рыночного.
−1 < «бета» < 0 — корреляция между активом и бенчмарком обратная. Они движутся в разные стороны, но актив ведет себя более стабильно.
«Бета» < −1 — корреляция обратная, но актив несет в себе больший риск в сравнении с рыночным.
«Бета» > 1 — означает, что актив коррелирует с индексом, но ведет себя более волатильно. Актив очень рисковый.
Разберем на примере. Предположим, портфель инвестора состоит из четырех активов.
Активы с разными бета-коэффициентами
| «Бета» | Доля | |
|---|---|---|
| Актив А | 1 | 25% |
| Актив B | 1,6 | 25% |
| Актив C | 0,75 | 25% |
| Актив D | 0,5 | 25% |
Посчитаем общую «бету» портфеля:
25% × 1 + 25% × 1,6 + 25% × 0,75 + 25% × 0,5 = 0,96
«Бета» 0,96 близка к 1 — значит, риск портфеля сопоставим с риском S&P 500. Предположим, инвестор хочет получить доходность больше и он готов взять на себя больший риск — его устроит «бета» портфеля 1,2. Этого можно добиться через корректировку долей активов, например так: забираем 5% от актива A и по 10% от активов C и D в пользу самого рискового актива — B.
Тогда мы получаем новую бету портфеля:
20% × 1 + 50% × 1,6 + 15% × 0,75 + 15% × 0,5 = 1,19
Таким образом происходит балансировка долей активов. Она позволяет инвестору приблизиться к оптимальному портфелю.
Пример оптимизации портфеля
Одной из самых известных и надежных стратегий считается всепогодный портфель Рэя Далио. Его принципы легли в основу фондов TRUR и OPNW. Классический вариант всепогодного портфеля можно воссоздать с помощью пяти ETF.
Пример классического всепогодного портфеля
| Тикер | Название фонда | Доля |
|---|---|---|
| VTI | Vanguard Total Stock Market ETF | 30% |
| TLT | iShares 20+ Year Treasury Bond ETF | 40% |
| IEF | iShares 7—10 Year Treasury Bond ETF | 15% |
| DBC | Invesco DB Commodity Tracking | 7,5% |
| GLD | SPDR Gold Shares | 7,5% |
Vanguard Total Stock Market ETF
iShares 20+ Year Treasury Bond ETF
iShares 7—10 Year Treasury Bond ETF
Invesco DB Commodity Tracking
Для анализа стратегии я буду использовать сервис Portfolio Visualizer.
Посмотрим на показатели всепогодного портфеля за последние 10 лет, с января 2011 года по ноябрь 2020, в сравнении с бенчмарком. Доходность берем без учета инфляции. Ребалансировка портфеля, то есть восстановление исходных пропорций, производится раз в год.
Показатели всепогодного портфеля и S&P 500 за 10 лет
| Портфель | Среднегодовая доходность | Бета | Стандартное отклонение | Корреляция с S&P 500 | Коэффициент Шарпа |
|---|---|---|---|---|---|
| Всепогодный | 8,15% | 0,16 | 6,17% | 0,37 | 1,21 |
| S&P 500 | 13,42% | 1 | 13,57% | 1 | 0,95 |
Среднегодовая доходность
8,15%
Стандартное отклонение
6,17%
Корреляция с S&P 500
0,37
Среднегодовая доходность
13,42%
Стандартное отклонение
13,57%
Индекс S&P 500 показывал в среднем в год доходность на 5,27 процентного пункта больше, чем всепогодный портфель. Но и его волатильность в два раза выше — то есть инвестор принял на себя в два раза больший риск. В сентябре 2011 он пережил просадку портфеля размером −16,31%, а в марте 2020 года — −19,63%. У всепогодного портфеля максимальная просадка случилась в декабре 2015 года и составила −6,95%.
В результате коэффициент Шарпа у S&P 500 ниже, чем у всепогодной стратегии. Коэффициент Шарпа показывает эффективность портфеля с точки зрения соотношения доходности к риску: чем больше коэффициент, тем выше доходность на единицу риска. И всепогодная стратегия оказалась более эффективной на тестируемом отрезке, но с точки зрения доходности она скорее подходит консервативным инвесторам.
Допустим, меня устраивает уровень риска всепогодной стратегии, но мне хочется зарабатывать больше — примерно 10% годовых. Перед тем как оптимизировать стратегию, взглянем на 10-летние показатели каждого инструмента в портфеле.
Показатели каждого актива за 10 лет
| Название фонда | Доходность | Макс. просадка | Корреляция с S&P 500 | Коэффициент Шарпа |
|---|---|---|---|---|
| Vanguard Total Stock Market ETF (VTI) | 13,37% | −20,84% | 1 | 0,92 |
| iShares 20+ Year Treasury Bond ETF (TLT) | 8,32% | −18,03% | −0,42 | 0,64 |
| iShares 7—10 Year Treasury Bond ETF (IEF) | 4,54% | −7,6% | −0,4 | 0,73 |
| Invesco DB Commodity Tracking (DBC) | −6,37% | −64,83% | 0,57 | −0,34 |
| SPDR Gold Shares (GLD) | 1,87% | −42,91% | 0,08 | 0,16 |
Vanguard Total Stock Market ETF (VTI)
iShares 20+ Year Treasury Bond ETF (TLT)
Корреляция с S&P 500
−0,42
iShares 7—10 Year Treasury Bond ETF (IEF)
Корреляция с S&P 500
−0,4
Invesco DB Commodity Tracking (DBC)
Корреляция с S&P 500
0,57
Корреляция с S&P 500
0,08
Мы видим, что самая слабая позиция в стратегии — ETF DBC, то есть коммодити. За десять лет они показали отрицательную доходность, в среднем давали ежегодный убыток 6,37%. А их корреляция с бенчмарком составляет 0,57 — это значительно выше остальных диверсификаторов в портфеле.
Еще отметим, что коэффициент Шарпа у акций выше, чем у длинных облигаций — то есть, хоть они и более рисковые, но они приносят больше прибыли на единицу риска.
Модифицируем классический всепогодный портфель двумя действиями:
- Заменим ETF DBC на коммунальный сектор — ETF Utilities Select Sector SPDR Fund (XLU). Показатели последнего намного лучше: высокий коэффициент Шарпа — 0,85 и низкая корреляция с рынком — 0,29. Он тоже предоставляет защиту от инфляции: коммунальные услуги — это предмет первой необходимости, они растут вслед за общим уровнем цен.
- Поменяем пропорции у акций и длинных облигаций. Им выделялось 30 и 40% соответственно — в новом портфеле сделаем наоборот. А доли других инструментов оставим как есть.
Пример оптимизированного всепогодного портфеля
| Тикер | Название фонда | Доля |
|---|---|---|
| VTI | Vanguard Total Stock Market ETF | 40% |
| TLT | iShares 20+ Year Treasury Bond ETF | 30% |
| IEF | iShares 7—10 Year Treasury Bond ETF | 15% |
| XLU | Utilities Select Sector SPDR ETF | 7,5% |
| GLD | SPDR Gold Shares | 7,5% |
Vanguard Total Stock Market ETF
iShares 20+ Year Treasury Bond ETF
iShares 7—10 Year Treasury Bond ETF
Utilities Select Sector SPDR ETF
Сравним результаты классического и оптимизированного портфелей за 10 лет. Посмотрим, что было бы, если бы мы в январе 2011 года вложили 10 000 $ в каждую из стратегий. Условия теста прежние: ежегодная ребалансировка, не учитываем инфляцию и дивиденды.
Показатели классического и оптимизированного портфелей и S&P 500 за 10 лет
| Портфель | Итог | Доходность | Макс. просадка | «Бета» | Стандартное отклонение | Коэффициент Шарпа |
|---|---|---|---|---|---|---|
| Классический | 21 741 $ | 8,15% | −6,95% | 0,16 | 6,17% | 1,21 |
| Оптимизированный | 25 535 $ | 9,91% | −6,33% | 0,28 | 6,44% | 1,41 |
| S&P 500 | 34 849 $ | 13,42% | −19,63 | 1 | 13,57% | 0,95 |
Стандартное отклонение
6,17%
Стандартное отклонение
6,44%
Стандартное отклонение
13,57%
Мы приблизились к желаемой доходности 10%, при этом заметно улучшив эффективность портфеля: коэффициент Шарпа вырос до 1,41. Портфель стал чуть более волатилен, хотя его максимальная просадка снизилась. Так как мы увеличили долю акций, «бета» и корреляция портфеля с S&P 500 увеличились. Но нам удалось сдвинуть планку доходности сильнее, чем возросли риски, — мы оказались ближе к эффективной границе.
Зачем искать альтернативные диверсификаторы
Как было показано, поиск оптимального портфеля связан с грамотным распределением долей активов в нем. При этом важно, чтобы инструменты слабо коррелировали между собой, а лучше — имели обратную корреляцию. Тогда движение по одному активу будет компенсироваться движением по другому — как результат, общая волатильность портфеля будет сглаживаться.
Альтернативные диверсификаторы — это активы, которые демонстрируют низкую корреляцию с традиционными инструментами, например золото, недвижимость, коммодити, венчурные инвестиции. Низкая корреляция делает их привлекательными дополнениями к портфелю.
В современных реалиях диверсификация только за счет акций и облигаций не работает так же хорошо, как несколько десятилетий назад. Характер рынков поменялся. Вот несколько аргументов в пользу добавления в портфель альтернативных инструментов.
Рынки стали более волатильными — об этом говорит исследование Blackstone. Если подсчитать количество торговых сессий, когда S&P 500 сдвинулся на 3% и больше, то с 2000 по 2009 год их было 95. А за предшествующие 50 лет был всего 81 случай.
Количество дней в каждом десятилетии, когда S&P 500 сдвинулся на 3% и более
| 1950—1959 | 5 |
| 1960—1969 | 9 |
| 1970—1979 | 16 |
| 1980—1989 | 24 |
| 1990—1999 | 27 |
| 2000—2009 | 95 |
| 2010—2019 | 50 |
Корреляции между активами также выросли. Это связано с более тесной интеграцией экономик, глобальными производственными цепочками и усилившимся влиянием рынков друг на друга. Если посмотреть на десятилетие перед кризисом 2008 года, то корреляция большинства классов активов с S&P 500 была ниже 0,5. Но после 2008 года корреляция заметно выросла. Только облигации по-прежнему остаются хорошим диверсификатором для акций, но их корреляция с отрицательной сменилась на положительную. Все это означает, что диверсифицироваться стало сложнее.
Корреляция различных классов активов с индексом S&P 500
| 1998—2007 | 2008—2020 | |
|---|---|---|
| Глобальные акции | 0,84 | 0,89 |
| Высоконадежные облигации | −0,21 | 0,01 |
| Высокодоходные облигации | 0,49 | 0,73 |
| Недвижимость | 0,32 | 0,74 |
| Товары | −0,01 | 0,59 |
Сложная макроэкономическая ситуация. В 2020 году мы вступили в рецессию — наблюдаем падение темпов роста ВВП. В условиях коронавируса ряд отраслей оказался под ударом: авиаперевозчики, отели, туризм, офлайн-ретейл, — многие компании оказались на грани банкротства и порезали дивиденды. В технологических отраслях оцененность акций по показателю P / E сильно выросла — акции стали более дорогими. Экономическая нестабильность и возможный пузырь на фондовом рынке пугают инвесторов, заставляя присматриваться к альтернативным классам активов.
Как менялись экономические показатели США
| 1985—2007 | 2008—2020 | |
|---|---|---|
| Темпы роста ВВП США | 3,2% | 1,6% |
| Доходность 10-летних казначейских облигаций | 6,4% | 2,2% |
| Оцененность S&P 500 по показателю P / E | 21,4 | 25,8 |
Доходность 10-летних казначейских облигаций
Оцененность S&P 500 по показателю P / E
Доходность по облигациям снижается. В мировой экономике сейчас дефляция, ключевые ставки стремятся к нулю. Соответственно, облигации развитых экономик дают околонулевую или отрицательную доходность. Да, они остаются хорошим диверсификатором акций, но практически не приносят прибыли.
Защита от инфляции. Альтернативные инструменты нередко предлагают такую защиту, главным образом это относится к коммодити и недвижимости. Несмотря на то что в конкретный момент уровень инфляции низкий, на стратегической дистанции она заметно сказывается на итоговой доходности портфеля.
Какие альтернативные диверсификаторы использовать
Под альтернативными инвестициями подразумевается все, что не относится к акциям, облигациям и наличным. Это может быть вложение в частный бизнес, венчурные инвестиции, хедж-фонды, криптовалюта, коммодити, предметы искусства и срочные инструменты — деривативы.
Сразу же обозначу минусы альтернативных активов:
- Часто это материальные активы, например физическая недвижимость, предметы искусства, антиквариат. У них низкая ликвидность — их продажа может занять время.
- Могут потребоваться специализированные знания. В частности, в случае с венчурными инвестициями, предметами искусства и деривативами — в этих сферах нужно ориентироваться и понимать все тонкости.
- Более сложный доступ. Например, для торговли деривативами нужен обеспеченный счет на срочной секции биржи. А в случае с хедж-фондами требуется большой капитал: в США порог входа составляет 5 млн долларов, в офшорах — порядка 100 тысяч долларов.
- Некоторые инструменты не регулируются со стороны государства — например, криптовалюта. А значит, в них вкладываться опасно.
Хорошая новость в том, что для рядовых инвесторов многие из этих инвестиций стали доступными благодаря различным фондам и ETF. Например, в широкий спектр недвижимости можно инвестировать через акции REIT, а в золото — через соответствующие ETF: FXGD, VTBG и TGLD или акции компаний-золотодобытчиков.
Стоит отметить, что отношение инвесторов к золоту за прошедшее столетие сильно менялось. В 1933 году Рузвельт подписал указ о конфискации золотых монет и слитков у населения в качестве меры борьбы с последствиями великой депрессии — до 1974 года частное владение золотом в США было запрещено. последующие десятилетия после 1974 года население ограничивалось хранением золота в виде золотых монет — как защита от апокалиптических сценариев вроде краха финансовой системы.
В новом тысячелетии золото приобретает в портфеле инвесторов статус стратегического актива, в том числе благодаря ETF. Если до 2008 года в сбалансированном портфеле золоту выделялась доля 2—3%, то сейчас нередко можно услышать мнение, что его доля должна составлять порядка 10%. Главным катализатором роста популярности золота можно назвать нулевые и отрицательные ставки инструментов с фиксированной доходностью.
Ежегодная доходность разных классов активов на стратегических отрезках времени
| С 1971 года | 20 лет | 10 лет | |
|---|---|---|---|
| Долларовый кэш | 5,10% | 1,79% | 0,58% |
| Облигации | 6,02% | 5,08% | 3,80% |
| Акции США | 10,94% | 6,93% | 13,45% |
| Глобальные акции | 11,30% | 5,55% | 6,42% |
| Акции развивающихся рынков | — | 11,19% | 5,13% |
| Коммодити | 10,69% | 2,77% | −3,88% |
| Золото | 10,61% | 9,65% | 4,54% |
Акции развивающихся рынков
Доля золота в оптимизированных портфелях
| Консервативный | 2,31—5,78% |
| Умеренный | 4—5,98% |
| Агрессивный | 4,5—10,2% |
Консервативный
2,31—5,78%
Оптимальное распределение инструментов для разных типов портфелей
| Консервативный портфель | Умеренный портфель | Агрессивный портфель | |
|---|---|---|---|
| Долларовый кэш | 4,49% | 2,58% | 0,74% |
| Акции | 25% | 37,01% | 44,02% |
| Облигации | 61,58% | 26,83% | 13,42% |
| Альтернативные активы | 6,42% | 27,95% | 32,40% |
| Золото | 2,51% | 5,63% | 9,42% |
Альтернативные активы
6,42%
Альтернативные активы
27,95%
Альтернативные активы
32,40%
В таблице выше портфели оптимизировали на основе данных по ежемесячной доходности инструментов в период с января 1989 по декабрь 2019 года. Характеристики «Консервативный», «Умеренный» и «Агрессивный» отражают составы гипотетических портфелей, основанных на опросах таких организаций, как Американская ассоциация индивидуальных инвесторов.
Например, распределение активов в умеренном портфеле, по их мнению, должно выглядеть примерно так: 28% облигаций и наличных, 42% акций и 30% золота и альтернативных инвестиций — REIT, хедж-фонды, частный бизнес, коммодити. Данные в таблице выше представляют оптимизированные значения долей активов, при которых достигается наилучшее соотношение доходности и риска: такой вариант портфеля находится ближе к эффективной границе.
Если инвестору не удается подобрать ETF для какого-то класса активов, можно найти отдельных представителей нужного сегмента, которые также могут послужить хорошими диверсификаторами.
Например, один из альтернативных типов активов — Luxury, брендовые вещи. Можно взять несколько представителей этого сегмента — например, акции Tiffany и Moet Hennessy Louis Vuitton. Они показывают достаточно низкую корреляцию с рынком — 0,35 и 0,58 соответственно. А вторая, помимо всего прочего, в последнем десятилетии дала высокий коэффициент Шарпа — 1,34. Включение в портфель таких активов может улучшить общий профиль риска.
Запомнить
- За счет балансирования долей активов можно управлять рисками портфеля и оптимизировать его доходность.
- Множество оптимальных портфелей с разным распределением долей активов образуют эффективную границу.
- Под риском подразумевается стандартное отклонение портфеля, то есть его волатильность. В вопросе оценки рисков важны метрики: стандартное отклонение, бета-коэффициент, коэффициент Шарпа и корреляция с широким рынком.
- В последние десятилетия рынки стали более капризными, а корреляция между различными классами активов возросла. Поэтому инвесторы все чаще используют в портфеле альтернативные диверсификаторы.
- Золото сейчас рассматривается как стратегический актив и считается важной частью сбалансированного портфеля.
Оптимизация инвестиционного портфеля по методу Марковица
Время на прочтение
4 мин
Количество просмотров 11K
Пример стандартной реализации на Python оптимизации инвестиционного портфеля по методу Марковица. Есть много реализаций данного метода. В том числе и на Python. Реализовал еще раз (см. ссылка на GitHub).
Источники
Немного теории возьмем из этих источников:
Лучший инвестиционный портфель через симуляцию Монте-Карло в Python
Портфельная теория Марковица (Википедиа)
Загрузка данных по котировкам
Используем данные с сервиса Yahoo.Finance
! pip install yfinance
import yfinance as yf
Берем несколько акций американского рынка за последние 3 месяца.
data = yf.download(['AAPL','GE','BAC','AMD','PLUG','F'],period='3mo')Курсы закрытия
В расчетах будем использовать дневные курсы закрытия
closeData = data.Close
closeData
Графики курсов
import matplotlib.pyplot as plt
for name in closeData.columns:
closeData[name].plot()
plt.grid()
plt.title(name)
plt.show()
Изменение курсов
Далее понадобятся относительные изменения к предыдущему дню.
dCloseData = closeData.pct_change()
dCloseData
Графики относительных изменений курсов
for name in dCloseData.columns:
dCloseData[name].plot()
plt.title(name)
plt.grid()
plt.show()
Средняя доходность
Средняя дневная доходность по каждой акции для расчета доходности портфеля.
dohMean = dCloseData.mean()
dohMean
Ковариация
Для расчета риска портфеля потребуется ковариационная матрица.
cov = dCloseData.cov()
cov
Случайный портфель
Будем генерить случайные портфели. В них сумма долей равна 1 (единице).
import numpy as np
cnt = len(dCloseData.columns)
def randPortf():
res = np.exp(np.random.randn(cnt))
res = res / res.sum()
return res
r = randPortf()
print(r)
print(r.sum())
[0.07519908 0.07594622 0.20932539 0.40973202 0.1234458 0.10635148]
1.0
Доходность портфеля
Доходность портфеля считаем как сумму долей доходностей по каждой акции в портфеле.
def dohPortf(r):
return np.matmul(dohMean.values,r)
r = randPortf()
print(r)
d = dohPortf(r)
print(d)
[0.0789135 0.13031559 0.25977124 0.21157419 0.13506695 0.18435853]
0.006588795350151513
Риск портфеля¶
Риск портфеля считаем через матричные произведения долей портфеля и матрицы ковариации.
def riskPortf(r):
return np.sqrt(np.matmul(np.matmul(r,cov.values),r))
r = randPortf()
print(r)
rs = riskPortf(r)
print(rs)
[0.10999361 0.13739338 0.20412889 0.13648828 0.24021123 0.17178461]
0.02483674110724784
Облако портфелей
Сгенерируем множество портфелей и выведем результат на график риск-доходность. Найдем параметры оптимального портфеля по минимальному риску и по максимальному коэффициенту Шарпа. Сравним с данными усредненного портфеля.
risk = np.zeros(N)
doh = np.zeros(N)
portf = np.zeros((N,cnt))
for n in range(N):
r = randPortf()
portf[n,:] = r
risk[n] = riskPortf(r)
doh[n] = dohPortf(r)
plt.figure(figsize=(10,8))
plt.scatter(risk*100,doh*100,c='y',marker='.')
plt.xlabel('риск, %')
plt.ylabel('доходность, %')
plt.title("Облако портфелей")
min_risk = np.argmin(risk)
plt.scatter([(risk[min_risk])*100],[(doh[min_risk])*100],c='r',marker='*',label='минимальный риск')
maxSharpKoef = np.argmax(doh/risk)
plt.scatter([risk[maxSharpKoef]*100],[doh[maxSharpKoef]*100],c='g',marker='o',label='максимальный коэф-т Шарпа')
r_mean = np.ones(cnt)/cnt
risk_mean = riskPortf(r_mean)
doh_mean = dohPortf(r_mean)
plt.scatter([risk_mean*100],[doh_mean*100],c='b',marker='x',label='усредненный портфель')
plt.legend()
plt.show()
Выведем данные найденных портфелей.
import pandas as pd
print('---------- Минимальный риск ----------')
print()
print("риск = %1.2f%%" % (float(risk[min_risk])*100.))
print("доходность = %1.2f%%" % (float(doh[min_risk])*100.))
print()
print(pd.DataFrame([portf[min_risk]*100],columns=dCloseData.columns,index=['доли, %']).T)
print()
print('---------- Максимальный коэффициент Шарпа ----------')
print()
print("риск = %1.2f%%" % (float(risk[maxSharpKoef])*100.))
print("доходность = %1.2f%%" % (float(doh[maxSharpKoef])*100.))
print()
print(pd.DataFrame([portf[maxSharpKoef]*100],columns=dCloseData.columns,index=['доли, %']).T)
print()
print('---------- Средний портфель ----------')
print()
print("риск = %1.2f%%" % (float(risk_mean)*100.))
print("доходность = %1.2f%%" % (float(doh_mean)*100.))
print()
print(pd.DataFrame([r_mean*100],columns=dCloseData.columns,index=['доли, %']).T)
print()
---------- Минимальный риск ----------
риск = 1.80%
доходность = 0.59%
доли, %
AAPL 53.890706
AMD 12.793389
BAC 4.117541
F 16.547201
GE 10.945462
PLUG 1.705701
---------- Максимальный коэффициент Шарпа ----------
риск = 2.17%
доходность = 0.88%
доли, %
AAPL 59.257114
AMD 8.317192
BAC 2.049882
F 8.689935
GE 4.772159
PLUG 16.913719
---------- Средний портфель ----------
риск = 2.33%
доходность = 0.68%
доли, %
AAPL 16.666667
AMD 16.666667
BAC 16.666667
F 16.666667
GE 16.666667
PLUG 16.666667
Выводы
Повторили классический метод расчета долей инвестиционного портфеля. Получили вполне конкретные результаты.
Оптимизация портфеля по методу Марковица предполагает сохранение параметров в будущем (корреляций между отдельными инструментами и уровня их доходности). Но это не гарантировано. В следующих работах предстоит это проверить.
Понятно, что положительного результата от обозначенной выше проверки ожидать не стоит. Но тогда можно поискать как доработать метод Марковица для получения более гарантированного дохода в будущем. Вот тема для еще одного исследования.
На чтение 10 мин Просмотров 66.3к.
Приведем пример формирования инвестиционного портфеля по модели Г. Марковица с помощью программы Excel, разберем достоинства и недостатки данной модели в современной экономике и пути их решения.
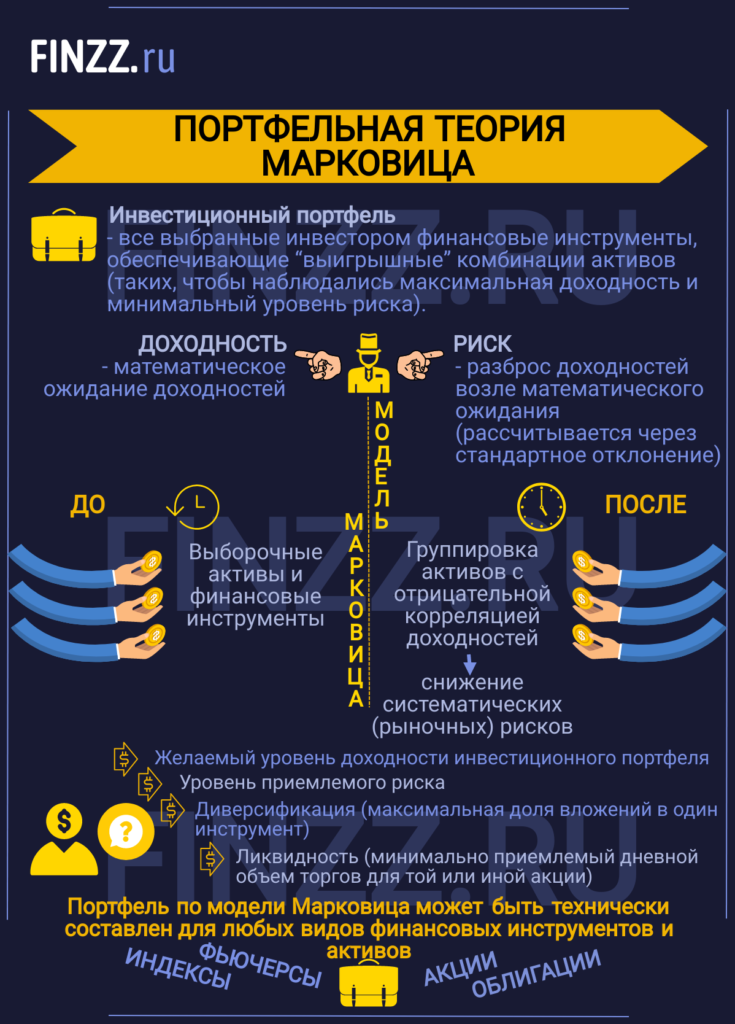
Инвестиционный портфель – это совокупность различных финансовых инструментов, удовлетворяющих цели инвестора и, как правило, заключается в создании таких комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска.
Содержание
- Инфографика: Портфельная теория Марковица (основная информация)
- Модель Марковица
- Цели формирования инвестиционного портфеля
- Расчет доходности инвестиционного портфеля Марковица
- Оценка риска инвестиционного портфеля Марковица
- Эконометрический вид модели Марковица
- Пример формирования инвестиционного портфеля Марковица в Excel
- Формирование инвестиционного портфеля минимального риска
- Формирование эффективного инвестиционного портфеля
- Достоинства и недостатки модели Г. Марковица
Инфографика: Портфельная теория Марковица (основная информация)
Модель Марковица
Г. Марковиц в 1952 году впервые предложил математическую модель формирования инвестиционного портфеля. В основе его модели лежат два ключевых показателя любого финансового инструмента: доходность и риск, которые были количественно измерены. Доходность по модели представляет собой математическое ожидание доходностей, а риск определяется как разброс доходностей возле математического ожидания и рассчитывается через стандартное отклонение.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
До модели Г. Марковица инвестирование происходило, как правило, в выборочные активы или финансовые инструменты, предложенная же им модель позволила снизить систематические (рыночные) риски за счет группировки активов с отрицательной корреляцией доходностей.
Следует заметить универсальность модели, так инвестиционный портфель может быть технически составлен для любых видов финансовых инструментов и активов: акций, облигаций, фьючерсов, индексов, недвижимости и т.д.
Цели формирования инвестиционного портфеля
Выделяют две инвестиционные стратегии при формировании портфеля:
► Максимизации доходности инвестиционного портфеля при ограниченном уровне риск.
► Минимизация риска инвестиционного портфеля при минимально допустимом уровне доходности.
Расчет доходности инвестиционного портфеля Марковица
Общая доходность портфеля будут представлять собой взвешенную сумму доходностей каждого отдельного финансового инструмента (актива):
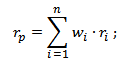
rp – доходность инвестиционного портфеля;
w – доля i-го финансового инструмента в портфеле;
ri – доходность i-го финансового инструмента.
Оценка риска инвестиционного портфеля Марковица
В модели Г. Марковица риск отдельно взятого финансового инструмента рассчитывается как стандартное отклонение доходностей. Для расчета общего риска портфеля необходимо отразить их совокупное изменение и взаимное влияние (через ковариацию), для этого воспользуемся следующей формулой:
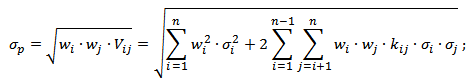
σp – риск инвестиционного портфеля;
σi – стандартное отклонение доходностей i-го финансового инструмента;
kij – коэффициент корреляции между I,j-м финансовым инструментом;
wi – доля i-го финансового инструмента (акций) в портфеле;
Vij – ковариация доходностей i-го и j-го финансового инструмента;
n – количество финансовых инструментов инвестиционного портфеля.
Эконометрический вид модели Марковица
Для того чтобы сформировать инвестиционный портфель необходимо решить оптимизационную задачу. Существует два вида задач: поиск долей акций в портфеле для достижения максимальной эффективности при заданном уровне риска (σp) и минимизация риска при заданном уровне доходности портфеля (rp). Помимо этого на уравнения накладываются дополнительные очевидные ограничения: сумма долей активов должна быть равна 1 и сами доли активов должны быть положительными.
В таблице ниже показаны формулы и наложенные на них ограничения для поиска оптимальных долей финансовых инструментов (акций).
Пример формирования инвестиционного портфеля Марковица в Excel
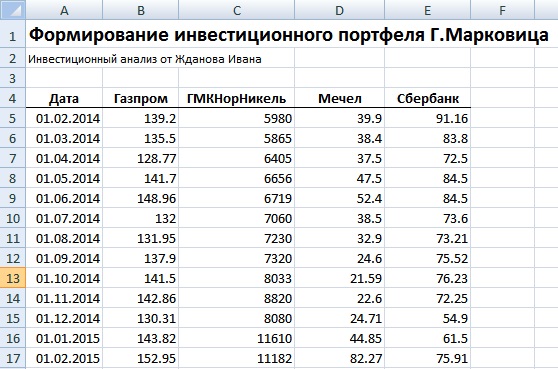
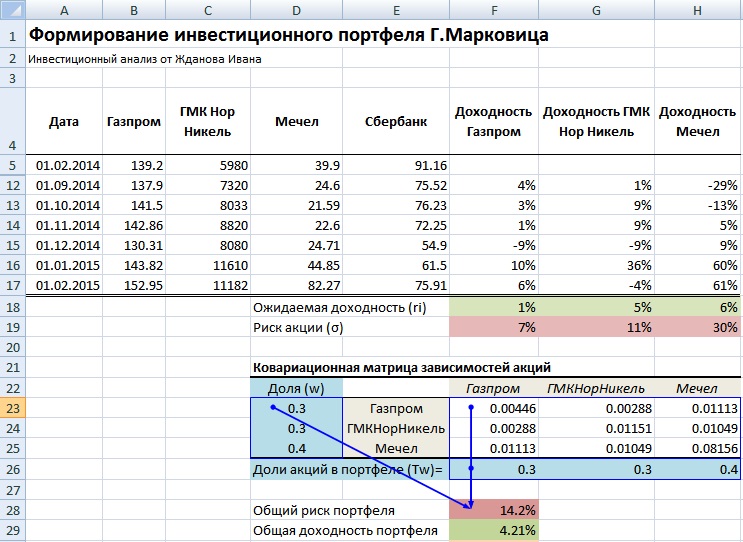
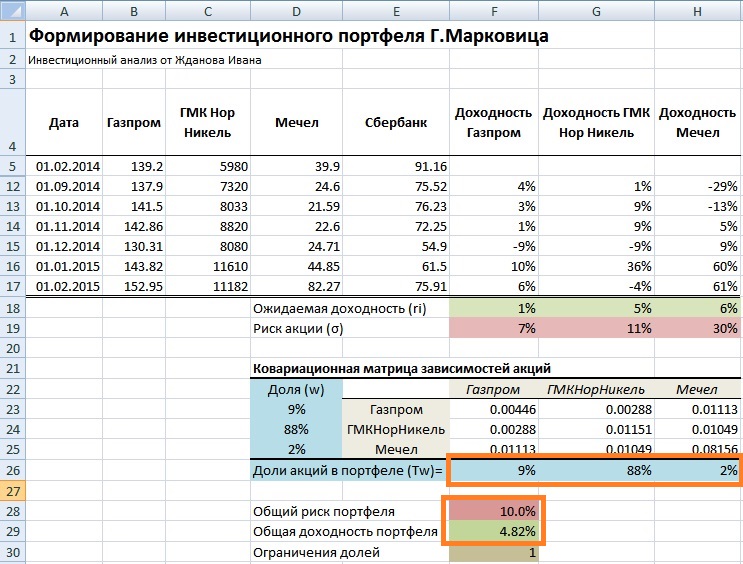
Рассмотрим наглядный пример формирования инвестиционного портфеля по модели Г. Марковица в программе Excel. Наш портфель будет состоять из четырех отечественных акций: ОАО «Газпром» (GAZP), ОАО «Норильский никель» (GMKN), ОАО «Мечел» (MTLR) и ОАО «Сбербанк» (SBER). Были взяты акции различных секторов: нефтегазового, промышленного и финансового, такой выбор увеличивает диверсификацию портфеля и снижает его рыночный риск.
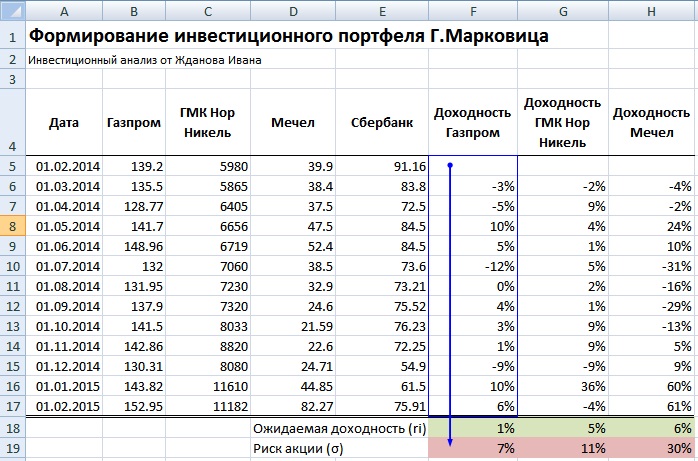
Рекомендуется брать период рассмотрения динамики изменения стоимости акций минимум один год. Это позволяет сделать более точный долгосрочный прогноз доходности и риска портфеля. На рисунке ниже показана ежемесячная стоимость акций за период с 01.02.2014 – 01.02.2015г.
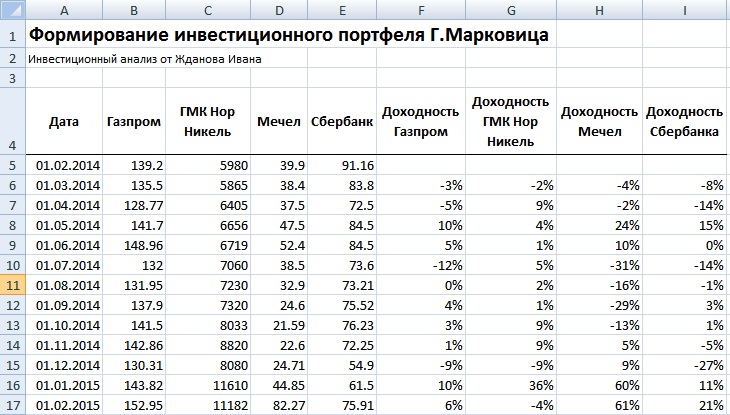
На следующем этапе формирования портфеля необходимо рассчитать ежемесячные доходности по каждой акции. Для этого воспользуемся формулой процентов в Excel:
Доходность Газпром =LN(B6/B5)
Доходность ГМКНорНикель =LN(C6/C5)
Доходность Мечел =LN(D6/D5)
Доходность Сбербанк =LN(E6/E5)
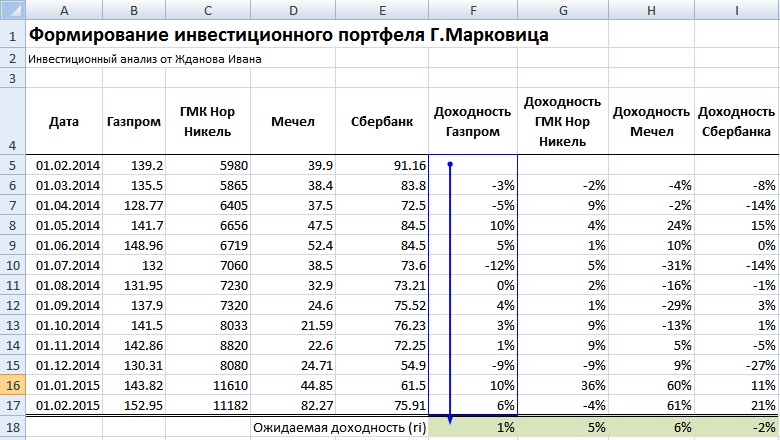
Далее определяем математическое ожидание доходностей по каждой акции, для этого найдем среднеарифметическое значение за весь период. Ожидаемая доходность по каждой акции будет следующая:
Ожидаемая доходность Газпром =СРЗНАЧ(F5:F17)
Ожидаемая доходность ГМКНорНикель =СРЗНАЧ(G5:G17)
Ожидаемая доходность Мечел =СРЗНАЧ(H5:H17)
Ожидаемая доходность Сбербанк =СРЗНАЧ(I5:I17)
Доходность акции ОАО «Сбербанк» имеет отрицательное ожидание доходности, поэтому ее следует исключить из портфеля. Оценка риска каждой акции – это ее изменчивость (волатильность) по отношению к математическому ожиданию доходностей.
Формула расчета риска акций следующая:
Риск Газпром =СТАНДОТКЛОН(F5:F17)
Риск ГМКНорНикель =СТАНДОТКЛОН(G5:G17)
Риск Мечел =СТАНДОТКЛОН(H5:H17)
Мы получили первоначальные необходимые данные для оценки долей данных акций в инвестиционном портфеле. Для оценки уровня риска всего инвестиционного портфеля воспользуемся надстройкой в Excel. Для этого зайдем в Главном меню → «Данные» → «Анализ данных» → «Ковариация».
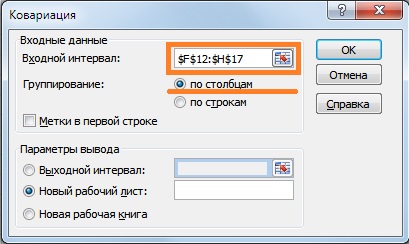
Далее в появившемся окне необходимо найти ковариации между доходностями акций. Указываем входной интервал – ежемесячных доходностей акций, а в опции «Группирование» выбираем функцию «по столбцам».
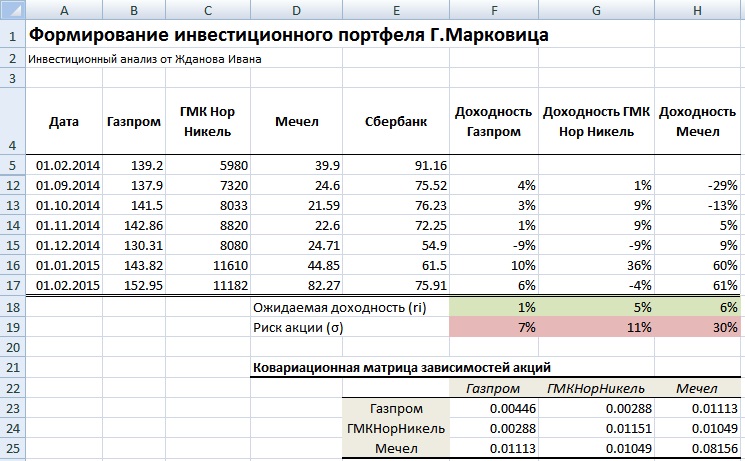
Результатом будет таблица ковариаций доходностей акций между собой. Расположим ее ниже под таблицей. Можно заметить, что диагональные значения представляют собой дисперсию доходностей акций.
Для расчета общего риска портфеля воспользуемся формулой рассмотренной выше и для этого нам необходимо перемножить доли весов акций между собой и значения ковариаций этих акций. Для того чтобы понять принцип расчета, установим доли акций 0.3, 0.3 и 0.4 и рассчитаем общий риск портфеля. Доходность портфеля рассчитывается как средневзвешенная сумма доходностей отдельных акций. Так как мы будем перемножать матрицы необходимо транспонировать столбец с долям (wT). Формула расчета риска инвестиционного портфеля будет иметь следующий вид:
Общий риск инвестиционного портфеля =КОРЕНЬ(МУМНОЖ(МУМНОЖ(F26:H26;F23:H25);D23:D25))
Общая доходность инвестиционного портфеля =F18*F26+G18*G26+H18*H26
Формирование инвестиционного портфеля минимального риска
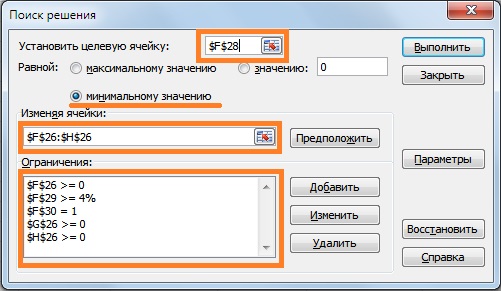
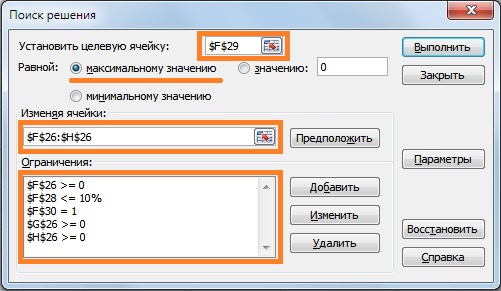
Для данной задачи необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp ≥ 4%. При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню Excel → «Данные» → «Поиск решений», а также введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля), ввести, какие параметры необходимо изменять (доли акций) и текущие ограничения. Целевая ячейка – это ячейка с формулой общего риска инвестиционного портфеля. Программа будет изменять значения долей акций при выставленных ограничениях. Формула ограничения размера доли в портфеле будет иметь следующий вид:
Ограничение на сумму долей акций (F30) =СУММ(F26:H26)
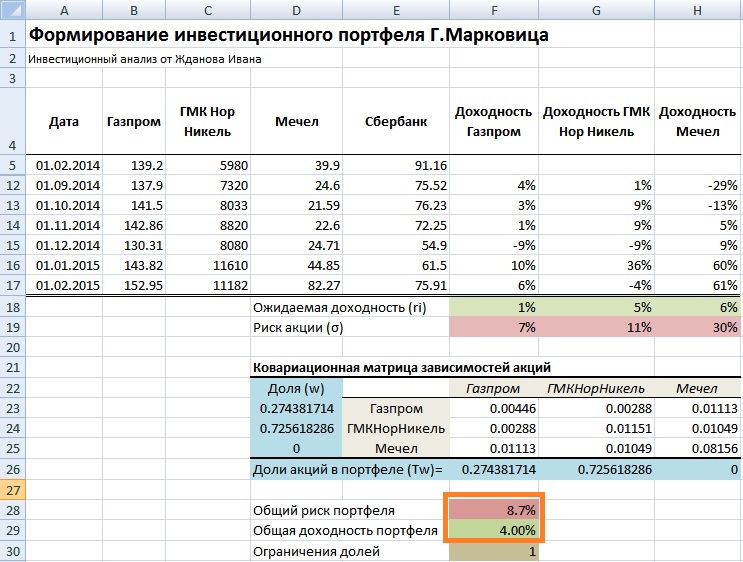
В результате мы получаем следующий расчет общего риска и доходности портфеля. Общий риск портфеля составил 8,7%, тогда как общая доходность 4%. Доли акций Газпрома получились равными 27%, доли ГМКНорНикель 73% и Мечела 0%. При заданных условиях эффективнее будет формирование портфеля из двух акций ОАО «Газпром» и ОАО «ГМКНорНикель».
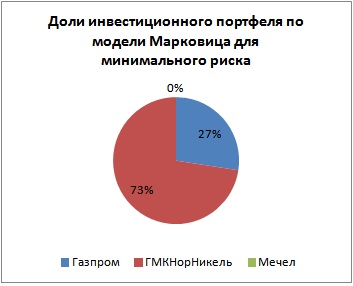
Визуально доли портфеля будут соотноситься следующим образом.
Формирование эффективного инвестиционного портфеля
Вторая задача, которая решается на основе модели Г. Марковица – посторонние портфеля с максимальным уровнем доходности и ограниченным уровнем риска. Разберем на примере данную задачу. Установим максимально допустимый уровень риска портфеля σp≤10%. С помощью надстройки «Поиск решений» определим доли акций в данной интерпретации задачи. Целевая ячейка будет ячейка с формулой доходности портфеля, ее следует максимизировать, изменяя значения долей акций при ограничениях по риску. На рисунке ниже показаны основные параметры для формирования портфеля с максимальной доходностью.
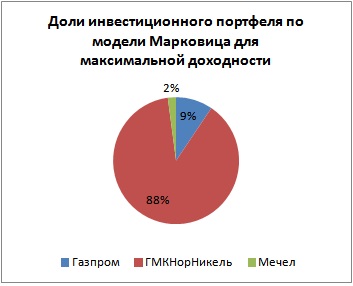
В результате мы получили доли акций в инвестиционном портфеле: 9% акций ОАО «Газпром», 88% акций ОАО «ГМКНорНикель» и 2% акций ОАО «Мечел». Общий риск портфеля не превысил 10%, а доходность составила 4,82%.
Визуально доли инвестиционного портфеля будут соотноситься следующим образом.
Достоинства и недостатки модели Г. Марковица
Рассмотрим ряд недостатков присущих модели Г. Марковица.
- Данная модель была разработана для эффективных рынков капитала, на которых наблюдается постоянный рост стоимости активов и отсутствуют резкие колебания курсов, что было в большей степени характерно для экономики развитых стран 50-80-х годов. Корреляция между акциями не постоянна и меняется со временем, в итоге в будущем это не уменьшает систематический риск инвестиционного портфеля.
- Будущая доходность финансовых инструментов (акций) определяется как среднеарифметическое. Данный прогноз основывается только на историческом значении доходностей акции и не включает влияние макроэкономических (уровень ВВП, инфляции, безработицы, отраслевые индексы цен на сырье и материалы и т.д.) и микроэкономических факторов (ликвидность, рентабельность, финансовая устойчивость, деловая активность компании).
- Риск финансового инструмента оценивается с помощью меры изменчивости доходности относительно среднеарифметического, но изменение доходности выше не является риском, а представляет собой сверхдоходность акции.
Многие из данных недостатков модели были решены последователями: прогнозирование доходности с помощью многофакторных моделей (Ю. Фама, К. Френч, Росс и др.), нейронных сетей; оценка риска на основе моделей ARCH, GARCH и т.д. Следует отметить одно из главных достоинств модели Г. Марковица: систематизация подхода к формированию инвестиционного портфеля и управление его доходностью и риском.
Резюме
В данной статье мы рассмотрели, как с помощью Excel можно сформировать инвестиционный портфель по модели Г. Марковица и решить две классические задачи: максимизация доходности портфеля при минимальном риске и минимизация риска при заданной доходности. Портфель Марковица позволяет снизить систематические риски за счет комбинации различных активов. Несмотря на сложности использования данной модели в современной экономике данная модель применима для таких низковолатильных активов как недвижимость, облигации товарные фьючерсы и т.д. В настоящее время сократился срок пересмотра активов в портфеле, так если раньше он мог составлять год, то сейчас это 2-6 месяцев. С вами был Иван Жданов, спасибо за внимание.
Автор: к.э.н. Жданов Иван Юрьевич
Сегодня в я решил написать суть, назначение и применение портфельной теории Гарри Марковица, который первым предложил метод математического составления инвестиционного портфеля и расчета соотношения доходности и риска, а не просто словесного обоснования инвестиционного решения.
В наше время составить портфель на основе методов Марковица может любой пользователь Excel, который мало-мальски знаком с данной программой. Но додуматься до того, что придумал Марковиц без компьютерных программ, вызывает восхищение. Именно поэтому прошло 38 (!) лет с момента публикации своей теории в 1952 году до получения Нобелевской премии лишь в 1990 году – в век компьютерных технологий.
Суть его теории заключается в 2-х положениях:
1. С помощью исторических данных о котировках акций определяется средняя доходность и риск (волатильность) по каждой ценной бумаге.
2. Составление портфеля подбором долей акций в нем таким образом, чтобы: при заданном риске максимизировать доходность или при заданной доходности минимизировать риск.
Понять суть теории поможет пошаговый расчет инвестиционного портфеля в Excel. Это выглядит следующим образом:
1. Выгружаются котировки акций. Чем больший период, тем лучше.
2. Рассчитывается доходность каждой акции за каждый промежуток времени, например, за месяц. Например, как ведет себя акция Газпрома каждый месяц, насколько она растет или падает.
3. Рассчитывается средняя доходность по акции за весь выгруженный период. Убираются те акции, доходность по которым получилась отрицательной. Кстати, в этом кроется недостаток модели, ведь могут быть фундаментально хорошие просевшие акции, которые, наоборот, нужно докупать. Об этом напишу ниже, т.к. в этом заключается моя стратегия и этим она отличается от модели Марковица.
4. Рассчитывается риск по каждой акции аналогично пункту 3. Для Марковица риском служила волатильность, т.е. колебание цены. Если 2 акции выросли одинаково, но первый из них сильно при этом колебался, то риск у первой акции будет больше. В Excel есть специальная формула для расчета данного риска – стандартное отклонение (отклонение цены акции от средних значений).
5. С помощью данных о ежемесячных доходностях акций рассчитывается ковариация между ценными бумагами, т.е. их взаимосвязи между собой. Например, насколько сильно влияет рост акций Газпрома на акции Газпромнефти? Наверное, сильнее, чем на акции условного Магнита. Это нужно для того, чтобы далее Excel мог методом подбора составить оптимальный портфель по соотношению доходность-риск.
6. Составляется произвольный портфель как база для дальнейшего расчета. Например, пусть в портфеле 3 акции: Газпром, Сбербанк и Норильский никель. Даются произвольные доли каждой акции. Пусть 40%, 30%, 30% соответственно.
7. Рассчитываются средневзвешенная доходность и риск данного портфеля. Мы знаем доли бумаг в портфеле, среднюю доходность и средний риск каждой из них (см. пункты 2, 3, 4). Поэтому можно рассчитать доходность и риск всего портфеля в целом.
8. Все предыдущие пункты были подготовкой для главного пункта – подбора оптимальных долей акций в портфеле. Как я написал выше, ставится одна из двух задач:
— максимизировать доходность при заданном риске — минимизировать риск при заданной доходности
В Excel есть возможность поставить такую задачу. Она называется «Поиск решений». Например, нам нужно найти такую структуру портфеля (доли акций в портфеле), чтобы при неизменном риске была максимальная доходность. Пусть риск (степень волатильности) будет 4%, и мы ставим задачу Excel, чтобы он нашел такое соотношение акций Газпрома, Сбербанка и Норникеля, чтобы доходность была максимальной при риске в 4%. И он найдет, зная средние значения доходности и риска каждой акции и их ковариацию между собой.
Также можно поставить задачу минимизировать риск при заданной доходности, где доходность будет фиксированная, а минимальный риск должен будет найти Excel с помощью подбора разных вариантов долей акций.
Вот так кратко звучит портфельная теория Марковица. Повторюсь, что человек додумался до этого без компьютерных программ. В данном посте попытался на словах объяснить, в чем состоит суть теории Марковица.
Более подробно, наглядно и детально с картинками расчет в Excel представлен на сайте БКС, у них есть статья «Составление инвестиционного портфеля по Марковицу для чайников». Не реклама, а сам оттуда брал информацию для данного поста, поэтому ссылок не оставляю.
Есть много недостатков портфельной теории Марковица, среди которых составление оптимального портфеля на основе исторических данных о доходности и риске акций. Мы знаем, что доходность в прошлом не гарантирует доходность в будущем.
Лично для меня еще более существенным недостатком модели является приравнивание волатильности к риску. Об этом я подробно писал в предыдущем посте. Для меня риск – это банкротство, снижение доли рынка, дефолт, плохое управление компанией, неверная оценка компании перед покупкой и т.д. Но никак не колебание акции фундаментально хорошей компании. Если компания привлекательна, а ее акции падают, то это для меня хорошо, и я докупаю. Но теория Марковица говорит об обратном.
Мой портфель ИИС схож с индексом МосБиржи по составу. Я увеличиваю покупки акций, когда рынок падает и таким образом получаю преимущество перед индексом МосБиржи. Если по методике Марковица посчитать доходность и риск моего ИИС и индекса МосБиржи, то получится, что оба параметра моего портфеля опережают индекс. Но их состав же одинаков (утрирую)! Да, волатильность высокая у моего портфеля, но это не говорит о том, что портфель более рискованный в инвестиционном плане. Это, пожалуй, основная мысль данного поста.