3.1. Канонические
уравнения прямой.
Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторы
коллинеарны, следовательно, их
соответствующие координаты пропорциональны:
(3.3.1)
Эти уравнения
называются каноническими
уравнениями прямой.
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору
Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:
Это канонические
уравнения прямой.
Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.
3.2.
Параметрические
уравнения прямой.
Пусть прямая
задана каноническими уравнениями
Обозначим тогда
Величина t
называется параметром и может принимать
любые значения:
.
Выразим x,
y
и z
через t
:
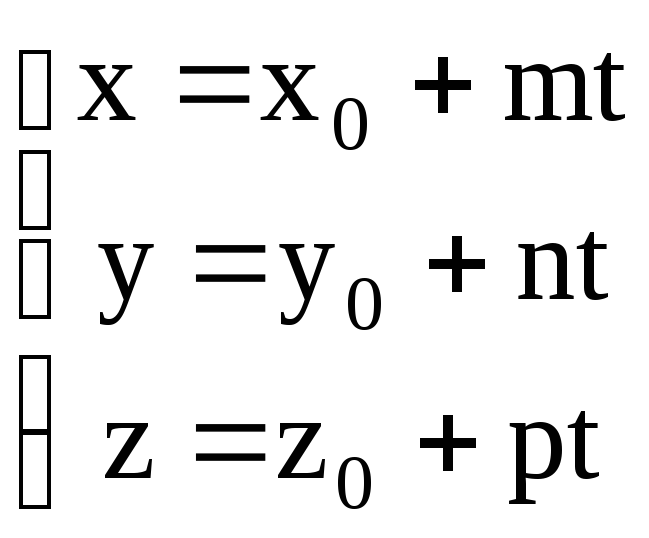
Полученные уравнения
называются параметрическими
уравнениями прямой.
Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору
Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:
Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):
Итак,

прямой.
Ответ:
Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).
Решение:
Вектор является направляющим
вектором искомой прямой.
Найдем вектор .
= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

параметрические уравнения прямой.
3.3. Уравнения
прямой, проходящей через две заданные
точки.
Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Вектор
можно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
наход
по формулам (3.1.1):).
(3.3.1)
Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
Применяем
формулу (3.3.1)
Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

уравнения прямой.
Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
По формулам
(3.3.1) получим:
Это канонические
уравнения.
Переходим к
параметрическим уравнениям:

уравнения.
Полученная прямая
параллельна оси oz
(см. рис.21).
3.4. Прямая как
линия пересечения двух плоскостей.
Пусть в
пространстве даны две плоскости
и
Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:
Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий вектор
Координаты точки
получим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть
Пример 1.
Составить
канонические уравнения прямой
Решение: Пусть
z
= 0. Решим систему
Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.
Итак, точка
лежит на искомой прямой.
Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:
Уравнения прямой
находим по формулам (3.1.1):
Ответ: .
Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).
Пример 2.
Составить канонические и параметрические
уравнения прямой
Решение:
Пусть y
= 0. Тогда система примет вид:
Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку
Для нахождения
второй точки положим x
= 0. Будем иметь:
То есть
Далее применяем
формулы (3.3.1):
Получили канонические
уравнения прямой.
Составим
параметрические уравнения прямой:
Ответ:
; 
3.5. Взаимное
расположение двух прямых в пространстве.
Пусть прямые
заданы уравнениями:
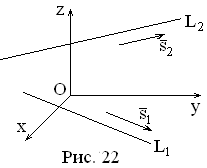
;
:
.
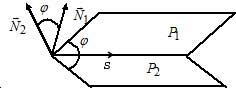
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот угол
находим по формуле из векторной алгебры:
или
(3.5.1)
Если прямые перпендикулярны
(),то
Следовательно,
(3.5.2)
Это условие
перпендикулярности двух прямых в
пространстве.
Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть
(3.5.3)
Это условие
параллельности двух прямых в пространстве.
Пример 1. Найти
угол между прямыми:
а).
и
б). и
Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему
Затем найдем их векторное произведение:
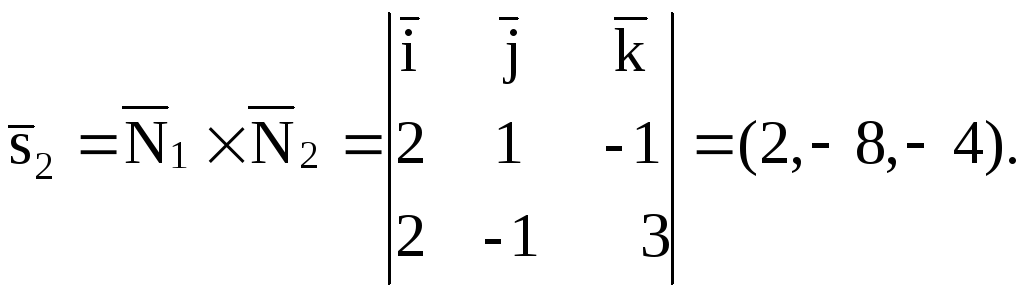
пункта 3.4).
По формуле (3.5.1)
получим:
Следовательно,
б). Запишем
направляющие векторы данных прямых:
Векторы
коллинеарны, так как их соответствующие
координаты пропорциональны:
Значит прямые
параллельны (
),
то есть
Ответ: а).
б).
Пример 2. Доказать
перпендикулярность прямых:
и
Решение:
Запишем направляющий вектор первой
прямой
Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:
Вычислим их векторное произведение:

Применим условие
перпендикулярности прямых (3.5.2):
Условие выполнено;
следовательно, прямые перпендикулярны
().
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
Уравнения прямой в пространстве векторное, общее, канонические, параметрические (Таблица)
Способ задания прямой в пространстве
Вид уравнения прямой
Векторное уравнение прямой, проходящей через точку М параллельно заданному вектору s .
s — направляющий вектор прямой
где t — скалярный множитель (параметр)
Канонические уравнения прямой, проходящей через точку M0(x0,y0,z0) и параллельно вектору s =
Параметрические уравнения прямой, проходящей через точку (x0,y0,z0) параллельно вектору s =
Прямая как линия пересечения двух непараллельных плоскостей (общие уравнения прямой)
Параметрические уравнения прямой на плоскости: описание, примеры, решение задач
Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.
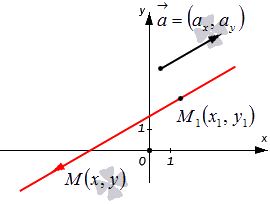
Вывод параметрических уравнений прямой на плоскости
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.
Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.
Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x — x 1 , y — y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) являются коллинеарными.
Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:
M 1 M → = λ · a → , где λ – некоторое действительное число.
Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.
В координатной форме оно имеет вид:
M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ
Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ
Составление параметрических уравнений прямой на плоскости
Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.
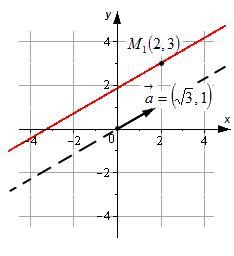
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .
Решение
На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ
Ответ: x = 2 + 3 · λ y = 3 + λ
Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .
К примеру, нам заданы направляющий вектор прямой a → = ( 2 , — 1 ) , а также точки М 1 ( 1 , — 2 ) и М 2 ( 3 , — 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = — 2 — λ или x = 3 + 2 · λ y = — 3 — λ .
Следует обратить внимание и на такой факт: если a → = ( a x , a y ) — направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .
Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.
Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = — 2 — 5 · λ . Тогда a → = ( 2 , — 5 ) — направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · — 5 ) = 2 μ , — 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор — 2 · a → = ( — 4 , 10 ) , ему соответствует значение μ = — 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 — 4 · λ y = — 2 + 10 · λ .
Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно
В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.
Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x — x 1 a x = y — y 1 a y .
Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y
При этом не должно смущать, если a x или a y будут равны нулю.
Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = — 2 — 4 · λ к каноническому уравнению.
Решение
Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = — 2 — 4 · λ
Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4
Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:
x — 3 0 = y + 2 — 4
Ответ: x — 3 0 = y + 2 — 4
В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y ⇔ ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ A x + B y + C = 0
Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = — 1 + 2 · λ y = — 3 · λ
Решение
Для начала осуществим переход к каноническому уравнению:
x = — 1 + 2 · λ y = — 3 · λ ⇔ λ = x + 1 2 λ = y — 3 ⇔ x + 1 2 = y — 3
Полученная пропорция идентична равенству — 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: — 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .
Ответ: 3 x + 2 y + 3 = 0
Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.
Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.
Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x — x 1 a x = y — y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :
x — x 1 a x = y — y 1 a y = λ ⇔ λ = x — x 1 a x λ = y — y 1 a y
Разрешим полученные уравнения относительно переменных x и y :
x = x 1 + a x · λ y = y 1 + a y · λ
Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x — 2 5 = y — 2 2
Решение
Приравняем части известного уравнения к параметру λ : x — 2 5 = y — 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x — 2 5 = y — 2 2 = λ ⇔ λ = x — 2 5 λ = y — 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ
Ответ: x = 2 + 5 · λ y = 2 + 2 · λ
Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.
Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x — 3 y — 3 = 0 .
Решение
Заданное общее уравнение преобразуем в уравнение канонического вида:
4 x — 3 y — 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4
Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:
x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = — 1 3 + 4 · λ
Ответ: x = 3 · λ y = — 1 3 + 4 · λ
Примеры и задачи с параметрическими уравнениями прямой на плоскости
Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.
- В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.
Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.
Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .
Решение
Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5
Ответ: 1 1 2 , 5
Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .
Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.
Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .
Решение
Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:
4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2
Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .
Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:
— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4
Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .
Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.
- В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.
Пример 8
Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .
Решение
По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ
Ответ: x = 1 2 + x · λ y = 2 3 — λ .
Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .
Решение
В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ
Ответ: x = 3 · λ y = — 7 — 2 · λ
- В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.
Пример 10
Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.
Решение
Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:
x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0
Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .
Параметрическое уравнение прямой в пространстве проходящей через точку параллельно вектору
Неверно введено число.
Точки должны быть разными.
Уравнение прямой в пространстве
Введите координаты точки A
Количество знаков после разделителя дроби в числах:
Каноническое уравнение прямой в пространстве:
Параметрическое уравнение прямой:
где вектор a( ; ; ) — направляющий вектор
Теория
Каноническим уравнением прямой в пространстве, проходящей через точку A(x0,y0,z0) параллельно вектору a(l,m,n) называется равенство:
Уравнением прямой в пространстве, проходящей через две точки A(x0,y0,z0) и B(x1,y1,z1) называется равенство:
Параметрическим уравнением прямой в пространстве, проходящей через точку A(x0,y0,z0) параллельно вектору a(l,m,n) называется:
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/parametricheskie-uravnenija-prjamoj-na-ploskosti/
http://www.math.by/geometry/eqline3d.html
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
Под углом
между двумя плоскостями будем понимать один из двугранных углов, образованных
этими плоскостями. Очевидно, что угол между нормальными векторами и
плоскостей α1
и α2 равен одному из указанных смежных двугранных углов или
. Поэтому

и
, то

Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.
Условие параллельности двух плоскостей.
Две плоскости α1 и α2
параллельны тогда и только тогда, когда их нормальные векторы и
параллельны, а значит
.
Итак, две плоскости параллельны друг другу тогда и только тогда, когда
коэффициенты при соответствующих координатах пропорциональны:
или
Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны
тогда и только тогда, когда их нормальные векторы перпендикулярны, а
следовательно, или
.
Таким образом, .
Примеры.
- Составить уравнение плоскости, проходящей через точку
M(-2; 1; 4) параллельно
плоскости 3x+2y-7z+8=0.Уравнение плоскости будем искать в виде Ax+By+Cz+D=0. Из условия
параллельности плоскостей следует, что:. Поэтому можно положить A=3, B=2, C=-7. Поэтому уравнение плоскости
принимает вид3x+2y-7z+D=0.Кроме того, так какMÎ α, то-6+2-28+D=0, D=32.
Итак, искомое уравнение 3x+2y-7z+32=0.
- Составить уравнение
плоскости, проходящей через точки M1(1;
1; 1), M2(0;
1; –1) перпендикулярно плоскости x+y+z=0.Так как M1Î α, то
используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.Далее, так как M2Î α, то
подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.
Выразим коэффициенты Aи
Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.Окончательно получаем -2x+y+z=0.
- Составить уравнение
плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно
плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.Так как MÎ α, то A(x+2)+B(x-3)+C(z-6)=0.
По условию задачи
, поэтому
Итак уравнение плоскости принимает вид
13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.
ПРЯМАЯ В ПРОСТРАНСТВЕ.
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Положение прямой в пространстве вполне определяется заданием какой-либо её
фиксированной точки М1 и вектора , параллельного этой прямой.
Вектор , параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая l проходит через точку М1(x1, y1, z1), лежащую
на прямой параллельно вектору .
Рассмотрим произвольную точку М(x,y,z)
на прямой. Из рисунка видно, что .
Векторы и
коллинеарны, поэтому найдётся такое число t, что
,
где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М1 и
М соответственно через и
,
получаем .
Это уравнение называется векторным уравнением прямой. Оно
показывает, что каждому значению параметра t соответствует радиус-вектор
некоторой точки М, лежащей на прямой.
Запишем это уравнение в координатной форме.
Заметим, что ,
и
отсюда
Полученные уравнения называются параметрическими
уравнениями прямой.
При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Пусть М1(x1, y1, z1) – точка,
лежащая на прямой l, и –
её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .
Ясно, что векторы и
коллинеарные, поэтому их соответствующие координаты
должны быть пропорциональны, следовательно,
– канонические
уравнения прямой.
Замечание 1. Заметим, что канонические
уравнения прямой можно было получить из параметрических,исключив параметр t. Действительно, из параметрических уравнений получаем или
.
Пример. Записать уравнение прямой в параметрическом виде.
Обозначим ,
отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.
Замечание 2. Пусть прямая
перпендикулярна одной из координатных осей, например оси Ox. Тогда
направляющий вектор прямой перпендикулярен
Ox,
следовательно, m=0. Следовательно,
параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае условимся формально
записывать канонические уравнения прямой в виде.
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает, что прямая
перпендикулярна соответствующей координатной оси.
Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz.
Примеры.
- Составить канонические и параметрические уравнения прямой,
проходящей через точку М1(1;0;-2) параллельно вектору.
Канонические уравнения:
.
Параметрические уравнения:
- Составить уравнения прямой,
проходящей через две точки М1(-2;1;3), М2(-1;3;0).Составим канонические уравнения прямой. Для
этого найдем направляющий вектор. Тогда l:
.
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые
две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения
любых двух таких плоскостей, рассматриваемые совместно представляют собой
уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.
Примеры.
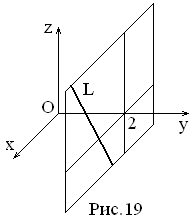
Построить прямую, заданную уравнениями
Для построения прямой
достаточно найти любые две ее точки. Проще всего выбрать точки пересечения
прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений
прямой, полагая z= 0:
Решив эту систему, найдем точку M1(1;2;0).
Аналогично, полагая y= 0, получим точку
пересечения прямой с плоскостью xOz:
От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти
какую-либо точку М1 на прямой и направляющий вектор прямой.
Координаты точки
М1
получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания
направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к
обоим нормальным векторам и
.
Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

Пример. Привести общие уравнения прямой
к каноническому виду.
Найдём точку,
лежащую на прямой. Для этого выберем произвольно одну
из координат, например, y= 0 и
решим систему уравнений:
Нормальные векторы
плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор
прямой будет

Следовательно, l: .
УГОЛ МЕЖДУ ПРЯМЫМИ
Углом
между прямыми в пространстве будем называть любой из смежных углов, образованных
двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими
векторами и
. Так как
, то по формуле для косинуса угла между векторами получим

Условия параллельности и
перпендикулярности двух прямых равносильны условиям параллельности и
перпендикулярности их направляющих векторов и
:
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда параллелен
.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна
нулю: .
Примеры.
- Найти угол между прямыми
и
.
- Найти уравнения прямой проходящей через точку М1(1;2;3) параллельно прямой l1:
Поскольку
искомая прямая l параллельна l1, то в качестве
направляющего вектора искомой прямой l можно взять направляющий вектор прямой l1. - Составить уравнения прямой,
проходящей через точку М1(-4;0;2) и перпендикулярной прямым:и
.
Направляющий
вектор прямой l можно найти как векторное произведение
векторови
:
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между прямой и плоскостью
будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
Рассмотрим векторы и
.
Если угол между ними острый, то он будет ,
где φ – угол между прямой и плоскостью. Тогда .
Если
угол между векторами и
тупой,
то он равен .
Следовательно .
Поэтому в любом случае .
Вспомнив формулу вычисления косинуса
угла между векторами, получим 
Условие перпендикулярности
прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда
направляющий вектор прямой и нормальный вектор
плоскости коллинеарны, т.е.
.
Условие параллельности прямой и плоскости.
Прямая и плоскость параллельны тогда и только тогда, когда векторы и
перпендикулярны.
Примеры.
- Написать уравнение плоскости, проходящей через точку М1(2;-3;4) параллельно прямым
и
.
Так как M1Î α, то уравнение плоскости
будем искать в виде.
Применяя
условие параллельности прямой и плоскости, получим систему линейных уравненийОтсюда
Итак,
или
.
- Найти угол между прямой
и плоскостью
.
Направляющий
вектор прямой.
Нормальный вектор плоскости.
Следовательно, - Найдите точку, симметричную данной М(0;-3;-2) относительно прямой
.
Составим уравнение плоскости α перпендикулярной l. MÎ α,
.
Следовательно,или
.
Найдём точку пересечения прямой l и α:
Итак,
N(0.5;-0.5;0.5). Пусть
искомая точка М1 имеет
координаты М1(x,y,z). Тогда очевидно равенство
векторов,
т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1,
y=2, z=3 или М1(1;2;3)..
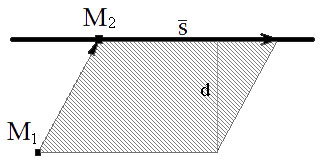
Составим уравнение прямой, проходящей через данную точку параллельно данному вектору
(рис. 22).
Пусть — некоторая прямая на плоскости; заданы точка
и вектор
=
— так называемый Направляющий вектор прямой. Пусть
— произвольная текущая точка на прямой
. Так как
, вектор
коллинеарен вектору
=
. Но у коллинеарных векторов координаты пропорциональны. Записывая данную пропорцию, получаем


Это уравнение называется Каноническим уравнением прямой на плоскости.
Здесь
— координаты точки, через которую проходит прямая,
— координаты направляющего вектора прямой,
— координаты текущих точек прямой.
Пример 27. Составить каноническое уравнение прямой, проходящей через точку и имеющей направляющий вектор
=
.
Решение.
=
ó
=
ó
Ответ: Искомое уравнение имеет вид . Прямая проходит параллельно оси
, пересекая ось
в точке
.
Рассмотрим снова каноническое уравнение прямой . Обозначив через
общее значение данной пропорции, получим:


,
Введя обозначения и
, получим:
(так называемые Параметрические уравнения прямой на плоскости).
Здесь:
— координаты некоторой точки, через которую проходит прямая;
— координаты текущей точки прямой;
— параметр, через который линейно выражаются координаты точек прямой;
— коэффициенты, определяющие координаты направляющего вектора прямой.
Согласно данным уравнениям, каждому значению параметра соответствует определенная точка прямой с координатами
.
| < Предыдущая | Следующая > |
|---|
Прямая в пространстве, всевозможные уравнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения прямой в пространстве:
1) $left{begin{array}{lcl}A_1x+B_1y+C_1z+D_1=0quad (P_1)\ A_2x+B_2y+C_2z+D_2=0quad (P_2)end{array}right. — $ общее уравнение прямой $L$ в пространстве, как линии пересечения двух плоскостей $P_1$ и $P_2.$
2) $frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p} -$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline{S}=(m, n, p).$ Вектор $overline S$ является направляющим вектором прямой $L.$
3) $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1} -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$
4) Приравнивая каждую из частей канонического уравнения 2 к прараметру $t,$ получаем параметрическое уравнение прямой:
$$left{begin{array}{lcl}x=x_0+mt\ y=y_0+nt\z=z_0+ptend{array}right. $$
Расположение двух прямых в пространстве.
Пусть $L_1:$ $frac{x-x_1}{m_1}=frac{y-y_1}{n_1}=frac{z-z_1}{p_1}$ $overline{S}_1=(m_1, n_1, p_1);$
$L_2:$ $frac{x-x_2}{m_2}=frac{y-y_2}{n_2}=frac{z-z_2}{p_2},$ $overline{S}_2=(m_2, n_2, p_2).$
Условие параллельности двух прямых: Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline{S}_1paralleloverline{S}_2Leftrightarrow$ $frac{m_1}{m_2}=frac{n_1}{n_2}=frac{p_1}{p_2}.$
Условие перпендикулярности двух прямых: $L_1perp L_2Leftrightarrow$ $overline{S}_1perpoverline{S}_2Leftrightarrow$ ${m_1}cdot{m_2}+{n_1}cdot{n_2}+p_1cdot p_2=0.$
Угол между прямыми:
$coswidehat{(L_1, L_2)}=$ $frac{overline{S}_1cdotoverline{S}_2}{|overline S_1|cdot|overline S_2|}=frac{{m_1}cdot{m_2}+{n_1}cdot{n_2}+p_1cdot p_2}{sqrt{m_1^2+n_1^2+p_1^2}cdotsqrt{m_2^2+n_2^2+p_2^2}}.$
Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на данную прямую.
Пусть прямая $L$ задана уравнением $frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p},$ следовательно $overline S=(m, n, p).$ Пусть также $M_2=(x_2, y_2, z_2) -$ произвольная точка, принадлежащая прямой $L.$ Тогда расстояние от точки $M_1=(x_1, y_1, z_1)$ до прямой $L$ можно найти по формуле: $$d(M_1, L)=frac{|[overline{M_1M_2}, overline S]|}{|overline S|}.$$
Примеры.
2.198. Написать каноническое уравнение прямой, проходящей через точку $M_0(2, 0, -3)$ параллельно:
а) вектору $q(2, -3, 5);$
б) прямой $frac{x-1}{5}=frac{y+2}{2}=frac{z+1}{-1};$
в) оси $OX;$
д) прямой $left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right. $
е) прямой $x=-2+t, y=2t, z=1-frac{1}{2}t.$
Решение.
а) Воспользуемся формулой (2) уравнения прямой в пространстве:
$frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p} -$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline{S}=(m, n, p).$
По условию $M_0(2, 0, -3)$ и $overline{S}=q(2,-3,5).$
Таким образом, $frac{x-2}{2}=frac{y-0}{-3}=frac{z-(-3)}{5}Rightarrowfrac{x-2}{2}=frac{y}{-3}=frac{z+3}{5}.$
Ответ: $frac{x-2}{2}=frac{y}{-3}=frac{z+3}{5}.$
б) Прямая, параллельная заданной прямой, должна быть параллельна ее направляющему вектору. Направляющий вектор прямой $frac{x-1}{5}=frac{y+2}{2}=frac{z+1}{-1}$ имеет координаты $overline S(5, 2, -1).$ Далее, находим уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(5, 2, -1)$ как и в пункте а):
$frac{x-2}{5}=frac{y-0}{2}=frac{z-(-3)}{-1}Rightarrowfrac{x-2}{5}=frac{y}{2}=frac{z+3}{-1}.$
Ответ: $frac{x-2}{5}=frac{y}{2}=frac{z+3}{-1}.$
в) ось OX имеет направляющий вектор $i=(1, 0, 0).$ Таким образом, ищем уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $i(1, 0, 0):$
$frac{x-2}{1}=frac{y-0}{0}=frac{z-(-3)}{0}Rightarrowfrac{x-2}{1}=frac{y}{0}=frac{z+3}{0}.$
Ответ: $frac{x-2}{1}=frac{y}{0}=frac{z+3}{0}.$
д) Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей, поэтому Направляющий вектор прямой
$left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right.$ можно найти как векторное произведение нормалей заданных плоскостей.
Для плоскости $P_1:$ $3x-y+2z-7=0$ нормальный вектор имеет координаты $N_1(3, -1, 2);$
для плосости $P_2:$ $x+3y-2z-3,$ нормальный вектор имеет координаты $N_2(1, 3, -2).$
Находим векторное произведение:
$[N_1, N_2]=begin{vmatrix}i&j&k\3&-1&2\1&3&-2end{vmatrix}=i(2-6)-j(-6-2)+k(9+1)=-4i+8j+10k.$
Таким образом, направляющий вектор прямой $left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right.$ имеет координаты $overline S (-4, 8, 10).$
Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(-4, 8, 10):$
$frac{x-2}{-4}=frac{y-0}{8}=frac{z-(-3)}{10}Rightarrowfrac{x-2}{-4}=frac{y}{8}=frac{z+3}{10}.$
Ответ: $frac{x-2}{-4}=frac{y}{8}=frac{z+3}{10}.$
{jumi[*4]}
е) Найдем направляющий вектор прямой $x=-2+t, y=2t, z=1-frac{1}{2}t.$ Для этого запишем уравнение этой прямой в каноническом виде:
$left{begin{array}{lcl}x=-2+t,\ y=2t,\z=1-frac{1}{2}t end{array}right.Rightarrow$ $left{begin{array}{lcl}t=x+2,\ t=frac{y}{2},\t=frac{z-1}{-frac{1}{2}} end{array}right.$ $Rightarrowfrac{x+2}{1}=frac{y}{2}=frac{z-1}{-frac{1}{2}}.$
Отсюда находим направляющий вектор $overline Sleft(1, 2, -frac{1}{2}right).$ Умножим координаты направляющего вектора на 2 (чтобы избавиться от дроби): $overline S_1(2, 4, -1).$
Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(2, 4, -1):$
$frac{x-2}{2}=frac{y-0}{4}=frac{z-(-3)}{-1}Rightarrowfrac{x-2}{2}=frac{y}{4}=frac{z+3}{-1}.$
Ответ: $frac{x-2}{2}=frac{y}{4}=frac{z+3}{-1}.$
2.199(a). Написать уравнение прямой, проходящей через две заданные точки $M_1 (1, -2, 1)$ и $M_2(3, 1, -1).$
Решение.
Воспользуемся формулой (3) уравнения прямой в пространстве:
$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1} -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$
Подставляем заданные точки:
$frac{x-1}{3-1}=frac{y+2}{1+2}=frac{z-1}{-1-1} Rightarrow$ $frac{x-1}{2}=frac{y+2}{3}=frac{z-1}{-2}.$
Ответ: $frac{x-1}{2}=frac{y+2}{3}=frac{z-1}{-2}.$
2.204. Найти расстояние между параллельными прямыми
$frac{x-2}{3}=frac{y+1}{4}=frac{z}{2}$ и $frac{x-7}{3}=frac{y-1}{4}=frac{z-3}{2}.$
Решение.
Расстояние между параллельными прямыми $L_1$ и $L_2$ равно расстоянию от произвольной точки прямой $L_1$ до прямой $L_2.$ Следовательно, его можно найти по формуле $$d(L_1, L_2)=d(M_1, L_2)=frac{|[overline{M_1M_2}, overline S]|}{|overline S|},$$ где $M_1-$ произвольная точка прямой $L_1,$ $M_2 — $произвольная точка прямой $L_2,$ $overline S -$ направляющий вектор прямой $L_2.$
Из канонических уравнений прямых берем точки $M_1=(2, -1, 0)in L_1,$ $M_2=(7, 1, 3)in L_2,$ $overline S=(3, 4, 2).$
Отсюда находим $overline{M_1M_2}=(7-2, 1-(-1),3-0)=(5, 2, 3);$
$[overline{M_1M_2}, overline S]=begin{vmatrix}i&j&k\5&2&3\3&4&2end{vmatrix}=i(4-12)-j(10-9)+k(20-6)=$ $=-8i-j+14k.$
$|[overline{M_1M_2},overline S]|=sqrt{8^2+1+14^2}=sqrt{64+1+196}=sqrt{261}=sqrt{9* 29}=3sqrt{29}.$
$|overline S|=sqrt{3^2+4^2+2^2}=sqrt{9+16+4}=sqrt{29}$
$$d(L_1, L_2)=frac{|[overline{M_1M_2}, overline S]|}{|overline S|}=frac{3sqrt{29}}{sqrt{29}}=3.$$
Ответ: 3.
2.205 (а). Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left{begin{array}{lcl}2x-2y+z+3=0,\ 3x-2y+2z+17=0 end{array}right.$
Решение.
Для того, чтобы найти расстояние от точки $A$ до прямой $L,$ нам необходимо выбрать произвольную точку $M,$ принадлежащую прямой $L$ и найти направляющий вектор этой прямой.
Выбираем точку $M.$ Пусть координата $z=0.$ Подставим это значение в данную систему:
$left{begin{array}{lcl}2x-2y+0+3=0,\ 3x-2y+0+17=0 end{array}right.Rightarrow$ $left{begin{array}{lcl}2x-2y+3=0,\ 3x-2y+17=0 end{array}right.-Rightarrow$ $left{begin{array}{lcl}x+14=0,\ 2x-2y+3=0 end{array}right.Rightarrow$ $left{begin{array}{lcl}x=-14,\ -28-2y+3=0 end{array}right.Rightarrow$ $left{begin{array}{lcl}x=-14,\ y=-frac{25}{2}. end{array}right.$
Таким образом, $M=(-14, -frac{25}{2}, 0)$
Направляющий вектор найдем, как векторное произведение нормалей заданных плоскостей:
Для плоскости $P_1:$ $2x-2y+z+3=0$ нормальный вектор имеет координаты $N_1(2, -2, 1);$
для плосости $P_2:$ $3x+2y+2z+17=0,$ нормальный вектор имеет координаты $N_2(3, -2, 2).$
Находим векторное произведение:
$[N_1, N_2]=begin{vmatrix}i&j&k\2&-2&1\3&-2&2end{vmatrix}=i(-4+2)-j(4-3)+k(-4+6)=-2i-j+2k.$
Таким образом, направляющий вектор прямой $left{begin{array}{lcl}2x-2y+z+3=0,\ 3x-2y+2z+17=0 end{array}right.$
имеет координаты $overline S (-2, -1, 2).$
Теперь можно воспользоваться формулой $$d(A, L)=frac{|[overline{AM}, overline S]|}{|overline S|}.$$
$overline{AM}=left(2-(-14),3-left(-frac{25}{2}right),-1-0right)=left(16, 15frac{1}{2}, -1right)$
$[overline{AM}, overline S]=begin{vmatrix}i&j&k\16&15,5&-1\-2&-1&2end{vmatrix}=i(31-1)-j(32-2)+k(-16+31)=$ $=30i-30j+15k.$
$|[overline{AM},overline S]|=sqrt{30^2+30^2+15^2}=sqrt{900+900+225}=sqrt{2025}=45.$
$|overline S|=sqrt{2^2+1^2+2^2}=sqrt{4+1+4}=3$
$$d(A, L)=frac{|[overline{AM}, overline S]|}{|overline S|}=frac{45}{3}=15.$$
Ответ: $d(A, L)=15.$
2.212. Написать каноническое уравнение прямой, которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $P: 3x-2y-3z-7=0$ и пересекает прямую $L: frac{x-2}{3}=frac{y+4}{-2}=frac{z-1}{2}.$
Решение.
Запишем уравнение плоскости $P_1,$ которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $3x-2y-3z-7=0:$
$P: 3x-2y-3z-7=0Rightarrow overline N=(3; -2; -3).$ Искомая плоскость проходит через точку $M_0(3, -2, -4)$ перпендикулярно вектору $overline N(3, -2, -3).$
$P_1: 3(x-3)-2(y+2)-3(z+4)=0Rightarrow $
$P_1: 3x-9-2y-4-3z-12=0 Rightarrow$
$P_1: 3x-2y-3z-25=0.$
Далее найдем точку пересечения плоскости $P_1$ и прямой $L.$ Для этого запишем уравнение прямой $L$ в параметрической форме:
$L: frac{x-2}{3}=frac{y+4}{-2}=frac{z-1}{2}=tRightarrow$
$left{begin{array}{lcl}x=3t+2,\ y=-2t-4,\z=2t+1. end{array}right.$
Далее, подставим значения $x, y$ и $z,$ выраженные через $t$ в уравнение плоскости $P_1,$ и из полученного уравнения выразм $t:$
$3x-2y-3z-25=0$
$3(3t+2)-2(-2t-4)-3(2t+1)-25=0$
$9t+6+4t+8-6t-3-25=0$
$7t-14=0$
$t=frac{14}{7}=2$
Подставляя найденное занчение $t$ в уравнение прямой $L,$ найдем координаты точки пересечения:
$left{begin{array}{lcl}x=3t+2,\ y=-2t-4,\z=2t+1. end{array}right.Rightarrow $ $left{begin{array}{lcl}x=6+2=8,\ y=-4-4=-8,\z=4+1=5. end{array}right.$
Таким образом, прямая $L$ и плоскость $P_1$ пересекаются в точке $M_1(8, -8, 5).$
Теперь запишем уравнение прямой, проходящей через точки $M_0(3, -2. -4)$ и $M_1(8, -8, 5)$— это и будет искомая прямая. Воспользуемся формулой (3) $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1} :$
$frac{x-3}{8-3}=frac{y+2}{-8+2}=frac{z+4}{5+4}Rightarrow$ $frac{x-3}{5}=frac{y+2}{-6}=frac{z+4}{9}.$
Ответ: $frac{x-3}{5}=frac{y+2}{-6}=frac{z+4}{9}.$
Домашнее задание.
2.199.
б) Написать уравнение прямой, проходящей через две заданные точки $M_1 (3, -1, 0)$ и $M_2(1, 0, -3).$
Ответ: $frac{x-3}{-2}=frac{y+1}{1}=frac{z}{-3}.$
2.205.
б) Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left{begin{array}{lcl}x=3t+5,\ y=2t,\z=-2t-25. end{array}right.$
Ответ: 21.
2.206. Доказать, что прямые $L_1: left{begin{array}{lcl}2x+2y-z-10=0,\ x-y-z-22=0, end{array}right.$ и $L_2: frac{x+7}{3}=frac{y-5}{-1}=frac{z-9}{4}.$ параллельны и найти расстояние $rho(L_1, L_2)$
Ответ: 25.
2.207. Составить уравнения прямой, проходящей через точки пересечения плоскости $x-3y+2z+1=0$ с прямыми $frac{x-5}{5}=frac{y+1}{-2}=frac{z-3}{-1}$ и $frac{x-3}{4}=frac{y+4}{-6}=frac{z-5}{2}.$
Ответ: $frac{x+1}{7}=frac{y-2}{-1}=frac{z-3}{-5}.$
2.211. Написать уравнение прямой, проходящей через точку $M_0(7, 1, 0)$ параллельно плоскости $2x+3y-z-15=0$ и пересекающей прямую $frac{x}{1}=frac{y-1}{4}=frac{z-3}{2}.$
Ответ: $frac{x-7}{67}=frac{y-1}{-28}=frac{z}{70}.$
{jcomments on}





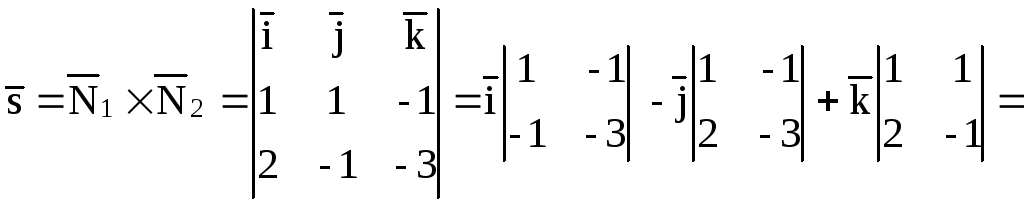






















 .
.