Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
Межотраслевой баланс представляется натуральными и стоимостными взаимозависимостями секторов экономической системы, показываемых в таблицах (матрицах) и аналитически (системами уравнений и неравенств).
Рассмотрим простой пример стоимостного баланса для экономической системы из трех секторов: сельского хозяйства, промышленности и домашних хозяйств. В каждом секторе, для производства товаров и услуг, расходуются ресурсы (сырье, рабочая сила, оборудование), создаваемые в нем и в других секторах экономической системы.
Каждый сектор в системе межотраслевых связей является одновременно производителем и потребителем.
Цель балансового анализа – определить, сколько продукции должен произвести каждый сектор для удовлетворения потребностей экономической системы в его продукции.
Единицей измерения объемов товаров и услуг является их стоимость.
1. Сельское хозяйство – 200 тыс. руб., в т. ч.:
- для своих нужд – 50 тыс. руб.,
- в промышленности – 40 тыс. руб.,
- в домашних хозяйствах – 110 тыс. руб.
2. Промышленность – 250 тыс. руб., в т. ч.:
- внутри своего сектора – 30 тыс. руб.,
- в сельском хозяйстве – 70 тыс. руб.,
- в домашних хозяйствах – 150 тыс. руб..
3. Домашние хозяйства – 300 тыс. руб., в т. ч.:
- внутри самого этого сектора – 40 тыс. руб.,
- в промышленности – 180 тыс. руб.,
- в сельском хозяйстве – 80 тыс. руб..
Эти данные сводятся в таблицу межотраслевого баланса: числа в строках таблицы отражают распределение продукции, произведенной в каждом секторе.
В последних клетках строк (в правом крайнем столбце) – отражается объем произведенной продукции в секторах экономики (общий выпуск).
Данные в столбцах показывают продукцию, потребляемую в процессе производства секторами экономической системы.
В нижней строке – суммарные затраты секторов.
| Производство | Сельское хоз-во | Промышленность | Домашнее хоз-во | Общий выпуск |
| Сельское хоз-во | 50 | 40 | 110 | 200 |
| Промышленность | 70 | 30 | 150 | 250 |
| Домашнее хоз-во | 80 | 180 | 40 | 300 |
| Затраты | 200 | 250 | 300 | 750 |
Здесь все секторы — производящие продукцию и они же потребляют всю продукцию.
Это замкнутая модель межотраслевых связей – в ней затраты секторов (суммы столбцов) равны объемам произведенной продукции (суммам строк).
Таблица межотраслевого баланса описывает потоки товаров и услуг между секторами экономики в течение конкретного промежутка времени (года, квартала).
Матричное представление межотраслевого баланса
Строки таблицы (матрицы) с производящими секторами имеют номера: i=1- n, где n – кол-во производящих секторов.
Столбцы таблицы (матрицы) с потребляющими секторами нумеруются j=1-n, где n – кол-во потребляющих секторов.
Матрица представляется квадратной. Адрес каждой клетки таблицы (матрицы) межотраслевого баланса состоит из номера строки и столбца. Стоимость продукции и услуг, производимых в секторе i и потребляемых в секторе j, обозначается {bij} .
Так стоимость продукции сельского хозяйства, потребляемой в самом сельском хозяйстве – b11=50; стоимость продукции промышленности, потребляемой в сельском хозяйстве – b21=70.
Баланс между совокупным выпуском и затратами в каждом секторе удовлетворяет системе уравнений:
Матрица межотраслевого баланса такого типа называется матрицей замкнутой модели «затраты – выпуск» Леонтьева, впервые описавшего ее в 1936 г.
Пример открытой системы межотраслевого баланса
Линейная модель «затраты-выпуск» отражает связь выпуска со спросом и определяет совокупный выпуск в каждом секторе для удовлетворения изменившихся потребностей (спроса).
Пусть экономика страны имеет n отраслей материального производства. Каждая отрасль выпускает некоторый продукт, часть которого потребляется другими отраслями (промежуточный продукт), а другая часть – идет на конечное потребление и накопление (конечный продукт).
Иными словами: в открытой системе вся произведенная продукция (совокупный продукт) делится на две части:
- одна (промежуточный продукт) расходуется в производящих секторах;
- другая (конечный продукт или конечный спрос) потребляется вне сферы материального производства, т.е. в секторе конечного спроса.
Обозначим через:
- Xi (i=1..n) — валовой продукт i-й отрасли;
- bij – стоимость продукта, произведенного в i-й отрасли и потребленного в j-й отрасли для изготовления продукции стоимостью Xj;
- Yi – конечный продукт i-й отрасли.
Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями и конечного продукта, то: xi = (xi1 + xi2 + … + xin) + yi (i = 1,2,…,n).
Эти уравнения называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в эти уравнения, имеют стоимостное выражение.
Введем коэффициенты прямых затрат: aij = bij / xj (i,j = 1,2,…,n),
показывающие какое количество продукции i-й отрасли необходимо (учитываются только прямые затраты) для производства единицы продукции j-й отрасли.
Если ввести:
- матрицу коэффициентов прямых затрат A = {aij},
- вектор-столбец валовой продукции X = (Xi)
- вектор-столбец конечной продукции Y = (Yi),
то математическая модель межотраслевого баланса примет вид X = AX +Y
Суть ее в том, что все затраты должны компенсироваться доходами. В основе создания балансовых моделей лежит балансовый метод – взаимное сопоставление имеющихся ресурсов и потребностей в них.
Коэффициент полных затрат {bij} показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции, получить единицу конечной продукции j-й отрасли.
Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.
В модели, описывающей экономику страны, сумма платежей производственных секторов в сектор конечного спроса образует национальный доход.
Критерии продуктивности матрицы А
1. Матрица {А} продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.
2. Для того, чтобы обеспечить положительный конечный выпуск по всем отраслям, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
- Определитель матрицы {E — A} не равен нулю, т.е. матрица {E — A} имеет обратную матрицу {E — A}-1.
- Наибольшее по модулю собственное значение матрицы {А}, т.е. решение уравнения |λE — A| = 0 строго меньше единицы.
- Все главные миноры матрицы {E — A} порядка от 1 до n положительны.
Матрица {A} имеет неотрицательные элементы (см. решение в скачанном файле) и удовлетворяет критерию продуктивности (при любом j сумма элементов 2-х столбцов ∑aij ≤ 1 (п. 1 условия).
Пример стоимостного межотраслевого баланса для открытой экономической системы с четырьмя секторами экономики:
| Производство | Сельское хоз-во | Промышленность | Транспорт | Конечный спрос | Общий выпуск |
| Сельское хоз-во | 50 | 16 | 120 | 60 | 246 |
| Промышленность | 30 | 10 | 180 | 100 | 320 |
| Транспорт | 15 | 14 | 140 | 80 | 249 |
Требуется определить новый вектор выпуска продукции Х при новом векторе спроса У (решение найдете в скачанном файле).
Скачать решение в MS Excel
7.2.2.1. Модель межотраслевого баланса
Балансовый метод применяется для анализа, нормирования, прогноза и планирования производства и распределения продукции на различных уровнях — от отдельного предприятия до народного хозяйства в целом.
Центральная идея межотраслевого баланса (МОБ) заключается в том, что каждая отрасль в нем рассматривается и как производитель, и как потребитель. Модель МОБ — одна из самых простых экономико-математических моделей. Она представляет собой единую взаимосвязанную систему информации о взаимных поставках продукции между всеми отраслями производства, а также об объеме и отраслевой структуре основных производственных фондов, обеспеченности народного хозяйства ресурсами труда и т. д.
Такая модель позволяет рассчитать сбалансированный план на основе точного учета всех межотраслевых связей и рассмот-
реть при этом множество возможных вариантов. В основе исследований балансовых моделей лежат балансовые таблицы, содержащие данные о производстве и потреблении продукции различных отраслей или предприятий. Характерные черты и особенности этого метода описываются с помощью матричных моделей баланса. Из математических методов здесь главным образом используется аппарат линейной алгебры.
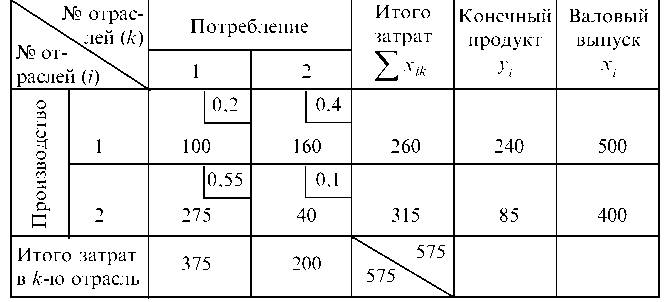
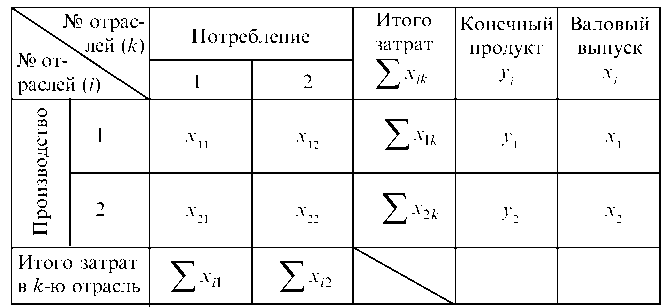
Рассмотрим пример предельно упрощенной системы, состоящей из двух производственных отраслей. Пусть исполнение баланса за предшествующий период характеризуется данными, приведенными в табл. 7.15.
Таблица 7.15
Продукция каждой отрасли частично идет на внешнее потребление (конечный продукт), а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции (1-й столбец продукции) и как ее потребитель (1-я строка таблицы). Приведенную таблицу конкретного примера можно записать и в более общем виде (табл. 7.16).
Обозначим через хг валовый выпуск продукции г-й отрасли за планируемый период и через у — конечный продукт, идущий на внешнее для рассматриваемой системы потребление (средства производства других экономических систем, потребление населения, образование запасов и т. д.). Таким образом, разность (хг — ^г) составляет часть продукции i-й отрасли, предназначенную для внутрипроизводственного потребления. Предполагаем, что баланс составляется в стоимостном разрезе. Обозначим через xik часть продукции i-й отрасли, которая потребляется k-й отраслью, для обеспечения выпуска ее продукции в размере xi.
Таблица 7.16
Очевидно, величины, расположенные в строках, связаны следующими балансовыми равенствами:
Отсюда стоимостной баланс в общем виде запишется уравнениями:
Рассмотрев отношение количества продукции i-й отрасли, поступающей в k-ю отрасль для обеспечения выпуска ее продукции в размере xk, получим затраты на единицу валовой продукции
откуда
Рассчитываем агк по формуле (7.21) и записываем в табл. 7.15 в углах соответствующих клеток.
Найденные коэффициенты прямых затрат и образуют неотрицательную матрицу прямых затрат:
(7.23)
Подставляя в уравнение (7.20) соотношения (7.22) получим:
(7.24)
Систему уравнений МОБ (7.24) запишем в матричной форме
(Е — А) X = Г, (7.25)
где Е — единичная матрица, А — матрица прямых затрат (7.23), X и Г — столбцовые матрицы
7.2.2.2. Полные внутрипроизводственные затраты
Пусть матрица
Р = (Е — А)-1, Р = || Р1к ||, (7.26)
тогда из (7.25): (Е — А)-1 ¦ (Е — А) ¦ X = (Е — А)-1 ¦ Г и, так как
(Е — А) ¦ (Е — А) = Е и ЕХ = X, то получаем, что объемы произ-
водства отраслей X определяются как
X = РГ
(7.27)
по заданным величинам конечного продукта потребления Г и матрице Р, которую называют матрицей коэффициентов полных затрат.
Элементы матрицы Р включают не только затраты i-й продукции, необходимой для создания одной единицы k-й продукции, но и те затраты, которые необходимы для создания в каждой отрасли одной единицы конечного продукта.
7.2.2.3. Косвенные затраты
Значит полные затраты Pik включают как прямые aik так и косвенные (Pik — aik) затраты. Очевидно, что всегда Pik > aik, точнее
Матрицы А2, А3, … , Ат,… называются матрицами коэффициентов косвенных затрат 1-го, 2-го и т. д. порядков и коэффициенты полных затрат получают в виде суммы коэффициентов прямых затрат и косвенных затрат.
Прямые затраты не отражают в полной мере сложных количественных взаимосвязей, наблюдающихся в народном хозяйстве. Они в частности не отражают обратных связей, имеющих далеко не маловажное значение.
Как возникают косвенные затраты? Например, на изготовление трактора в виде прямых затрат расходуется чугун, сталь, и т. д., но для производства стали также нужен чугун. Таким образом, кроме прямых затрат чугуна, имеются и косвенные затраты чугуна, связанные с производством трактора. В эти косвенные затраты входит и чугун, необходимый для создания того количества чугуна, которое составляет прямые затраты. Эти косвенные затраты могут иногда существенно превышать прямые затраты.
Исходя из (7.27), валовый выпуск k-й отрасли хк определяется как
Модель межотраслевого баланса (7.24), (7.25) или (7.29) позволяет решить следующие задачи:
1) определить объем конечной продукции отраслей y1, y2, ., yn по заданным объемам валовой продукции х1, х2, …, хп;
2) по заданной матрице коэффициентов прямых затрат А определить матрицу коэффициентов полных затрат P, элементы которой служат важными показателями для планирования развития отраслей;
3) определить объем валовой продукции отраслей хь х2, ., хп по заданным объемам конечной продукции у1, у2, …, уп.
4) по п заданным объемам конечной или валовой продукции отраслей х1, .у2, х3, .у4, … определить оставшиеся п объемов.
7.2.2.4. Решение типовой задачи
Рассмотрим пример составления межотраслевого баланса производства и распределения продукции для трехотраслевой экономической системы, заданной матрицей коэффициентов прямых затрат А и вектором конечной продукции Г:
Найти коэффициенты полных затрат: плановые объемы валовой продукции X = (х1; х2, Х3); величину межотраслевых потоков, т. е. значения хгк (г = 1, 2, 3; к = 1, 2, 3); матрицу косвенных затрат; по заданному вектору увеличения косвенного выпуска продукции ДГ определить изменение плана ДХ.
Находим матрицу (Е — А):
Для определения матрицы полных затрат (7.28) обращаем матрицу К.
Первый способ нахождения К 1 = (Е — А)-1. Вычисляем определитель
Так как | К | ф 0, то существует матрица К 1 = Р обратная заданной матрице К.
Находим алгебраические дополнения для элементов матрицы К.
Из алгебраических дополнений составляем транспонированную матрицу и, деля ее на | К |, получаем обратную матрицу К -1:
Рассмотрим другой способ нахождения обратной матрицы К 1 с помощью жордановых исключений. Составляем табл. 7.17.
Таблица 7.17
Совершаем последовательно три шага жордановых исключений, меняя местами Ьг — и х., получаем табл. 7.18—7.20.
Таблица 7.19
Таблица 7.20
Внутри табл. 7.20 стоит обратная матрица K 1. Округляя до третьего знака после запятой, имеем:
| (1,580 0,469 0,359^ | ( 56 ^ | (102,197^ | ||
| X = PY = | 0,276 1,220 0,100 | 20 | = | 41,047 |
| 0Д87 0,117 1Д31 0 | I12 0 | 26,383 |
Следовательно, плановые объемы валовой продукции трех отраслей, необходимые для обеспечения заданного уровня конечной продукции равны:
х1 = 102,2; х2 = 41,0; х3 = 26,4.
Для составления баланса рассчитываем межотраслевые потоки средств производства по формуле (7.22):
x11 = 0,3 • 102,2 = 37,7; x21 = 0,15 • 102,2 = 15,3; x31 = 0,1 • 102,2 = 10,2; x12 = 0,25 • 41,0 = 10,2; x22 = 0,12 • 41,0 = 4,9; x32 = 0,05 • 41,0 = 2,1; x13 = 0,2 • 26,4 = 5,3; x23 = 0,03 • 26,4 = 0,8; x33 = 0,08 • 26,4 = 2,1.
Результаты вычислений представим в форме межотраслевого баланса (табл. 7.21). Величина чистой продукции определяется здесь как разница между валовой продукцией отрасли и суммой межотраслевых потоков в каждом столбце.
Таблица 7.21
| ^^^Потребляющие отрасли Произво-^^^^ дящие отрасли^^ | 1 | 2 | 3 | Конечная
продукция |
Валовая
продукция |
| 1 | 30,7 | 10,2 | 5,3 | 56 | 102,2 |
| 2 | 15,3 | 4,9 | 0,8 | 20 | 41,0 |
| 3 | 10,2 | 2,1 | 2,1 | 12 | 26,4 |
| Чистая продукция | 46,0 | 23,8 | 18,2 | — | — |
| Валовая продукция | 102,2 | 41,0 | 26,4 | — | 169,6 |
На основе заданных матриц Y и A по уровню конечного продукта и коэффициентов прямых затрат получен полностью сбалансированный план общего производства продукции и ее рас-
пределения как между отраслями в качестве средств производства, так и для конечного использования.
Матрицу косвенных затрат найдем из формулы (7.28):
Определяем изменение плана ДХ, которое потребуется при увеличении конечного выпуска продукции 1-й отрасли на 20, 2-й — на 10 и 3-й — на 5 (единиц).
Следовательно, потребуется увеличить валовый выпуск 1-й отрасли на Дх1 = 38,1, 2-й отрасли на Дх2 = 18,2 и 3-й отрасли на 10,6 (единиц).
| < Предыдущая | Следующая > |
|---|
Три
отрасли промышленности (I,
II
и III)
являются производителями и в то же время
потребителями некоторой продукции. Их
взаимосвязи определяет матрица
коэффициентов прямых затрат

в
которой на пересечении i-й
строки и j-го
столбца находятся значения величин
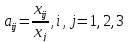
гдеxij
– поток средств производства из i-й
отрасли в j-ю,
xj
– валовой объем продукции j-й
отрасли (все объемы выражены в стоимостных
единицах).
Задан
также вектор объемов конечной продукции
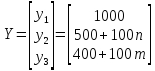
-
Составить
уравнения межотраслевого баланса. -
Решить
систему уравнений межотраслевого
баланса, то есть найти коэффициенты
полных затрат bij,
объемы валовой продукции каждой отрасли
xi,
обеспечивающие потребности всех
отраслей и изготовление конечной
продукции Y.
(Расчеты рекомендуется производить с
точностью до трех знаков после запятой). -
Составить
матрицу межотраслевых потоков средств
производства xij. -
Определить
объем условно-чистой продукции каждой
отрасли:
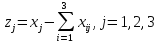
-
Результаты
расчетов оформить в виде таблицы
межотраслевого
баланса:
|
Потребляющие
отрасли Производящие
отрасли |
I |
II |
III |
конечный yi |
валовой xi |
|
I |
x11 |
x12 |
x13 |
y1 |
x1 |
|
II |
x21 |
x22 |
x23 |
y2 |
x2 |
|
III |
x31 |
x32 |
x33 |
y3 |
x3 |
|
условно-чистый |
z1 |
z2 |
z3 |
||
|
валовой |
x1 |
x2 |
x3 |
|
-
Составить
матрицу коэффициентов косвенных затрат
С
= (сij)
= B
— A
—
E. -
Определить
изменение плана ΔX,
которое потребуется при увеличении
выпуска конечной продукции 1-й отрасли
на 10·n
единиц, 2-й – на 5·m
единиц и 3-й – на 5 единиц.
Решение типовой задачи моб
3-х
отраслевая экономическая система задана
матрицей коэффициентов прямых затрат
А и
вектором конечной продукции Y:

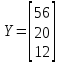
Найти:
-
коэффициенты
полных затрат: В
= (bij); -
плановые
объемы валовой продукции: Х
= (xi)
= (x1,
x2,
x3); -
величину
межотраслевых потоков средств
производства, т.е. значения xij,
i=1,
2, 3; j
= 1, 2, 3; -
объемы
условно-чистой продукции zj; -
матрицу
косвенных затрат С
= (сij)
= B
— A
— E. -
По
заданному вектору увеличения выпуска
конечной продукции ΔY=(Δy1,Δy2,Δy3)=(20,
10, 5) определить изменение плана
производства валовой продукции ΔX.
Результаты
вычислений п.п. 1-4 представить в форме
МОБ.
Решение
Используем
уравнения МОБ
в
развернутом виде:
в
матричном виде: X
= (E
— A)-1
· Y
= B
Y.
-
Находим
матрицу полных затрат В
= (E
— A)-1:
E
— A
=
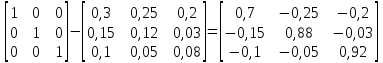
Обращаем
матрицу E
— A,
т.е. найдем В
= (E
— A)-1.
Вычисляем
определитель Δ=|E
— A|=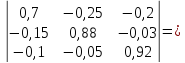
Так
как Δ≠0, то существует матрица В
= (E
— A)-1,
обратная заданной матрице E—A.
Находим
алгебраические дополнения для элементов
матрицы K
= E
— A:
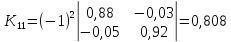
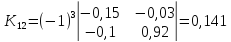
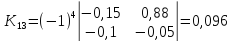
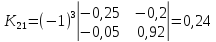
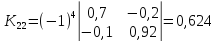
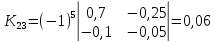
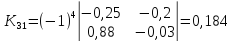
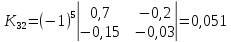
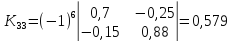
Составляем
матрицу из алгебраических дополнений:
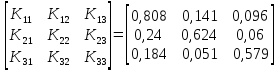
Транспонируем
эту матрицу (получим приведенную матрицу)
и делим ее на определитель Δ=0,511; в
результате получаем обратную матрицу
В
= (E
— A)-1:
В
= (E
— A)-1
=
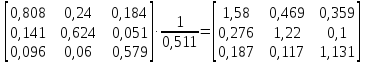
Таким
образом, матрица коэффициентов полных
затрат
В
= (E
— A)-1
=
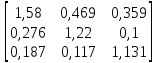
-
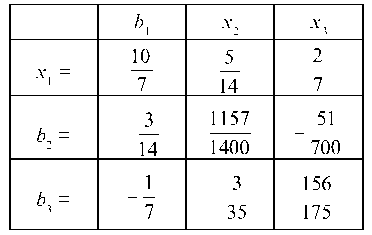
Находим
объемы производства отраслей (валовая
продукция):
X
= B
Y
=
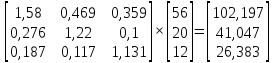
Следовательно,
плановые объемы валовой продукции трех
отраслей, необходимые для обеспечения
заданного уровня конечной продукции,
равны:
х1=102,197;
х2=41,047;
х3=26,383.
-
Рассчитываем
значения межотраслевых потоков xij=aij·
xj:
x11=0,3·102,2=30,7; x12=0,25·41,0=10,2; x13=0,2·26,4=5,3;
x21=0,15·102,2=15,3; x22=0,12·41,0=4,9; x23=0,03·26,4=0,8;
x31=0,1·102,2=10,2; x32=0,05·41,0=2,1; x33=0,08·26,4=2,1.
-
Результаты
вычислений представим в форме МОБ.
Величина условно-чистой продукции zj
определяется как разница между валовой
продукцией отрасли xj
и суммой межотраслевых потоков в каждом
столбце:
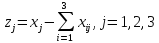
|
Потребляющие
отрасли Производящие
отрасли |
1 |
2 |
3 |
Конечный yi |
Валовой xi |
|
1 |
30,7 |
10,2 |
5,3 |
56 |
102,2 |
|
2 |
15,3 |
4,9 |
0,8 |
20 |
41,0 |
|
3 |
10,2 |
2,1 |
2,1 |
12 |
26,4 |
|
Условно-чистый |
46,0 |
23,8 |
18,2 |
||
|
Валовой |
102,2 |
41,0 |
26,4 |
169,6 |
Таким
образом, на основе заданных матриц по
уровню конечного продукта Y
и коэффициентов прямых затрат A
получен полностью сбалансированный
план общего производства продукции и
ее распределения в качестве средств
производства между отраслями и в качестве
продукции для конечного использования.
-
Найдем
матрицу косвенных затрат по формуле:
С
= (сij)
= B
— A
— E
= =
-
Определяем
изменение плана ΔX,
которое потребуется при увеличении
выпуска конечной продукции 1-й отрасли
на 20 ед., 2-й – на 10 ед. и 3-й – на 5 ед.
ΔX
= B
ΔY
=
Следовательно,
потребуется увеличить выпуск валовой
продукции 1-й отрасли на Δx1=38,1
ед., 2-й отрасли – на Δx2=18,2
ед., 3-й отрасли – на 10,6 ед.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача
Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках
и векторе объемов конечного использования
.
Требуется:
Указание:
При вычислениях производить округление с точностью до тысячных.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Матрица прямых затрат
Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора
:
Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:
Подставляя
числовые значения, получаем:
Матрица «Затраты — выпуск»
Найдем матрицу
«Затраты — выпуск»
Вектор конечного использования Y для валового объема выпуска X
Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения:
Для этого выполним умножение двух матриц
Матрица полных затрат
Найдем
матрицу коэффициентов полных материальных затрат
-она будет равна обратной матрице
:
Определитель матрицы
:
Алгебраические
дополнения:
Обратная матрица:
Вектор валового объема выпуска X для конечного использования Y
Вектор валового объема выпуска
для конечного продукта
определим формуле:
Приросты валовых объемов выпуска
Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на
по сравнению с
:
Матрица полных затрат ресурсов S
Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:
Суммарная потребность в ресурсах
Суммарная потребность в ресурсах для вектора Y0:
Суммарная потребность в ресурсах для вектора Yn:
Матрицы косвенных затрат и сумма затрат
Найдем
матрицы косвенных затрат первого, второго и третьего порядка
Сумма затрат:
Разность
матриц:
Вектор потребности в продукции
Найдем
вектор потребности в продукции всех отраслей материального производства bij
для получения единицы конечного продукта bj вида. Для этого
просуммируем столбцы матрицы полных затрат:
Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.
Аннотация: Лекция посвящена анализу балансовых моделей средствами программы Mathcad. Приведены основные параметры и уравнения межотраслевого баланса (МОБ). Рассмотрена задача нахождения совокупного выпуска по матрице прямых затрат, задача построения структурной матрицы по данным межотраслевых поставок и вектору конечного спроса, задача межотраслевого баланса затрат труда и использования трудовых ресурсов. Mathcad удобен для. моделирования и расчета межотраслевого баланса. Таблицы МОБ представляются в виде матриц, и решение задач реализуется быстро и легко.
Цель лекции. Научить строить модель МОБ. Вводить данные в виде матриц. Производить действия с матрицами: транспонирование, умножение, находить суммы элементов. Рассчитывать матрицы межотраслевого баланса.
3.1. Моделирование межотраслевого баланса
Межотраслевой баланс — инструмент анализа и прогнозирования структурных взаимосвязей в экономике. Метод построения межотраслевого баланса состоит в двойственном рассмотрении различных отраслей и секторов экономики: с одной стороны, как потребляющих продукцию, с другой — как выпускающих те или иные виды товаров и услуг для собственного потребления и нужд других отраслей экономики. Метод «затраты-выпуск»,.разработанный Леонтьевым, позволяет анализировать межотраслевые связи первичных затрат выпуска продукции в отдельных отраслях и конечного спроса на них и предоставляет информацию, которую практически невозможно получить, применяя другие методы и модели макроэкономического анализа [15,16,17].
Основу межотраслевого баланса составляет совокупность всех отраслей материального производства. Предположим, что экономическую систему имеет n отраслей, производящих определенные товары и услуги. При производстве товаров и услуг в каждой отрасли расходуются определенные ресурсы, которые производятся как в других отраслях, так и в данной отрасли. Каждая отрасль экономики выступает в системе межотраслевых связей одновременно производителем и потребителем.
Цель балансового анализа — определить, сколько продукции должна произвести каждая отрасль для того, чтобы удовлетворить все потребности экономической системы в его продукции [15]. Процесс производства рассматривается за некоторый период времени, например, за год. Часть продукции идет на производственное потребление данной отраслью и другими отраслями, а другая часть предназначена для потребления вне сферы материального производства. В зависимости от того, в каких единицах измерения записываются соотношения баланса, различают натуральный или стоимостной межотраслевые балансы.
Все отрасли производственной сферы экономики представляются в виде таблицы (

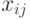




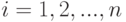


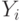
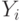


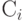
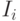
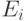






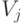

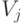

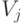

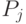
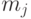
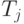
Элементы 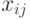


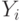


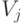

 |
( 3.1) |
 |
( 3.2) |
Делается допущение, что материальные издержки пропорциональны объему производимой продукции.
Для любой пары отраслей можно записать 

 |
( 3.3) |
Величины 


Соотношения баланса, записанные через коэффициенты прямых затрат, имеют вид::
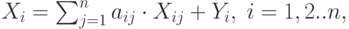 |
( 3.4) |
Уравнения описывают технологию производства и структуру экономических связей и означают, что в сектор конечного спроса от каждого производственного сектора поступает та часть произведенной продукции, которая остается после того, как обеспечены потребности производящих секторов.
Записывая уравнения в матричной форме получаем
 |
( 3.5) |
где 


Свойства коэффициентов прямых материальных затрат
- 1. Неотрицательность, т.е.
. Это утверждение следует из неотрицательности величин x_{ij} и положительности валовых выпусков
.
- 2. Поставки самому себе по определению меньше валового выпуска
. Следовательно:
.
- 3. Сумма элементов матрицы
по любому из столбцов меньше единицы, т.е.
Обозначая 
 |
( 3.6) |
Если существует обратная матрица 
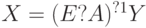 |
( 3.7) |
Однако, для того, чтобы решение имело экономический смысл, необходимо, чтобы 

Матрица A называется продуктивной, если для любого вектора 

Справедливы следующие критерии продуктивности.
Обратную матрицу обозначим через 
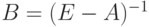
 |
( 3.8) |
Элементы матрицы 
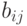
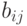



![Rendered by QuickLaTeX.com [sumlimits_{j = 1}^n {mathop bnolimits_{kj} } = sumlimits_{i = 1}^n {mathop bnolimits_{ik} } ;,;k = 1,2,....n]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-d3ad7a1880f4db6741cece5f2cbfc34d_l3.png)
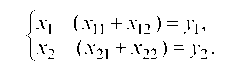
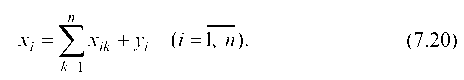

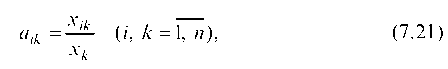
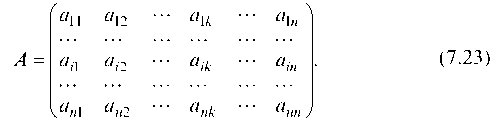
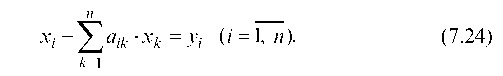

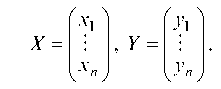
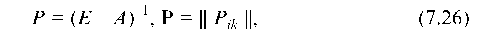

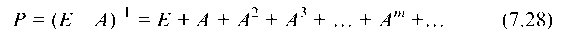
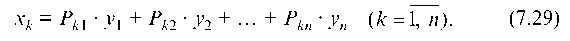
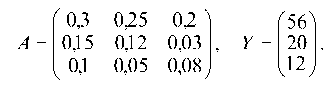
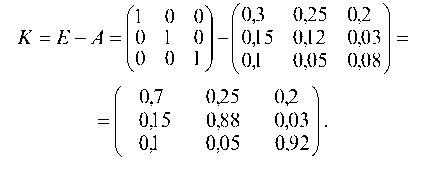
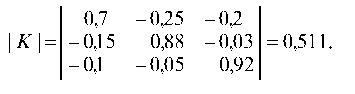
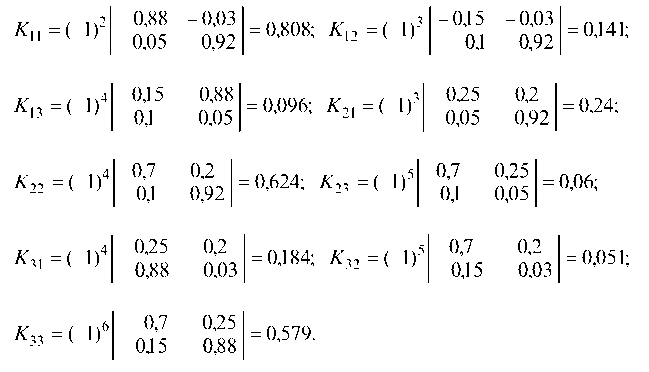
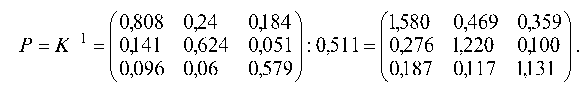

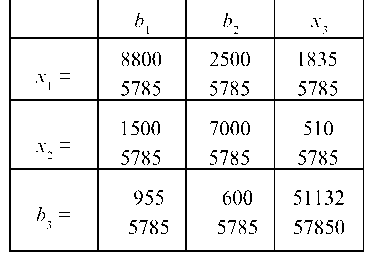
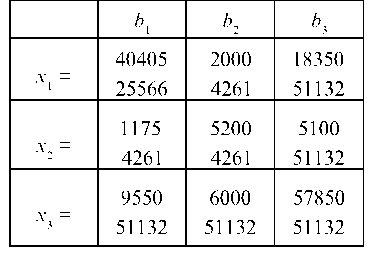
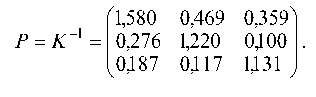
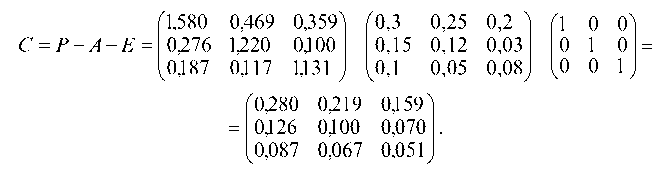
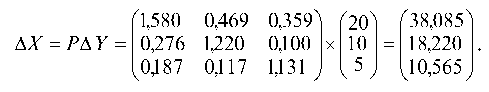
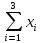
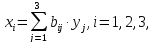
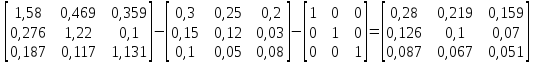
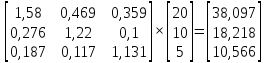

 . Это утверждение следует из неотрицательности величин x_{ij} и положительности валовых выпусков
. Это утверждение следует из неотрицательности величин x_{ij} и положительности валовых выпусков  .
.