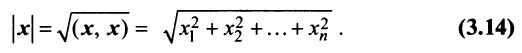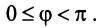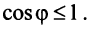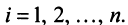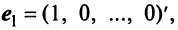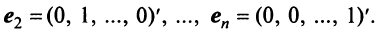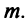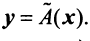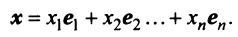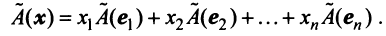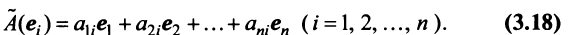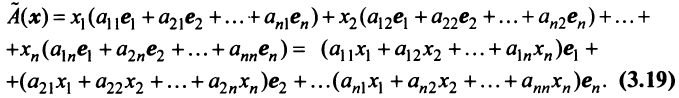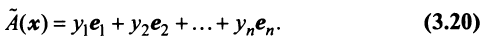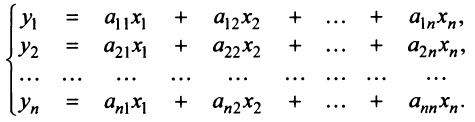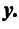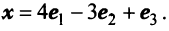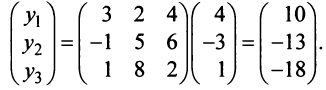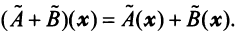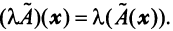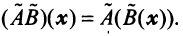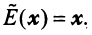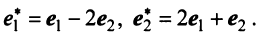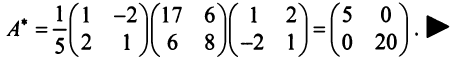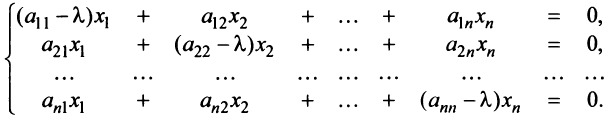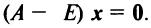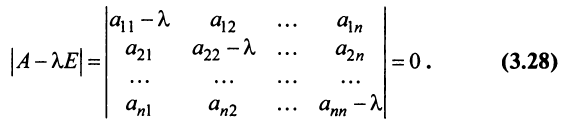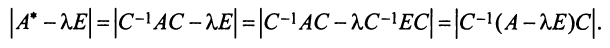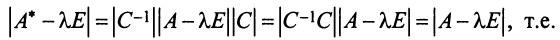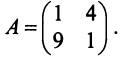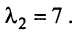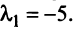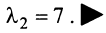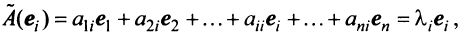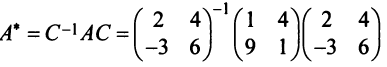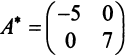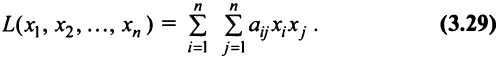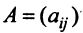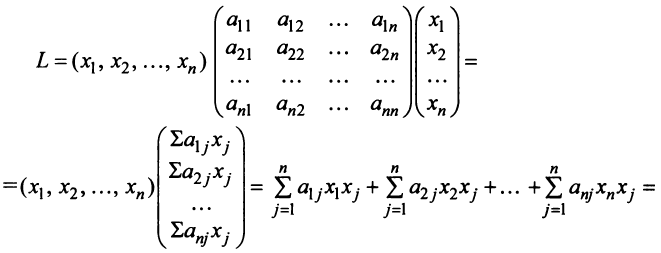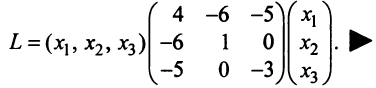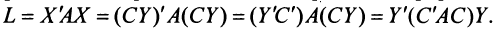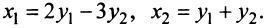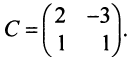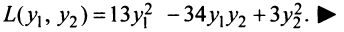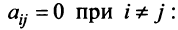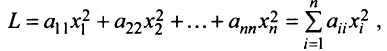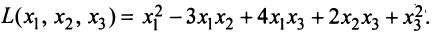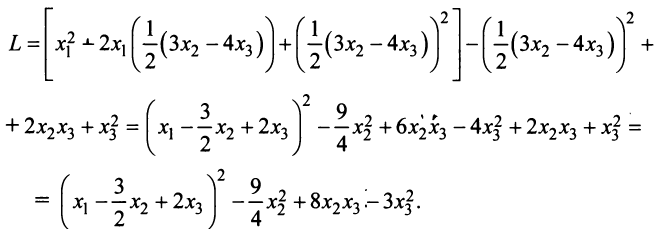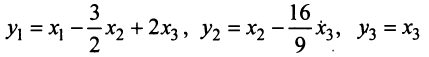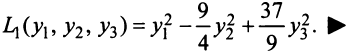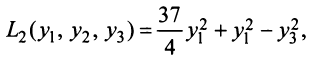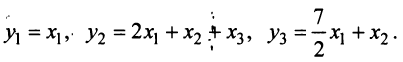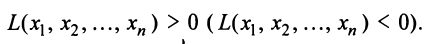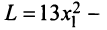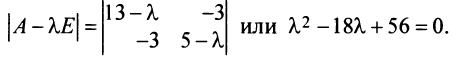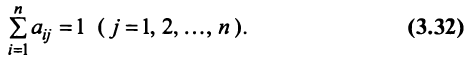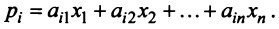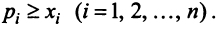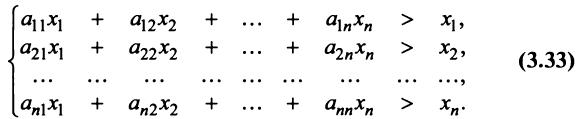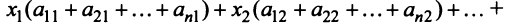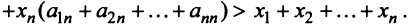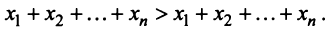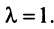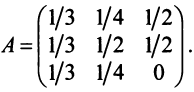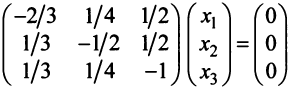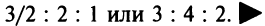Межотраслевой баланс
С помощью сервиса в онлайн режиме можно:
- найти коэффициенты полных материальных затрат, определить вектор валовой продукции;
- составить межотраслевой баланс, составить схему межотраслевого баланса труда;
- проверить продуктивность матрицы.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
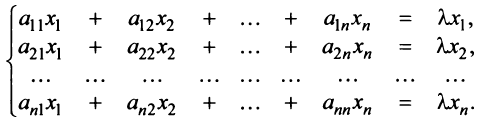
Система уравнений X = AX + Y называется экономико-математической моделью межотраслевого баланса (МОБ) или моделью «затраты — выпуск». C помощью нее можно выполнить следующие расчеты:
- подставив в модель объемы валовой продукции каждой отрасли Xi, можно определить объем конечной продукции отрасли Yj: Y = (E — A)X
- задав величины конечной продукции всех отраслей Yj, можно определить величины валовой продукции каждой отрасли Xi: X = (E — A) -1 Y
- установив для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти объемы конечной продукции первых отраслей и объемы валовой продукции вторых.
Здесь A – матрица прямых затрат, коэффициенты которой, aij показывают затраты i-й отрасли на производство единицы продукции j-й отрасли. Введем обозначение B = (E — A) -1 . Матрица B называется матрицей полных материальных затрат, коэффициенты которой, bij показывают полный объем продукции i-й отрасли, используемой для производства единицы продукции j-й отрасли. С учетом линейности соотношений эффект распространения спроса ΔX, вызванный изменением конечного спроса на величину ΔY рассчитывается как: ΔX = B·ΔY
Через C=A-B обозначают матрицу косвенных затрат.
Пример №1 . Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y .
Пример №2 . Дан межотраслевой баланс трехотраслевой модели хозяйства:
| № отрасли потребления | 1 | 2 | 3 | Конечный продукт | Валовый продукт | Y’ | |
| № отрасли | 1 | 20 | 20 | 60 | 100 | 200 | 150 |
| отрасли | 2 | 20 | 40 | 60 | 80 | 200 | 100 |
| производства | 3 | 20 | 0 | 10 | 70 | 100 | 100 |
Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
4) определить валовый выпуск X’ на новый ассортимент конечной продукции Y’;
Решение.
Находим валовой объем продукции xi;
x1 = 20 + 20 + 60 + 100 = 200
x2 = 20 + 40 + 60 + 80 = 200
x3 = 20 + 0 + 10 + 70 = 100
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | 20 | 20 | 60 | 100 | 200 |
| 20 | 40 | 60 | 80 | 200 | |
| 20 | 0 | 10 | 70 | 100 |
По формуле aij = xij / xj находим коэффициенты прямых затрат:
a11 = 20/200 = 0.1; a12 = 20/200 = 0.1; a13 = 60/100 = 0.6; a21 = 20/200 = 0.1; a22 = 40/200 = 0.2; a23 = 60/100 = 0.6; a31 = 20/200 = 0.1; a32 = 0/200 = 0; a33 = 10/100 = 0.1;
| 0.1 | 0.1 | 0.6 |
| 0.1 | 0.2 | 0.6 |
| 0.1 | 0 | 0.1 |
Определим матрицу коэффициентов полных затрат с помощью формул обращения невырожденных матриц.
а) Находим матрицу (E-A):
| (E-A) = |
|
б) Вычисляем обратную матрицу (E-A) -1 :
| 0,9 | -0,1 | -0,6 |
| -0,1 | 0,8 | -0,6 |
| -0,1 | 0 | 0,9 |
Найдем величины валовой продукции трех отраслей
| X’ = (B -1 *Y’) = |
|
* | = |
Пример №3 . В модели межотраслевого баланса
| Производство | Потребление | Конечная продукция | Валовая продукция | ||
| 1 | 2 | 3 | |||
| 1 | 10 | 5 | 15 | 70 | 100 |
| 2 | 20 | … | … | … | … |
| 3 | 30 | … | … | … | … |
| Оплата труда | 30 | … | … | … | … |
| Прибыль D | D | … | … | … | … |
прибыль D равна:
D = Валовая продукция – Затраты на производство – Оплата труда = 100 – (10+20+30) – 30 = 10.
ВЕКТОР И МАТРИЦА КОЭФФИЦИЕНТОВ КОРРЕЛЯЦИИ
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Для оценивания силы линейной зависимости объясняемой переменной (у) от потенциальных объясняющих переменных (лсь х2, . хт) по приведенной ниже формуле рассчитываются коэффициенты корреляции, которые записываются в виде вектора корреляции R0:
Коэффициенты корреляции между потенциальными объясняющими переменными хи х2, . хт рассчитываются по приведенной ниже формуле и записываются в виде матрицы корреляции R:
Матрица R симметрична относительно единичной диагонали, т е. Гу = />
Тесноту влияния всех объясняющих переменных на результат позволяет определять коэффициент (индекс) множественной корреляции:
Величина индекса множественной корреляции лежит в пределах от 0 до 1 и должна быть больше или равна максимальному парному индексу корреляции: RyXx. Xn ^гух.(тах).
Чем ближе значение индекса множественной корреляции к 1, тем теснее связь результативного признака и набора исследуемых переменных.
Сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности (величина индекса множественной корреляции существенно отличается от индекса парной корреляции) включения в уравнение регрессии того или иного фактора.
При линейной зависимости совокупный коэффициент множественной корреляции определяется через матрицу парных коэффициентов корреляции:
где Аг= — определитель матрицы парных коэф-
фициентовкорреляции; Агп = » —определитель
матрицы межфакгорной корреляции.
В [9, с. 33] коэффициент множественной корреляции рассчитывается по формуле
где AR — определитель матрицы R коэффициентов корреляции попарно объединенных объясняющих переменных хь х2, . х„; AW— определитель матрицы W, представленной в следующем виде:
где R0 — вектор коэффициентов корреляции между переменной у и объясняющими переменными хь х2. хп.
Частные коэффициенты корреляции характеризуют тесноту линейной зависимости между результатом и соответствующим фактором при устранении влияния других факторов. Если вычисляется, например, г уХхХ2 (частный коэффициент корреляции между у и х<
при фиксированном влиянии х2), то это означает, что определяется количественная мера линейной зависимости у от хь которая будет иметь место, если устранить влияние на эти признаки фактора х2.
Частные коэффициенты корреляции, измеряющие влияние на у фактора х,- при неизменном уровне других факторов, можно определить так:
или по рекуррентной формуле:
Для двухфакторного уравнения частные коэффициенты корреляции рассчитывают по следующим формулам:
Частные коэффициенты корреляции изменяются в пределах от — 1 до +1.
Сравнение значений парного и частного коэффициентов корреляции показывает направление воздействия фиксируемого фактора. Если частный коэффициент корреляции гуХ[^ получится меньше, чем соответствующий парный коэффициент гуХ<, значит, взаимосвязь признаков у и Х в некоторой степени обусловлена воздействием на них фиксируемой переменной х2. И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная х2 ослабляет своим воздействием связь у и х.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, г уХх2
коэффициент частной корреляции первого порядка.
Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент множественной корреляции:
Качество построенной модели в целом оценивает коэффициент (индекс) множественной детерминации, который рассчитывается как квадрат индекса множественной корреляции (RyxY. Xn ) 2 ? Коэффициент множественной детерминации фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как 1 — R 2 .
Если число параметров при х,- близко к объему наблюдений, то коэффициент множественной корреляции приближается к единице даже при слабой связи факторов с результатом. Чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс множественной корреляции, который содержит поправку на число степеней свободы:
где к — число объясняющих переменных; п — число элементов в выборке.
Чем больше к, тем сильнее различия R 2 и R 2 .
Содержание
В этом документе собраны основные сведения из алгебры матриц и векторов, которые используются в хемометрике. Приведенный текст не может служить учебником по матричной алгебре — он скорее является конспектом, справочником в этой области. Более глубокое и систематическое изложение может быть найдено в литературе.
Текст разбит на две части названные — «Базовые сведения» и «Дополнительная информация». В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части — факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls, которая сопровождает этот документ.
Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.
Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x ( a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2 ) = x (C 1 )+ x (C 2 ). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера — хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии — это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 . x n , характеризующих набор концентраций C 1 ,C 2 , . C m веществ, присутствующих в изучаемой системе.
Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на Рис. 1, где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый ( x 1 ) и второй ( x 2 ) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?
Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.
1. Базовые сведения
1.1 Матрицы
Матрицей называется прямоугольная таблица чисел, например
Матрицы обозначаются заглавными полужирными буквами ( A ), а их элементы — соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй — столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как < a ij , i = 1. I ; j = 1. J >. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.
Пара чисел I и J называется размерностью матрицы и обознается как I × J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.
1.2. Простейшие операции с матрицами
Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Например —
Рис. 3 Умножение матрицы на число
Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. Например,
Рис. 4 Сложение матриц
В результате умножения на число и сложения получается матрица той же размерности.
Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A + O = A , A − A = O и 0 A = O .
Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A ‘ или индексом A t . Таким образом, если A = < a ij , i = 1. I ; j = 1. J >, то A t = < a ji , j = 1. J ; i = 1. I >. Например
Рис. 5 Транспонирование матрицы
Очевидно, что ( A t ) t = A , ( A + B ) t = A t + B t .
1.3. Умножение матриц
Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I × K , и матрицы B , размерностью K × J , называется матрица C , размерностью I × J , элементами которой являются числа
Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц —
Рис.6 Произведение матриц
Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца ( c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B
Рис.7 Элемент произведения матриц
Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = ( AB ) C = A ( BC ). Кроме того, оно еще и дистрибутивно, т.е. A ( B + C ) = AB + AC . Очевидно, что AO = O .
1.4. Квадратные матрицы
Если число столбцов матрицы равно числу ее строк ( I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.
Очевидно AI = IA = A .
Матрица называется диагональной , если все ее элементы, кроме диагональных ( a ii ) равны нулю. Например
Рис. 8 Диагональная матрица
Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i > j . Например
Рис. 9 Верхняя треугольная матрица
Аналогично определяется и нижняя треугольная матрица.
Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например
Рис. 10 Симметричная матрица
Матрица A называется ортогональной , если
Матрица называется нормальной если
1.5. След и определитель
Следом квадратной матрицы A (обозначается Tr( A ) или Sp( A )) называется сумма ее диагональных элементов,
Рис. 11 След матрицы
Sp(α A ) = α Sp( A ) и
Sp( A + B ) = Sp( A )+ Sp( B ).
Можно показать, что
Sp( A ) = Sp( A t ), Sp( I ) = N ,
Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det( A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда
Для матрицы (3×3) определитель будет равен
В случае матрицы ( N × N ) определитель вычисляется как сумма 1·2·3· . · N = N ! слагаемых, каждый из которых равен
Индексы k 1 , k 2 . k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, . , N ). Вычисление определителя матрицы — это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,
Рис. 12 Определитель матрицы
Отметим только очевидные свойства:
det( I ) = 1, det( A ) = det( A t ),
det( AB ) = det( A )det( B ).
1.6. Векторы
Если матрица состоит только из одного столбца ( J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например
Можно рассматривать и матрицы, состоящие из одной строки, например
Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело — со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.
Размерностью вектора называется число его элементов.
Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.
В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .
1.7. Простейшие операции с векторами
Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,
Рис. 13 Операции с векторами
Два вектора x и y называются колинеарными , если существует такое число α, что
1.8. Произведения векторов
Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = ( x 1 , x 2 . x N ) t и y = ( y 1 , y 2 . y N ) t . Руководствуясь правилом перемножения «строка на столбец», мы можем составить из них два произведения: x t y и xy t . Первое произведение
называется скалярным или внутренним . Его результат — это число. Для него также используется обозначение ( x , y ) = x t y . Например,
Рис. 14 Внутреннее (скалярное) произведение
называется внешним . Его результат — это матрица размерности ( N × N ). Например,
Рис. 15 Внешнее произведение
Векторы, скалярное произведение которых равно нулю, называются ортогональными .
1.9. Норма вектора
Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина
определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение
Рис. 16 Норма вектора
Вектор единичной длины (|| x || = 1) называется нормированным. Ненулевой вектор ( x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = || x || ( x/ || x ||) = || x || e . Здесь e = x/ || x || — нормированный вектор.
Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.
1.10. Угол между векторами
Скалярное произведение определяет и угол φ между двумя векторами x и y
Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.
1.11. Векторное представление матрицы
Каждую матрицу A размера I × J можно представить как набор векторов
Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A
1.12. Линейно зависимые векторы
Векторы одинаковой размерности ( N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 . x K и столько же чисел α α 1 , α 2 . α K . Вектор
y = α 1 x 1 + α 2 x 2 +. + α K x K
называется линейной комбинацией векторов x k .
Если существуют такие ненулевые числа α k ≠ 0, k = 1. K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2 x 2 = 0
1.13. Ранг матрицы
Рассмотрим набор из K векторов x 1 , x 2 . x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе
имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.
Очевидно, что если векторов в наборе больше, чем их размерность ( K > N ), то они обязательно линейно зависимы.
Рангом матрицы (обозначается rank( A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.
rank( A ) = rank( A t ).
1.14. Обратная матрица
Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями
Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является
det( A ) ≠ 0 или rank( A ) = N .
Обращение матрицы — это сложная процедура, для выполнения которой существуют специальные программы. Например,
Рис. 17 Обращение матрицы
Приведем формулы для простейшего случая — матрицы 2×2
Если матрицы A и B невырождены, то
1.15. Псевдообратная матрица
Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что
Псевдобратная матрица — не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза.
Если число столбцов меньше числа строк, то
A + =(A t A) −1 A t
Рис. 1 7a Псевдообращение матрицы
Если же число столбцов больше числа строк, то
A + =A t (AA t ) −1
1.16. Умножение вектора на матрицу
Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка — слева x t A . Если размерность вектора J , а размерность матрицы I × J то в результате получится вектор размерности I . Например,
Рис. 18 Умножение вектора на матрицу
Если матрица A — квадратная ( I × I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что
A (α 1 x 1 + α 2 x 2 ) = α 1 Ax 1 + α 2 Ax 2 .
Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .
2. Дополнительная информация
2.1. Системы линейных уравнений
Пусть A — матрица размером I × J , а b — вектор размерности J . Рассмотрим уравнение
относительно вектора x , размерности I . По сути — это система из I линейных уравнений с J неизвестными x 1 . x J . Решение существует в том, и только в том случае, когда
rank( A ) = rank( B ) = R ,
где B — это расширенная матрица размерности I ×( J+1 ), состоящая из матрицы A , дополненной столбцом b , B = ( A b ). В противном случае уравнения несовместны.
Если R = I = J , то решение единственно
Если R I , то существует множество различных решений, которые можно выразить через линейную комбинацию J − R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A ( N × N ) имеет нетривиальное решение ( x ≠ 0 ) тогда и только тогда, когда det( A ) = 0. Если R = rank( A ) N , то существуют N − R линейно независимых решений.
2.2. Билинейные и квадратичные формы
Если A — это квадратная матрица , а x и y — вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой , определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.
2.3. Положительно определенные матрицы
Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора x ≠ 0 ,
Аналогично определяются отрицательно ( x t Ax x t Ax ≥ 0) и неположительно ( x t Ax ≤ 0) определенные матрицы.
2.4. Разложение Холецкого
Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой
Рис. 19 Разложение Холецкого
2.5. Полярное разложение
Пусть A — это невырожденная квадратная матрица размерности N × N . Тогда существует однозначное полярное представление
где S — это неотрицательная симметричная матрица, а R — это ортогональная матрица. Матрицы S и R могут быть определены явно:
S 2 = AA t или S = ( AA t ) ½ и R = S −1 A = ( AA t ) −½ A .
Рис. 20 Полярное разложение
Если матрица A вырождена, то разложение не единственно — а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .
2.6. Собственные векторы и собственные значения
Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A , если
где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и α v — тоже собственный вектор.
2.7. Собственные значения
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению
являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид
Рис. 21 Собственные значения
Набор собственных значений λ 1 . λ N матрицы A называется спектром A .
Спектр обладает разнообразными свойствами. В частности
det( A ) = λ 1 ×. ×λ N , Sp( A ) = λ 1 +. +λ N .
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная ( A t = A ), то ее собственные значения вещественны.
2.8. Собственные векторы
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений
Она имеет нетривиальное решение, поскольку det( A − λ n I ) = 0.
Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.
2.9. Эквивалентные и подобные матрицы
Две прямоугольные матрицы A и B одной размерности I × J эквивалентны , если существуют такие квадратные матрицы S , размерности I × I , и T , размерности J × J , что
Эквивалентные матрицы имею один и тот же ранг.
Две прямоугольные матрицы A и B одной размерности N × N подобны , если существует такая невырожденная матрица T , что
Матрица T называется преобразованием подобия.
Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.
2.10. Приведение матрицы к диагональному виду
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —
Здесь Λ = diag(λ 1 . λ N ) — это диагональная матрица, элементами которой являются собственные значения матрицы A , а T — это матрица, составленная из соответствующих собственных векторов матрицы A , т.е. T = ( v 1 . v N ).
Рис. 23 Приведение к диагональному виду
2.11. Разложение по сингулярным значениям (SVD)
Пусть имеется прямоугольная матрица A размерностью I × J ранга R ( I ≤ J ≤ R ). Ее можно разложить в произведение трех матриц P R ( I × R ), D R ( R × R ) и Q R ( J × R ) —
.
Здесь P R — матрица, образованная R ортонормированными собственными векторами p r матрицы AA t , соответствующим R наибольшим собственным значениям λ r ;
AA t p r = λ r p r ;
Q R — матрица, образованная R ортонормированными собственными векторами q r матрицы A t A ;
A t Aq r = λ r q r .
D R = diag (σ 1 . σ R ) — положительно определенная диагональная матрица , элементами которой являются σ 1 ≥. ≥σ R ≥0 — сингулярные значения матрицы A , равные квадратным корням из собственных значений матрицы A t A —
Рис. 24 SVD разложение
Дополняя матрицы P R и Q R ортонормированными столбцами, а матрицу D R нулевыми значениями, можно сконструировать матрицы P ( I × J ), D ( J × J ) и Q ( J × J ) такие, что
2.12. Линейное пространство
Рассмотрим все возможные векторы размерности N . Это множество называется линейным пространством размерности N и обозначается R N . Так как в R N включены все возможные векторы, то любая линейная комбинация векторов из R N будет также принадлежать этому пространству.
2.13. Базис линейного пространства
Любой набор из N линейно независимых векторов называется базисом в пространстве R N . Простейший пример базиса — это набор векторов
в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = ( x 1 , x 2 . x N ) t может быть представлен как линейная комбинация x = x 1 e 1 + x 2 e 2+ . + x N e N базисных векторов.
Базис, составленный из попарно ортогональных векторов, называется ортогональным , а если базисные вектора еще и нормированы, то этот базис называется ортонормированным .
2.14. Геометрическая интерпретация
Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N -мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x = ( x 1 , x 2 . x N ) t можно изобразить точкой в этом пространстве с координатами ( x 1 , x 2 . x N ).
Рис. 25 Координатное пространство
2.15. Множественность базисов
В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса
можно установить и другой ортонормированный базис, например
Каждый базис можно представить матрицей B = ( b 1 . b N ), составленной из базисных векторов. Переход от одного базиса к другому осуществляется с помощью невырожденной квадратной матрицы T , т.е. B 2 = TB 1 .
2.16. Подпространство
Пусть имеется набор из K линейно независимых векторов x 1 , x 2 . x K в пространстве R N . Рассмотрим все возможные линейные комбинации этих векторов
x = α 1 x 1 + α 2 x 2 +. + α K x K
О получившимся множестве Q говорят, что оно является линейной оболочкой или что оно натянуто на векторы x 1 , x 2 . x K . По определению линейного пространства это множество Q само является линейным пространством размерности K . При этом оно принадлежит пространству R N , поэтому Q называется линейным подпространством R K в пространстве R N .
2.17. Проекция на подпространство
Рассмотрим подпространство R K , натянутое на векторы X = ( x 1 , x 2 . x K ) в пространстве R N . Матрица базиса X имеет размерность ( N × K ). Любой вектор y из R N может быть спроецирован на подпространство R K , т.е. представлен в виде
где вектор y || принадлежит R K , а вектор y ⊥ ортогонален y || .
Рис. 26 Проекция на подпространство
Проекцию y || можно представить как результат действия проекционной матрицы P
Проекционная матрица определяется как
Рис. 27 Проекционное разложение
Заключение
Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.
http://studref.com/706993/ekonomika/vektor_matritsa_koeffitsientov_korrelyatsii
http://www.chemometrics.ru/old/Tutorials/matrix.htm
Чтобы проверить
является ли система векторов
линейно-зависимой, необходимо составить
линейную комбинацию этих векторов
,
и проверить, может ли она быть рана нулю,
если хот один коэффициент равен нулю.
Случай 1. Система
векторов заданна векторами
Составляем линейную
комбинацию
Мы получили
однородную систему уравнений. Если она
имеет ненулевое решение, то определитель
должен быть равен нулю. Составим
определитель и найдём его значение.
Определитель равен
нулю, следовательно, вектора линейно
зависимы.
Случай 2. Система
векторов заданна аналитическими
функциями:
a)
,
если тождество верно, значит система
линейно зависима.
Составим линейную
комбинацию.
Необходимо
проверить, существуют ли такие a,
b,
c
(хотя бы одна из которых не равна нулю)
при которых данное выражение равно
нулю.
Запишем гиперболические
функции
,
,
тогда
,
тогда линейная
комбинация векторов примет вид:
,
откуда
,
возьмём, например,,
тогда линейная комбинацияравна нулю, следовательно, система
линейно зависима.
Ответ: система
линейно зависима.
b)
,
составим линейную комбинацию
Линейная комбинация
векторов, должна быть равна нулю для
любых значений x.
Проверим для
частных случаев.
Линейная комбинация
векторов равна нулю, только если все
коэффициенты равны нулю.
Следовательно,
система линейно не зависима.
Ответ: система
линейно не зависима.
5.3. Найти какой-нибудь базис и определить размерность линейного пространства решений.
Сформируем
расширенную матрицу и приведём её к
виду трапеции методом Гаусса.
Получим
Чтоб
получить какой-нибудь базис подставим
произвольные значения:
Получим
остальные координаты
Ответ:
5.4. Найти координаты вектора X в базисе , если он задан в базисе .
Нахождение координат
вектора в новом базисе сводится к решению
системы уравнений
Способ 1.
Нахождение при помощи матрицы перехода
Составим матрицу
перехода
Найдём вектор в
новом базисе по формуле
Найдём обратную
матрицу и выполним умножение

Способ 2.
Нахождение путем составления системы
уравнений.
Составим базисные
вектора из коэффициентов базиса
,
,
Нахождение вектора
в новом базисе имеет вид
,
где d
это заданный вектор x.
Полученное уравнение
можно решить любым способом, ответ будет
аналогичным.
Ответ: вектор в
новом базисе
.
5.5. Пусть x = (
x1,
x2,
x3
).
Являются ли линейными следующие
преобразования.
Составим матрицы
линейных операторов из коэффициентов
заданных векторов.
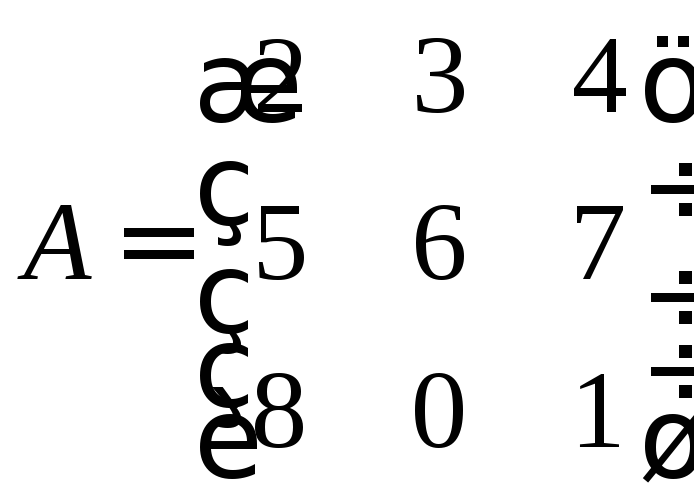
Проверим свойство
линейных операций для каждой матрицы
линейного оператора.
Левую часть найдём
умножением матрицы А
на вектор
Правую часть
найдем, умножив заданный вектор на
скаляр
.
Мы видим, что
значит, преобразование не является
линейным.
Проверим другие
вектора.
,
преобразование не является линейным.
,
преобразование является линейным.
Ответ: Ах
– не линейное преобразование, Вх
– не линейное, Сх
– линейное.
Примечание.
Можно выполнить данное задание гораздо
проще, внимательно посмотрев на заданные
вектора. В Ах
мы видим, что есть слагаемые которые не
содержат элементы х,
что не могло быть получено в результате
линейной операции. В Вх
есть элемент х
в третьей степени, что также не могло
быть получено умножением на вектор х.
5.6. Дано x
= {
x1,
x2,
x3
},
Ax
= {
x2
–
x3,
x1,
x1
+ x3
},
Bx
= {
x2,
2x3,
x1
}.
Выполнить заданную операцию: (
A(
B
– A
))x
.
Выпишем матрицы
линейных операторов.
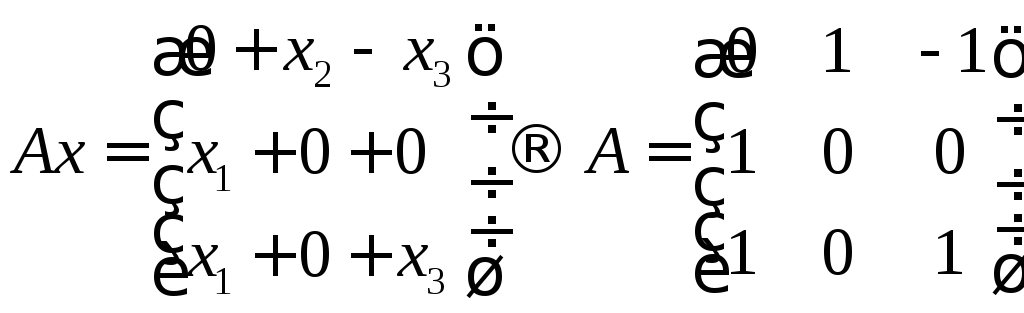
Выполним операцию
над матрицами
При умножении
полученной матрицы на Х, получим
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2016959.94 Кб5PT.pdf
- #
Содержание:
Векторы на плоскости и в пространстве:
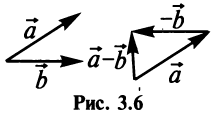
Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.
Вектором называется направленный отрезок
Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, либо выделяться жирным шрифтом, например:
Длиной (или модулем) 
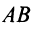
Векторы, лежащие на одной прямой или на параллельных прямых, называются коминеарными.
Если начало и конец вектора совпадают, например 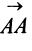
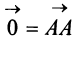
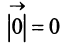
Произведением вектора 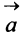
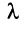
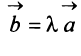
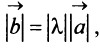
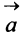
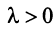
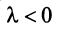
Противоположным вектором 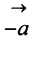
Рис. 32
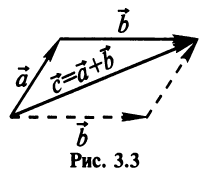
Суммой двух векторов 

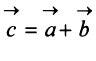




Очевидно, что вектор 


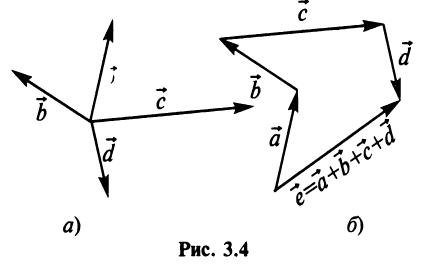
Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов 
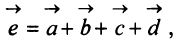

Нетрудно убедиться. что вектор 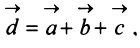


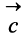
Разностью двух векторов 


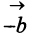

Легко убедиться в том, что в параллелограмме, построенном на векторах 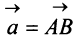
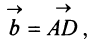


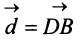
Перенесем вектор 

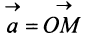
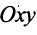
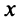
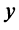
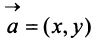
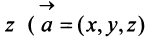
В соответствии с определениями, приведенными выше, нетрудно показать, что суммой и разностью векторов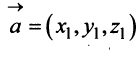
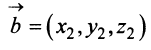
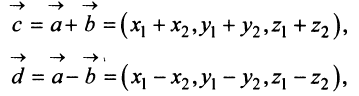
а произведение вектора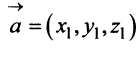
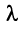
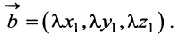
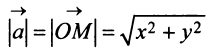
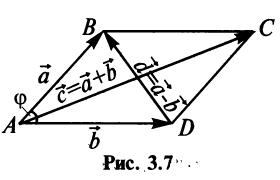
Определение. Скалярным произведением 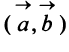


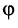
Выразим скалярное произведение через координаты векторов 

Из треугольника 
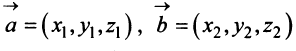
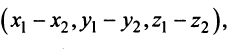
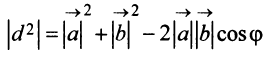
Учитывая формулу длины вектора (3.1) найдем
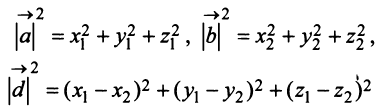
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Заметим, что при 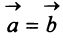
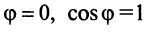
т.е. скалярный квадрат вектора равен квадрату его длины.
В частности, расстояние 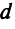
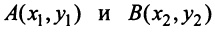
Поэтому
Угол между векторами

Пример:
Даны векторы
Найти: а)векторы 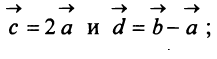
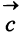
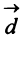
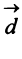
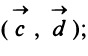
Решение:
а) По определению
б) По формуле (3.1) найдем длины векторов
в) По формуле (3.4) скалярный квадрат равен квадрату модуля вектора, т.е.
г) По формуле (3.3) скалярное произведение
д) По формуле (3.6) угол между векторами 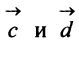
 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
Определение.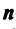
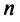
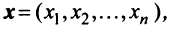
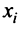
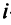
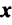
Понятие 
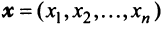
Два 
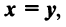
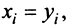
Суммой двух векторов одинаковой размерности п называется вектор 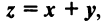
Произведением вектора 
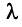
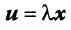
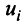
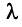

Линейные операции над любыми векторами удовлетворяют следующим свойствам:
— коммутативное (переместительное) свойство суммы:
— ассоциативное (сочетательное) свойство суммы;
— ассоциативное относительно числового множителя свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;
—дистрибутивное относительно суммы числовых множителей свойство;
- Существует нулевой вектор
такой, что
для любого вектора
(особая роль нулевого вектора);
- Для любого вектора
существует противоположный вектор
такой, что
для любого вектора
(особая роль числового множителя 1).
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
Следует отметить, что под 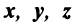
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа 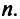



Из определения векторного (линейного) пространства, в частности из аксиом 1-8, вытекает существование единственного нулевого вектора, равного произведению произвольного вектора 
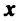
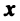
Размерность и базис векторного пространства
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано в § 1.6 для строк матрицы.
Определение. Вектор 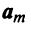

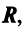
где 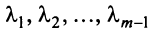
Определение. Векторы 
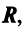
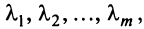
В противном случае векторы 
Из приведенных выше определений следует, что векторы 
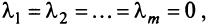
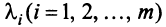
Можно показать (аналогично § 1.6), что если векторы 
Примером линейно независимых векторов являются два не-коллинеарных, т.е. не параллельных одной прямой, вектора 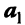
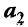
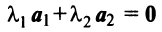
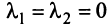
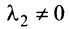
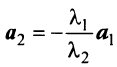
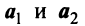
Отметим некоторые свойства векторов линейного пространства:
- Если среди векторов
имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например,
то равенство (3.8) справедливо при
- Если часть векторов
являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы
линейно зависимы, то справедливо равенство
в котором не все числа равны нулю. Но тогда с теми же числами
и
будет справедливо равенство (3.8).
Пример:
Выяснить, являются ли векторы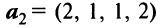
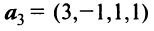
Решение:
Составим векторное равенство 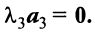
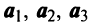
Задача свелась таким образом к решению системы:
Решая систему методом Гаусса (см. § 2.3), приведем ее к виду:
откуда найдем, бесконечное множество ее решений 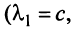
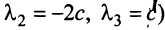
Итак, для ‘данных векторов условие (3.8) выполняется не только при 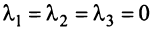
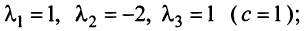
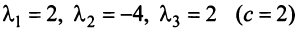
Определение. Линейное пространство 
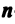
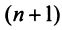


Определение. Совокупность 


Теорема. Каждый вектор 

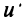

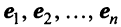




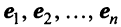

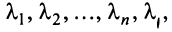
При этом 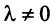
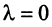
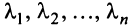
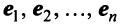
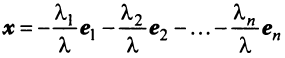
где
Это выражение 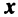

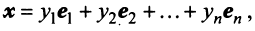
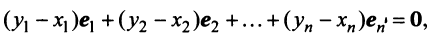

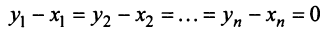
Равенство (3.9) называется разложением вектора 

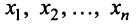

Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, — противоположные по знаку координаты.
Важное значение имеет следующая теорема.
Теорема. Если 

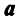




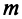

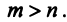

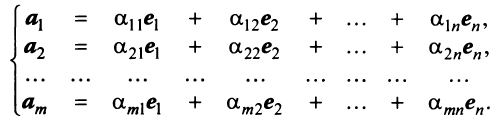
Ранг этой матрицы не превосходит 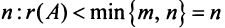
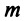
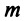
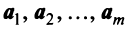

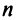

Пример:
В базисе 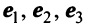
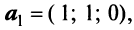
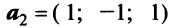
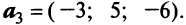
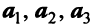
Решение:
Векторы 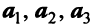
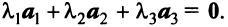
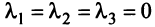
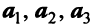
Переход к новому базису
Пусть в пространстве 

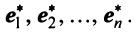
Полученная система означает, что переход от старого базиса 
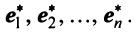
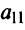
причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица 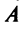
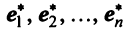
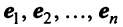
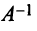
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 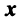
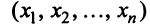
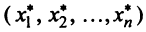
Подставив значения 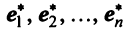
т.е. в матричной форме
Пример:
По условию примера 3.3 вектор 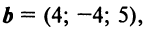
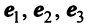
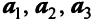
Решение:
Выразим связь между базисами:
Матрица перехода от базиса 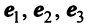
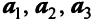
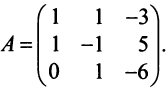
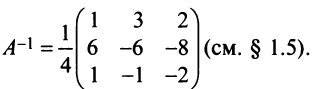
т.е. новые координаты вектора 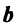
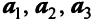
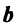
Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.
Определение. Скалярным произведением двух векторов 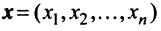
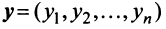
Скалярное произведение имеет экономический смысл. Если 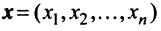
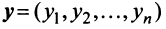
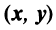
Скалярное произведение имеет следующие свойства:
— коммутативное свойство;
— дистрибутивное свойство;
— для любого действительного числа;
если
— ненулевой вектор;
, если
— нулевой вектор.
Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
Длиной (нормой) вектора 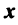
Имеют место следующие свойства длины вектора:
1. 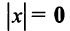
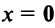
2. 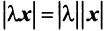
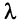
3.
(неравенство Коши—Буняковского);
4. 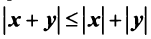
Угол 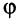

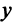

Такое определение вполне корректно, так как согласно неравенству Коши—Буняковского (3.15) 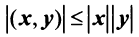
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен 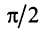
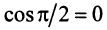
Векторы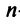
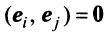
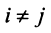
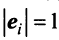
Для установления корректности приведенного определения необходимо убедиться в том, что входящие в него векторы 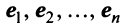
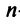

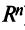
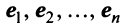
справедливо лишь при
Действительно, умножая скалярно равенство (3.17) на любой вектор 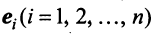
откуда, учитывая, что 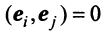
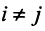
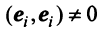
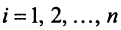
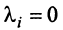
Сформулируем теперь (без доказательства) основную теорему.
Теорема. Во всяком 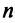
Примером ортонормированного базиса является система 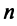
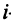
Линейные операторы
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.
Рассмотрим два линейных пространства: 
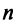

Определение. Если задан закон (правило), по которому каждому вектору 


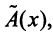


Оператор (преобразование) называется линейным, если для любых векторов 
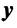

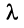
Вектор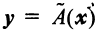


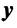
Если пространства 



Выберем в пространстве 

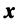
В силу линейности оператора 
Поскольку 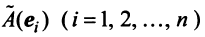


Тогда
С другой стороны, вектор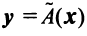

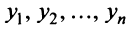
Ввиду единственности разложения вектора по базису равны правые части равенства (3.19) и (3.20), откуда
Матрица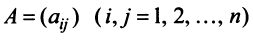


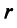
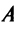

Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице 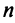
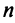
Связь между вектором 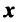
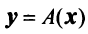
где 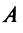
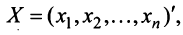
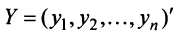

Пример:
Пусть в пространстве 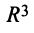

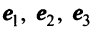
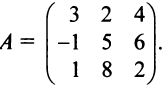
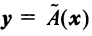
Решение:
По формуле (3.21) имеем
Следовательно, 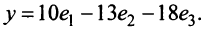
Определим действия над линейными операторами.
Суммой двух линейных операторов 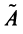
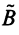
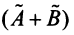
Произведением линейного оператора 
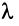
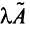
Произведением линейных операторов 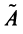
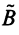
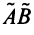
Можно убедиться в том, что операторы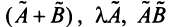
Определим нулевой оператор 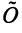
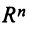
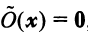
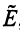
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема. Матрицы 
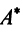

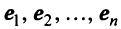
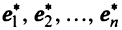
где 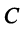



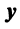
(в новом базисе). Так как 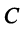
Умножим равенство (3.24) слева на матрицу 
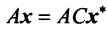
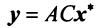
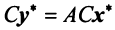
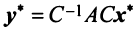
Пример:
В базисе 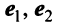

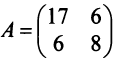

Решение:
Матрица перехода здесь 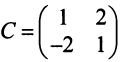
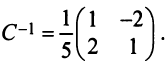
Собственные векторы и собственные значения линейного оператора
Определение. Вектор 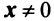

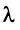
Число 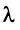


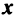
Из определения следует, что собственный вектор под действием линейного оператора 
Равенство (3.26) можно записать в матричной форме:
где вектор 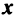
Перепишем систему так, чтобы в правых частях были нули:
или в матричном виде
Полученная однородная система всегда имеет нулевое решение 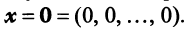
Определитель 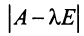
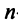
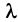




Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен 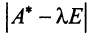
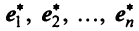
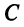
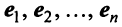
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц (см. §1.4), получим
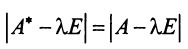
Пример:
Найти собственные значения и собственные векторы линейного оператора 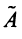
Решение:
Составляем характеристическое уравнение
откуда собственные значения линейного оператора
Находим собственный вектор 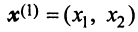
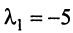
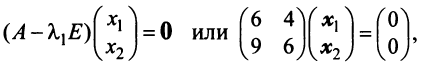
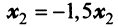
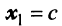
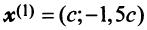
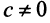

Аналогично можно убедиться в том, что векторы 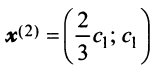
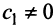

Наиболее простой вид принимает матрица 

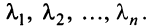
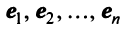
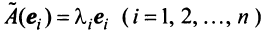
откуда 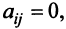
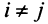
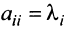
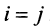

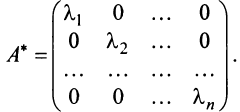


Можно доказать, что если линейный оператор имеет 
- Заказать решение задач по высшей математике
Пример:
Привести матрицу 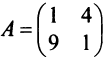

Решение:
В примере 3.7 были найдены собственные значения матрицы 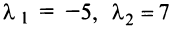
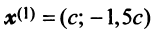
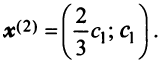
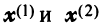
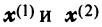
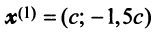
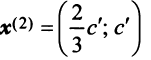
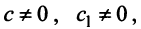
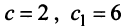
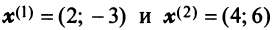
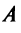
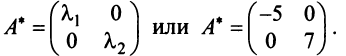
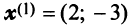
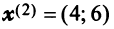
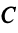
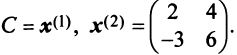
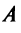
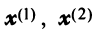
или после вычислений (которые мы опускаем)
т.е. получим ту же диагональную матрицу, элементы которой по главной диагонали равны собственным значениям матрицы 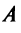
Квадратичные формы
При решении различных прикладных задач часто приходится исследовать квадратичные формы.
Определение. Квадратичной формой 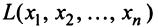
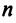
Предполагаем, что коэффициенты квадратичной формы 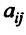
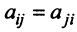
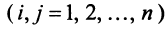
где 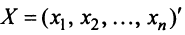
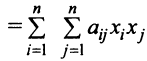
Пример:
Дана квадратичная форма 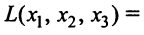
Решение:
Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, -3, а другие элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть матрицы-столбцы переменных 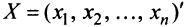
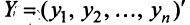
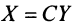
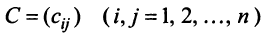
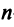
, Итак, при невырожденном линейном преобразовании 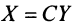
Пример:
Дана квадратичная форма 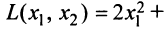
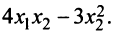
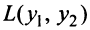
Решение:
Матрица данной квадратичной формы 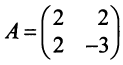
Следовательно, по (3.31) матрица искомой квадратичной формы 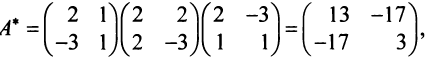
Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.
Квадратичная форма 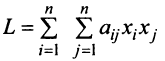
а ее матрица является диагональной. Справедлива следующая теорема.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Пример:
Привести к каноническому виду квадратичную форму
Решение:
Вначале вьделим полный квадрат при переменной 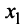
Теперь выделяем полный квадрат при переменной 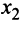
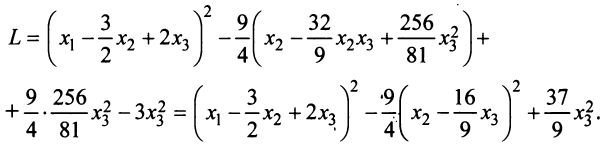
приводит данную квадратичную форму к каноническому виду
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.
Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.
Например, квадратичную форму 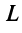
применив невырожденное линейное преобразование
Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.
Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичная форма 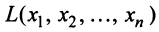
Так, например, квадратичная форма 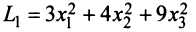
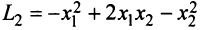
Теорема. Для того чтобы квадратичная форма 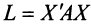
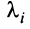
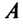
В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 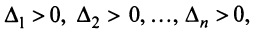

Пример:
Доказать, что квадратичная форма 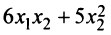
Решение:
Первый способ. Матрица 
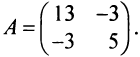

Решая уравнение, найдем 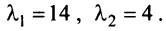

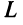
Второй способ. Так как главные миноры матрицы 
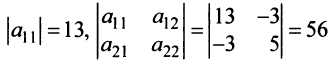
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется 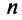
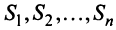
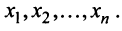
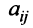
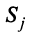
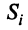
Рассмотрим матрицу
которая получила название структурной матрицы торговли. В соответствии с (3.32) сумма элементов любого столбца матрицы 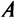
Для любой страны 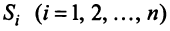
Для сбалансированной торговли необходима бездефицитность торговли каждой страны 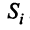
Если считать, что 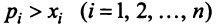
Сложив все неравенства системы (3.33), получим после группировки
Учитывая (3.32), выражения в скобках равны единице, и мы приходим к противоречивому неравенству
Таким образом, неравенство 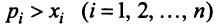
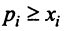
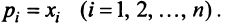
Вводя вектор 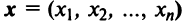
В котором вектор х записан в виде вектор-столбца, т.е. задача свелась к отысканию собственного вектора матрицы 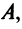
Пример:
Структурная матрица торговли трех стран 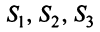
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
Находим собственный вектор 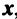
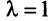
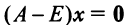
методом Гаусса. Найдем 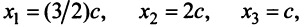
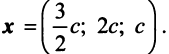
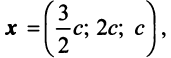
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
- Степенные ряды
Содержание:
- n-мерный вектор и векторное пространство
- Линейные (векторные) n — мерные пространства
- Линейные операции над n — измеримыми векторами
- Скалярное произведение двух векторов
- Линейная зависимость и независимость векторов
- Базис n -мерного пространства. Разложение вектора по базису
- Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений
- Однородная система уравнений. Особенности решения
n-мерный вектор и векторное пространство
Множество всех векторов, которые мы рассматривали на плоскости или в пространстве и для которых определены операции сложения векторов, умножение вектора на число являются простыми примерами векторного пространства.
Определение 1. Упорядоченное множество n действительных чисел, записанных в виде (a1, a2, a3, …, an) называется n- мерным вектором. Числа a1, a2, a3, …, an называются координатами вектора 

Понятие n-мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать вектором 

Если у n-мерного вектора одна координата равна единице, а все остальные равны нулю, то такой вектор называется единичным. Очевидно, что существует n различных единичных векторов
исходящих из начала координат — точки О. Все определения и действия для двумерных и трехмерных векторов, заданных в координатной форме, распространяются и на n-мерные векторы (n ≥ 4).
Два n-мерных вектора равны тогда и только тогда, когда их соответствующие компоненты равны.
Вектор 

Суммой двух n-мерных векторов 




Произведением вектора 


Вектор, у которого все координаты равны нулю, называется нулевым вектором и обозначается
Операции над произвольными векторами удовлетворяют свойствам:
1. 
2. 
3. 
4. 
5. 
6. Существует нулевой вектор 


7. Для произвольного вектора 

8. 

Определение. Множество векторов с действительными координатами, в
котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие выше приведенным восьми свойствам, называется векторным пространством.
Замечания. Если под векторами 

Линейным пространством, например, множество всех алгебраических многочленов, степени которых не превышают натуральное число n. Если множество всех многочленов точно равно натуральному числу n, то не будет линейным пространством, потому что сумма двух многочленов может оказаться многочленом, степень которого меньше n.
Линейные (векторные) n — мерные пространства
Линейные 
В школьном курсе математики понятие вектора обозначалось как направленный отрезок. Положение (расположение) вектора на прямой 


Математический подход к изучению различных явлений (процессов) окружающего мира, в том, числе и экономических, требует обобщения понятия вектора, связано с увеличением количества его координат. Такое обобщение не подразумевает геометрической интерnретации, но является удобным для математического моделирования.
Вектором размерности 






Согласно определению 



Нулевым вектором 

Два вектора 

Линейные операции над n — измеримыми векторами
1. Суммой 



Следовательно:
Следствие. Для любого вектора 
2. Произведением вектора 




Следствие. Если 



Векторы 


Суммой взаимно противоположных векторов есть нулевой вектор той же размерности.
Разность векторов 



Векторы 




Если 
прямой или на параллельных прямых.
В частном случае, когда 

где 


Совокупность всех 


Скалярное произведение двух векторов
Аналогично тому, как рассматривался произведение матриц вводят понятие скалярного произведения векторов 


Скалярным произведением двух 
Действие умножения для получения скалярного произведения обозначают точкой между векторами:
Произведение 
На основе скалярного произведения приведем определение понятий, которые вводились для векторов размерностью 
Длиной 


то есть
Единичным 


Возведение любого ненулевого вектора к единичному называется его нормированием.
Среди единичных векторов выделяют векторы, для которых одна из координат равна единице, а все остальные — нулю. Такие векторы обозначают маленькой буквой 



В частности, в трехмерном пространстве эти векторы называются ортами координатных осей, они имеют собственные обозначения:
Кутом между двумя векторами 


Согласно (4.9) скалярное произведение можно рассматривать как общую числовую характеристику двух векторов.
Свойства скалярного произведения:
Линейное пространство, для которого определено скалярное произведение векторов со свойствами (4.10), называется евклидовым пространством.
В тeopии линейных пространств любое множество векторов одинаковой размерности называется системой векторов.
Пусть имеем систему, которая состоит из 







С помощью этой системы векторов систему линейных алгебраических уравнений с 
или кратко:
Действительно, если по правилам сложения векторов и умножения на скаляр умножить каждый вектор 


Замечания. На основе тeopии 
Линейная зависимость и независимость векторов
Пусть имеется система векторов 






Векторы называются линейно зависимыми, если хотя бы один из векторов системы является линейной комбинацией других. В противном случае, когда в системе векторов нет ни одного, который был бы линейной комбинацией других, векторы называются линейно независимыми.
Теорема 4.1 (про линейную зависимость системы векторов). Если среди чисел 

то система векторов 
Доказательство. Пусть в равенстве (4.14) среди чисел 

Отсюда получаем:
а согласно (4.13) это означает, что система векторов 

Последствие из теоремы 4.1 (о линейной независимости системы векторов).
Система векторов есть линейно независимой, если векторное равенство
выполняется только в случае 
Доказательство. Предположим, что система векторов линейно независима, и при этом существуют 

Одной из основных задач теории линейных пространств является задача исследования системы векторов на линейную независимость, то есть выяснения вопрос о том, какова есть заданная система векторов — линейно зависимой или линейно независимой.
Решение этой задачи сводится к решению систем линейных уравнений.
Запишем равенство (4.14) в координатной форме:
выполним умножение векторов системы на скаляры

По следствием из теоремы 4.1 система векторов линейно независимая, если система однородных уравнений (4.15) имеет только тривиальное решение: 

Проведем исследование на линейную независимость системы векторов:
Запишем векторное равенство:
Отсюда получаем систему уравнений:
Вычислим определитель основной матрицы системы:
Поскольку 

Преобразование основной матрицы системы по методу Жордана-Гаусса позволяет определить количество линейно независимых векторов в заданной системе векторов:
Ранг матрицы системы 
Подставляя найденные коэффициенты в векторное равенство (4.14), получим
Таким образом, векторы 





В линейной алгебре широко применяется система п единичных векторов 



Рассмотрим питания о наибольшее количество векторов, которое может содержать линейно независимая система 
Выберем из пространства 

запишем векторное равенство
и соответствующую ей однородную линейную систему 

Для ответа на поставленный вопрос будем исходить из сравнения количества векторов системы 

1. Если количество векторов больше измеримости пространства 


2. Если количество векторов равно размерности пространства 


Из проведенного анализа следует, что наибольшее количество линейно независимых векторов равно размерности линейного пространства.
Базис n -мерного пространства. Разложение вектора по базису
Понятие 






Теорема 4.2 (о разложении 
Произвольный вектор 


Доказательство. Согласно определению линейной комбинации системы векторов (4.13) надо показать существование единого набора цифр 

Представим векторы 

и запишем соответствующую систему линейных уравнений:
Поскольку определитель основной матрицы системы отличается от нуля (по условию векторы 
Представление вектора 


Система 



Запись 


Определение базиса пространства и разложения вектора по базису можно выполнять одновременно, аналогично тому, как выбор базисных неизвестных и нахождения решений СЛАУ осуществляли при применении методов Гаусса и Жордана-Гаусса.
Осуществить разложение вектора 

Для решения задачи представим вектор 


где 


Представим векторы 


Проверку на линейную независимость векторов 


Для этого запишем расширенную матрицу системы и проведем ее преобразования по методу Жордана-Гаусса:
Поскольку элементарными преобразования на месте основной матрицы системы получено единичную матрицу третьего порядка, то определитель исходной матрицы отличен от нуля, и система векторов 



Следовательно, координатами вектора 

В другом базисе вектор 

Любой вектор с 
Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений
Представим произвольный вектор 

где 

Выясним, как можно осуществить переход от одного базиса линейного пространства к другому и найти координаты вектора 
Пусть в пространстве 


Запишем систему (4.17) в матричном виде: 
Неособенная матрица 


Можно показать, что зависимость между координатами вектора в разных базисах определяется формулами:
где 

Переход к новому базису широко используется в задачах линейного программирования и в других задачах математических методов в экономике.
Задан вектор 







В предыдущем примере было показано, что векторы 
Матрица перехода от базиса 



Транспонируем матрицу 
Для нее существует обратная матрица, поскольку 
По соотношению (4.18) определяем координаты вектора 


Рассмотрим разложение вектора по новому базису для нахождения базисных решений СЛАУ.
Запишем систему линейных алгебраических уравнений в векторной форме
где коэффициентами при неизвестных системы являются векторы 





Система линейных уравнений называется сводной к единичному базису, если среди векторов 

В общем случае, если количество векторов, образующих базис, меньше количества векторов системы 
Таким образом, для нахождения всех базисных решений системы можно предложить такой алгоритм:
1) сводим систему линейных уравнений элементарными преобразованиями к единичному базису;
2) находим значения неизвестных, что соответствуют данном базису, то есть координаты вектора 
3) выполняем преобразование системы уравнений с целью введения в базис других векторов системы. Тогда координаты вектора 
Заметим, что максимальное количество базисных решений равно количеству сопряжений с 


Найдем все базисные решения системы линейных уравнений
В векторной форме система уравнений имеет вид
где
Среди заданных векторов 

Есть четыре вектора двумерного пространства, среди которых необходимо определить базисные. Поскольку наибольшее количество линейно независимых векторов в этом пространстве равно двум, то все четыре вектора не могут быть линейно независимыми. Сводим систему линейных уравнений к единичному базису. Запишем матрицу коэффициентов системы в таблице 4.1 и выполним элементарные преобразования этой системы по методу Жордана-Гаусса.
Сведение системы уравнений к единичному базису Таблица 4.1
По результатам последней операции получено единичную матрицу.
Следовательно, векторы 








Количество базисов для данного примера определяется количеством соединений из четырех векторов 

В таблице 4.2 первым из базисных решений системы приведено именно то, которое получили в таблице 4.1.
Нахождение базисных решений Таблица 4.2
Заметим, что среди шестерых базисных решений данной системы линейных уравнений только 

В рамках учебной дисциплины 


Однородная система уравнений. Особенности решения
Рассмотрим векторный подход к нахождению общего решения систем линейных уравнений (1.9):
где 


В векторной форме система однородных линейных уравнений имеет вид:
где 




Если ранг основной матрицы меньше количества неизвестных 
Пусть коэффициенты при неизвестных 
где 

По свойству 3 (п. 3.2) любая линейная комбинация решений однородной системы также является решением этой системы.
Фундаментальной системой решений однородной системы уравнений называется такая линейно независимая система векторов 
Теорема 4.3 (пpo фундаментальную систему решений). Однородная система уравнений (4.20) имеет фундаментальную систему решений, количество векторов которой равно 

Доказательство. Предоставим свободным неизвестным 

(Конечно, при 
Выражения базисных неизвестных 


Вектор
где 
Если числа 


Следовательно, для нахождения общего решения однородной системы уравнений выполняем следующее:
1. Выражает базисные неизвестные системы (4.20) через свободные.
2. Предоставляем значение свободным 
3. Подставляемые в (4.21) последовательно значение свободных неизвестных (4.22), находим базисные неизвестные, получая таким образом фундаментальную систему решений:
4. Записываем общее решение системы как линейную комбинацию фундаментальных решений (4.23).
Найдем фундаментальную систему решений однородной системы уравнений:
Чтобы выразить базисные неизвестные системы через свободные неизвестные, воспользуемся методом Жордана-Гаусса. Выполняем элементарные преобразования основной матрицы системы для получения в ней единичной матрицы:
Выбираем за базисные неизвестные 


Если свободным неизвестным последовательно предоставить значения 





Общее решение системы уравнений в векторной форме находим как линейную комбинацию фундаментальных решений, а именно:
где
Тогда общее решение однородной системы уравнений, составленный из фундаментальных решений системы, имеет вид:
Замечания. Аналогично можно представить общее решение и неоднородной системы уравнений, которая имеет множество решений.
Пусть система неоднородных уравнений
совместима, но ранг матрицы системы меньше количества неизвестных 
где 
— общее решение (4.22) соответствующей однородной системы уравнений (4.20).
Найдем общее решение неоднородной системы уравнений:
Если праве части всех уравнений положить равными нулю, то получим однородной систему уравнений (4.24), общее решение которой определен в предыдущем примере:
где
Найдем произвольный частное решение неоднородной системы. Например, возьмем свободные неизвестные равными нулю: 



где
или
Такое представление общего решения неоднородной системы линейных алгебраических уравнений обобщается на произвольные неоднородные системы, которые имеют множество решений.
Лекции:
- Исследовать ряд на абсолютную сходимость
- Комплексные числа: примеры решения
- Уравнение окружности и прямой
- Область определения функции примеры решения
- Неопределенный интеграл
- Объемы многогранников
- Приложения определенного интеграла
- Дифференциальное вычисление функции одной переменной
- Решение слау
- Каноническое уравнение параболы

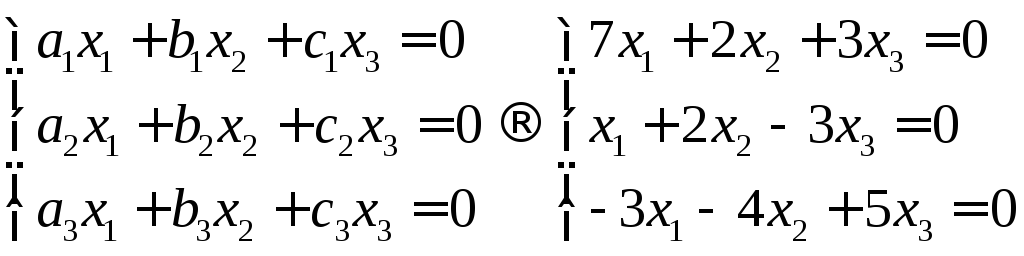
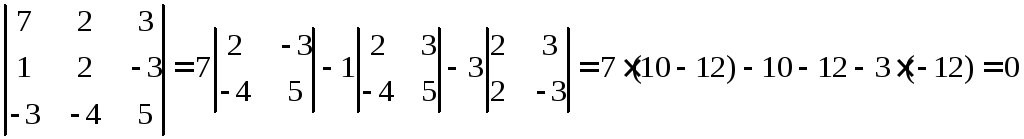
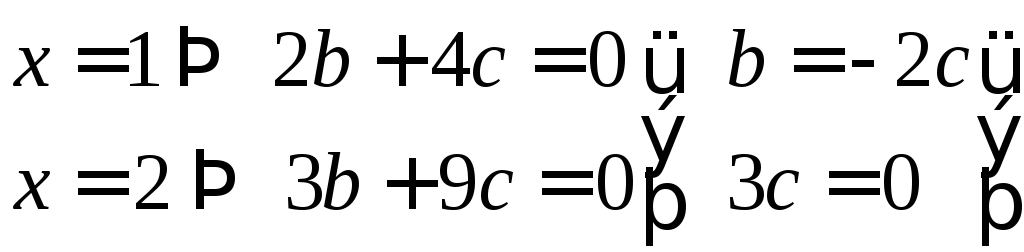

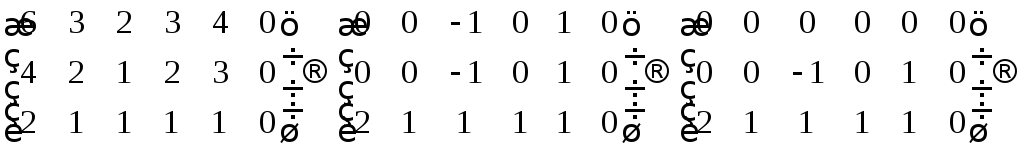
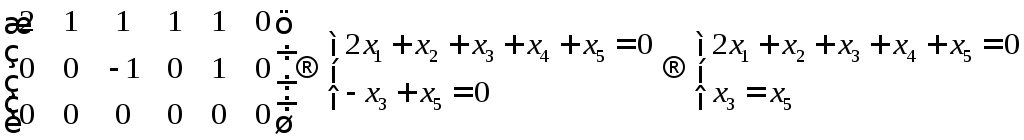
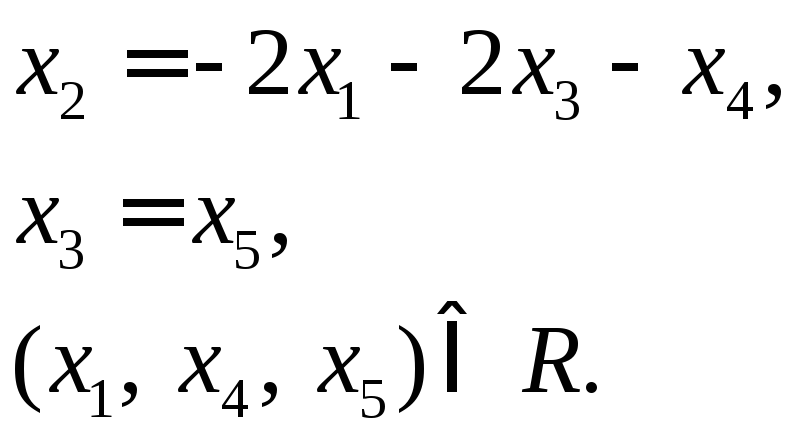
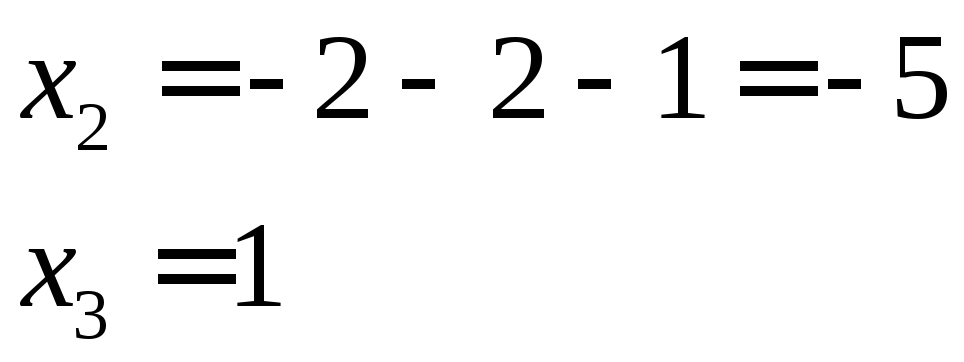

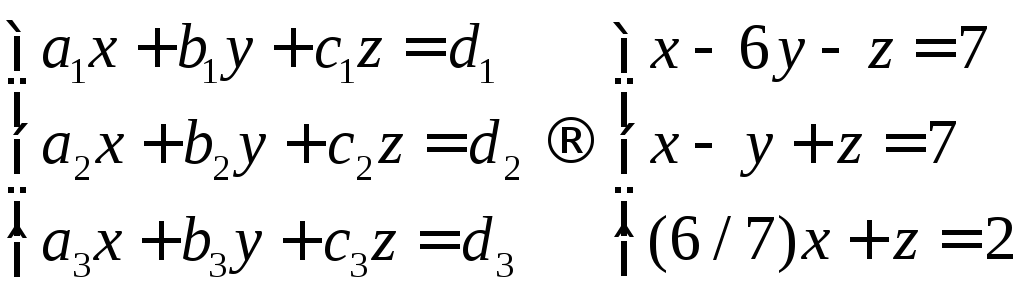
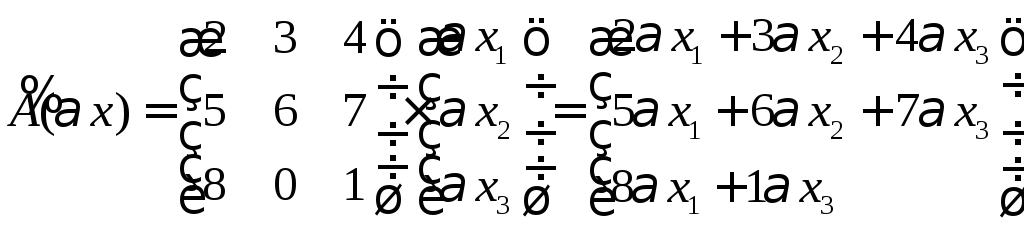
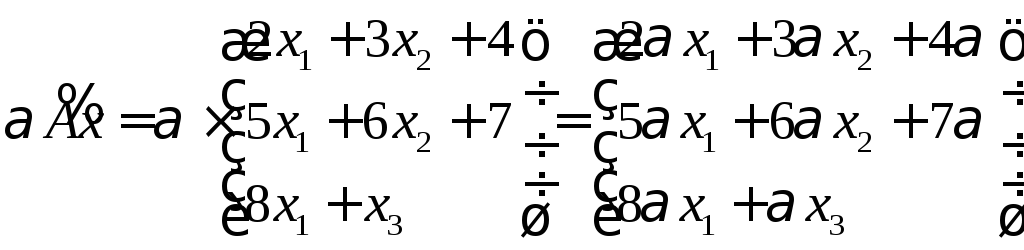
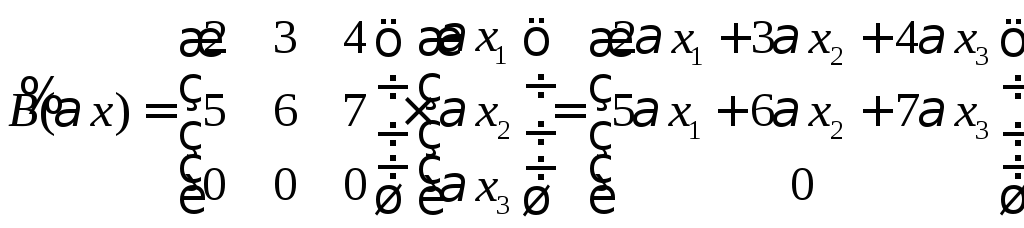
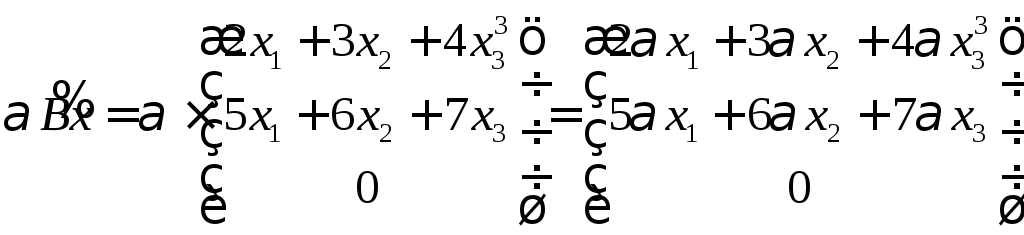
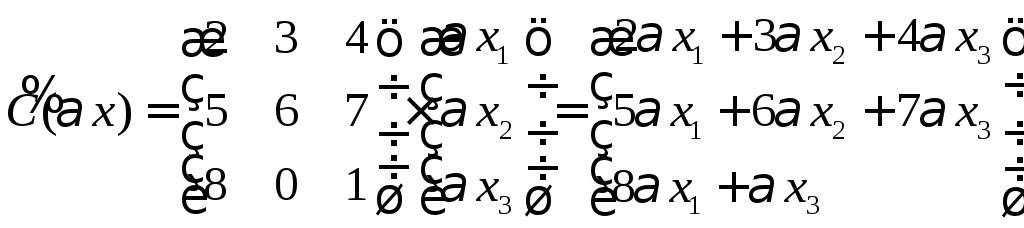
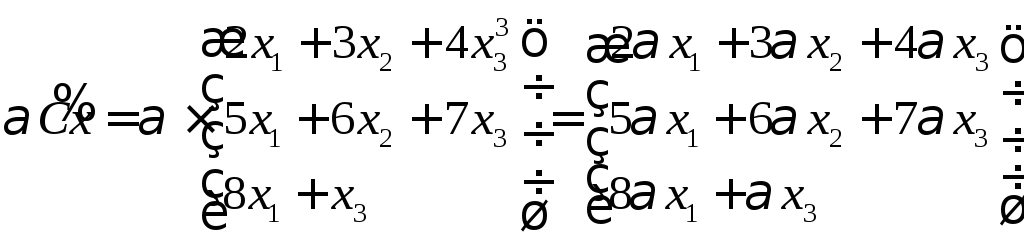
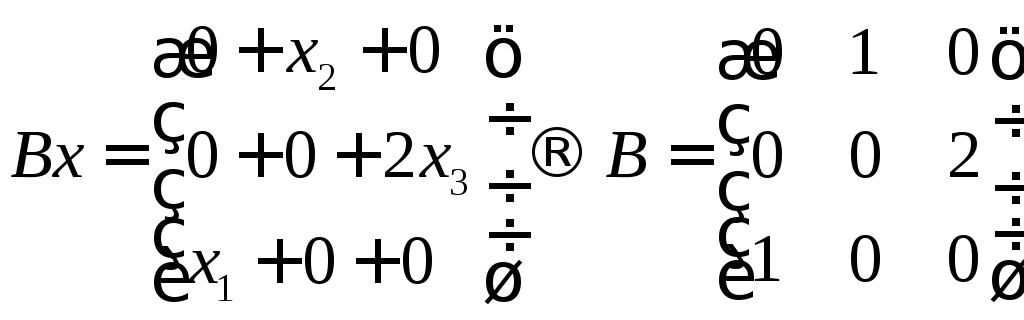
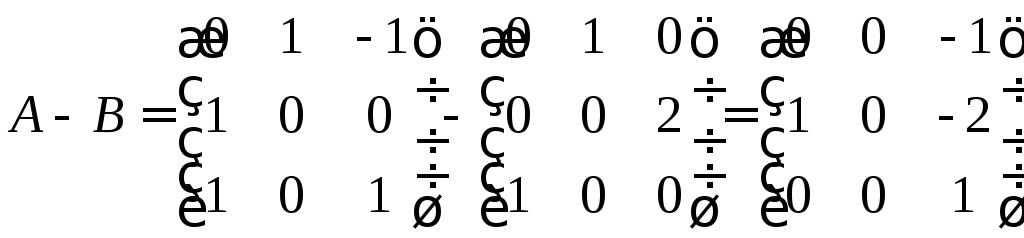
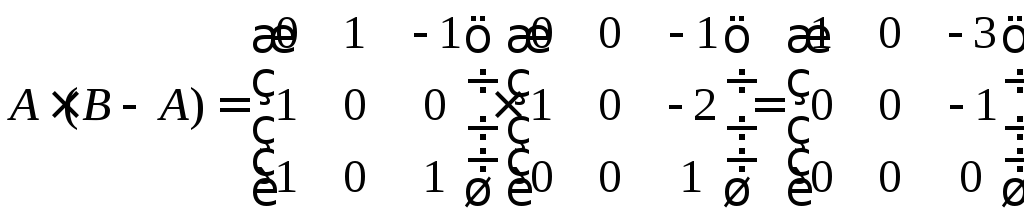
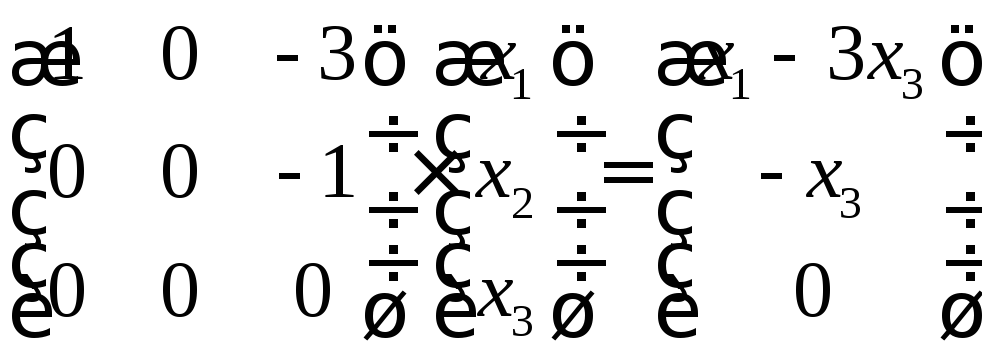
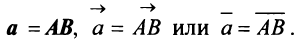
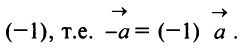
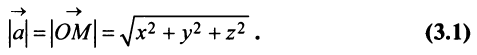
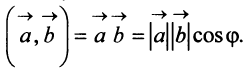
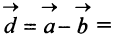
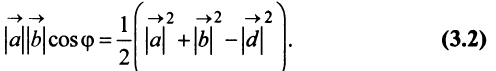
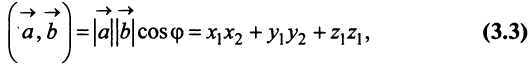
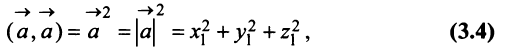
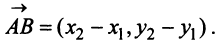
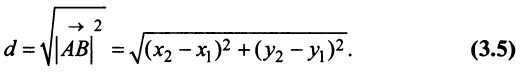
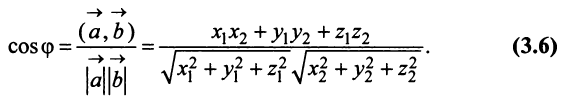
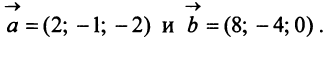
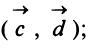
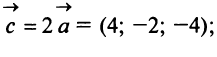
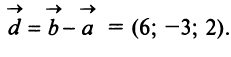
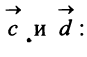
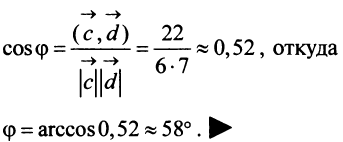
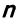 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство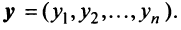
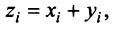
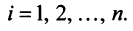
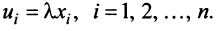
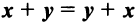 — коммутативное (переместительное) свойство суммы:
— коммутативное (переместительное) свойство суммы: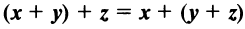 — ассоциативное (сочетательное) свойство суммы;
— ассоциативное (сочетательное) свойство суммы;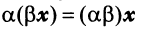 — ассоциативное относительно числового множителя свойство;
— ассоциативное относительно числового множителя свойство;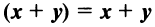 — дистрибутивное (распределительное) относительно суммы векторов свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;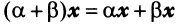 —дистрибутивное относительно суммы числовых множителей свойство;
—дистрибутивное относительно суммы числовых множителей свойство;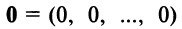 такой, что
такой, что 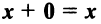 для любого вектора
для любого вектора 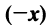 такой, что
такой, что 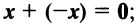
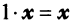 для любого вектора
для любого вектора 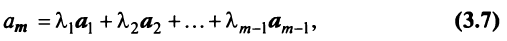
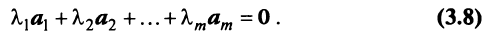
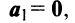 то равенство (3.8) справедливо при
то равенство (3.8) справедливо при 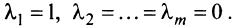
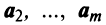 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство 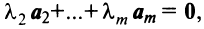 в котором не все числа равны нулю. Но тогда с теми же числами
в котором не все числа равны нулю. Но тогда с теми же числами 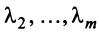 и
и 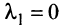 будет справедливо равенство (3.8).
будет справедливо равенство (3.8).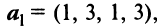
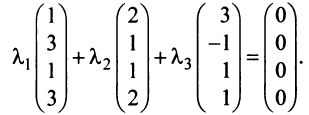
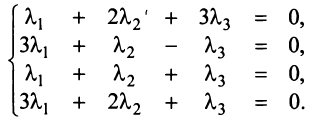
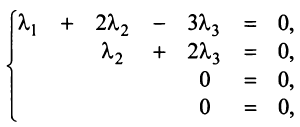
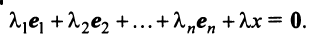
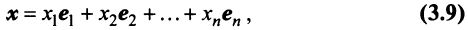
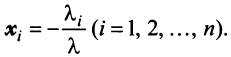
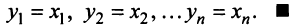
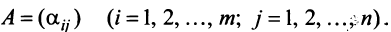


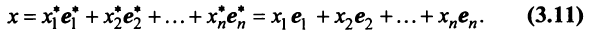
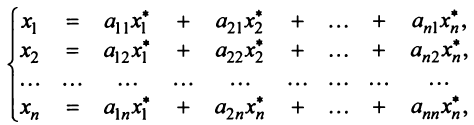
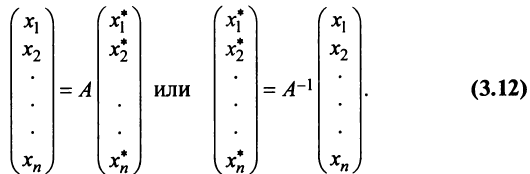
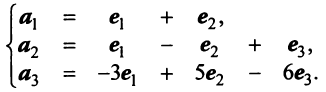
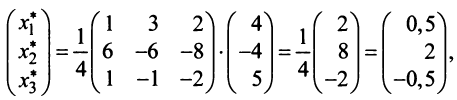
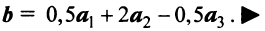
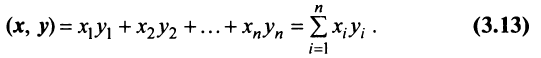
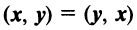 — коммутативное свойство;
— коммутативное свойство;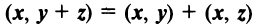 — дистрибутивное свойство;
— дистрибутивное свойство;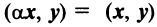 — для любого действительного числа;
— для любого действительного числа;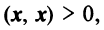 если
если 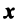 — ненулевой вектор;
— ненулевой вектор; 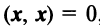 , если
, если