Как составить математическую модель фирмы

Разработка математической модели по формированию производственной программы предприятия

Содержание

Введение

. Роль
экономико-математических методов в оптимизации экономических решений

.1 История
применения математических методов в экономике

.2 Сущность
экономико-математического моделирования

.3 Основные
понятия и типы моделей. Их классификация

.4 Этапы
экономико-математического моделирования

.5 Принцип
работы симплекс-метода

.6 Симплекс
метод в общем виде

. Разработка
математической модели по формированию производственной программы

.1
Составление математической модели

.
Оптимизационные расчеты, связанные с выбором производственной программы

.1 Решение
задачи средствами Microsoft Excel

.2 Решение
задачи на максимум прибыли

.3 Решение
задачи на минимум себестоимости

.4 Анализ
полученных данных

Заключение

Список
использованных источников

Приложения

Введение

В современном мире начинающие, а так же опытные предприниматели
сталкиваются с проблемой грамотного распределения ресурсов для производства той
или иной продукции. Постоянно меняющиеся условия рынка влияют на многие сферы
экономики. Одним из путей решения этой проблемы является применение методов
экономико-математического моделирования в управлении предприятиями, в том числе
и железнодорожным транспортом.

Математические модели и методы — это необходимый элемент современной
экономической науки, как на микро-, так и макроуровне, изучаются в таких её
разделах, как математическая экономика и эконометрика.

Эконометрика — это раздел экономической науки, которая изучает
количественные и качественные экономические взаимосвязи с помощью
математических и статистических методов и моделей.

Математическая экономика занимается анализом, разработкой и поиском
решений математических моделей разных экономических процессов, среди них
выделяют макро- и микроэкономические классы моделей. Макроэкономические модели изучают
экономику в целом, опираясь на такие укрупнённые показатели, как валовый
национальный продукт, инвестиции, потребление, занятость и т.д. При
моделировании рыночной экономики особое место в этом классе занимают модели
равновесия и экономического роста.

Равновесные модели описывают такие состояния экономики, когда
результирующая всех сил, стремящихся вывести её из некоторого состояния, равна
нулю (модель «затраты — выпуск» В. Леонтьева, модель Эрроу-Добре).

Модели экономического роста описывают экономическую динамику и приводят к
поиску и анализу траекторий стационарного роста: (модель Харрода-Домара, модель
Солоу, модели магистрального типа).

Микроэкономические модели описывают экономические процессы на уровне
предприятий и фирм, помогая решать стратегические и оперативные вопросы
планирования и оптимального управления в рыночных условиях. Важное место среди
микроэкономических моделей занимают оптимизационные модели (задачи
распределения ресурсов и финансирования, транспортная задача, максимизация прибыли
фирмы, оптимальное проектирование).

. Роль экономико-математических методов в оптимизации экономических
решений

.1 История применения математических методов в экономике

Применение математических методов, в том числе и
методов математического моделирования, в экономике в целом имеет длинную
историю. В качестве примера хочу привести характеристику математического метода
исследования основателем классической школы буржуазной политической экономии В.
Петти (1623 — 1687). В предисловии к «Политической арифметике» В. Петти писал о
том, что его способ исследования не обычный, ибо вместо того, чтобы употреблять
слова только в сравнительной и превосходной степени и прибегать к умозрительным
аргументам, я вступил на путь выражения своих мнений на языке чисел, весов и
мер, что я уже давно стремился пойти по этому пути, чтобы показать пример политической
арифметики.

Экономист домарксовского периода Н. Г. Чернышевский
(1828 — 1889) в замечаниях на трактат Д, С. Миля «Основания политической
экономии» написал: Мы видели уже много примеров тому, какими приемами
пользуется политическая экономия для решения своих задач. Эти приемы
математические. Иначе и быть не может, потому что предмет науки — количества,
подлежащие счету и мере, понимаемые только через вычисление и измерение.

Понятие об экономике как науке возникло в период
расцвета греческой рабовладельческой демократии, когда были сделаны первые
попытки не просто заметить, а теоретически осмыслить факты жизни экономической.
Слово «экономия», от которого произошли такие понятия, как «экономика»,
«экономическая наука» и т. д., в переводе с греческого имеет смысл науки о
ведении домашнего хозяйства. По своему основному содержанию она должна была
заниматься вопросами целесообразного хозяйствования. Однако поскольку богатое
греческое хозяйство рабовладельческое являлось сложной системой
производственной, отражающей на себе все процессы, которые происходили в
обществе, то эта наука неизбежно затрагивала и более общие проблемы: из каких
хозяйственных единиц должно состоять грамотно построенное государство; в каком
отношении эти единицы должны обменивать производимые ими товары; какую роль
играют деньги и торговля? Проблемы науки экономической в таком виде
сформулировал великий греческий философ Аристотель, которого считать принято ее
основателем. Аристотель первым пытался рассмотреть экономические закономерности,
господствующие в обществе, выдвинул идею о различии между меновой и
потребительной стоимостями товаров, высказал мысль о превращении денег в
капитал и т. д. Таким образом, еще в Древней Греции в экономической науке
возникли два направления исследований: во-первых, это анализ методов
рационального управления народным хозяйством и, во-вторых, изучение основных
экономических закономерностей. В дальнейшем первое направление превратилось в
науку о грамотном управлении деятельностью производительных единиц любого
уровня — от производственного участка до экономики в целом. Второе направление
дало начало экономической теории — науке, изучающей основные экономические
закономерности сменяющих друг друга общественно-экономических формаций. Оба
направления экономической науки развивались и развиваются в тесной связи между
собой, их общность особенно заметна в исследованиях, направленных на изучение
экономики страны как целого.

В системе экономических наук главенствующее положение
занимает экономическая теория: она служит теоретической и методологической
основой всего комплекса экономических наук. Применение математических методов в
экономике началось именно в теоретико-экономических исследованиях. Обычно в
качестве исторически первой модели общественного производства называют
экономическую таблицу Ф. Кене (1694 — 1774). В 1758 г. он опубликовал первый
вариант своей «Экономической таблицы», второй вариант — «Арифметическая
формула» — был опубликован в 1766 году. К. Маркс высоко оценил таблицу Ф. Кенэ.
«Это попытка, — писал Маркс, — сделанная во второй трети XIII столетия, в
период детства политической экономии, была в высшей степени гениальной идеей,
бесспорно самой гениальной из всех, какие только выдвинула до сего времени
политическая экономия».

Представители буржуазной политической экономии уже с
середины XIX века в своих теоретических исследованиях начинают использовать все
более и более сложный математический аппарат. В последнее тридцатилетие XIX
века складывается самостоятельное математическое направление в буржуазной
политической экономии.

Школа математическая возникла в рамках так называемого
неоклассического направления в экономии политической, главным содержанием
которого является теория предельной полезности (маржинализм). В ходе развитие
неоклассического направления, проблемы социально-экономической динамики
исчезают незаметно из анализа, осуществляется постепенно переход к общим
проблемам функционирования систем экономических, ценовых и рыночных механизмов,
реализации принципа рациональности и экономичности в условиях совершенной
конкуренции, условий общего и частного равновесия. Родоначальником
математической школы считается ученый французской школы О. Курно (1801 — 1877).
В 1838 г. была опубликована его книга «Исследование математических принципов
теории богатства» (О. Курно был известным философом, экономистом, историком и
математиком).

Видными представителями школы математической являются
Г. Кассель (1866 — 1944) в Швеции, Ф. Эджворд (1845 — 1926) в Англии В. Джевонс
(1835 — 1882) в Англии, В. Парето (1848 — 1923) в Италии Г. Госсен (1810 —
1859) в Германии, Л. Вальрас (1834 — 1910) в Швейцарии, Г. Кассель (1866 —
1944) в Швеции, Л. Вальрас (1834 — 1910) в Швейцарии, Ф. Эджворд (1845 — 1926)
в Англии, В. Парето (1848 — 1923) в Италии, В. Дмитриев )1868 — 1913) в России.
Математического направления представители в буржуазной политической экономии
достигли известных успехов в области моделирования математического, в раскрытии
ряда объективных закономерностей обмена, производства, потребления и
распределения. В этой связи необходимо отметить важность работ экономиста
русского В. К. Дмитриева. Его основная работа «Экономические очерки. Опыт
органического синтеза трудовой ценности и теории предельной полезности» была
опубликована в 1904 году. В своих работах В, К. Дмитриев выдвинул ряд выводов,
которые позднее были получены В. Леонтьевым на основе анализа моделей «затраты
— выпуск». В частности, эти выводы важны для подсчета коэффициентов полных
трудовых и материальных затрат. Кроме того, стремясь примирить трудовую теорию
стоимости с теорией предельной полезности, что, естественно, сделать
невозможно, он тем не менее поставил проблему соотношения категорий полезности
и стоимости.

Основатели школы математической рассматривали
математические методы, математическое моделирование связей между элементами
экономической системы как методы исследования, а не как методы изложения,
иллюстраций положений и законов экономических, которые получены другим путем.
Изложение же выводов, полученных математически, может быть дано и на обычном
языке, или в математической форме, но без доказательства. Так, Л. Вальрас
писал:

«Весьма немногие из нас в состоянии прочесть
«Математические начала натуральной философии» Ньютона или «Небесную механику»
Лапласа, и тем не менее мы все принимаем на веру сделанное сведущими людьми
описание мира астрономических явлений согласно закону всеобщего тяготения.
Почему точно таким же образом не принять описание мира экономических явлений,
сделанного согласно закону свободной конкуренции».

Представители математической школы с помощью
математических методов стремились разрешить не отдельные частные проблемы
экономической теории, а охватить весь экономический процесс в целом, дать общую
картину взаимозависимости всех экономических явлений. Так, по мнению Парето, процесс
научного прогресса проходит через три стадии:

·        мы ограничиваемся констатированием
существованиям взаимодействия между отдельными элементами экономической
системы, не изучая из в дальнейшем;

·        мы знаем отдельные связи, которые
существуют между отдельными элементами;

·        мы имеем возможность вычислить
величину всех этих элементов и дать совершенно точное выражение условий
равновесия. Идеал всякой науки — достижение третьей стадии.

Математический метод рассматривается как основной,
важнейший метод, который только один в состоянии дать экономической теории
научную законченность.

Основным результатом научным неоклассического
направления является разработка моделей частного и общего равновесия и, условий
использования ресурсов, их оптимального распределения по различным
направлениям, условий равновесия потребления и обмена. Сюда относятся
разработка построение функций спроса, зависимостей спроса от дохода и цен,
моделей поведения потребителя, построение производственной функции, моделей
общего экономического равновесия, моделей поведения фирмы, моделей общего
экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций.

.2 Сущность экономико-математического моделирования

Что бы понять сущность моделирования важно не упускать
из виду, что моделирование — это не единственный источник знаний об объекте.
Процесс моделирования «погружён» в более общий процесс познания. Это
обстоятельство учитывается не только на этапе построения модели, но и на
завершающей стадии, когда происходит обобщение и объединение результатов
исследования, получаемых на основе многообразных средств познания.

Моделирование является процессом циклическим. Это
означает, что за первым четырёхэтапным циклом может последовать второй, третий
и т. д. При этом знания об исследуемом объекте уточняются и расширяются, а
первоначальная модель постепенно совершенствуется. Недостатки, которые могут
быть обнаружены после первого цикла моделирования, обусловливаются малым
знанием объекта и неточностями в построении модели, их можно исправить в
последующих циклах. В методологии моделирования, таким образом, заложены весьма
большие возможности саморазвития.

Проникновение математики в Экономическую науку связано
с преодолением значительных трудностей, которые лежат в специфике экономической
науки и в природе экономических процессов.

Множество объектов, которые изучаются экономической
наукой, могут быть охарактеризованы понятием — «сложная система».

Наиболее распространено понимание системы как
совокупности элементов, которые находятся во взаимодействии и образуют
некоторое единство, целостность. Важным качеством любой системы является
эмерджентность — наличие таких свойств, которые не присущи ни одному из
элементов, входящих в систему. Следовательно, изучая систему, недостаточно
пользоваться методом их разбития на элементы с последующим изучением этих
элементов в отдельности. Одна из трудностей экономических исследований
заключается в том, что почти не существует экономических объектов, которые
можно было бы рассматривать как отдельные (внесистемные) элементы.

Определить сложно систему можно по количеству
элементов входящих в неё, связями между этими элементами, а также
взаимоотношениями между системой и средой. Экономика любого предприятия
обладает всеми признаками очень сложной системы. Она объединяет большое
количество элементов, отличающихся многообразием внутренних связей и связей с
другими системами (природная среда, экономика других стран и т. д.). В
управлении экономикой взаимодействуют природные, социальные процессы,
технологические, субъективные и объективные факторы.

Сложность экономики иногда рассматривалась как
обоснование невозможности её моделирования, изучения средствами математики. Но
такая точка зрения неверна. Моделировать можно объект любой природы и любой
сложности, чем сложнее объект моделирования, тем интереснее модель. Благодаря
моделированию мы можем получить результаты, которые невозможно получить иными
способами исследования.

Потенциальная возможность математического
моделирования любых экономических объектов и процессов не означает, её успешной
осуществимости при данном уровне экономических и математических знаний,
имеющейся конкретной информации и вычислительной технике. И, хотя нельзя
указать абсолютные границы математической формализуемости экономических
проблем, всегда будут существовать неформализованные проблемы, для которых
математическое моделирование недостаточно эффективно.

С экономической точки зрения оптимальные решения,
которые можно получить с помощью экономическо-математического моделирования,
обладают следующими основными свойствами:

·        Оптимальность решения зависит oт целей, поставленных при
планировании процесса. Например, выбор типа продукта по критерию стоимости
будет отличаться от выбора по критерию качества.

·        Оптимальность решения зависит oт текущей хозяйственной обстановки
(иными словами, оптимум всегда конкретен, его нельзя вычислять абстрактно).

·        Существенные изменения оптимального
варианта происходят только при значительных изменениях обстановки — это
свойство называется устойчивостью базиса оптимального плана относительно малых
изменений условий (т.е. оптимальные решения можно находить достаточно надёжно,
несмотря на приблизительный характер почти всей экономической информации).

·        При определении взаимозависимости
решений по всем объектам экономики особое значение имеют обратная связь
объектов и издержки обратной связи. Например, если предприятия А и Б потребляют
один и тот же ограниченный ресурс, то увеличение доли предприятия А уменьшает
долю предприятия Б (обратная связь). Вероятно, что потребление данного ресурса
(топлива, сырья и др.) снижает производственные издержки. Тогда, увеличение
доли предприятия А приведёт к экономии на этом предприятии и к дополнительным
издержкам на предприятии Б в результате замены ресурса менее эффективным
(издержки обратной связи).

·        Оценка рациональности конкретного
мероприятия зависит от уровня управления: решение, оптимальное для отдельного
предприятия, может быть неоптимальным для отрасли или экономики в целом.

1.3 Основные
понятия и типы моделей. Их классификация

В процессе исследования объекта часто бывает нецелесообразно или даже
невозможно иметь дело непосредственно c этим объектом. Удобнее бывает заменить его другим объектом, подобным
данному в тех аспектах, которые важны в данном исследовании. В общем виде модель
можно определить как условный образ реального объекта (процессов), создаваемый
для более детального изучения действительности. Метод исследования, который
базируется на использовании и разработке моделей, называется моделированием.
Необходимость моделирования обусловлена сложностью, а порой и невозможностью
прямого изучения реального объекта (процессов). Значительно доступнее создавать
и изучать прообразы реальных объектов (процессов), т.е. модели. Можно сказать,
что теоретическое знание o
чем-либо, как правило, представляет собой совокупность различных моделей. Эти
модели отражают существенные свойства реального объекта (процессов), хотя на
самом деле действительность значительно содержательнее и богаче.

Модель — это материально реализованная или мысленно представляемая
система, которая, отображая или воспроизводя объект исследования, способна
замещать его так, что изучение ее дает новую информацию об этом объекте.

На сегодняшний день общепризнанной единой классификации моделей не
существует. Однако из множества моделей можно выделить физические, графические,
экономико-математические, словесные, графические и некоторые другие типы
моделей.

Экономико-математические модели — это модели экономических объектов или
процессов, в которых при описании используются математические средства. Цели их
создания очень разнообразны: они строятся для анализа тех или иных положений и
предпосылок экономической теории, логического обоснования экономических
закономерностей, обработки и приведения в систему эмпирических данных. В
практическом плане экономико-математические модели используются как инструмент
планирования, прогноза, управления и совершенствования различных сторон
экономической деятельности общества.

Экономико-математические модели отражают наиболее существенные свойства
реального объекта или процесса с помощью системы уравнений. Единой
классификации экономико-математических моделей не существует, хотя можно
выделить наиболее значимые их группы в зависимости от признака классификации.
По целевому назначению модели делятся на:

·        Теоретико-аналитические (используются в исследовании общих
свойств и закономерностей экономических процессов);

·        Прикладные (применяются в решении конкретных экономических
задач, таких как задачи экономического анализа, прогнозирования, управления).

По учету фактора времени модели подразделяются на:

·        Статистические (экономическая система описана в статистике,
применительно к одному определенному моменту времени; это как бы снимок, срез,
фрагмент динамической системы в какой-то момент времени).

·        Динамические (описывают экономическую систему в развитии);

По длительности рассматриваемого периода времени различают модели:

·        Краткосрочного прогнозирования или планирования (до года);

·        Среднесрочного прогнозирования или планирования (до 5 лет);

·        Долгосрочного прогнозирования или планирования (более 5 лет).

По цели создания и применения различают модели:

·        Балансовые;

·        Оптимизационные;

·        Эконометрические;

·        Сетевые;

·        Имитационные (экспертные).

·        Систем массового обслуживания;

Балансовые модели отражают требования соответствия наличия ресурсов и их
использования. Оптимизационные модели позволяют найти из множества возможных
(альтернативных) вариантов наилучший вариант производства, потребления или
распределения. При этом ограниченные ресурсы будут использованы наилучшим
образом для достижения поставленной цели. Параметры эконометрических моделей
оцениваются с помощью методов математической статистики. Наиболее
распространены модели, которые представляют собой системы регрессионных
уравнений. В этих уравнениях отражается зависимость зависимых переменных от
независимых переменных. Данная зависимость в основном выражается через тренд
(длительную тенденцию) основных показателей моделируемой системы экономической.
Эконометрические модели принято использовать для прогнозирования и анализа
конкретных экономических процессов с использованием реальной статистической
информации. Сетевые модели используются наиболее широко в управлении проектами.
Сетевая модель отображает комплекс работ (операций) и событий, и их взаимосвязь
во времени. Обычно сетевая модель предназначается для выполнения работ в такой
последовательности, чтобы сроки выполнения проекта были минимальными. В этом
случае ставится задача нахождения критического пути. Но существуют и такие
сетевые модели, которые ориентированы не на критерий времени, а, например, на
минимизацию стоимости работ.

Имитационная модель, наряду с машинными решениями, содержит блоки, где
решения принимаются человеком (экспертом). Вместо непосредственного участия
человека в принятии решений может выступать база знаний. В этом случае
персональный компьютер, специализированное программное обеспечение, база данных
и база знаний образуют экспертную систему. Экспертная система предназначена для
решения одной или ряда задач методом имитации действий человека, эксперта в
данной области.

Модели систем массового обслуживания создаются для минимизации затрат
времени на ожидание в очереди и времени простоев каналов обслуживания.

По учету фактора неопределенности модели подразделяются на:

·        Детерминированные (с однозначно определенными результатами);

·        Стохастические (вероятностные; с различными, вероятностными
результатами).

По типу математического аппарата различают модели:

·        Линейного программирования (оптимальный план достигается в
крайней точке области изменения переменных величин системы ограничений);

·        Нелинейного программирования ( оптимальных значений целевой
функции может быть несколько);

·        Корреляционно-регрессионные;

·        Сетевые;

·        Теории игр;

·        Матричные;

·        Теории массового обслуживания и т.д.

С развитием экономико-математических исследований проблема классификации
применяемых моделей усложняется. Наряду с появлением новых типов моделей и
новых признаков их классификации, осуществляется процесс интеграции моделей
разных типов в более сложные модельные конструкции.

В данной работе рассмотрен пример решения задачи линейного
программирования. Для начала рассмотрим вопрос — что же такое «линейное
программирование»? Это один из первый разделов математического
программирования. Термин «программирование» в названии не имеет
ничего общего с термином «программирование» для ЭВМ, так как
«линейное программирование» появилось задолго до того времени, когда
ЭВМ стали широко применятся для решения разнообразных экономических,
математических и других задач. Термин «линейное программирование» возник в
результате неточного перевода английского «linear programming». Одно из
значений слова «programming» — составление планов, планирование. Следовательно,
правильным переводом «linear programming» было бы не «линейное
программирование», а «линейное планирование», что точнее отражает содержание
термина.

 Задачами
линейного программирования являются задачи, в которых линейны как целевая
функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного
программирования можно сформулировать следующим образом: найти вектор значений
переменных, доставляющих экстремум линейной целевой функции при m ограничениях
в виде линейных равенств или неравенств. Линейное программирование представляет
собой наиболее часто используемый метод оптимизации. К числу задач линейного
программирования можно отнести такие задачи как:

·        рационального использования материалов и; задачи оптимизации
раскроя;

·        оптимизации производственной программы предприятий;

·        оптимального размещения и концентрации производства;

·        составления оптимального плана перевозок, работы транспорта;

·        управления производственными запасами;

·        и многие другие, принадлежащие сфере оптимального
планирования.

 В настоящее
время линейное программирования широко применяется предприятиями для
оптимизации производственного плана.

Подведем небольшой итог. Линейное программирование — это наука о методах
исследования и отыскания наибольших или наименьших значений линейной функции.
На неизвестные переменные накладываются ограничения. Таким образом задачи
линейного программирования можно отнести к задачам на условный экстремум
функции.

1.4 Этапы
экономико-математического моделирования

Процесс экономико-математического моделирования — это описание социальных
и экономических систем и процессов в виде экономико-математических моделей.
Данная разновидность моделирования обладает рядом существенных особенностей,
связанных как с объектом моделирования, так и с применяемыми аппаратом и
средствами моделирования. Поэтому целесообразно более детально проанализировать
последовательность и содержание этапов экономико-математического моделирования,
выделив следующие шесть этапов:

·        Постановка экономической проблемы и ее качественный анализ;

·        Построение математической модели;

·        Математический анализ модели;

·        Подготовка исходной информации;

·        Численное решение;

·        Анализ численных результатов и их применение.

Рассмотрим каждый из этапов более подробно.

Постановка экономической проблемы и ее качественный анализ. На данном
этапе нужно четко сформулированная сущность проблемы, принимаемые допущения и
те вопросы, на которые требуется получить ответы. Сначала нужно обозначить
важнейшие черты и свойства моделируемого объекта; изучение структуры объекта и
основных зависимостей, связывающих его элементы; формулирование гипотез (хотя
бы предварительных), объясняющих развитие и поведение объекта.

Построение математической модели. Это — этап формализации экономической
проблемы, выражения ее в виде конкретных математических отношений и зависимостей
(функций, уравнений, неравенств и т.д.). Обычно сначала определяется основная
конструкция (тип) модели математической, а дальше уточняются детали этой
конструкции (конкретный перечень переменных и параметров, форма связей). Таким
образом, построение модели можно разбить на несколько стадий.

Неправильно полагать, что чем больше фактов учитывает модель, тем она
лучше «работает» и дает лучшие результаты. То же можно сказать о таких
характеристиках сложности модели, как используемые формы математических зависимостей
(линейные и нелинейные), учет факторов случайности и неопределенности и т.д.

Лишняя сложность модели затрудняет процесс исследования. Нужно учитывать
не только реальные возможности информационного и математического обеспечения,
но и сопоставлять затраты на моделирование с получаемым эффектом.

Одна из важный особенностей математических моделей — потенциальная
возможность их использования для решения разнокачественных проблем. Поэтому,
даже сталкиваясь с новой экономической задачей, не нужно стремиться
«изобретать» модель; сначала необходимо попытаться применить для решения этой
задачи уже известные модели.

Математический анализ модели. Целью этого этапа является выяснение общих
свойств модели. Здесь применяются чисто математические приемы исследования.
Наиболее важный момент — это доказательство существования решений в
сформулированной модели. Если удается доказать, что математическая задача не
имеет решения, то необходимость в последующей работе по первоначальному
варианту модели отпадает и следует скорректировать либо постановку
экономической задачи, либо способы ее математической формализации. При
аналитическом исследовании модели выясняются такие вопросы, как, например,
единственное ли решение, в каких пределах и в зависимости исходных условий они
изменяются, какие переменные (неизвестные) могут входить в решение, каковы
будут соотношения между ними, каковы тенденции их изменения и т.д.
Аналитической исследование модели по сравнению с эмпирическим (численным) имеет
то преимущество, что получаемые выводы сохраняют свою силу при различных
конкретных значениях внешних и внутренних параметров модели.

Подготовка исходной информации. Моделирование предъявляет жесткие
требования к системе информации. В то же время реальные возможности получения
информации ограничивают выбор моделей, предназначаемых для практического
использования. При этом принимается во внимание не только принципиальная
возможность подготовки информации (за определенные сроки), но и затраты на
подготовку соответствующих информационных массивов.

Эти затраты не должны превышать эффект от использования дополнительной
информации.

В процессе подготовки информации широко используются методы теории
вероятностей, теоретической и математической статистики. При системном
экономико-математическом моделировании исходная информация, используемая в
одних моделях, является результатом функционирования других моделей.

Численное решение. Этот этап включает разработку алгоритмов для
численного решения задачи, составление программ на ЭВМ и непосредственное проведение
расчетов. Трудности этого этапа обусловлены, прежде всего, большой размерностью
экономических задач, необходимостью обработки значительных массивов информации.

Исследование, проводимое численными методами, может существенно дополнить
результаты аналитического исследования, а для многих моделей оно является
единственно осуществимым. Класс экономических задач, которые можно решать
численными методами, значительно шире, чем класс задач, доступных
аналитическому исследованию.

Анализ численных результатов и их применение. На этом заключительном
этапе цикла встает вопрос о полноте и полноте результатов моделирования, о
степени практической применимости последних.

Математические методы проверки могут выявить некорректные построения
модели и тем самым сужать класс потенциально правильных моделей. Неформальный
анализ теоретических выводов и численных результатов, получаемых посредством
модели, сопоставление их с имеющимися знаниями и фактами действительности также
позволяют обнаруживать недостатки постановки экономической задачи,
сконструированной математической модели, ее математического и информационного
обеспечения.

.5 Принцип работы симплекс-метода

Симплекс-метод позволяет решать задачи линейного программирования любой
размерности, т.е. с любым количеством переменных. Решение задач линейного
программирования на основе симплекс-метода состоит в целенаправленном переборе
угловых точек области допустимых решений (далее ОДР) в направлении улучшения
значения целевой функции.

Можно доказать, что экстремум (минимум или максимум) целевой функции
всегда достигается при значениях переменных X₁, ₂,…,X_n, соответствующих одной из угловых
точек ОДР. Другими словами, оптимальное решение всегда находится в угловой
точке ОДР.

Принцип работы симплекс-метода состоит в следующем. Находится какое-либо
допустимое решение, соответствующее одной из угловых точек ОДР.

Проверяются смежные с ней угловые точки ОДР. Под смежной здесь понимается
угловая точка, расположенная на той же границе ОДР, что и текущая угловая точка
(для двухмерной ОДР — на той же стороне многоугольника, для трехмерной — на том
же ребре многогранника, и т.д.). Если ни в одной из смежных угловых точек
значение целевой функции не улучшается, то решение задачи завершается; текущая
угловая точка ОДР соответствует оптимальному решению задачи. Если имеются
смежные угловые точки ОДР, для которых значение целевой функции улучшается, то
выполняется переход в ту из них, для которой достигается наиболее быстрое
улучшение значения целевой функции.

Для новой угловой точки ОДР процесс повторяется, т.е. проверяются смежные
угловые точки. Перебор угловых точек происходит до тех пор, пока не будет
найдено оптимальное решение, т.е. пока не будет достигнута угловая точка ОДР,
для которой ни в одной из смежных точек значение целевой функции не улучшается.

Поиск решения на основе симплекс-метода реализуется с помощью
симплекс-таблиц. Основные этапы реализации симплекс-метода следующие.

. Задача линейного программирования приводится к стандартной форме. 2.
Определяется начальное допустимое решение (начальная угловая точка ОДР).

. Строится исходная симплекс-таблица. Выполняются преобразования
симплекс-таблиц, соответствующие перебору угловых точек ОДР, до получения
оптимального решения.

Реализация симплекс-метода существенно различается в зависимости от вида
математической модели задачи. В данном разделе рассматривается реализация
симплекс-метода для случая, когда математическая модель задачи состоит только
из ограничений «меньше или равно», и целевая функция подлежит
максимизации. Реализация симплекс-метода для задач с математической моделью
любого вида рассматривается в разделе 3.

.6 Симплекс метод в общем виде

Требуется найти максимум целевой функции:

 (1)

При ограничениях:

 (2)

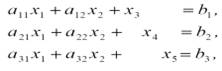
И условиях неотрицательности:

x_i ≥ 0, i=1,
2, …, n (3)

Из системы (2) видно, что если за свободные неизвестные принять х₁,
х₂ и положить их равными нулю, то базисные неизвестные х₃,
х₄, х₅ будут равны правым частям системы. в результате
получаем план:

х₁=0, х₂=0, х₃=b₁, x₄=b₂, x₅=b₃ (4)

Для которого целевая функция равна

 (5)

Выразим из (2) базисные неизвестные х₃, х₄, х₅
через свободные х₁, х₂:

 (6)

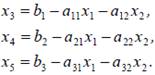
Подставим (6) в целевую функцию (1) и после приведения подобных членов
будем иметь:

f = (c1-c3a11-c4a21-c5a31)x1 + (c2-c3a12-c4a22-c5a32)x2 +
c3b1 + c4b2 + c5b3. (7)

Если коэффициенты перед х₁, х₂ в (7) окажутся отрицательными,
то целевую функцию нельзя увеличить, переводя эти свободные неизвестные в
базисные, то есть давая им какие-то положительное значения. Отрицательность
коэффициентов перед неизвестными в (7) есть признак того, что найдено
оптимальное решение. Коэффициенты перед свободными неизвестными в выражении для
целевой функции принято называть оценками. Введем обозначения:

Z1 = c3a11 + c4a21 + c5a31, Z2 = c3a12 + c4a22 + c5a32. (8)

В этих обозначениях условия максимальности запишутся:

c1 — Z1 < 0, c2 — Z2 < 0, (9)

Пусть условии оптимальности (9) не выполнены, а именно пусть, для
определенности, коэффициент перед х₁ в (7) положителен, тогда,
увеличивая х₁, мы увеличим целевую функцию по сравнению с ее
значением (5). Посмотрим, насколько может быть увеличена переменная х₁по
сравнению с нулем, при условии, что х₂ остается свободной, то есть
будет иметь неизменное значение х₂=0. Из (6) видно, что увеличение х₁
будет вести к уменьшению х₃, х₄, х₅, если
коэффициенты перед х₁ в (6) отрицательны. Увеличивать х₁
можно лишь до значения, при котором первая из неизвестных х₃, х₄,
х₅ обратится в нуль. Положив нулю левые части (6), получим три
уравнения: 0 = b1 — a11x1, 0 = b2 — a21x1, 0 = b3 — a31x1.

Если положить:

 (10)

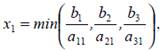
то только одна неизвестная из х₃, х₄, х₅ обратится
в нуль, то есть станет свободной, а остальные останутся положительными.
Предположим, что это будет х₃, тогда будем иметь в качестве
свободных неизвестных х₂, х₃ и в качестве базисных х₁,
х₄, х₅.

Для удобства дальнейших вычислений желательно преобразовать систему
ограничений к виду (2), который характерен тем, что столбцы коэффициентов при
базисных неизвестных образуют единичную матрицу. Так как старая базисная
переменная х₃ заменяется новой базисной переменной х₁, то
в первом уравнении коэффициент перед х₁ должен быть равен 1.

Это достигается делением первого уравнения на a₁₁. Далее следует исключить неизвестную х₁ из
второго и третьего уравнений. Для этого преобразованное первое уравнение
умножим сначала на а₂₁ и вычтем из второго, затем на а₃₁
и вычтем из третьего. В результате этих преобразований система (2) примет вид:

 (11)

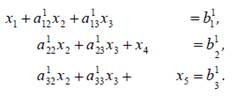
Здесь через a¹_ij обозначены новые значения
коэффициентов. Заметим, что подобные преобразования выполняются в методе Гаусса
при решении систем линейных уравнений.

Описание выше действия по работе с системой ограничений (2) следует
повторить для системы (11) и т.д., до тех пор, пока не будет выполнены условия
оптимальности.

. Описание объекта и логическая формулировка проблемы

Хлебобулочный завод производит 20 различных видов хлебобулочных изделий.
Стоимость и возможные запасы основных ингредиентов представлены в таблице 1.

Таблица 1 — Исходные данные

Наименование	Цена за кг., руб.	Запасы (день), кг.
Мука высшего сорта	20	280
Мука 1-го сорта	15	200
Мука ржаная	14	80
Дрожжи	150	9
Соль	10	8
Сахар	50	25
Маргарин	60	10

Завод установил контракты с различными магазинами на продажу
хлебобулочных изделий. Контрактом установлены минимальное количество изделий на
поставку каждого вида в день. В таблице 2 отражен спрос в день для каждого вида
выпечки, цена по каждому виду (стоимость указана без учета начинки для
некоторых изделий).

Таблица 2 — Спрос в день по каждому виду выпечки, цена каждого вида

Вид хлебобулочного изделия	Цена за штуку, руб.	Минимальный выпуск продукции в день, шт.	максимальный выпуск продукции в день, шт.
Батон	16	420	500
Хлеб «Столичный»	17	70	110
Батон с отрубями	12	30	45
Батон с изюмом	13	20	50
Хлеб «Дарницкий»	17	270	300
Хлеб «Аромантый»	18	40	65
Хлеб «Паляница»	19	180	220
Докторская булочка	10	25	40
Плюшка московская	12	110	130
Сдоба с курагой	11	15	27
Марципан	12	90	112
Плетенка	14	40	60
Булочка столичная	7	25	45
Булочка для хот-догов	7	230	250
Сдоба с маком	12	165	180
Бублик с маком	20	90	110
Пирог с маком	45	15	25
Сдоба с изюмом	10	85	90
Рогалик с шоколадом	11	20	35
Ватрушка с творогом	15	20	30

В таблице 3 отражены количество ингредиентов для создания одной единицы
продукции.

Таблица 3 — Рецептура хлебобулочных изделий

Наименование	Мука в/с, кг	Мука 1-го сорта, кг	Мука ржаная, кг	Дрожжи, кг	Соль, кг	Сахар, кг	Маргарин, кг
Батон	0,2	—	—	0,003	0,0045	0,012	0,011
Хлеб «Столичный»	—	0,3	0,22	0,004	0,008	0,008	—
Батон с отрубями	0,15	—	—	0,007	0,002	0,02	—
Батон с изюмом	0,15	—	—	0,007	0,002	0,02	—
Хлеб «Дарницкий»	—	0,24	0,22	0,003	0,009	—	—
Хлеб «Аромантый»	—	0,35	—	0,012	0,005	0,025	—
Хлеб «Паляница»	—	0,5	—	0,01	0,01	—	—
Докторская булочка	0,15	—	—	0,007	0,002	0,02
Плюшка московская	0,07	—	—	0,003	0,0007	0,014	0,01
Сдоба с курагой	0,05	—	—	0,002	0,0004	0,008	0,004
Марципан	0,05	—	—	0,002	0,0004	0,008	0,004
Плетенка	0,15	—	—	0,007	0,002	0,02	—
Булочка столичная	0,044	—	—	0,0024	0,0008	0,0008	0,0008
Булочка для хот-догов	0,04	—	—	0,002	0,0006	0,0009	0,0009
Сдоба с маком	0,05	—	—	0,002	0,0004	0,008	0,004
Бублик с маком	0,6	—	—	0,0006	0,0006	0,004	0,004
Пирог с маком	1,06	—	—	0,042	0,011	0,106	0,011
Сдоба с изюмом	0,05	—	—	0,002	0,0004	0,008	0,004
Рогалик с шоколадом	0,068	—	—	0,003	0,001	0,014	0,01
Ватрушка с творогом	0,068	—	—	0,003	0,0007	0,014	0,01

Исходя из данных, представленных в таблице 2 и таблице 3, определим
себестоимость ассортимента, чтобы вычислить чистую прибыль от продажи.

Таблица 4 — Вспомогательная таблица

Наименование	Себестоимость	Стоимость продажи	Чистая прибыль
Батон	5,76	16	10,25
Хлеб «Столичный»	8,66	17	8,34
Батон с отрубями	5,07	12	6,93
Батон с изюмом	5,07	13	7,93
Хлеб «Дарницкий»	7,22	17	9,78
Хлеб «Аромантый»	8,35	18	9,65
Хлеб «Паляница»	9,10	19	9,90
Докторская булочка	5,07	10	4,93
Плюшка московская	3,16	12	8,84
Сдоба с курагой	1,94	11	9,06
Марципан	1,94	12	10,06
Плетенка	5,07	14	8,93
Булочка столичная	1,34	7	5,66
Булочка для хот-догов	1,21	7	5,80
Сдоба с маком	1,94	12	10,06
Бублик с маком	12,54	20	7,46
Пирог с маком	33,57	45	11,43
Сдоба с изюмом	1,94	10	8,06
Рогалик с шоколадом	3,12	11	7,88
Ватрушка с творогом	3,12	15	11,88

.1 Составление математической модели

Обозначения:

i —
индекс изделия

j —
индекс ингредиента

x_i — объем i-го изделия

y_j — объем j-го ингредиента

p_i — цена i-го
изделия

z_i — себестоимость i-го
изделия

h_i — ограничение по объему выпуска i-ой продукции

k_j — ограничение j-го
ингредиента

Теперь можно составить математическую модель функции (чистой прибыли) и
системы ограничений.

Необходимо найти такие значения x_i, которые обеспечивают максимум целевой функции

 _ix_i→max,

где
i=1, 2, …, n.=16x₁+17x₂+12x₃+13x₄+17x₅+18x₆+19x₇+10x₈+12x₉+11x₁₀+12x₁₁+14x₁₂+7x₁₃++7x₁₄+12x₁₅+20x₁₆+45x₁₇+10x₁₈+11x₁₉+15x₂₀→max.

При ограничениях по ингредиентам:

_ij  y_j,

где i=
1, 2, …, n; j= 1, 2, …, n.₁*0,2+x₃*0,15+x₄*0,15+x₈*0,15+x₉*0,07+x₁₀*0,05+x₁₁*0,05+x₁₂*0,15+x₁₃*0,044+x₁₄*0,04+x₁₅*0,05+x₁₆*0,6+x₁₇*1,06+x₁₈*0,05+x₁₉*0,068+
x₂₀*0,068280 x₂*0,3+x₅*0,24+x₆*0,35+x₇*0,575₂*0,22+x₅*0,2260

x₁*0,003+x₂*0,004+x₃*0,007+x₄*0,007+x₅*0,003+x₆*0,012+x₇*0,01+x₈*0,007+x₉*0,003+x₁₀*0,002+x₁₁*0,002+x₁₂*0,007+x₁₃*0,0024+x₁₄*0,002+x₁₅*0,0006+x₁₆*0,0006+x₁₇*0,042+x₁₈*0,002+x₁₉*0,003+ x₂₀*0,0037

x₁*0,0045+x₂*0,008+x₃*0,002+x₄*0,002+x₅*0,009+x₆*0,005+x₇*0,01+x₈*0,002+x₉*0,0007+x₁₀*0,0004+x₁₁*0,0004+x₁₂*0,002+x₁₃*0,0008+x₁₄*0,0006+x₁₅*0,0004+x₁₆*0,0006+x₁₇*0,011+x₁₈*0,0004+x₁₉*0,001+ x₂₀*0,00075

x₁*0,012+x₂*0,008+x₃*0,02+x₄*0,02+x₆*0,025+x₈*0,02+x₉*0,014+x₁₀*0,008+x₁₁*0,008+x₁₂*0,02+x₁₃*0,0008+x₁₄*0,0009+x₁₅*0,008+x₁₆*0,004+x₁₇*0,106+x₁₈*0,008+x₁₉*0,014+ x₂₀*0,01415

x₁*0,011+x₉*0,01+x₁₀*0,004+x₁₁*0,004+x₁₃*0,0008+x₁₄*0,0009+x₁₅*0,004+x₁₆*0,004+x₁₇*0,011+x₁₈*0,004+x₁₉*0,01+ x₂₀*0,0110

При ограничениях по объему выпуска:

≤x₁≤ 500

≤x₂≤ 110

≤x₃≤ 45

≤x₄≤ 50

≤x₅≤ 300

≤x₆≤ 65

≤x₇≤ 220

≤x₈≤ 40

≤x₉≤ 130

≤x₁₀≤ 27

≤x₁₁≤ 112

≤x₁₂≤ 60

≤x₁₃≤ 45

≤x₁₄≤ 250

≤x₁₅≤ 180

≤x₁₆≤ 110

≤x₁₇≤ 25

≤x₁₈≤ 90

≤x₁₉≤ 35

≤x₂₀≤ 30

. Оптимизационные расчеты, связанные с выбором производственной программы

.1 Решение задачи средствами Microsoft Excel

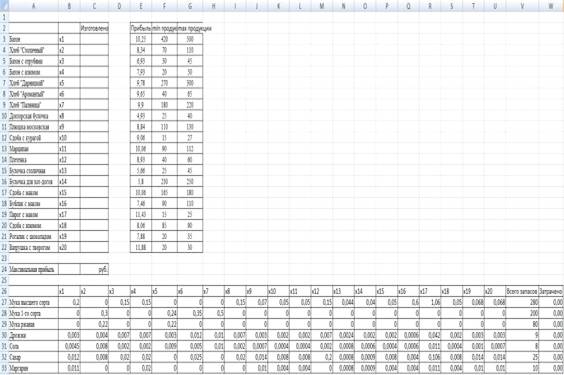
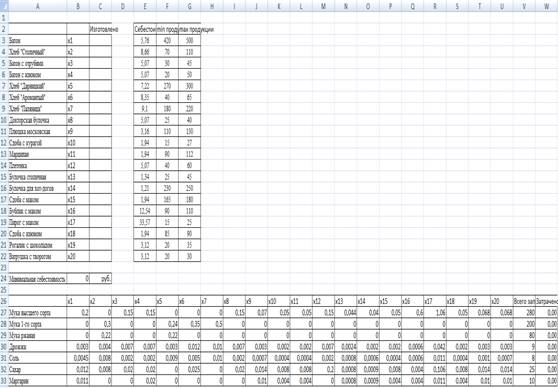
Исходные данные в Microsoft Excel 2007 выглядят таким образом.

Далее через верхнее меню заходим в раздел «Данные», нажимаем на функцию
«Поиск решения». Перед нами открывается окно параметров поиска решения.
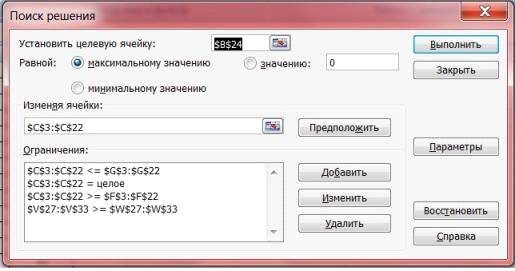
Заполняем окно в соответствии с задачей (Рис 1.).

Рис. 1. Окно параметров поиска решения

Алгоритм настройки окна параметров выглядит следующим образом.

. Устанавливаем целевую ячейку.

. Устанавливаем переключатели, задающие значение целевой ячейки, —
максимальное значение, минимальное значение или конкретное значение.

. Указываем в поле «Изменяя ячейки», в каких ячейках программа должна изменять
значения в поисках оптимального результата.

. Создаем ограничения в списке «Ограничения». Для этого щелкаем на кнопке
«Добавить» и в диалоговом окне «Добавление ограничения определить ограничения».

. Нажимаем кнопку «Найти решение», и программа подсчитает оптимальное
решение.

.2 Решение задачи на максимум прибыли

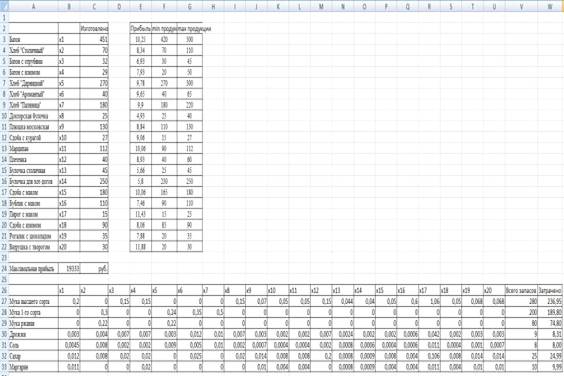
Максимальная прибыль составит 19 333 рублей.

В соответствии с оптимальным планом производства для достижения
максимальной прибыли следует производить следующее количество каждого из видов хлебобулочных
изделий (Таблица5):

Таблица 5 — Результаты расчетов

Наименование	Количество, шт.
Батон	451
Хлеб «Столичный»	70
Батон с отрубями	32
Батон с изюмом	29
Хлеб «Дарницкий»	270
Хлеб «Аромантый»	40
Хлеб «Паляница»	180
Докторская булочка	25
Плюшка московская	130
Сдоба с курагой	27
Марципан	112
Плетенка	40
Булочка столичная	45
Булочка для хот-догов	250
Сдоба с маком	180
Бублик с маком	110
Пирог с маком	15
Сдоба с изюмом	90
Рогалик с шоколадом	35
Ватрушка с творогом	30

При этом будет затрачено ингредиентов (Таблица 6):

Таблица 6 — Результаты расчетов

Ингредиенты	Используемое количество, кг.
Мука высшего сорта	236,95
Мука 1-го сорта	189,8
Мука ржаная	74,8
Дрожжи	8,31
Соль	8
Сахар	24,99
Маргарин	9,99

.3 Решение задачи на минимум себестоимости

экономический
математический модель оптимизация

Исходные данные:

Целевая функция примет следующий вид:

_ix_i→max,

где i=1, 2, …, n, ограничения остаются прежними.

Исходные данные выглядят таким образом.

Решение:

Как и в предыдущем пункте используем функцию «Поиск решения». вводим
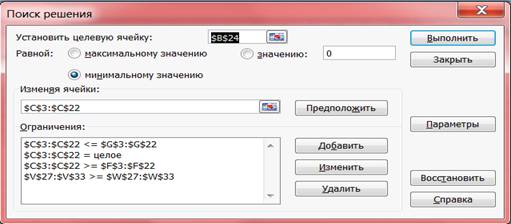
ограничения (рис. 2).

Рис. 2. Окно параметров поиска решения

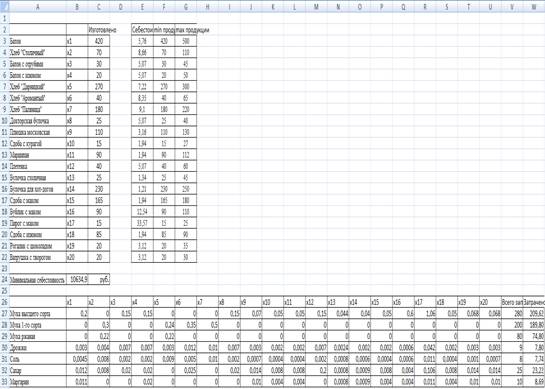
Повторяем алгоритм настройки окна параметров из п.3. Получаем решение. Из
приложения 4 мы видим, что при решение задачи на минимальную себестоимость,
затраты составят 10634,9 руб. При этом будет произведено следующее количество
каждого из видов хлебобулочных изделий (Таблица7):

Таблица 7 — Результаты расчетов

Наименование	Количество, шт.
Батон	420
Хлеб «Столичный»	70
Батон с отрубями	30
Батон с изюмом	20
Хлеб «Дарницкий»	270
Хлеб «Аромантый»	40
Хлеб «Паляница»	180
Докторская булочка	25
Плюшка московская	110
Сдоба с курагой	15
Марципан	90
Плетенка	40
Булочка столичная	25
Булочка для хот-догов	230
Сдоба с маком	165
Бублик с маком	90
Пирог с маком	15	85
Рогалик с шоколадом	20
Ватрушка с творогом	20

При этом будет затрачено ингредиентов (Таблица 8):

Таблица 8 — Результаты расчетов

Ингредиенты	Используемое количество, кг.
Мука высшего сорта	209,62
Мука 1-го сорта	189,80
Мука ржаная	74,80
Дрожжи	7,80
Соль	7,74
Сахар	23,22
Маргарин	8,69

.4 Анализ полученных данных

Посчитаем себестоимость для решения задачи на максимизацию прибыли, так же
посчитаем прибыль для задачи, решенной на минимум себестоимости.

Таблица 9 — Вспомогательная таблица

	Прибыль, руб	Себестоимость, руб
Решение 1	19 333	17 616,6
Решение 2	11 417	10634,9

Объединим результаты таблицы 5 и таблицы 7.

Таблица 9 — Результаты

Наименование	Количество произведенной продукции при расчете на max прибыли	Количество произведенной продукции при расчете на min себестоимости
Батон	451	420
Хлеб «Столичный»	70	70
Батон с отрубями	32	30
Батон с изюмом	29	20
Хлеб «Дарницкий»	270	270
Хлеб «Аромантый»	40	40
Хлеб «Паляница»	180	180
Докторская булочка	25	25
Плюшка московская	130	110
Сдоба с курагой	27	15
Марципан	112	90
Плетенка	40	40
Булочка столичная	45	25
Булочка для хот-догов	250	230
Сдоба с маком	180	165
Бублик с маком	110	90
Пирог с маком	15	15
Сдоба с изюмом	90	85
Рогалик с шоколадом	35	20
Ватрушка с творогом	30	20

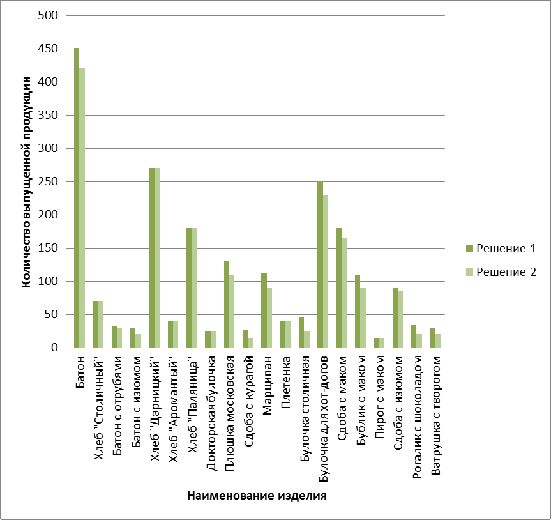
По данным таблицы 9 составляется диаграмма, на которой наглядно видно,
какой продукции выпущено больше, а какой меньше при разных интерпретациях задачи.

Заключение

Использование математики в экономической науке, дало толчок в развитии
как самой экономической науке, так и прикладной математике, в части методов
экономико-математической модели. Расчеты по моделям предостерегают от ошибок,
поскольку позволяют заранее оценить последствия каждого решения, исключить
недопустимые варианты и выбрать оптимальный вариант.

Практическими задачами экономико-математического моделирования являются,
во-первых, анализ экономических объектов; во-вторых, экономическое
прогнозирование, предвидение развития хозяйственных процессов и поведения
отдельных показателей; в-третьих, выработка управленческих решений на всех
уровнях управления.

Список использованных источников

1. Википедия
https://ru.wikipedia.org

. Тарасов В.
Л. Экономико-математические методы и модели. Учебное пособие. Нижний Новгород,
2003

. Иванилов Ю.
П., Лотов А.В. Математические модели в экономике. — М.: Наука, 2007.

. Гранберг А.
Г. Математические модели социалистической экономики. — М.: Экономика, 1988.

. Пинегина М.В. Математические методы и
модели в экономике. М.: Издательство «Экзамен», 2002 г.

. Шикин Е. В., Чхартишвили А.Г.
Математические методы и модели в управлении. М.: Издательство «Дело», серия
«Наука управления», 2000 г.

7. Солопахо
А. В. Математика в экономике. Учебно-практическое пособие. — Тамбов: Изд-во
Тамб. гос. техн. ун-та, 2001.

Приложения

Приложение 1

Исходные данные общей задачи линейного программирования на максимизацию
прибыли

Приложение 2

Оптимальное решение общей задачи линейного программирования на
максимизацию прибыли

Приложение 3

Исходные данные общей задачи линейного программирования на минимизацию
себестоимости

Приложение 4

Оптимальное решение общей задачи линейного программирования на
минимизацию себестоимости

Приложение 5

Сравнительная диаграмма

Mathematical modeling is now the basis of managerial decision-making in modern business, this article on the example of LLC «Zheldorservis» clearly presents theoretical as well as empirical evidence that mathematical modeling helps to solve and answer the above questions.

Keywords: method, economic model, Economics, economic processes.

В настоящее время предпринимательство в России активно развивается. И в условиях такой тенденции у предпринимателей часто возникают вопросы: «Как увеличить прибыль?», «Какие инструменты использовать?» «Как заполучить выигрышную позицию в сравнении с конкурентами?». В последнее время всё чаще для решения этих проблем используются математические модели. И появляются уже другие вопросы: «Как правильно строить математические модели», «Как их использовать?», «Как с их помощью можно получить конкурентное преимущество?». Математическое моделирование в настоящее время является основой принятия управленческих решений в современном бизнесе, в данной статье на примере компании ООО «Желдорсервис» наглядно представлено теоретическое, а также практическое доказательство того, что математическое моделирование помогает успешно решить и ответить на вышеупомянутые вопросы.

При помощи математического моделирования строятся различные модели, описывающие различные ситуации, включающие в себя данные о конкретном предприятии. Построение и использование этих моделей способствует принятию важных управленческих решений в различных сферах, в частности — в бизнесе. Все задачи имеют многовариантные решения, которые могут быть найдены с помощью составления и построения математических моделей.

 1.Математический инструментарий принятия решений компании ООО «Желдорсервис»

Данный инструментарий (экономико-математические модели и методы — ЭМММ) представляет собой логический системный подход к решению проблемы управления (рис. 1).

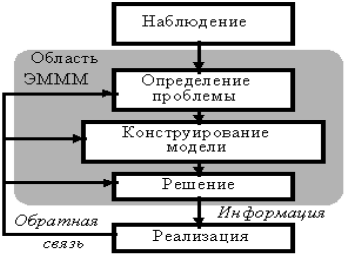
Рис. 1 Использование ЭМММ при принятии решения

 

Менеджер не прямо применяет полученный результат как решение, а сравнивает его со своими оценками и прогнозами. Если менеджер не использует результаты ЭМММ, то это означает, что они не могут быть реализованы. Если это так, то необходимо ввести дополнительные ресурсы или усилия при решении проблемы, конструировании модели и ее решении. Результаты моделирования и решения основываются на оригинальной модели, которая в процессе испытания в различных условиях, а также будущих решений менеджера, может быть изменена.

На практике в менеджменте наибольшее значение придается следующим моделям:

          сетевым;

          имитационным;

          теории очередей (задачам массового обслуживания);

          линейному программированию;

          графам (деревьям) решений;

          анализу замещения;

          интегральному программированию.

Математические модели используются при решении разного типа задач. Рассмотрим несколько примеров их использования в реальной деятельности компании ООО «Желдорсервис». Первое, что стоит отметить, изучают издержки фирмы на простейших математических моделях, которые строятся на линейной зависимости всех издержек от постоянных и переменных. В данном случае рассматривается таблица, которую предлагается заполнить, используя простые формулы.

 

Таблица 1

Исходные данные

Q	AFC	AVC	VC	AC	MC	TC
1					20
2				79
3			54
4		17
5	24					200

TC=VC+FC, AFC=FC/Q, AVC=VC/Q, AC=TC/Q, MC=(TC)’

Таблица 2

Решение задачи

Q	AFC	AVC	VC	AC	MC	TC
1	120	18	18	138	20	138
2	60	19	38	79	16	158
3	40	18	54	58	14	174
4	30	17	68	47	12	188
5	24	16	80	40	—	200

В результате человек, решающий данную задачу получает показатели, которые может иметь фирма, и в дальнейшем использовать их для определения оптимального выпуска и цены в различных рыночных условиях.

После того, как изучается взаимосвязь издержек, решается задача на определение оптимума фирмы. В бизнесе более вероятны ситуации, когда математическая модель может стать ключом к решению поставленной задачи, в частности, при определении антикризисной стратегии или способе осуществления конкурентной борьбы. Например, когда происходит «ценовая война». Фирмы или группа фирм устанавливают заниженные цены и работают в убыток для того, чтобы освободить пространство на рынке. Здесь модель чётко покажет, сколько может работать фирма в условиях такой борьбы, и даст прогноз, сколько смогут продержаться конкуренты.

 2. Использование математического инструментария в финансовой сфере компании ООО «Желдорсервис»

Математический инструментарий активно используется в финансовой сфере компании ООО «Желдорсервис». Для определения доходности компаний и инвестиционных портфелей в зависимости от различных факторов используются такие коэффициенты, как Альфа, Бета, Шарпа, Сортино и Треёнора. ООО «Желдорсервис» необходимо знать, насколько доходным будет тот или иной портфель. Кратко остановимся на этих ключевых показателях, используемых в работе компании.

Коэффициент альфа — параметр, с помощью которого можно точно оценить эффективность управления капиталом при учете рисковой составляющей. Коэффициент альфа отображает, насколько результаты работы на рынке зависят от качества торговой системы, а не от рыночных колебаний. Бета-коэффициент — показатель, рассчитываемый для портфеля ценных бумаг. Является мерой рыночного риска, отражая изменчивость доходности портфеля по отношению к доходности другого портфеля, в роли которого часто выступает среднерыночный портфель. Коэффициент Шарпа — показатель эффективности инвестиционного портфеля (актива), который вычисляется как отношение средней премии за риск к среднему отклонению портфеля. Другими словами, этот коэффициент показывает связь доходности портфеля и его волатильности. Коэффициент Сортино — представляет собой показатель, обуславливающий связь между изменчивостью портфеля и доходностью. Отличается он от коэффициента Шарпа тем, что при его расчёте используется так называемая «волатильность вниз». В этом случае волатильность рассчитывается по доходностям ниже минимального допустимого уровня доходности портфеля (MAR). Коэффициент Трейнора —отношение средней доходности, превышающей без рисковую процентную ставку, к систематическому риску β.

Данные показатели являются базовым инструментарием при определении доходности портфеля компании ООО «Желдорсервис». Само собой, каждый из них представляет собой математическую формулу с чётко определёнными переменными. С другой стороны, практически каждый из них имеет определённые ограничения, которые объясняют неточности всей модели в целом. Построение моделей помогает решить многие проблемы в бизнесе, если их рационально использовать в сочетании с другими математическими методами. Тем не менее, нужно всегда учитывать экономическую составляющую и понимать сущность экономических процессов. Из вышесказанного следует, что работать модели могут как в определённом конкретном случае, так и при решении общих задач, стоящих перед компанией.

 3. Этапы экономико-математического моделирования в компании ООО «Желдорсервис»

Под применением экономико-математических моделей подразумевается не просто выполнение разнообразных экономических расчетов, а использование математики в целях нахождения наиболее выгодных и удачных экономических решений, а также изучения экономических зависимостей и закономерностей, получения новых теоретических выводов.

Синтез инновационных экономических и математических знаний даёт новые возможности в сфере экономического анализа.

Рассмотрим содержание процесса экономико-математического моделирования поэтапно. Обычно выделяют шесть основных этапов:

1.                Определение и постановка экономической проблемы, ее рассмотрение и тщательный анализ
2.                Построение математической модели;
3.                Математический анализ построенной модели;
4.                Подготовка исходной информационной базы;
5.                Решение поставленной задачи в числах;
6.                Анализ, обработка и рассмотрение возможных вариантов применения полученных числовых результатов,

Рассмотрим этапы процесса экономико-математического моделирования более развернуто и в примерах.

1.                На этом этапе происходит четкое формулирование сути проблемы, принимаемые допущения, а также происходит четкая постановка вопросов, на которые необходимо будет найти ответы. Этот этап подразумевает выделение важнейших черт и свойств объекта моделирования, второстепенные черты уходят на второй план. Тщательно изучается структура объекта, взаимосвязь составляющих его элементов, также обычно формулируется предварительная гипотеза, разъясняющая характер поведения и развития объекта.
2.                Построение математической модели означает представление нашей поставленной экономической проблемы в виде определенных математических зависимостей и отношений: уравнений, неравенств, функций. Как в любой модели, сначала строится каркас- основная типовая конструкция, затем каркас совершенствуется при помощи добавления деталей и параметров. Неправильно полагать, что чем больше фактов учитывает модель, тем она лучше «работает» и дает лучшие результаты. То же можно сказать о таких характеристиках сложности модели, как используемые формы математических зависимостей (линейные и нелинейные), учет факторов случайности т неопределенности и т. д. Положение о том, что, чем сложнее модель, тем она лучше, является ошибочным. Громоздкость и ёмкость модели затрудняют процесс исследования.

Если планируется усложнить модель, с целью сделать ее более точной и подробной, нужно помнить и справедливо оценивать, будут ли соответствовать затраченные силы на вычисления точности прогнозируемых результатов. И обратно, если принято решение исключить какой-либо элемент из модели, чтобы упростить модель, необходимо оценить вероятные потери в ее достоверности.

1.                На этом этапе в основном применяются математические приемы исследования.

Одна из наиболее важных задач на этапе — доказательство возможности существования решений в сформулированной модели. Если доказано, что поставленная математическая задача не имеет решения, то автоматически исчезает смысл дальнейшей работы по первоначальному варианту модели, а значит, следует скорректировать либо саму постановку экономической задачи, либо способы ее точного математического представления — формализации. Аналитической исследование модели имеет одно преимущество по отношению к численному (эмпирическому): выводы, которые мы получаем сохраняют своё значение при подстановке различных конкретных значений внешних и внутренних параметров модели, то есть мы имеем своеобразный шаблон.

1.      Моделирование ставит жесткие требования к систематизированию исходной информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования. В случае, если нам недостаточно одной лишь подготовки определенной информации, а необходимы дополнительные затраты на подготовку иных информационных массивов, нужно помнить, что такие затраты не должны превышать получаемый эффект от использования дополнительной информации. В процессе подготовки информационной базы часто и широко используются методы теории вероятностей, а также теоретической и математической статистики. При системном экономико-математическом моделировании информационные потоки взаимосвязаны друг с другом: выходные результаты функционирования одних моделей являются исходной информацией, используемой в других моделях.
2.      Непосредственный этап численного решения задачи. Разработка алгоритмов, составление программ на ЭВМ и само проведение расчетов. Сложности на этом этапе могут возникать ввиду большого объема решаемых экономических задач и информационных массивов для обработки. Непосредственное исследование в числах может значительно дополнить результаты аналитического исследования, а для многих моделей оно даже является единственно осуществимым. Количество задач, которые доступны к решению численными методами, значительно больше, чем количество задач, которые могут быть подвержены аналитическому исследованию.
3.      На этом заключительном этапе цикла основным и самым важным является вопрос о правильности и полноте полученных результатов моделирования, а также о возможности реального практического применения этих результатов. Неформальный, обычно человеческий анализ теоретических выводов и численных результатов, которые были получены на выходе из модели, сопоставление их с имеющимися знаниями, информационными массивами и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели, а также ее информационного и математического обеспечения.

 4. Пример применения простейшей двухпродуктовой балансовой экономико-математической модели ООО «Желдорсервис»

Пусть производится два товара, один — в количестве x1 и другой — в количестве x2 (измеряются в одинаковых единицах). На производство первого товара тратится 0,1 общего выпуска этого же товара и 0,15 единиц второго товара. Кроме того, 3300 единиц первого товара производится на другие нужды. На производство единицы второго товара затрачивается 0,2 единицы первого товара и 0,05 единиц второго товара. Кроме того, 6600 единиц второго товара производится на другие нужды. Задача: определить требуемые объемы производства одного и второго товара (m1 и m2)

Двухпродуктовая балансовая модель выглядит следующим образом:

m1 — объем производства первого товара;

m2 — объем производства второго товара;

b11 — доля первого товара, затрачиваемая на его же производство;

b12 — доля первого товара, затрачиваемая на производство второго;

b21 — доля второго товара, затрачиваемая на производство первого;

b22 — доля второго товара, затрачиваемая на его же производство;

m1v — объем производства первого товара на другие нужды;

m2v — объем производства второго товара на другие нужды.

Приводимая простейшая балансовая модель представляет систему двух линейных уравнений относительно неизвестных m1 и m2.

Согласно условиям задачи: b11== 0,1; b12 = 0,15; b21 = 0,2; b22 = 0,05; m1v =3300; m2v = 6600.

В итоге приходим к системе уравнений баланса:

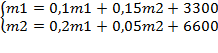
Решаем систему, находим искомые объемы производства: m1 = 5000 единиц; m2 = 8000 единиц. Исходную модель можно использовать для поиска любых элементов системы при заданных значениям других величин, включенных в систему.

 4. Экономико-математическая модель на примере задачи планирования производства ООО «Желдорсервис»

Таблица 3

Данные задачи по планированию производства

Виды сырья	Запасы сырья	Количество единиц сырья, затрачиваемых на изготовление единицы продукции
P1	P2
S1 S2 S3	b1 b2 b3	a11 a21 a31	a12 a22 a32
Прибыль от единицы продукции (в руб.)	с1	c2

Для изготовления двух видов продуктовP1 и P2 используют три вида сырья: S1, S2 и S3. В таблице представлены запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции и величина прибыли, получаемая от единицы продукции.

Задача: составить план выпуска продукции, чтобы получать максимально возможную прибыль при реализации.

Далее переходим к составлению экономико-математической модели задачи.

Пусть x1, x2 — количество единиц продукции P1 и P2 соответственно, запланированных к производству. Тогда учитывая количество единиц сырья, которые затрачиваются на изготовление единицы продукции, а также запасы сырья получают систему неравенств.

Суммарная прибыль F(x) составит c1x1 руб. от реализации продукции P1 и c2x2 руб. — от реализации продукции P2, т. е.

F(x)=c1x1+c2x2

Итого получаем экономико-математическую модель задачи: найти такой план выпуска продукции X=(x1,x2), удовлетворяющий системе неравенств и условию x1>=0; x2>=0, при котором функция F(x) будет принимать максимальное значение.

Задачу легко обобщить, если будет выпускаться n видов продукции с использованием m видов сырья.

 5. Актуальность применения экономико-математического моделирования

Экономико-математическое моделирование в настоящее время является неотъемлемой частью любого исследования в области экономики. Активное развитие математического анализа, исследования и анализа операций, теории вероятностей и математической статистики повлияло на развитие формирования разнообразных моделей экономики.

В течение последних 30–40 лет методы моделирования в экономике разрабатывались особенно прогрессивно. В основном создание и развитие этих методов было предназначено для достижения теоретических целей экономического анализа и для реализации практических целей структурного планирования, прогноза и управления.

Объединяя в себе основные процессы, экономические модели по содержанию включают в себя: производство, планирование, управление, финансы и т. д. Однако в каждой из соответствующих моделей упор всегда делается на какой-нибудь один процесс, в то время как все остальные включены туда в сокращенном упрощенном виде.

Применение экономико-математических моделей в настоящее время является очень актуальнымпри решении экономических задач. Тему делает актуальным то, что применение математических методов существенно увеличивает и преумножает возможности экономического анализа, позволяет определить новые постановки экономических задач, повышает выгоду принимаемых управленческих решений.

Экономические задачи, которые решаются в процессе этапа финансового анализа, планирования, проектирования и напрямую направлены на определение искомых неизвестных величин на основе известных входных данных, не всегда удается свести лишь к расчетам, в отличие от математических задач. Решение экономических задач сопровождается поиском необходимых недостающих данных, экспертным обсуждением и оцениванием, принятием дополнительных решений.

Актуальность применения экономико-математических моделей также подтверждается тем, что они используются не только в рамках производства и с точки зрения глобальной экономики, но и всеми нами в повседневной жизни. Кроме того, каждый человек старается максимально выгодно для себя использовать имеющуюся у него «информационную базу», качественно спланировать свои действия, иначе: смоделировать своё поведение. Простой пример: модель планирования и распределения семейного бюджета.

Экономико-математические методы тесно взаимодействуют и напрямую связаны с инновационной сферой, и, разумеется, применимы не только для отдельных индивидов, но и для общества в целом.

В экономической и управленческой сфере деятельности экономико-математические методы являются одним из важнейших «помощников», позволяющих принимать верные, выгодные разумные решения.

Впрочем, далеко не во всех случаях данные, полученные на выходе из экономико-математических моделей, могут использоваться непосредственно как готовые управленческие решения. Чаще всего они лишь являются вспомогательными, консультирующими средствами, принятие же непосредственно управленческих решений остается за человеком. Экономические и социально-экономические процессы очень сложны. Экономико-математические модели являются лишь вспомогательными элементами в сложном процессе взаимодействия вычислительных машин и человека, планирования и управления.

Применение экономико-математических методов в различных областях однозначно можно считать эффективным потому, что экономические объекты, как микро-, так и макроуровней можно рассматривать с точки зрения системного подхода. Кроме того, присутствие таких характеристик поведения экономических систем, как: динамичность, противоречивость и неоднозначность поведения, тенденция к ухудшению, подверженность воздействию внешних факторов предопределяет выбор метода их исследования.

В современном бизнесе всё чаще используются математические средства для определения оптимальной стратегии поведения фирмы. Моделирование может использоваться во многих целях, например: определение антикризисной стратегии — математически определяется поведение фирмы в резко меняющихся условиях, причём не только при резком или затяжном спаде, но и на подъёме экономической конъюнктуры; конкурирование с другими фирмами — высчитывается оптимальная стратегия взаимодействия с конкурентами на рынке; расширение производства на своём рынке — этот процесс необходимо планировать и моделировать так же точно, как предыдущие, так как при принятии управленческих решений в этом случае существует риск не просто провалить поставленную задачу, но и принести огромные убытки фирме; по аналогии — сокращение производства; выход на рынки других продуктов или на международную торговлю — при принятии такого решения фирма должна быть уверена, что это не будет стоить больше, чем может принести, для чего и будет строиться множество математических моделей для прогнозирования последствий осуществления таких задач.

В настоящее время идет поиск новых математических понятий и методов, которые будут полезны для построения и исследования, как единичных моделей, так и их систем. Системы представляют собой сложные комплексы с переменной структурой, изменчивым характером, содержащие недостаточную и не полностью формализованную информацию. Все это делает математико-статистическое моделирование, машинную имитацию всё более влиятельными и используемыми разделами математики в современной экономике.

Изучение математических дисциплин и методов, которые составляют основу современного аппарата моделирования в экономике, позволит специалистам в будущем сформировать необходимые составляющие мышления — уровень, кругозор и культуру, которые понадобятся профессионала своего дела, как для успешной работы, так и для совершенствования знаний и повышения своей квалификации. Обосновано, что применение экономико-математических методов позволяет значительно повысить качество и выгоду принимаемых решений. 

Литература:

1.      http://www.dginh.ru/content/glavnay/ucheb_deyatel/uposob/up-fgos-14–15-pmit-15.pdf
2.      Баканов М. И., Мельник М. В., Шеремет А. Д. Теория экономического анализа. — М.: Финансы и статистика, 2005,
3.      Лотов А. В. Введение в экономико-математическое моделирование. — М.:Наука, 2008.
4.      http://www.imf.org/external/pubs/ft/fandd/basics/models.htm
5.      http://bibliofond.ru/view.aspx?id=560479
6.      http://economic_mathematics.academic.ru/5085
7.      http://www.grandars.ru/student/vysshaya-matematika/ekonomiko-matematicheskaya-model.html
8.      http://www.math.mrsu.ru/text/courses/method/primer_linprog_zad.htm
9.      Годин В. В. Информационное обеспечение управленческой деятельности / В.ВГодин, И. К. Корнеев. — М.: Мастерство, Высшая школа, 2001;
10. Менеджмент: учебник / Э. М. Коротков. — М.: Издательство Юрайт, 2010, — 640 с. — (Университеты России);
11. Прохоров А. П. Русская модель управления. — М.: Эксмо, 2006;
12. http://www.unn.ru/books/met_files/EconMatMetMod.pdf

Несмотря
на большое разнообразие математических
моделей, существуют важнейшие элементы,
которые присутствуют практически во
всех моделях.

Все
факторы, входящие в описание операции,
можно разделить на две группы:

— постоянные факторы
(условия проведения операции), на которые
мы влиять не можем. Обозначим их

,


,
…;

—
зависимые факторы (элементы решения)


,


,
…; оперирующая сторона может выбирать
их по своему усмотрению, учитывая
определенные ограничения.

Для
применения количественных методов
исследования требуется построить
математическую модель операции. Модель
операции – это достаточно точное
описание операции с помощью математического
аппарата (различного рода функций,
уравнений, систем уравнений и неравенств
и др.)

Эффективность
операции, то есть степень соответствия
хода операции поставленной цели,
количественно выражается в виде критерия
эффективности, который представляет
собой некоторую целевую функцию,
зависящую от определенного набора
факторов. В математической модели
эквивалентом цели операции является
требование оптимизации (максимизации
или минимизации) целевой функции.

Оптимизационную
задачу можно сформулировать в общем
виде:

Найти
переменные

,

,
…
,
удовлетворяющие системе неравенств
(уравнений)

и
обращающие в максимум (или минимум)
целевую функцию

,

условия
неотрицательности переменных, входят
в систему ограничений.

С
целью иллюстрации основных понятий
исследования операций и составляющих
элементов математических моделей
рассмотрим несколько простых примеров
построения моделей для содержательных
задач.

Для
построения математической модели
конкретной задачи рекомендуется
выполнить следующую последовательность
работ:

1.     
изучение условия задачи,

2.     
определение важнейших факторов,

3.     
выделение известных и неизвестных
факторов,

4.     
выявление постоянных и зависимых
факторов,

5.     
дополнение условия задачи недостающими
сведениями,

6.     
введение системы обозначений,

7.     
составление математической модели
(математическое описание важнейших
факторов, соотношений и связей между
параметрами).

Пример 1.
Планирование суточного выпуска продукции
– задача об использовании ресурсов

Процесс
изготовления изделий двух видов состоит
в последовательной обработке каждого
из них на трех станках. Известны время
эксплуатации станка в сутки, время
обработки каждого изделия на каждом
станке, стоимость реализации единицы
каждого изделия.

Требуется
составить для фирмы план суточного
выпуска изделий так, чтобы доход от их
продажи был максимальным.

Решение:

На
основании сведений, указанных в условии
задачи, имеем:

—       
оперирующая сторона – фирма,

—       
цель – максимизация дохода от
продажи выпущенных за сутки изделий
двух видов,

—       
зависимые факторы: принятие решения
состоит в определении суточных объемов
выпуска каждого из двух видов изделий,

—       
ограничения: возможности ограничены
временными ресурсами эксплуатации
станков трех видов.

После
выявления важнейших факторов нужно
анализировать все параметры задачи:
значение каких параметров известно
(задано), какие параметры являются
неизвестными (искомыми) величинами,
какие из параметров являются постоянными
и какие зависимыми факторами.

В
нашем примере известными являются
следующие параметры:

—       
суточная норма

 эксплуатации
станка j, j=1,2,3,

—       
время

 обработки
единицы изделия вида i
(i=1,2) на станке типа j,
(j=1,2,3),

—       
стоимость

 продажи
единицы продукции вида i
(i=1,2).

Все
эти параметры являются постоянными.

Неизвестными
(искомыми) являются величины:

—       
объем

 суточного
выпуска изделия вида i
(i=1,2).

Эти
параметры считаем зависимыми, так как
фирма сама определяет их величину
(исходя из реальных условий). По смыслу
задачи

.

Тогда
доход F от продажи составит


 от
реализации изделия вида 1 и

 от
реализации изделия вида 2, то есть

.

Время,
необходимое для обработки

 единиц
изделий на станке j,
равняется величине

,

Теперь
первоначальную задачу можно сформулировать
математически:

.                                       
(4.1)

                                       
(4.2)

Экономико-математическая
модель данной задачи формулируется в
следующем виде: Найти план

 выпуска
изделий, удовлетворяющий системе (4.2),
при котором функция (4.1) принимает
максимальное значение.

Рассмотрим
примеры экономико-математических
моделей некоторых известных задач.

Пример
2. Задача составления рациона (задача
о диете, задача о смесях).

Имеется
два вида крома I и II,
содержащие питательные вещества
(витамины) S₁ , S₂
, S₃. Содержание числа
единиц питательных веществ в 1 кг каждого
вида корма и необходимый минимум
питательных веществ приведены в следующей
таблице.

Питательное вещество (витамин)	Необходимый минимум питательных веществ	Число единиц питательных веществ в 1 кг корма
I	II
S1	9	3	1
S2	8	1	2
S3	12	1	6

Стоимость
1 кг корма I и II
соответственно равна 4 и 6 рублей.

Необходимо
составить дневной рацион, имеющий
минимальную стоимость, в котором
содержание каждого вида питательных
веществ было бы не менее установленного
предела.

Экономико-математическая
модель задачи имеет вид:

Составить
дневной рацион Х=(х₁,х₂),
удовлетворяющий следующей системе:

и
условию

х₁  0, х₂
 0,

при
котором функция F

F=4х₁ +6х₂

принимает
минимальное значение.

Пример
3. Задача об использовании мощностей
(задача о загрузке)

Предприятию
задан план производства продукции:
требуется за время T
выпустить n₁, n₂,…,
n_k
единиц продукции P₁,
P₂,…, P_k.
Продукция производится на станках S₁,
S₂,…, S_k.
Для каждого станка известны
производительность a_ij
(то есть число единиц продукции P_j,
которое можно произвести на станке S_i)
и затраты b_ij
на изготовление продукции P_j
на станке S_i
в единицу времени.

Необходимо
составить такой план работы станков
(то есть так распределить выпуск продукции
между станками), чтобы затраты на
производство всей продукции были
минимальными.

Обозначим
x_ij –
время, в течение которого на станке S_i
будут изготовлять продукцию P_j
.

Экономико-математическая
модель задачи имеет вид:

Найти
такое решение Х=(x₁₁,x₁₂,…,x_mk),
удовлетворяющее следующим системам:

и
условию

x_ij0,
i=1,2,…,m;
j=1,2,…,k

при
котором функция F

F = b₁₁x₁₁
+ b₁₂x₁₂
+ …+ b_mkx_mk

принимает
минимальное значение.

Пример
4. Задача о раскрое материалов.

На
раскрой поступает материал одного
образца в количестве а единиц.
Требуется изготовить из него l
разных комплектующих изделий в
количествах, пропорциональным числам
b₁, b₂,
b_l (условие
комплектности). Каждая единица материала
может быть раскроена n
различными способами, причем использование
i-того способа
(i=1,2,…,n) дает a_ik
единиц k-того изделия
(k=1,2,…,l).

Необходимо
найти план раскроя, обеспечивающий
максимальное число комплектов.

Обозначим
x_i –
число единиц материала, раскраиваемых
i-тым способом, и х
– число изготавливаемых комплектов
изделий.

Экономико
математическая модель задачи имеет
вид:

Найти
такое решение Х=(x₁₁,x₁₂,…,x_nm),
удовлетворяющее следующей системе:

и условию x_ij

0,

при
котором функция F =
x принимает
максимальное значение.

Приведенные
выше задачи являются задачами
математического программирования,
точнее — задачами линейного программирования
с целевой функцией F и
множеством допустимых решений, которое
описывается системой неравенств.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

  13.04.201529.06 Mб33Matlab7NaiboleePolnoeRukovodstvo.djvu

• #
• #