Как составить магический квадрат по математике 4 класс

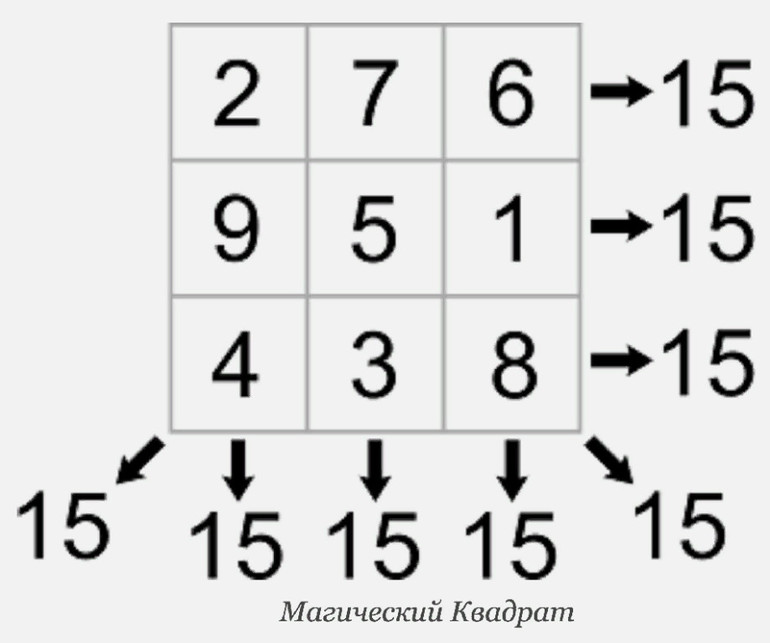
Магическая константа M — сумма чисел в каждой строке, столбце и на диагоналях.

Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:

M = n(n² + 1)/2

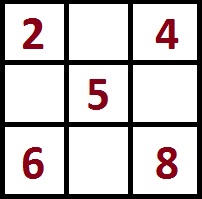
I. Магический квадрат 3×3

Для квадрата размера 3×3 минимально возможная магическая константа будет равна:

3(3² + 1)/2 = 3(9 + 1)/2 = 15

Подчеркнём, что 15 — это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.

Важное правило, которое вам пригодится при построении магического квадрата 3×3:

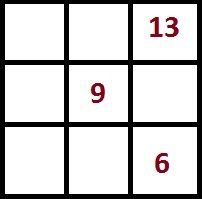
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.

То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять

15:3 = 5.

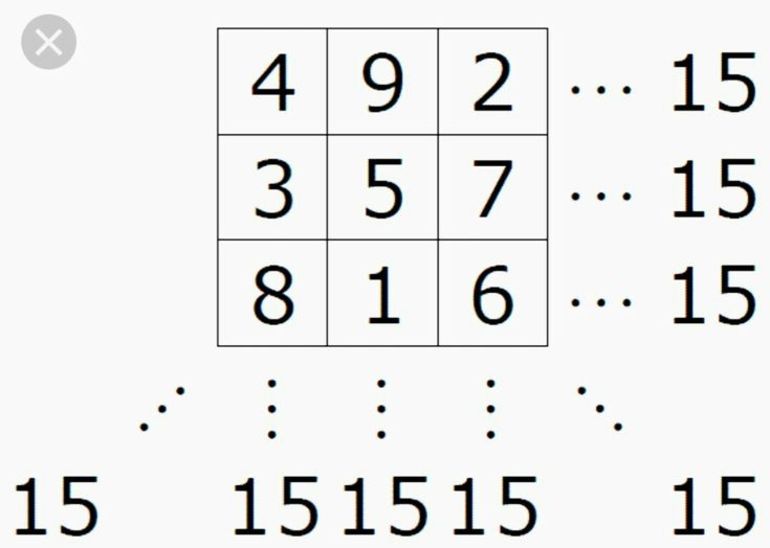
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.

Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто — надо из магической константы вычесть два числа из ряда или столбца.

Применив этот метод, мы получим полностью заполненный магический квадрат:

Ещё одно важное правило построения магических квадратов:

Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.

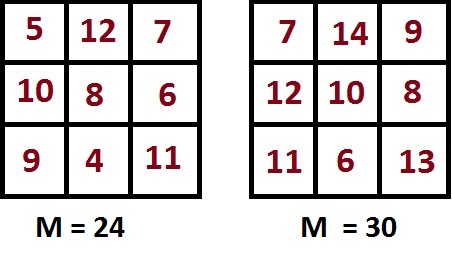
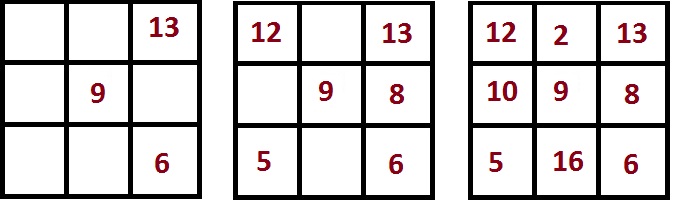
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5

Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.

У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).

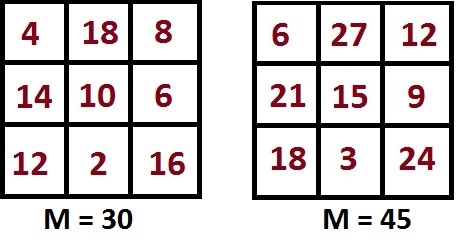
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3

Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 — та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные — а вот число в центральном квадрате одно и то же — это 10.

Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.

Задача 1.

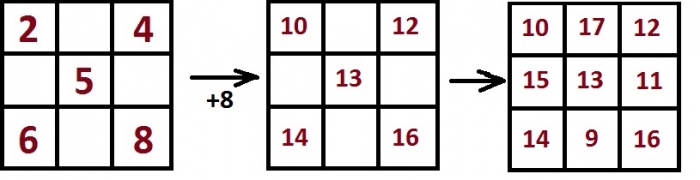
Постройте магический квадрат с магической константой 39.

Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке — нужно магическую константу разделить на 3. 39:3 = 13.

Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Напомним этот квадрат:

В центре этого квадрата — число 5. В центре того квадрата, который мы должны построить — число 13.

Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.

Достаточно запомнить, что в центре минимального магического квадрата — 5, а по углам — чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).

В итоге получится вот такой квадрат:

Задача 2.

Достройте магический квадрат

В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.

Решение:

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

II. Магический квадрат 4×4

Мы не будем подробно останавливаться на магических квадратах 4×4 — они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.

Минимально возможная магическая константа вычисляется всё по той же формуле:

M = n(n² + 1)/2

M = 4(4² + 1)/2 = 34.

У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.

Однако, у этого квадрата есть другие закономерности:

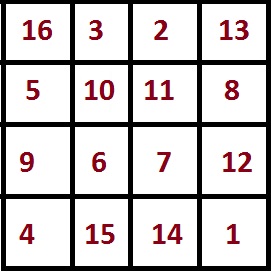
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.

Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.

Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.

Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34

История

Археологи нашли свидетельства того, что волшебные таблицы были известны еще древним грекам и китайцам. «Магическими» эти фигуры назвали арабы, которые наделяли их сверхъестественными защитными свойствами.

В середине XVI в. европейские математики занялись исследованиями загадочных таблиц, положив начало их новой жизни. Они искали общий метод построения магических квадратов и пытались описать все возможные их варианты.

На уроках математики в школе

Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Дети учатся планировать и контролировать свою работу. В клетки магических квадратов можно записывать не только числа, но и выражения. Все зависит от изучаемой темы. Задания с магическими квадратами часто дают как дополнительные или олимпиадные уже в начальной школе.

Один из способов решения магического квадрата

Нетрудно решить магический квадрат третьего порядка (у которого по три столбца и строки). Можно воспользоваться тем фактом, что число (выражение), стоящее на пересечении его диагоналей, всегда равно ⅓ волшебной суммы. Отсюда следует алгоритм построения:

1. Вписываем  в первую строку или столбец 3 любых числа.

1. Вычисляем магическую сумму (0 + 2 + 4 = 6).
2. Ищем ее третью часть (6/3 = 2).
3. Полученное число записываем на пересечении диагоналей.

1. Подбираем остальные числа и заполняем ими пустые клеточки квадрата.

Как рассчитать магический квадрат Пифагора самому?

Пифагор — математик, заложивший основы нумерологии. Ученый верил, что миром правят числа. Даже человеческая сущность зависит от них, ведь дата рождения не что иное, как число.

Магический квадрат Пифагора — фигура третьего порядка, клетки которой заполнены числами от 1 до 9. Он делится на 3 уровня: материальный, души и разума.

Цифры даты рождения вписываются в определенном порядке. Полученная комбинация рассказывает о заложенных природой способностях человека.

Материал может быть использован на занятии математического кружка, на внеклассном мероприятии. Цель — развить и расширить познавательный кругозор и логическое мышление.

Решаем магический квадрат Пифагора: пример

Дата рождения: 17.09.2005 г. Складываем эти цифры, не учитывая нули: 1 + 7 + 9 + 2 + 5 = 24. Аналогично поступаем с цифрами результата: 2 + 4 = 6.

Из первой суммы вычитаем удвоенную первую цифру дня рождения: 24 -2 = 22. Снова складываем: 2 + 2 = 4. Полученные числа: 17; 9; 25; 24; 6; 22; 4.

Цифры вписываем в магический квадрат так, чтобы все единицы оказались в первой клеточке, двойки — во второй и так далее. Нули не учитываем.

Результат:

Значение:

Задачи на составление магических квадратов часто включаются в сборники нестандартных заданий. Они встречаются на олимпиадах. Увлеченным математикой школьникам будет полезно узнать об этом классе задач. 

Об авторе: Филиппова Оксана, учитель математики, физики и информатики.

Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Квадрат нечётного порядка

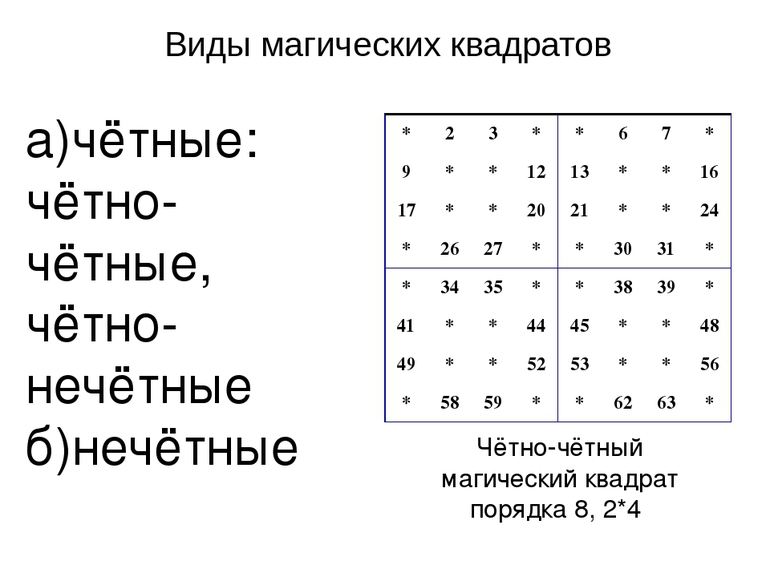
Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

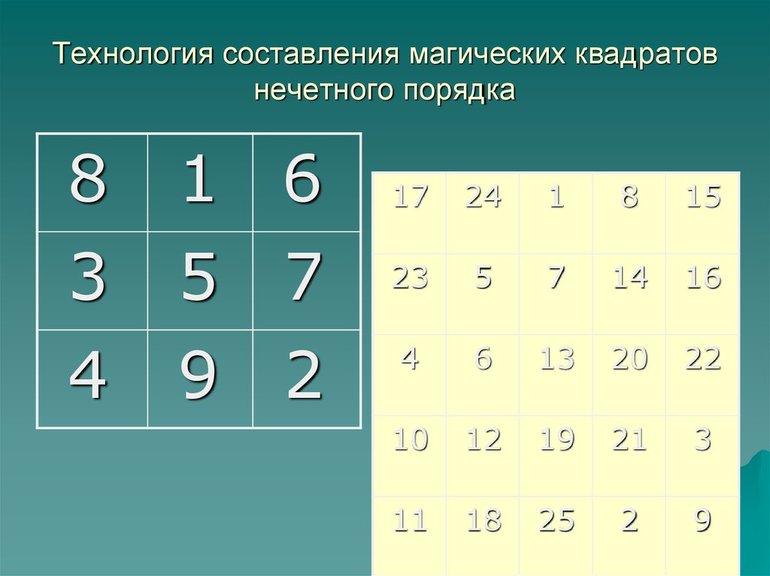
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.

Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.

Вычисление магической константы

Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.

Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.

Дальнейшие действия

Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.

Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.

Алгоритм действий:

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.

Двойной порядок

Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.

Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:

Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.

Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:

По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.

Предыдущая

МатематикаАлгоритм Евклида — формулы, правила и примеры решения задач

Следующая

МатематикаМинор матрицы — способы, порядок и примеры вычисления

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Квадрат нечётного порядка

Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

1. Подсчитывается сумма, которая должна получиться в каждой строке. Для этого используется формула: 3 * (32 +1) / 2 = 3 * 10 / 2. Ответом будет число 15.
2. Числа в ячейках расставляются так, чтобы сумма их была равна 15 в каждой строчке. Это требует смекалки и воображения.
3. В средней клетке верхней строки вписывается 1.
4. Каждое следующее число ставится справа по диагонали вверх. Поставить цифру 2 нельзя, так как выше нет строк. Если мысленно добавить сверху ещё один квадрат, цифра 2 окажется в его нижнем правом углу. Значит, цифра 2 вписывается в нижнюю правую клетку.
5. По тому же принципу вписывается цифра 3. Она попадает в среднюю ячейку слева.
6. Если нужная клетка уже занята, очередной символ вписывается ниже предыдущего. Таким образом, 4 ставится под 3.
7. Записывается цифра 5 по диагонали вправо и вверх, а 6 в верхний угол справа.
8. Поскольку место цифры 7 уже занято, она вписывается ниже 6.
9. Восьмёрка занимает место в левом нижнем углу.
10. Оставшуюся клетку занимает девятка.

Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.

Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.

Вычисление магической константы

Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.

Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.

Дальнейшие действия

Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.

Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

1. Минимальное число, которым начинается заполнение ячеек, всегда ставится в верхнем ряду посередине. У каждой части эта ячейка находится отдельно.
2. Каждая часть заполняется как новый математический объект. Даже если есть пустое место в другом квадрате, его в этих случаях игнорируют.

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.

Алгоритм действий:

1. Начинать нужно с крайней левой клетки в верхней строке. Если фигура имеет размеры 6х6, выделяется только первая верхняя строка части А. В ней должно быть вписано число 8. Если величина таблицы составляет 10х10, выделяют 2 первые клетки в верхнем ряду. В них стоят 17 и 24.
2. Из выделенных клеток формируется промежуточный квадрат. В таблице с количеством строк и столбцов 6х6 он будет состоять из 1 клетки. Его условно обозначают А1.
3. Если размер 10х10, в верхней строке выделяется 2 первые ячейки. Вместе с ними выделяется ещё 2 клетки, во второй строке получается поле из 4 прилежащих друг к другу ячеек.
4. В следующей строке первая ячейка пропускается, затем выделяется столько клеток, сколько было в промежуточной таблице А1. Полученную фигуру можно обозначить А2.
5. Таким же способом строят промежуточный квадрат А3.
6. Эти 3 промежуточных фигуры формируют выделенную область А.
7. Далее переходят в квадрант D и формируют обособленную область D.

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.

Двойной порядок

Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.

Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:

1. Если длина стороны составляет 4 ячейки, промежуточные зоны будут иметь по 1 клетке.
2. В таблице 8х8 эти области включают 4 элемента (2х2).
3. В квадрате 12х12 выделяются промежуточные фигуры размером 3х3.

Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.

Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:

1. В первой сверху строке и первом слева столбце пишется 1. В верхней клетке четвертого столбика — 4.
2. В центр второй горизонтальной строчки ставятся цифры 6 и 7.
3. В четвёртой строке слева пишется 13, а справа — 16.

По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.

История появления магических
квадратов.

     
В давние времена, научившись считать и выполнять арифметические действия, люди
с удивление обнаружили, что числа имеют самостоятельную жизнь, удивительную и
таинственную.

     Китайский император Ню, живший 4 тысячи лет
назад,  однажды  гулял по берегу реки. И вдруг увидел черепаху. На её панцире
был изображён рисунок из белых и чёрных кружков.

« Да, она священна!», — воскликнул он.

Если заменить каждую фигуру числом, показывающим,
сколько в ней кружков, получится такая таблица.

(Сумма чисел строк равна сумме чисел столбцов, равна
сумме чисел диагоналей и равна 15.)

     Сейчас любую квадратную таблицу, составленную из
чисел и обладающую таким свойством, называют магическим квадратом.

Определение магического квадрата.

    
Магический квадрат — квадратная таблица из целых чисел, в которой суммы чисел
вдоль любой строки, любого столбца и любой из двух главных диагоналей равны
одному и тому же числу.

     Наверное, эту легенду китайцы придумали, когда
нашли расположение чисел от 1 до 9 со столь замечательным свойством. Рисунок
они назвали «ло-шу» и стали считать его магическим символом.  Первое
специальное упоминание о таком квадрате найдено около 1 века до н.э. Вплоть до
10 века н.э. магические квадраты были воплощены в амулетах, заклинаниях.
Они  использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах
удачи, медицинских кружках. До сих пор они используются у некоторых восточных
народов как талисман.

    Полного описания всех возможных магических
квадратов не получено и до сего времени. Магических квадратов 2*2 не
существует. Существует единственный магический квадрат 3_*3, так как
остальные магические квадраты 3_*3 получаются из него либо
перестановкой строк (рис. 4а) или столбцов (рис. 4б) либо путем поворота
исходного квадрата на 90⁰ (рис. 4в) или на 180⁰ (рис 4г).

      
а                                   б                                       в              
              г

     В IX веке интерес к магическим квадратам вспыхнул
с новой силой. Получение магических квадратов считалось популярным развлечением
среди математиков. Ими создавались огромные квадраты, например, 45*45,
содержащий числа от 1 до 2025, Были придуманы способы построения магических
квадратов любого размера.

          В XIII веке математик Ян Хэй занялся
проблемой методов построения магических квадратов. Его исследования были, потом
продолжены другими китайскими математиками. Из Китая магические квадраты распространились
сначала в Индию, а затем и в другие страны.

      Редкостью является
использование магического квадрата в изобразительном искусстве, а не в научном
или литературном произведении.  Впервые это сделал немецкий художник Альбрехт
Дюрер (1471 – 1528), выпустивший в гравюру «Меланхолия», на которой есть
изображение магического квадрата четвёртого порядка. Причем два числа в
середине нижней строки  указывают на год создания гравюры – 1514.Этот факт
говорит об умении в то время составлять магические квадраты с определённым
заданным расположением некоторых чисел. Говорят, что гравюра А.Дюрера послужила
толчком для знаменитых пророчеств его современника Мишеля Нострадамуса
(1503-1566).

Применение магических квадратов .

Традиционной сферой
применения магических квадратов являются талисманы. К примеру, талисман Луны
обладает определенными свойствами: предохраняет от кораблекрушения и болезней,
делает человека любезным, способствует предотвращению дурного намерения, а так
же укрепляет здоровье. Его гравируют на серебре в день и час Луны, когда Солнце
или Луна находится в первых десяти градусах Рака. Магический квадрат 9-ого
порядка вписывается в девятиугольник (9 — число Луны, см. ниже) и окружается
специальными символами.

    
В наши дни магические квадраты  можно встретить на палубах больших пассажирских
судов как площадку для игры. Известная головоломка – пазл с числами — судоку,
появившаяся примерно 30 лет назад и популярная во многих странах мира, тоже
содержит магические квадраты.

    
За последнее столетие  значительно возросло число книг по занимательной
математике, в которых содержатся головоломки и задачки, связанные с необычными
квадратами. В наше время магические квадраты продолжают привлекать к себе
внимание не только специалистов, но и любителей математических игр и
развлечений.