Как составить магический квадрат 3х3 2 класс

Магическая константа M — сумма чисел в каждой строке, столбце и на диагоналях.

Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:

M = n(n² + 1)/2

I. Магический квадрат 3×3

Для квадрата размера 3×3 минимально возможная магическая константа будет равна:

3(3² + 1)/2 = 3(9 + 1)/2 = 15

Подчеркнём, что 15 — это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.

Важное правило, которое вам пригодится при построении магического квадрата 3×3:

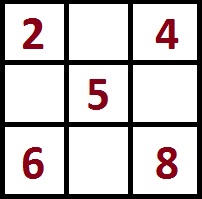
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.

То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять

15:3 = 5.

Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.

Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто — надо из магической константы вычесть два числа из ряда или столбца.

Применив этот метод, мы получим полностью заполненный магический квадрат:

Ещё одно важное правило построения магических квадратов:

Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.

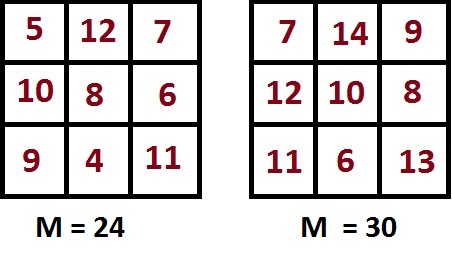
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5

Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.

У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).

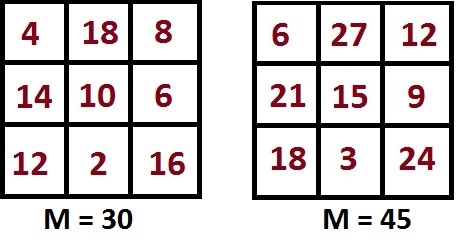
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3

Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 — та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные — а вот число в центральном квадрате одно и то же — это 10.

Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.

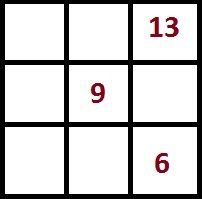
Задача 1.

Постройте магический квадрат с магической константой 39.

Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке — нужно магическую константу разделить на 3. 39:3 = 13.

Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

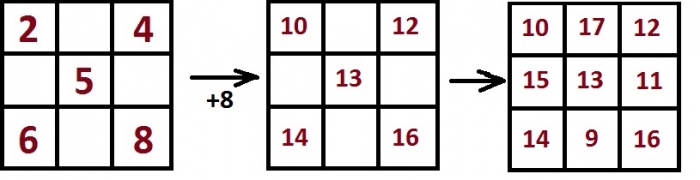
Напомним этот квадрат:

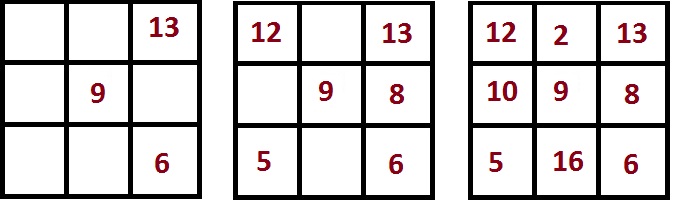
В центре этого квадрата — число 5. В центре того квадрата, который мы должны построить — число 13.

Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.

Достаточно запомнить, что в центре минимального магического квадрата — 5, а по углам — чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).

В итоге получится вот такой квадрат:

Задача 2.

Достройте магический квадрат

В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.

Решение:

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

II. Магический квадрат 4×4

Мы не будем подробно останавливаться на магических квадратах 4×4 — они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.

Минимально возможная магическая константа вычисляется всё по той же формуле:

M = n(n² + 1)/2

M = 4(4² + 1)/2 = 34.

У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.

Однако, у этого квадрата есть другие закономерности:

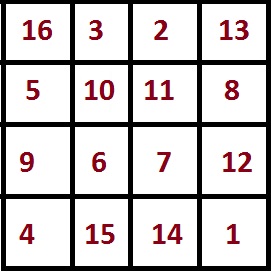
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.

Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.

Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.

Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34

Учитель начальных классов

2 класс

Таникеева В.Д.

Мастер – класс по математике по теме

«Построение магических квадратов»

                    
                                   Ход урока

Орг. Момент.

—Ребята,  проверили свои рабочие места. Что вы
заметили необычного? (много гостей, парты расставлены дугообразно…). Чтобы не
отвлекаться, посмотрите на гостей и подарите им свои улыбки. А сейчас тихо
занимаем свои места.

1.    
 Сообщение
темы и целей занятия

 Уважаемые коллеги, ребята,   я приглашаю вас в удивительный мир
магических квадратов, одним из основоположников которого является  известный швейцарский
ученый Леонард Эйлер. По его мнению, их составление есть превосходная
умственная гимнастика.

«Составление магических квадратов

представляет собой превосходную

умственную гимнастику,

развивающую способность

понимать идеи

размещения,

сочетания

 и симметрии».

                                              Леонард Эйлер

Цели   занятия:  

·       
развитие процессов  
индукции и дедукции на основе выработки навыка построения    латинского и
магического квадрата       методом террас, методом Эйлера и методом Делаира;

·       
выражаю надежду, что   вы
увидите красоту геометрической фигуры на основе взаимодействия   науки и
искусства.

Оборудование:

·       
работаем мы на основе раздаточного 
дидактического материала и презентаций учителя и школьников.

Методы
работы:

·       
основные методы работы – объяснение
принципов построения магических квадратов, упражнение в их построении, а
также иллюстрирование объяснения. Прошу проявлять активность в работе.   

2. Актуализация знаний, постановка проблемы и
осознание познавательных задач.

     2.1. Подготовительная работа.

—
Ребята, а что вы видите на сладе?

-Где вы видели такие квадраты?  (в книжке, у Наташи)

— Кто решал такие удивительные задачи?

    На математических олимпиадах, в досуговых журналах и познавательных
книгах   очень часто встречаются задачи, когда необходимо в квадрат так вставить
цифры от 1 до 9 , чтобы сумма этих цифр по строкам, столбцам и диагоналям
была одной и той же,  постоянной. Конечно для этого нужно иметь  время и
терпение. При решении таких задач  используем   метод   подбора.

— Итак, посмотрите  внимательно на доску.

-Мы должны подобрать цифры т.о., чтобы сумма  в строках, столбцах,
диагоналях была равна 15.

 2.2. Введение нового понятия.

У нас получился квадрат, в котором сумма цифр в строках, столбцах и
диагоналях равна 15 ( проверка). Такую фигуру называют магическим квадратом
порядка 3.

   В
математике под  магическим квадратом
обычно понимают квадратную таблицу, так заполненную различными натуральными
числами, что их сумма в строках, столбцах и двух диагоналях таблицы
одинакова. Значение этой суммы принято называть «магической
постоянной».

— Давайте
вспомним правило о натуральных числах!

— А в этом
нам поможет наш справочник.           

  Итак,
вписать числа от 1 до 9 в квадрат, чтобы он стал магическим, не составляет
особого труда. Как же быть, если нужно вписать в квадрат числа от 1 до 25 или
от 1 до 49, или от 2 до 50 так, чтобы квадрат получился магическим?  

7 сл. –
Ребята, сложно было решить магический квадрат?

           
Тема……

         Предположение
…. – Что должны составить для дальнейшей работы?                                  
  

9 сл.

3.Изучение
нового материала

Рассмотрим один 
способ построения магического квадрата нечетного порядка. Итак, первый
способ – метод террас.

— Ребята, сможете
объяснить слово терраса?

— Давайте обратимся к словарю.

( у нас в школе тоже
есть терраса, только без крыши)

-А в магическом
квадрате, как вы думаете,  где терраса?

 3.1. Объяснение. Построение магического квадрата
методом террас.

Если магический квадрат третьего порядка не трудно
построить простым перебором всевозможных комбинаций, то, уже начиная с квадрата
четвёртого порядка, дело осложняется. Математики изобрели несколько
методов построения магических квадратов. Начнём с метода террас,
который применяется для построения магических квадратов нечётного порядка:
пятого, седьмого и т. д.

 Рассмотрим его на примере магического квадрата  порядка
3.

      С
четырёх сторон к исходному квадрату 3х3 добавляются террасы.            В
полученной фигуре располагают числа от 1 до 9 в естественном порядке косыми
рядами снизу вверх. Числа в террасах, не попавшие в квадрат, перемещаются как
бы вместе с террасами внутрь него так, чтобы они примкнули к противоположным
сторонам квадрата (числа, не попавшие в заштрихованный квадрат, сдвигаем на n=3
единицы: 1 – вниз, 3 – влево, 9 – вверх, 7 – вправо).         

Итак, рассмотрим метод террас, заполнения
магического квадрата нечётного порядка на примере квадратов порядка 3 .
Записываем числа следующим образом:

-Вот для чего нужен нам метод террас!

     Числа, не
попавшие в заштрихованный квадрат, сдвигаем на n=3 единицы: 1 – вниз, 3 –
влево, 9 – вверх, 7 – вправо. Получаем:

Магический квадрат 3*3.
Сумма = 15.

 3.2. Практическая
работа.  

  У вас на столах
лежит таб.  №3. Сейчас построим с вами  магический квадрат пятого порядка,
используя метод террас.

   Будем заполнять
квадрат по шагам, по алгоритму.

1.      С четырёх сторон к исходному
квадрату 5х5 добавлены террасы.              В полученной фигуре расположим
числа от 1 до 25 в естественном порядке косыми рядами снизу вверх, как в
примере с квадратом третьего порядка.

                         Числа, не попавшие в выделенный квадрат,
сдвигаем на n=5 единиц: 1,2,6 – вниз, 4,5,10– влево, 24,25,20 – вверх, 16,21,20
– вправо. Получаем:

Важное наблюдение: заметим, что методом террас можно построить не
только традиционный магический квадрат нечётного порядка, но и квадрат,
заполненный любыми другими числами, лишь бы разность между каждым
последующим и предыдущим числом была постоянной. Так, на рисунке вы
видите нетрадиционный магический квадрат пятого порядка,
заполненный чётными числами от 2 до 50, построенный методом террас.

4. Объяснение
на основе иллюстраций.

  Построение
магического квадрата методом Делаира,  или методом  латинских квадратов.

    Переходим ко второму способу
составления магических квадратов и рассмотрим его на примере построения магического
квадрата порядка 5.        

1.    
Из целых чисел от 0 до
4 строят два  латинских квадрата размером 5 *5.

Первый строят
следующим образом:

· 
произвольно заполняют
нижний горизонтальный ряд квадратной таблицы  

5*5 целыми числами от
0 до 4, следя лишь за тем, чтобы последняя клетка        горизонтального ряда
была заполнена числом 2=[5-1/2]; (k=[n-1/2], n— количество различных цифр в квадрате);

· 
остальные горизонтальные
ряды таблицы заполняют снизу вверх так, чтобы каждый следующий ряд получался из
предыдущего перестановкой – первое число переносится в конец строки.

На этой иллюстрации
приведён такой первый латинский квадрат

Построение второго
латинского квадрата.

· 
произвольно заполняют  верхний
горизонтальный ряд квадратной таблицы 5*5 целыми числами от 0 до 4, следя лишь
за тем, чтобы последняя клетка горизонтального ряда была заполнена числом 2=[5-1/2];
(k=[n-1/2], n— количество различных цифр в квадрате);

· 
остальные горизонтальные
ряды таблицы заполняют сверху вниз так, чтобы каждый следующий ряд получался из
предыдущего перестановкой – первое число переносится в конец строки.

На этой иллюстрации приведён второй латинский квадрат

         2. Преобразовываю полученные два латинских
квадрата путём умножения   каждого числа первого квадрата на 5 и увеличения на
1 каждого числа другого квадрата.

        3.  Произвожу поклеточное суммирование двух
преобразованных на втором этапе квадратов.

    Итак, построим магический квадрат, используя два
выше построенных латинских квадрата:

5. Итог 
занятия

— Итак, мы научились
строить магические квадраты тремя способами.   Назовите их.

 — Какой квадрат
называется магическим?

 — Какие операции
мышления мы использовали?

   Да, проведенная умственная  гимнастика , надеюсь, помогла понять 
Вам идеи размещения, сочетания и симметрии. Эти идеи расположены рядом с
нами, надо только их увидеть.  Предлагаю  увидеть их в   искусстве, в быту, в
науке на основе школьных презентаций.

Коллеги, наша совместная работа была  не так проста, как умножение на  десять,
но и не так трудна, чтобы не познать основных принципов построения совершенной,
по мнению В.Малевича,  геометрической фигуры  — квадрата. А сделать его
магическим  нам под силу.

Магический квадрат

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Магические квадраты… От этого словосочетания сразу веет волшебством. Великие учёные древности считали количественные отношения основой сущности мира. Они увидели, что числа имеют какую-то самостоятельную жизнь, свои тайны. Позже выяснилось, что располагая числа правильными рядам, складывая слева направо и сверху вниз, каждый раз получаются равные числа. Так в ходе времени образовался магический квадрат, который мы встречаем по сей день.

Я выбрала эту тему для исследования, потому что считаю её актуальной и познавательной. При выборе темы исследования у меня появилось желание узнать, влияет ли дата моего рождения на мой характер. Это и стало гипотезой данной работы.

Актуальность моего исследования заключается в умение составлять магические квадраты 3х3, повышать и развивать интерес к новым загадочным головоломкам, развивать любознательность и логическое мышление.

Цель данной работы – знакомство с различными магическими квадратами, способов заполнения магических квадратов 3х3.

Данная цель исследования предполагает решение следующих задач:

определить, что такое магический квадрат;

узнать какие магические квадраты существуют;

3) научиться составлять магический квадрат 3х3;

4) определить влияет ли дата моего рождения на мой характер.

Предмет исследования: история магических квадратов, их разновидности, особенности построения.

Объектом исследования данной работы является магический квадрат.

В своей работе я применяла такие методы исследования:

1) Исследовательский

2) Описательный

3) Метод анализа и обобщения (при работе с информацией)

4) Метод анализа и сравнения.

1. История появления магических квадратов

Магические квадраты возникли в глубокой древности в Китае. Вероятно, самым «старым» из дошедших до нас магических квадратов является таблица Ло Шу (около 2200 г. до н. э.). Она имеет размер 3×3 и заполнена натуральными числами от 1 до 9. В этом квадрате сумма чисел в каждой строке, столбце и диагонали равна 15. Согласно одной из легенд, прообразом Ло Шу стал узор из связанных черных и белых точек, украшавший панцирь огромной черепахи, кото­рую встретил однажды на берегу реки Ло-Шуй ми­фический прародитель китайской цивилизации Фуси. Жители Поднебесной считали таблицу Ло Шу священной, у них даже не возникало мысли о составлении аналогичных квадратов большего размера, поэтому последние стали появляться только три тысячелетия спустя.

В средневековой Европе, как и на Востоке, магическим квадратам часто приписывали различ­ные мистические свойства. Поэтому не удиви­тельно, что они пользовались особой популярно­стью у прорицателей, астрологов и врачевателей. Бытовало даже поверье, что выгравированный на серебряной пластине магический квадрат защи­щает от чумы.

Название «магические» квадраты получили от арабов, которые усмотрели в их свойствах нечто мистическое, и потому принимали квадраты за своеобразные талисманы, защищавшие тех, кто их носит, от многих несчастий. К удивительным квадратам проявляли интерес и средневековые арабские математики, приводившие их примеры в своих сочинениях. Из Китая магические квадраты распространи­лись сначала в Индию, затем в Японию и другие страны. На востоке их считали волшебными, полными тайного смысла символами, и использовали при заклинаниях. 

В наше время магические квадраты продолжа­ют привлекать к себе внимание не только специалистов, но и любителей математических игр и развлечений. За последнее столетие значительно возросло число книг по занимательной матема­тике, в которых содержатся головоломки и задачи, связанные с необычными квадратами. Для их успешного решения требуются не столько специ­альные знания, сколько смекалка и умение под­мечать числовые закономерности. Решение таких задач не только доставит удовольствие тем, кто интересуется математикой, но и послужит пре­красной «гимнастикой для ума».

2. Что такое магический квадрат и его виды

Магическим квадратом (МК)¹ n-го порядка называется квадратная таблица размером n х n, заполненная натуральными числами от 1 до n², суммы которых по всем строкам, столбцам и обеим диагоналям одинаковы.

Магический квадрат имеет по горизонтали – строки, по вертикали – столбцы и клетки диагонального направления.

Строка

Диагональ

Столбец

Клетки магического квадрата заполняются цифрами, сумма которых по строкам, столбцам и диагоналям должны иметь постоянное значение т.е. постоянную магического квадрата.

Полного описания всех возможных магических квадратов не получено и до сего времени, однако отмечено, что магических квадратов 2х2 не существует. Существует единственный магический квадрат 3х3, так как остальные магические квадраты 3х3 получаются из него либо поворотом вокруг центра, либо отражением относительно одной из его осей симметрии.

Нормальный МК — магический квадрат, заполненный целыми числами от 1 до n² (рис. 1)

Полумагический квадрат — квадрат, заполненный числами от 1 до n².

называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется (рис. 2)

Ассоциативный, или симметричный МК, такой МК, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n² (рис. 3)

Пандиагональный (дьявольский) МК — такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата (рис. 4)

Идеальный МК — магический квадрат, который одновременно пандиагональный и ассоциативный (рис. 5)

Совершенный МК — магический пандиагональный квадрат порядка 4k (рис. 6)

Бимагический квадрат — такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует (рис. 7)

Нетрадиционный квадрат – если в таблицу заносится не строго натуральный ряд чисел (рис.

Латинский квадрат или судоку — мудрость востока называют квадратnхn клеток, в которых написаны числа 1,2,3… при том так, что в каждой строке и каждом столбце встречаются цифры по одному разу (рис. 9)

3. Магический квадрат 3х3

Полного описания всех возможных магических квадратов не получено и до сего времени. Можно попробовать перебрать различные варианты расстановки чисел от 1 до 9 в клетках таблицы. Если повезет — вы получите магический квадрат. Однако при этом надо иметь в виду, что всего существует почти 400 000 перестановок в этом квадрате, 9х8х7х6х5х4х3х2х1.

Гораздо интереснее составить такой магический квадрат с помощью рассуждений. Найдём наименьшую магическую константу Волшебного квадрата 3х3 и числа, расположенного посередине этого квадрата

Первый способ:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9= (1+9) + (2+8)+ (3+7)+ (4+6) + 5 = 45

45 : 3 = 15

Магическая константа равна 15, чтобы квадрат был магическим, в каждом столбце и на каждой диагонали сумма чисел тоже должна быть равна 15.

Всего в квадрате три строки. Значит, в каждой строке магического квадрата сумма чисел должна быть равна 45 : 3 = 15. Выпишем все возможные представления числа 15 в виде суммы трех слагаемых от 1 до 9: 9+5+1, 9+4+2, 8+6+1, 8+5+2, 8+4+3, 7+6+2, 7+5+3, 6+5+4.

Заметим, что число, стоящее в центре таблицы, должно встречаться в выписанных суммах четыре раза (столбец, строка и две диагонали). Каждое число, стоящее в углу таблицы, должно встречаться в суммах три раза (строка, столбец, диагональ). А число, стоящее на одном из оставшихся четырех мест, должно встречаться в суммах только два раза (строка и столбец).

Поскольку в полученных суммах четыре раза встречается только число 5, оно и должно стоять в центре таблицы.

Трижды встречаются в суммах числа 2, 4, 6 и 8. Значит, они должны стоять в углах таблицы, причем так, чтобы 2 и 8 были на одной диагонали (2+5+8=15), а 4 и 6—на другой. Остальной процесс — простая арифметика (Приложение 4, рис. 10)

Второй способ: Постоянная магического квадрата также определяется по формуле, где n число строк, а М – магическая константа:

Давайте построим волшебный квадрат 3х3, зная, что магическая константа равна 2.

Вспомним, как строится волшебный 3х3 квадрат по наименьшей константе 15. По крайним полям записываются чётные числа

2, 4, 6, 8, а в середине число 5 (15:3)

По условию надо построить квадрат по магической константе 21. В центре искомого квадрата должно быть число 7, т.е. 21:3. Найдём, насколько больше каждый член искомого квадрата каждого члена с наименьшей магической константой 7 – 5 = 2.

Строим искомый волшебный квадрат ( Приложение 4, рис. 11)

21 – (4 + 6) =11

21 – (6 + 10) = 5

21 – (8 + 10) = 3

21 – (4 + = 9

Если можешь построить один магический квадрат, то нетрудно построить их любое количество. Поэтому запомним приёмы построения магического квадрата 3х3 с константой 15.

Существует единственный магический квадрат 3х3, так как остальные магические квадраты 3х3 получаются из него либо перестановкой строк или столбцов либо путем поворота исходного квадрата на 90° или на 180°

4. Магический квадрат Пифагора

Квадрат Пифагора – это очень мощный аналитический инструмент. Он позволяет выявить основные особенности личности, обусловленные датой рождения. Сохранившиеся исторические источники свидетельствуют, что знаменитый математик Пифагор долго учился потаенным знаниям у египетских жрецов. У них, говорят, в племени дагонов сохранились фрагменты наук о предыдущей цивилизации. Пифагор изучил в Египте, а потом привез в Европу цифровые матрицы, известные ранее только узкому кругу избранных. В адаптированном варианте тайные таблицы дошли до наших дней и ныне известны как квадрат Пифагора. Пифагор постиг истину связи числа рождения с судьбой человека.

Представленный вам магический квадрат Пифагора пришёл именно из тех лет, когда нумерология только начинала свой долгий путь. При помощи этой таблицы и некоторых несложных подсчётов, можно увидеть характер по квадрату Пифагора свой и своих близких. Все манипуляции числовой квадрат Пифагора обуславливает, как решение уравнения, а это вполне научное действие.

Для примера я взяла дату своего рождения 26.10.2007 г. Сложим цифры дня, месяца и года рождения (без нулей): 2+6+1+2+7=18. Далее складываем цифры результата: 1+8=9. Затем из первой суммы вычитаем удвоенную первую цифру дня рождения: 18-4=14. И вновь складываем цифры последнего числа: 1+4=5. Получили числа 26.10.2007,18,9,14,5.

И составляем магический квадрат так, чтобы все единицы этих чисел вошли в ячейку 1, все двойки – в ячейку 2 и т.д. Нули при этом во внимание не принимаются. В результате квадрат будет выглядеть следующим образом:

Согласно расшифровки (Приложение 4) показатели моего характера следующие:

1. У меня покладистый характер.

2. Бионергии достаточно.

3. Цифра 3 отсутствует в дате моего рождения.

4. Болезни настигнут меня только в пожилом возрасте.

5. Совершаю ошибки, но редко.

6. Я обычный человек, который думает об образовании.

7. Талант не явно выражен, но при желании его можно развить.

8. Развитое чувство ответственности.

9. необходимо умственное развитие.

Заключение

В результате данной работы я расширила свои знания о магических квадратах, выяснила, что такое магический квадрат, как они появились, какие виды магических квадратов существуют. Я узнала: способы построения квадрата 3х3, новые понятия, например магический квадрат, магическая константа.

С целью подтверждения выдвинутой гипотезы я составила магический квадрат Пифагора, используя дату моего рождения. Я проанализировала и выявила следующее: исходя из полученных данных, я могу сказать, что магический квадрат Пифагора, который составляется по дате рождения, может частично определить свойства характера человека. Безусловно, не следует слепо верить всему магическому. Возможно, некоторые черты характера и заложены в дате рождения человека, но человек всегда может найти способы что-то изменить в своей судьбе.

Выполняя эту работу, я много узнала о Магических квадратах, однако так же многое мною осталось не изучено. Я считаю, что «точку» в моей работе ещё ставить рано, я  буду стремиться к  дальнейшему исследованию способов заполнения магических квадратов.

Библиография

М. М. Постников «Магические квадраты. Выпуск 131» Издательство: «URSS» (2017).

Т. Ушакова «Тренировочные упражнения. Математика. Магические квадраты». Издательство: «Литера ИД» (2017).

Ю. В. Чебраков «Магические квадраты» С Петербург (1995).

Сайты в Интернете

https://all-psih.ru/magicheskij-kvadrat-pifagora.html

http://ru.wikipedia.org/wiki

http://xreferat.ru/54/540-1-magicheskie-kvadraty.html

 http://www.krugosvet.ru/articles/15/1001543/print.htm 

 http://www.kspu.ru/magazine/no4/pub/pr3-4.htm 

Приложение 1

Рисунок 1.Нормальный магический квадрат.

Рисунок 2.Полумагический квадрат. 

Рисунок 3.Ассоциативный, или симметричный МК.

Приложение 2

Рисунок 4.Пандиагональный (дьявольский) МК. 

Рисунок 5.Идеальный МК. 

Рисунок 6.Совершенный МК. 

Приложение 3

Рисунок 7.Бимагический квадрат. 

Рисунок 8.Нетрадиционный квадрат.

Рисунок 9. Латинский квадрат (судоку)

Приложение 4

Рисунок 10.

Рисунок 11.

РАСШИФРОВКА КВАДРАТА ПИФАГОРА

Цифра 1 (эгоизм). Количество единиц определяет интенсивность эгоизма.

1 — утонченный эгоист (только я должен жить, я, я, я,)

11 — близок к эгоизму (все время себя хвалит, как на продажу, боится переоценить)

111 — хороший характер (покладистый)

1111 — очень волевой, сильный

11111 — диктатор, самодур

111111 — (очень редко) человек жесткий, в то же время для близкого человека может совершить невозможное, с ним очень трудно.

Цифра 2 (биоэнергия, поведение человека в семье). Соответственно, количество двоек определяет интенсивность проявления способности.

0 двоек – нет биоэнергии, канал биоэнергии открыт для интенсивного набора, эти люди любят старые вещи, неплохо относятся к окружающим, стараясь этим самим подпитаться от других, воспитаны от природы.

2 — биоэнергии достаточно для жизни, но сейчас, на данном этапе маловато. Спорт обязателен, чувствителен к изменениям в атмосфере.

22 — биоэнергии достаточно (уже может лечить других)

222 — хороший экстрасенс

2222 — этих людей любит противоположный пол и очень любят люди со знаком 666.

Цифра 3 (порядочность). Нет троек – очень чистоплотный или пунктуальный, что-то выделяет их из окружающей среды своим языком (все время чистят)

3 — этих людей не беспокоит порядок, но относительно, (хочу — делаю, хочу -нет) все зависит от настроения.

33 — склонность к наукам (хорошие математики, физики, химики, ученые)

333 — склонность к наукам (с увеличенной силой, невозможная педантичность, есть не реализованной в науке)

Цифра 4 (здоровье). Пустой квадрат – этот человек будет болеть очень сильно (особенно, если при расчете много двоек)

4 — в основном болезни настигают только в пожилом возрасте.

44 — темперамент живой, человек крайне здоровый.

444 — уровень сопротивляемости инфекциям и заболеваниям очень высок.

Цифра 5 (интуиция). Пустой квадрат – открытый канал при рождении, поэтому этот человек всегда пытается что-то предпринять, что-то доказать, всегда голова в раздумье, сам в эксперименте, в расчете. Жизненный опыт показывает, что с этим человеком трудно жить. Все достается (пробивает) своей головой.

5 — интуиция есть, ошибки происходят, но редко.

55 — сильно развита интуиция – следователь и юрист.

555 — это ясновидение. Такой человек всегда знает, как поступать в любых ситуациях.

5555 — есть возможность проникнуть в другие измерения, контролирует время и пространство.

Цифра 6 (отвечает за склонность человека к физическому труду и склонность к власти). Пустой квадрат – человек пришел приобрести ремесло, физический труд необходим, но он его не любит.

6 — обычный человек, который думает об образовании, не исключая возможности физического труда.

66 — трудолюбие, но физическая работа — не более, чем увлечение.

666 — нужно быть очень осторожным. Привлекательная и темпераментная личность, но от партнера потребует значительных денежных трат.

6666 — в прошлых жизнях работал тяжело и много.

,

Цифра 7 (называется знаком везения или знаком ангела. Семерок нет -в этой жизни возьмет меньшее от судьбы. Он будет талантлив в следующих жизнях.

7 — талант не явно выражен, при желании, можно развить.

77 — для них нет закрытых дверей судьбы. Такой человек обладает всем — хорошим и плохим. Имеет вкус, хорошо рисует, очень талантлив. В случае неприятностей выходит сухим из воды.

777 — сталкиваются с особыми трудностями.

7777 — сигнал тревоги. Нужно быть предельно осторожным.

Цифра 8 (чувство долга). Пустой квадрат — человек что-то возьмет, но не спешит отдавать.

8 — развитое чувство ответственности.

88 — всегда поможет другим, ответственность высока.

888 — существует для народа.

8888 — парапсихолог, большой талант в точных науках.

Цифра 9 – отвечает за ум, память и способность к ясновидению. Все эти качества представляют собой звенья одной цепочки: полученные человеком знания.

9 — необходимо умственное развитие.

99 — лентяй, но с умной головой.

999 — ум и удачливость на его стороне.

9999 — исключительный ум, но человек груб и немилосерден.

1 МК- магический квадрат

Просмотров работы: 2872