С помощью линейной диаграммы пользователь представляет наглядно вариацию, динамику и взаимосвязь. Графически изображение представляет собой последовательность точек, соединенных отрезками прямой в ломаные линии. Как происходит построение линейной диаграммы в Excel.
Для какой цели используется линейная диаграмма
Линейные диаграммы графики целесообразно использовать в следующих ситуациях:
- Динамический ряд имеет достаточно большое количество значений. Непрерывная линия, соединяющая их, подчеркивает непрерывность процесса.
- Нужно показать общую тенденцию развития явления.
- Необходимо в пределах одной геометрической плоскости сравнить несколько динамических рядов.
- В сопоставлении нуждаются не абсолютные значения, а темпы роста явления.
На оси абсцисс, как правило, показывается временная характеристика явления. На оси ординат – значение показателя.
Как построить линейную диаграмму в Excel
С помощью линейного графика в Excel можно быстро сопоставить продажи в компании за определенные промежутки времени, проанализировать баланс, доходы и расходы, значения какого-либо эксперимента и т.п. Рассмотрим на примере как сделать линейную диаграмму в Excel.
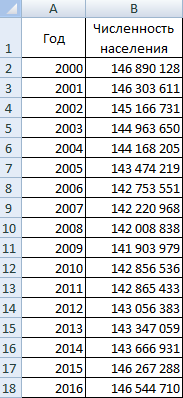
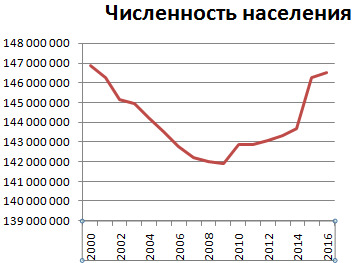
Создадим таблицу в Excel «Численность населения России за 2000-2016 гг.»:
- Все ячейки в колонках должны быть заполнены.
- Данные имеют одинаковый формат.
- В одном столбце – значения одного типа (даты, численность).
Выделяем всю таблицу, включая заголовки. Переходим на вкладку «Вставка» — в меню «Диаграммы». Выбираем «График».
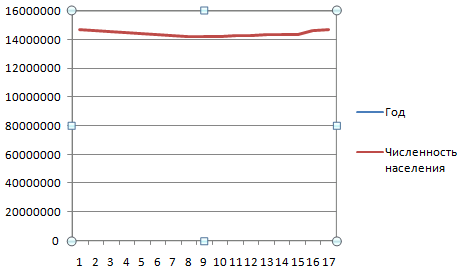
Можно выбрать «с накоплением», «нормированный», «с маркерами» и т.п. Щелкаем по иконке выбранной разновидности графика левой кнопкой мыши. Получаем:
Такой график нас не устраивает – он построен не совсем правильно. Поэтому щелкаем по области построения, чтобы активировалась вкладка «Работа с диаграммами». Нажимаем кнопку «Выбрать данные».
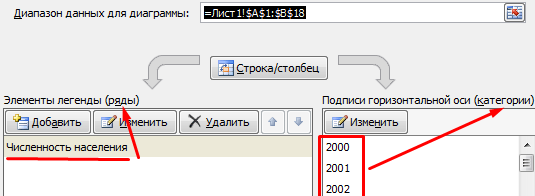
В окне «Выбор источника данных» мы сначала изменим подписи горизонтальной оси.
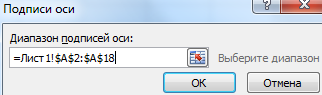
После нажатия кнопки «Изменить» откроется поле для назначения диапазона подписей. Выбираем столбец с датами.
Нажимаем ОК. Программа возвращает нас к диалоговому окну «Выбор источника данных».
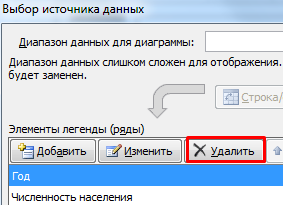
В «Элементы легенды» попали данные столбца «Год» и «Численность населения». «Год» удалим.
По умолчанию подписи горизонтальной и вертикальной оси принимают горизонтальное направление. Каждое значение года имеет 4 цифры. Они сливаются – и плохо видно. Чтобы изменить их направление, щелкаем правой кнопкой мыши по подписям. Нажимаем кнопку «Формат оси».
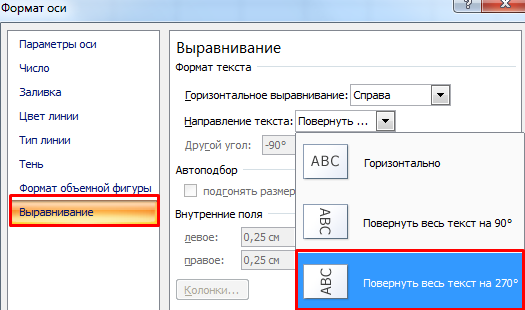
В открывшемся диалоговом окне переходим на вкладку «Выравнивание». Здесь мы можем изменить направление текста.
Получаем график вида:
Построить линейную диаграмму по таблице достаточно просто. Готовые график можно менять (цвет, толщину линии, размер шрифта, подписи и т.п.), используя доступные инструменты на вкладках «Конструктор», «Макет», «Формат».
Линейчатая диаграмма
В Excel 2007 имеется такой тип. По сути, это столбчатая гистограмма, где столбики повернуты горизонтально. Столбчатая гистограмма и линейчатая диаграмма взаимозаменяемы. Они применяются для анализа изменений показателя за определенный промежуток времени.
Каждый столбик (прямоугольник) показывает величину уровня в анализируемом статистическом ряду. Сравниваемые данные имеют одинаковые единицы измерения. Поэтому удается проанализировать рассматриваемый процесс.
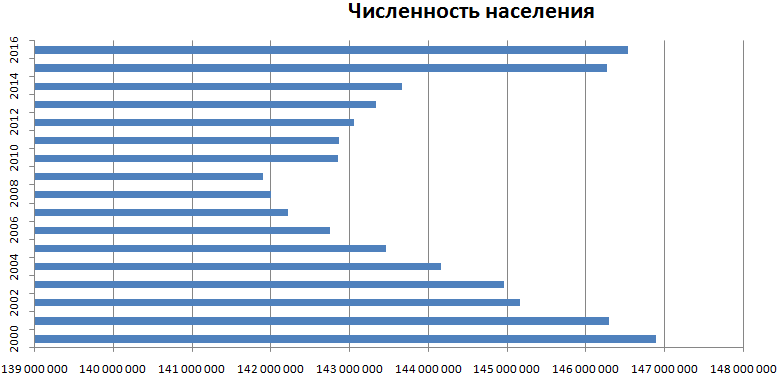
На основе уже имеющихся данных по численности населения построим линейчатую диаграмму.
Обратите внимание: так как столбики имеют горизонтальное направление, диаграмма как будто ложится на бок.
Теперь годы – это подписи вертикальной оси, а численность – горизонтальной. Но при выборе источника данных для диаграммы нужно придерживаться прежнего порядка:
Значения для категорий и рядов должны остаться теми же.
What Is a Linear Price Scale?
A linear (arithmetic) price scale is a charting scale used by traders that is plotted with real values spaced equidistant from one another on the vertical y-axis. Each unit change is represented by the same vertical distance on the chart, regardless of what price level the asset is at when the change occurs.
A linear scale can be compared with a logarithmic scale. The interpretation of a stock chart can vary among different traders depending on the type of price scale used when viewing the data.
Key Takeaways
- Linear price scales—also referred to as arithmetic—represent an asset’s price on the y-axis using equidistant spacing between price marks.
- A linear price scale chart displays changes in absolute terms and does not depict price movements in relation to their percent change.
- A logarithmic price scale chart, on the other hand, is plotted to show the percentage change that occurs when a price moves from one quote to the next so that each price mark is larger by a factor of ten.
How Linear Price Scales Work
Linear price scales and logarithmic (log) price scales are two common types of charts used in the financial industry. Both types of charts can be used by technical analysts. Each of the charts is typically generated from software automation. Linear price scale charts can more easily be drawn manually since they rely on static units representative of absolute values.
Logarithmic charts typically require the use of advanced chart programming since their unit value movements are not constant but rather expressed in percentages. Both linear and logarithmic charts will use the same x-axis dates for their charting.
A linear price scale can also be known as an arithmetic chart. The linear price scale chart doesn’t depict or scale movements in any relation to their percent change. The linear price scale plots price level changes with each unit change corresponding to a constant unit value. Since each value change on the grid is constant, linear price scales can more easily be drawn manually.
linear versus logarithmic stock chart.
FreeStockCharts.com
Logarithmic Price Scales and Charting
A logarithmic price scale chart is plotted to show the percentage change that occurs when a price moves from one quote to the next. They chart the price’s percentage move by mathematically portraying it in the vertical movement.
Therefore, if a price increases by 1%, its higher vertical movement will be much less than a vertical movement depicting the price change of a 50% increase. To allow for mathematically scaled price movements per unit change, advanced charting software creates a non-static y-axis. In a logarithmic price scale, the y-axis changes its scale with each price movement.
Important
While the difference between linear and logarithmic price scales is important to understand when reading charts, there are other forms of technical analysis that you can use to identify and capitalize on price trends.
A linear and logarithmic price scale chart will have the same visual appearance in the body of the chart. However, a logarithmic chart will have an adjustable y-axis that can more clearly show breakout levels at which a price has made large percentage moves. If price changes are occurring in low percentages then a logarithmic price chart will also depict that with concentrated price levels on the y-axis rather than large spaces shown between prices.
Example of a Linear Price Scale
A linear price scale is easy to identify because the y-axis will always be charted with values equidistant apart.
For example, a linear scale disregards the fact that a $5 move is more substantial when the price of an asset is $10 than when the price of the asset is $50. The price movement that is plotted on the chart is represented as being the same distance on the scale, even though a $5 increase from $10 is equal to a 50% increase, while a $5 increase from $50 is a 10% increase.
Сравнение равномерной, логарифмической и степенной шкал
Выбор типа шкал для графика, всегда казалось мне интуитивно понятной задачей. Однако, когда мне нужно было объяснить, чем они отличаются, то я не смог привести понятных аргументов. В интернете хорошей информации мне не попалось. Поэтому решил разобраться, откуда растут ноги у разных видов шкал и как их следует применять. Я решил рассмотреть три самых распространенных вида шкал — равномерную, логарифмическую и степенную.
Равномерная шкала
Самый распространенный и привычный вид шкал. Также их называют арифметическими или линейными шкалами. На такой шкале значения равноудалены друг друг от друга.
Например значения 100 и 200, и 200 и 300 отстают друг от друга на одно и тоже расстояние.
Например, на этом графике по оси Y — равномерная шкала с шагом в 20 лет средней продолжительности жизни, а по оси X — равномерная шкала с шагом 10 календарных лет.
Логарифмическая шкала
Этот вид шкал тоже используется достаточно часто, особенно когда речь идёт о научных исследованиях. Она используется для отображения широко диапазона величин, когда значения, которые попадают на график отличаются на много порядков. То есть когда мы хотим одновременно видеть и значения 0.1, 0.2 и значения 100, 200 на одном графике. Зачастую это связанно с физикой процесса. Так, например, в музыке ноты, различающиеся по частоте в два раза это ноты на октаву выше (Ля и Ля следующей октавы). Чтобы показать частоты двух нот будет удобно использовать логарифмическую шкалу.
Но бывает, что в наборе данных просто содержаться большой разброс данных. Например, как на этом графике из Beautiful Evidence Тафти, где он использует логарифмические шкалы для сравнения массы тела и мозга различных существ. Так как бывают и крошечные рыбки и огромные киты, то на таком графике удобно использовать логарифмические шкалы.
Чаще всего используются логарифмические шкалы с основанием 10. Это значит, что одинаковые расстояние на графике откладываются между значениями отличающимися на один порядок. Но бывают логарифмические шкалы с другими основаниями. Например 2.
Степенная шкала
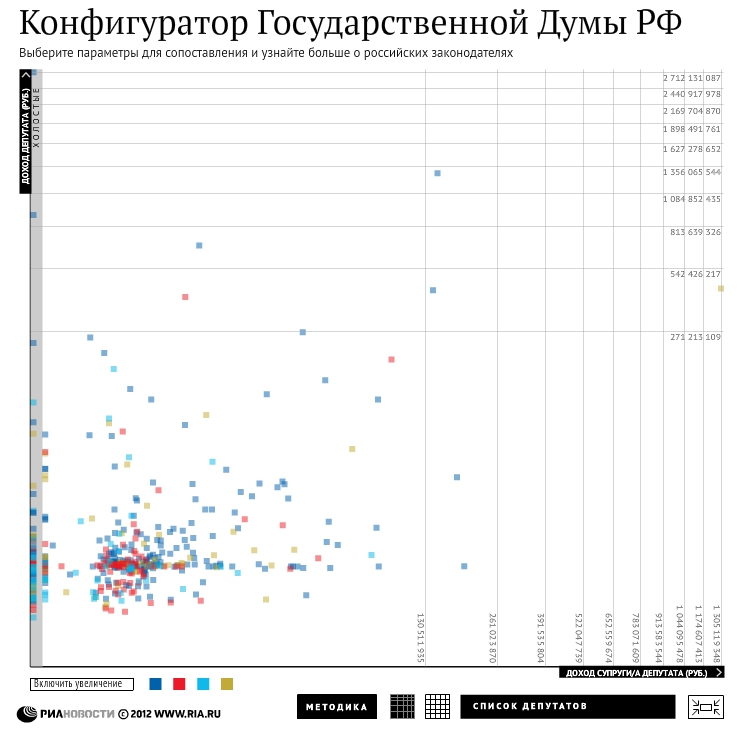
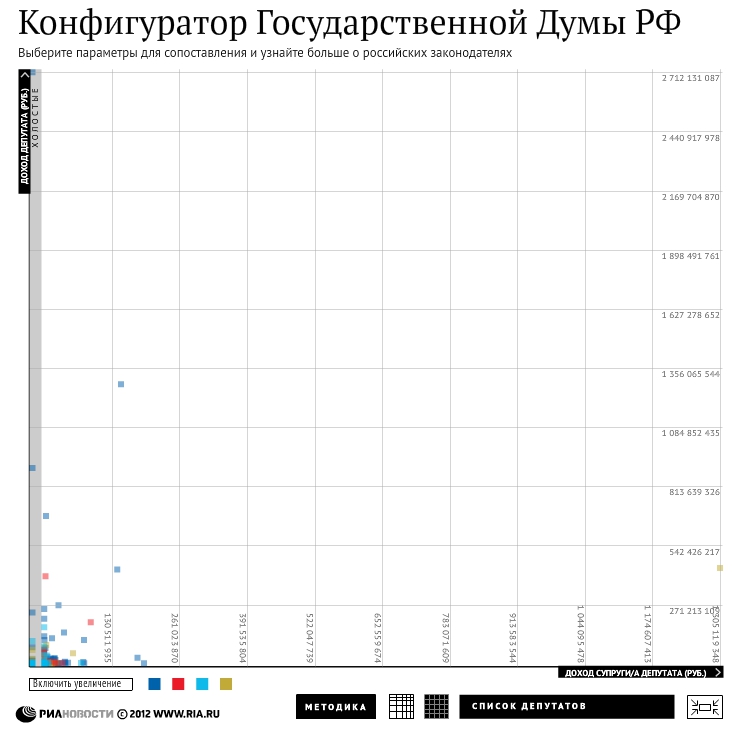
Это менее известный тип шкал. Он отличается от остальных тем, что расстояние между рисками, соответствует числам возведенным в степень. То есть получается, что расстояние между соседними рисками постоянно растёт или уменьшается. Такие шкалы удобны, когда мы хотим показать на одном графике более детально какую-то группу значений, но при это не хотим потерять из вида, значения которые, сильно отличаются от этой группы. Чем-то это похоже на логарифмическую шкалу, но здесь идёт акцент не на всем промежутке, а только на отдельной его части. Это хорошо видно на примере РИА новости, где они использовали степенные шкалы, чтобы сгладить выбросы по доходам отдельных депутатов.
Со степенной шкалой
С равномерной шкалой
То есть степенные шкалы используются когда данные смещены в ту или иную сторону.
Сравнение шкал
Чтобы удобно сравнить и понять как использовать ту или иную шкалу, я сделал небольшой инструмент. На нём можно выбрать разные наборы данных и понять, как они выглядят на разных шкалах.
Интерполяция + (линейная | логарифмическая) шкала + С++
В этой статье я распишу теорию (а также базовые виртуальные классы), в следующей возьмусь за конкретные реализации средствами Qt.
Осторожно: в тексте много графики!
Откуда растут ноги у задачи
В общем, надо мне сделать регулятор холостого хода — такая штука для автомобиля, которая при холостом ходе в зависимости от температуры двигателя должна поддерживать определенные обороты. Поддерживает она их, регулируя заслонку шаговым двигателем.
В общем, мне надо знать текущую температуру. Было решено измерять ее штатными средствами — с терморезистора. Измеряем падение напряжения на нем — получаем сопротивление. Далее из таблицы (поскольку это микроконтроллер) получаем требуемые обороты.
Таблицу эту надо задать (для этого программа пишется средствами Qt). У меня есть несколько точек «сопротивление => температура». Мне надо для каждого кода АЦП (для ряда значений сорпотивлений) получить соответствующую температуру. Поскольку у разных автомобилей эти значения могут быть разными, то надо на экране, сверившись с таблицей, задать несколько точек на кривой.
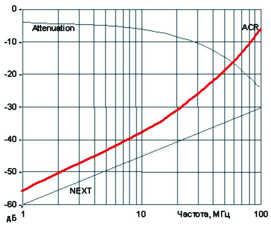
По ходу дела оказалось, что график этот будет явно в логарифмическом масштабе. Значит, надо его вывести на экран. Как это сделать — читаем дальше.
Постановка задачи
Давайте немного подробнее опишем что нам надо:
- задание функции — необходимо задать несколько точек, по которым строится график. Вобщем, вспоминаем интерполяцию;
- построение графика функции — да-да, я знаю про Qwt. Может, не очень хорошо я его знаю, т. к. я не нашел в нем следующей возможности:
- интерактивное задание функции — мне нужно двигать точки, по которым строится функция, прямо на экране, в текущих экранных координатах шкалы, которые переводятся в реальное значение;
- линейная/логарифмическая шкала — поскольку значения вот такие, как я написал, мне пришлось заложить возможность менять шкалу. Причем как одну, так и обе сразу.
Вот такое ТЗ… Ну да ничего, я справился! Давайте и вам помогу.
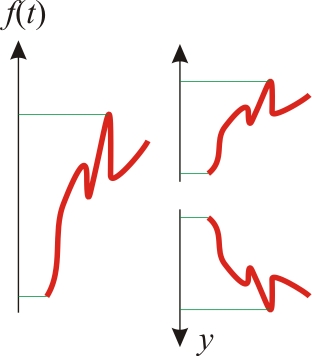
Да, пока не нырнули — спасибо Equation Editor-у от CodeCogs! С их помощью я лихо построил все математические формулы без всяких Microsoft Equation Editor, которые потом надо еще экспортировать в графику со вставкой сюда. Кстати, там есть и русский редактор. В общем, рекомендую!
Ну и если вместо формул вы видите пустые квадратики — это тоже «спасибо» Equation Editor-у…
Прикрепленный Excel-файл
По ходу написания статьи я все расчеты строил и проверял в таблице Excel с формулами. Оказалось очень удобно. И я решил его выложить для общественного пользования. Там внизу перечислены страницы по разделам. На каждой странице параметры, которые можно менять, отмечены как ячейки с желтым фоном. Остальные клетки лучше не трогать. Впрочем, все формулы можно смело смотреть. Скачивайте файлик и пробуйте на здоровье! Если проблемы с файлом — пишите, вышлю.
Функциональная зависимость
Итак, у нас есть некоторая зависимость — обозначим ее как 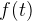

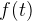

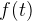
Почему не 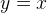
только в школе в простейшем случае.

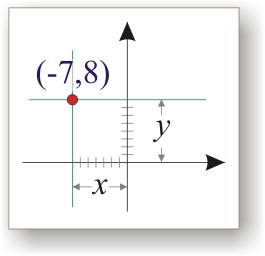
задает вертикальное смещение горизонтальной оси относительно нуля,
задает горизонтальное смещение вертикальной оси относительно нуля.
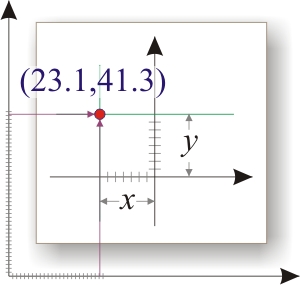

Ну и не забываем о том, что это все эти красивые рассуждения справедливы пока что для линейной шкалы, а у нас маячит за горизонтом логарифмическая. Там вообще черт знает что будет!
Но это только лишь точка. А у нас будет какая-то линия, точнее — много линий. Что там будут за преобразования?
Вот именно поэтому мы с самого начала должны четко разделить функциональную зависимость и преобразования координат.
Итак, давайте договоримся о следующем: у нас есть некоторый абстрактный процесс, который описывается функциональной зависимостью 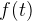
, где
,
. Следующие шаги — это прояснить эти самые
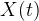
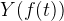
Но отложим пока в сторону координаты — нам надо как-то задать нашу функцию (помните ТЗ)? Причем задать в тех самых абстрактных координатах 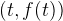
Интерполяция
В моем случае был известен ряд точек 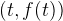
 , Ω , Ω |
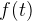 , ˚ , ˚ |
|---|---|
| 180 | 100 |
| 6 000 | 0 |
| 30 000 | -30 |
Не ахти какая сложна и большая таблица, но тут явно куча пустых мест. А какое сопротивление соответствует 60˚, -40˚, . В общем, надо проставить отсутствующие точки. И в этом нам помогут интерполяция, аппроксимация и экстраполяция. Впрочем, не пугайтесь — одной интерполяции хватит за глаза.


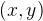
Многочлен вычисляется как , где .
Математика испугала? Хм… Ладно, напишу на языке С++:
Как видите, все достаточно тривиально (насколько тривиальными могут быть полиномы).
Еще одно большое достоинство полиномов Лагранжа — их легко можно промоделировать в таблице Excel-я, что я и делал.
Потом, правда, все стало немного печально, т. к. у этих полиномов, как и у любых других, на графике видны вибрации. Т. е. они не могут дать прямые линии — постоянные значения. В моем случае я не смог их настроить дОлжным образом — они выгибались в явно недопустимые числа. Поэтому мне пришлось от них отказаться…
Работая в Corel, я был близко знаком с кривыми Безье — тоже достаточно удобное и простое представление табличных данных. Весьма легко реализуется в программировании. Однако это уже не интерполяция, а, скорее, аппроксимация, т. к. тут приходится подгонять кривую к нужному виду.

Говоря языком математики, мы между точками и проводим прямые линии вида .
Опять же, на языке С++ это будет выглядеть так:
Тоже ничего революционного, не так ли?
Есть одно существенное различие между полиномом Лагранжа и линейной интерполяцией: у первого нельзя явно задать значения за пределами точек — они вычисляются, у второго можно это дело контролировать. Также и поэтому я в конечном итоге остановился на линейном варианте. Более того — в логарифмическом масштабе, к которому я стремился, линейные отрезки дают более подходящий мне вариант.
Впрочем, не будем заморачиваться сейчас на методах интерполяции. Давайте лучше мы сделаем базовый класс, от которого будем наследовать реализации различных методов $#*@!поляции.
Базовый класс для задания/расчета функции
Что этот класс должен уметь делать? Мне кажется, что такой класс должен:
- давать значение функции в зависимости от аргумента — собственно, ради чего мы его и городим;
- реагировать (перемещать и пересчитывать) на изменение точек интерполяции — на вход подается факт нажатия/отпускания в некоторой координате, в результате чего производится пересчет параметров;
- различать одиночный и двойной щелчок мышки — одиночное нажатие, как по мне, указывает на передвижение точки; двойное создает новую точку;
- прорисовывать точки интерполяции как при их движении, так и без оного — т. к. у разных методов интерполяции будет разное интуитивно понятное значение точек интерполяции, то и выводить их должен производный класс (например, в интерполяции точка является частью графика; в аппроксимации точка не обязательно лежит на графике; в кривых Безье часть точек лежит на графике, часть задают форму);
- давать координаты текущей передвигаемой точки — это нужно для вывода текста координаты данной точки;
- давать сервисную информацию — например, «определена ли функция?», «сколько точек для интерполяции используется?», «получить координаты точек» и т. п. Эти данные позволят сохранить текущие настройки;
- производить настройку — «распределить столько-то точек», «задать координаты точки» — это нам позволит восстановить сохраненные настройки.
Еще есть мысли? Если будут — пишите в комментариях, добавим!
Получается такой вот класс:
(Тем, кто недоволен моим стилем и структурой — предложите объективно лучше!)
(Тем, кто найдет ошибки в коде — спасибо!)
Думаю, тут все очевидно.
Для координат используется представление точки в виде QPointF (пара чисел в виде qreal, qreal. «На всех платформах, кроме ARM, используется double» — так написано для Qt 4.8).
Нажатия на кнопки мышки реализованы функциями MouseClicked , MouseDblClicked , MouseReleased и MouseMove . Предполагается, что в конкретных реализациях будут соответствующие реакции.
Для прорисовки точек используются методы DrawPoints и DrawCurPoint . Если для всех методов, кроме этих, координаты используются абстрактные, то тут нужны самые что ни на есть экранные. Поэтому сюда передаются два объекта класса ScaleBase для преобразований. Этот класс — тоже виртуальный. Его предки реализуют преобразование из абстрактных координат в текущие экранные. Сам же этот класс будет описан ниже.
Текущее значение функции возвращает метод f (const qreal) и перегруженная операторная функция operator() (const qreal) .
Для задания структуры используются функции set_points (Num) — задание количества точек, point (Num) , set_point (Num) , get_point (Num) — задание координат конкретной точки. num_points () const — возвращает количество точек, point (Num) const , get_point (Num) const возвращают координаты точки. is_specified () const возвращает true , если структура функции задана.
В следующей статье мы распишем пару вариантов реализации этого класса.
Функция преобразования для вертикальной/горизонтальной шкалы
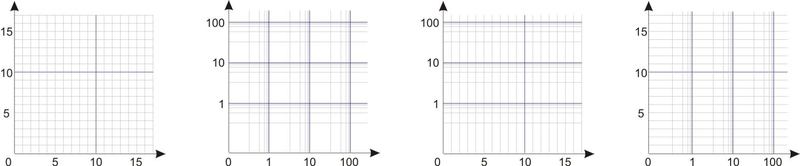
Есть линейные и логарифмические шкалы. Учитывая, что вертикальная шкала может быть сделана в одном формате, а горизонтальная — в другом, мы получаем четыре варианта графика:
Вариант первый — обе шкалы линейные. Вариант второй — обе логарифмические. Варианты третий и четвертый — смешанные графики. Кстати, в моем случае именно смешанный случай в итоге и подошел, т. к. по горизонтали у меня потребовался логарифмический масштаб, по вертикали — линейный.
Следовательно, задачу отображения нужно решать отдельно для обеих осей.
Напомним, что при отображении на экран используется преобразование в координаты , где
,
. Наша дальнейшая задача — построить эти функции для линейного и логарифмического случаев.
Что это за функции такие? На вход они получают координату в абстрактных (для компьютерной подпрограммы отображения на экран) координатах, на выход дают в экранных («экранные» координаты будут для разных операционных систем разными»). Для расчета им нужно знать следующее:
- пределы абстрактных координат — те предельные значения аргумента и функции, что нас интересуют. Это будут
,
для горизонтальной оси и
,
для вертикальной. Не нужно допускать классическую ошибку:
,
! В приведенном примере это проиллюстрировано;
- пределы экранных координат — границы картинки, в которой рисуется график. Естественно, в текущих экранных координатах. На графике это
,
для горизонтальной оси и
,
для вертикальной;
- шаг экранной координаты — текущий шаг пикселя
,
. В простом случае это будет единица. Но в Qt вертикальный ноль — это верх окна. Следовательно,
. А еще могут быть применены всякие трансформации, и шаг уже будет отнюдь не единичным.
Обратите внимание — для задачи преобразования не важно, вертикальная это ось или нет! Она (задача) оперирует граничными значения входного, выходного, а также шагом выходного параметров. Следовательно, задачу можно обобщить: необходимо преобразовать параметр на основе его пределов , в выходную величину с учетом ее пределов , и шага . Тут намеренно введены обозначения , вместо привычных alt=»image» />, alt=»image» />, т. к. иначе будет путаница. Одно существенное дополнение: .
Базовый класс для преобразований шкал
Давайте сформулируем желаемую функциональность виртуального класса преобразований для шкалы, от которого будут унаследованы реализации шкал:
- преобразований из экранных координат в абстрактные и наоборот — логично, ради этого мы его и делаем;
- настройка преобразования — это тоже логично;
- свойства — текущие свойства преобразования (минимальные/максимальные значения, шаг для разных значений);
- информация по сетке — позиции для крупной и мелкой сетки, подписи под шкалой.
Реализация может выглядеть так:
Настройка шкалы производится функциями set_. (Val) . Пересчет необходимых значений должен производится в этих же функциях. При изменении размера окна вызывается метод Resized (Size) .
Для повышения производительности можно один раз рассчитать соответствие точки на экране и ее значение в исходных, абстрактных координатах. Этот массив возвращается методом scr_values () const . Далее, для построения крупной и мелкой сетки рассчитываются массивы (возвращают их, соответственно, функции scr_maj_grid () и scr_min_grid () ). Длина массива соответствует количеству оных линий, значение — смещению относительно начала шкалы на экране (т. е. индексу первого массива). Также заранее рассчитываются два массива — текст подписи к шкале (функция scr_text_str () ) и смещения этих подписей относительно начала (функция scr_text_pos () ).
Наконец, прямое преобразование — из абстрактных в экранные координаты — производится функцией scr (Val) , обратное — функцией val (Scr) .
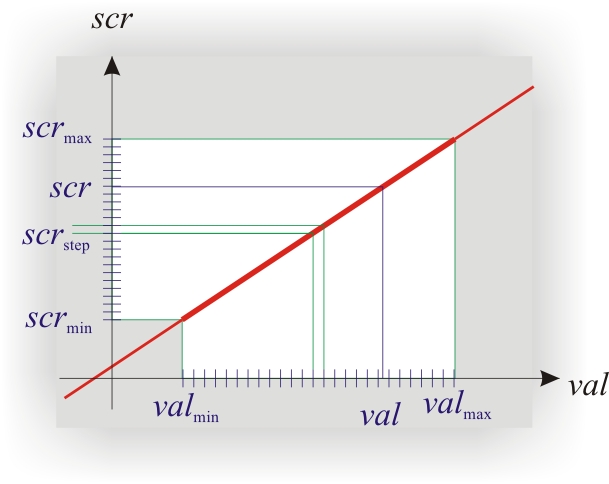
Линейное преобразование
Давайте отдельно рассмотрим линейное преобразование для горизонтальной и вертикальной оси.
Мы имеем некоторую функцию — кривую в одном представлении. Для другого нам пришлось ее сузить и сместить вправо (окно на экране уменьшили и сдвинули вправо). Для другого представления нам пришлось сместить ее влево (окно сдвинули влево). Как это описывается математически? Достаточно просто: alt=»image» />. В первом случае, похоже, , во втором alt=»image» />.
В другом случае нам пришлось сузить вертикальное представление кривой и сдвинуть вверх. А потом и вообще — перевернуть. Оба этих преобразования описываются как alt=»image» />. В первом случае , . Во втором случае alt=»image» />.
Оба преобразования имеют одно и то же математическое описание: . В данном описании есть две константы, которые определяют преобразование — alt=»image» />и alt=»image» />. Первая определяет угол наклона, вторая — смещение относительно нуля.
Расчет этих констант достаточно прост — это решение системы двух уравнений:
Еще важно уметь делать обратное преобразование — скажем, координаты указателя мыши перевести в абстрактные координаты. Также ничего сложного:
Шаг в данном случае для расчета не используется, но он потом нам пригодится в реализации на С++ для расчета смещения.
Как это будет использоваться на практике? Да все просто! Горизонтальное преобразование: — граница картинки графика, соответствующая (как правило, слева), — (как правило, справа), — шаг вывода картинки по горизонтали. Вертикальное преобразование — аналогично, но по вертикали (у нас в Qt будет нижней границей картинки, — верхней, причем ).
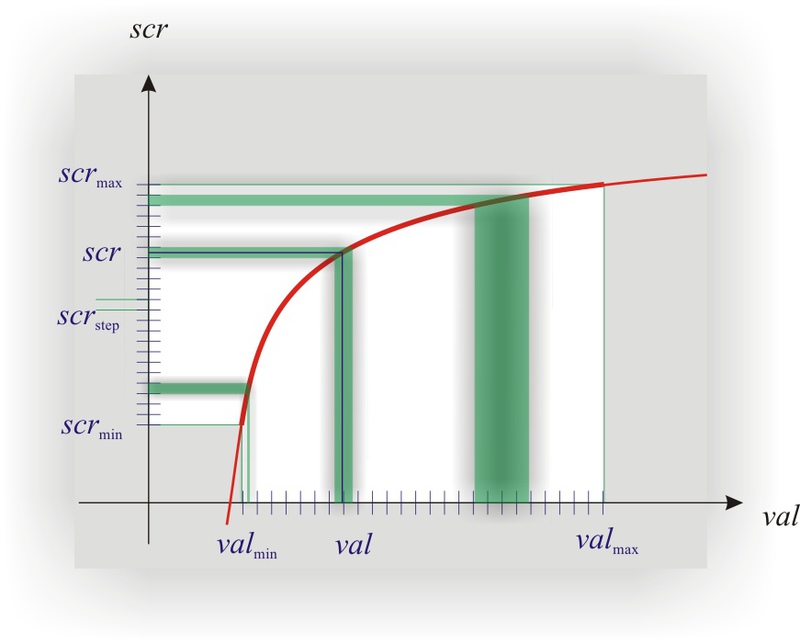
Логарифмическое преобразование
А теперь окунемся туда, ради чего все это закрутилось:
(на графике не логарифм нарисован, а что-то похожее на него. Сделано это специально, т. к. логарифм тут будет не очень нагляден)
Если один и тот же на всей шкале, то будет везде разным! По какому закону он меняется? Правильно — по логарифмическому! Давайте первым делом научимся определять этот самый .
Всего точек у нас будет (например, , , ; тогда у нас будет 3 точки). Этому соответствует диапазон входных значений . Значению соответствует , соответствует . Последняя точка имеет индекс . Чему соответствует ?
Для линейной шкалы , где определяется диапазоном входных значений. Тут можно поступить аналогично, только вместо умножения будет возведение в степень: (помним, что ). Есть один, правда, ньюанс: при у нас , а должно бы. Это решается просто — вычтем единицу: . И тогда для нулевого случая все сходится. Как рассчитать в данном случае? Есть разные варианты. Я это предпочитаю сделать следующим образом.
Нам известно, что . В то же время мы теперь знаем, что . Получается уравнение: . Решим его относительно : . Вспомнив, чему равно и заменив корень возведением в степень, получим приемлемый для компьютера вид: (напоминаю, что ). Прекрасно, базовая величина получена!
Фактически, мы получили алгоритм преобразования из экранной координаты в абстрактную — обратная задача. Теперь режим прямую задачу — преобразование из абстрактной координаты в экранную. Задача решается несложно. Фактически, нужно найти , а для него несложно и .
Для нахождения надо решить уравнение относительно : . Ну а дальше уже из свойств логарифма получим, что . Ну и далее, рассматривая экранные координаты как линию с наклоном, получим, что (для полной красоты надо еще заменить на ).
Вроде бы базовую математику рассмотрели. Нашли ошибки или неточности — пишите в комментариях, буду благодарен!
Со временем напишу следующую статью — реализацию этой математики средствами Qt языка C++.
Какую шкалу графика выбрать
При подготовке инструкции по работе с графиками на сайте Stockcharts.com я не уточнила такой важной момент, как выбор шкалы. Уточняю. Если вы посмотрите на график движения цены, то увидите на нем две оси. По горизонтальной оси X отложено время, по вертикальной оси Y – цена.
Для оси X используется арифметическая (линейная) шкала. Для оси Y может применяться как арифметическая, так и логарифмическая шкала. В чем их отличие?
Арифметическая шкала показывает простое изменение цены в количестве пунктов или долларов. Логарифмическая шкала показывает не абсолютное изменение цены, а относительное, то есть не в количестве пунктов или долларов, а в процентном соотношении.
На арифметической шкале все единичные отрезки имеют одинаковую длину. Интервалы логарифмической шкалы не равны, так как с ростом цены процентные изменения уменьшаются и, как следствие, отрезки становятся уже, а деления чаще.
Принцип построения арифметической шкалы
Арифметическая шкала строится от нуля и с помощью сложения и вычитания. При перемещении вправо от нуля значения складываются, а при перемещении влево от нуля – вычитаются. Значение показателя по мере продвижения оси изменяется на равную величину. В результате отрезок шкалы 10-20 будет равен отрезку 100-110, несмотря на то, что в первом варианте изменение составит 100% (2 раза), а во втором – лишь 10%.
Принцип построения логарифмической шкалы
В логарифмической шкале равным отрезкам соответствует одинаковое процентное изменение показателя. Например, отрезок шкалы 10-20 будет равен отрезкам 20-40 и 40-80, т.е. изменение показателя во всех случаях составит 2 раза. Данная шкала строится от единицы с помощью умножения и деления. И для того чтобы переместиться на такое же расстояние как в арифметической шкале, например, на 10, необходимо 1 умножить на 10. В свою очередь, для перемещения на 10 влево, нужно 1 разделить на 10.
Отображение графиков с разной шкалой
При работе с графиками на коротких интервалах времени разница между арифметическим и логарифмическим способами шкалирования едва заметна. Однако при больших ценовых колебаниях и длительных периодах различия существенны. Эта хорошо видно на рисунке ниже. На нем я наложила графики индекса NYSE Composite ($NYA) за более чем 20-летний период. Менее четкая линия – это линия графика, построенного по логарифмической шкале.
График индекса NYSE Composite ($NYA), построенный по арифметической и логарифмической шкале
Живая версия графиков доступна здесь и здесь.
Обратите внимание, что диапазон колебаний на графике с арифметической шкалой выше, чем с логарифмической. Кроме этого, на графике с арифметической шкалой есть ощущение более существенного движения и изменения. Поэтому такой способ построения любят СМИ: он позволяет преувеличить значения показателей и раздуть новость. Этого не происходит, когда данные отображаются на логарифмической шкале. И именно ее я рекомендую использовать при работе с графиками, охватывающими данные за длительный период.
Данное руководство расскажет, как в Excel создать линейчатую диаграмму со значениями, автоматически отсортированными по убыванию или по возрастанию, как создать линейчатую диаграмму с отрицательными значениями, как настраивать ширину полос линейчатой диаграммы и многое другое.
Линейчатые диаграммы, наравне с круговыми диаграммами, входят в число самых популярных диаграмм. Построить линейчатую диаграмму не сложно, а понять – ещё проще. Для каких данных лучше всего использовать линейчатую диаграмму? Для любых числовых данных, которые нужно сравнить: числа, проценты, температуры, частоты и прочие измерения. В целом, линейчатая диаграмма подойдёт для того, чтобы сравнить отдельные значения нескольких категорий данных. Особый вид линейчатой диаграммы – диаграмма Ганта, часто используется в приложениях для управления проектами.
В данном руководстве мы рассмотрим следующие вопросы, касающиеся линейчатых диаграмм в Excel:
- Линейчатые диаграммы в Excel – основы
- Как создать линейчатую диаграмму в Excel
- Создание линейчатых диаграмм разного типа
- Настройка линейчатых диаграмм в Excel
- Изменение ширины полос и расстояния между полосами диаграммы
- Построение линейчатой диаграммы с отрицательными значениями
- Сортировка данных в линейчатых диаграммах Excel
Содержание
- Линейчатые диаграммы в Excel – основы
- Как построить линейчатую диаграмму в Excel
- Как увидеть все доступные типы линейчатой диаграммы
- Выбираем макет и стиль линейчатой диаграммы
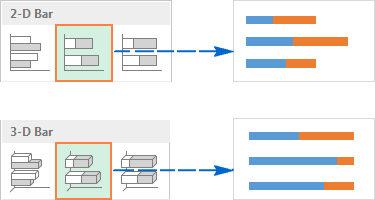
- Типы линейчатых диаграмм в Excel
- Линейчатая с группировкой
- Линейчатая с накоплением
- Нормированная линейчатая с накоплением
- Цилиндры, конусы и пирамиды
- Как в Excel 2013 и 2016 при построении диаграммы использовать цилиндр, конус или пирамиду
- Настройка линейчатых диаграмм в Excel
- Изменение ширины полос и расстояния между полосами диаграммы
- Построение линейчатой диаграммы с отрицательными значениями
- Настраиваем подписи вертикальной оси
- Меняем цвет заливки для отрицательных значений
- Сортировка данных в линейчатых диаграммах Excel
- Расставляем данные в линейчатой диаграмме Excel в порядке убывания/возрастания без сортировки исходных данных
- Изменяем порядок рядов данных в линейчатой диаграмме
- Изменяем порядок рядов данных при помощи диалогового окна «Выбор источника данных»
- Изменяем порядок рядов данных при помощи формул
Линейчатые диаграммы в Excel – основы
Линейчатая диаграмма – это график, показывающий различные категории данных в виде прямоугольных полос (линеек), длины которых пропорциональны величинам элементов данных, которые они отображают. Такие полосы могут быть расположены горизонтально (линейчатая диаграмма) или вертикально. График с вертикальными полосами – это отдельный тип диаграммы в Excel, называется гистограмма.
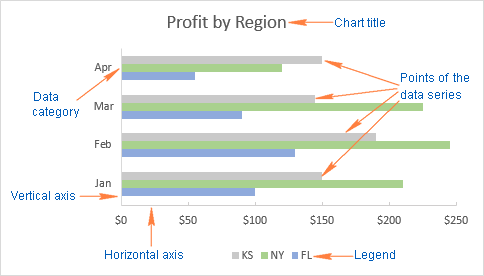
Чтобы упростить дальнейшее изучение данного руководства и точно знать, что мы с Вами правильно понимаем друг друга, давайте определим основные термины, которыми обозначены элементы линейчатой диаграммы в Excel. На следующем рисунке показана стандартная линейчатая диаграмма с группировкой, которая содержит 3 ряда данных (серый, зелёный и голубой) и 4 категории данных (Jan, Feb, Mar и Apr).
Как построить линейчатую диаграмму в Excel
Нет ничего проще, чем построить линейчатую диаграмму в Excel. Сначала выделите данные, которые нужно показать на диаграмме, затем на вкладке Вставка (Insert) в разделе Диаграммы (Charts) кликните иконку линейчатой диаграммы и выберите, какой подтип нужно создать.
В данном примере мы создаём самую простую диаграмму – Линейчатая с группировкой (2-D clustered Bar):
Линейчатая диаграмма с группировкой, вставленная на рабочий лист Excel, будет выглядеть примерно так:
Показанная на рисунке выше линейчатая диаграмма Excel, отображает только один ряд данных, поскольку исходные данные содержат только один столбец с числами. Если в исходных данных окажется два или более столбцов с числами, то линейчатая диаграмма будет содержать несколько рядов данных, окрашенных в разные цвета:
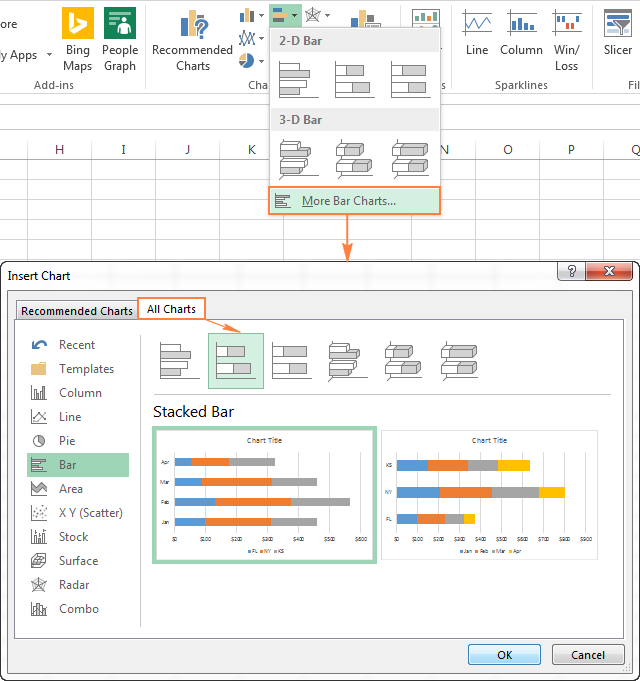
Как увидеть все доступные типы линейчатой диаграммы
Чтобы увидеть все доступные в Excel типы линейчатой диаграммы, нажмите ссылку Другие линейчатые диаграммы (More Column Charts) и в открывшемся диалоговом окне Вставка диаграммы (Insert Chart) выберите один из доступных подтипов диаграммы.
Выбираем макет и стиль линейчатой диаграммы
Если предложенный по умолчанию макет или стиль линейчатой диаграммы, вставленной на рабочий лист Excel, не вызывает восторга, то выделите её, чтобы на Ленте меню появилась группа вкладок Работа с диаграммами (Chart Tools). После этого на вкладке Конструктор (Design) можно сделать следующее:
- В разделе Макеты диаграмм (Chart Layouts) нажмите кнопку Экспресс-макет (Quick Layout) и попробуйте различные готовые макеты линейчатой диаграммы;
- Или поэкспериментируйте со стилями линейчатой диаграммы в разделе Стили диаграмм (Chart Styles).
Типы линейчатых диаграмм в Excel
Создавая линейчатую диаграмму в Excel, можно выбрать один из следующих подтипов:
Линейчатая с группировкой
Линейчатая диаграмма с группировкой (2-D или 3-D) сравнивает значения в категориях данных. В линейчатой диаграмме с группировкой категории обычно построены по вертикальной оси (ось Y), а значения – по горизонтальной (ось X). 3-D линейчатая диаграмма с группировкой не отображает третью ось, а просто делает полосы графика объёмными.
Линейчатая с накоплением
Линейчатая диаграмма с накоплением показывает пропорции отдельных элементов в отношении к целому. Как и линейчатая диаграмма с группировкой, она может быть плоской (2-D) или объёмной (3-D):
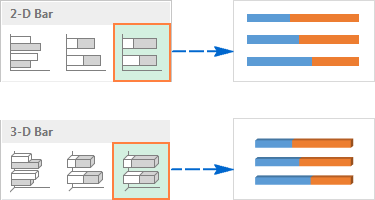
Нормированная линейчатая с накоплением
Этот тип линейчатой диаграммы похож на предыдущий, но показывает долю в процентах каждого элемента относительно целого для каждой категории данных.
Цилиндры, конусы и пирамиды
Кроме стандартных прямоугольников, для построения всех перечисленных подтипов линейчатой диаграммы можно использовать цилиндры, конусы или пирамиды. Разница только в форме фигуры, которая отображает исходные данные.
В Excel 2010 и более ранних версиях диаграмму с цилиндрами, конусами или пирамидами можно было построить, выбрав соответствующий тип графика на вкладке Вставка (Insert) в разделе Диаграммы (Charts).
На Ленте меню Excel 2013 и Excel 2016 не предлагается использовать цилиндры, конусы или пирамиды. Как сообщает Microsoft, эти типы диаграмм были убраны, поскольку слишком большое разнообразие типов диаграмм в ранних версиях Excel затрудняло пользователю выбор нужного типа. Тем не менее, возможность использовать цилиндр, конус или пирамиду доступна и в современных версиях Excel, правда для этого потребуется сделать несколько дополнительных действий.
Как в Excel 2013 и 2016 при построении диаграммы использовать цилиндр, конус или пирамиду
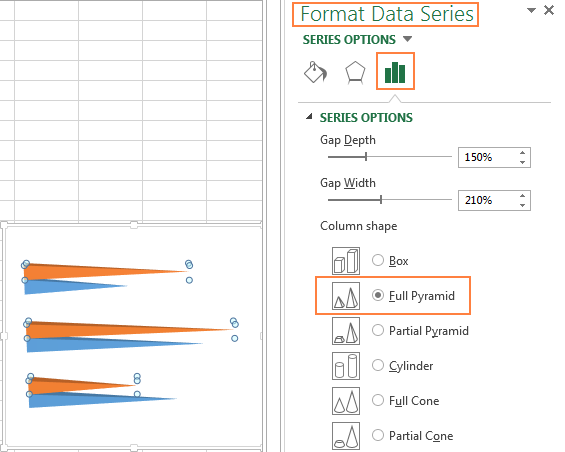
Чтобы в Excel 2013 и 2016 при построении диаграммы использовать цилиндр, конус или пирамиду, создайте объёмную линейчатую диаграмму нужного типа (с группировкой, с накоплением или нормированную с накоплением) и затем измените фигуры, использованные для построения рядов:
- Выделите все полосы на диаграмме, кликните по ним правой кнопкой мыши и в контекстном меню нажмите Формат ряда данных (Format Data Series), либо просто дважды кликните по полосе графика.
- В появившейся панели в разделе Параметры ряда (Series Options) выберите подходящую Фигуру (Column shape).
Замечание: Если на диаграмме построено несколько рядов данных, то описанную процедуру необходимо повторить для каждого ряда в отдельности.
Настройка линейчатых диаграмм в Excel
Как и другие типы диаграмм Excel, линейчатые диаграммы предоставляют множество настроек для таких элементов, как название диаграммы, оси, подписи данных и прочее. Более подробную информацию Вы сможете найти по ссылкам ниже:
- Добавляем название диаграммы
- Настраиваем оси диаграммы
- Добавляем подписи данных
- Добавляем, убираем, перемещаем и настраиваем формат легенды
- Показываем или скрываем линии сетки
- Изменяем или скрываем ряды данных
- Изменяем тип и настраиваем стиль диаграммы
- Изменяем стандартные цвета диаграммы
А теперь давайте рассмотрим некоторые специфические приёмы, применимые к линейчатым диаграммам в Excel.
Изменение ширины полос и расстояния между полосами диаграммы
В линейчатой диаграмме, созданной в Excel с использованием настроек по умолчанию, между полосами остаётся слишком много пустого пространства. Чтобы сделать полосы шире и визуально приблизить их друг к другу, выполните следующие шаги. Таким же способом можно сделать полосы уже и увеличить расстояние между ними. В плоской 2-D диаграмме полосы могут даже накладываться одна на другую.
- В линейчатой диаграмме Excel кликните правой кнопкой мыши по любому ряду данных (полосе) и в контекстном меню нажмите Формат ряда данных (Format Data Series)
- В появившейся панели в разделе Параметры ряда (Series Options) сделайте одно из следующих действий:
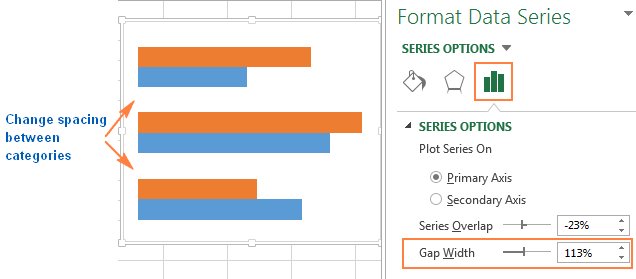
- Для плоской или для объёмной диаграммы: чтобы изменить ширину полосы и промежуток между категориями, переместите ползунок параметра Боковой зазор (Gap Width) или введите значение в процентах от 0 до 500 в поле ввода. Чем меньше значение, тем тоньше полосы и меньше зазор между ними, и наоборот.
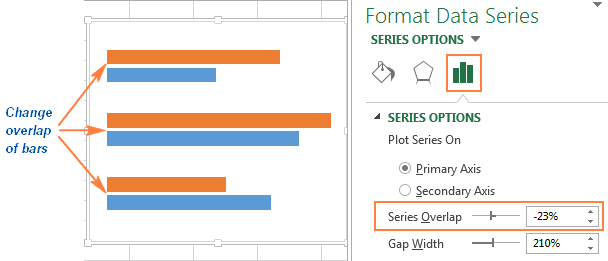
- Для плоской диаграммы: чтобы изменить зазор между рядами в одной категории, переместите ползунок параметра Перекрытие рядов (Series Overlap) или введите в поле ввода значение в процентах от -100 до 100. Чем больше значение, тем больше перекрытие рядов. Отрицательное значение приведёт к появлению зазора между рядами, как на картинке ниже:
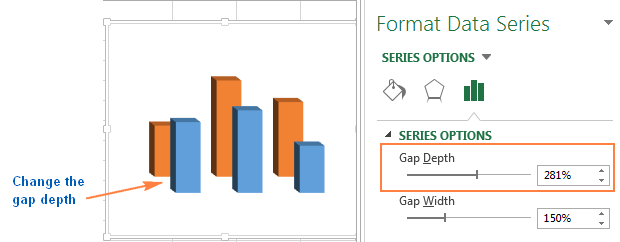
- Для объёмной (3-D) диаграммы: чтобы изменить зазор между рядами данных, переместите ползунок параметра Фронтальный зазор (Gap Depth) или введите значение от 0 до 500 процентов. Чем больше значение, тем больше расстояние между полосами. Изменение фронтального зазора заметно отражается в большинстве линейчатых диаграмм Excel, но лучше всего – в объёмной гистограмме, как показано на следующей картинке:
- Для плоской или для объёмной диаграммы: чтобы изменить ширину полосы и промежуток между категориями, переместите ползунок параметра Боковой зазор (Gap Width) или введите значение в процентах от 0 до 500 в поле ввода. Чем меньше значение, тем тоньше полосы и меньше зазор между ними, и наоборот.
Построение линейчатой диаграммы с отрицательными значениями
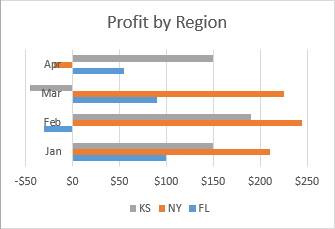
Для построения линейчатой диаграммы в Excel исходные значения не обязательно должны быть больше нуля. В целом, в Excel нет никаких проблем с отображением отрицательных значений на стандартной линейчатой диаграмме, но вид диаграммы, вставляемой по умолчанию на рабочий лист Excel, заставляет задуматься о правках в макете и оформлении.
Чтобы как-то улучшить вид диаграммы на рисунке выше, во-первых, было бы неплохо сместить подписи вертикальной оси влево, чтобы они не накладывались на полосы отрицательных величин, и во-вторых, можно использовать другие цвета для отрицательных значений.
Настраиваем подписи вертикальной оси
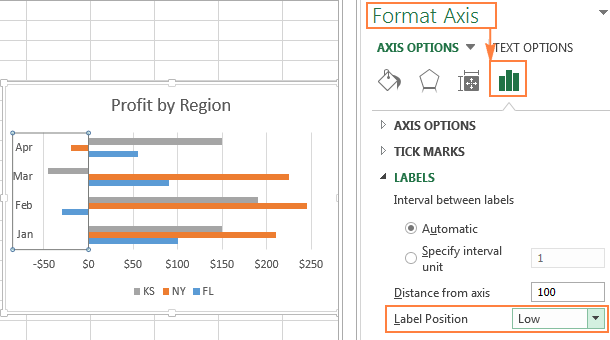
Чтобы изменить параметры оформления вертикальной оси, кликните по любой из её подписей и в контекстном меню нажмите Формат оси (Format Axis), или просто дважды кликните по подписям оси. В правой части рабочего листа появится панель.
Откройте вкладку Параметры оси (Axis Options), разверните раздел Подписи (Labels) и установите для параметра Положение метки (Labels Position) значение Внизу (Low).
Меняем цвет заливки для отрицательных значений
Если нужно привлечь внимание к отрицательным значениям на диаграмме, то это с успехом можно сделать, если полосы отрицательных значений будут окрашены в другой цвет.
Если в линейчатой диаграмме Excel построен только один ряд данных, то отрицательные значения, как это часто делается, можно окрасить в красный цвет. Если рядов данных на диаграмме несколько, то отрицательные значения в каждом из них нужно будет окрасить в свой цвет. Например, можно использовать определенные цвета для положительных значений, а для отрицательных — их более бледные оттенки.
Для того, чтобы изменить цвет отрицательных полос, выполните следующие действия:
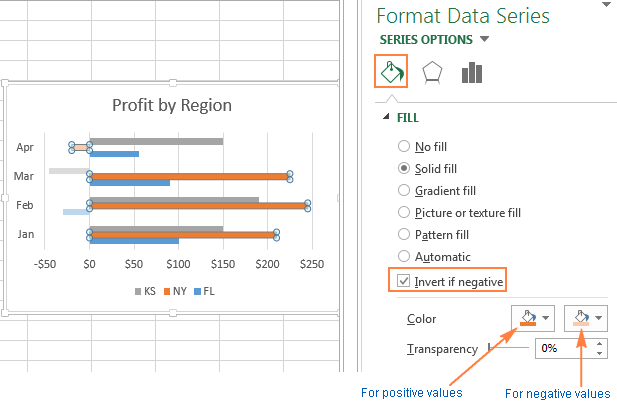
- Кликните правой кнопкой мыши по любой полосе ряда данных, цвет которого нужно изменить (в нашем примере это оранжевая полоса) и в контекстном меню нажмите Формат ряда данных (Format Data Series).
- В появившейся панели на вкладке Заливка и границы (Fill & Line) отметьте галочкой параметр Инверсия для чисел <0 (Invert if Negative)
- Сразу после этого появится два поля выбора цвета – для положительных и для отрицательных значений.
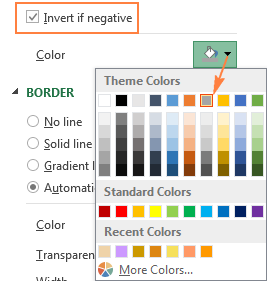
Совет: Если второе поле выбора цвета не появилось, кликните маленькую чёрную стрелку в пока единственном доступном поле и укажите цвет для положительных значений (можете выбрать тот же, что назначен по умолчанию). Сразу после этого появится второе поле выбора цвета для отрицательных значений:
Сортировка данных в линейчатых диаграммах Excel
При создании линейчатой диаграммы в Excel категории данных по умолчанию выстраиваются в обратном порядке. То есть, если исходные данные отсортированы от А до Я, то в линейчатой диаграмме они будут расположены от Я до А. Почему так принято в Excel? Никто не знает. Зато мы знаем, как это исправить.
Примечание переводчика: Автор не знает почему так, хотя с точки зрения математики всё вполне логично: Microsoft Excel строит график от начала координат, которое находится стандартно в левом нижнем углу. То есть первое значение, верхнее в таблице данных, будет отложено первым снизу и так далее. Это работает и для диаграмм, построенных на трёх осях. В таком случае первый ряд данных в таблице будет отложен ближним по оси Z и далее по порядку.
Простейший способ развернуть порядок категорий на линейчатой диаграмме – выполнить обратную сортировку в исходной таблице.
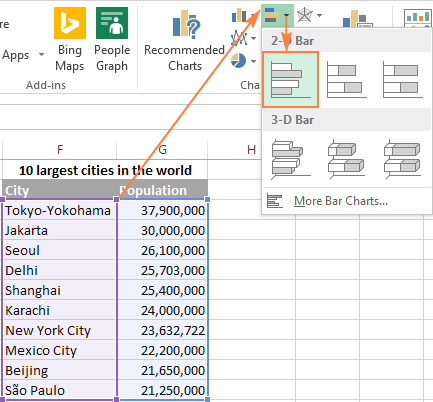
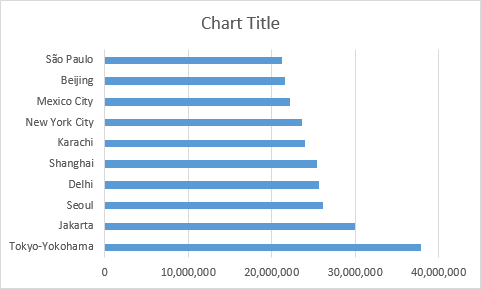
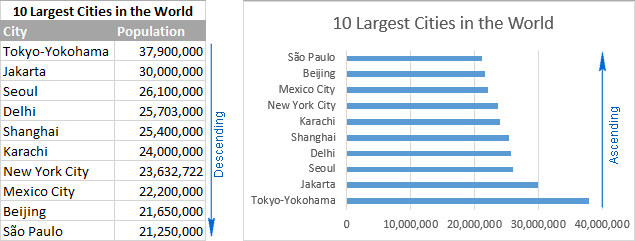
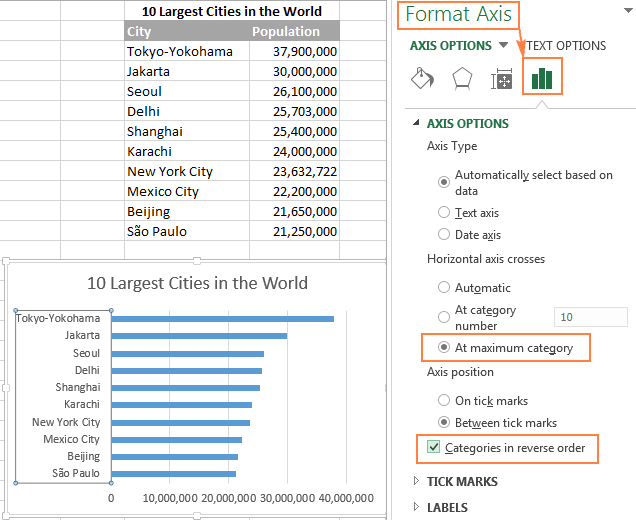
Проиллюстрируем это на примере простого набора данных. На рабочем листе содержится список из 10 крупнейших городов мира, расставленных в порядке убывания числа населения. В линейчатой диаграмме данные будут расположены сверху вниз по возрастанию.
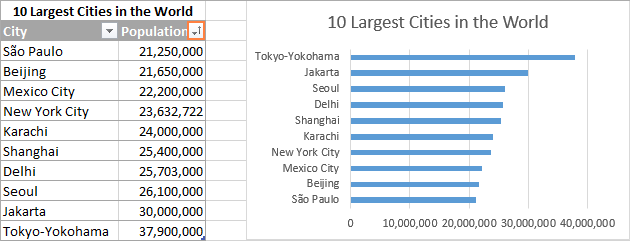
Чтобы на диаграмме Excel данные расположились от больших к меньшим сверху вниз, достаточно упорядочить их в исходной таблице в обратном порядке, т.е. от меньших к большим:
Если по каким-либо причинам сортировка данных в таблице невозможна, то далее будет показан способ изменить порядок расположения данных на диаграмме Excel, не изменяя порядок данных в исходной таблице.
Расставляем данные в линейчатой диаграмме Excel в порядке убывания/возрастания без сортировки исходных данных
Если порядок исходных данных на рабочем листе имеет значение и изменён быть не может, давайте заставим полосы диаграммы появиться в точности в том же порядке. Это просто – нужно лишь включить пару дополнительных опций в настройках параметров.
- В линейчатой диаграмме Excel кликните правой кнопкой мыши по любой из подписей вертикальной оси и в контекстном меню нажмите Формат оси (Format Axis). Или просто дважды кликните по подписям вертикальной оси.
- В появившейся панели в разделе Параметры оси (Axis Options) настройте следующие параметры:
- В группе Пересечение с горизонтальной осью (Horizontal axis crosses) выберите В точке с максимальным значением категории (At maximum category).
- В группе Положение оси (Axis position) выберите Обратный порядок категорий (Categories in reverse order).
Готово! Данные в линейчатой диаграмме Excel немедленно выстроятся в том же порядке, что и в исходной таблице, – по возрастанию или по убыванию. Если порядок исходных данных будет изменён, то данные на диаграмме автоматически повторят эти изменения.
Изменяем порядок рядов данных в линейчатой диаграмме
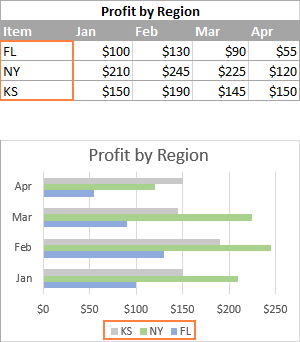
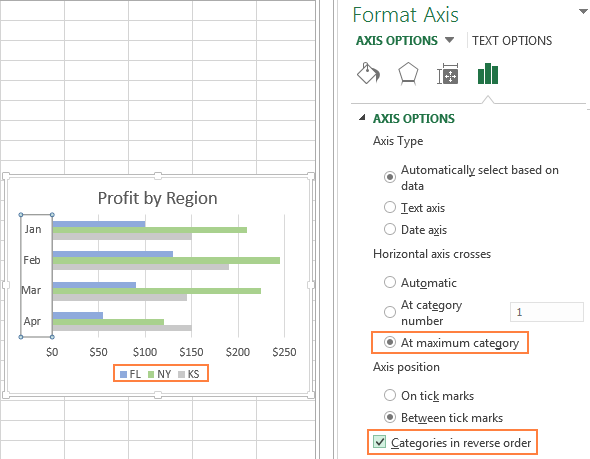
Если в линейчатой диаграмме Excel содержится несколько рядов данных, то по умолчанию они также построены в обратном порядке. Обратите внимание на рисунок ниже: регионы в таблице и на диаграмме расположены в противоположном порядке.
Чтобы расположить ряды данных в линейчатой диаграмме в том же порядке, как и на рабочем листе, используйте параметры В точке с максимальным значением категории (At maximum category) и Обратный порядок категорий (Categories in reverse order), как мы сделали это в предыдущем примере. Порядок построения категорий при этом также изменится, как видно на следующем рисунке:
Если нужно расставить ряды данных в линейчатой диаграмме в порядке, отличающемся от порядка данных на рабочем листе, то это можно сделать при помощи:
- Диалогового окна «Выбор источника данных»
- Формулы ряда данных
Изменяем порядок рядов данных при помощи диалогового окна «Выбор источника данных»
Этот метод позволяет изменить порядок построения рядов данных в линейчатой диаграмме для каждого ряда в отдельности и сохранить при этом неизменным порядок исходных данных на рабочем листе.
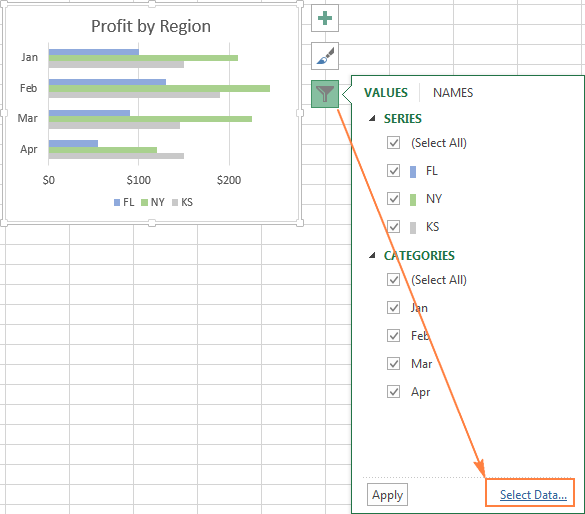
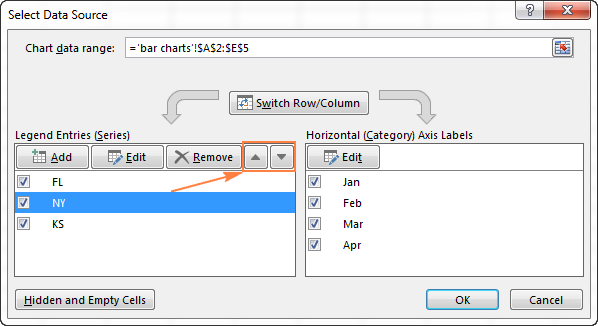
- Выделите диаграмму, чтобы на Ленте меню появилась группа вкладок Работа с диаграммами (Chart Tools). Откройте вкладку Конструктор (Design) и в разделе Данные (Data) нажмите кнопку Выбрать данные (Select Data). Или нажмите иконку Фильтры диаграммы (Chart Filters) справа от диаграммы и кликните ссылку Выбрать данные (Select Data) внизу открывшегося меню.
- В диалоговом окне Выбор источника данных (Select Data Source) выберите ряд данных, для которого нужно изменить порядок построения, и переместите его вверх или вниз при помощи стрелок:
Изменяем порядок рядов данных при помощи формул
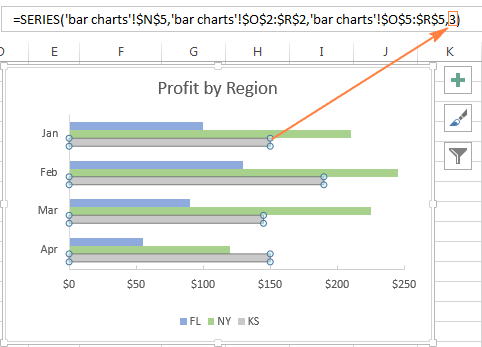
Каждый ряд данных в диаграммах Excel (не только линейчатой – любой диаграммы) задан формулой, поэтому можно изменить ряд данных, изменяя его формулу. В рамках этой статьи нам интересен только последний аргумент этой формулы, который определяет порядок построения рядов. Более подробно о формуле ряда данных Вы можете прочитать в этой статье.
Например, серый ряд данных линейчатой диаграммы в следующем примере занимает третье место.
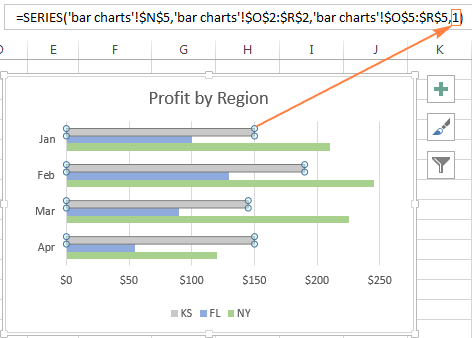
Чтобы изменить порядок построения данного ряда данных, выделите его в диаграмме, затем в строке формул измените последний аргумент формулы на любое другое число. В нашем примере, чтобы переместить ряд данных на одну позицию вверх, введите «2», а чтобы сделать его первым в диаграмме, введите «1» в качестве последнего аргумента.
Как и настройка параметров в диалоговом окне Выбор источника данных (Select Data Source), редактирование формулы ряда данных приводит к изменению порядка рядов данных только в диаграмме; исходные данные на рабочем листе остаются неизменными.
Вот так происходит построение линейчатой диаграммы в Excel. Для тех, кто желает узнать больше о диаграммах Excel, рекомендую изучить статьи из этого раздела сайта. Спасибо за внимание!
Оцените качество статьи. Нам важно ваше мнение:
На чтение 11 мин. Просмотров 549
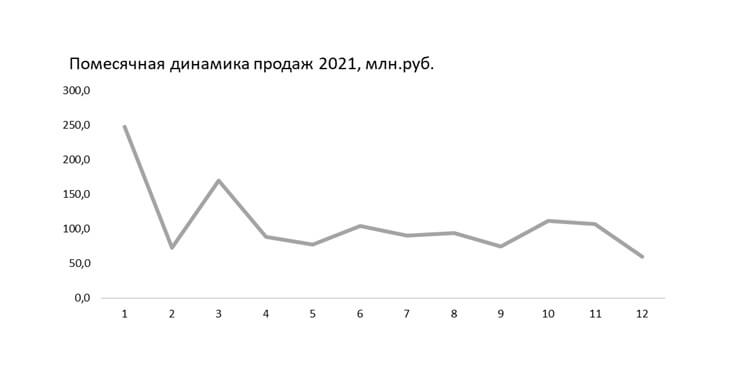
Линейный график — это простой графический способ визуализации информации, который отлично подходит для отображения непрерывных данных. В рамках данной статьи, читатель сможет понять, как легко можно построить линейный график в Excel и в других инструментах визуализации. Однако, несмотря на свою простоту, есть масса особенностей и нюансов, которые позволят сделать визуальную составляющую удобной и более читаемой, но об этом далее.
Содержание
- Общее понимание линейного графика
- Для какой цели используется линейная диаграмма
- Типы линейных диаграмм в Excel
- Плюсы и минусы линейного графика
- Добавляем линейную диаграмму в Excel
- Другие инструменты построения линейного графика
- Линейный график в Google Таблицах
- Линейный график в в Power BI
- Онлайн сервисы для построения линейного графика
- Строим линейный график в Yandex DataLens
- Линейный график с помощью Python
- 7 примеров улучшения визуализации графика в Excel и не только
- Выбирайте подходящий интервал измерения
- Расхламление основной области диаграммы
- Предоставьте дополнительный контекст
- Не добавляйте слишком много линий
- Сохраняйте острые углы
- Использование двойной оси
- График начинаться с нуля?
- FAQ по линейным графикам
Общее понимание линейного графика
Линейный график [англ. line graph] — это график, который использует точки и линии для отображения изменений во времени. По сути это вид диаграммы, которая показывает линию, соединяющую несколько точек массива данных. Линейные графики являются распространенными и эффективными диаграммами, потому как они просты, понятны и эффективны.
Всякий раз, когда вы слышите эту ключевую фразу «с течением времени», это подсказка, чтобы рассмотреть возможность использования линейного графика для ваших данных. По большей части, линейные графики лучше всего подходят, когда вы хотите показать, как значения меняются с течением времени, или сравнить, как несколько вещей изменяются в динамике по отношению друг к другу. По сути это идеальный вариант применения такого типа визуализации, но не единственный.
Для какой цели используется линейная диаграмма
Ввиду того, что в этой статьи старались описать «правильные» принципы работы с линейным графиком, нельзя не упомянуть о том, что график должен представлять значимую информацию для пользователя. Поэтому и выбирать этот тип визуализации необходимо для соответствующих целей.
Линейные диаграммы отлично подходят для:
- отображения изменений и тенденций в динамике
- сравнения большого количества данных одновременно
- фиксирования аномалий или среднего значения на столбчатой диаграмме
- включения важного контекста и аннотации
- отображения данных прогноза и вероятности
При этом, линейный график не самый лучшим выбором для:
- отображение количества вещей
- работа с категориальными данными
- сравнения части с целым
- отображения разреженных наборов данных
Всегда стоит помнить, что элементов визуализаций много, но для каждого отдельного случая необходимо выбирать наиболее подходящий элемент. Идеальный вариант для линейного графика — это динамика.
Типы линейных диаграмм в Excel
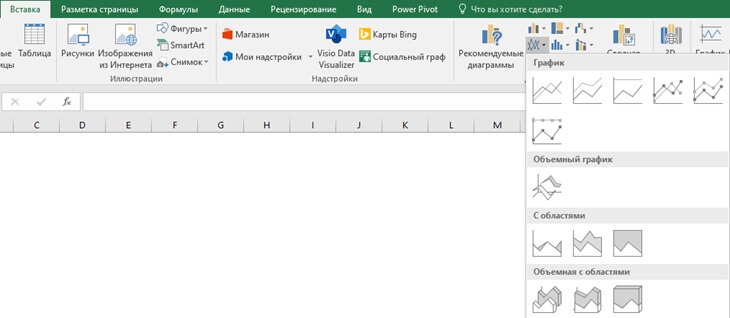
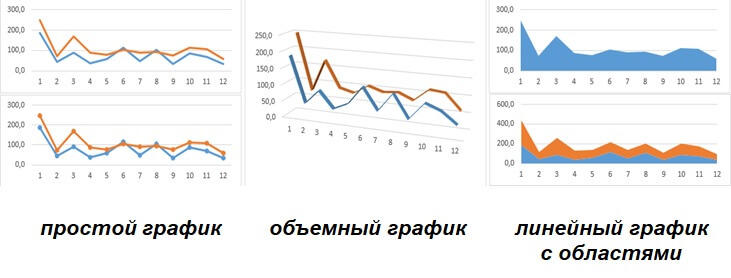
Любая диаграмма и график в Microsoft Excel добавляются в меню ВСТАВКА — Раздел ДИАГРАММЫ. Для построения линейного графика в Excel возможно выбрать три различных варианта:
- простой график, в т.ч. с накоплением или маркерами
- объемный график
- линейный график с областями
Простые линейные графики. Базовый линейный график, который соединяет точки массива данных простой линией. Если, для построения графика выбирается несколько рядов данных, они будут отображаться в одной области диаграммы независимыми линиями.
Объемный график. Тоже что и простой линейный график, только в 3D. Визуальная составляющая так себе, но нужно танцевать от задач, иногда может пригодиться
График с областями. Не совсем линейный, но… Применяется, если важен порядок категорий либо, когда необходимо показать вклад одного показателя в другом. Интересный вариант для наглядной демонстрации выполнения плана, при котором план — это вся область, а факт второй набор данных.
Спарклайн. Данный тип визуализации также можно отнести к линейному графику, просто сам график размещается в ячейке с данными, а не отдельной областью. Это особый элемент визуализации данных, который заслуживает отдельного внимания и выделен в отдельную статью на страницах этого сайта. Спарклайн-график поможет вам избежать рутины в создании большой диаграммы, которая иногда может запутать во время анализа.
Плюсы и минусы линейного графика
Некоторые недостатки линейного графика:
- при размещении большого количества линий в одной области, график становится нечитаемым
- линейный график ограничен только числовым набором данных
- при наличии дробных значений в массиве данных, линейный график трудно детализировать
Теперь о плюсах:
- помогает отобразить тенденции за разный период
- легко воспринимается пользователем
- вполне подходит для сравнения небольшого количества сопоставимых показателей
Добавляем линейную диаграмму в Excel
От теории пора переходить к практике. Линейный график в Excel строится в 3 простых шага:
Шаг 1 Для начала выделите таблицу данных, включая заголовки столбцов.
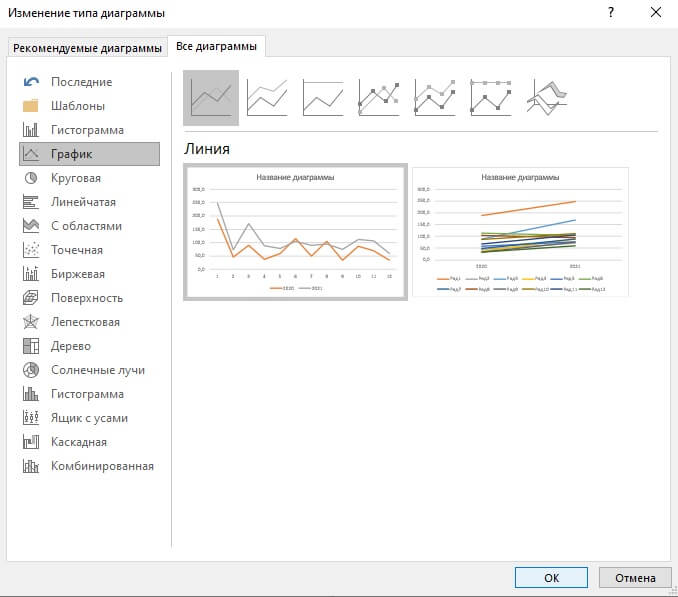
Шаг 2 Выбрать меню «Вставка» и выберите значок линейной диаграммы либо меню «Рекомендуемые диаграммы».
Шаг 3 Выбрать наиболее подходящий вариант графика и нажать ОК.
Теперь у нас есть простой линейный график, но это не совсем то, что мы себе представляли. Excel сделал точки данных, например, месяца отдельной линией (нужно будет удалить этот ряд), а визуальная составляющая и вовсе хромает. Далее уже остается настроить визуальную привлекательность графика и все готово.
Другие инструменты построения линейного графика
Несмотря на то, что Excel является самым востребованным способом построения линейного графика, однако есть и другие инструменты. Кратко пробежимся по основным из них.
Линейный график в Google Таблицах
Всего тремя кликами мыши можно сделать вполне читаемый линейный график в Google Таблицах, а впоследствии настроить его применяя некоторые рекомендации по визуализации.
- Выбор и выделение массива данных.
- Переход в меню «Вставка» и подменю «Диаграмма».
- Отобразится график, при этом откроется боковая панель для настройки диаграммы.
- Выбирается вариант, который больше всего подходит под цели визуализации.
Наглядный пример как создать линейный график в Google Таблицах в коротеньком видео ниже
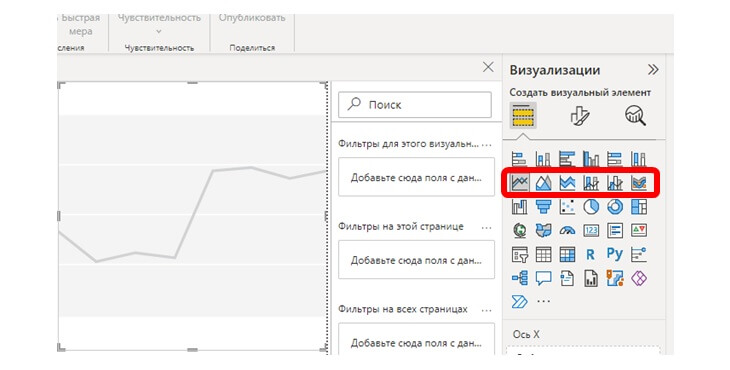
Линейный график в в Power BI
В Power BI добавление линейного графика проще, чем Excel, так как панель инструментов доступна сразу. Выбираем нужный тип графика, и он добавляется в рабочую область. Далее перетаскиваем нужные поля, удерживая их кнопкой мыши и всё.
Онлайн сервисы для построения линейного графика
Случаются моменты, когда картинка необходима быстро, а под рукой нет нужного инструмента. Ниже добавлены 2 сайта, где можно сделать простой линейный график быстро и онлайн. Вносим данные и готово. Согласен, что это не самое удобное решение, но оно есть:
- https://www.mathsisfun.com/data/data-graph.php
- https://www.rapidtables.com/tools/line-graph.html
Строим линейный график в Yandex DataLens
В справочном описании Yandex Cloud есть подробное пошаговое руководство по вставке линейного графика в Yandex DataLens, очень рекомендую прочитать более детально, а краткая выжимка ниже.
Линейный график с помощью Python
Есть несколько способов построить линейный график с помощью Python. Самый простой, с помощью импорта библиотеки Matplotlib или Plotly, хотя таких библиотек несколько. Сначала производится импорт библиотеки, а затем указываются значения данных по осям.
код:
import matplotlib.pyplot as plt
import numpy as np
# Define X and Y variable data
x = np.array([1, 2, 3, 4])
y = x*2
plt.plot(x, y)
plt.xlabel(«X-axis») # add X-axis label
plt.ylabel(«Y-axis») # add Y-axis label
plt.title(«Any suitable title») # add title
plt.show()
7 примеров улучшения визуализации графика в Excel и не только
Для настройки визуализации необходимы простые изменения дизайна значений по умолчанию Excel, однако они сделают график более понятным и легким для понимания данных аудиторией.
Выбирайте подходящий интервал измерения
Важным аспектом создания линейного графика является выбор правильного интервала на горизонтальной оси. Для временных данных слишком широкий интервал измерения может означать, что потребуется слишком много времени, чтобы увидеть в данных какую-либо тенденцию. С другой стороны, слишком короткий интервал измерения может выявить только шум, а не сигнал.
Тестируя различные интервалы или полагаясь на свои знания, вы можете определить хороший выбор размера шага. Также можно использовать несколько линий: одну линию для мелкозернистого интервала, а затем вторую линию для общего тренда с усреднением по скользящему окну.
Расхламление основной области диаграммы
Необходимо сосредоточиться на удалении элементов, которые занимают место, но не добавляют информативности.
Убираем границы диаграммы. Часто мы используем границу, чтобы различать части нашего слайда или визуального элемента. В большинстве случаев мы можем удалить границу графика и использовать пустое пространство, чтобы лучше отделить их друг от друга.
Удаление горизонтальных линий сетки. Этот шаг вносит дополнительный контраст, который позволяет линиям выделяться больше. Щелкните правой кнопкой мыши линии сетки, а затем выберите «Удалить» в меню, чтобы добиться этого. Эти два небольших изменения упрощают график и облегчают просмотр данных. В крайнем случае, если без линий нельзя, сделайте их еле заметным пунктиром.
Регулировка толщины и цвет линии. Сделайте акцент на данных и сделать их более заметными. Щелкните правой кнопкой мыши в любом месте строки и выберите «Формат ряда данных» в меню «Заливки и границы» можно редактировать толщину и цвет линии графика. Оптимальная толщина линии 3pt.
Ставим легенду. Уменьшите усилия пользователя необходимые для перехода от легенды к строке и обратно. Для этого необходимо переместить легенду в верхнюю часть графика в виде подзаголовка, чтобы аудитория прочитала ее до того, как доберется до диаграммы.
После изменения цвета и ширины линии у нас получился примерно вот такой график
Предоставьте дополнительный контекст
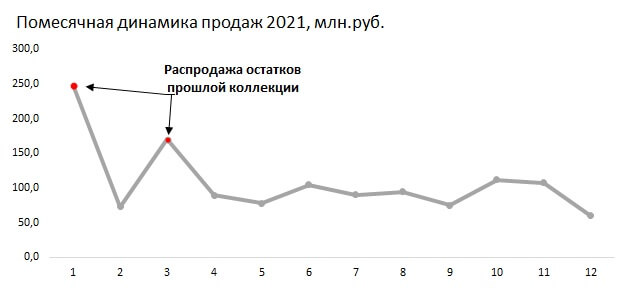
Наш график теперь выглядит значительно лучше, но мы можем сделать больше, чтобы улучшить ее еще немного. Есть некоторые элементы, которые нужно добавить в нашу линейную диаграмму, чтобы дать нашей аудитории дополнительное понимание того, на что обратить внимание.
Теперь у нас есть элегантная линейная диаграмма, показывающая основные реперные точки и причину акцентирования на них внимания пользователя. Данный прием не всегда актуален, но вполне приемлем в некоторых случаях.
Не добавляйте слишком много линий
Людям трудно уследить за более чем четырьмя или пятью вещами одновременно, поэтому рассмотрите возможность использования это количество в качестве ориентира. Если вам абсолютно необходимо показать больше линий, попробуйте использовать цвет, толщину линий и маркировку, а лучше столбчатую диаграмму, чтобы сосредоточиться на наиболее важных линиях или точках.
Сохраняйте острые углы
На стандартной линейной диаграмме каждая точка соединена со следующей отрезком прямой линии от первой до последней. Однако может возникнуть эстетическое искушение попытаться связать все точки плавно, сопоставив кривую, которая проходит через все точки одновременно. Не допускайте этого!
Попытка такой подгонки обязательно приведет к искажению восприятия трендов в данных. Предполагается, что направление и крутизна линии указывают на изменение значения, и поэтому кривая может в конечном итоге означать наличие дополнительных точек данных между фактическими измерениями, которых не существует.
Использование двойной оси
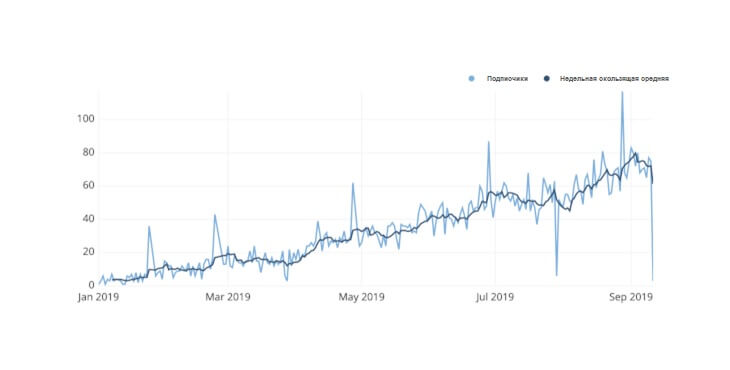
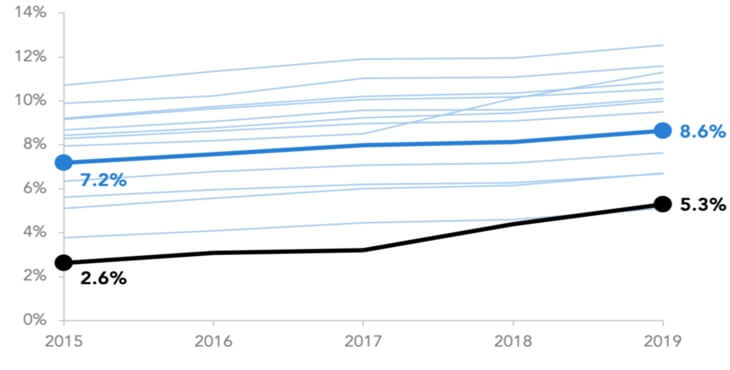
Когда линейный график включает в себя две линии, каждая из которых отображает сводку разных переменных, мы получаем график с двумя осями.
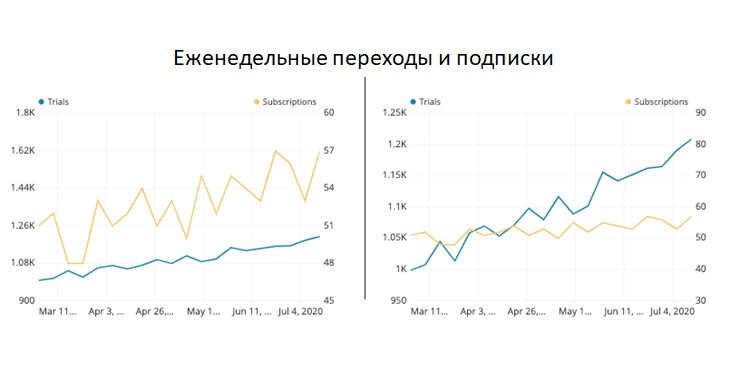
Проблема с двухосным графиком заключается в том, что им можно легко манипулировать, чтобы он вводить пользователя в заблуждение. В зависимости от того, как масштабируется каждая ось, воспринимаемое отношение между двумя линиями может быть изменено. На двух графиках ниже количество еженедельных переходов и подписок нанесено на двухосевые графики. Данные абсолютно одинаковы для каждой из них, но из-за выбора вертикального масштабирования для каждой переменной предполагаемая взаимосвязь между переменными изменится. Будьте с этим очень аккуратны.
График начинаться с нуля?
Когда мы смотрим на линейные графики, мы сравниваем линии друг с другом больше, чем их высоту от оси X. По своей природе линейные графики лучше показывают изменение значений с течением времени, чем точное количество в каждой измеряемой точке.
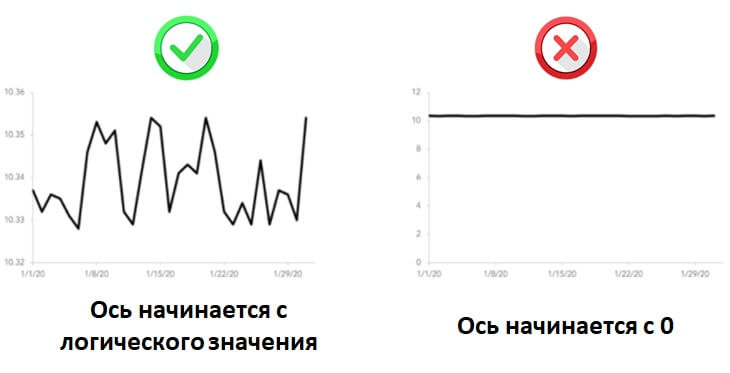
Таким образом, линейные графики не обязаны иметь нулевую базовую линию, но в большинстве случаев это все же целесообразно. Пользователя меньше смущает, если ось Y начинается с нуля, поскольку это нормальное ожидание при первом просмотре графика. Должны быть веские причины, чтобы подорвать эти ожидания.
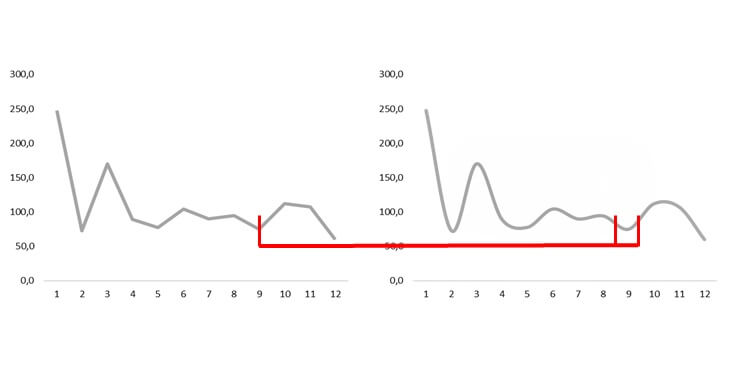
Ниже конкретный пример, для которого нулевой базовый уровень может быть не оптимальным
FAQ по линейным графикам
Для чего используется линейный график?
Как правило, линейные графики или линейные диаграммы используются для отслеживания изменений во времени, которые могут быть долгосрочными или краткосрочными. Также линейный график может применяться для сравнения изменений за один и тот же период для более чем одной группы.
Из каких частей состоит линейный график?
Линейный график включает в себя 4 основных элементов:
- шкала измерения (оси)
- заголовок
- область построения
- ряд данных
Может ли быть более одной линии на линейном графике?
Да, на линейном графике может быть более одной линии. Обычно это делается, когда нам нужно сравнить два или более набора информации, каждый набор представлен линией.
Всегда ли линейный график — это прямая линия?
Нет. Линия, образованная путем соединения всех точек данных на линейном графике, может быть прямой, а может и не быть таковой. График с прямой линией можно построить если точек 2, при большем их количестве возможны отклонение.
Сколько места необходимо оставить вверху и внизу графика?
Конкретный ответ на этот вопрос будет варьироваться в зависимости от каждого графика, который необходимо сделать. Полезной отправной точкой является создание диапазона от наименьшего значения до наибольшего, занимающего около 70-80% доступного вертикального пространства вашего графика с примерно равным количеством пустого пространства над и под ним. Сверху свободное пространство будет занимать название диаграммы, внизу — показатель по оси Х.