Как составить латинский квадрат

Н. Макарова

МЕТОДЫ ПОСТРОЕНИЯ
ЛАТИНСКИХ КВАДРАТОВ

Здесь
рассмотрены некоторые схемы построения классических латинских квадратов. При
этом латинские квадраты будем представлять в символьном виде, то есть заполнять
их не числами 1, 2, 3, …, n, а символьными элементами a1, a2, a3, …, an. Понятно, что от
символьного латинского квадрата очень легко перейти к латинскому квадрату,
заполненному числами, присвоив символьным элементам числовые значения 1, 2, 3,
… , n (или 0, 1, 2, … , n – 1) в любой комбинации.
Все латинские квадраты, получаемые варьированием значений символьных элементов,
будут изоморфными. Можно сказать, что эти квадраты получаются друг из
друга преобразованием, которое я назвала трансформацией тождественной
перестановки чисел. Понятно, что группа получаемых таким преобразованием
изоморфных латинский квадратов будет содержать n! квадратов.

ЦИКЛИЧЕСКИЙ СДВИГ

Циклический
сдвиг – очень простая схема построения латинских квадратов. Она работает для
латинских квадратов любого порядка. Каждая следующая строка (или каждый
следующий столбец) латинского квадрата получается из предыдущей строки (или
столбца) циклическим сдвигом с постоянным шагом k. Для квадрата порядка n шаг k может быть таким, что у k нет общих делителей с n, кроме 1.

Интересно
отметить, что для порядков, являющихся простым числом, этим методом строится
полная группа взаимно ортогональных латинских квадратов.

 На рис. 1
– 5 вы видите латинские квадраты порядков 2 — 6, построенные данным методом.

Рис. 1

a1

a2

a3

a1

a2

a3

a2

a3

a1

a3

a1

a2

a3

a1

a2

a2

a3

a1

Рис. 2

a1

a2

a3

a4

a1

a2

a3

a4

a2

a3

a4

a1

a4

a1

a2

a3

a3

a4

a1

a2

a3

a4

a1

a2

a4

a1

a2

a3

a2

a3

a4

a1

Рис. 3

a1

a2

a3

a4

a5

a1

a2

a3

a4

a5

a1

a2

a3

a4

a5

a1

a2

a3

a4

a5

a2

a3

a4

a5

a1

a3

a4

a5

a1

a2

a4

a5

a1

a2

a3

a5

a1

a2

a3

a4

a3

a4

a5

a1

a2

a5

a1

a2

a3

a4

a2

a3

a4

a5

a1

a4

a5

a1

a2

a3

a4

a5

a1

a2

a3

a2

a3

a4

a5

a1

a5

a1

a2

a3

a4

a3

a4

a5

a1

a2

a5

a1

a2

a3

a4

a4

a5

a1

a2

a3

a3

a4

a5

a1

a2

a2

a3

a4

a5

a1

Рис. 4

a1

a2

a3

a4

a5

a6

a1

a2

a3

a4

a5

a6

a2

a3

a4

a5

a6

a1

a6

a1

a2

a3

a4

a5

a3

a4

a5

a6

a1

a2

a5

a6

a1

a2

a3

a4

a4

a5

a6

a1

a2

a3

a4

a5

a6

a1

a2

a3

a5

a6

a1

a2

a3

a4

a3

a4

a5

a6

a1

a2

a6

a1

a2

a3

a4

a5

a2

a3

a4

a5

a6

a1

Рис. 5

Для
порядков 3 и 5 получились полные группы MOLS. Понятно, что квадраты
4-го порядка (а тем более – 6-го порядка) не ортогональны.

Все
латинские квадраты одного и того же порядка, построенные данным методом,
получаются друг из друга перестановкой строк.

Покажу ещё
одну схему циклического сдвига, когда циклически сдвигаются блоки 2х2. Таким
методом строятся латинские квадраты, состоящие из латинских подквадратов 2х2.
По приведённым конкретным примерам легко понять, как работает данная схема. Для
большей наглядности латинские квадраты заполнены числами. На рис. 6 показан латинский
квадрат 6-го порядка, на рис. 7 – латинский квадрат 8-го порядка, на рис. 8 –
латинский квадрат 20-го порядка. Понятно, что данный метод применим для
построения латинских квадратов чётных порядков n > 2.

0

1

2

3

4

5

1

0

3

2

5

4

2

3

4

5

0

1

3

2

5

4

1

0

4

5

0

1

2

3

5

4

1

0

3

2

Рис. 6

0

1

2

3

4

5

6

7

1

0

3

2

5

4

7

6

2

3

4

5

6

7

0

1

3

2

5

4

7

6

1

0

4

5

6

7

0

1

2

3

5

4

7

6

1

0

3

2

6

7

0

1

2

3

4

5

7

6

1

0

3

2

5

4

Рис. 7

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

1

0

3

2

5

4

7

6

9

8

11

10

13

12

15

14

17

16

19

18

18

19

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

19

18

1

0

3

2

5

4

7

6

9

8

11

10

13

12

15

14

17

16

16

17

18

19

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

17

16

19

18

1

0

3

2

5

4

7

6

9

8

11

10

13

12

15

14

14

15

16

17

18

19

0

1

2

3

4

5

6

7

8

9

10

11

12

13

15

14

17

16

19

18

1

0

3

2

5

4

7

6

9

8

11

10

13

12

12

13

14

15

16

17

18

19

0

1

2

3

4

5

6

7

8

9

10

11

13

12

15

14

17

16

19

18

1

0

3

2

5

4

7

6

9

8

11

10

10

11

12

13

14

15

16

17

18

19

0

1

2

3

4

5

6

7

8

9

11

10

13

12

15

14

17

16

19

18

1

0

3

2

5

4

7

6

9

8

8

9

10

11

12

13

14

15

16

17

18

19

0

1

2

3

4

5

6

7

9

8

11

10

13

12

15

14

17

16

19

18

1

0

3

2

5

4

7

6

6

7

8

9

10

11

12

13

14

15

16

17

18

19

0

1

2

3

4

5

7

6

9

8

11

10

13

12

15

14

17

16

19

18

1

0

3

2

5

4

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

0

1

2

3

5

4

7

6

9

8

11

10

13

12

15

14

17

16

19

18

1

0

3

2

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

0

1

3

2

5

4

7

6

9

8

11

10

13

12

15

14

17

16

19

18

1

0

Рис. 8

В символьном виде латинский
квадрат с рис. 6 будет выглядеть так (рис. 8а):

a1

a2

a3

a4

a5

a6

a2

a1

a4

a3

a6

a5

a3

a4

a5

a6

a1

a2

a4

a3

a6

a5

a2

a1

a5

a6

a1

a2

a3

a4

a6

a5

a2

a1

a4

a3

Рис. 8а

АЛГОРИТМ АГРИППЫ

Алгоритм
Агриппы применяется для построения латинских квадратов любого чётного порядка n > 2. Я получила этот
алгоритм, разложив на пару ортогональных латинских квадратов известный
полумагический квадрат 12-го порядка, автором которого является Агриппа. К
сожалению, второй латинский квадрат в этой паре ОЛК является обобщённым
латинским квадратом. Начну демонстрацию алгоритма Агриппы с латинского квадрата
4-го порядка (рис. 9).

a1

a2

a3

a4

a4

a3

a2

a1

a2

a1

a4

a3

a3

a4

a1

a2

Рис. 9

Схема
очень проста. В первой строке записывается тождественная перестановка
элементов. В следующей строке эта перестановка пишется в обратном порядке.
Теперь во второй строке производится циклический сдвиг с шагом 2, полученная
перестановка записывается в третью строку. В четвёртой строке записывается
перестановка третьей строки в обратном порядке.

На рис. 10
показываю латинский квадрат 6-го порядка, построенный по этому алгоритму.

a1

a2

a3

a4

a5

a6

a6

a5

a4

a3

a2

a1

a4

a3

a2

a1

a6

a5

a5

a6

a1

a2

a3

a4

a3

a4

a5

a6

a1

a2

a2

a1

a6

a5

a4

a3

Рис. 10

Теперь,
думаю, схема стала совсем понятна. Здесь в четвёртой строке производится
циклический сдвиг с шагом 4. Соответственно в латинском квадрате 8-го порядка в
шестой строке производится циклический сдвиг с шагом 6, в латинском квадрате
10-го порядка в восьмой строке производится циклический сдвиг с шагом 8 и так
далее.

Покажу ещё
два примера – латинские квадраты 8-го и 10-го порядка (рис. 11 – 12).

a1

a2

a3

a4

a5

a6

a7

a8

a8

a7

a6

a5

a4

a3

a2

a1

a6

a5

a4

a3

a2

a1

a8

a7

a7

a8

a1

a2

a3

a4

a5

a6

a3

a4

a5

a6

a7

a8

a1

a2

a2

a1

a8

a7

a6

a5

a4

a3

a4

a3

a2

a1

a8

a7

a6

a5

a5

a6

a7

a8

a1

a2

a3

a4

Рис. 11

a1

a2

a3

a4

a5

a6

a7

a8

a9

a10

a10

a9

a8

a7

a6

a5

a4

a3

a2

a1

a8

a7

a6

a5

a4

a3

a2

a1

a10

a9

a9

a10

a1

a2

a3

a4

a5

a6

a7

a8

a3

a4

a5

a6

a7

a8

a9

a10

a1

a2

a2

a1

a10

a9

a8

a7

a6

a5

a4

a3

a6

a5

a4

a3

a2

a1

a10

a9

a8

a7

a7

a8

a9

a10

a1

a2

a3

a4

a5

a6

a5

a6

a7

a8

a9

a10

a1

a2

a3

a4

a4

a3

a2

a1

a10

a9

a8

a7

a6

a5

Рис. 12

Во всех
латинских квадратах (рис. 9 – 12) оранжевым цветом выделены строки, содержащие
перестановку предыдущей строки, записанную в обратном порядке.

Вот как
выглядит нормализованный латинский квадрат с рис. 12 (рис. 13):

0

1

2

3

4

5

6

7

8

9

9

8

7

6

5

4

3

2

1

0

7

6

5

4

3

2

1

0

9

8

8

9

0

1

2

3

4

5

6

7

2

3

4

5

6

7

8

9

0

1

1

0

9

8

7

6

5

4

3

2

5

4

3

2

1

0

9

8

7

6

6

7

8

9

0

1

2

3

4

5

4

5

6

7

8

9

0

1

2

3

3

2

1

0

9

8

7

6

5

4

Рис. 13

ПОСТРОЕНИЕ С ПОМОЩЬЮ
КВАЗИ-РАЗНОСТНОЙ МАТРИЦЫ

Метод
построения латинских квадратов с помощью квази-разностной матрицы (КРМ)
подробно описан в статье http://www.natalimak1.narod.ru/quazi.htm . Сначала я разработала
свою схему построения латинского квадрата любого чётного порядка n > 2, когда ещё не знала
о КРМ. Потом увидела, что к этой схеме можно применить КРМ. Покажу здесь
латинский квадрат 8-го порядка, построенный по этой схеме (рис. 14).

0

2

4

6

a

3

5

1

6

1

3

5

0

a

4

2

5

0

2

4

6

1

a

3

a

6

1

3

5

0

2

4

3

a

0

2

4

6

1

5

2

4

a

1

3

5

0

6

1

3

5

a

2

4

6

0

4

5

6

0

1

2

3

a

Рис. 14

На рис. 15 изображена КРМ
этого латинского квадрата.

a

0

0

0

0

0

0

0

0

0

a

3

0

1

2

4

5

6

1

4

a

0

6

5

3

2

1

Рис. 15

Латинские
квадраты, построенные данным методом нельзя представить в символьном виде, так
как далеко не всякая трансформация тождественной перестановки чисел даёт
латинский квадрат такой же структуры. Возможна, например, такая трансформация,
как циклический сдвиг. Применим к латинскому квадрату преобразование следующей
трансформации тождественной перестановки чисел, являющейся циклическим сдвигом:

0  1  2  3  4  5 
6  7

1  2  3  4  5 
6  7  0

На рис. 16
вы видите преобразованный латинский квадрат. Он изоморфен латинскому квадрату с
рис. 14.

1

3

5

7

0

4

6

2

7

2

4

6

1

0

5

3

6

1

3

5

7

2

0

4

0

7

2

4

6

1

3

5

4

0

1

3

5

7

2

6

3

5

0

2

4

6

1

7

2

4

6

0

3

5

7

1

5

6

7

1

2

3

4

0

Рис. 16

Все
латинские квадраты, построенные по этой схеме, содержат подквадрат 1х1 и имеют
определённую структуру, КРМ этих латинских квадратов тоже подобны; можно
составить КРМ в общем виде для любого чётного порядка n > 2.

Найденная
мной в Интернете пара ОЛК 10-го порядка, автором которой является А. И. Лямзин,
тоже состоит из латинских квадратов, построенных по описанной схеме. Эти
латинские квадраты тоже содержат подквадрат 1х1 и имеют такую же структуру.
Подробно схема Лямзина описана в указанной статье. Здесь покажу латинские
квадраты 10-го, 12-го и 14-го порядков, построенные по схеме Лямзина (рис. 17 —
19).

9

5

8

3

2

7

0

6

4

1

5

9

6

0

4

3

8

1

7

2

8

6

9

7

1

5

4

0

2

3

3

0

7

9

8

2

6

5

1

4

2

4

1

8

9

0

3

7

6

5

7

3

5

2

0

9

1

4

8

6

0

8

4

6

3

1

9

2

5

7

6

1

0

5

7

4

2

9

3

8

4

7

2

1

6

8

5

3

9

0

1

2

3

4

5

6

7

8

0

9

Рис. 17

11

6

2

1

7

4

10

3

9

0

5

8

6

11

7

3

2

8

5

0

4

10

1

9

2

7

11

8

4

3

9

6

1

5

0

10

1

3

8

11

9

5

4

10

7

2

6

0

7

2

4

9

11

10

6

5

0

8

3

1

4

8

3

5

10

11

0

7

6

1

9

2

10

5

9

4

6

0

11

1

8

7

2

3

3

0

6

10

5

7

1

11

2

9

8

4

9

4

1

7

0

6

8

2

11

3

10

5

0

10

5

2

8

1

7

9

3

11

4

6

5

1

0

6

3

9

2

8

10

4

11

7

8

9

10

0

1

2

3

4

5

6

7

11

Рис. 18

13

7

2

12

5

3

10

4

11

1

9

0

6

8

7

13

8

3

0

6

4

11

5

12

2

10

1

9

2

8

13

9

4

1

7

5

12

6

0

3

11

10

12

3

9

13

10

5

2

8

6

0

7

1

4

11

5

0

4

10

13

11

6

3

9

7

1

8

2

12

3

6

1

5

11

13

12

7

4

10

8

2

9

0

10

4

7

2

6

12

13

0

8

5

11

9

3

1

4

11

5

8

3

7

0

13

1

9

6

12

10

2

11

5

12

6

9

4

8

1

13

2

10

7

0

3

1

12

6

0

7

10

5

9

2

13

3

11

8

4

9

2

0

7

1

8

11

6

10

3

13

4

12

5

0

10

3

1

8

2

9

12

7

11

4

13

5

6

6

1

11

4

2

9

3

10

0

8

12

5

13

7

8

9

10

11

12

0

1

2

3

4

5

6

7

13

Рис. 19

Эти латинские квадраты
интересны тем, что они симметричны относительно главной диагонали.

Для квадратов
этой группы так же возможно построение изоморфных латинских квадратов, как это
было показано для предыдущей группы квадратов. Для порядка 10 мне удалось найти
неизоморфный латинский квадрат такой же структуры (по программе). Вы видите
этот квадрат на рис. 20.

9

7

5

2

4

0

8

3

6

1

7

9

8

6

3

5

1

0

4

2

5

8

9

0

7

4

6

2

1

3

2

6

0

9

1

8

5

7

3

4

4

3

7

1

9

2

0

6

8

5

0

5

4

8

2

9

3

1

7

6

8

1

6

5

0

3

9

4

2

7

3

0

2

7

6

1

4

9

5

8

6

4

1

3

8

7

2

5

9

0

1

2

3

4

5

6

7

8

0

9

Рис. 20

Для
латинских квадратов 4-го, 8-го и 10-го порядков, построенных по схеме Лямзина,
существуют ортогональные соквадраты. Существуют ли ортогональные соквадраты для
следующих чётных порядков, я не выяснила. Этот вопрос остаётся открытым.
Хорошая задача для читателей!

Работая с
КРМ, я нашла ещё одну интересную схему построения латинских квадратов для
любого чётного порядка n > 2. Покажу латинские квадраты, построенные по
этой схеме, для порядков 4 – 12 (рис. 21 – 22).

4

1

5

2

6

3

7

0

7

5

2

6

3

0

4

1

3

1

4

2

5

0

5

7

6

3

0

4

1

2

5

4

2

0

3

1

2

6

7

0

4

1

5

3

2

1

3

0

4

5

0

3

1

2

6

3

0

7

1

5

2

4

3

0

2

1

2

0

5

1

4

3

3

0

4

1

7

2

6

5

0

3

1

2

0

3

1

5

2

4

0

4

1

5

2

7

3

6

1

2

0

3

1

2

3

4

0

5

1

2

3

4

5

6

0

7

Рис. 21

6

1

7

2

8

3

9

4

10

5

11

0

11

7

2

8

3

9

4

10

5

0

6

1

5

1

6

2

7

3

8

4

9

0

7

11

8

3

9

4

10

5

0

6

1

2

9

6

2

7

3

8

4

0

5

1

2

8

11

9

4

10

5

0

6

1

7

3

6

9

7

3

8

4

0

5

1

2

8

3

9

11

10

5

0

6

1

7

2

4

2

7

9

8

4

0

5

1

6

3

3

9

4

10

11

0

6

1

7

2

8

5

7

3

8

9

0

5

1

6

2

4

9

4

10

5

0

11

1

7

2

8

3

6

3

8

4

0

9

1

6

2

7

5

4

10

5

0

6

1

11

2

8

3

9

7

8

4

0

5

1

9

2

7

3

6

10

5

0

6

1

7

2

11

3

9

4

8

4

0

5

1

6

2

9

3

8

7

5

0

6

1

7

2

8

3

11

4

10

9

0

5

1

6

2

7

3

9

4

8

0

6

1

7

2

8

3

9

4

11

5

10

1

2

3

4

5

6

7

8

0

9

1

2

3

4

5

6

7

8

9

10

0

11

Рис. 22

Помимо
того, что схема расположения чисел в этих латинских квадратах очень изящная,
эти квадраты обладают интересным свойством: они являются нетрадиционными
магическими квадратами, то есть в них сумма чисел в обеих главных диагоналях
равна магической константе квадрата, хотя диагональными они не являются (кроме
квадрата 4-го порядка). В одной главной диагонали этих квадратов все элементы
различны. А в другой главной диагонали содержится набор таких чисел: 0, 1, n – 1 и n/2 (n – 3) раза. Сумма этих
чисел равна:

1 + n – 1 + (n – 3)*n/2 =
n*(n – 1)/2

К
сожалению, ортогональный соквадрат мне удалось построить только для порядка 4.
Покажу оба квадрата данной пары ОЛК (рис. 23):

2

1

3

0

2

3

0

1

3

0

2

1

1

0

3

2

0

3

1

2

3

2

1

0

1

2

0

3

0

1

2

3

Рис. 23

Для
порядков, начиная с 8, нахождение ортогонального соквадрата – сложная задача,
но её стоит решать. Если удастся
найти ортогональные соквадраты для всех латинских квадратов данной группы,
которые тоже будут являться нетрадиционными магическими квадратами, то мы
получим уникальный алгоритм, дающий нам пары ОЛК любого чётного порядка (кроме
2 и 6), сразу пригодные для построения магических квадратов.

Не буду
описывать здесь метод составных квадратов, который был описан в статьях: “Построение
пар диагональных латинских квадратов методом составных квадратов” (http://www.natalimak1.narod.ru/aspekty5.htm ) и “Построение пар
ортогональных латинских квадратов методом составных квадратов” (http://www.natalimak1.narod.ru/olk.htm ).

В
заключение покажу построение латинских квадратов нечётного порядка не кратного
3 методом циклического сдвига. Эти латинские квадраты замечательны тем, что они
являются нетрадиционными магическими квадратами, обладающими свойством
ассоциативности и пандиагональности и, кроме того, для этих латинских квадратов
существуют ортогональные соквадраты, обладающие такими же свойствами. Таким
образом, мы имеем замечательные пары ОЛК, из которых строятся методом латинских
квадратов идеальные магические квадраты. Подробно смотрите об этом в статье http://www.natalimak1.narod.ru/aspekty4.htm

Продемонстрирую
метод на примере построения пары ОЛК 7-го порядка. Первый латинский квадрат
строится методом циклического сдвига, описанным в начале данной статьи, только
в первой строке записывается не произвольная, а конкретная перестановка чисел.
Эта перестановка для любого порядка n рассматриваемой группы
порядков составляется так: в первой ячейке записывается 0, а дальше записываются
числа от  n – 1 до 1 в убывающем порядке.
Смотрите первый латинский квадрат на рис. 24. В этом примере циклический сдвиг
выполняется с шагом 5. В общем случае для порядка n циклический сдвиг
выполняется с шагом n – 2.

0

6

5

4

3

2

1

2

1

0

6

5

4

3

4

3

2

1

0

6

5

6

5

4

3

2

1

0

1

0

6

5

4

3

2

3

2

1

0

6

5

4

5

4

3

2

1

0

6

Рис. 24

Ортогональный
соквадрат можно получить из этого латинского квадрата несколькими способами:
отражением относительно горизонтальной (или вертикальной) оси симметрии,
отражением относительно одной из главных диагоналей. Покажу ортогональный
соквадрат, полученный отражением относительно главной диагонали, начинающейся с
0 (рис. 25).

0

2

4

6

1

3

5

6

1

3

5

0

2

4

5

0

2

4

6

1

3

4

6

1

3

5

0

2

3

5

0

2

4

6

1

2

4

6

1

3

5

0

1

3

5

0

2

4

6

Рис. 25

Ещё раз подчеркну: данный
метод работает для любого нечётного порядка не кратного 3.

Наверное, существует ещё
множество интересных схем построения латинских квадратов. Если вы знаете такие
схемы, пишите мне.

15 апреля 2009 г.

г. Саратов.

Читайте мою виртуальную
книгу “Волшебный мир магических квадратов”:

http://www.klassikpoez.narod.ru/glavnaja.htm

Скачайте
электронную версию этой книги:

http://narod.ru/disk/5834353000/Magic_squares.pdf.html

Заодно прихватите книгу “Позиционные системы счисления”, авось,
пригодится:

http://narod.ru/disk/5936760000/pozic4.pdf.html

       Пишите мне!

        Приглашаю всех на форум!

Рейтинг@Mail.ru

На главную страницу

Источник

Латинский квадрат: вызываем демонов во имя математики

Время на прочтение
7 мин

Количество просмотров 9.7K

Привет, Хабр, я Олег, преподаватель Elbrus Bootcamp. Возможно, вы слышали о латинских квадратах. Раньше считали, что они защищают от зла и помогают в магических ритуалах, а теперь их используют в криптографии и играх.

В моем пет-проекте футошики латинский квадрат является игровым полем. Потребовалось генерировать такие квадраты быстро, не задерживая пользователя даже на 100 миллисекунд, но делать их непредсказуемыми и разнообразными. Оказалось, что генерация латинского квадрата — все еще проблема. Я погуглил и выяснил, что на русском языке информации о способах ее решения почти нет.

Решил исправить ситуацию: в этой статье расскажу об алгоритмах генерации и их ограничениях, и покажу, как реализовал один из алгоритмов на JavaScript. А еще объясню, почему магический и латинский квадрат — не одно и то же.

История латинского квадрата

Латинские квадраты — это такие квадратные таблицы, в которых символы не должны повторяться в каждой строке и в каждом столбце.

Первые находки, связанные с латинскими квадратами, датируют ещё 10-11 веком [1]. Тогда люди верили в то, что амулеты, содержащие латинские квадраты, защищают от зла и помогают в магических ритуалах для призыва демонов. Самая первая книга, содержащая латинские квадраты, опубликована примерно в 1200 году.

Может возникнуть ассоциация с другими квадратами, которые называются магическими. Но между этими двумя квадратами есть очень большая разница. Магические квадраты, в отличие от латинских, могут быть построены только для чисел и требуют, чтобы совпадала сумма всех элементов в каждой строке и столбце и на диагоналях, а сами числа не повторялись во всём квадрате. В латинских же квадратах набор чисел в каждой строке и столбце одинаковый, меняется только их порядок.

Одной из важнейших вех в развитии латинских квадратов стало исследование Эйлера. Именно он дал название латинским квадратам и первым описал их математически, а также применил для их исследования математические методы.

В современном мире латинские квадраты активно используются для протоколов шифрования, в планировании научных экспериментов, в коммуникационных протоколах для коррекции ошибок, в статистике и играх.

Первое практическое применение латинского квадрата было как раз для шифрования — полиалфавитный шифр Тритемия использовал простейший латинский квадрат. Но и в современной криптографии латинский квадрат используется часто. В 2005 году разработчики потокового шифра Edon80 использовали в своём алгоритме целый конвейер из 80-ти специально подобранных латинских квадратов. Кроме этого, латинский квадрат используется и в схемах разделения секрета.

Есть и совершенно неожиданные способы применения. Например, латинские квадраты использовались в агрономических исследованиях, для минимизации влияния разных экспериментов друг на друга.

И, конечно, нельзя не упомянуть использование латинских квадратов в других играх, кроме уже упомянутой футошики. Поле знаменитой игры «Судоку», конечно, является латинским квадратом, но добавляет к нему несколько новых правил, чтобы играть было интересно. Кстати, на занятиях в Elbrus Bootcamp студенты создают для нее автоматический решатель.

Алгоритмы генерации

Хотя правила латинского квадрата очень просты, а история их исследования насчитывает не одну сотню лет, всё ещё существует проблема генерации латинского квадрата. Разные задачи требуют разных характеристик алгоритма. Среди прочего важны:

  • Алгоритмическая сложность в зависимости от размера квадрата

  • Количество памяти, необходимое для генерации

  • Равномерность вероятности попадания каждой цифры в каждую ячейку квадрата

Квадрат характеризуется числом n— размером одной его стороны. Давайте рассмотрим некоторые из существующих алгоритмов генерации латинского квадрата [2].

Метод Косельни

Самым быстрым способом сгенерировать латинский квадрат является метод Косельни. Он создаёт новый квадрат на основе двух других, меньшего размера. Сложность этого алгоритма O(n^2) и это самый быстрый из известных алгоритмов. Большим минусом этого метода является то, что итоговый квадрат не будет равномерно распределённым, а потому не может быть использован в криптографии. Да и в игре его не особо используешь, готовые квадраты уж слишком похожи друг на друга.

Реализацию метода можно посмотреть здесь.

SeqGen с перегенерацией строки

Это единственный алгоритм, обладающий равномерной вероятностью попадания каждой цифры в каждую ячейку. К сожалению, это одновременно один из самых медленных методов. Вряд ли вы дождётесь окончания его работы для квадратов размером более 200, так как время его работы экспоненциально зависит от размера. Можем оценить его вычислительную сложность как O(e^n)

Реализацию метода можно посмотреть здесь.

SeqGen с графом замен

Этот алгоритм — нечто среднее между предыдущими двумя. С одной стороны, он достигает приемлемого равномерного распределения только на очень больших размерах квадратов, 256 и больше. С другой стороны, он способен сгенерировать квадраты такого размера за приемлемое время. Сложность этого алгоритма приближается к O(n^3)

Реализацию метода можно посмотреть здесь.

Метод Джейкобсона и Мэтьюза

Отличный выбор, если мы хотим как можно ближе приблизиться к равномерному распределению чисел при адекватной алгоритмической сложности. Этот алгоритм способен дать нам квадрат очень хорошего качества, но при этом работает строго за O(n^3), в отличие от предыдущего, который часто может закончить генерацию быстрее.

Реализацию метода можно посмотреть здесь.

Разбор алгоритма Джейкобсона и Мэтьюза

Хотя для моей задачи, для генерации совсем небольших квадратов, хватило бы и SeqGen с перегенерацией строки, я всё же выбрал именно алгоритм Джейкобсона и Мэтьюза. Он одновременно и достаточно быстрый, и даёт очень близкое к равномерному распределение. А еще он весьма интересен в реализации, что в итоге стало главным критерием. В отличие от всех предыдущих, этот алгоритм рассматривает латинский квадрат не как матрицу, а как трехмерный куб.

Куб инцидентности

Куб инцидентности — это альтернативное представление матрицы латинского квадарата. Он представляет собой куб размером n times n times n, где каждая ось соответствует строкам, колонкам и символам латинского квадрата.

Ячейка куба (a, b, c)содержит 1, если на пересечении строки a и колонки b находится символ c. В ином случае ячейка содержит 0.

defarraystretch{1.3} begin{array}{|c|c|c|c|} hline 0 & 1 & 2 & 3 \ hline 1 & 2 & 3 & 0 \ hline 2 & 3 & 0 & 1 \ hline 3 & 0 & 1 & 2 \ hline end{array}

Для этого квадрата у нас будут следующие ненулевые ячейки:

defarraystretch{1.3} begin{array}{|c|c|c|c|} hline (0, 0, 0) & (1, 0, 1) & (2, 0, 2) & (3, 0, 3) \ hline (0, 1, 1) & (1, 1, 2) & (2, 1, 3) & (3, 1, 0) \ hline (0, 2, 2) & (1, 2, 3) & (2, 2, 0) & (3, 2, 1) \ hline (0, 3, 3) & (1, 3, 0) & (2, 3, 1) & (3, 3, 2) \ hline end{array}

Соответствующий матрице куб инцидентности:

Куб инцидентности с разных сторон

Куб инцидентности с разных сторон

Описание шага

Шагом алгоритма мы будем называть добавление и вычитание единицы в некоторых ячейках куба таким образом, чтобы не изменять сумму элементов в каждой строке по всем трём осям куба. Эта сумма всегда должна быть равна 1. В процессе хода может образоваться ячейка, содержащая значение -1. Так как сумма строки обязана быть неизменной, в строке со значением -1 будет присутствовать две ячейки со значением 1.

Куб, содержащий ячейку со значением -1, мы будем называть незаконченным.

Будем различать два типа шагов: из законченного куба и из незаконченного куба.

  1. Для шага из законченного куба мы выбираем из куба любую ячейку со значением 0. Назовём эту ячейкуt, её координаты будут (t.x, t.y, t.z)Эта ячейка связана с тремя строками в кубе, каждая из строк параллельна одной из осей и в каждой строке находится только одна ячейка со значением 1. Назовём координаты таких ячеек x_1, y_1и z_1соответственно. Таким образом мы получаем подкуб размером 2 times 2 times 2. Этот подкуб не обязательно будет состоять из соседних клеток. Шагом в таком случае будет добавление 1к(t.x, t.y, t.z)и вычитание 1таким образом, чтобы в каждой строке по каждой оси сумма всех ячеек осталась равна. Визуальное отображение шага показано выше. Если после совершения шага противоположная tячейка c координатами (x_1, y_1, z_1)содержит значение -1, то получившийся куб считается незаконченным. В ином случае куб законченный.

  2. Для шага из незаконченного куба алгоритм вычитания и добавления остаётся прежним, но меняется алгоритм вычисления tи координат x_1y_1и z_1. В качестве значения tмы берём ячейку со значением -1. Такая ячейка в кубе может быть только одна. В строке x, соответствующей координате t.xнаходится одна ячейка со значением -1 и две ячейки со значением 1. В качестве x_1выбираем любую из этих двух ячеек. Аналогично поступаем с y_1и z_1После этого хода мы точно так же можем получить как законченный, так и незаконченный куб.

Джейкобсон и Мэтьюз доказали [3], что любые два куба инцидентности связаны между собой конечным числом шагов. При этом таких шагов будет всегда не более 2(n-1)^3.

Получается, для генерации куба с максимально равномерным распределением необходимо соблюсти три ключевых условия:

  • для всех случайных значений нужно использовать качественный генератор случайных чисел;

  • необходимо повторить шаг алгоритма как минимум n^3раз;

  • только законченный куб можно преобразовать в корректный латинский квадрат.

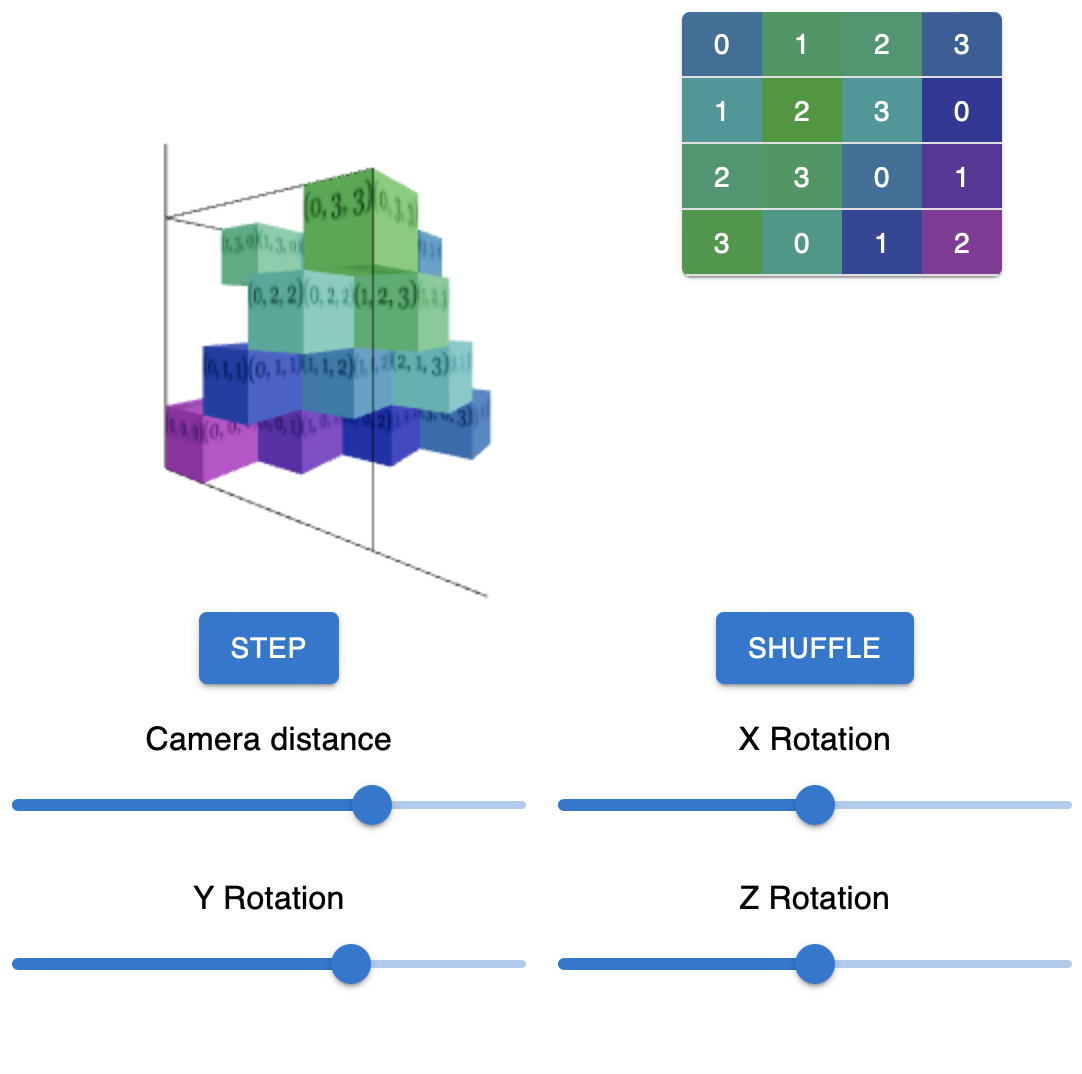
Наивная реализация на JavaScript

Я написал неэффективную, но легко читаемую реализацию алгоритма на JavaScript с визуализацией на React и Three.js, она доступна здесь. Вы можете вращать куб по всем осям с помощью соответствующих слайдеров, а также запускать алгоритм пошагово с помощью кнопки «Step» и запускать алгоритм целиком с помощью кнопки «Shuffle». Справа от куба отображается соответствующий ему латинский квадрат.

Реализация самого алгоритма находится в файле src/bl/IncidenceCube.js.

Что дальше?

Мы рассмотрели краткую историю латинских квадратов и варианты их применения, взглянули на уже известные подходы к генерации этих квадратов. Мы выяснили, что существующие алгоритмы очень сильно различаются по своим характеристикам, а потому должны подбираться в зависимости от конкретной задачи.

Мы взглянули на простейшую реализацию алгоритма Джейкобсона и Мэтьюза, которая, конечно, далеко не самая оптимальная. Сложность моего алгоритма — O(n^4)но его можно сократить как минимум до O(n^3)

Проблема текущей реализации состоит в том, что для каждого шага, зная x и y, мы можем очень долго искать местоположение ячейки, содержащей 1. В худшем случае это займёт O(n)Это можно значительно ускорить, например, сохраняя значения z-координат всех ячеек со значением 1 и, таким образом, сведя скорость поиска к O(1)Похожая оптимизация алгоритма Джейкобсона и Мэтьюза частично описана в работе Gallego Sagastume [4].

Код на JavaScript, представленный выше, генерирует квадрат 100 на 100 за 9 секунд. Слабо сделать на JS быстрее, чем за секунду?

Ссылки

  1. https://vbn.aau.dk/ws/portalfiles/portal/13649565/R-2007-32.pdf

  2. https://github.com/bluemontag/igs-lsgp

  3. https://onlinelibrary.wiley.com/doi/epdf/10.1002/(SICI)1520-6610(1996)4%3A6<405%3A%3AAID-JCD3>3.0.CO%3B2-J

  4. http://sedici.unlp.edu.ar/bitstream/handle/10915/42155/Documento_completo.pdf?sequence=1

Источник

In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column. An example of a 3×3 Latin square is

The name «Latin square» was inspired by mathematical papers by Leonhard Euler (1707–1783), who used Latin characters as symbols,[2] but any set of symbols can be used: in the above example, the alphabetic sequence A, B, C can be replaced by the integer sequence 1, 2, 3. Euler began the general theory of Latin squares.

History[edit]

The Korean mathematician Choi Seok-jeong was the first to publish an example of Latin squares of order nine, in order to construct a magic square in 1700, predating Leonhard Euler by 67 years.[3]

Reduced form[edit]

A Latin square is said to be reduced (also, normalized or in standard form) if both its first row and its first column are in their natural order.[4] For example, the Latin square above is not reduced because its first column is A, C, B rather than A, B, C.

Any Latin square can be reduced by permuting (that is, reordering) the rows and columns. Here switching the above matrix’s second and third rows yields the following square:

This Latin square is reduced; both its first row and its first column are alphabetically ordered A, B, C.

Properties[edit]

Orthogonal array representation[edit]

If each entry of an n × n Latin square is written as a triple (r,c,s), where r is the row, c is the column, and s is the symbol, we obtain a set of n2 triples called the orthogonal array representation of the square. For example, the orthogonal array representation of the Latin square

is

{ (1, 1, 1), (1, 2, 2), (1, 3, 3), (2, 1, 2), (2, 2, 3), (2, 3, 1), (3, 1, 3), (3, 2, 1), (3, 3, 2) },

where for example the triple (2, 3, 1) means that in row 2 and column 3 there is the symbol 1. Orthogonal arrays are usually written in array form where the triples are the rows, such as:

r c s
1 1 1
1 2 2
1 3 3
2 1 2
2 2 3
2 3 1
3 1 3
3 2 1
3 3 2

The definition of a Latin square can be written in terms of orthogonal arrays:

  • A Latin square is a set of n2 triples (r, c, s), where 1 ≤ r, c, s ≤ n, such that all ordered pairs (r, c) are distinct, all ordered pairs (r, s) are distinct, and all ordered pairs (c, s) are distinct.

This means that the n2 ordered pairs (r, c) are all the pairs (i, j) with 1 ≤ i, j ≤ n, once each. The same is true of the ordered pairs (r, s) and the ordered pairs (c, s).

The orthogonal array representation shows that rows, columns and symbols play rather similar roles, as will be made clear below.

Equivalence classes of Latin squares[edit]

Many operations on a Latin square produce another Latin square (for example, turning it upside down).

If we permute the rows, permute the columns, and permute the names of the symbols of a Latin square, we obtain a new Latin square said to be isotopic to the first. Isotopism is an equivalence relation, so the set of all Latin squares is divided into subsets, called isotopy classes, such that two squares in the same class are isotopic and two squares in different classes are not isotopic.

Another type of operation is easiest to explain using the orthogonal array representation of the Latin square. If we systematically and consistently reorder the three items in each triple (that is, permute the three columns in the array form), another orthogonal array (and, thus, another Latin square) is obtained. For example, we can replace each triple (r,c,s) by (c,r,s) which corresponds to transposing the square (reflecting about its main diagonal), or we could replace each triple (r,c,s) by (c,s,r), which is a more complicated operation. Altogether there are 6 possibilities including «do nothing», giving us 6 Latin squares called the conjugates (also parastrophes) of the original square.[5]

Finally, we can combine these two equivalence operations: two Latin squares are said to be paratopic, also main class isotopic, if one of them is isotopic to a conjugate of the other. This is again an equivalence relation, with the equivalence classes called main classes, species, or paratopy classes.[5] Each main class contains up to six isotopy classes.

Number of n × n Latin squares[edit]

There is no known easily computable formula for the number Ln of n × n Latin squares with symbols 1, 2, …, n. The most accurate upper and lower bounds known for large n are far apart. One classic result[6] is that

{displaystyle prod _{k=1}^{n}left(k!right)^{n/k}geq L_{n}geq {frac {left(n!right)^{2n}}{n^{n^{2}}}}.}

A simple and explicit formula for the number of Latin squares was published in 1992, but it is still not easily computable due to the exponential increase in the number of terms. This formula for the number Ln of n × n Latin squares is

{displaystyle L_{n}=n!sum _{Ain B_{n}}^{}(-1)^{sigma _{0}(A)}{binom {operatorname {per} A}{n}},}

where Bn is the set of all n × n {0, 1}-matrices, σ0(A) is the number of zero entries in matrix A, and per(A) is the permanent of matrix A.[7]

The table below contains all known exact values. It can be seen that the numbers grow exceedingly quickly. For each n, the number of Latin squares altogether (sequence A002860 in the OEIS) is n! (n − 1)! times the number of reduced Latin squares (sequence A000315 in the OEIS).

The numbers of Latin squares of various sizes

n reduced Latin squares of size n
(sequence A000315 in the OEIS) 		all Latin squares of size n
(sequence A002860 in the OEIS)
1 1 1
2 1 2
3 1 12
4 4 576
5 56 161,280
6 9,408 812,851,200
7 16,942,080 61,479,419,904,000
8 535,281,401,856 108,776,032,459,082,956,800
9 377,597,570,964,258,816 5,524,751,496,156,892,842,531,225,600
10 7,580,721,483,160,132,811,489,280 9,982,437,658,213,039,871,725,064,756,920,320,000
11 5,363,937,773,277,371,298,119,673,540,771,840 776,966,836,171,770,144,107,444,346,734,230,682,311,065,600,000
12 1.62 × 1044
13 2.51 × 1056
14 2.33 × 1070
15 1.50 × 1086

For each n, each isotopy class (sequence A040082 in the OEIS) contains up to (n!)3 Latin squares (the exact number varies), while each main class (sequence A003090 in the OEIS) contains either 1, 2, 3 or 6 isotopy classes.

Equivalence classes of Latin squares

n main classes

(sequence A003090 in the OEIS)

isotopy classes

(sequence A040082 in the OEIS)

structurally distinct squares

(sequence A264603 in the OEIS)

1 1 1 1
2 1 1 1
3 1 1 1
4 2 2 12
5 2 2 192
6 12 22 145,164
7 147 564 1,524,901,344
8 283,657 1,676,267
9 19,270,853,541 115,618,721,533
10 34,817,397,894,749,939 208,904,371,354,363,006
11 2,036,029,552,582,883,134,196,099 12,216,177,315,369,229,261,482,540

The number of structurally distinct Latin squares (i.e. the squares cannot be made identical by means of rotation, reflection, and/or permutation of the symbols) for n = 1 up to 7 is 1, 1, 1, 12, 192, 145164, 1524901344 respectively (sequence A264603 in the OEIS).

Examples[edit]

We give one example of a Latin square from each main class up to order five.

{begin{bmatrix}1end{bmatrix}}quad {begin{bmatrix}1&2\2&1end{bmatrix}}quad {begin{bmatrix}1&2&3\2&3&1\3&1&2end{bmatrix}}

{begin{bmatrix}1&2&3&4\2&1&4&3\3&4&1&2\4&3&2&1end{bmatrix}}quad {begin{bmatrix}1&2&3&4\2&4&1&3\3&1&4&2\4&3&2&1end{bmatrix}}

{begin{bmatrix}1&2&3&4&5\2&3&5&1&4\3&5&4&2&1\4&1&2&5&3\5&4&1&3&2end{bmatrix}}quad {begin{bmatrix}1&2&3&4&5\2&4&1&5&3\3&5&4&2&1\4&1&5&3&2\5&3&2&1&4end{bmatrix}}

They present, respectively, the multiplication tables of the following groups:

Transversals and rainbow matchings[edit]

A transversal in a Latin square is a choice of n cells, where each row contains one cell, each column contains one cell, and there is one cell containing each symbol.

One can consider a Latin square as a complete bipartite graph in which the rows are vertices of one part, the columns are vertices of the other part, each cell is an edge (between its row and its column), and the symbols are colors. The rules of the Latin squares imply that this is a proper edge coloring. With this definition, a Latin transversal is a matching in which each edge has a different color; such a matching is called a rainbow matching.

Therefore, many results on Latin squares/rectangles are contained in papers with the term «rainbow matching» in their title, and vice versa.[8]

Some Latin squares have no transversal. For example, when n is even, an n-by-n Latin square in which the value of cell i,j is (i+j) mod n has no transversal. Here are two examples:

{displaystyle {begin{bmatrix}1&2\2&1end{bmatrix}}quad {begin{bmatrix}1&2&3&4\2&3&4&1\3&4&1&2\4&1&2&3end{bmatrix}}}

In 1967, H. J. Ryser conjectured that, when n is odd, every n-by-n Latin square has a transversal.[9]

In 1975, S. K. Stein and Brualdi conjectured that, when n is even, every n-by-n Latin square has a partial transversal of size n−1.[10]

A more general conjecture of Stein is that a transversal of size n−1 exists not only in Latin squares but also in any n-by-n array of n symbols, as long as each symbol appears exactly n times.[9]

Some weaker versions of these conjectures have been proved:

  • Every n-by-n Latin square has a partial transversal of size 2n/3.[11]
  • Every n-by-n Latin square has a partial transversal of size n − sqrt(n).[12]
  • Every n-by-n Latin square has a partial transversal of size n − 11 log2
    2    (n).[13]

Algorithms[edit]

For small squares it is possible to generate permutations and test whether the Latin square property is met. For larger squares, Jacobson and Matthews’ algorithm allows sampling from a uniform distribution over the space of n × n Latin squares.[14]

Applications[edit]

Statistics and mathematics[edit]

  • In the design of experiments, Latin squares are a special case of row-column designs for two blocking factors.[15][16]
  • In algebra, Latin squares are related to generalizations of groups; in particular, Latin squares are characterized as being the multiplication tables (Cayley tables) of quasigroups. A binary operation whose table of values forms a Latin square is said to obey the Latin square property.

Error correcting codes[edit]

Sets of Latin squares that are orthogonal to each other have found an application as error correcting codes in situations where communication is disturbed by more types of noise than simple white noise, such as when attempting to transmit broadband Internet over powerlines.[17][18][19]

Firstly, the message is sent by using several frequencies, or channels, a common method that makes the signal less vulnerable to noise at any one specific frequency. A letter in the message to be sent is encoded by sending a series of signals at different frequencies at successive time intervals. In the example below, the letters A to L are encoded by sending signals at four different frequencies, in four time slots. The letter C, for instance, is encoded by first sending at frequency 3, then 4, 1 and 2.

{displaystyle {begin{matrix}A\B\C\D\end{matrix}}{begin{bmatrix}1&2&3&4\2&1&4&3\3&4&1&2\4&3&2&1\end{bmatrix}}quad {begin{matrix}E\F\G\H\end{matrix}}{begin{bmatrix}1&3&4&2\2&4&3&1\3&1&2&4\4&2&1&3\end{bmatrix}}quad {begin{matrix}I\J\K\L\end{matrix}}{begin{bmatrix}1&4&2&3\2&3&1&4\3&2&4&1\4&1&3&2\end{bmatrix}}}

The encoding of the twelve letters are formed from three Latin squares that are orthogonal to each other. Now imagine that there’s added noise in channels 1 and 2 during the whole transmission. The letter A would then be picked up as:

{displaystyle {begin{matrix}12&12&123&124end{matrix}}}

In other words, in the first slot we receive signals from both frequency 1 and frequency 2; while the third slot has signals from frequencies 1, 2 and 3. Because of the noise, we can no longer tell if the first two slots were 1,1 or 1,2 or 2,1 or 2,2. But the 1,2 case is the only one that yields a sequence matching a letter in the above table, the letter A.
Similarly, we may imagine a burst of static over all frequencies in the third slot:

{displaystyle {begin{matrix}1&2&1234&4end{matrix}}}

Again, we are able to infer from the table of encodings that it must have been the letter A being transmitted. The number of errors this code can spot is one less than the number of time slots. It has also been proven that if the number of frequencies is a prime or a power of a prime, the orthogonal Latin squares produce error detecting codes that are as efficient as possible.

Mathematical puzzles[edit]

The problem of determining if a partially filled square can be completed to form a Latin square is NP-complete.[20]

The popular Sudoku puzzles are a special case of Latin squares; any solution to a Sudoku puzzle is a Latin square. Sudoku imposes the additional restriction that nine particular 3×3 adjacent subsquares must also contain the digits 1–9 (in the standard version). See also Mathematics of Sudoku.

The more recent KenKen and Strimko puzzles are also examples of Latin squares.

Board games[edit]

Latin squares have been used as the basis for several board games, notably the popular abstract strategy game Kamisado.

Agronomic research[edit]

Latin squares are used in the design of agronomic research experiments to minimise experimental errors.[21]

Heraldry[edit]

The Latin square also figures in the arms of the Statistical Society of Canada,[22] being specifically mentioned in its blazon. Also, it appears in the logo of the International Biometric Society.[23]

Generalizations[edit]

  • A Latin rectangle is a generalization of a Latin square in which there are n columns and n possible values, but the number of rows may be smaller than n. Each value still appears at most once in each row and column.
  • A Graeco-Latin square is a pair of two Latin squares such that, when one is laid on top of the other, each ordered pair of symbols appears exactly once.
  • A Latin hypercube is a generalization of a Latin square from two dimensions to multiple dimensions.

See also[edit]

  • Block design
  • Combinatorial design
  • Eight queens puzzle
  • Futoshiki
  • Magic square
  • Problems in Latin squares
  • Rook’s graph, a graph that has Latin squares as its colorings
  • Sator Square
  • Vedic square
  • Word square

Notes[edit]

  1. ^ Busby, Mattha (27 June 2020). «Cambridge college to remove window commemorating eugenicist». The Guardian. Retrieved 2020-06-28.
  2. ^ Wallis, W. D.; George, J. C. (2011), Introduction to Combinatorics, CRC Press, p. 212, ISBN 978-1-4398-0623-4
  3. ^ Colbourn, Charles J.; Dinitz, Jeffrey H. (2 November 2006). Handbook of Combinatorial Designs (2nd ed.). CRC Press. p. 12. ISBN 9781420010541. Retrieved 28 March 2017.
  4. ^ Dénes & Keedwell 1974, p. 128
  5. ^ a b Dénes & Keedwell 1974, p. 126
  6. ^ van Lint & Wilson 1992, pp. 161-162
  7. ^ Jia-yu Shao; Wan-di Wei (1992). «A formula for the number of Latin squares». Discrete Mathematics. 110 (1–3): 293–296. doi:10.1016/0012-365x(92)90722-r.
  8. ^ Gyarfas, Andras; Sarkozy, Gabor N. (2012). «Rainbow matchings and partial transversals of Latin squares». arXiv:1208.5670 [CO math. CO].
  9. ^ a b Aharoni, Ron; Berger, Eli; Kotlar, Dani; Ziv, Ran (2017-01-04). «On a conjecture of Stein». Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 87 (2): 203–211. doi:10.1007/s12188-016-0160-3. ISSN 0025-5858. S2CID 119139740.
  10. ^ Stein, Sherman (1975-08-01). «Transversals of Latin squares and their generalizations». Pacific Journal of Mathematics. 59 (2): 567–575. doi:10.2140/pjm.1975.59.567. ISSN 0030-8730.
  11. ^ Koksma, Klaas K. (1969-07-01). «A lower bound for the order of a partial transversal in a latin square». Journal of Combinatorial Theory. 7 (1): 94–95. doi:10.1016/s0021-9800(69)80009-8. ISSN 0021-9800.
  12. ^ Woolbright, David E (1978-03-01). «An n × n Latin square has a transversal with at least n−n distinct symbols». Journal of Combinatorial Theory, Series A. 24 (2): 235–237. doi:10.1016/0097-3165(78)90009-2. ISSN 0097-3165.
  13. ^ Hatami, Pooya; Shor, Peter W. (2008-10-01). «A lower bound for the length of a partial transversal in a Latin square». Journal of Combinatorial Theory, Series A. 115 (7): 1103–1113. doi:10.1016/j.jcta.2008.01.002. ISSN 0097-3165.
  14. ^ Jacobson, M. T.; Matthews, P. (1996). «Generating uniformly distributed random latin squares». Journal of Combinatorial Designs. 4 (6): 405–437. doi:10.1002/(sici)1520-6610(1996)4:6<405::aid-jcd3>3.0.co;2-j.
  15. ^ Bailey, R.A. (2008), «6 Row-Column designs and 9 More about Latin squares», Design of Comparative Experiments, Cambridge University Press, ISBN 978-0-521-68357-9, MR 2422352
  16. ^ Shah, Kirti R.; Sinha, Bikas K. (1989), «4 Row-Column Designs», Theory of Optimal Designs, Lecture Notes in Statistics, vol. 54, Springer-Verlag, pp. 66–84, ISBN 0-387-96991-8, MR 1016151
  17. ^ Colbourn, C.J.; Kløve, T.; Ling, A.C.H. (2004). «Permutation arrays for powerline communication». IEEE Trans. Inf. Theory. 50: 1289–1291. doi:10.1109/tit.2004.828150. S2CID 15920471.
  18. ^ Euler’s revolution, New Scientist, 24 March 2007, pp 48–51
  19. ^ Huczynska, Sophie (2006). «Powerline communication and the 36 officers problem». Philosophical Transactions of the Royal Society A. 364 (1849): 3199–3214. doi:10.1098/rsta.2006.1885. PMID 17090455. S2CID 17662664.
  20. ^ C. Colbourn (1984). «The complexity of completing partial latin squares». Discrete Applied Mathematics. 8: 25–30. doi:10.1016/0166-218X(84)90075-1.
  21. ^ The application of Latin square in agronomic research
  22. ^ «Letters Patent Confering the SSC Arms». ssc.ca. Archived from the original on 2013-05-21.
  23. ^ The International Biometric Society Archived 2005-05-07 at the Wayback Machine

References[edit]

  • Bailey, R.A. (2008). «6 Row-Column designs and 9 More about Latin squares». Design of Comparative Experiments. Cambridge University Press. ISBN 978-0-521-68357-9. MR 2422352.
  • Dénes, J.; Keedwell, A. D. (1974). Latin squares and their applications. New York-London: Academic Press. p. 547. ISBN 0-12-209350-X. MR 0351850.
  • Shah, Kirti R.; Sinha, Bikas K. (1989). «4 Row-Column Designs». Theory of Optimal Designs. Lecture Notes in Statistics. Vol. 54. Springer-Verlag. pp. 66–84. ISBN 0-387-96991-8. MR 1016151.
  • van Lint, J. H.; Wilson, R. M. (1992). A Course in Combinatorics. Cambridge University Press. p. 157. ISBN 0-521-42260-4.

Further reading[edit]

  • Dénes, J. H.; Keedwell, A. D. (1991). Latin squares: New developments in the theory and applications. Annals of Discrete Mathematics. Vol. 46. Paul Erdős (foreword). Amsterdam: Academic Press. ISBN 0-444-88899-3. MR 1096296.
  • Hinkelmann, Klaus; Kempthorne, Oscar (2008). Design and Analysis of Experiments. Vol. I, II (Second ed.). Wiley. ISBN 978-0-470-38551-7. MR 2363107.
    • Hinkelmann, Klaus; Kempthorne, Oscar (2008). Design and Analysis of Experiments, Volume I: Introduction to Experimental Design (Second ed.). Wiley. ISBN 978-0-471-72756-9. MR 2363107.
    • Hinkelmann, Klaus; Kempthorne, Oscar (2005). Design and Analysis of Experiments, Volume 2: Advanced Experimental Design (First ed.). Wiley. ISBN 978-0-471-55177-5. MR 2129060.
  • Knuth, Donald (2011). The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1. Reading, Massachusetts: Addison-Wesley. ISBN 978-0-201-03804-0.
  • Laywine, Charles F.; Mullen, Gary L. (1998). Discrete mathematics using Latin squares. Wiley-Interscience Series in Discrete Mathematics and Optimization. New York: John Wiley & Sons, Inc. ISBN 0-471-24064-8. MR 1644242.
  • Shah, K. R.; Sinha, Bikas K. (1996). «Row-column designs». In S. Ghosh and C. R. Rao (ed.). Design and analysis of experiments. Handbook of Statistics. Vol. 13. Amsterdam: North-Holland Publishing Co. pp. 903–937. ISBN 0-444-82061-2. MR 1492586.
  • Raghavarao, Damaraju (1988). Constructions and Combinatorial Problems in Design of Experiments (corrected reprint of the 1971 Wiley ed.). New York: Dover. ISBN 0-486-65685-3. MR 1102899.
  • Street, Anne Penfold; Street, Deborah J. (1987). Combinatorics of Experimental Design. New York: Oxford University Press. ISBN 0-19-853256-3. MR 0908490.
  • Berger, Paul D.; Maurer, Robert E.; Celli, Giovana B. (November 28, 2017). Experimental Design with Applications in Management, Engineering, and the Sciences (2nd edition (November 28, 2017) ed.). Springer. pp. 267–282.

External links[edit]

  • Weisstein, Eric W. «Latin Square». MathWorld.
  • Latin Squares in the Encyclopaedia of Mathematics
  • Latin Squares in the Online Encyclopedia of Integer Sequences
Источник

Давно, под влиянием книг Перельмана, Гарднера, Азимова и прочих, а также журналов вроде «Наука и жизнь» и «Квант», планировал на будущее писать собственные научно-популярные книги обо всем. Но к счастью вовремя понял, что бумажная литература в XXI веке — жанр не то чтобы вымирающий, но откровенно ретроградный, и в итоге переквалифицировался в блогеры. Многие посты из тех, что можно найти по тегу «занимательные бредни» (и не только) — это несостоявшиеся статьи/главы. Да, в ЖЖ есть свои «научпоперы» вроде sly2m‘а с его физико-математической серией «На пальцах», и мои работы — полнейшая неихуровня ©, зато охват тем у меня поширше будет. Настолько, что даже сам не знаю, про что будет следующий пост.

Сейчас же, отсылаясь к первой главе гарднеровских «Математических досугов», хочу написать про латинские квадраты, конечные аффинные и проективные плоскости и обобщенно-круговые турниры. Что это за звери такие, как они связаны друг с другом и зачем это всё.

Начнем по порядку. Латинский квадрат — это матрица NxN, заполненная N различными элементами по правилам судоку — в каждой строке и в каждом столбце встречается ровно по одному экземпляру каждого из различных элементов.

Существуют также греко-латинские квадраты — комбинации из двух латинских квадратов одного порядка, в которых каждая упорядоченная пара элементов встречается только один раз. Составляющие их латинские квадраты называют ортогональными.

Количество возможных попарно ортогональных латинских квадратов зависит от N. Эйлер, изучавший тему, показал, что при N=6 таких нет (то есть греко-латинский составить нельзя). Для остальных N>3 есть хотя бы одна пара, а теоретический максимум — N-1 — достигается при простом N (и не только, например, есть «полная группа» из 3 латинских квадратов 4х4).

Именно для простых N полная группа латинских квадратов строится алгоритмически: закрепив одну строчку/столбец, делаем копирование элементов вдоль всевозможных так называемых «ломаных диагоналей», всегда перемещаясь на X шагов по одной оси и на Y по другой, считая противоположные стороны квадрата склеенными по правилам модели тора (бублика). Полную группу из двух квадратов 3х3 можно видеть на картинке выше, группа из четырех квадратов 5х5 выглядит так (два получены ходом шахматного слона, два — ходом коня):

Добавим к полной группе еще два квадрата, уже не латинских — в нашем случае из пяти столбцов, заполненных числами 1-2-3-4-5 и из пяти строк, также заполненных 1-2-3-4-5 (процесс копирования не по диагоналям, а вдоль осей) — и держим расширенную группу из N+1=6 получившихся матриц в уме.
___

Что такое конечная плоскость? Мы привыкли иметь дело с плоскостями бесконечными, евклидовыми; конечные же отличаются от них тем, что содержат конечное число точек, которые могут принадлежать прямым. Размерность плоскости (2 измерения) обеспечивает прописанное в «правилах игры» отсутствие скрещивающихся прямых — есть только пересекающиеся (содержащие общую точку) либо, опционально, параллельные (не содержащие ее). Обращаю внимание на то, что параллельность здесь не в евклидовом понимании, да и вообще при отображении на евклидову плоскость прямые превращаются в кривые, причем конечные.

Эта опциональность порождает два варианта:

1) Аффинные конечные плоскости. Их точки разбиваются на несколько равновеликих подмножеств, рассматривающихся как пучки параллельных прямых. При этом через каждую точку проходит несколько прямых (так, что любые две точки принадлежат одной прямой).

Простейшая аффинная плоскость топологически соответствует четырехугольнику с диагоналями (4 точки, 3 семейства по 2 параллельных прямых). Это второй порядок. Третий порядок — так называемая конфигурация Гессе из 9 точек и 12 прямых в составе 4 семейств по 3 штуки, которую можно визуализировать, например, так:

4 семейства здесь — вертикальные прямые, горизонтальные и 2 вида диагональных (ломано-диагональных). Кто знаком с понятием определителя матрицы 3-го порядка, узнает здесь удобный метод их расчета (произведения троек вдоль главной диагонали берутся с плюсом, вдоль побочной — с минусом). Но постойте, где-то мы уже сталкивались с ломаными диагоналями… Правильно! Эти аффинные модели соответствуют расширенным полным группам латинских квадратов. А нашему примеру 5х5 соответствует 25 точек и 6 семейств по 5 параллельных прямых, каждая из которых соединяет одноименные элементы.

2) А вот конечные плоскости без параллельных прямых называются проективными. В них точки и прямые полностью двойственны — через любые две точки проходит одна прямая, но и любые две прямые проходят через одну точку. Проективная плоскость (не обязательно конечная, и бесконечная тоже) может быть получена операцией дополнения: а) каждый пучок параллельных прямых дополняется одной точкой (в случае с преобразованием евклидовой плоскости она называется бесконечно удаленной точкой); б) все бесконечно удаленные точки «объединяются» в прямую.

В итоге такая «дополненная» проективная плоскость обладает полной внутренней симметрией — все ее однотипные структуры с точки зрения топологии полностью симметричны. Собственно, название происходит из того факта, что такая плоскость позволяет уйти от противоречий и парадоксов при проекции с одной евклидовой плоскости на другую, при которых некоторые точки уходят в никуда и оттуда же (причем даже с противоположной на 180° стороны) возвращаются, делая пересекающиеся прямые параллельными и наоборот.

Так вот. В случае с конечной геометрией эти дополнения строятся аналогично: каждый пучок параллельных «прямых» продлевается до новой точки, через все новые точки проводится еще одна прямая. Конструкция из 25 точек и 30 прямых превращается в 31-31, где на каждой прямой находится ровно 6 точек. А конструкция 4-6 (четырехугольник с диагоналями) — в 7-7, известную как плоскость Фано:


И конфигурация Гессе, и плоскость Фано принадлежат к семейству троек Штейнера — частного случая систем Штейнера, комбинаций подмножеств определенного множества, где каждая пара элементов встречается в одном и том же количестве подмножеств. Конфигурация Гессе является еще и «тройкой Киркмана» — частным случаем систем Штейнера, когда все подмножества разбиваются на группы без перекрытий, каждая из которых содержит все элементы. 4х3 подмножеств на 9 элементов — простейшая из троек, сам Киркман изначально описал случай из 7х5 подмножеств на 15 элементов.
___

Итак, и самое главное — зачем это всё? С практической точки зрения. А затем, что вышеописанные конструкции могут служить математической основой для турнирных схем, для которых ввожу определение обобщенные круговые турниры. От обычных круговых турниров — дуэлей «каждый с каждым по N раз» — обобщенные турниры включают в себя игры, в которых задействовано не 2, а большее фиксированное количество игровых единиц (игроков, команд). В подвижных спортивных играх это довольно редкое явление, а вот в настольных, киберспорте, викторинах такое сплошь и рядом. Год назад писал про частные случаи для 27 человек, играющих тройками. Скажем, конфигурация Гессе — это турнир на 9 человек, играющих тройками в 4 захода, чем я и воспользовался однажды при организации дартс-турнира на девятерых. (Мы играем чаще всего не один на один, а группами от 3 до 5 человек сразу). Играли и по плоскости Фано всемером.

Кроме того, схема обобщенного турнира может быть применена для оптимизации расписания обычного кругового турнира. Допустим, разбивка 16 человек на 20 четверок (аффинная конечная плоскость 4-го порядка) — это разбивка 120 дуэлей на группы по 6. Все игроки делятся на четыре четверки-микрогруппы, которые могут одновременно играть внутренние мини-турниры по 6 игр (как в футболе). Потом тасуются, и так 5 подэтапов. Именно такую схему даже применял в одной забаве в институтское время. А проективную плоскость из 13 игроков и игр (то есть точек и прямых) советовал кому-то в useful_faq, когда требовалось составить расписание для игры в пинг-понг, когда было лишь два стола и время на 3 поединка на каждом столе в день.

А системы Штейнера с несколькими встречами между каждой парой игроков весьма удачно применил Андрей Полозов для организации личных первенств в рамках командных видов спорта. Подключив фантазию, можно ввернуть эти математические схемы и еще куда-нибудь.

Да, кстати, если кто не знал, я в принципе увлекаюсь разнообразными турнирными схемами и помогу подобрать оптимальную по вашим входным условиям. Что характерно, бесплатно :-)

Тема может быть интересна для spamsink, doncunita, aaamibor, avva и всех, кто видит прелесть в математике и может осилить вышенаписанное.

Источник

ПОСТРОЕНИЕ
ИДЕАЛЬНЫХ КВАДРАТОВ ЧЁТНО-ЧЁТНОГО ПОРЯДКА

С ПОМОЩЬЮ
ЛАТИНСКИХ КВАДРАТОВ

В статье http://www.klassikpoez.narod.ru/idlat.htm показано построение
идеальных квадратов нечётного порядка с помощью латинских квадратов. Здесь
покажу этот метод для идеальных квадратов чётно-чётного порядка. Рассмотрю
пример построения идеального квадрата 8-ого порядка.

Сразу отмечу один нюанс: сначала
я буду идти от известного мне идеального квадрата. Как составить латинские
квадраты для построения идеального квадрата 8-ого порядка, мне неизвестно. В
своей книге “Магические квадраты. Теория чисел, алгебра, комбинаторный анализ”
(С.-Петербург, 1995 г.) Ю. В. Чебраков даёт метод построения пандиагонального
квадрата 8-ого порядка (в терминологии Чебракова – совершенного). Этот
квадрат строится с помощью двух обобщённых ортогональных латинских квадратов. И
он действительно получается не только пандиагональным, но и совершенным (не в
смысле терминологии Чебракова, а в смысле моей терминологии: я называю
совершенными такие пандиагональные квадраты, которые обладают дополнительными
свойствами). Этот метод я изложила подробно в статье http://www.klassikpoez.narod.ru/latsov.htm

Однако для построения
идеальных квадратов 8-ого порядка данный метод не годится.

Итак, на рис. 1 вы видите
идеальный квадрат 8-ого порядка, с которым я буду работать. Этот идеальный
квадрат был построен методом качелей.

1

32

41

56

49

48

25

8

63

34

23

10

15

18

39

58

4

29

44

53

52

45

28

5

62

35

22

11

14

19

38

59

6

27

46

51

54

43

30

3

60

37

20

13

12

21

36

61

7

26

47

50

55

42

31

2

57

40

17

16

9

24

33

64

Рис. 1

Раскладываю этот квадрат на
латинские квадраты (как это делается, показывалось в предыдущих статьях). На
рис. 2 и на рис. 3 изображены полученные латинские квадраты. Эти квадраты
обобщённые и ортогональные, они очень похожи на квадраты в методе Чебракова для
построения совершенного квадрата 8-ого порядка (см. в книге стр. 119, рис.
2.15).

0

3

5

6

6

5

3

0

7

4

2

1

1

2

4

7

0

3

5

6

6

5

3

0

7

4

2

1

1

2

4

7

0

3

5

6

6

5

3

0

7

4

2

1

1

2

4

7

0

3

5

6

6

5

3

0

7

4

2

1

1

2

4

7

Рис. 2

0

7

0

7

0

7

0

7

6

1

6

1

6

1

6

1

3

4

3

4

3

4

3

4

5

2

5

2

5

2

5

2

5

2

5

2

5

2

5

2

3

4

3

4

3

4

3

4

6

1

6

1

6

1

6

1

0

7

0

7

0

7

0

7

Рис. 3

Если посмотреть на эти
латинские квадраты как на нетрадиционные магические, они являются идеальными
квадратами с магической константой 28, то есть они не просто магические, но и
ассоциативные, и пандиагональные.

Интересно отметить, что
заполнение первого латинского квадрата связано с номерами циклов качания
качелей, как и в идеальных квадратах нечётного порядка. Смотрите: всем числам
начальной цепочки в идеальном квадрате в латинском квадрате соответствуют нули
(нулевой цикл качания качелей); далее, всем числам следующего цикла качания
качелей k=3
в идеальном квадрате в латинском квадрате соответствует число 3 и так далее.
Чтобы лучше увидеть эту связь, читателям надо посмотреть построение идеальных
квадратов такого вида методом качелей. В идеальном квадрате и в первом
латинском квадрате раскрашены нулевой цикл и следующий цикл качания качелей k=3.

А теперь по аналогии с
построением идеальных квадратов нечётного порядка сверну эти латинские квадраты
в такую матрицу (рис. 4):

0000

0313

1100

1213

1200

1113

0300

0013

1312

1001

0212

0101

0112

0201

1012

1301

0003

0310

1103

1210

1203

1110

0303

0010

1311

1002

0211

0102

0111

0202

1011

1302

0011

0302

1111

1202

1211

1102

0311

0002

1303

1010

0203

0110

0103

0210

1003

1310

0012

0301

1112

1201

1212

1101

0312

0001

1300

1013

0200

0113

0100

0213

1000

1313

Рис. 4

При формировании этой
матрицы использована следующая формула для разложения десятичных чисел:

                   N = 32a + 8b + 4c + d = 8(4a + b) + 4c + d

где параметры a, b, c, d принимают значения 0, 1, 2,
3.

Если мы посмотрим на эту
матрицу как на магический нетрадиционный квадрат, заполненный десятичными
числами, это будет не просто магический, а идеальный квадрат с магической
константой 5252. А можно посмотреть на элементы этой матрицы как на числа в
любой другой системе счисления с основанием n>3, например, в
пятеричной. На рис. 4а представлен нетрадиционный идеальный квадрат,
построенный с помощью данной матрицы в пятеричной системе счисления.
Представляете, сколько можно построить нетрадиционных идеальных квадратов таким
способом!

1

84

151

184

176

159

76

9

208

127

58

27

33

52

133

202

4

81

154

181

179

156

79

6

207

128

57

28

32

53

132

203

7

78

157

178

182

153

82

3

204

131

54

31

29

56

129

206

8

77

158

177

183

152

83

2

201

134

51

34

26

59

126

209

Рис. 4а

Получился нетрадиционный
идеальный квадрат с магической константой 840.

А вот нетрадиционный
идеальный квадрат (рис. 4б), который получается, если  смотреть на элементы
матрицы как на числа в четверичной системе счисления, используя стандартное
представление чисел в этой системе счисления по формуле

N = 64a + 16b + 4c + d

1

56

81

104

97

88

49

8

119

66

39

18

23

34

71

114

4

53

84

101

100

85

52

5

118

67

38

19

22

35

70

115

6

51

86

99

102

83

54

3

116

69

36

21

20

37

68

117

7

50

87

98

103

82

55

2

113

72

33

24

17

40

65

120

Рис. 4б

Этот нетрадиционный
идеальный квадрат имеет магическую константу 484.  Интересно отметить, что в
этом квадрате начальная цепочка точно такая же, как в традиционном идеальном
квадрате (рис. 1).

Примечание: нетрадиционным идеальным квадратам
посвящена отдельная страница:

http://www.klassikpoez.narod.ru/idnet.htm

Осталось по данной матрице написать
символьную матрицу (рис. 5):

AAAA

ADbD

BBAA

BCBD

BCAA

bbbD

ADAA

AABD

BDBC

BAAB

ACBC

ABAB

ABBC

ACAB

BABC

BDAB

AAAD

ADBA

BBAD

BCBA

BCAD

BBBA

ADAD

AABA

BDBB

BAAC

ACBB

ABAC

ABBB

ACAC

BABB

BDAC

AABB

ADAC

BBBB

BCAC

BCBB

BBAC

ADBB

AAAC

BDAD

BABA

ACAD

ABBA

ABAD

ACBA

BAAD

BDBA

AABC

ADAB

BBBC

BCAB

BCBC

BBAB

ADBC

AAAB

BDAA

BABD

ACAA

ABBD

ABAA

ACBD

BAAA

BDBD

Рис. 5

На рис. 6 вы видите
табличку значений символом матрицы, при которых получается исходный идеальный
квадрат с рис. 1.

1

2

3

4

A

0

0

0

0

B

32

8

4

1

C

16

8

2

D

24

12

3

Рис. 6

Символы С и D не встречаются в первой
позиции ни в одном элементе матрицы (позиции считаются слева, как в таблице
значений; номера позиций в таблице значений записаны в верхней строке).
Напомню, как вычисляется значение элементов матрицы. Например:

ADBD = 0 + 24 + 4 + 3 = 31

Для приведения квадрата к
традиционному виду надо увеличить все элементы на единицу.

А теперь построим идеальный
квадрат с такими значениями символов (рис. 7):

1

2

3

4

A

32

8

4

1

B

0

0

0

0

C

24

12

3

D

16

8

2

Рис. 7

Просто поменялись местами
значения символов: A и B, C и D. На рис. 8 вы видите новый идеальный квадрат.

46

51

6

27

30

3

54

43

20

13

60

37

36

61

12

21

47

50

7

26

31

2

55

42

17

16

57

40

33

64

9

24

41

56

1

32

25

8

49

48

23

10

63

34

39

58

15

18

44

53

4

29

28

5

52

45

22

11

62

35

38

59

14

19

Рис. 8

Ещё один пример: циклически
переставим значения всех символов (рис. 9).

1

2

3

4

A

0

0

0

0

B

4

1

32

8

C

8

2

16

D

12

3

24

Рис. 9

Новый идеальный квадрат,
построенный с такими значениями символов, изображён на рис. 10.

1

60

6

63

7

62

4

57

56

13

51

10

50

11

53

16

25

36

30

39

31

38

28

33

48

21

43

18

42

19

45

24

41

20

46

23

47

22

44

17

32

37

27

34

26

35

29

40

49

12

54

15

55

14

52

9

8

61

3

58

2

59

5

64

Рис. 10

Интересно привести для
сравнения матрицу для построения пандиагональных квадратов 8-ого порядка,
которая была найдена мной в Интернете по следующей ссылке:

http://www.grogono.com/magic/8x8.php

Эту матрицу вы видите на рис. 11.

ACDE

BD

ABCE

ACF

DEF

ABCDF

BEF

BCDF

ABEF

CF

ADEF

ABD

BCE

A

CDE

AC

DE

ABCD

BE

F

ACDEF

BDF

ABCEF

ABDF

BCEF

AF

CDEF

BCD

ABE

C

ADE

BDE

ABC

E

ACD

ABCDEF

BF

ACEF

DF

CEF

ADF

BCDEF

ABF

AE

CD

ABDE

BC

ABCDE

B

ACE

D

BDEF

ABCF

EF

ACDF

AEF

CDF

ABDEF

BCF

CE

AD

BCDE

AB

Рис. 11

Значения символов в этой
матрице такие: A=16, B=32, C=4, D=8, E=1, F=2. При этом можно
перебрать все перестановки этих значений и таким образом построить по данной
матрице 720 пандиагональных квадратов, но ни один из них не будет идеальным.
Это очевидно: в левой верхней ячейке квадрата стоит число 0, а в правой нижней
ячейке стоит элемент АВ, максимальное значение которого равно 48. Поэтому ни
один из построенных квадратов не будет ассоциативным. Видимо, автор статьи не
ставил цель построить идеальные квадраты, а просто пандиагональные.

В своей статье о магических
квадратах 8-ого порядка я показала построение пандиагональных квадратов с
помощью этого матричного метода и построила по программе все 720
пандиагональных квадратов (они есть в Приложении к статье). Как автор построил
эту символьную матрицу, заинтересовавшиеся читатели могут посмотреть по
указанной ссылке.

По представленной мной
символьной матрице (рис. 5) строятся идеальные квадраты.

К сожалению, у меня нет
идеальных квадратов следующих порядков, подобных рассмотренному квадрату 8-ого
порядка. Поэтому не могу показать построение таких квадратов с помощью
латинских квадратов.

Но есть ещё одна группа
идеальных квадратов, в которых начальная цепочка строится ходом шахматного
коня. Интересно посмотреть, как будет работать данный метод построения для
таких идеальных квадратов. Начну опять с идеального квадрата 8-ого порядка. На
рис. 12 представляю один из квадратов данной группы.

1

63

54

36

41

23

30

12

27

10

8

61

51

34

48

21

47

22

28

9

7

62

52

33

50

40

45

19

26

16

5

59

6

60

49

39

46

20

25

15

32

13

3

58

56

37

43

18

44

17

31

14

4

57

55

38

53

35

42

24

29

11

2

64

Рис. 12

Если строить этот идеальный
квадрат методом качелей, получится следующая образующая таблица (рис. 13):

1

63

54

36

41

23

30

12

-1

2

64

53

35

42

24

29

11

-2

4

57

55

38

44

17

31

14

1

3

58

56

37

43

18

32

13

-3

6

60

49

39

46

20

25

15

1

5

59

50

40

45

19

26

16

-2

7

62

52

33

47

22

28

9

-1

8

61

51

34

48

21

27

10

k=7

k=6

k=4

k=5

k=2

k=3

k=1

Рис. 13

Теперь разложу этот квадрат
на два латинских квадрата (рис. 14 и рис. 15).

0

7

6

4

5

2

3

1

3

1

0

7

6

4

5

2

5

2

3

1

0

7

6

4

6

4

5

2

3

1

0

7

0

7

6

4

5

2

3

1

3

1

0

7

6

4

5

2

5

2

3

1

0

7

6

4

6

4

5

2

3

1

0

7

Рис. 14

Очевидно, что этот
латинский квадрат обобщённый.

Посмотрите на первую строку
этого квадрата! Как и в случае для идеальных квадратов нечётного порядка, в
первой строке первого латинского квадрата записаны номера циклов качания
качелей (смотрите на нижнюю строку образующей таблицы; начальной цепочке, как
вы знаете, соответствует нулевой цикл качания качелей k=0). А дальше латинский
квадрат заполняется в точном соответствии с номерами циклов качания качелей:
всем числам начальной цепочки в идеальном квадрате в латинском квадрате
соответствуют нули; всем числам в идеальном квадрате из набора следующего цикла
качания качелей k=7 в латинском квадрате соответствует число 7 и так
далее. Удивительная закономерность! В идеальном квадрате (рис. 12) и в
латинском квадрате (рис. 14) эта закономерность показана раскраской первых трёх
циклов качания качелей, считая нулевой.

Можно отметить также, что
каждая следующая строка в этом латинском квадрате получается из предыдущей
циклическим сдвигом с постоянным шагом.

Составляю второй латинский
квадрат (рис. 15):

0

6

5

3

0

6

5

3

2

1

7

4

2

1

7

4

6

5

3

0

6

5

3

0

1

7

4

2

1

7

4

2

5

3

0

6

5

3

0

6

7

4

2

1

7

4

2

1

3

0

6

5

3

0

6

5

4

2

1

7

4

2

1

7

Рис. 15

Как строится второй
латинский квадрат – не вижу правила. Но этот квадрат должен быть ортогональным
к первому латинскому квадрату. Возможно, существуют методы построения
ортогональных латинских квадратов (пока не изучала эту тему подробно). Этот
латинский квадрат тоже обобщённый. Если смотреть на оба латинских квадрата как
на нетрадиционные магические квадраты, они являются идеальными с магической
константой 28.

По аналогии с первым
примером можно составить символьную матрицу для построения идеальных квадратов,
подобных квадрату с рис. 12. Оставляю это читателям.

А я рассмотрю идеальные
квадраты 12-ого порядка из этой же группы квадратов (с начальной цепочкой “ход
конём”). Один из таких квадратов вы видите на рис. 16.

1

140

75

45

35

55

121

20

87

117

107

67

106

65

12

138

74

40

34

53

132

18

86

112

93

119

103

61

8

135

81

47

31

49

128

15

126

14

88

118

101

72

6

134

76

46

29

60

25

56

123

21

95

115

97

68

3

141

83

43

82

41

36

54

122

16

94

113

108

66

2

136

9

143

79

37

32

51

129

23

91

109

104

63

102

62

4

142

77

48

30

50

124

22

89

120

85

116

99

69

11

139

73

44

27

57

131

19

130

17

96

114

98

64

10

137

84

42

26

52

33

59

127

13

92

111

105

71

7

133

80

39

78

38

28

58

125

24

90

110

100

70

5

144

Рис. 16

Этот квадрат тоже построен
методом качелей и вот его образующая таблица (рис. 17):

1

140

75

45

35

55

121

20

87

117

107

67

-4

5

144

78

38

28

58

125

24

90

110

100

70

-2

7

133

80

39

33

59

127

13

92

111

105

71

-3

10

137

84

42

26

52

130

17

96

114

98

64

-1

11

139

73

44

27

57

131

19

85

116

99

69

7

4

142

77

48

30

50

124

22

89

120

102

62

-5

9

143

79

37

32

51

129

23

91

109

104

63

7

2

136

82

41

36

54

122

16

94

113

108

66

-1

3

141

83

43

25

56

123

21

95

115

97

68

-3

6

134

76

46

29

60

126

14

88

118

101

72

-2

8

135

81

47

31

49

128

15

93

119

103

61

-4

12

138

74

40

34

53

132

18

86

112

106

65

k=11

k=6

k=3

k=2

k=4

k=10

k=1

k=7

k=9

k=8

k=5

Рис. 17

А теперь попробую составить
первый латинский квадрат не путём разложения исходного идеального квадрата, а
по номерам циклов качания качелей, то есть по выявленной для идеального
квадрата 8-ого порядка закономерности. Записываю в первой строке латинского
квадрата номера циклов качания качелей из нижней строки образующей таблицы; в
первой ячейке запишется число 0, соответствующее нулевому циклу качания качелей
(начальной цепочке). А дальше буду заполнять квадрат в соответствии с номерами
циклов качания качелей. Вот какой латинский квадрат у меня получился (рис. 18):

0

11

6

3

2

4

10

1

7

9

8

5

8

5

0

11

6

3

2

4

10

1

7

9

7

9

8

5

0

11

6

3

2

4

10

1

10

1

7

9

8

5

0

11

6

3

2

4

2

4

10

1

7

9

8

5

0

11

6

3

6

3

2

4

10

1

7

9

8

5

0

11

0

11

6

3

2

4

10

1

7

9

8

5

8

5

0

11

6

3

2

4

10

1

7

9

7

9

8

5

0

11

6

3

2

4

10

1

10

1

7

9

8

5

0

11

6

3

2

4

2

4

10

1

7

9

8

5

0

11

6

3

6

3

2

4

10

1

7

9

8

5

0

11

Рис. 18

Всё получилось совершенно
аналогично латинскому квадрату 8-ого порядка. Латинский квадрат получился
обобщённый. Кроме того, это нетрадиционный идеальный квадрат с магической
константой 66. Ну, а второй латинский квадрат надо составить так, чтобы он был
ортогональным к первому. И он тоже должен быть нетрадиционным идеальным
квадратом с магической константой 66. Этот латинский квадрат вы видите на рис.
19.

0

7

2

8

10

6

0

7

2

8

10

6

9

4

11

5

1

3

9

4

11

5

1

3

8

10

6

0

7

2

8

10

6

0

7

2

5

1

3

9

4

11

5

1

3

9

4

11

0

7

2

8

10

6

0

7

2

8

10

6

9

4

11

5

1

3

9

4

11

5

1

3

8

10

6

0

7

2

8

10

6

0

7

2

5

1

3

9

4

11

5

1

3

9

4

11

0

7

2

8

10

6

0

7

2

8

10

6

9

4

11

5

1

3

9

4

11

5

1

3

8

10

6

0

7

2

8

10

6

0

7

2

5

1

3

9

4

11

5

1

3

9

4

11

Рис. 19

Напомню читателям, что
идеальный квадрат порядка n=4k, k=2, 3, 4… строится из двух латинских (обобщённых)
ортогональных квадратов по следующей формуле:

cij = n*aij + bij + 1

где aij – элементы первого
латинского квадрата, bij  – соответствующие элементы
второго латинского квадрата, cij – соответствующие элементы
идеального квадрата. Если не прибавлять единицу, получится идеальный квадрат,
заполненный числами от 0 до n2 — 1.

Покажу ещё пример для
идеального квадрата 16-ого порядка из этой группы квадратов. На рис. 20 вы
видите идеальный квадрат, построенный методом качелей, на рис. 21 – его
образующую таблицу, на рис. 22 – первый латинский квадрат. Второй латинский
квадрат предлагаю составить читателям. Первый латинский квадрат составлен точно
так же, как для квадрата 12-ого порядка.

1

251

174

237

220

152

199

130

177

75

126

61

108

40

23

82

19

86

16

255

170

233

213

148

195

134

192

79

122

57

101

36

104

39

18

81

11

254

173

236

216

151

194

129

187

78

125

60

121

53

100

35

22

96

15

250

169

229

212

147

198

144

191

74

190

77

124

56

103

34

17

91

14

253

172

232

215

146

193

139

208

143

186

73

117

52

99

38

32

95

10

249

165

228

211

150

210

145

203

142

189

76

120

55

98

33

27

94

13

252

168

231

164

227

214

160

207

138

185

69

116

51

102

48

31

90

9

245

12

248

167

226

209

155

206

141

188

72

119

50

97

43

30

93

26

89

5

244

163

230

224

159

202

137

181

68

115

54

112

47

107

46

29

92

8

247

162

225

219

158

205

140

184

71

114

49

118

64

111

42

25

85

4

243

166

240

223

154

201

133

180

67

183

66

113

59

110

45

28

88

7

242

161

235

222

157

204

136

197

132

179

70

128

63

106

41

21

84

3

246

176

239

218

153

221

156

200

135

178

65

123

62

109

44

24

87

2

241

171

238

175

234

217

149

196

131

182

80

127

58

105

37

20

83

6

256

Рис. 20

1

251

174

237

220

152

199

130

177

75

126

61

108

40

23

82

-5

6

256

175

234

217

149

196

131

182

80

127

58

105

37

20

83

4

2

241

171

238

221

156

200

135

178

65

123

62

109

44

24

87

-1

3

246

176

239

218

153

197

132

179

70

128

63

106

41

21

84

-4

7

242

161

235

222

157

204

136

183

66

113

59

110

45

28

88

3

4

243

166

240

223

154

201

133

180

67

118

64

111

42

25

85

-4

8

247

162

225

219

158

205

140

184

71

114

49

107

46

29

92

3

5

244

163

230

224

159

202

137

181

68

115

54

112

47

26

89

-7

12

248

167

226

209

155

206

141

188

72

119

50

97

43

30

93

3

9

245

164

227

214

160

207

138

185

69

116

51

102

48

31

90

-4

13

252

168

231

210

145

203

142

189

76

120

55

98

33

27

94

3

10

249

165

228

211

150

208

143

186

73

117

52

99

38

32

95

-4

14

253

172

232

215

146

193

139

190

77

124

56

103

34

17

91

-1

15

250

169

229

212

147

198

144

191

74

121

53

100

35

22

96

4

11

254

173

236

216

151

194

129

187

78

125

60

104

39

18

81

-5

16

255

170

233

213

148

195

134

192

79

122

57

101

36

19

86

k=15

k=10

k=14

k=13

k=9

k=12

k=8

k=11

k=4

k=7

k=3

k=6

k=2

k=1

k=5

Рис. 21

0

15

10

14

13

9

12

8

11

4

7

3

6

2

1

5

1

5

0

15

10

14

13

9

12

8

11

4

7

3

6

2

6

2

1

5

0

15

10

14

13

9

12

8

11

4

7

3

7

3

6

2

1

5

0

15

10

14

13

9

12

8

11

4

11

4

7

3

6

2

1

5

0

15

10

14

13

9

12

8

12

8

11

4

7

3

6

2

1

5

0

15

10

14

13

9

13

9

12

8

11

4

7

3

6

2

1

5

0

15

10

14

10

14

13

9

12

8

11

4

7

3

6

2

1

5

0

15

0

15

10

14

13

9

12

8

11

4

7

3

6

2

1

5

1

5

0

15

10

14

13

9

12

8

11

4

7

3

6

2

6

2

1

5

0

15

10

14

13

9

12

8

11

4

7

3

7

3

6

2

1

5

0

15

10

14

13

9

12

8

11

4

11

4

7

3

6

2

1

5

0

15

10

14

13

9

12

8

12

8

11

4

7

3

6

2

1

5

0

15

10

14

13

9

13

9

12

8

11

4

7

3

6

2

1

5

0

15

10

14

10

14

13

9

12

8

11

4

7

3

6

2

1

5

0

15

Рис. 22

Этот обобщённый латинский
квадрат является нетрадиционным идеальным квадратом с магической константой
120. Второй латинский квадрат должен быть ортогональным первому, и он тоже
будет идеальным квадратом с той же магической константой. Если вы умеете
строить ортогональные латинские квадраты, то постройте ортогональный квадрат
для латинского квадрата, изображённого на рис. 22. А если нет, то второй
латинский квадрат можно построить разложением исходного идеального квадрата с
рис. 20.

У меня есть ещё идеальный
квадрат 20-ого порядка из этой группы квадратов, который я тоже построила
методом качелей и ещё нигде не показала в своих статьях (показала только на
научном форуме; там один товарищ высказал мнение, что у меня не получится
построить такой сложный квадрат, пришлось построить и показать товарищу этот
квадрат).

Посетите этот форум, вот
прямая ссылка на тему “Магические квадраты”:

http://dxdy.ru/topic12959.html

Не пропадать же квадрату!
Покажу его сейчас, он здесь как раз к месту. Читателям предлагаю составить
образующую таблицу этого квадрата и два обобщённых ортогональных латинских
квадрата, из которых этот квадрат может быть построен (иными словами: на которые
этот идеальный квадрат раскладывается). На рис. 23 вы видите идеальный квадрат
20-ого порядка из рассматриваемой группы квадратов. Смотрите, как всё похоже в
идеальных квадратах этой группы. Чудесная аналогия!

1

393

258

371

357

315

214

229

325

122

281

113

278

71

177

195

94

49

25

142

23

148

20

399

256

372

347

306

204

230

323

128

300

119

276

72

167

186

84

50

89

45

22

141

13

398

251

377

355

314

209

225

322

121

293

118

271

77

175

194

166

184

90

43

28

160

19

396

252

367

346

304

210

223

328

140

299

116

272

67

277

75

174

189

85

42

21

153

18

391

257

375

354

309

205

222

321

133

298

111

296

112

267

66

164

190

83

48

40

159

16

392

247

366

344

310

203

228

340

139

333

138

291

117

275

74

169

185

82

41

33

158

11

397

255

374

349

305

202

221

208

240

339

136

292

107

266

64

170

183

88

60

39

156

12

387

246

364

350

303

345

302

201

233

338

131

297

115

274

69

165

182

81

53

38

151

17

395

254

369

244

370

343

308

220

239

336

132

287

106

264

70

163

188

100

59

36

152

7

386

15

394

249

365

342

301

213

238

331

137

295

114

269

65

162

181

93

58

31

157

32

147

6

384

250

363

348

320

219

236

332

127

286

104

270

63

168

200

99

56

98

51

37

155

14

389

245

362

341

313

218

231

337

135

294

109

265

62

161

193

180

199

96

52

27

146

4

390

243

368

360

319

216

232

327

126

284

110

263

68

262

61

173

198

91

57

35

154

9

385

242

361

353

318

211

237

335

134

289

105

290

103

268

80

179

196

92

47

26

144

10

383

248

380

359

316

212

227

326

124

334

129

285

102

261

73

178

191

97

55

34

149

5

382

241

373

358

311

217

235

207

226

324

130

283

108

280

79

176

192

87

46

24

150

3

388

260

379

356

312

351

317

215

234

329

125

282

101

273

78

171

197

95

54

29

145

2

381

253

378

259

376

352

307

206

224

330

123

288

120

279

76

172

187

86

44

30

143

8

400

Рис. 23

Возвращаюсь к квадратам
8-ого порядка из этой группы квадратов (с начальной цепочкой “ход конём”).
Итак, установлено, на какие два латинских обобщённых ортогональных квадрата
раскладывается рассмотренный идеальный квадрат 8-ого порядка (с рис. 12).
Теперь можно пойти обратным путём, то есть сначала составить латинские
квадраты, а затем построить из них идеальный квадрат. Алгоритм очень простой.
Сначала заполняем первую строку первого латинского квадрата. Подчеркну, что нам
неизвестен тот идеальный квадрат, который построится из составленных латинских
квадратов. Первую строку первого латинского квадрата заполняем так: в левой
верхней ячейке записываем число 0. Из остальных семи чисел 1, 2, 3, 4, 5, 6, 7
образуем всевозможные перестановки. Каждую из таких перестановок запишем в
первую строку. Каждая следующая строка получается из предыдущей, как мы видели
в рассмотренном примере, циклическим сдвигом с постоянным шагом. Сформировав
таким образом квадрат, надо проверить, чтобы получился идеальный магический
(нетрадиционный) квадрат с магической константой 28. Вот и весь алгоритм для
первого латинского квадрата. Программа, написанная по этому алгоритму, выдала
48 латинских квадратов. Приступаем к составлению второго латинского квадрата.
Как я уже говорила, второй латинский квадрат должен быть ортогонален к первому
и тоже должен являться идеальным (нетрадиционным) магическим квадратом с той же
магической константой 28. Составляю этот квадрат по аналогии с тем, как
составлен латинский квадрат на рис. 15; если присмотреться, можно увидеть связь
этого квадрата с латинским квадратом на рис. 14.

Из 48 вариантов программа
выдала только 6 пар ортогональных латинских квадратов, которые удовлетворяют
всем условиям. Наконец, последний этап – построение из полученной пары
латинских квадратов идеального квадрата. Это совсем простой этап, просто надо
запрограммировать известную формулу:

cij = 8*aij + bij +1

Итак, по программе получены
шесть идеальных квадратов 8-ого порядка. Все они начинаются с числа 1, так как
в левой верхней ячейке первого латинского квадрата мы записали число 0 (и второй
латинский квадрат здесь тоже начинается с числа 0). Среди полученных решений,
конечно, есть идеальный квадрат с рис. 12, поэтому я не буду его показывать.
Остальные пять решений покажу (рис. 24 – рис. 28).

1

60

30

15

41

20

54

39

51

37

8

58

27

13

48

18

44

22

55

33

4

62

31

9

29

16

42

19

53

40

2

59

6

63

25

12

46

23

49

36

56

34

3

61

32

10

43

21

47

17

52

38

7

57

28

14

26

11

45

24

50

35

5

64

Рис. 24

Покажу для примера пару
ортогональных обобщённых латинских квадратов, выданных программой для этого
идеального квадрата:

            0  7  3  1  5 
2  6  4                           0  3  5  6  0  3  5  6

            6  4  0  7  3 
1  5  2                           2  4  7  1  2  4  7  1 

            5  2  6  4  0 
7  3  1                           3  5  6  0  3  5  6  0 

            3  1  5  2  6 
4  0  7                           4  7  1  2  4  7  1  2

                        0 
7  3  1  5  2  6  4                           5  6  0  3  5  6  0  3              

                        6 
4  0  7  3  1  5  2                           7  1  2  4  7  1  2  4 

                        5 
2  6  4  0  7  3  1                           6  0  3  5  6  0  3  5

                        3 
1  5  2  6  4  0  7                           1  2  4  7  1  2  4  7

1

60

31

22

49

12

47

38

42

37

8

59

26

21

56

11

52

15

46

33

4

63

30

17

29

24

51

10

45

40

3

58

7

62

25

20

55

14

41

36

48

35

2

61

32

19

50

13

54

9

44

39

6

57

28

23

27

18

53

16

43

34

5

64

Рис. 25

1

62

44

15

25

38

52

23

53

19

8

58

45

11

32

34

30

36

55

17

6

60

47

9

43

16

26

37

51

24

2

61

4

63

41

14

28

39

49

22

56

18

5

59

48

10

29

35

31

33

54

20

7

57

46

12

42

13

27

40

50

21

3

64

Рис. 26

1

62

47

36

49

14

31

20

26

19

8

61

42

35

56

13

54

15

28

17

6

63

44

33

43

40

53

10

27

24

5

58

7

60

41

38

55

12

25

22

32

21

2

59

48

37

50

11

52

9

30

23

4

57

46

39

45

34

51

16

29

18

3

64

Рис. 27

1

63

52

22

25

39

44

14

45

10

8

59

53

18

32

35

31

36

46

9

7

60

54

17

50

24

27

37

42

16

3

61

4

62

49

23

28

38

41

15

48

11

5

58

56

19

29

34

30

33

47

12

6

57

55

20

51

21

26

40

43

13

2

64

Рис. 28

Прекрасные идеальные
квадратики! Теперь можно сказать, что метод построения идеальных квадратов
8-ого порядка с помощью двух обобщённых ортогональных латинских квадратов
полностью разработан. Алгоритм реализован, есть программа и вот готовые
идеальные квадраты.

Таким образом, мы имеем альтернативный
метод построения идеальных квадратов чётно-чётного порядка. Напомню, что мной
рассмотрен ещё один метод построения таких квадратов – с помощью обратимых
квадратов. Из этой статьи я сейчас возьму один идеальный квадрат 8-ого порядка,
который не входит в полученную группу квадратов. Все полученные здесь идеальные
квадраты начинаются с числа 1. Но ведь идеальные квадраты могут начинаться с
других чисел. А как построить идеальный квадрат 8-ого порядка, начинающийся,
например, с числа 2? Если применить к идеальному квадрату с рис. 28
преобразование параллельного переноса на торе так чтобы он начинался с числа 2,
квадрат утратит ассоциативность и уже не будет идеальным. В указанной статье я
построила идеальный квадрат, начинающийся с числа 2, из обратимого квадрата.
Вот этот квадрат [копирую его из указанной статьи http://www.klassikpoez.narod.ru/obratid1.htm ] (рис. 29):

2

61

48

35

50

13

32

19

25

20

7

62

41

36

55

14

53

16

27

18

5

64

43

34

44

39

54

9

28

23

6

57

8

59

42

37

56

11

26

21

31

22

1

60

47

38

49

12

51

10

29

24

3

58

45

40

46

33

52

15

30

17

4

63

Рис. 29

Обратите внимание: этот
идеальный квадрат связан с квадратом с рис. 27 преобразованием “плюс-минус 1”.

Интересно посмотреть, на
какие латинские квадраты разложится этот идеальный квадрат. Выполняю разложение
и показываю латинские квадраты на рис. 30 и рис. 31.

0

7

5

4

6

1

3

2

3

2

0

7

5

4

6

1

6

1

3

2

0

7

5

4

5

4

6

1

3

2

0

7

0

7

5

4

6

1

3

2

3

2

0

7

5

4

6

1

6

1

3

2

0

7

5

4

5

4

6

1

3

2

0

7

Рис. 30

Как видите, первый
латинский квадрат строится точно так же, как для рассмотренной выше группы
идеальных квадратов. Смотрим на второй латинский квадрат (рис. 29).

1

4

7

2

1

4

7

2

0

3

6

5

0

3

6

5

4

7

2

1

4

7

2

1

3

6

5

0

3

6

5

0

7

2

1

4

7

2

1

4

6

5

0

3

6

5

0

3

2

1

4

7

2

1

4

7

5

0

3

6

5

0

3

6

Рис. 31

Этот латинский квадрат
строится по-другому, нежели в рассмотренном выше примере. Однако он тоже
является идеальным магическим (нетрадиционным) квадратом с магической константой
28 и ортогонален к первому латинскому квадрату. Можно составить программу и для
этой группы идеальных квадратов. Эта программа выдаст все решения, в которых в
левой верхней ячейке идеального квадрата 8-ого порядка стоит число 2.

Примечание: об идеальных квадратах 8-ого
порядка смотрите далее статью

http://www.klassikpoez.narod.ru/id8all.htm

Понятно, что аналогичный
алгоритм можно разработать и для построения идеальных квадратов следующих порядков.

Есть ещё одна группа
идеальных квадратов порядка n=8k, k=1, 2, 3… Эту группу я построила доработкой
пандиагонального квадрата Франклина 16-ого порядка. Сейчас посмотрю на эти
идеальные квадраты с точки зрения построения их с помощью латинских квадратов.

Для примера возьму
идеальный квадрат 16-ого порядка. Этот квадрат был получен из готового
пандиагонального квадрата Франклина комбинацией различных преобразований.
Вероятно, во времена Франклина ещё не рассматривались идеальные квадраты, иначе
Франклин не мог не увидеть в своём пандиагональном квадрате явный прообраз
идеального квадрата. Как помнят читатели, знакомые с этим методом построения
идеальных квадратов, построение осуществляется в два этапа: сначала строится
методом качелей пандиагональный квадрат, подобный пандиагональному квадрату
Франклина 16-ого порядка, а затем простым преобразованием пандиагональный
квадрат превращается в идеальный. Идеальный квадрат 16-ого порядка был построен
мной самым первым и исследован досконально. Я составила для него даже
образующую таблицу, которая получилась бы, если бы этот идеальный квадрат сразу
строился методом качелей, минуя первый этап. Эту образующую таблицу, кажется,
нигде ещё не показала. Сейчас нашла её в черновых записях и покажу здесь. С
помощью этой образующей таблицы я с ходу составила первый латинский квадрат.
Тут точно такая же связь: всё определилось номерами циклов качания качелей!

Замечу, что здесь
образующая таблица имеет несколько необычный вид. Это и понятно: квадрат-то
строится в два этапа. Если составить образующую таблицу для пандиагонального
квадрата, из которого получен идеальный квадрат, она будет иметь обычный вид.
Итак, сначала покажу сам идеальный квадрат 16-ого порядка (рис. 32), а затем
его образующую таблицу (рис. 33).

1

240

225

223

210

63

50

80

65

176

161

159

146

127

114

16

254

19

30

36

45

196

205

179

190

83

94

100

109

132

141

243

2

128

113

160

145

175

162

79

66

64

49

224

209

239

226

15

253

131

142

99

110

84

93

180

189

195

206

35

46

20

29

244

7

234

231

217

216

57

56

74

71

170

167

153

152

121

120

10

252

21

28

38

43

198

203

181

188

85

92

102

107

134

139

245

8

122

119

154

151

169

168

73

72

58

55

218

215

233

232

9

251

133

140

101

108

86

91

182

187

197

204

37

44

22

27

246

11

230

235

213

220

53

60

70

75

166

171

149

156

117

124

6

248

25

24

42

39

202

199

185

184

89

88

106

103

138

135

249

12

118

123

150

155

165

172

69

76

54

59

214

219

229

236

5

247

137

136

105

104

90

87

186

183

201

200

41

40

26

23

250

13

228

237

211

222

51

62

68

77

164

173

147

158

115

126

4

242

31

18

48

33

208

193

191

178

95

82

112

97

144

129

255

14

116

125

148

157

163

174

67

78

52

61

212

221

227

238

3

241

143

130

111

98

96

81

192

177

207

194

47

34

32

17

256

Рис. 32

1

240

225

223

210

63

50

80

65

176

161

159

146

127

114

-6

7

234

231

217

216

57

56

74

71

170

167

153

152

121

120

-4

11

230

235

213

220

53

60

70

75

166

171

149

156

117

124

-2

13

228

237

211

222

51

62

68

77

164

173

147

158

115

126

10

3

238

227

221

212

61

52

78

67

174

163

157

148

125

116

-2

5

236

229

219

214

59

54

76

69

172

165

155

150

123

118

-4

9

232

233

215

218

55

58

72

73

168

169

151

154

119

122

-6

15

226

239

209

224

49

64

66

79

162

175

145

160

113

128

k=0

k=14

k=13

k=3

k=4

k=10

k=9

k=7

241

242

17

32

34

47

194

207

177

192

81

96

98

111

130

143

-6

247

248

23

26

40

41

200

201

183

186

87

90

104

105

136

137

-4

251

252

27

22

44

37

204

197

187

182

91

86

108

101

140

133

-2

253

254

29

20

46

35

206

195

189

180

93

84

110

99

142

131

10

243

244

19

30

36

45

196

205

179

190

83

94

100

109

132

141

-2

245

246

21

28

38

43

198

203

181

188

85

92

102

107

134

139

-4

249

250

25

24

42

39

202

199

185

184

89

88

106

103

138

135

-6

255

256

31

18

48

33

208

193

191

178

95

82

112

97

144

129

k=15

k=1

k=2

k=12

k=11

k=5

k=6

k=8

Рис. 33

Невероятно гармоничен этот
идеальный квадрат! Браво, Франклин!

А сейчас покажу первый
латинский квадрат (рис. 34), и вы ещё более поразитесь удивительной связи этого
латинского квадрата с образующей таблицей, а точнее – с номерами циклов качания
качелей. Все номера циклов качания качелей в точном соответствии с образующей
таблицей записаны в первых двух строках этого латинского квадрата. А далее
первые две строки просто дублируются: один раз с переворотом, другой раз –
точной копией.

0

14

14

13

13

3

3

4

4

10

10

9

9

7

7

0

15

1

1

2

2

12

12

11

11

5

5

6

6

8

8

15

0

7

7

9

9

10

10

4

4

3

3

13

13

14

14

0

15

8

8

6

6

5

5

11

11

12

12

2

2

1

1

15

0

14

14

13

13

3

3

4

4

10

10

9

9

7

7

0

15

1

1

2

2

12

12

11

11

5

5

6

6

8

8

15

0

7

7

9

9

10

10

4

4

3

3

13

13

14

14

0

15

8

8

6

6

5

5

11

11

12

12

2

2

1

1

15

0

14

14

13

13

3

3

4

4

10

10

9

9

7

7

0

15

1

1

2

2

12

12

11

11

5

5

6

6

8

8

15

0

7

7

9

9

10

10

4

4

3

3

13

13

14

14

0

15

8

8

6

6

5

5

11

11

12

12

2

2

1

1

15

0

14

14

13

13

3

3

4

4

10

10

9

9

7

7

0

15

1

1

2

2

12

12

11

11

5

5

6

6

8

8

15

0

7

7

9

9

10

10

4

4

3

3

13

13

14

14

0

15

8

8

6

6

5

5

11

11

12

12

2

2

1

1

15

Рис. 34

Вы где-нибудь видели такой
красивый латинский (обобщённый) квадрат? Если посмотреть на него как на
магический нетрадиционный квадрат, он является идеальным квадратом с магической
константой 120.

В идеальном квадрате (рис.
32) и в латинском квадрате (рис. 34) раскрашены первые четыре цикла качания
качелей, считая нулевой цикл (начальную цепочку). Связь с номерами циклов
качания качелей в латинском квадрате очевидна.

Ну, а теперь осталось
составить второй латинский квадрат. Как вы уже знаете, этот латинский квадрат
должен быть ортогонален первому латинскому квадрату, и обязан являться
нетрадиционным идеальным квадратом с магической константой 120. Вы можете
составить такой латинский квадрат? Я пока не знаю, как это сделать. А поэтому
составляю второй квадрат, исходя из разложения исходного идеального квадрата на
два латинских квадрата. Второй латинский квадрат вы видите на рис. 35.

0

15

0

14

1

14

1

15

0

15

0

14

1

14

1

15

13

2

13

3

12

3

12

2

13

2

13

3

12

3

12

2

1

15

0

15

0

14

1

14

1

15

0

15

0

14

1

14

12

2

13

2

13

3

12

3

12

2

13

2

13

3

12

3

6

9

6

8

7

8

7

9

6

9

6

8

7

8

7

9

11

4

11

5

10

5

10

4

11

4

11

5

10

5

10

4

7

9

6

9

6

8

7

8

7

9

6

9

6

8

7

8

10

4

11

4

11

5

10

5

10

4

11

4

11

5

10

5

10

5

10

4

11

4

11

5

10

5

10

4

11

4

11

5

7

8

7

9

6

9

6

8

7

8

7

9

6

9

6

8

11

5

10

5

10

4

11

4

11

5

10

5

10

4

11

4

6

8

7

8

7

9

6

9

6

8

7

8

7

9

6

9

12

3

12

2

13

2

13

3

12

3

12

2

13

2

13

3

1

14

1

15

0

15

0

14

1

14

1

15

0

15

0

14

13

3

12

3

12

2

13

2

13

3

12

3

12

2

13

2

0

14

1

14

1

15

0

15

0

14

1

14

1

15

0

15

Рис. 35

Сложив теперь матрицы этих
латинских квадратов по формуле:

cij = 16*aij + bij + 1

вы получите исходный идеальный квадрат с рис. 32.

А теперь напомню, что в
этом примере мы опять шли от известного идеального квадрата. Можете ли вы, основываясь
на приведённом примере, составить пару латинских квадратов для построения
идеального квадрата следующего – 24-ого – порядка? Ведь номера циклов качания
качелей для этого идеального квадрата вы не знаете. Как заполнить первую строку
первого латинского квадрата? Ну, положим, что в первой и в последней ячейке
надо записать число 0. Заметьте, что во второй строке числа комплементарны
соответствующим числам в первой строке, то есть сумма этих чисел всегда равна
15. Для порядка n=24 сумма двух комплементарных чисел будет равна 23
(то есть n – 1). Остаётся заполнить первую строку между первой
и последней ячейкой. А дальше всё элементарно. Составив первый латинский
квадрат, строим второй – ортогональный первому и являющийся идеальным
нетрадиционным магическим квадратом с магической константой 276. И, наконец, с
помощью двух латинских квадратов по приведённой выше формуле строим идеальный
квадрат. Положим, подбор чисел в первой строке первого латинского квадрата
можно выполнить по программе. Но как построить второй латинский квадрат? Нужно
увидеть связь между этими двумя квадратами. Или просто знать методы построения
ортогональных латинских квадратов. Не забудьте, что второй латинский квадрат
должен быть не только ортогональным первому, он должен быть ещё нетрадиционным
идеальным магическим квадратом с той же самой магической константой, что и
первый латинский квадрат.

Предлагаю читателям по
черновому наброску схемы разработать этот алгоритм. Тогда можно будет написать
программу и по этой программе получить множество подобных идеальных квадратов.

Примечание: магическая константа латинского квадрата
порядка n вычисляется
очень просто, это есть сумма чисел от 0 до n – 1.
Например, для n=24
имеем:

S = (0 + 23)*24/2 = 276.

14-18 июля 2008 г.

г. Саратов.

       Пишите мне!

        Приглашаю всех на форум!

Рейтинг@Mail.ru

На главную страницу

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти формулу сульфата меди
  • Подключено кроме аудио как исправить на андроид
  • Как найти нужную фразу в поисковике
  • Касперский обновлены не все компоненты как исправить
  • Как найти нужную папку на андроиде

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии