Как составить квадрат суммы двух одночленов - AvtoShod.ru

Квадрат суммы

Квадрат суммы двух чисел можно искать как произведение двух множителей. Но удобнее один раз вывести формулу и в дальнейшем сумму возводить в квадрат уже с помощью этой формулы.

Формула квадрата суммы двух чисел — одна из формул сокращенного умножения, которые называются так потому, что позволяют сократить вычисления.

Квадрат суммы двух одночленов называют квадратом двучлена.

$[{(a + b)^2} = (a + b)(a + b) = ]$

$[ = {a^2} + ab + ab + {b^2} = {a^2} + 2ab + {b^2}]$

Таким образом, формула квадрата суммы двух чисел —

$[{(a + b)^2} = {a^2} + 2ab + {b^2}]$

Найти квадрат суммы выражений:

$[1){(x + 5)^2};]$

$[2){(3x + 7y)^2};]$

$[3){(2{x^3} + 5{x^7})^2};]$

$[4){(10a + b{c^5})^2}.]$

Решение:

$[1){(x + 5)^2} = ]$

Первое слагаемое — x, второе — 5. Значит, a=x, b=5. Применяем формулу квадрата суммы:

$[ = {x^2} + 2 cdot x cdot 5 + {5^2} = {x^2} + 10x + 25.]$

$[2){(3x + 7y)^2} = ]$

Все, что стоит до знака «+» — это a, все после «+» — b. В данном случае a=3x, b=7y.

На начальном этапе обучения может помочь работе с формулой квадрата двучлена рисунок.

Если выражение, стоящее до знака «+», заключить в квадрат, а выражение после «+» — в круг, то схематически формулу квадрата суммы можно представить так:

Рисунок позволяет наглядно показать, что стоит на месте a и b в каждом конкретном случае.

Применив эту схему к нашему примеру, получим

В традиционной записи возведение в квадрат суммы записывают так:

$[{(3x + 7y)^2} = {(3x)^2} + 2 cdot 3x cdot 7y + {(7y)^2} = ]$

$[ = 9{x^2} + 42xy + 49{y^2};]$

Важно помнить — при возведении в квадрат произведения или степени их обязательно записывать в скобках!

При возведении в квадрат используем свойства степеней.

$[3){(2{x^3} + 5{x^7})^2} = ]$

$[ = {(2{x^3})^2} + 2 cdot 2{x^3} cdot 5{x^7} + {(5{x^7})^2} = ]$

$[ = 4{x^6} + 20{x^{10}} + 25{x^{14}};]$

$[4){(10a + b{c^5})^2} = {(10a)^2} + 2 cdot 10a cdot b{c^5} + {(b{c^5})^2} = ]$

$[ = 100{a^2} + 20ab{c^5} + {b^2}{c^{10}}.]$

Источник

Светило науки — 5593 ответа — 17687 раз оказано помощи

Составьте квадрат суммы двух одночленов.Ответ запишите в виде степени и в виде многочлена.(2x + 5)² = 4x² + 20x + 25
(x + 3)² = x² + 6x + 9
(6a + 7b)² = 36a² + 84ab + 49b²
(2k + 3)² = 4k² + 12k + 9

Пользуясь формулой квадрата суммы,вычислите значение выражения:10,2

² = (10+0,2)² = 100 + 4 + 0,04 = 104,04
104²=(100+4)² = 10000 + 800 + 16 = 10816
32² = (30 + 2)² = 900 + 120 + 4 = 1024
51² = (50 + 1)² = 2500 + 100 + 1 = 2601
ПРИМЕЧАНИЕ:все числа во второй степени.

Представьте многочлен в виде квадрата суммы:4a

²+4ab+b² = (2a + b)²
k²+2kb+b² = (k + b)²
1+2m+m² = (1 + m)²
1/4+p+p² = (1/2 + p)²
ПРИМЕЧАНИЕ:4a,b k,b m p во второй степени

Источник

Составьте квадрат суммы двух одночленов.

Ответ запишите в виде степени и в виде многочлена.

2x и 5 x и 3y 6a и 7b 2k и 3 Пользуясь формулой квадрата суммы, вычислите значение выражения : 10, 2 = (10 + 0, 2) 104 = (100 + 4) 32 51 ПРИМЕЧАНИЕ : все числа во второй степени.

Представьте многочлен в виде квадрата суммы : 4a + 4ab + b k + 2kb + b 1 + 2m + m одна четвертая + p + p ПРИМЕЧАНИЕ : 4a, b k, b m p во второй степени ПОМОГИТЕ СРОЧНО!

Перед вами страница с вопросом Составьте квадрат суммы двух одночленов?, который относится к
категории Алгебра. Уровень сложности соответствует учебной программе для
учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.

Источник

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Бином Ньютона

Одними из основных формул сокращенного умножения является формулы квадрата суммы и квадрата разности двух одночленов.

Данные формулы можно вывести с помощью Бинома Ньютона.

Формула бинома Ньютона для натуральных чисел имеет следующий вид:

Здесь $C^0_n, C^1_n,dots ,C^{n-1}_n,C^n_n$ — коэффициенты Бинома Ньютона.

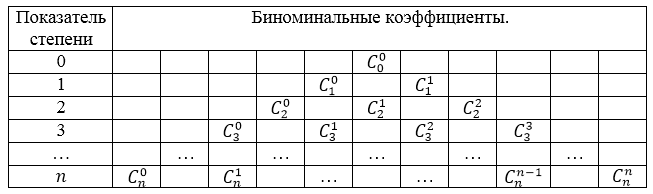
Коэффициенты разложения Бинома Ньютона можно находить с помощью треугольника Паскаля.

Треугольник Паскаля имеет следующую структуру (рис. 1).

Рисунок 1. Структура треугольника Паскаля

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

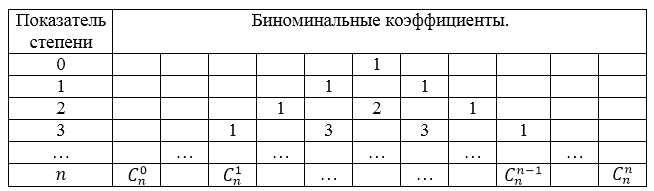
Значения коэффициентов треугольника паскаля приведены в следующей таблице (рис. 2):

Рисунок 2. Коэффициенты треугольника Паскаля

Формула квадрата суммы

Выведем с использованием формулы Бинома Ньютона формулу квадрата суммы ${(a+b)}^2$. Из формулы Бинома Ньютона получаем:

Используя таблицу 2, получим:

Таким образом, квадрат суммы двух выражений равен сумме квадрата первого выражения с удвоенным произведением первого выражения на второе и квадратом второго выражения:

Пример 1: возвести в квадрат $(2x+3y)$

Используя формулу квадрата суммы, получим:

Замечание

!!! Здесь стоит обратить особое внимание, что формулу надо применяя к одночленам, входящим в сумму, целиком. Типичной ошибкой в данном случае бывает то, что зачастую в квадрат возводят только часть одночлена (к примеру, возводят не $2x$ целиком, а только $x$, что является ошибкой!!!)

«Квадрат суммы и квадрат разности» 👇

Формула квадрата разности

Найдем теперь формулу разности суммы. Для этого вначале представим выражение в следующем виде:

Воспользуемся формулой Бинома Ньютона:

Используя таблицу 2, получим:

Таким образом, квадрат разности двух выражений равен сумме квадрата первого выражения с квадратом второго выражения без удвоенного произведения первого выражения на второе:

Примеры задач на использование формул квадрата суммы и разности

Пример 1

Выполнить возведение в квадрат:

а) ${(-9a+4b)}^2$

б) ${(-8a-5b)}^2$

в) ${(x^2-7)}^2$

Решение:

а) ${(-9a+4b)}^2$

Поменяем одночлены, стоящие в скобке, местами:

[{(-9a+4b)}^2={(4b-9a)}^2]

Воспользуемся формулой квадрата разности:

[{(4b-9a)}^2={(4b)}^2-2cdot 4bcdot 9a+{(9a)}^2={16b}^2-72ab+{81a}^2]

б) ${(-8a-5b)}^2$

Так как квадрат всегда положительное число, то получим:

[{(-8a-5b)}^2={(8a+5b)}^2]

Воспользуемся формулой квадрата суммы:

[{(8a+5b)}^2={(8a)}^2+2cdot 5bcdot 8a+{(5b)}^2={64a}^2+80ab+{25b}^2]

в) ${(x^2-7)}^2$

Воспользуемся формулой квадрата разности:

[{(x^2-7)}^2={(x^2)}^2-2cdot x^2cdot 7+7^2=x^4-14x^2+49]

Пример 2

Представить в виде квадрата:

а) $4a^2+12a+9$

б) $x^2-20xy^2+100y^4$

Решение:

а) $4a^2+12a+9$

Воспользуемся формулой квадрата суммы:

[4a^2+12a+9={(2a)}^2+2cdot 2acdot 3+3^2=(2a+3)^2]

б) $x^2-20xy^2+100y^4$

Воспользуемся формулой квадрата разности:

[x^2-20xy^2+100y^4=x^2-2cdot xcdot 10y^2+{(10y)}^2=(x-10y)^2]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

☰

Квадрат суммы нескольких слагаемых

Рассмотрим квадрат трех слагаемых:

(a + b + c)²

Представим его в таком виде:

((a + b) + c)²

Если рассматривать (a + b) как одно слагаемое, то мы можем применить формулу квадрата суммы для двух слагаемых:

((a + b) + c)² = (a + b)² + 2(a + b)c + c² = a² + 2ab + b² + 2ac + 2bc + c²

Итак в результате преобразования мы получили:

(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc

Если бы слагаемых было 4, то в результате преобразования выглядели так:

(a + b + c + d)² = ((a + b) + (c + d))² = (a + b)² + 2(a+b)(c+d) + (c + d)² = a² + 2ab + b² + 2ac + 2ad + 2bc + 2bd + c² + 2cd + d²

В результате была бы получена следующая формула:

(a + b + c + d)² = a² + b² + c² + d² + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd

Вообще независимо от того, сколько слагаемых в квадрате суммы, при раскрытии скобок получается сумма квадратов всех слагаемых плюс удвоенные пары произведений этих слагаемых.

Источник

Бином Ньютона

Формула квадрата суммы

Формула квадрата разности

Примеры задач на использование формул квадрата суммы и разности

Квадрат суммы нескольких слагаемых

Не пропустите также: