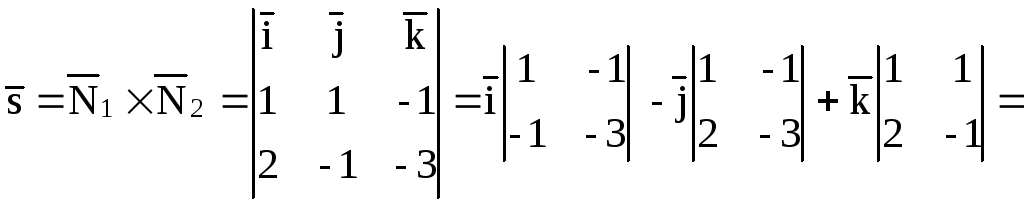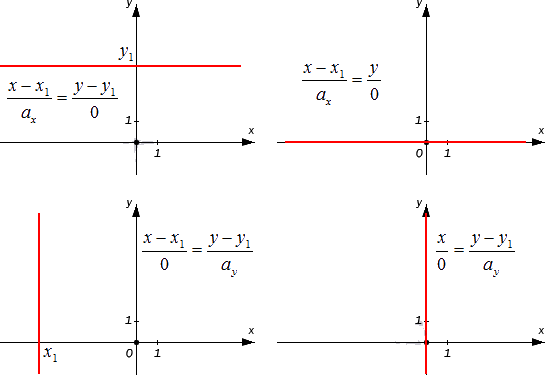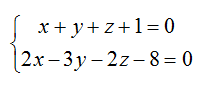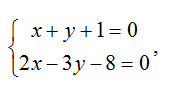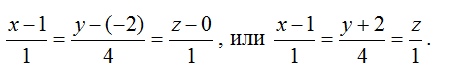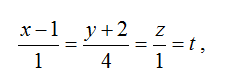3.1. Канонические
уравнения прямой.
Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторы
коллинеарны, следовательно, их
соответствующие координаты пропорциональны:
(3.3.1)
Эти уравнения
называются каноническими
уравнениями прямой.
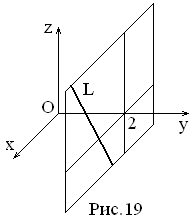
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору
Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:
Это канонические
уравнения прямой.
Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.
3.2.
Параметрические
уравнения прямой.
Пусть прямая
задана каноническими уравнениями
Обозначим тогда
Величина t
называется параметром и может принимать
любые значения:
.
Выразим x,
y
и z
через t
:
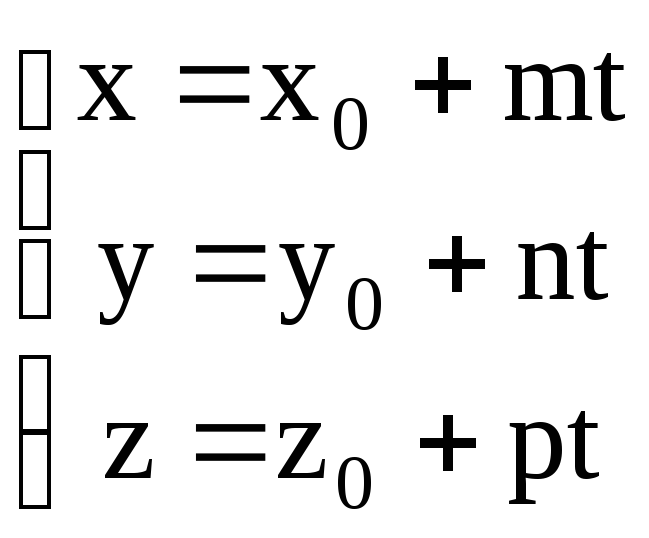
Полученные уравнения
называются параметрическими
уравнениями прямой.
Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору
Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:
Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):
Итак,

прямой.
Ответ:
Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).
Решение:
Вектор является направляющим
вектором искомой прямой.
Найдем вектор .
= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

параметрические уравнения прямой.
3.3. Уравнения
прямой, проходящей через две заданные
точки.
Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Вектор
можно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
наход
по формулам (3.1.1):).
(3.3.1)
Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
Применяем
формулу (3.3.1)
Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

уравнения прямой.
Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
По формулам
(3.3.1) получим:
Это канонические
уравнения.
Переходим к
параметрическим уравнениям:

уравнения.
Полученная прямая
параллельна оси oz
(см. рис.21).
3.4. Прямая как
линия пересечения двух плоскостей.
Пусть в
пространстве даны две плоскости
и
Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:
Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий вектор
Координаты точки
получим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть
Пример 1.
Составить
канонические уравнения прямой
Решение: Пусть
z
= 0. Решим систему
Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.
Итак, точка
лежит на искомой прямой.
Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:
Уравнения прямой
находим по формулам (3.1.1):
Ответ: .
Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).
Пример 2.
Составить канонические и параметрические
уравнения прямой
Решение:
Пусть y
= 0. Тогда система примет вид:
Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку
Для нахождения
второй точки положим x
= 0. Будем иметь:
То есть
Далее применяем
формулы (3.3.1):
Получили канонические
уравнения прямой.
Составим
параметрические уравнения прямой:
Ответ:
; 
3.5. Взаимное
расположение двух прямых в пространстве.
Пусть прямые
заданы уравнениями:
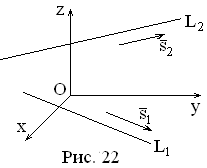
;
:
.
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот угол
находим по формуле из векторной алгебры:
или
(3.5.1)
Если прямые перпендикулярны
(),то
Следовательно,
(3.5.2)
Это условие
перпендикулярности двух прямых в
пространстве.
Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть
(3.5.3)
Это условие
параллельности двух прямых в пространстве.
Пример 1. Найти
угол между прямыми:
а).
и
б). и
Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему
Затем найдем их векторное произведение:
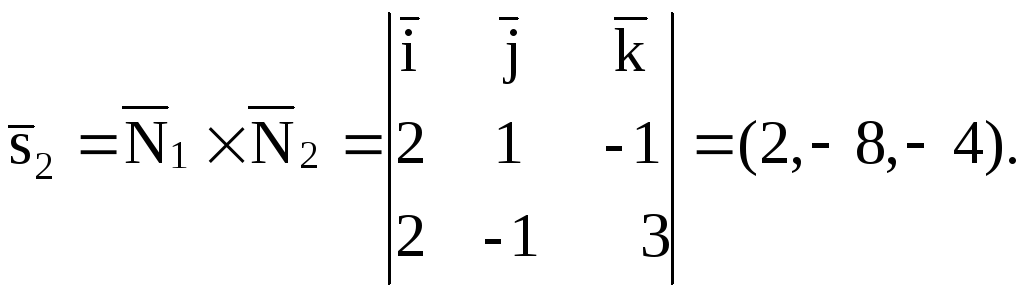
пункта 3.4).
По формуле (3.5.1)
получим:
Следовательно,
б). Запишем
направляющие векторы данных прямых:
Векторы
коллинеарны, так как их соответствующие
координаты пропорциональны:
Значит прямые
параллельны (
),
то есть
Ответ: а).
б).
Пример 2. Доказать
перпендикулярность прямых:
и
Решение:
Запишем направляющий вектор первой
прямой
Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:
Вычислим их векторное произведение:

Применим условие
перпендикулярности прямых (3.5.2):
Условие выполнено;
следовательно, прямые перпендикулярны
().
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
Понятие канонического уравнения прямой
Чтобы разобраться, что такое каноническое уравнение, нужно рассмотреть следующий пример. Дана прямоугольная система координат, в которой задана некая произвольная прямая. Известны координаты произвольной точки на отрезке [M_{1}left(x_{1}, y_{1}right)] и координаты направляющего вектора [bar{a}=left(a_{x^{prime}} a_{y}right)]. Используя все имеющиеся данные составим и запишем уравнение, которое будет описывать данную заданную прямую.
Рассмотрим точку [mathrm{M}(x, y)]. Вектор [overline{M_{1} M}] можно отнести к направляющим исходной линии в координатной плоскости. Координатами вектора будут точки [left(x-x_{1}, y-y_{1}right)]. Чтобы правильно определить векторные координаты, необходимо вспомнить основное правило решения векторов.
Произвольные точки [M(x, y)] будут являться основой для необходимой прямой с направляющим вектором [bar{a}=left(a_{x}, a_{y}right)], только тогда, когда вектора [overline{M_{1} M}] и [bar{a}=left(a_{x}, a_{y}right)] будут являться коллинеарными по отношению друг к другу.
Исходя из этого можно составить формулу коллинеарности двух векторов.
Формула
[overline{M_{1} M}=lambda cdot overline{mathrm{a}}, lambda in R]
Где:
После преобразования данного равенства в координатную форму, можно получить следующее уравнение:
[begin{aligned}
&x-x_{1}=lambda cdot a_{x} \
&y-y_{1}=lambda cdot a_{y}
end{aligned}]
Однако, обязательно выполнение главных условий: [a_{x} neq 0] и [a_{y} neq 0].
При выполнении вышеперечисленных условий, получаем следующие равенства:
[begin{aligned}
&x-x_{1}=lambda cdot a_{x} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&y-y_{1}=lambda cdot a_{y} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}
end{aligned}]
Все выполненные преобразования привели к тому, что мы получили окончательную формулу канонического уравнения на плоскости [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Иначе такое равенство, еще называют уравнением прямой канонического вида.
Используя данную запись [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], можно в прямоугольной системе координат задать прямую, которой будет характерен направляющий вектор [bar{a}=left(a_{x}, a_{y}right)]. Также данная линия будет проходить через заданную точку [M_{1}left(x_{1}, y_{1}right)].
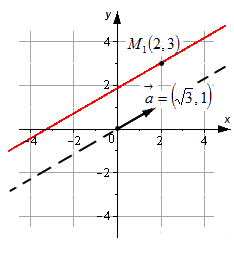
Например: задано уравнение [frac{x-2}{sqrt{3}}=frac{y-3}{1}]. Задается линия, которая будет проходить через точки [M_{1}(2,3)]. Ее направляющий вектор имеет координатные точки: [bar{a}=(sqrt{3}, 1)].
Когда любая прямая в системе координат проходит через две любые точки [M_{1}left(x_{1}, y_{1}right)] и [M_{2}left(x_{2}, y_{2}right)] и имеет направляющий вектор [bar{a}=left(a_{x}, a_{y}right)], множество всех векторов можно записать как [mu cdot overline{mathrm{a}}=left(mu cdot mathrm{a}{x^{prime}} mu cdot a{y}right), mu in R, mu neq 0].
Таким образом, каждое уравнение прямой канонического вида [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], будет соответствовать заданной прямой на плоскости.
Пример 1
В системе координат задана прямая, которая проходит через точки [M_{1}(2,4)], и имеет направляющий вектор [bar{a}=(1,-3)].
Решение задачи:
Составим и запишем общий вид канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Далее подставим в него заданные значения [x_{1}=2, y_{1}=-4, a_{x}=1, a_{y}=-3].
Проведем необходимый расчет и получим следующую запись:
[frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-2} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}].
Ответ: [frac{x-2}{1}=frac{y+4}{-3}]
Каноническое уравнение на плоскости с точками ax и ay равными нулевому значению
При условии, что одно из значений переменной является нулю, будет использоваться первоначальный вид уравнения. Две переменные нулевыми быть не могут, так как это невозможно по определению. Направляющий вектор не может быть нулевым.
В такой ситуации выражение [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] считается условным, и его нужно понимать как равенство [a_{y}left(x-x_{1}right)=a_{x}left(y-y_{1}right)].
Если [frac{x-x_{1}}{0}=frac{y-y_{1}}{a_{y}}] при [a_{x}=0], а заданная прямая проходит через точки [M_{1}left(x_{1}, y_{1}right)]. В данном случае она является параллельной относительно оси ординат. Если [x_{1}=0], то прямая будет совпадать с осью координат.
Утверждение необходимо доказать. Для заданной прямой вектор [bar{a}=left(a_{x}, a_{y}right)] является направляющим. Также данный вектор будет являться коллинеарным по отношению к координатному вектору [bar{j}=(0.1)].
Если второй параметр является нулевым значением, то [a_{y}=0] и мы получим равенство [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{0}]. Данное уравнение характеризует прямую, которая проходит через точку [M_{1}left(x_{1}, y_{1}right)] и располагается параллельно оси абсцисс. Это утверждение будет правдивым, так как [bar{a}=left(a_{x^{prime}} 0right)], и является для прямой направляющим вектором. А вектор, в свою очередь, коллинеарен по отношению к вектору координат [bar{j}=(0.1)].
Примеры 2 — 3
На координатной плоскости задана прямая, которая расположена параллельно оси Oy. Она проходит через точку
[M_{1}left(sqrt[3]{2},-frac{1}{7}right)].
Необходимо составить каноническое уравнение для заданной прямой, используя исходные данные.
Решение:
Так как прямая по отношению к координатной оси является параллельной, можно использовать координатный вектор
[bar{j}=(0.1)]. Данный вектор будет служить, как направляющий.
Искомое уравнение будет выглядеть в следующем виде:
[frac{x-sqrt[3]{2}}{0}=frac{y-left(-frac{1}{7}right)}{1} Leftrightarrow
frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
Ответ: [frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
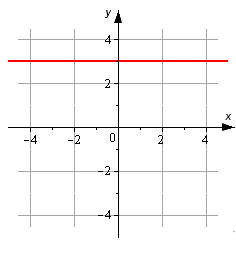
Согласно графику, нужно составить каноническое уравнение прямой.
Решение:
Исходя из графика можно сказать, что линия параллельна оси Ox и проходит через точку [M_{1}(0,3)].
Используем координатный вектор как направляющий.
Записываем каноническое уравнение: [frac{x-0}{1}=frac{y-3}{0} Leftrightarrow
frac{x}{1}=frac{y-3}{0}].
Ответ: [frac{x}{1}=frac{y-3}{0}].
Преобразование канонического уравнения прямой в уравнение другого вида
Стандартную форму канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] можно поставить в систему параметрических уравнений для плоскости.
Для преобразования одного вида уравнения в другой необходимо одну часть уравнения приравнять к другой.
[begin{aligned}
&frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow frac{x-x_{1}}{a_{y}}=lambda Rightarrow \
&frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow x=x_{1}+a_{x} cdot lambda Rightarrow y=y_{1}+a_{y} cdot lambda
end{aligned}]
Примеры 4 — 5
Задана прямая на плоскости в виде канонического уравнения [frac{x+2}{3}=frac{y-1}{11}].
Необходимо записать параметрическое уравнение для прямой.
Принцип решения задачи:
Нужно поставить знак равенства между отдельными частями уравнения и переменной [lambda]. Получается
следующий вид уравнения: [frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda].
Далее можно записать необходимы уравнения параметрического вида:
[frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda.].
[Leftrightarrow x+2=3 cdot lambda] и
[y-1=11 cdot lambda Leftrightarrow x=-2+3 cdot lambda] и [y=1+11 cdot lambda]
Ответ: [x=-2+3 cdot lambda] и [y=1+11 cdot lambda].
Задана на плоскости прямая при помощи канонического уравнения [frac{x-1}{2}=frac{y+4}{0}].
Необходимо составить общей вид канонического уравнения для данной прямой.
Решение:
Аналогичным образом решаем задачу, как в предыдущем примере:
[frac{x-1}{2}=lambda] и [frac{y+4}{0}=lambda].
[Leftrightarrow x-1=2 cdot lambda] и [y+4=0
cdot lambda Leftrightarrow x=-2+1 cdot lambda] и [y=-4+0 cdot lambda]
[Leftrightarrow 0
cdot(x-1)=2 cdot(y+4) Leftrightarrow y+4=0]
Ответ: [y+4=0].
Нет времени решать самому?
Наши эксперты помогут!
Принцип решения задач на составление канонических уравнений
Первым делом канонические уравнения применяется для тех задач, где необходимо вычислить принадлежность точки к заданному отрезку на плоскости.
Рассмотрим несколько вариантов задач, и подробно опишем их решение.
Примеры 6 — 8
Задана линия, каноническое уравнение которой выглядит следующим образом:
[frac{x-1}{2}=frac{y+frac{1}{2}}{-3}].
Нужно определить принадлежат ли две точки [M_{1}left(3,-3 frac{1}{2}right)] и [M_{2}(5,-4)]
прямой.
Решение:
Для того чтобы проверить принадлежность прямой, нужно подставить заданные координаты точек в каноническое
уравнение.
Выполнив данное действие получим верное равенство: [frac{3-1}{2}=frac{-3 frac{1}{2}+frac{1}{2}}{-2}
Leftrightarrow 1=1].
Согласно результату, можно сказать что точка [M_{1}left(3,-3 frac{1}{2}right)] принадлежит заданному
отрезку.
Аналогичным образом нужно поступить и с другой точкой.
[frac{5-1}{2}=frac{-4 frac{1}{2}+frac{1}{2}}{-3} Leftrightarrow 2=frac{7}{6}]
Полученное в ходе решения равенство не является верным, следовательно, точка [M_{2}(5,-4)] не будет ей
принадлежать.
Ответ: прямой принадлежат координаты точки [M_{1}left(3,-3 frac{1}{2}right)], координаты точки
[M_{2}(5,-4)] нет.
Заданы координаты двух точек [M_{1}(2,4)] и [M_{2}(-1,3)]. Нужно определить, будет ли заданная прямая на
плоскости с помощью уравнения [frac{x-2}{0}=frac{y-3}{2}], проходить через заданные координаты.
Решение:
Уравнение [frac{x-2}{0}=frac{y-3}{2}] можно преобразовать, и записать как [2 cdot(x-2)=0 cdot(y-3)
Leftrightarrow x-2=0].
Заданные координаты точек подставим преобразованное уравнение, и произведем проверку.
Для точки [M_{1}(2,4) 2-2=0 Leftrightarrow 0=0].
Так как равенство верное, можно сделать вывод, что точка принадлежит прямой.
Аналогичным образом проводится проверка второй точки: [M_{2}(-1,3)]
[-1-2=0 Leftrightarrow-3=0].
Равенство неверное, поэтому точка [M_{2}(-1,3)] не принадлежит прямой.
Ответ: через точку [M_{1}(2,4)] прямая будет проходить, так как равенство верное, через точку
[M_{2}(-1,3)] нет.
Задачи, в которых заданы точки с координатами, будут являться наиболее простыми по отношению нахождения
канонического уравнения прямой.
Наиболее сложнее решаются задачи, когда предварительно необходимо определить координаты точек, через которые
проходит прямая.
Наиболее распространенной является тип задач, где нужно доказать прохождение прямой, через заданные точки.
Задана прямая, которая проходит через точки [M_{1}(0,-3)] и [M_{2}(2,-2)] в прямоугольной системе координат. Согласно условию задачи, необходимо составить каноническое уравнение.
Решение:
Вычислим координаты вектора [overline{M_{1} M_{2}}=(2.1)], по уже известной методике решения, используя заданные точки. По отношению к прямой данный вектор будет направляющим.
[frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}]
Ответ: [frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}].
Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей
Решение
1) Найдем координаты фиксированной точки. Из исходной системы уравнений
исключим z.
Положим z=0, тогда:
откуда находим: x=1, y= -2.
Таким образом, нашли координаты фиксированной точки M0(1,-2,0).
2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:
3) Запишем канонические уравнения:
4) Обозначив,
получаем параметрические уравнения:
x=t+1, y=4t-2, z=4
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
(схема 27)
Пусть задан
вектор 
однозначно определяется в пространстве точкой M0(x0;y0;z0) и вектором 
Обозначим

с точностью до коллинеарности (рис. 2.21).
Пусть точка M(x;y;z) – текущая точка прямой l,
тогда текущий вектор прямой имеет координаты 


следствию из теоремы 2.5 данное условие
можно записать в виде:

канонические уравнения прямой в
пространстве. Равенство нулю одного из знаменателей означает обращение
в нуль соответствующего числителя.
Пусть прямая l проходит через две точки,
одна из которых – уже введенная в
рассмотрение точка M0(x0;y0;z0). Другую точку обозначим M1(x1;y1;z1). Тогда в качестве направляющего вектора 


уравнения прямой в пространстве, проходящей
через две заданные точки.
Все
соотношения (2.43) равны между собой, следовательно, может быть введен
коэффициент пропорциональности t,
называемый параметром прямой:

Можно записать
частный случай уравнений (2.45) для плоскости: 
прямой линии на плоскости. Проводя аналогичные рассуждения, в качестве
направляющего вектора прямой на плоскости можно взять вектор 
M0(x0;y0) – в качестве произвольной точки
прямой. Заметим, что канонические уравнения (2.4) прямой на плоскости
представляют собой частный случай уравнений (2.44).
Чтобы задать прямую l в пространстве в общем виде
надо рассмотреть её как линию пересечения двух
плоскостей, которые обозначим через α
и β, и зададим уравнениями соответственно: 
означает, что прямая задается системой, состоящей из уравнений плоскостей α и β:

–
общее уравнение прямой в пространстве.
Здесь 
или совпадают).
Поставим
задачу – привести общее уравнение (2.46) прямой к ее каноническим уравнениям (2.43). Решение
состоит из трех этапов.
1. Отыскание точки M0(x0;y0;z0), лежащей на данной прямой.
Координаты
точки M0 должны удовлетворять системе (2.46), так как
точка принадлежит обеим плоскостям α и β.
Ранг
системы (2.46) равен 2, сама система является совместной неопределенной.
Объявим базисными переменными, например, x и y,
тогда z – свободная переменная. Придадим ей конкретное
значение z=z0. Система примет вид: 

достаточно найти одно ее частное решение.
Для простоты вычислений можно придать свободной переменной нулевое значение, то есть z0=0. После этого определенную систему уравнений решают известными методами. Решение
системы x=x0; y=y0
в совокупности со значением свободной переменной представляет собой координаты
искомой точки M0(x0;y0;z0).
2. Рассмотрим нахождение направляющего вектора 



то его можно найти по теореме 2.5 как векторное произведение указанных
векторов:

3. Найденную точку M0 и вектор 
уравнение (2.43). Таким образом, задача о приведении общего уравнения прямой к
каноническому виду решена.
Пример 2.16.
Привести общее уравнение прямой в
пространстве 
каноническому виду.
Решение. Найдем точку M0(x0;y0;z0), принадлежащую данной прямой. Достаточно найти одно
частное решение заданной системы, например, при z0=0. Решение будет представлять собой координаты точки M0:

вспомогательные определители системы: 
По формулам (1.6):


заданной прямой.
Найдем направляющий вектор 
пересечением которых задана прямая, есть 
2.5:

Подставляя координаты точки M и вектора
в (2.43), получим искомое каноническое
уравнение прямой l:
Вопросы
для самопроверки