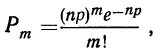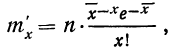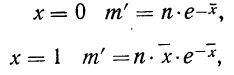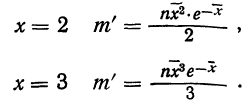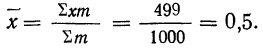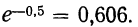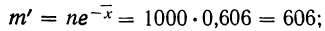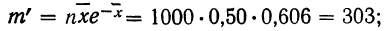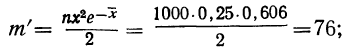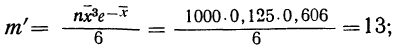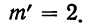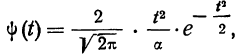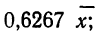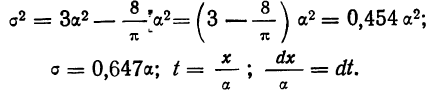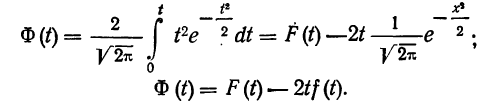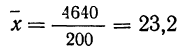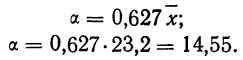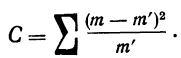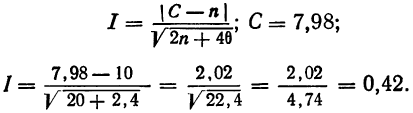Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k — число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) — середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) — результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | — |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Функция распределения случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть
– действительное число. Вероятность события,
состоящего в том, что
примет значение, меньшее
, то есть вероятность
события
обозначим через
. Разумеется, если
изменяется, то, вообще говоря, изменяется и
, то есть
– функция от
.
Функцией распределения называют функцию
, определяющую вероятность
того, что случайная величина
в результате испытания примет значение,
меньшее
, то есть:
Геометрически
это равенство можно истолковать так:
есть вероятность того, что случайная величина примет
значение, которое изображается на числовой оси точкой, лежащей левее точки
.
Иногда
вместо термина «функция распределения» используют термин «интегральная
функция».
Функцию
распределения дискретной случайной величины
можно представить следующим соотношением:
Это
соотношение можно переписать в развернутом виде:
Функция
распределения дискретной случайной величины есть разрывная ступенчатая функция,
скачки которой происходят в точках, соответствующих возможным значениям
случайной величины и равны вероятностям этих значений. Сумма всех скачков
функции
равна 1.
Свойства функции распределения
Свойство 1.
Значения
функции распределения принадлежат отрезку
:
Свойство 2.
– неубывающая функция, то есть:
,
если
Свойство 3.
Если возможные значения случайной величины
принадлежат интервалу
,
то:
1)
при
;
2)
при
Свойство 4.
Справедливо равенство:
Свойство 5.
Вероятность того, что непрерывная случайная
величина
примет одно определенное значение, равна нулю.
Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый.
Заметим, что было бы неправильным думать, что
равенство нулю вероятности
означает, что событие
невозможно (если, конечно, не ограничиваться
классическим определением вероятности). Действительно, в результате испытания
случайная величина обязательно примет одно из возможных значений; в частности,
это значение может оказаться равным
.
Свойство 6.
Если возможные значения непрерывной случайной величины
расположены на всей оси
,
то справедливы следующие предельные соотношения:
Свойство 7.
Функция распределения непрерывная слева, то есть:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Примеры решения задач
Пример 1
Дан ряд
распределения случайной величины
:
|
|
1 | 2 | 6 | 8 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти и изобразить ее функцию распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Будем задавать различные значения
и находить для них
1. Если
,
то, очевидно,
в том числе и при
2. Пусть
(например
)
Очевидно, что и
3. Пусть
(например
);
Очевидно, что и
4. Пусть
Очевидно, что и
5. Пусть
Итак:
График функции распределения
Пример 2
Случайная
величина
задана функцией распределения:
Найти
вероятность того, что в результате испытания
примет значение:
а) меньше
0,2;
б) меньше
трех;
в) не
меньше трех;
г) не
меньше пяти.
Решение
а) Так
как при
функция
, то
то есть
при
б)
в)
События
и
противоположны, поэтому
Отсюда:
г) сумма
вероятностей противоположных событий равна единице, поэтому
Отсюда, в
силу того что при
функция
, получим:
Пример 3
Задана
непрерывная случайная величина X своей плотностью
распределения вероятностей f(x). Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики функций f(x) и F(x);
4)
вычислить математическое ожидание и дисперсию X;
5)
определить вероятность того, что X примет значение из
интервала (a,b).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем отметить,
что:
и
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
3) Построим графики функций:
График плотности распределения
График функции распределения
4) Вычислим
математическое ожидание:
В нашем случае:
Вычислим дисперсию:
Искомая дисперсия:
5) Вероятность того, что
примет значение из интервала
:
Задачи контрольных и самостоятельных работ
Задача 1
Закон
распределения случайной величины X задан таблицей.
Найти ее
математическое ожидание, дисперсию и значение функции распределения в заданной
точке.
F(1)=
M[X]=
D[X]=
Задача 2
Случайная
величины X задана функцией распределения
Найти
плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить графики дифференциальной и интегральной функций.
Найти вероятность попадания случайной величины X в интервалы (1,2; 1,8),
(1,8; 2,3)
Задача 3
Дискретная
случайная величина X задана рядом распределения. Найти:
1)
функцию распределения F(x) и ее график;
2)
математическое ожидание M(X);
3)
дисперсию D(X).
|
|
-5 | 5 | 25 | 45 | 65 |
|
|
0.2 | 0.15 | 0.3 | 0.25 | 0.1 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В задаче
дискретная случайная величина задана рядом распределения.
Найти
; M(X), D(X), P(0≤X≤2); F(x).
Начертить график F(x)
Задача 5
В задаче
непрерывная случайная величина X задана функцией
распределения F(x).
Найти a; f(x); M(X); D(X); P(X<0.2)
Начертить
графики функций f(x);F(x).
Задача 6
Функция
распределения непрерывной случайной величины X (времени безотказной работы
некоторого устройства) равна
(
). Найти вероятность безотказной
работы устройства за время x больше либо равно T.
Задача 7
Функция
распределения непрерывной случайной величины задана выражением:
Найдите:
1)
параметр a;
2)
плотность вероятностей;
4) P(0<x<1)
Постройте
графики интегральной и дифференциальной функции распределения.
Задача 8
Дана
интегральная функция распределения. Найти: дифференциальную функцию f(x),M(X),σ(X),D(X).
Задача 9
Дана
функция распределения F(х) случайной величины Х.
Найти плотность
распределения вероятностей f(x), математическое ожидание M(X),
дисперсию D(X) и вероятность попадания X на
отрезок [a,b]. Построить графики
функций F(x) и f(x).
Задача 10
НСВ X имеет
плотность вероятности (закон Коши)
Найти:
а)
постоянную C=const;
б)
функцию распределения F(x);
в)
вероятность попадания в интервал -1<x<1
г)
построить графики f(x), F(x).
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Интегральная функция распределения вероятностей случайной величины
ТЗР-3. Интегральная функция распределения
вероятностей СВ
Это наиболее
универсальный способ задания закона
распределения. Его можно применять и
для дискретных и для непрерывных СВ.
Часто, говоря об этом способе, слова
«интегральная» и «вероятностей»
отбрасывают и используют термин «функция
распределения СВ» .
Интегральная
функция распределения вероятностей
представляет собой вероятность того,
что некоторая случайная величина Х
принимает значение меньшее, чем текущее
х:
F(х)
= Р(Х < х)
(20)
Например,
если для такой СВ, как ток в ЛЭП, функция
распределения F(90)
= 0,3, то это означает, что вероятность
принятия током в ЛЭП значения, меньше
90 А, равна 0,3.
Если
для напряжения в сети функция распределения
F(215)
= 0,4, то 0,4 –это вероятность того, что
напряжение в сети меньше 215 В.
Функция
распределения вероятностей может быть
задана аналитически, таблично или
графически.
Пример
27
По
заданному ряду распределения оценок
студентов на экзамене (табл. 8, строки 1
и 2) записать интегральную функцию
распределения (табл. 8, строка 3) и построить
её график.
Таблица 8. Ряд и интегральная функция
распределения оценок на экзамене
|
Оценка Х |
2 |
3 |
4 |
5 |
6 |
|
Вероятность |
0,1 |
0,5 |
0,3 |
0,1 |
— |
|
Функция |
0 |
0,1 |
0,6 |
0,9 |
1,0 |
Для нахождения
значений функции распределения необходимо
воспользоваться её определением (20):
-
для
Х
= 2 F(2)
= Р(Х
< 2) = 0, так
как оценок меньше 2 на экзамене не
бывает; -
для
Х =
3 F(3)
= Р(Х
< 3) = Р(Х =
2) = 0,1, т.к. меньше 3 есть только оценка
2; -
для
Х
= 4 F(4)
= Р(Х
< 4) = Р(Х
= 2) + Р(Х
= 3) = 0,1 + 0,5 =
0,6, т.к. меньше 4 есть две оценки – 2 или
3 (получение оценки меньше 4 равнозначно
получению или
оценки 2 или
оценки 3 и для нахождения F(4)
можно воспользоваться формулой сложения
вероятностей несовместных событий); -
для
Х
= 5 F(5)
= Р(Х
< 5) = Р(Х
< 4) + Р(Х
= 4) = 0,6 + 0,3 =
0,9, то есть к F(4)
добавляется вероятность того, что
оценка равна 4.
Анализируя порядок
нахождения значений F(х),
видим, что к вероятности наименьшего
значения СВ сначала добавляется
вероятность второго значения, затем –
третьего и т.д. То есть вероятности как
бы накапливаются. Поэтому интегральную
функцию распределения иначе называют
«функцией накопленных вероятностей».
В
литературе по статистике функцию
накопленных вероятностей достаточно
часто называют кумулятой.
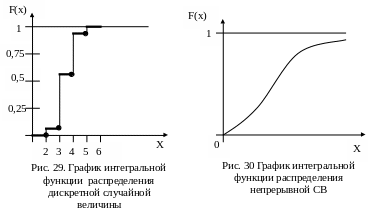
На
основе данных табл. 8 может быть построен
график интегральной функции дискретной
случайной величины (рис. 29). Эта функция
является разрывной. Скач
ки
соответствуют отдельным дискретным
значениям Х, а высоты «ступенек»
— соответствующим вероятностям. В
местах разрыва функция (рис. 29) принимает
значения обозначенные точками, т.е.
непрерывна слева. В общем виде для
дискретной СВ можно записать: F(х)
= Р(Х < х) =
.
(21)
Для
того чтобы понять, как будет выглядеть
график интегральной функции распределения
для непрерывной СВ, можно прибегнуть к
следующим рассуждениям. Если представить,
что количество значений дискретной СВ
возрастает, то мест разрыва будет
становиться больше, а высота ступенек
будет уменьшаться. В пределе, когда
количество возможных значений станет
бесконечным (а это и есть непрерывная
СВ), ступенчатый график превратится в
непрерывный (рис. 30).
Поскольку
интегральная
функция распределения вероятностей СВ
имеет первостепенное значение, рассмотрим
подробнее ее свойства:
Свойство 1. Такой способ задания
закона распределения универсален,
т. к. пригоден для задания закона
распределения как дискретных, так и
непрерывных СВ.
Свойство
2. Поскольку
интегральная функция распределения –
это вероятность, то ее
значения лежат на отрезке от 0 до 1.
Свойство
3. Функция
распределения безразмерна,
как и любая вероятность.
Свойство
4. Функция
распределения есть неубывающая
функция, т.
е. большему значению аргумента
соответствует то же или большее значение
функции: при х2
> х1
F(х2)
≥
F(х1).
Это
свойство вытекает из того (рис. 31), что
вероятность попадания на больший отрезок
(от -∞ до х2)
никак не может быть меньше вероятности
попадания на меньший отрезок (от -∞ до
х1).
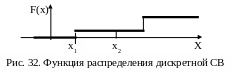
Если
на участке от х2
до х1
(рис. 32)
нет возможных
значений СВ (это возможно для дискретных
СВ), то F(х2)
= F(х1).
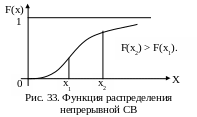
Для
функции распределения непрерывной СВ
(рис.33) F(х2)
всегда больше F(х1).
Свойство
4 имеет два следствия.
Следствие
1
Вероятность
того, что величина Х примет значение в
интервале (х1;х2)
равна разности значений интегральной
функции на границах интервала:
Р(х1
≤ Х <
х2)
= F(х2)
– F(х1). (15)
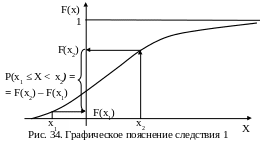
Это
следствие можно пояснить следующим
образом (рис.31):
F(х2)
= Р(Х <
х2)
–
вероятность
того, что СВ принимает значения левее
точки х2.
F(х1)
= Р(Х <
х1)
– вероятность того, что СВ принимает
значения левее точки х1.
Отсюда
разность
Р(Х
< х2)
— Р(Х <
х1)
есть
вероятность того, что значения СВ
расположены на участке от х1
до х2
(рис.34).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
- число попаданий при п выстрелах, если известна вероятность попадания при 1 выстреле. Число попаданий может быть 0, 1, 2….. n;
- число появлений герба при n бросаниях монеты.
Примеры непрерывных случайных переменных:
- ошибка измерения;
- дальность полета снаряда.
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
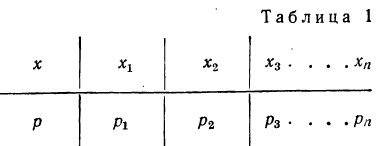
Закон распределения имеет чаще всего табличную -форму изложения. В этом случае перечисляются все возможные значения случайной переменной и соответствующие им вероятности:
Такая таблица называется также рядом распределения случайной переменной.
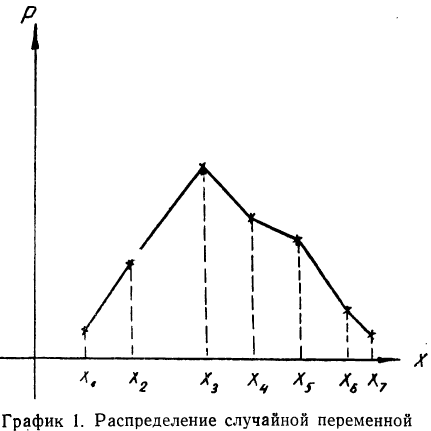
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х<х, зависит от текущей переменной х и является функцией от х. Эта функция носит название функции распределения случайной переменной X.
F(x) = P(X
Функция распределения является одной из форм выражения закона распределения. Она является универсальной характеристикой случайной переменной и может существовать для прерывных и непрерывных случайных переменных.
Функция распределения F(x) называется также интегральной функцией распределения, или интегральным законом распределения.
Основные свойства функции распределения могут быть сформулированы так:
- F(x) всегда неотрицательная функция, т. е.
- Так как вероятность не может быть больше единицы, то
- Ввиду того что F(x) является неубывающей функцией, то при
- Предельное значение функции распределения при х=
равно нулю, а при х=
равно единице.
Если случайная переменная X дискретна и задана рядом распределения, то для нахождения F(x) для каждого х необходимо найти сумму вероятностей значений X, которые лежат до точки х.
Графическое изображение функции распределения представляет собой некоторую неубывающую кривую, значения которой начинаются с 0 и доходят до 1.
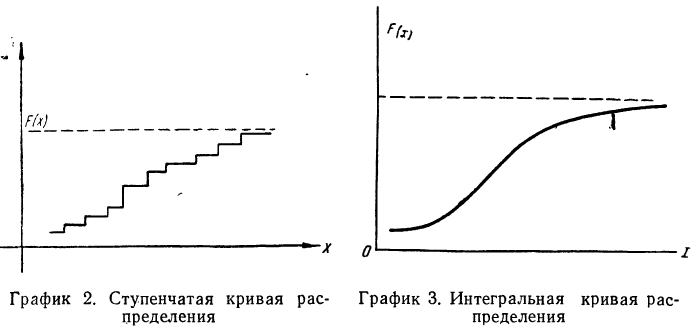
В случае дискретной случайной переменной величины вероятность F(x) увеличивается скачками всякий раз, когда х при своем изменении проходит через одно из возможных значений 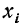
В случае непрерывной случайной переменной величины функция F(x) при графическом изображении дает плавную, монотонно возрастающую кривую следующего вида (см. график 3).
Обычно функция распределения непрерывной случайной переменной представляет собой функцию, непрерывную во всех точках. Эта функция является также дифференцируемой функцией. График функции распределения такой случайной переменной является плавной кривой и имеет касательную в любой ее точке.
Плотность распределения
Если для непрерывной случайной переменной X с функцией распределения F(x) вычислять вероятность попадания ее на участок от х до х+ 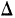
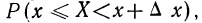
Если величину 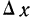
т. е. производной от функции распределения, которая характеризует плотность, с которой распределяются значения случайной переменной в данной точке. Эта функция называется плотностью распределения и часто обозначается f(x). Ее называют также дифференциальной функцией распределения, или дифференциальным законом распределения.
Таким образом, функция плотности распределения f(x) является производной интегральной функции распределения F(x).
Вероятность того, что случайная переменная X примет значение, лежащее в границах от а до 6, равна определенному интегралу в тех же пределах от плотности вероятности, или:
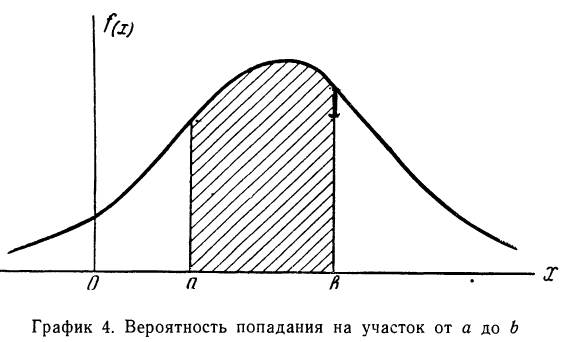
Кривая, изображающая плотность распределения случайной переменной, называется кривой распределения (дифференциальной).
Построим кривую некоторой заданной функции плотности вероятности и найдем участок, ограниченный абсциссами а и b. Площадь, ограниченная соответствующими ординатами кривой распределения самой кривой и осью абсцисс, и отобразит вероятность того, что случайная переменная будет находиться в данных пределах (см. график 4).
Плотность распределения является одной из форм закона распределения, но существует только для непрерывных случайных величин.
Основные свойства плотности распределения могут быть сформулированы так:
1. Плотность распределения есть функция, не могущая принимать отрицательных значений, т. е.
Отсюда в геометрическом изображении плотности распределения (в кривой распределения) не может быть точек, лежащих ниже оси абсцисс.
2.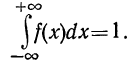
Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона и нормальное распределение.
Биномиальное распределение
Если производится n независимых испытаний, в каждом из которых вероятность появления данного события А есть величина постоянная, равная р, и, следовательно, вероятность непоявления события А также постоянна и равна q=1—р, то число появлений события А во всех n испытаниях представляет собой случайную переменную. Вероятность того, что событие А появится в n испытаниях m раз, равна:
т. е. m+1, члену разложения бинома 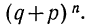
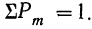
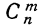
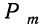
Ввиду того что вероятности 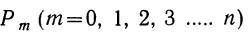
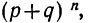
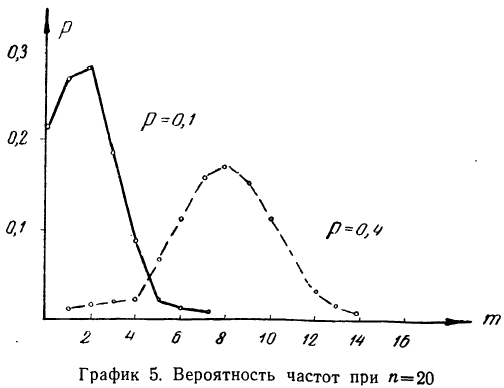
График биномиального распределения, на котором по оси абсцисс откладываются числа наступлений события, а по оси ординат — вероятности этих чисел, представляет собой ломаную линию. Форма графика зависит от значений р, q и n.
Если р и q одинаковы, то график распределения симметричен. Если же р и q неодинаковы, то график распределения будет скошенным.
Одна из частот на графике имеет максимальное значение. Это наиболее вероятная частота. Ее значение можно определить приближенно, аналитически как произведение nр.
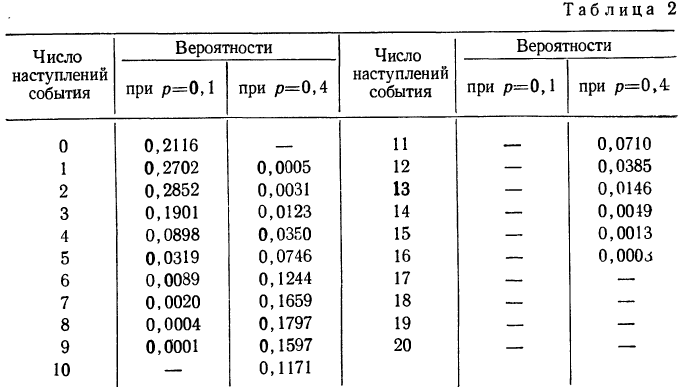
Найдем вероятности числа наступления события А при 20 испытаниях при p = 0,1 и р = 0,4 и построим график их распределений (см. график 5). Найдем вероятности частот при n = 20 для p = 0,1 и р=0,4.
График показывает, что приближение р к 0,5 вносит в распределение большую симметрию. Оказывается также, что при увеличении n распределение становится симметричным и для
Биномиальное распределение имеет широкое распространение в практической деятельности людей. Например, продолжительное наблюдение за качеством выпускаемой заводом продукции показало, что p-я часть ее является браком. Иначе говоря, мы выражаем через р вероятность для любого изделия оказаться бракованным. Биномиальное распределение показывает вероятность того, что в партии, содержащей n изделий, окажется m бракованных, где m = 0, 1, 2, 3 … n.
Предположим, имеется 100 изделий из партии изделий, в ко торой доля брака равна 0,05. Вероятность того, что из этих из делий окажется 10 бракованных, равна:
Закон биномиального распределения называется также схемой Бернулли. .
Нормальное распределение
Расчет вероятностей по формуле биномиального распределения при больших n очень громоздок. При этом значении m прерывны, и нет возможности аналитически отыскать их сумму в некоторых границах. Лаплас нашел закон распределения, являющийся предельным законом при неограниченном возрастании числа испытаний n и называемый законом нормального распределения.
Плотность вероятности нормального распределения выражается при этом формулой:
где t представляет собой нормированное отклонение частоты т от наиболее вероятной частоты nр, т. е. 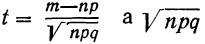
Максимальная ордината кривой соответствует точке m=nр, т. е. математическому ожиданию случайной переменной m; величина этой ординаты равна 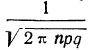
Для практического нахождения вероятностей используют таблицу значений f(t).
Эмпирические и теоретические распределения
В примерах распределений, приведенных в разделе I, мы пользовались данными, почерпнутыми из наблюдений.
Поэтому всякий наблюденный ряд распределения назовем эмпирическим, а график, изображающий распределение
частот этого ряда, — эмпирической кривой распределения. Эмпирические кривые распределения могут быть представлены полигоном и гистограммой. При этом изображение в виде полигона применяется для рядов с прерывными значениями признака, а гистограмма— для рядов с непрерывными значениями признака.
Наблюдая многочисленные ряды распределения, математики стремятся описать эти распределения путем анализа образования величины признака, пытаются построить теоретическое распределение, исходя из данных об эмпирическом распределении.
Мы уже видели на примере распределения случайной переменной, что распределение ее задается законом распределения. Закон распределения, заданный в виде функции распределения, позволяет математически описать ряды распределения некоторых совокупностей.
Теоретическим законом распределения многих совокупностей, наблюдаемых на практике, является нормальное распределение. Иначе говоря, многие эмпирические подчинены закону нормального распределения, функция плотности вероятности которого приведена в предыдущем параграфе.
Чтобы эту формулу применять для нахождения теоретических данных по некоторому эмпирическому ряду, необходимо вероятностные характеристики заменить данными эмпирического ряда. При этой замене величина стандартизованного отклонения t будет представлять собой 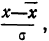
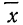
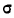
Следовательно, нормальное распределение ряда распределения зависит от величин средней арифметической и его среднего квадратического отклонения.
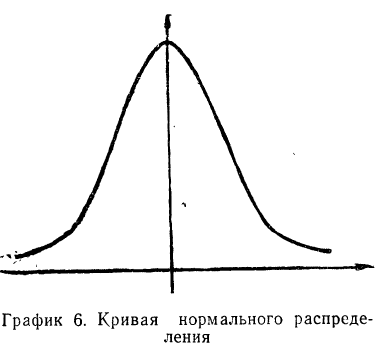
Свойства кривой нормального распределения
Дифференциальный закон нормального распределения, заданный функцией:
имеет ряд свойств. Полагая 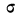
Рассмотрим ее свойства.
- Кривая нормального распределения имеет ветви, удаленные в бесконечность, причем кривая асимптотически приближается к оси Ot.
- Функция является четной: t(—t) = f(t). Следовательно, кривая нормального распределения симметрична относительно оси Оу.
- Функция имеет максимум при t = 0. Величина этого максимума равна
Следовательно, модального значения кривая
достигает при t = 0, а так как 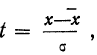
Наибольшую частоту кривая будет иметь при значении х, равном среднему арифметическому из отдельных вариантов. Средняя арифметическая является центром группирования частот ряда.
4. При t=±1 функция имеет точки перегиба. Это означает, что кривая имеет точки перегиба при отклонениях от центра
группирования 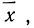
5. Сумма частостей, лежащих в пределах от а до b, равна определенному интегралу в тех же пределах от функции f(t), т. е.
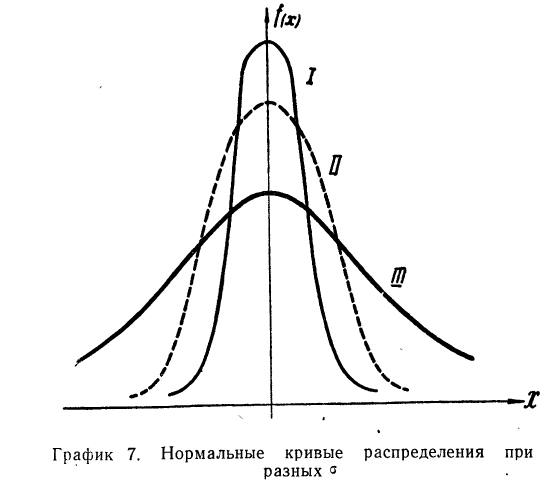
Если учесть действительную величину среднего квадратического отклонения, то окажется, что при больших величинах о значение f(t) мало, при малых, наоборот, велико. Отсюда изменяется и форма кривой распределения. При больших 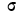
На графике 7 показаны 3 кривые нормального распределения (I, II, III) при 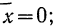
Зная общие свойства кривой нормального распределения, рассмотрим те условия, которые приводят к образованию кривых данного типа.
Формирование нормального распределения
Закон нормального распределения является наиболее распространенным законом не только потому, что он наиболее часто встречается, но и потому, что он является предельным законом распределения, к которому приближается ряд других законов распределения.
Нормальное распределение образуется в том случае, когда действует большое число независимых (или слабо зависимых), случайных причин. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Основное условие формирования нормального распределения состоит в том, чтобы все случайные величины, действующие вместе, играли в общей сумме примерно одинаковую роль. Если одна из случайных ошибок окажется по своему влиянию резко превалирующей над другими, то закон распределения будет обусловлен действием этой величины.
Если есть основания рассматривать изучаемую величину как сумму многих независимых слагаемых, то при соблюдении указанного выше условия ее распределение будет нормальным, независимо от характера распределения слагаемых.
Нормальное распределение встречается часто в биологических явлениях, отклонениях размеров изделий от их среднего размера, погрешностях измерения и т. д.
Если взять распределение людей по номеру носимой ими обуви, то это распределение будет нормальным. Но это правило применимо только в том случае, когда численность совокупности велика и сама совокупность однородна.
Из того факта, что нормальное распределение встречается нередко в разных областях, не следует, что всякий признак распределяется нормально. Наряду с нормальным распределением существуют другие различные распределения.
Но все же умение выявить нормальное распределение в некоторой эмпирической совокупности является важным условием для ряда практических расчетов и действий. Зная, что эмпирическое распределение является нормальным, можно определить оптимальные размеры предприятий, размеры резервов и т. д.
Важным условием определения характера данной эмпирической кривой является построение на основе эмпирических данных теоретического нормального распределения.
Построение кривой нормального распределения
Первый способ. Для того чтобы построить кривую нормального распределения, пользуются следующей егo формулой:
где N — число проведенных испытаний, равное сумме частот эмпирического распределения
k — величина интервала дробления эмпирического ряда распределения;
t—нормированное отклонение, т. е.
Величина 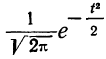
Для нахождения значений теоретических частот (см. пример 1) сначала необходимо найти среднюю арифметическую эмпирического ряда распределения, т. е. 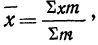
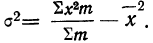
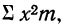
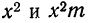
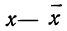
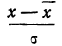
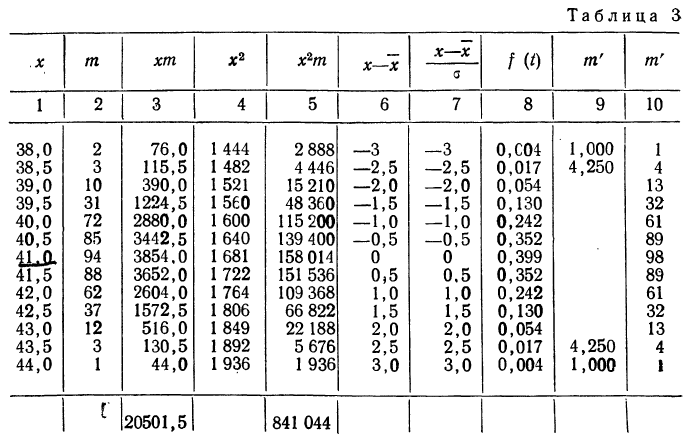
Найденная при умножении величина и составляет теоретическую частоту каждого варианта, записанного в строке (графа 9). Ввиду того что частоты могут быть только целыми числами, округляем их до целых и получим теоретические частоты, которые будем обозначать 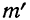
Пример 1.
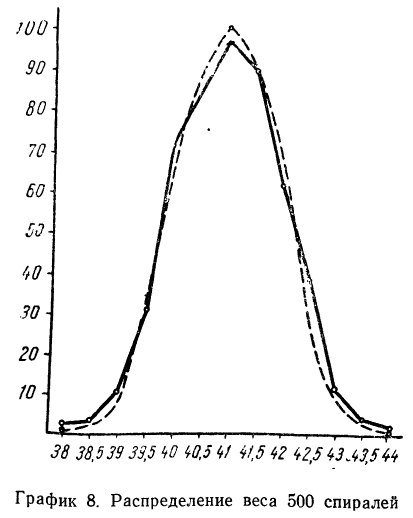
В таблице 3 приведено эмпирическое распределение веса 500 спиралей и расчет частот нормального распределения. (Вес спиралей х дан в миллиграммах.)
Из таблицы находим:
Строим график эмпирических и теоретических данных. На графике 8 сплошной линией дано изображение эмпирического распределения, а пунктирной — построенного на его основе теоретического распределения.
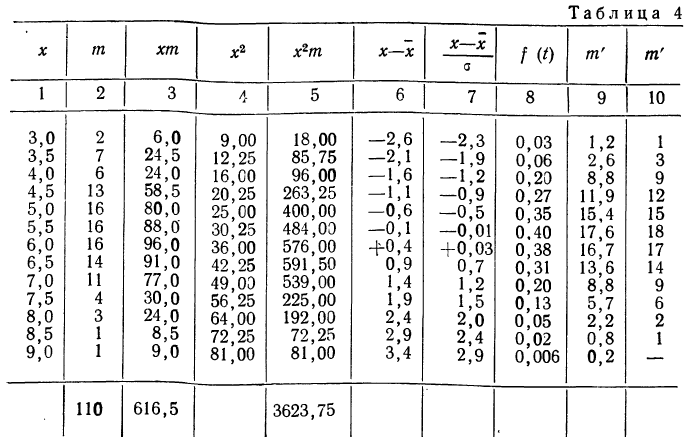
Пример 2.
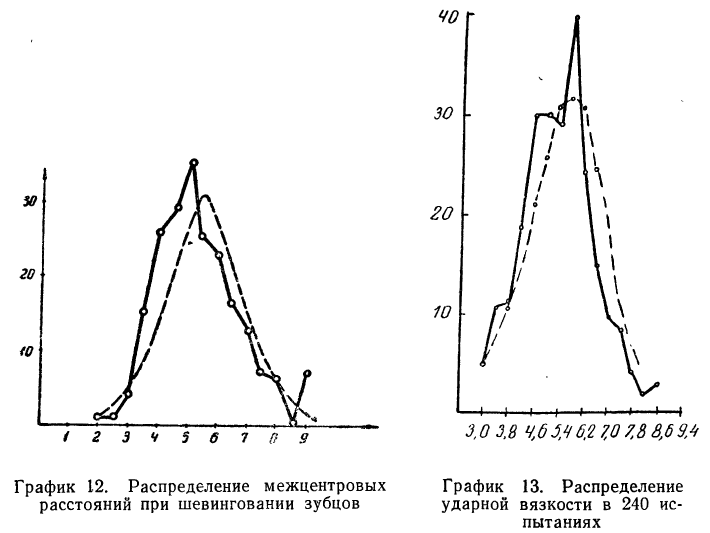
В таблице 4 дается эмпирическое распределение ПО замеров межцентрового расстояния при шевинговании зубцов динамомашины 110412 и расчет теоретических частот.
Исчислим:
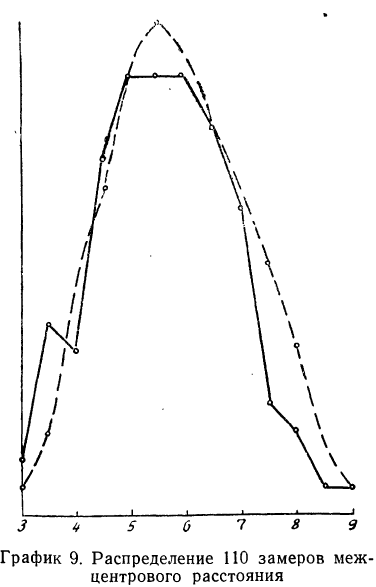
Построим графики эмпирического и теоретического распределений (см. график 9).
Оба эмпирических распределения хорошо воспроизводятся теоретическим нормальным распределением.
Второй способ построения кривой нормального распределения основан на применении функции стандартизованного нормального распределения, в котором 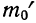
За начало отсчета признака при этом способе построения берется его средняя арифметическая. Ей соответствует наибольшая ордината.
Вычисление ординат производится по формуле:
где N — число наблюдений;
k — величина интервала эмпирического распределения.
Так как значение наибольшей ординаты получается при
t = 0, когда 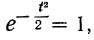
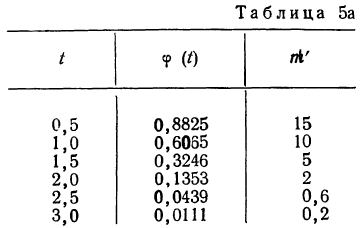
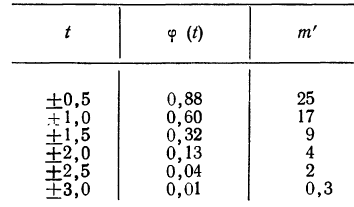
Придавая t последовательно значения 0,5; 1,0; 1,5; 2,0, т. е. сначала меньшие, а потом увеличивающиеся, находим в таблице стандартизованного нормального распределения для данных t соответствующие 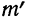
Например, при t = 0,5 величина стандартизованного нормального распределения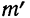
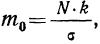
Пример 3.
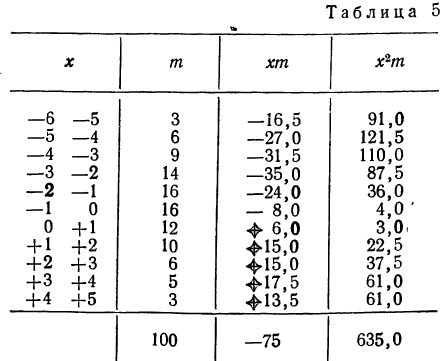
Взяты результаты измерения 100 отклонений шага резьбы х от всей длины резьбы. Получен следующий ряд распределения, для которого по общим правилам производится расчет средней и дисперсии.
Отсюда;
Рассчитаем наибольшую ординату:
так как величина 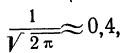
Взяв значение t = 0,5 по таблице стандартизованного нормального распределения, находим 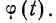
Для данного примера будем иметь:
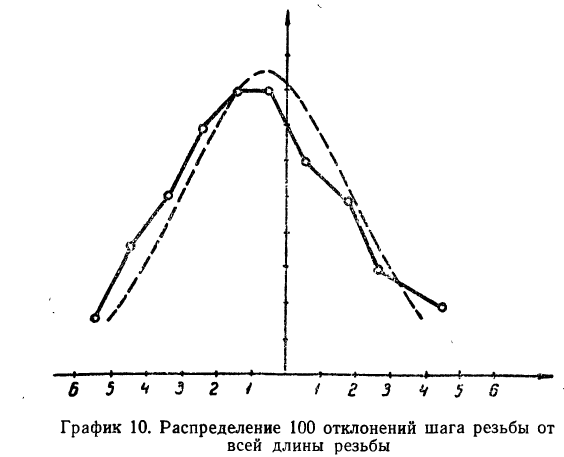
Полученный результат наносим на график, а для сравнения наносим на график и результаты непосредственных измерений отклонений (см. график 10).
Как видно из графика, теоретическая кривая довольно близко воспроизводит полигон эмпирического распределения.
Пример 4.
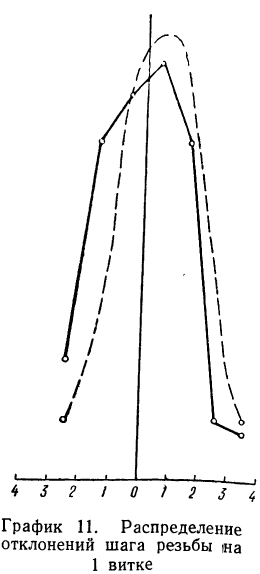
Даны результаты измерений отклонений шага резьбы (х) в микронах на 1 витке от среднего значения. Приводятся эти данные с соответствующими расчетами:
Теоретические частоты (ординаты) рассчитываются так же, как и в предыдущем примере. Сначала находится величина наибольшей частоты:
затем другие частоты:
Эмпирические и теоретические частоты наносим на график (см. график 11) и убеждаемся, что эмпирическое распределение довольно близко воспроизводится теоретическим распределением.
Третий способ построения кривой нормального распределения (или вычисления теоретических частот) по имеющимся эмпирическим данным основан на применении функции:
которая дает площадь нормальной кривой, заключенной между —t и +t.
Вообще говоря, можно находить площадь нормальной кривой, заключенную между любыми точками 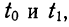
применяя функцию F(t). Искомая площадь будет представлять собой 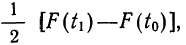
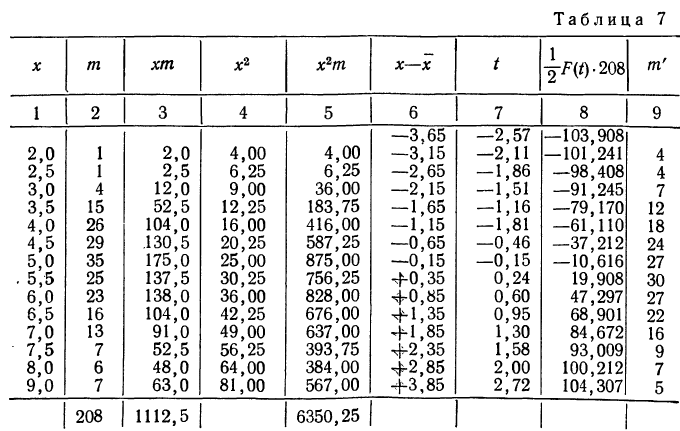
Пример 5.
Получены результаты 208 измерений межцентровых расстояний при шевинговании зубцов шестерни динамо-машины (см. табл. 7). Вычислим нужные параметры и теоретические частоты и построим графики эмпирического и теоретического распределений.
Колонки 1, 2, 3, 4 и 5 необходимы для расчетов 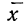
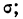
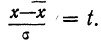
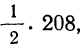
Чтобы получить теоретическую частоту для каждого интервала, достаточно из верхней строки (в 8-й колонке) вычесть число той же колонки, стоящее строкой ниже.
На графике 12 показано, что теоретическое распределение достаточно точно отражает эмпирически полученный материал, только наблюдается некоторое смещение теоретической кривой вправо, что, очевидно, вызвано большим удельным весом правого конца эмпирического распределения.
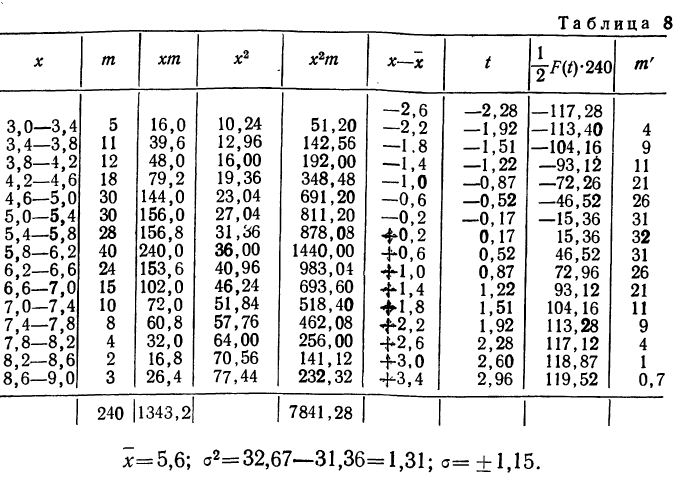
Пример 6.
Дается ряд распределения ударной вязкости в 240 испытаниях. Приведем этот ряд распределения и построим для него теоретическое распределение (см. график 13).
Критерии согласия
Определение близости эмпирических распределений к теоретическому нормальному распределению по графику может быть недостаточно точным, субъективным и по-разному оценивать расхождения между ними. Поэтому математики выработали ряд объективных оценок для того, чтобы определить, является ли данное эмпирическое распределение нормальным. Такие оценки называются критериями согласия. Критерии согласия были предложены разными учеными, занимавшимися этим вопросом. Рассмотрим критерии согласия Пирсона, Романовского, Колмогорова и Ястремского.
Критерий согласия Пирсона основан на определении величины 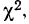
где m — эмпирические частоты;
m’ — теоретические частоты.
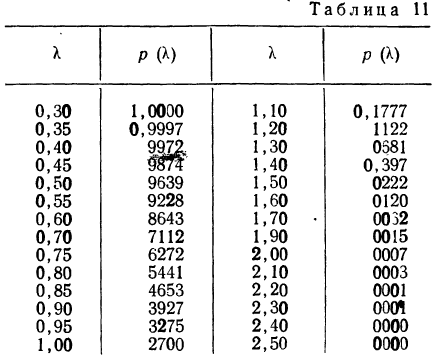
Для оценки того, насколько данное эмпирическое распределение воспроизводится нормальным распределением, исчисляют по распределению Пирсона вероятности достижения 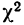
Значения 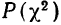
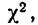
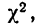
Пересечение данного столбца с соответствующей строкой дает искомую вероятность
При вероятностях, значительно отличающихся от нуля, расхождение между теоретическими и эмпирическими частотами можно считать случайным.
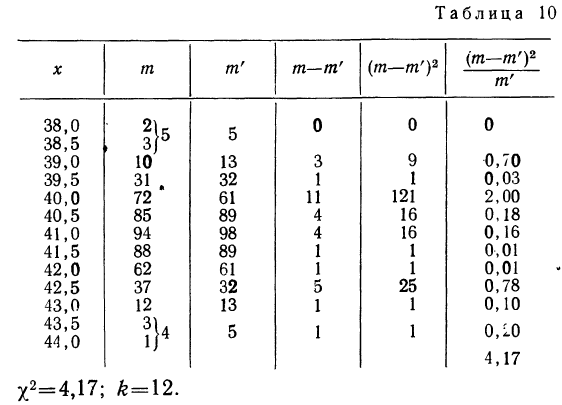
Проф. В. И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину
Он предложил вычислять отношение:
где k — число степеней свободы.
Если указанное отношение имеет абсолютное значение, меньшее трех, то предлагается расхождение между теоретическим и эмпирическим распределениями считать несущественным; если же это отношение больше трех, то расхождение существенно. Несущественность расхождения (когда величина отношения Романовского меньше трех) говорит о возможности принять за закон данного эмпирического распределения нормальное распределение.
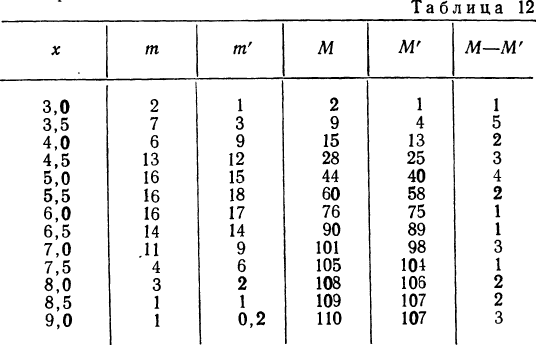
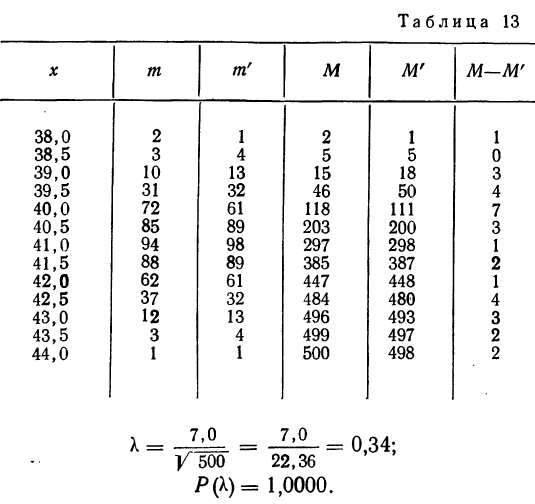
По данным примера 2 рассчитаем величину
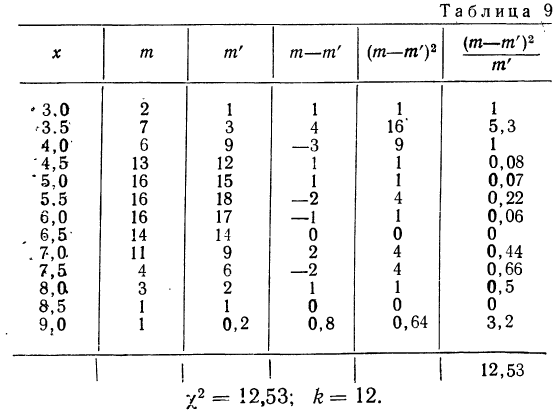
Пример 7.
Вычисление 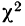
Из таблицы 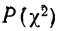
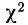
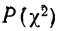
Находим отношение Романовского:
Это отношение значительно меньше трех, поэтому расхождение между теоретическими и эмпирическими частотами можно считать несущественными, и, таким образом, теоретическое распределение достаточно хорошо воспроизводит эмпирическое.
Пример 8.
Вычислим критерий 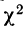
По таблице находим вероятность 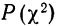
Отношение Романовского
также значительно меньше трех, поэтому теоретическое воспро* изведение эмпирического ряда достаточно удовлетворительное.
Критерий 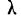
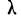
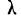
где D — максимальная граница разности: 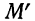
Приведем таблицу значений 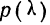
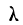
Если найденному значению 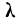
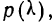
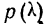
Рассмотрим применение этого критерия на двух примерах.
Пример 9.
В таблице вероятностей 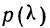
Эта большая вероятность указывает на то, что расхождение между наблюдением и теоретическим распределением вполне могло быть случайным.
Пример 10.
Величина вероятности 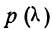
Критерий Б. С. Ястремского. В общем виде критерий Ястремского можно записать следующим неравенством:
где
Для числа групп, меньших 20, 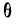
Значение I, меньшее 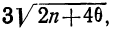
При значениях I, больших 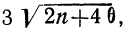
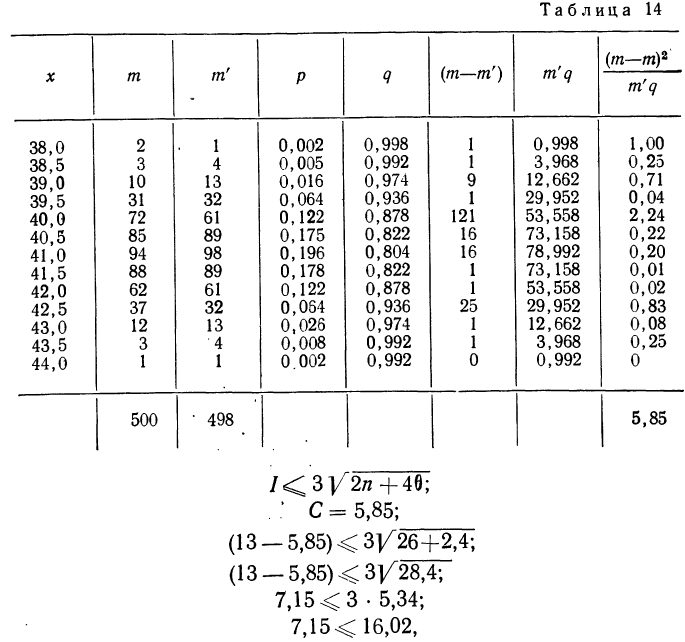
Пример 11.
Определим величину I и оценим эмпирическое распределение 500 спиралей (m) по сравнению с соответствующим нормальным (m’).
что говорит о нормальном распределении исследуемой совокупности.
Элементарные приемы определения «нормальности» распределения. Для определения элементарными способами близости данного опытного распределения к нормальному прибегают к числам Вестергарда и к сравнению средней арифметической, моды и медианы.
Числами Вестергарда являются: 0,3; 0,7; 1,1; 3. Для пользования ими определяют сначала основные характеристики — среднюю арифметическую 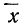
Для того чтобы данное эмпирическое распределение было подчинено закону нормального распределения, необходимо, чтобы распределение удовлетворяло следующим условиям:
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
было расположено
всей совокупности;
- в промежутках от —3 до +3 было расположено 0,998 всей совокупности.
Для приводимого распределения 500 спиралей по весу (пример 1) все эти условия соблюдаются, что говорит о подчинении данного распределения закону нормального распределения.
К элементарным приемам определения «нормальности» следует отнести применение графического метода, особенно удобное с помощью полулогарифмической сетки Турбина. На сетке накопленные эмпирические частоты при нормальном их распределении дают прямую линию. Всякое отклонение от прямой свидетельствует об отклонении эмпирического распределения от «нормального».
Распределение Пуассона
Вероятности частот событий, редко встречающихся при некотором числе испытаний, находят по формуле:
где m — частота данного события;
n — число испытаний;
р — вероятность события при одном испытании;
е= 2,71828.
Это выражение носит название закона распределения Пуассона.
Подставим вместо nр среднее число фактически наблюдавшихся случаев в эмпирическом материале. Теоретические ординаты кривой распределения по закону Пуассона m’ найдем по формуле:
где х — переменное значение числа раз;
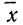
n — число наблюдений.
При
Пример 12.
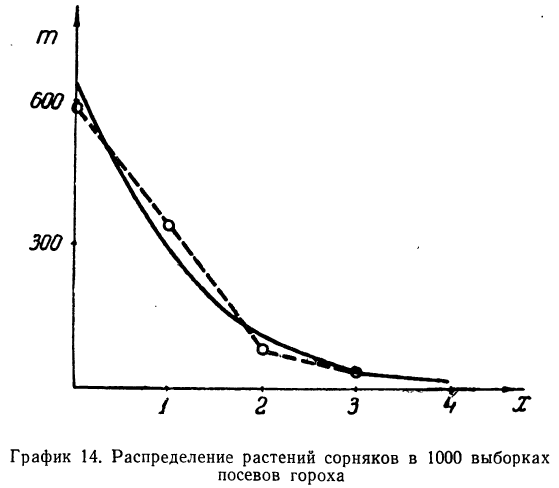
Наблюдалось следующее распределение растений сорняков в 1000 выборках посевов гороха. Результаты эксперимента записаны в следующей таблице:
Определим по закону Пуассона теоретические частоты разного числа растений сорняков. Для этого предварительно исчислим среднее число растений сорняков в одной выборке:
Из таблицы находим
Определим теоретическое число выборок, в которых число растений сорняков будет равно 0:
то же:
для числа растений сорняков, равного 1:
для числа растений сорняков, равного 2:
для числа растений сорняков, равного 3:
для числа растений сорняков более 3:
Графическое сопоставление обоих распределений говорит о соответствии между эмпирическим и теоретическим распределениями.
Распределение Максвелла
В технике часто встречается распределение по закону Максвелла. Это — распределение существенно положительных величин. Например, эмпирическое распределение эксцентриситетов биений теоретически воспроизводится распределением Максвелла.
Дифференциальный закон распределения Максвелла выражается следующей формулой:
где 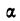
Интегральный закон распределения выразится тогда:
Пример 13.
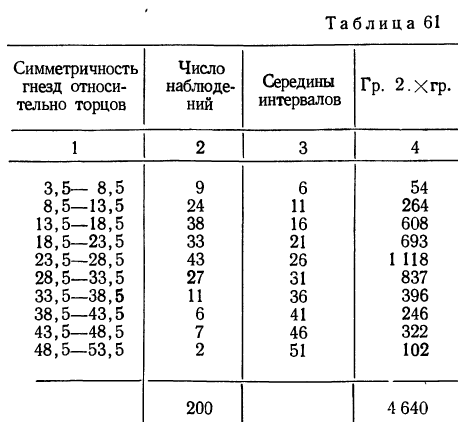
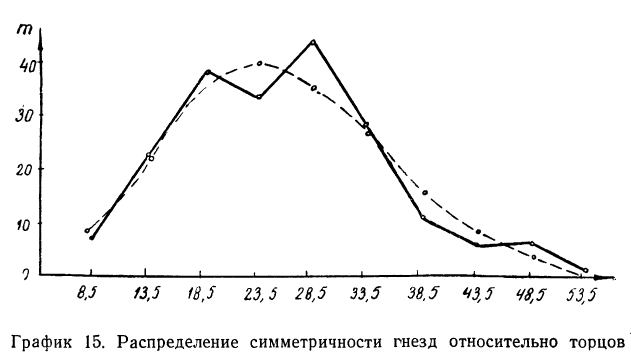
Заимствуем из книги А. М. Длина таблицу распределения симметричности гнезд относительно торцов в круглых плашках (в 0,01 мм) и проведем дополнительные расчеты.
Из этой таблицы легко определим среднюю симметричность:
и параметр рассеяния:
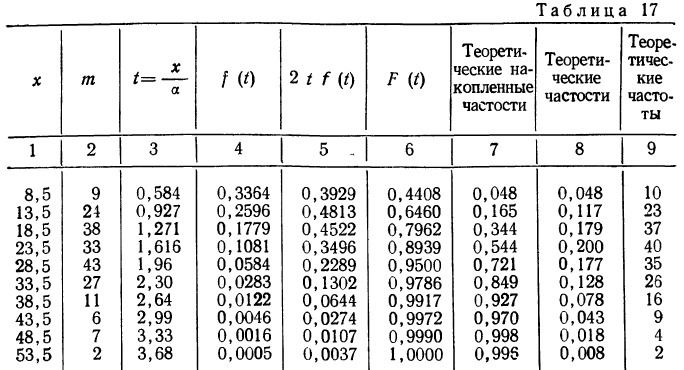
Формула интегрального распределения по закону Максвелла позволяет найти накопленные, а затем теоретические частости и частоты.
Изобразим на графике 15 данные эмпирического и теоретического рядов распределения.
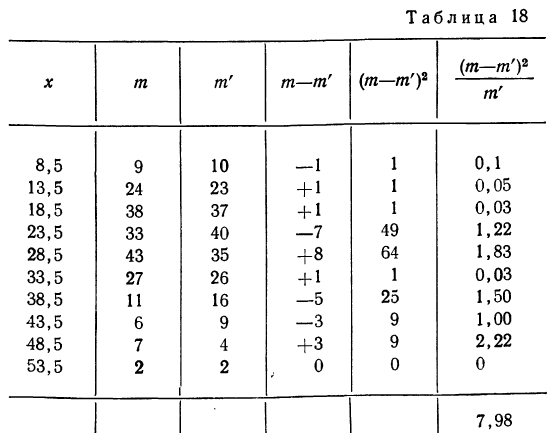
Определим близость их по критерию согласия Ястремского. Для этого приведем в табл. 18 расчет величины С:
По критерию Ястремского находим
Величина I значительно меньше 3. Следовательно, данное эм лирическое распределение хорошо согласуется с законом распределения Максвелла.
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
- Элементы теории ошибок
- Статистические оценки
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд







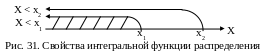

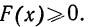
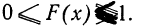
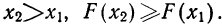
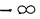 равно нулю, а при х=
равно нулю, а при х=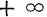 равно единице.
равно единице.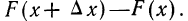
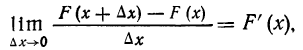
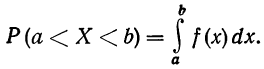
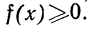
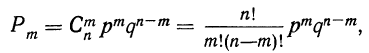
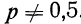
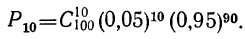
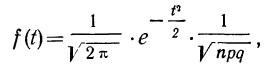
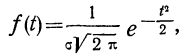
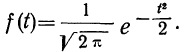
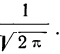
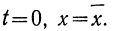
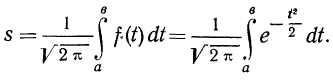
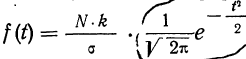
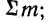
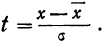
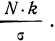
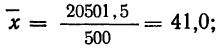
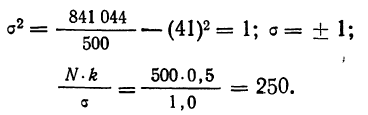
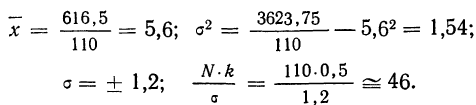
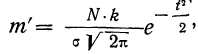
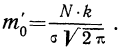
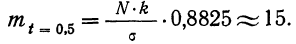
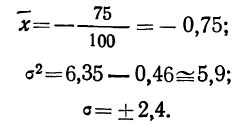
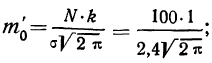
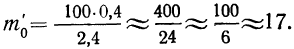

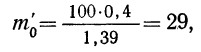
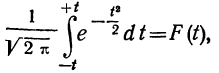
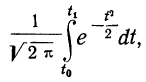
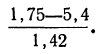
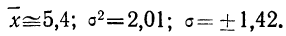
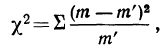
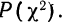
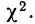
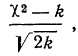
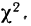
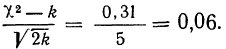
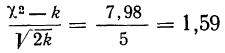
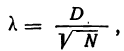
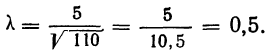
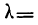
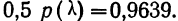
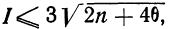
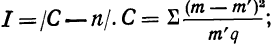
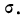
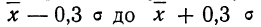 была расположена
была расположена 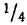 часть всей совокупности;
часть всей совокупности;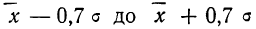 была расположена
была расположена 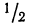 часть всей совокупности;
часть всей совокупности;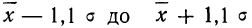 было расположено
было расположено  всей совокупности;
всей совокупности;