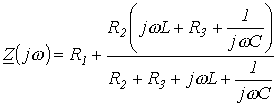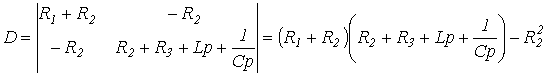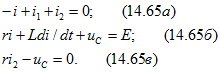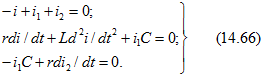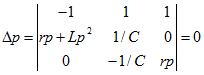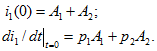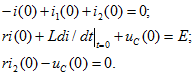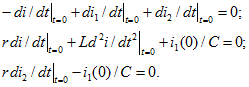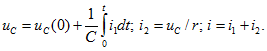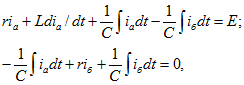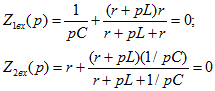Как составить характеристическое уравнение для неразветвленной цепи - AvtoShod.ru

Характеристическое уравнение составляется для цепи после коммутации. Оно может
быть получено следующими способами:

непосредственно на основе дифференциального уравнения вида (2) (см. лекцию
№24), т.е. путем исключения из системы уравнений, описывающих электромагнитное
состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных
величин, кроме одной, относительно которой и записывается уравнение (2);
путем использования выражения для входного сопротивления цепи на синусоидальном
токе;
на основе выражения главного определителя.

Согласно первому способу в предыдущей лекции было получено дифференциальное
уравнение относительно напряжения на конденсаторе для последовательной
R-L-C-цепи, на базе которого записывается характеристическое уравнение.

Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом,
корни характеристического уравнения являются общими для всех свободных составляющих
напряжений и токов ветвей схемы, параметры которых входят в характеристическое
уравнение. Поэтому по первому способу составления характеристического уравнения
в качестве переменной, относительно которой оно записывается, может быть выбрана
любая.

Применение второго и третьего способов составления характеристического уравнения
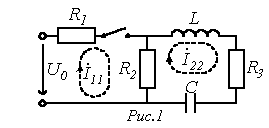
рассмотрим на примере цепи рис. 1.

Составление характеристического уравнения по методу входного сопротивления
заключается в следующем:

записывается входное сопротивление цепи на переменном токе;

jw заменяется на оператор р;

полученное выражение приравнивается к нулю.

Уравнение

совпадает с характеристическим.

Следует подчеркнуть, что входное сопротивление может быть записано относительно
места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным
по аналогии с методом эквивалентного генератора. Данный способ составления характеристического
уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии
таковых необходимо осуществить их предварительное развязывание.

Для цепи на рис. 1 относительно зажимов источника

Заменив jw на р и приравняв полученное выражение к нулю, запишем

или

(1)

При составлении характеристического уравнения на основе выражения главного
определителя число алгебраических уравнений, на базе которых он записывается,
равно числу неизвестных свободных составляющих токов. Алгебраизация исходной
системы интегро-дифференциальных уравнений, составленных, например, на основании
законов Кирхгофа или по методу контурных токов, осуществляется заменой символов
дифференцирования и интегрирования соответственно на умножение и деление на
оператор р. Характеристическое уравнение получается путем приравнивания записанного
определителя к нулю. Поскольку выражение для главного определителя не зависит
от правых частей системы неоднородных уравнений, его составление можно производить
на основе системы уравнений, записанных для полных токов.

Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных
токов имеет вид

Отсюда выражение для главного определителя этой системы

Приравняв D к нулю, получим результат, аналогичный (1).

Общая методика расчета переходных процессов классическим
методом

В общем случае методика расчета переходных процессов классическим методом включает
следующие этапы:

Запись выражения для искомой переменной в виде

(2)

Нахождение принужденной составляющей общего решения на основании расчета
установившегося режима послекоммутационной цепи.
Составление характеристического уравнения и определение его корней (для
цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней
можно находить постоянную времени t — см. лекцию №26). Запись
выражения свободной составляющей в форме, определяемой типом найденных корней.
Подстановка полученных выражений принужденной и свободной составляющих в
соотношение (2).
Определение начальных условий и на их основе – постоянных интегрирования.

Примеры расчета переходных процессов классическим методом

1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения

Такие
процессы имеют место, например, при подключении к источнику питания электромагнитов,
трансформаторов, электрических двигателей и т.п.

Рассмотрим два случая:

а)

б) .

Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать

(3)

Тогда для первого случая принужденная составляющая тока

(4)

Характеристическое уравнение

откуда и постоянная времени .

Таким образом,

(5)

Подставляя (4) и (5) в соотношение (3), запишем

В соответствии с первым законом коммутации . Тогда

откуда .

Таким образом, ток в цепи в переходном процессе описывается уравнением

а напряжение
на катушке индуктивности – выражением

Качественный вид кривых и , соответствующих полученным решениям,
представлен на рис. 3.

При втором типе источника принужденная составляющая рассчитывается с использованием
символического метода:

где .

Отсюда

Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,

Поскольку , то

Таким образом, окончательно получаем

(6)

Анализ полученного выражения (6) показывает:

При начальной фазе напряжения постоянная интегрирования А=0.
Таким образом, в этом случае коммутация не повлечет за собой переходного процесса,
и в цепи сразу возникнет установившийся режим.
При свободная составляющая максимальна
по модулю. В этом случае ток переходного процесса достигает своей наибольшей
величины.

Если значительна по величине, то за
полпериода свободная составляющая существенно не уменьшается. В этом случае
максимальная величина тока переходного процесса может существенно превышать амплитуду
тока установившегося режима. Как видно из рис. 4, где

, максимум тока имеет место примерно
через . В пределе при .

Таким образом, для линейной цепи максимальное значение тока переходного режима
не может превышать удвоенной амплитуды принужденного тока: .

Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное
напряжение равно своему амплитудному значению и постоянная времени цепи достаточно велика, то примерно
через половину периода напряжение на конденсаторе достигает своего максимального
значения , которое не может превышать удвоенной
амплитуды принужденного напряжения: .

2. Переходные процессы при отключении катушки индуктивности от источника питания

При размыкании ключа в цепи
на рис. 5 принужденная составляющая тока через катушку индуктивности .

Характеристическое уравнение

откуда и .

В соответствии с первым законом коммутации

Таким образом, выражение для тока в переходном режиме

и напряжение на катушке индуктивности

(7)

Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы,
могут возникать большие перенапряжения, которые без принятия специальных мер
могут вывести аппаратуру из строя. Действительно, при модуль напряжения на катушке
индуктивности в момент коммутации будет во много раз превышать напряжение источника:
. При отсутствии гасящего резистора
R указанное напряжение прикладывается к размыкающимся контактам ключа, в результате
чего между ними возникает дуга.

3. Заряд и разряд конденсатора

При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:

Принужденная составляющая напряжения на конденсаторе .

Из характеристического уравнения

определяется корень . Отсюда постоянная времени .

Таким образом,

При t=0 напряжение на конденсаторе равно (в общем случае к моменту коммутации
конденсатор может быть заряженным, т.е. ). Тогда и

Соответственно для зарядного тока можно записать

В зависимости от величины : 1 — ; 2 — ; 3 — ; 4 — — возможны четыре вида кривых
переходного процесса, которые иллюстрирует рис. 7.

При разряде конденсатора на резистор (ключ на рис.6 переводится в
положение 2) . Постоянная времени .

Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения
(в частном случае ), для напряжения на нем в переходном
режиме можно записать

Соответственно разрядный ток

(8)

Как видно из (8), во избежание значительных бросков разрядного тока величина
должна быть достаточно большой.

В заключение отметим, что процессы заряда и разряда конденсатора используются
в генераторах пилообразного напряжения, широко применяемых в автоматике. Для
этого ключ в схеме на рис. 6 заменяется на электронный.

Литература

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи
с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

Контрольные вопросы

Составить характеристическое уравнение для цепи на рис. 1, используя выражение
входного сопротивления относительно места разрыва ветви с резистором .
Может ли в одной части линейной цепи протекать колебательный переходный
процесс, а в другой – апериодический?
Для чего в схеме на рис. 5 служит цепочка, состоящая из диода и резистора
R?
Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным
элементом?
Почему корни характеристического уравнения не зависят от того, относительно
какой переменной было записано дифференциальное уравнение?
Для цепи на рис. 8 составить характеристическое уравнение и определить,
при каких значениях переходный процесс в ней будет
носить апериодический характер, если .

Ответ: .

Определить в цепи на рис. 9, если , , , .

Ответ: .

Источник

Характеристическое
уравнение составляется для цепи после
коммутации. Оно может быть получено
следующими способами:

непосредственно на основе дифференциального
уравнения вида (2) (см. лекцию №24), т.е.
путем исключения из системы уравнений,
описывающих электромагнитное состояние
цепи на основании первого и второго
законов Кирхгофа, всех неизвестных
величин, кроме одной, относительно
которой и записывается уравнение (2);
путем использования выражения для
входного сопротивления цепи на
синусоидальном токе;
на основе выражения главного определителя.

Согласно
первому способу в предыдущей лекции
было получено дифференциальное уравнение
относительно напряжения

на
конденсаторе для последовательной
R-L-C-цепи, на базе которого записывается
характеристическое уравнение.

Следует
отметить, что, поскольку линейная цепь
охвачена единым переходным процессом,
корни характеристического уравнения
являются общими для всех свободных
составляющих напряжений и токов ветвей
схемы, параметры которых входят в
характеристическое уравнение. Поэтому
по первому способу составления
характеристического уравнения в качестве
переменной, относительно которой оно
записывается, может быть выбрана любая.

П
рименение
второго и третьего способов составления
характеристического уравнения рассмотрим
на примере цепи рис. 1.

Составление
характеристического уравнения по методу
входного сопротивления заключается в
следующем:

записывается
входное сопротивление цепи на переменном
токе;

jw
заменяется на оператор р;

полученное
выражение

приравнивается
к нулю.

Уравнение

совпадает
с характеристическим.

Следует
подчеркнуть, что входное сопротивление
может быть записано относительно места
разрыва любой ветви схемы. При этом
активный двухполюсник заменяется
пассивным по аналогии с методом
эквивалентного генератора. Данный
способ составления характеристического
уравнения предполагает отсутствие в
схеме магнитосвязанных ветвей; при
наличии таковых необходимо осуществить
их предварительное развязывание.

Для
цепи на рис. 1 относительно зажимов
источника

Заменив
jw на р и приравняв полученное выражение
к нулю, запишем

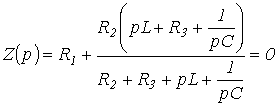
или

(1)

При
составлении характеристического
уравнения на основе выражения главного
определителя число алгебраических
уравнений, на базе которых он записывается,
равно числу неизвестных свободных
составляющих токов. Алгебраизация
исходной системы интегро-дифференциальных
уравнений, составленных, например, на
основании законов Кирхгофа или по методу
контурных токов, осуществляется заменой
символов дифференцирования и интегрирования
соответственно на умножение и деление
на оператор р. Характеристическое
уравнение получается путем приравнивания
записанного определителя к нулю.
Поскольку выражение для главного
определителя не зависит от правых частей
системы неоднородных уравнений, его
составление можно производить на основе
системы уравнений, записанных для полных
токов.

Для
цепи на рис. 1 алгебраизованная система
уравнений на основе метода контурных
токов имеет вид

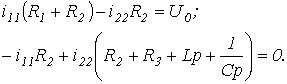
Отсюда
выражение для главного определителя
этой системы

Приравняв
D к нулю, получим результат, аналогичный
(1).

Источник

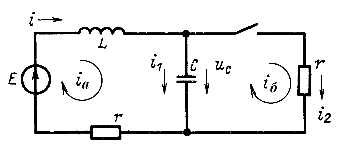
В предыдущих разделах был дан анализ переходных процессов в неразветвленных цепях. Порядок анализа переходных процессов в разветвленных цепях рассмотрим на достаточно простом примере расчета тока в цепи рис. 14.24, чтобы нетрудно было проследить путь анализа и все его этапы. Далее будут даны необходимые пояснения.

1. Для цепи после коммутации составим систему дифференциальных уравнений по первому и второму законам Кирхгофа:

где . После подстановки в (14.65) и дифференцирования уравнений (14.65 6 и в) получим систему уравнений для трех неизвестных токов:

2. Независимые начальные условия — ток в индуктивном элементе и напряжение на емкостном элементе — неизвестны. Поэтому определим их из расчета режима цепи до коммутации с применением законов коммутации.
Считая, что до коммутации в левом контуре был установившийся режим, при остоянной ЭДС Е конденсатор был заряжен до напряжения , т. е. , а ток был равен нулю, т. е. . Это и есть независимые начальные условия.

3. Запишем искомую величину в виде суммы установившейся и свободной составляющих: .

4. Установившуюся составляющую найдем, рассчитав режим цепи постоянного тока (ЭДС в цепи постоянная) после коммутации.
В установившемся режиме после коммутации ток есть только во внешнем контуре, a .

5. Составим характеристическое уравнение и найдем его корни.
Из системы трех уравнений (14.66) с тремя неизвестными можно исключить токи и для полученного дифференциального уравнения записать характеристическое уравнение. Однако для определения корней можно составить главный определитель системы (14.66) и приравнять его к нулю:

Рис. 14.24

или
Корень р = 0 соответствует установившемуся режиму, который уже найден. Два других корня определяются из характеристического уравнения Они могут быть действительные разные , равные или комплексные сопряженные (действительная часть корней не может быть положительной, так как в рассматриваемых цепях переходные процессы затухают).

6. Запишем свободную составляющую с постоянными интегрирования, обращая внимание на вид корней (действительные различные, равные, комплексные сопряженные):

Далее для определенности будем предполагать случай действительных разных корней.

7. Искомое решение с двумя постоянными интегрирования

8. Для определения двух постоянных интегрирования запишем полученное решение и его производную для начального момента времени

Это два алгебраических уравнения, из которых можно найти постоянные при известных значениях Начальное значение тока определим из системы дифференциальных уравнений цепи (14.65), записанной для момента t = 0:

В этой системе алгебраических уравнений с тремя токами, производной тока и напряжением две величины и были уже найдены с применением законов коммутации. Следовательно, остальные три величины можно вычислить.
Для определения начального значения производной дифференцируем систему уравнений Кирхгофа (14.65) и подставляем t = 0:

Это система трех алгебраических уравнений с тремя неизвестными , которые и можно вычислить. В рассматриваемой задаче достаточно найти
При трех корнях характеристического уравнения потребовалось бы еще раз продифференцировать уравнения Кирхгофа для определения третьего начального значения — второй производной искомой величины при t = 0, и т. д.

9. После определения постоянных остается подставить их в искомое решение, и расчет закончен.
Для определения других токов и напряжений не требуется заново выполнять все этапы расчета. Действительно,

О системе дифференциальных уравнений.
Необходимое число уравнений, составляемых по первому и второму законам Кирхгофа, определяется так же, как и при расчете установившихся режимов в цепях постоянного и переменного токов. Независимые контуры выбираются по тем же правилам, что и для цепей постоянного и переменного токов.

Независимые начальные условия.
В цепи рис. 14.24 ЭДС Е постоянная. Если ЭДС синусоидальная , то ток до коммутации , т. e. и , напряжение , т. е.

Установившийся режим после коммутации.
При синусоидальной ЭДС в цепи рис. 14.24 ток , т .e. и аналогично .

Характеристическое уравнение дифференциального уравнения n-го порядка, как известно, составляется алгебраизацией соответствующего однородного уравнения. Например, у дифференциального уравнения тока

характеристическое уравнение

имеет n корней, среди которых могут быть действительные и комплексные сопряженные, различные и одинаковые. Степень называется порядком цепи. Так были получены характеристические уравнения цепей, рассмотренных в предыдущих разделах.
Однако, как указывалось выше, при анализе переходных процессов классическим методом в цепи, для которой составлена система уравнений Кирхгофа, можно получить характеристическое уравнение, составив главный определитель системы дифференциальных уравнений. Для понижения порядка определителя, при помощи которого находятся корни характеристического уравнения, можно записать уравнения цепи с контурными токами. Например, для цепи на рис. 14.24, выбрав контуры с токами , составим систему уравнений

главный определитель которой

Уравнение имеет те же корни, что и характеристическое уравнение (14.68), т. е также является характеристическим.
Нетрудно заметить, что элементы определителя [в отличие от элементов ] — это собственные и общие комплексные сопротивления контуров той же самой цепи при замене оператором р: и т.д.
Таким образом, определитель (14.69) можно записать сразу без составления дифференциальных уравнений.
Составив комплексное входное сопротивление цепи для источника синусоидальной ЭДС (вместо источника ЭДС Е в цепи рис. 14.24) после замены оператором р получим

Как будет показано в разделе, уравнение

— это тоже характеристическое.
Источник ЭДС можно считать включенным в любую из ветвей цепи, т. е.

— это тоже характеристические уравнения.
Характеристическим является и уравнение

где — главный определитель системы, составленной методом узловых потенциалов с заменой оператором р. Например, для цепи на рис. 14.24 (с двумя узлами) определитель (первого порядка)

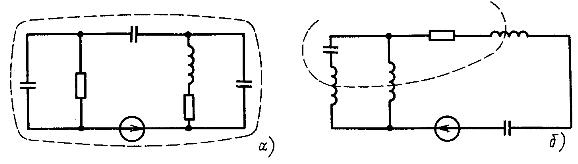
Число корней характеристического уравнения не может быть больше числа накопителей энергии в цепи после коммутации, т. е. числа ее индуктивных и емкостных элементов. Если схема замещения цепи не содержит особых контуров, состоящих только из емкостных элементов и источников ЭДС, и особых сечений, у которых в каждой ветви есть индуктивные элементы или источники тока, то число корней характеристического уравнения равно числу накопителей энергии. На рис. 14.25, а и б штриховой линией показаны особые контур и сечение. Число корней для цепи на рис. 14.25, а равно не 4, а 3 (один емкостной контур), для цепи на рис. 14.25,6 оно равно не 5, а 4 (одно индуктивное сечение).

Рис. 14.25

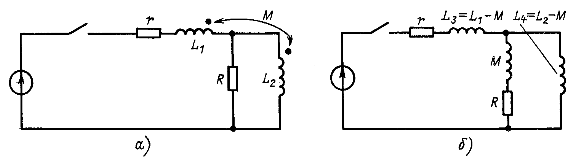
Наличие индуктивных связей не увеличивает числа корней характеристического уравнения. Например, для цепи на рис. 14.26, а запишем характеристическое уравнение, составив входное сопротивление для источника ЭДС после развязки индуктивной связи (рис. 14.26,6):

или

у которого два корня. Для цепи на рис. 14.26, а при отсутствии индуктивной связи характеристическое уравнение

или

т. е. тоже второго порядка (корни, конечно, другие).

Рис. 14.26

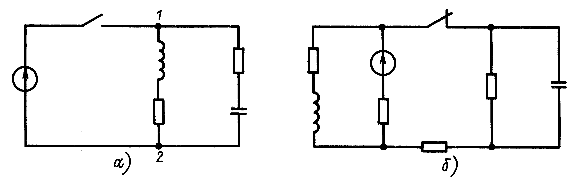
Корни характеристического уравнения определяются только топологией цепи после коммутации и значением ее параметров. В общем случае они одинаковы для любого из токов и напряжений цепи. Но следует обратить внимание на то, что в частных случаях, например в цепях на рис. 14.27, а и б, общее правило не выполняется. В цепи на рис. 14.27, а после замыкания рубильника задано напряжение между узлами 1 и 2. Поэтому на переходный процесс в каждой из ветвей с индуктивным и емкостным элементами не влияет вторая ветвь. Цепь на рис. 14.27, б после коммутации распадается на две отдельные цепи.

Рис. 14.27

Корни характеристического уравнения, как указывалось, имеют отрицательные действительные части (свободные составляющие процесса затухают). Это справедливо для всех цепей с потерями, в которых действуют только независимые источники ЭДС и тока. Следовательно, на комплексной плоскости точки, изображающие корни, располагаются на левой полуплоскости. В цепях с зависимыми источниками, например четырехполюсники — операционные усилители с обратной связью, возможно самовозбуждение. В этом случае характеристическое уравнение имеет хотя бы один корень (полюс передаточной функции) с положительной действительной частью, изображающая точка которого находится на правой полуплоскости (неустойчивость). Существуют критерии (Гурвица, Михайлова, Найквиста), дающие возможность судить об устойчивости без вычисления корней характеристического уравнения, т. е. полюсов.

Смотри пример по разделу

Источник

Не пропустите также: