Понятие функции
Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:
-
Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
-
Графический способ — наглядно.
-
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
-
Словесный способ.
Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Например, для функции вида
область определения выглядит так
-
х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): (-∞; 0) ⋃ (0; +∞).
Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
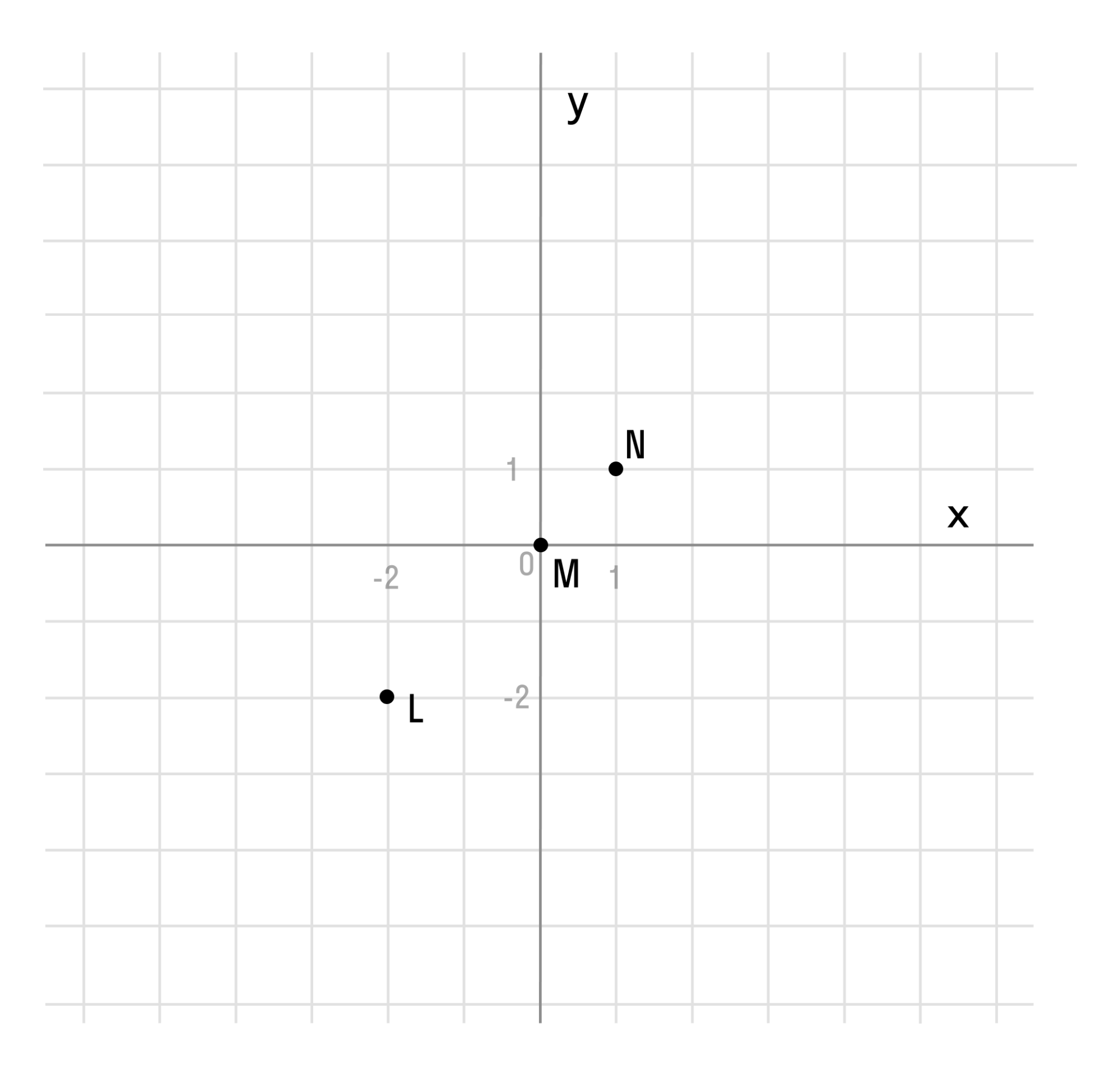
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Запоминаем!
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
-
стационарные и критические точки;
-
точки экстремума;
-
нули функции;
-
точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых значение функции равно нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
-
Найти область определения функции.
-
Найти область допустимых значений функции.
-
Проверить не является ли функция четной или нечетной.
-
Проверить не является ли функция периодической.
-
Найти точку пересечения с осью OY (если она есть).
-
Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.
-
Промежутки знакопостоянства.
-
Асимптоты.
-
На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
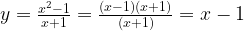
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Задача 3. Построить графики функций:
а) y = 3x — 1
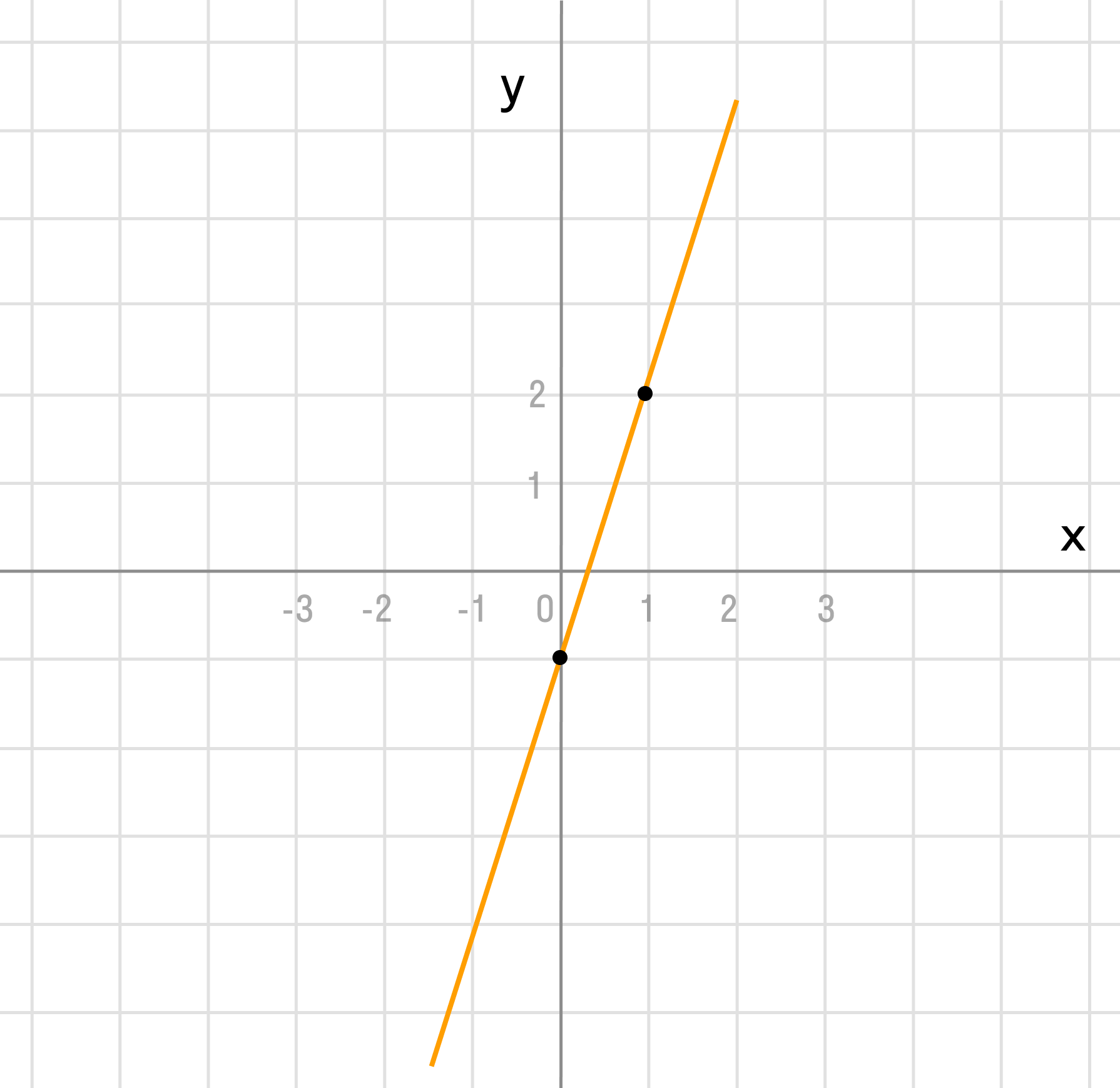
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
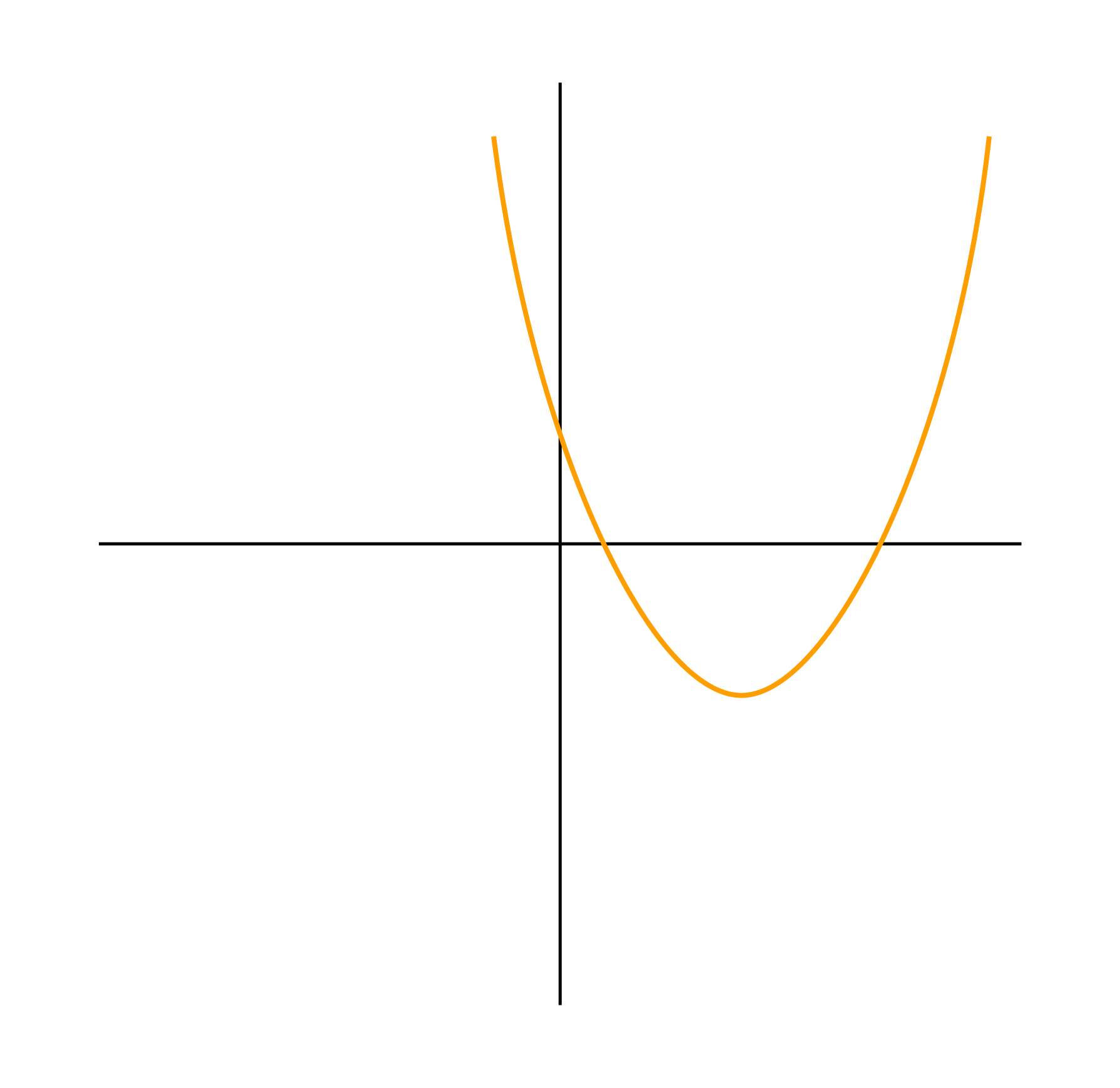
-
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 5. Построить графики функций:
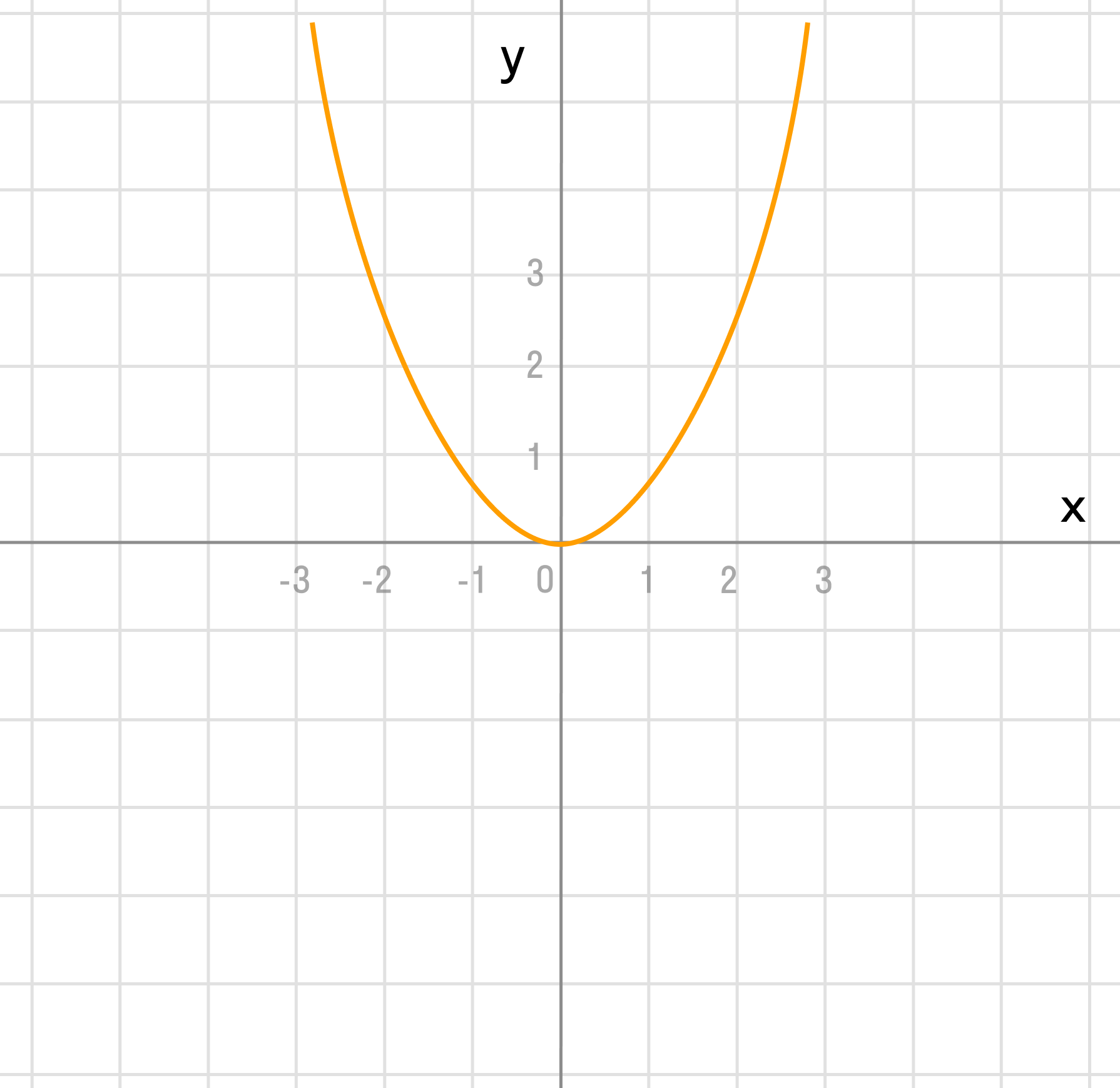
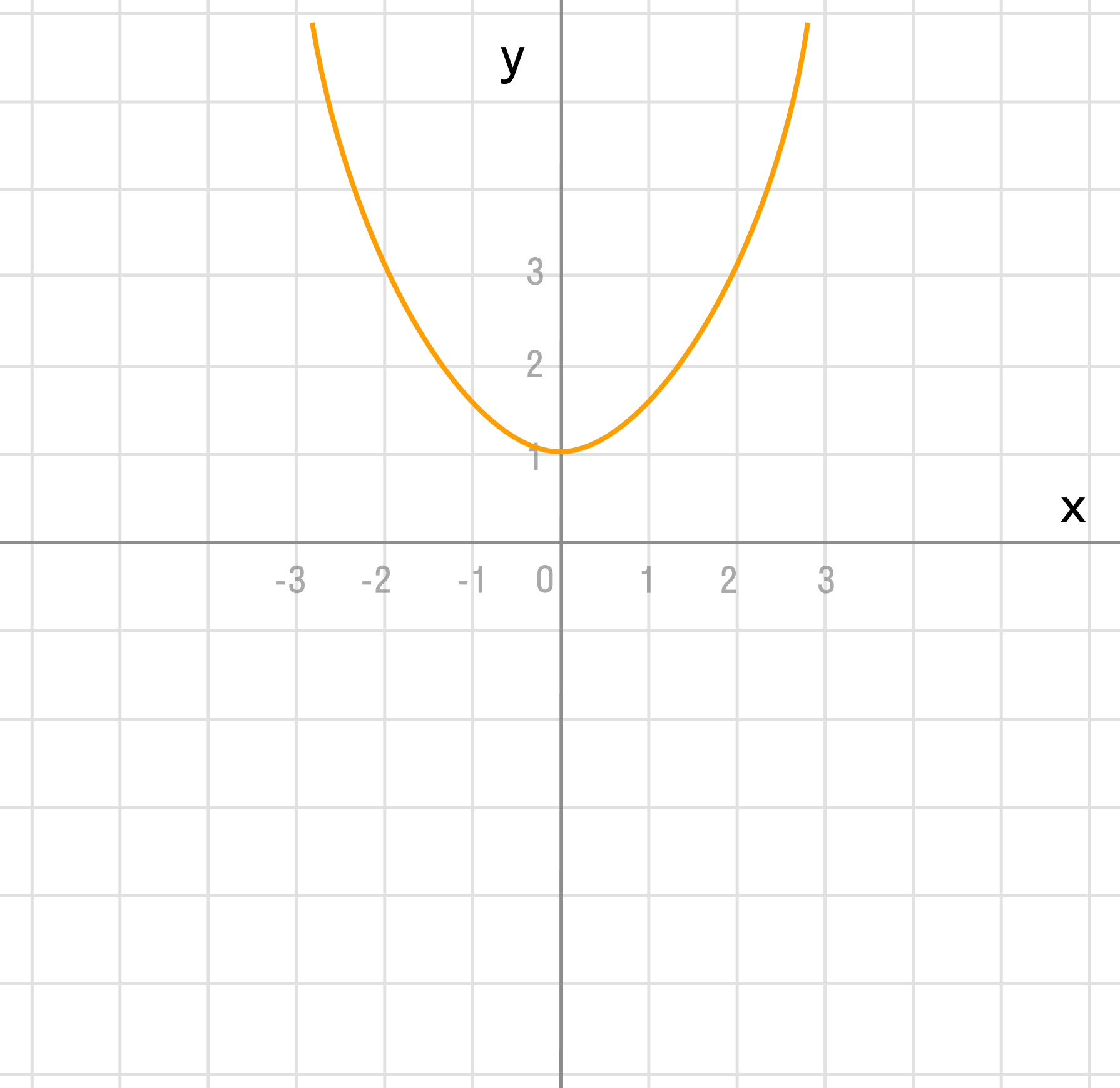
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Построить графики можно при помощи элементарных преобразований.
Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).
-
y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;
-
y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;
-
y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;
-
y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.
Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.
-
Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.
-
Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
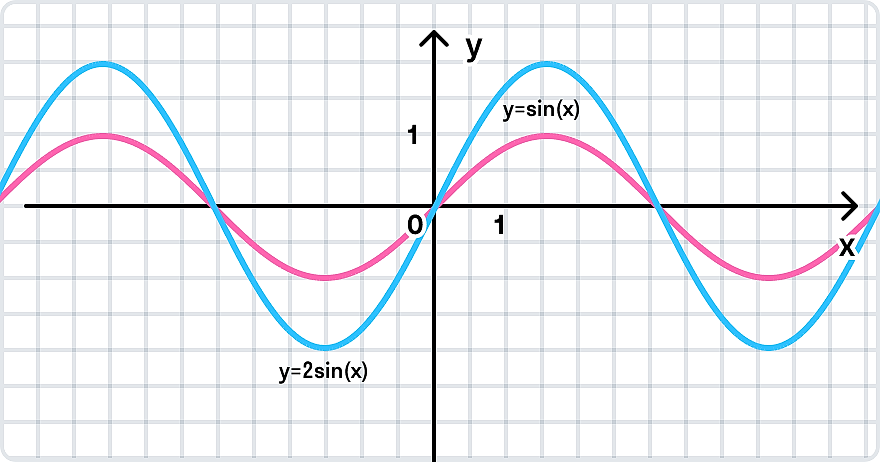
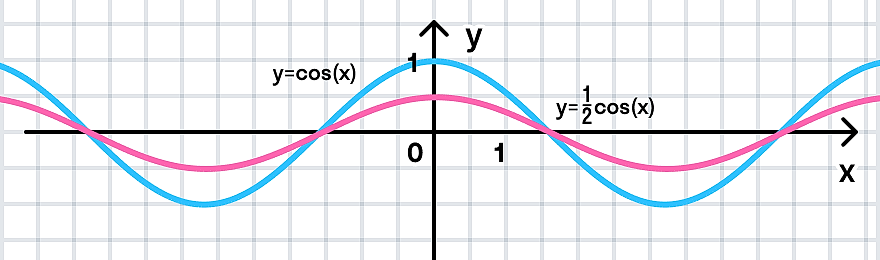
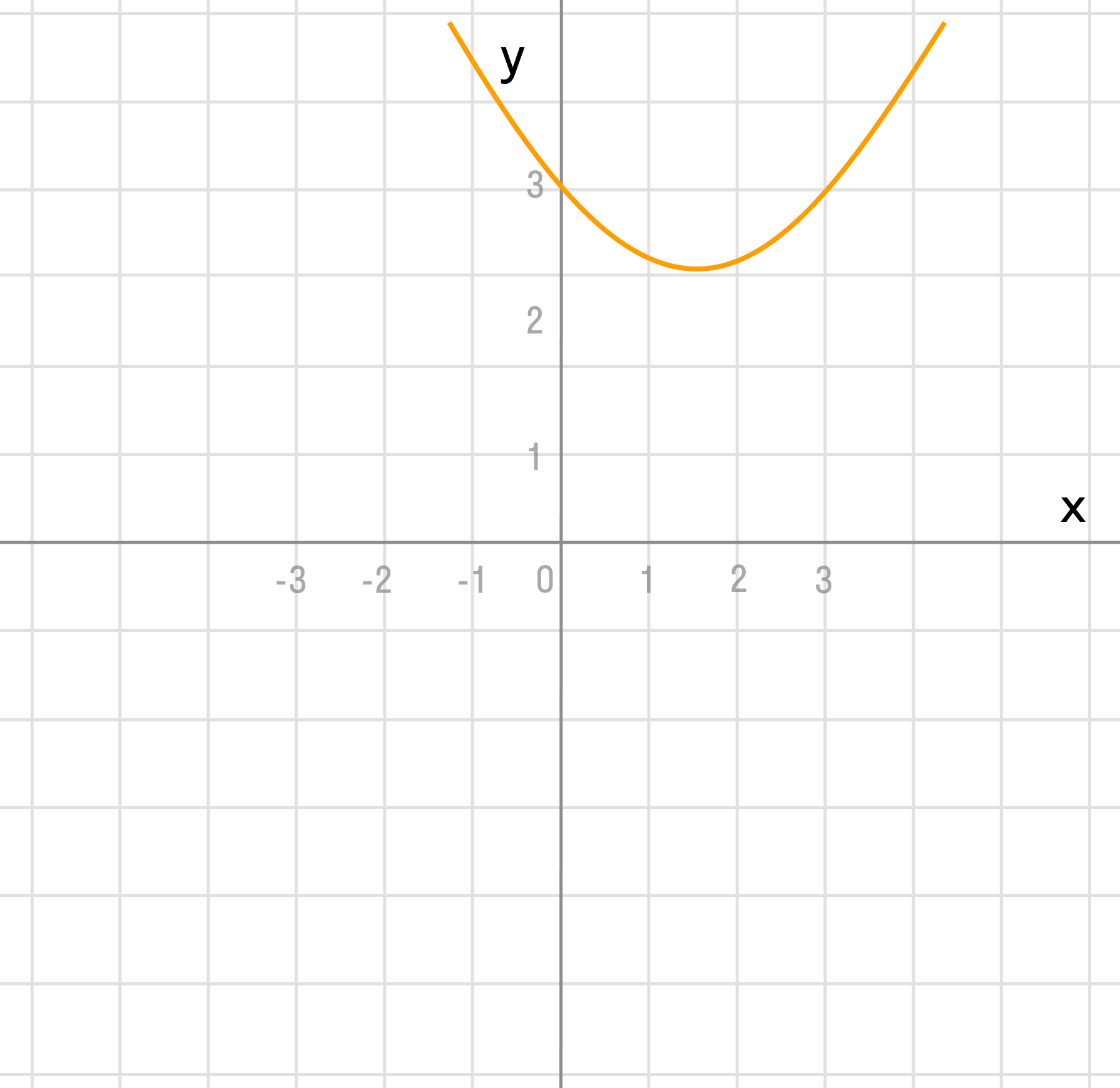
г)
Преобразование в одно действие типа
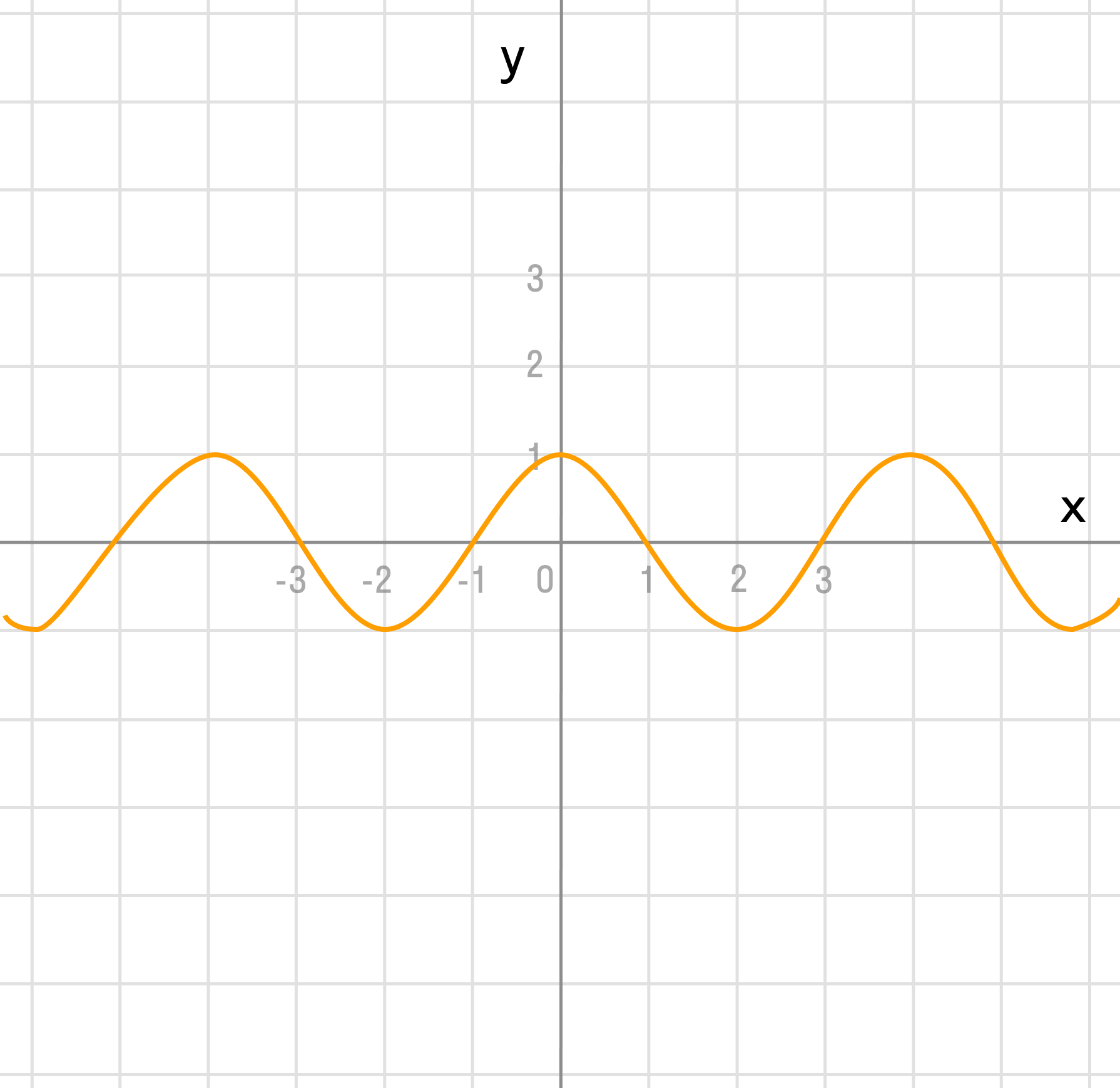
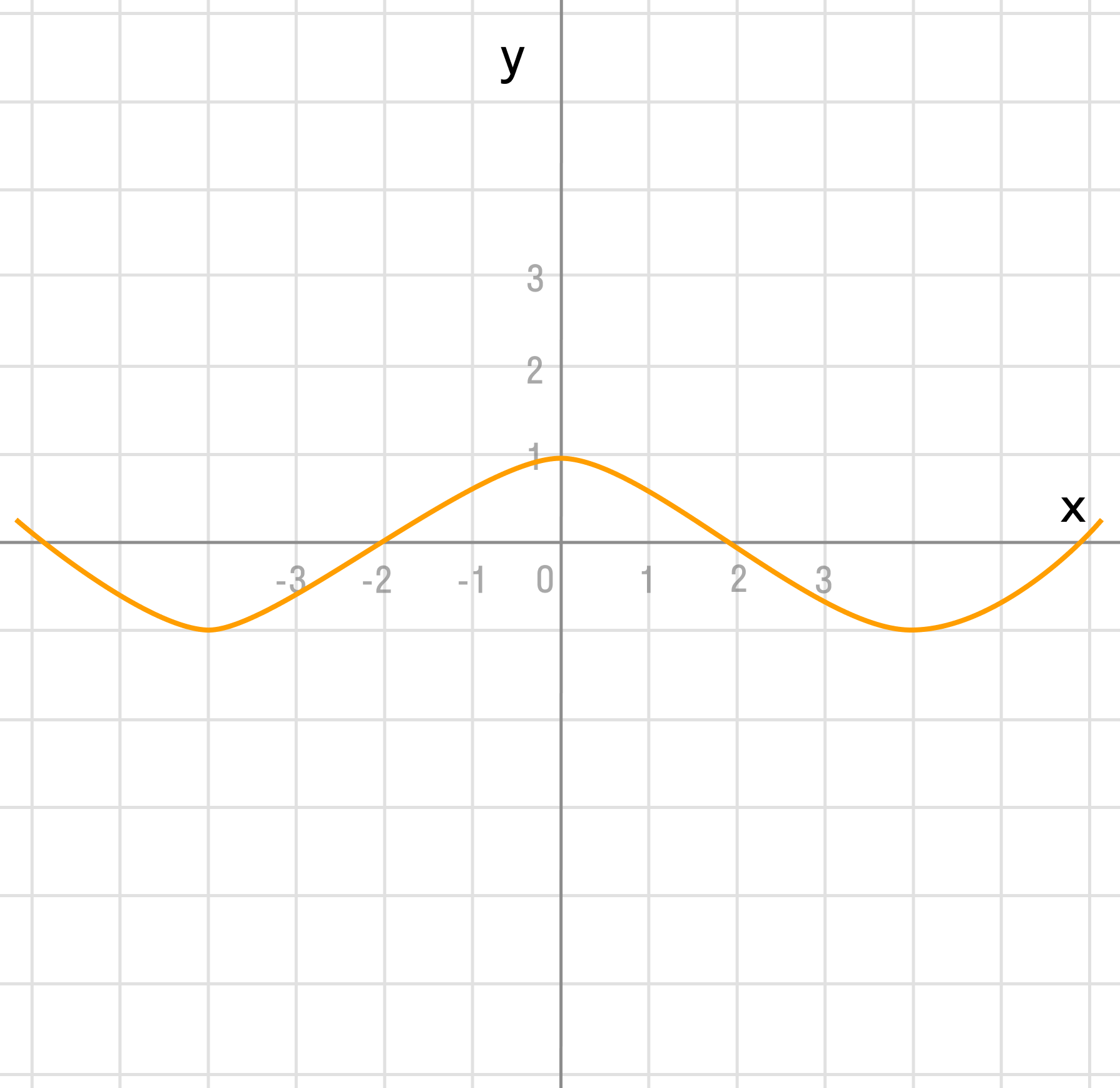
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
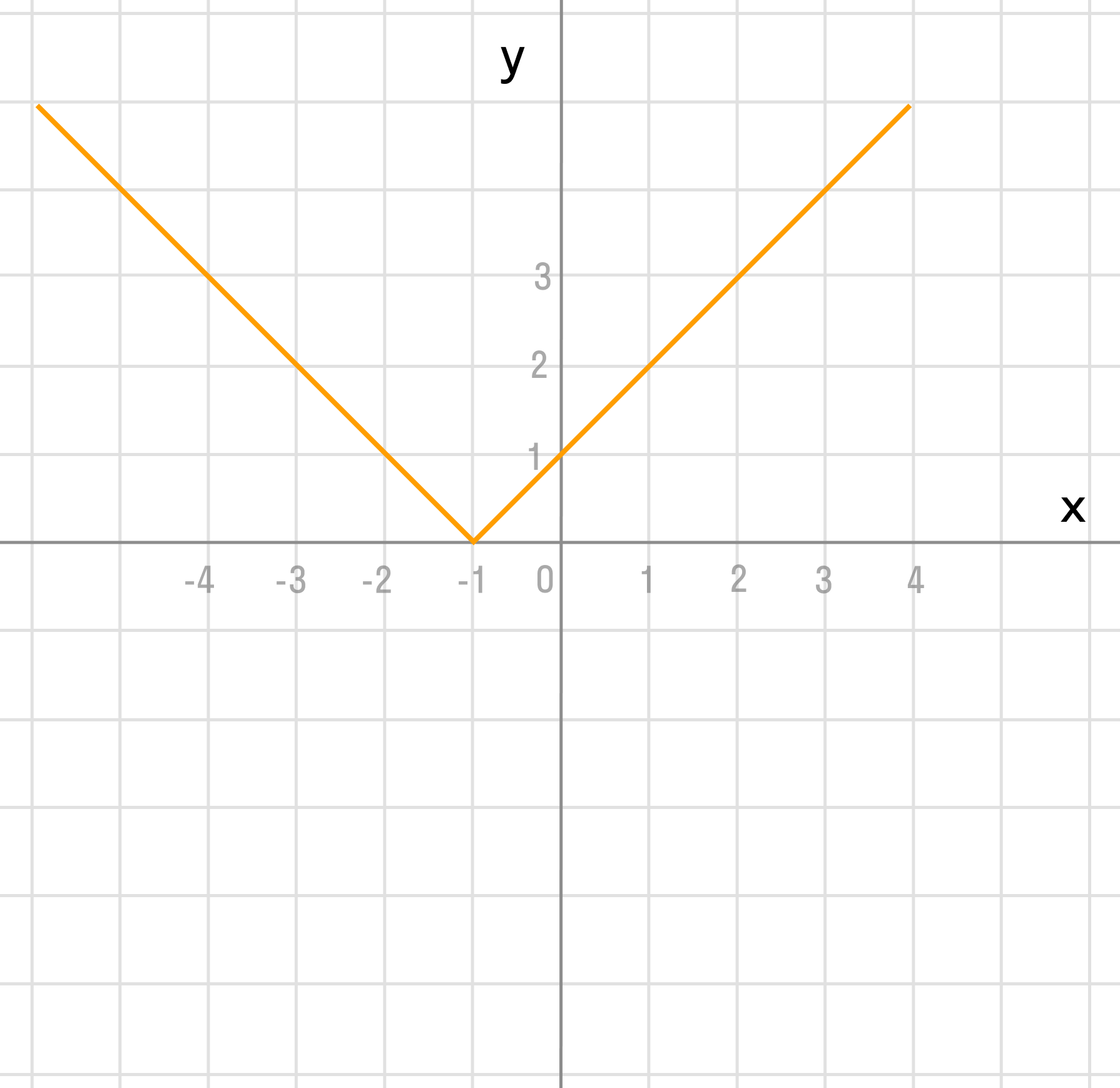
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
На чтение 11 мин. Просмотров 554
Линейный график — это простой графический способ визуализации информации, который отлично подходит для отображения непрерывных данных. В рамках данной статьи, читатель сможет понять, как легко можно построить линейный график в Excel и в других инструментах визуализации. Однако, несмотря на свою простоту, есть масса особенностей и нюансов, которые позволят сделать визуальную составляющую удобной и более читаемой, но об этом далее.
Содержание
- Общее понимание линейного графика
- Для какой цели используется линейная диаграмма
- Типы линейных диаграмм в Excel
- Плюсы и минусы линейного графика
- Добавляем линейную диаграмму в Excel
- Другие инструменты построения линейного графика
- Линейный график в Google Таблицах
- Линейный график в в Power BI
- Онлайн сервисы для построения линейного графика
- Строим линейный график в Yandex DataLens
- Линейный график с помощью Python
- 7 примеров улучшения визуализации графика в Excel и не только
- Выбирайте подходящий интервал измерения
- Расхламление основной области диаграммы
- Предоставьте дополнительный контекст
- Не добавляйте слишком много линий
- Сохраняйте острые углы
- Использование двойной оси
- График начинаться с нуля?
- FAQ по линейным графикам
Общее понимание линейного графика
Линейный график [англ. line graph] — это график, который использует точки и линии для отображения изменений во времени. По сути это вид диаграммы, которая показывает линию, соединяющую несколько точек массива данных. Линейные графики являются распространенными и эффективными диаграммами, потому как они просты, понятны и эффективны.
Всякий раз, когда вы слышите эту ключевую фразу «с течением времени», это подсказка, чтобы рассмотреть возможность использования линейного графика для ваших данных. По большей части, линейные графики лучше всего подходят, когда вы хотите показать, как значения меняются с течением времени, или сравнить, как несколько вещей изменяются в динамике по отношению друг к другу. По сути это идеальный вариант применения такого типа визуализации, но не единственный.
Для какой цели используется линейная диаграмма
Ввиду того, что в этой статьи старались описать «правильные» принципы работы с линейным графиком, нельзя не упомянуть о том, что график должен представлять значимую информацию для пользователя. Поэтому и выбирать этот тип визуализации необходимо для соответствующих целей.
Линейные диаграммы отлично подходят для:
- отображения изменений и тенденций в динамике
- сравнения большого количества данных одновременно
- фиксирования аномалий или среднего значения на столбчатой диаграмме
- включения важного контекста и аннотации
- отображения данных прогноза и вероятности
При этом, линейный график не самый лучшим выбором для:
- отображение количества вещей
- работа с категориальными данными
- сравнения части с целым
- отображения разреженных наборов данных
Всегда стоит помнить, что элементов визуализаций много, но для каждого отдельного случая необходимо выбирать наиболее подходящий элемент. Идеальный вариант для линейного графика — это динамика.
Типы линейных диаграмм в Excel
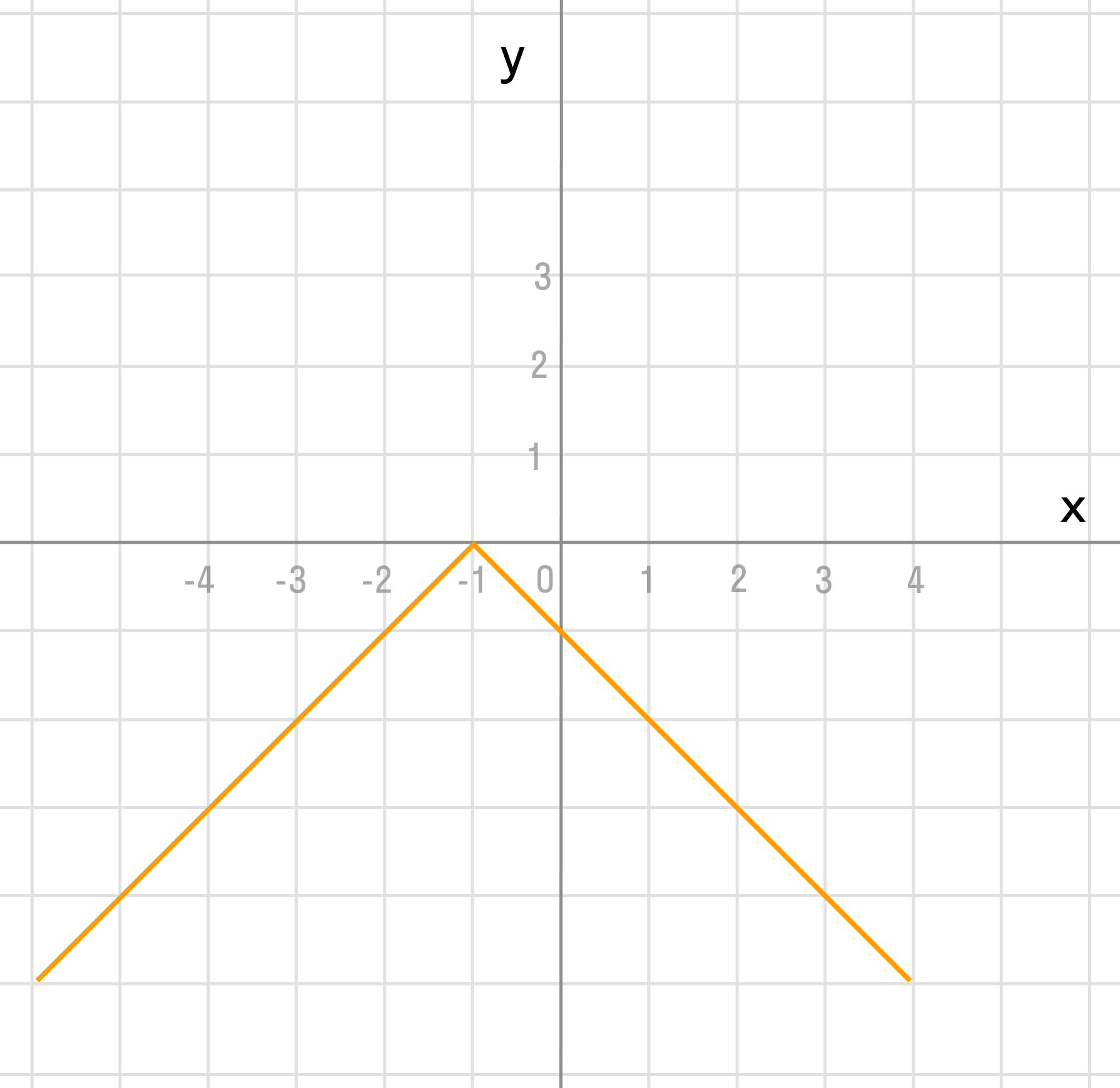
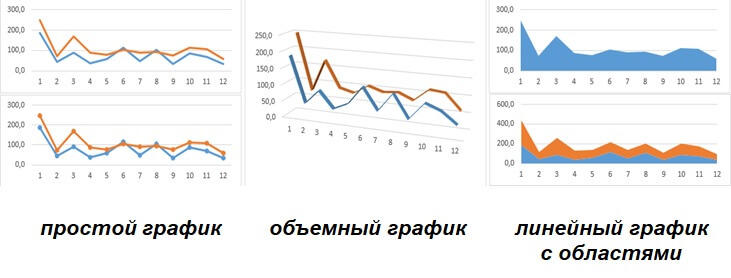
Любая диаграмма и график в Microsoft Excel добавляются в меню ВСТАВКА — Раздел ДИАГРАММЫ. Для построения линейного графика в Excel возможно выбрать три различных варианта:
- простой график, в т.ч. с накоплением или маркерами
- объемный график
- линейный график с областями
Простые линейные графики. Базовый линейный график, который соединяет точки массива данных простой линией. Если, для построения графика выбирается несколько рядов данных, они будут отображаться в одной области диаграммы независимыми линиями.
Объемный график. Тоже что и простой линейный график, только в 3D. Визуальная составляющая так себе, но нужно танцевать от задач, иногда может пригодиться
График с областями. Не совсем линейный, но… Применяется, если важен порядок категорий либо, когда необходимо показать вклад одного показателя в другом. Интересный вариант для наглядной демонстрации выполнения плана, при котором план — это вся область, а факт второй набор данных.
Спарклайн. Данный тип визуализации также можно отнести к линейному графику, просто сам график размещается в ячейке с данными, а не отдельной областью. Это особый элемент визуализации данных, который заслуживает отдельного внимания и выделен в отдельную статью на страницах этого сайта. Спарклайн-график поможет вам избежать рутины в создании большой диаграммы, которая иногда может запутать во время анализа.
Плюсы и минусы линейного графика
Некоторые недостатки линейного графика:
- при размещении большого количества линий в одной области, график становится нечитаемым
- линейный график ограничен только числовым набором данных
- при наличии дробных значений в массиве данных, линейный график трудно детализировать
Теперь о плюсах:
- помогает отобразить тенденции за разный период
- легко воспринимается пользователем
- вполне подходит для сравнения небольшого количества сопоставимых показателей
Добавляем линейную диаграмму в Excel
От теории пора переходить к практике. Линейный график в Excel строится в 3 простых шага:
Шаг 1 Для начала выделите таблицу данных, включая заголовки столбцов.
Шаг 2 Выбрать меню «Вставка» и выберите значок линейной диаграммы либо меню «Рекомендуемые диаграммы».
Шаг 3 Выбрать наиболее подходящий вариант графика и нажать ОК.
Теперь у нас есть простой линейный график, но это не совсем то, что мы себе представляли. Excel сделал точки данных, например, месяца отдельной линией (нужно будет удалить этот ряд), а визуальная составляющая и вовсе хромает. Далее уже остается настроить визуальную привлекательность графика и все готово.
Другие инструменты построения линейного графика
Несмотря на то, что Excel является самым востребованным способом построения линейного графика, однако есть и другие инструменты. Кратко пробежимся по основным из них.
Линейный график в Google Таблицах
Всего тремя кликами мыши можно сделать вполне читаемый линейный график в Google Таблицах, а впоследствии настроить его применяя некоторые рекомендации по визуализации.
- Выбор и выделение массива данных.
- Переход в меню «Вставка» и подменю «Диаграмма».
- Отобразится график, при этом откроется боковая панель для настройки диаграммы.
- Выбирается вариант, который больше всего подходит под цели визуализации.
Наглядный пример как создать линейный график в Google Таблицах в коротеньком видео ниже
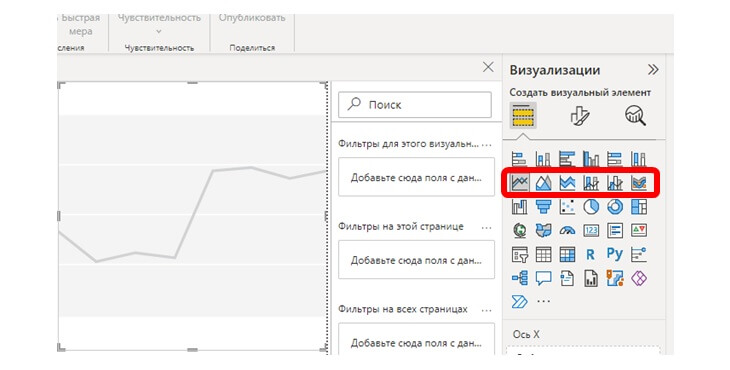
Линейный график в в Power BI
В Power BI добавление линейного графика проще, чем Excel, так как панель инструментов доступна сразу. Выбираем нужный тип графика, и он добавляется в рабочую область. Далее перетаскиваем нужные поля, удерживая их кнопкой мыши и всё.
Онлайн сервисы для построения линейного графика
Случаются моменты, когда картинка необходима быстро, а под рукой нет нужного инструмента. Ниже добавлены 2 сайта, где можно сделать простой линейный график быстро и онлайн. Вносим данные и готово. Согласен, что это не самое удобное решение, но оно есть:
- https://www.mathsisfun.com/data/data-graph.php
- https://www.rapidtables.com/tools/line-graph.html
Строим линейный график в Yandex DataLens
В справочном описании Yandex Cloud есть подробное пошаговое руководство по вставке линейного графика в Yandex DataLens, очень рекомендую прочитать более детально, а краткая выжимка ниже.
Линейный график с помощью Python
Есть несколько способов построить линейный график с помощью Python. Самый простой, с помощью импорта библиотеки Matplotlib или Plotly, хотя таких библиотек несколько. Сначала производится импорт библиотеки, а затем указываются значения данных по осям.
код:
import matplotlib.pyplot as plt
import numpy as np
# Define X and Y variable data
x = np.array([1, 2, 3, 4])
y = x*2
plt.plot(x, y)
plt.xlabel(«X-axis») # add X-axis label
plt.ylabel(«Y-axis») # add Y-axis label
plt.title(«Any suitable title») # add title
plt.show()
7 примеров улучшения визуализации графика в Excel и не только
Для настройки визуализации необходимы простые изменения дизайна значений по умолчанию Excel, однако они сделают график более понятным и легким для понимания данных аудиторией.
Выбирайте подходящий интервал измерения
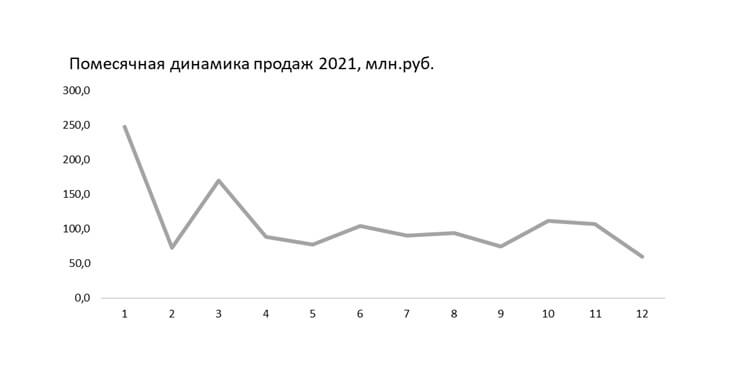
Важным аспектом создания линейного графика является выбор правильного интервала на горизонтальной оси. Для временных данных слишком широкий интервал измерения может означать, что потребуется слишком много времени, чтобы увидеть в данных какую-либо тенденцию. С другой стороны, слишком короткий интервал измерения может выявить только шум, а не сигнал.
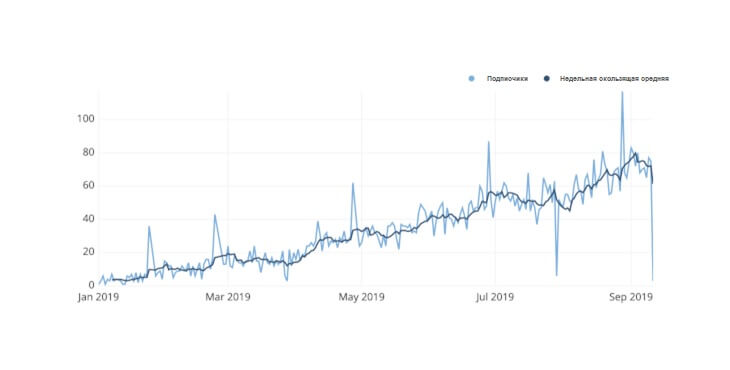
Тестируя различные интервалы или полагаясь на свои знания, вы можете определить хороший выбор размера шага. Также можно использовать несколько линий: одну линию для мелкозернистого интервала, а затем вторую линию для общего тренда с усреднением по скользящему окну.
Расхламление основной области диаграммы
Необходимо сосредоточиться на удалении элементов, которые занимают место, но не добавляют информативности.
Убираем границы диаграммы. Часто мы используем границу, чтобы различать части нашего слайда или визуального элемента. В большинстве случаев мы можем удалить границу графика и использовать пустое пространство, чтобы лучше отделить их друг от друга.
Удаление горизонтальных линий сетки. Этот шаг вносит дополнительный контраст, который позволяет линиям выделяться больше. Щелкните правой кнопкой мыши линии сетки, а затем выберите «Удалить» в меню, чтобы добиться этого. Эти два небольших изменения упрощают график и облегчают просмотр данных. В крайнем случае, если без линий нельзя, сделайте их еле заметным пунктиром.
Регулировка толщины и цвет линии. Сделайте акцент на данных и сделать их более заметными. Щелкните правой кнопкой мыши в любом месте строки и выберите «Формат ряда данных» в меню «Заливки и границы» можно редактировать толщину и цвет линии графика. Оптимальная толщина линии 3pt.
Ставим легенду. Уменьшите усилия пользователя необходимые для перехода от легенды к строке и обратно. Для этого необходимо переместить легенду в верхнюю часть графика в виде подзаголовка, чтобы аудитория прочитала ее до того, как доберется до диаграммы.
После изменения цвета и ширины линии у нас получился примерно вот такой график
Предоставьте дополнительный контекст
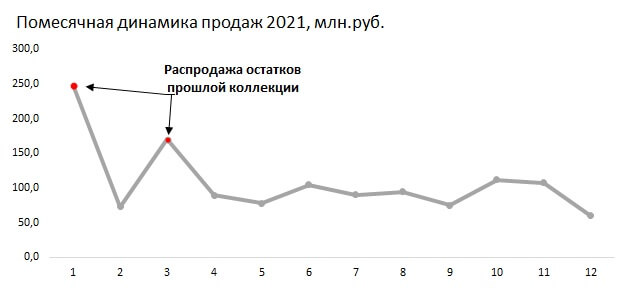
Наш график теперь выглядит значительно лучше, но мы можем сделать больше, чтобы улучшить ее еще немного. Есть некоторые элементы, которые нужно добавить в нашу линейную диаграмму, чтобы дать нашей аудитории дополнительное понимание того, на что обратить внимание.
Теперь у нас есть элегантная линейная диаграмма, показывающая основные реперные точки и причину акцентирования на них внимания пользователя. Данный прием не всегда актуален, но вполне приемлем в некоторых случаях.
Не добавляйте слишком много линий
Людям трудно уследить за более чем четырьмя или пятью вещами одновременно, поэтому рассмотрите возможность использования это количество в качестве ориентира. Если вам абсолютно необходимо показать больше линий, попробуйте использовать цвет, толщину линий и маркировку, а лучше столбчатую диаграмму, чтобы сосредоточиться на наиболее важных линиях или точках.
Сохраняйте острые углы
На стандартной линейной диаграмме каждая точка соединена со следующей отрезком прямой линии от первой до последней. Однако может возникнуть эстетическое искушение попытаться связать все точки плавно, сопоставив кривую, которая проходит через все точки одновременно. Не допускайте этого!
Попытка такой подгонки обязательно приведет к искажению восприятия трендов в данных. Предполагается, что направление и крутизна линии указывают на изменение значения, и поэтому кривая может в конечном итоге означать наличие дополнительных точек данных между фактическими измерениями, которых не существует.
Использование двойной оси
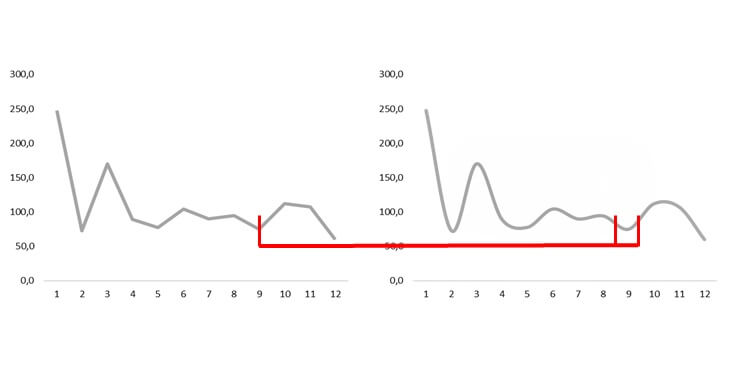
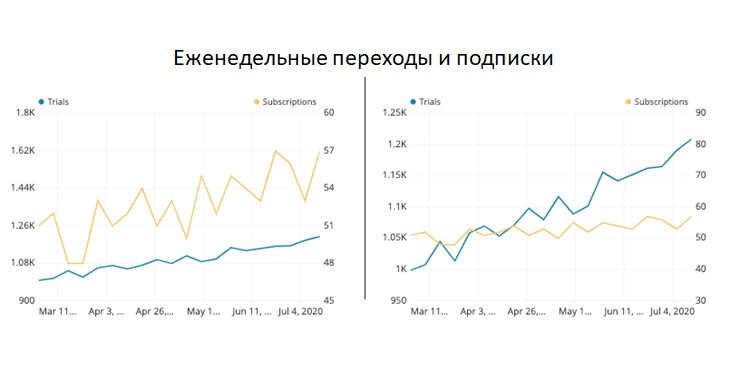
Когда линейный график включает в себя две линии, каждая из которых отображает сводку разных переменных, мы получаем график с двумя осями.
Проблема с двухосным графиком заключается в том, что им можно легко манипулировать, чтобы он вводить пользователя в заблуждение. В зависимости от того, как масштабируется каждая ось, воспринимаемое отношение между двумя линиями может быть изменено. На двух графиках ниже количество еженедельных переходов и подписок нанесено на двухосевые графики. Данные абсолютно одинаковы для каждой из них, но из-за выбора вертикального масштабирования для каждой переменной предполагаемая взаимосвязь между переменными изменится. Будьте с этим очень аккуратны.
График начинаться с нуля?
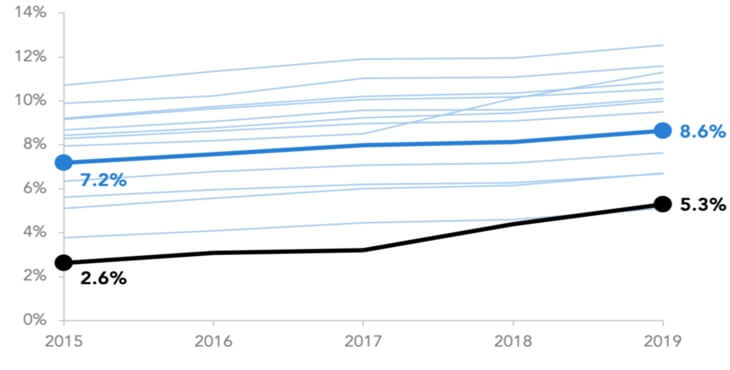
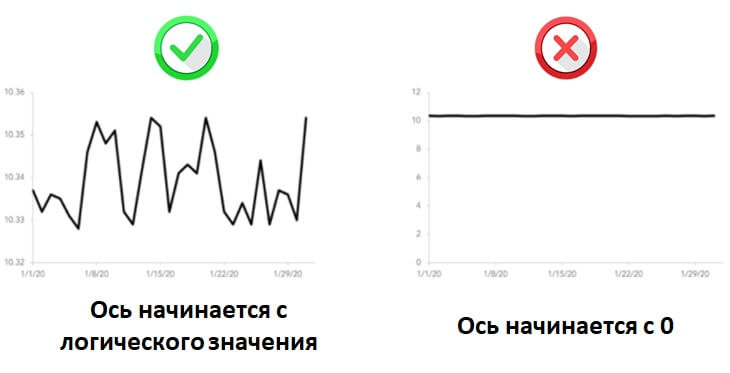
Когда мы смотрим на линейные графики, мы сравниваем линии друг с другом больше, чем их высоту от оси X. По своей природе линейные графики лучше показывают изменение значений с течением времени, чем точное количество в каждой измеряемой точке.
Таким образом, линейные графики не обязаны иметь нулевую базовую линию, но в большинстве случаев это все же целесообразно. Пользователя меньше смущает, если ось Y начинается с нуля, поскольку это нормальное ожидание при первом просмотре графика. Должны быть веские причины, чтобы подорвать эти ожидания.
Ниже конкретный пример, для которого нулевой базовый уровень может быть не оптимальным
FAQ по линейным графикам
Для чего используется линейный график?
Как правило, линейные графики или линейные диаграммы используются для отслеживания изменений во времени, которые могут быть долгосрочными или краткосрочными. Также линейный график может применяться для сравнения изменений за один и тот же период для более чем одной группы.
Из каких частей состоит линейный график?
Линейный график включает в себя 4 основных элементов:
- шкала измерения (оси)
- заголовок
- область построения
- ряд данных
Может ли быть более одной линии на линейном графике?
Да, на линейном графике может быть более одной линии. Обычно это делается, когда нам нужно сравнить два или более набора информации, каждый набор представлен линией.
Всегда ли линейный график — это прямая линия?
Нет. Линия, образованная путем соединения всех точек данных на линейном графике, может быть прямой, а может и не быть таковой. График с прямой линией можно построить если точек 2, при большем их количестве возможны отклонение.
Сколько места необходимо оставить вверху и внизу графика?
Конкретный ответ на этот вопрос будет варьироваться в зависимости от каждого графика, который необходимо сделать. Полезной отправной точкой является создание диапазона от наименьшего значения до наибольшего, занимающего около 70-80% доступного вертикального пространства вашего графика с примерно равным количеством пустого пространства над и под ним. Сверху свободное пространство будет занимать название диаграммы, внизу — показатель по оси Х.
Визуальное представление информации помогает облегчить ее восприятие. Вероятно, самый простой способ превращения сухих данных в доступную для визуального восприятия форму — это создание графиков и таблиц. Ни один аналитик не может обойтись без них.
Графики имеют ряд преимуществ перед другими способами визуального представления информации. Во-первых, они позволяют быстро обрабатывать доступные числовые значения и делать определенные прогнозы. Помимо прочего, планирование позволяет проверить достоверность доступных числовых данных, так как неточности могут появиться после создания графика.
Слава богу, Excel превращает создание диаграмм в простой и легкий процесс, просто основываясь на существующих числовых значениях.
Создание графика в Excel возможно разными методами, каждый из которых имеет значительные преимущества и ограничения. Но давайте посмотрим все более подробно.
Содержание
- Элементарный график изменения
- Создание графика с несколькими кривыми
- Создание второй оси
- Excel: методика создания графика функции
- Как объединить несколько графиков
- Графики зависимости
- Настройка внешнего вида графика Excel
- Общие рекомендации по созданию графиков
- Выводы
Элементарный график изменения
График необходим, если от человека требуется продемонстрировать, насколько определенный показатель изменился за конкретный период времени. И обычного графика для выполнения этой задачи вполне достаточно, а вот различные вычурные диаграммы на деле могут только сделать информацию менее читаемой.
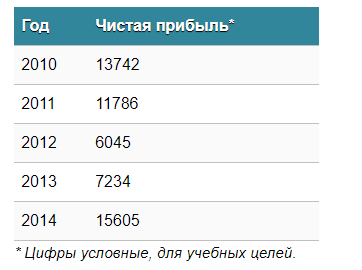
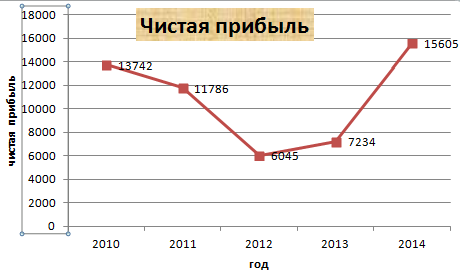
Предположим, у нас есть таблица, которая предоставляет информацию о чистой прибыли компании за последние пять лет.
Важно. Эти цифры не представляют фактические данные и могут быть нереалистичными. Они предоставляются только в образовательных целях.
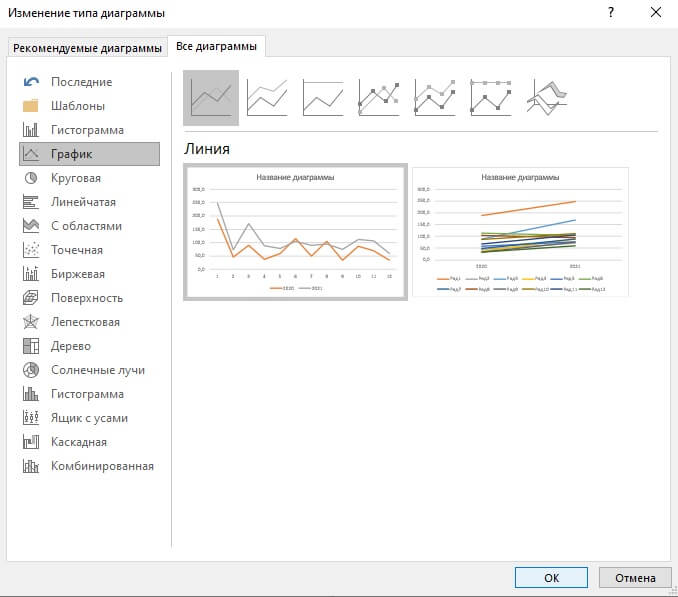
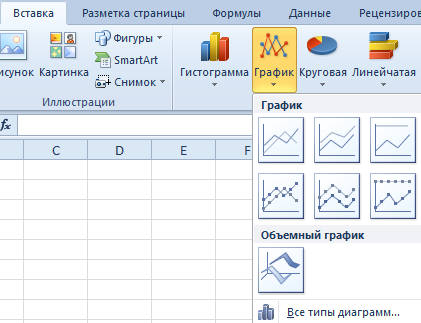
Затем отправьтесь к вкладке «Вставка», где у вас есть возможность осуществить выбор типа графика, который будет подходящим в конкретной ситуации.
Нас интересует тип «График». После нажатия на соответствующую кнопку, появится окошко с настройками внешнего вида будущего графика. Чтобы понять, какой вариант подходит в конкретном случае, вы можете навести указатель мыши на определенный тип, и появится соответствующее приглашение.
После выбора нужного вида диаграммы вам необходимо скопировать таблицу данных связать ее с графиком. Результат будет следующим.
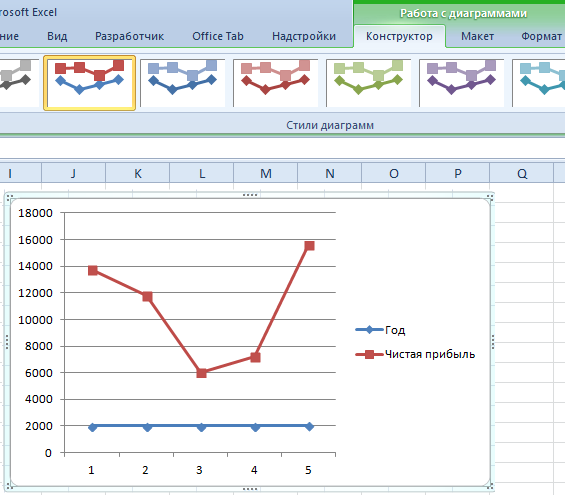
В нашем случае на диаграмме представлено две линии. Первая имеет красный цвет. Вторая — синий. Последняя нам не нужна, поэтому мы можем удалить ее, выбрав ее и нажав кнопку «Удалить». Поскольку мы имеем лишь одну линию, легенда (блок с названиями отдельных линий графика) также может быть удалена. Но маркеры лучше назвать. Найдите панель «Работа с диаграммами» и блок «Подписи данных» на вкладке «Макет». Здесь вы должны определить положение чисел.
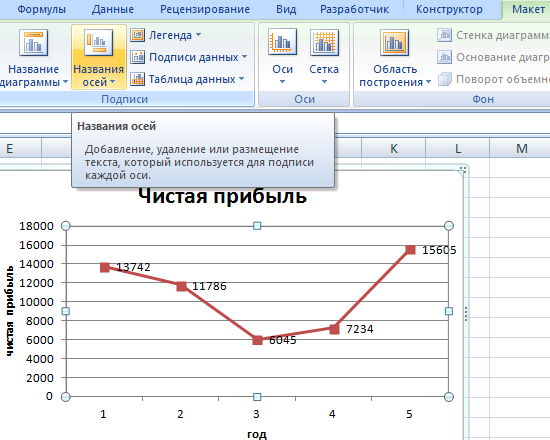
Оси рекомендуется называть, чтобы обеспечить большую удобочитаемости графика. На вкладке «Макет» найдите меню «Названия осей» и задайте имя для вертикальной или горизонтальной осей соответственно.
Но вы можете смело обходиться без заголовка. Чтобы удалить его, вам нужно переместить его в область графика, которая невидима для постороннего глаза (над ним). Если вам все еще нужно название диаграммы, вы можете получить доступ ко всем необходимым настройкам через меню «Название диаграммы» на той же вкладке. Вы также можете найти его на вкладке «Макет».
Вместо порядкового номера отчетного года достаточно оставить только сам год. Выберите требуемые значения и щелкните по ним правой кнопкой мышки. Затем кликните по пункту «Выбор данных» — «Изменить подпись горизонтальной оси». Далее вам следует задать диапазон. В случае с нами, это первая колонка таблицы, являющейся источником информации. Результат такой.
Но вообще, можно все оставить, этот график вполне рабочий. Но если есть необходимость сделать привлекательный дизайн графика, то к вашим услугам — Вкладка «Конструктор», которая позволяет указать фоновый цвет графика, его шрифт, а также разместить его на другом листе.
Создание графика с несколькими кривыми
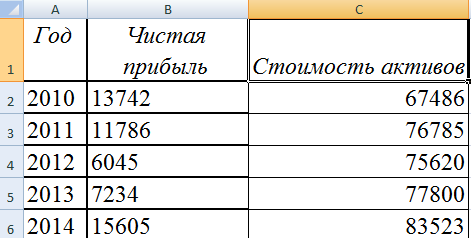
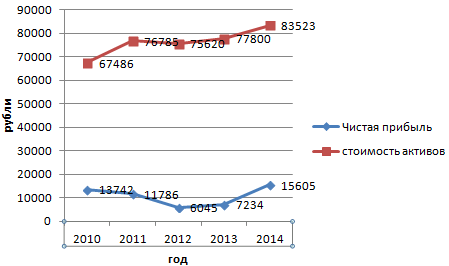
Предположим, нам надо продемонстрировать инвесторам не одну лишь чистую прибыль предприятия, но и то, сколько в общей сумме будут стоить ее активы. Соответственно, выросло количество информации.
Невзирая на это, в методике создания графика принципиальных отличий нет по сравнению с описанным выше. Просто теперь легенду надо оставить, поскольку ее функция отлично выполняется.
Создание второй оси
Какие же действия необходимо предпринять, чтобы создать еще одну ось на графике? Если мы используем общие метрические единицы, то необходимо применить советы, описанные ранее. Если применяются данные различных типов, то придется добавлять еще одну ось.
Но перед этим нужно построить обычный график, как будто используются одни и те же метрические единицы.
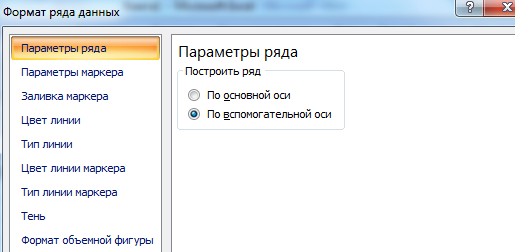
После этого главная ось выделяется. Затем вызовите контекстное меню. В нем будет много пунктов, один из которых – «Формат ряда данных». Его нужно нажать. Затем появится окно, в котором необходимо найти пункт меню «Параметры ряда», а далее выставить опцию «По вспомогательной оси».
Далее закройте окно.
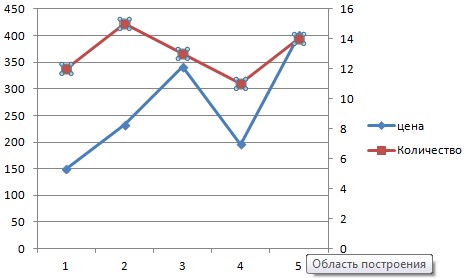
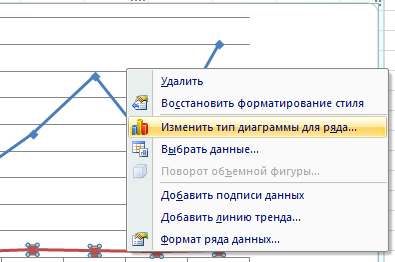
Но это всего лишь один из возможных методов. Никто не мешает, например, использовать для вторичной оси диаграмму другой разновидности. Надо определиться, какая линия требует того, чтобы мы добавили дополнительную ось, и потом кликнуть правой кнопкой мыши по ней и выбрать пункт «Изменить тип диаграммы для ряда».
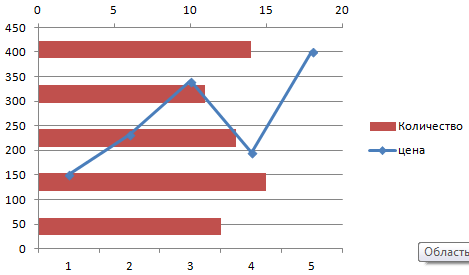
Далее нужно настроить «внешность» второго ряда. Мы решили остановиться на линейчатой диаграмме.
Вот, как все просто. Достаточно сделать лишь пару кликов, и появляется еще одна ось, настроенная под иной параметр.
Excel: методика создания графика функции
Это уже более нетривиальная задача, и для ее выполнения необходимо выполнить два основных действия:
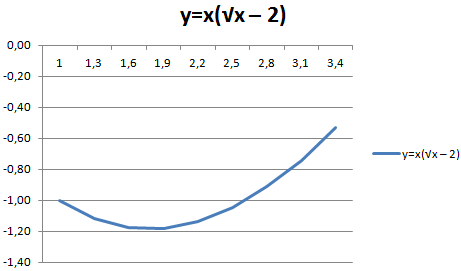
- Сформировать таблицу, служащую источником информации. Сперва следует определиться с тем, какая будет конкретно в вашем случае использоваться функция. Например, y=x(√x – 2). При этом в качестве используемого шага мы выберем значение 0,3.
- Собственно, построить график.
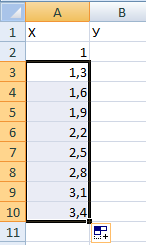
Итак, нам необходимо сформировать таблицу, где есть два столбца. Первый – это горизонтальная ось (то есть, X), второй – вертикальная (Y). Вторая строка содержит первое значение, в нашем случае это единица. На третьей строке нужно написать значение, которое будет на 0,3 большим предыдущего. Это можно сделать как с помощью самостоятельных подсчетов, так и записав непосредственно формулу, которая в нашем случае будет следующей:
=A2+0,3.
После этого нужно применить автозаполнение к следующим ячейкам. Для этого нужно выделить ячейки A2 и A3 и перетащить квадратик на нужное количество строк вниз.
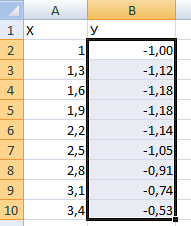
В вертикальной колонке мы указываем формулу, используемую, чтобы на основе готовой формулы построить график функции. В случае с нашим примером это будет =А2*(КОРЕНЬ(А2-2). После этого подтверждает свои действия с помощью клавиши Enter, и программа автоматически рассчитает результат.
Далее нужно создать новый лист или перейти на другой, но уже существующий. Правда, если есть острая необходимость, можно вставить диаграмму здесь же (не резервируя под эту задачу отдельный лист). Но лишь при условии, что есть много свободного пространства. Затем нажимаем следующие пункты: «Вставка» – «Диаграмма» – «Точечная».
После этого надо решить, какой тип диаграммы нужно использовать. Далее делается правый клик мышью по той части диаграммы, для которой будут определяться данные. То есть, после открытия контекстного меню следует нажать на кнопку «Выбрать данные».
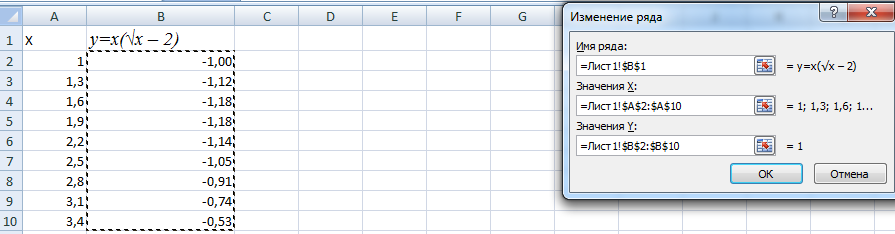
Далее нужно выделить первый столбик, и нажать «Добавить». Появится диалоговое окно, где будут настройки названия ряда, а также значения горизонтальной и вертикальной осей.
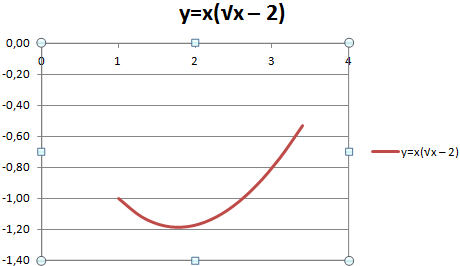
Ура, результат есть, и выглядит очень даже мило.
Аналогично графику, построенному в начале, можно удалять легенду, поскольку мы имеем только одну линию, и нет необходимости ее дополнительно подписывать.
Но есть одна проблема – на оси X не нанесены значения, лишь номер точек. Чтобы скорректировать эту проблему, надо дать названия этой оси. Чтобы это сделать, нужно кликнуть правой кнопкой мыши по ней, а затем выбрать пункт «Выбрать данные» – «Изменить подписи горизонтальной оси». По окончании этих операций выделяется требуемый набор значений, и график станет выглядет так.
Как объединить несколько графиков
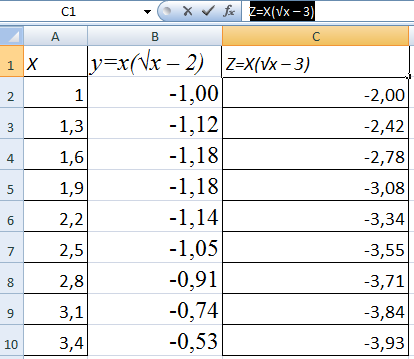
Для создания двух графиков на одном поле особых каких-то компетенций не нужно. Для старта необходимо добавить следующую колонку с функцией Z=X(√x – 3).
Чтобы все было более наглядно, приводим табличку.
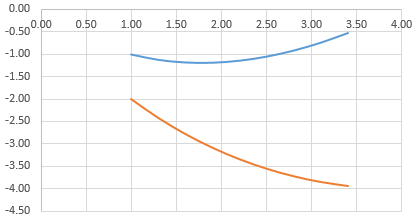
Обнаруживаем ячейки с требуемой информацией и выделяем их. После этого их необходимо вставить в диаграмму. Если что-то идет не по плану (например, случайно были написаны неправильные названия рядов или неверные цифры на оси), то можно воспользоваться пунктом «Выбрать данные» и отредактировать их. Как следствие, появится вот такой график, где две линии совмещены вместе.
Графики зависимости
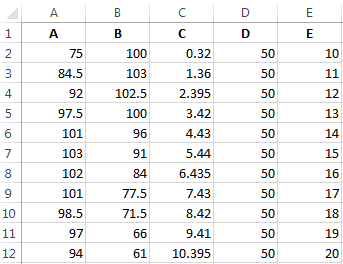
Это вид графика, где содержимое одной строки или колонки прямо влияет на результат другой. Чтобы его создать, необходимо сформировать табличку типа этой.
Условия, заложенные в график: А = f (E); В = f (E); С = f (E); D = f (E).
В случае с нами, нужно найти точечную диаграмму с маркерами и гладкими кривыми, поскольку этот тип больше всего подходит под наши задачи. Затем нажмите на следующие кнопки: Выбор данных – Добавить. Пусть название ряда будет «А», а значения Х будут значениями А. В свою очередь, значения, расположенные по вертикали, будут значениями Е. Опять нужно нажать «Добавить». Второй ряд будет называться B, а значения, расположенные по оси Х, будут находиться в колонке B, а по оси вертикали – в колонке E. Далее по этому механизму создается вся таблица.
Настройка внешнего вида графика Excel
После того, как график будет создан, необходимо уделить отдельное внимание его настройке. Важно, чтобы его внешний вид был привлекательным. Принципы настройки одинаковые, независимо от используемой версии программы.
Важно понимать, что любая диаграмма – по сути своей сложный объект. Поэтому в его состав входит множество более мелких частей. Каждая из них может настраиваться путем вызова контекстного меню.
Здесь нужно отличать настройку общих параметров графика и конкретных объектов. Так, для настройки его базовых характеристик, необходимо нажать на фон диаграммы. После этого программа покажет мини-панель, где можно управлять основными общими параметрами, а также разные пункты меню, где можно настраивать их более гибко.
Чтобы задать фон диаграммы, нужно выбрать пункт «Формат области диаграммы». Если регулируются свойства конкретных объектов, то количество пунктов меню значительно уменьшится. Например, чтобы отредактировать легенду, достаточно просто вызвать контекстное меню и кликнуть там по пункту, который всегда начинается со слова «Формат». Обычно его можно найти в самом низу контекстного меню.
Общие рекомендации по созданию графиков
Есть несколько рекомендаций, как правильно создавать графики, чтобы они были читаемыми и информативными:
- Не нужно использовать слишком много линий. Достаточно лишь двух-трех. Если необходимо отобразить больше информации, лучше создать отдельный график.
- Нужно особое внимание уделить легенде, а также осям. От того, насколько качественно они подписаны, зависит то, насколько легко будет читать график. Это важно, поскольку любая диаграмма создается для упрощения представления определенной информации, но если подойти к этому безответственно, человеку будет тяжелее разобраться.
- Несмотря на возможность настраивать внешний вид диаграммы, не рекомендуется использовать слишком много цветов. Это будет сбивать с толку человека, читающего диаграммы.
Выводы
Простыми словами, абсолютно несложно создать график, используя в качестве источника данных конкретный диапазон значений. Достаточно нажать пару кнопкой, и все остальное программа сделает самостоятельно. Конечно, для профессионального овладения этим инструментом надо немного потренироваться.
Если следовать общим рекомендациям по созданию графиков, а также красиво оформлять график таким образом, чтобы получилась очень красивая и информативная картинка, которая не будет вызывать трудностей при ее чтении.
Оцените качество статьи. Нам важно ваше мнение:
Загрузить PDF
Загрузить PDF
График функции – это наглядное представление поведения некоторой функции на координатной плоскости. Графики помогают понять различные аспекты функции, которые невозможно определить по самой функции. Можно построить графики множества функций, причем каждая из них будет задана определенной формулой. График любой функции строится по определенному алгоритму (если вы забыли точный процесс построения графика конкретной функции).
-
1
-
2
Воспользуйтесь константой, чтобы отметить точку на оси Y. Константа (b) является координатой «у» точки пересечения графика с осью Y. То есть это точка, координата «х» которой равна 0. Таким образом, если в формулу подставить х = 0, то у = b (константе). В нашем примере
константа равна 5, то есть точка пересечения с осью Y имеет координаты (0,5). Нанесите эту точку на координатную плоскость.
-
3
Найдите угловой коэффициент прямой. Он равен множителю при переменной. В нашем примере
при переменной «х» находится множитель 2; таким образом, угловой коэффициент равен 2. Угловой коэффициент определяет угол наклона прямой к оси X, то есть чем больше угловой коэффициент, тем быстрее возрастает или убывает функция.
-
4
Запишите угловой коэффициент в виде дроби. Угловой коэффициент равен тангенсу угла наклона, то есть отношению вертикального расстояния (между двумя точками на прямой) к горизонтальному расстоянию (между этими же точками). В нашем примере угловой коэффициент равен 2, поэтому можно заявить, что вертикальное расстояние равно 2, а горизонтальное расстояние равно 1. Запишите это в виде дроби:
.
- Если угловой коэффициент отрицательный, функция убывает.
-
5
От точки пересечения прямой с осью Y нанесите вторую точку, используя вертикальное и горизонтальное расстояния. График линейной функции можно построить по двум точкам. В нашем примере точка пересечения с осью Y имеет координаты (0,5); от этой точки передвиньтесь на 2 деления вверх, а затем на 1 деление вправо. Отметьте точку; она будет иметь координаты (1,7). Теперь можно провести прямую.
-
6
При помощи линейки проведите прямую через две точки. Во избежание ошибок найдите третью точку, но в большинстве случаев график можно построить по двум точкам. Таким образом, вы построили график линейной функции.
Реклама
-
1
Определите функцию. Функция обозначается как f(x). Все возможные значения переменной «у» называются областью значений функции, а все возможные значения переменной «х» называются областью определения функции. Например, рассмотрим функцию y = x+2, а именно f(x) = x+2.
-
2
Нарисуйте две пересекающиеся перпендикулярные прямые. Горизонтальная прямая – это ось Х. Вертикальная прямая – это ось Y.
-
3
Обозначьте оси координат. Разбейте каждую ось на равные отрезки и пронумеруйте их. Точка пересечения осей – это 0. Для оси Х: справа (от 0) наносятся положительные числа, а слева отрицательные. Для оси Y: сверху (от 0) наносятся положительные числа, а снизу отрицательные.
-
4
Найдите значения «у» по значениям «х». В нашем примере f(x) = х+2. Подставьте в эту формулу определенные значения «х», чтобы вычислить соответствующие значения «у». Если дана сложная функция, упростите ее, обособив «у» на одной стороне уравнения.
- -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
-
5
Нанесите точки на координатную плоскость. Для каждой пары координат сделайте следующее: найдите соответствующее значение на оси Х и проведите вертикальную линию (пунктиром); найдите соответствующее значение на оси Y и проведите горизонтальную линию (пунктиром). Обозначьте точку пересечения двух пунктирных линий; таким образом, вы нанесли точку графика.
-
6
Сотрите пунктирные линии. Сделайте это после нанесения на координатную плоскость всех точек графика. Примечание: график функции f(х) = х представляет собой прямую, проходящую через центр координат [точку с координатами (0,0)]; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).[2]
Реклама
-
1
-
2
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. Имейте в виду, что нули имеют не все функции, но это первый шаг процесса построения графика любой функции. Чтобы найти нули функции, приравняйте ее к нулю. Например:
-
3
Найдите и отметьте горизонтальные асимптоты. Асимптота – это прямая, к которой график функции приближается, но никогда не пересекает ее (то есть в этой области функция не определена, например, при делении на 0). Асимптоту отметьте пунктирной линией. Если переменная «х» находится в знаменателе дроби (например,
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
-
4
Найдите координаты нескольких точек и нанесите их на координатную плоскость. Просто выберите несколько значений «х» и подставьте их в функцию, чтобы найти соответствующие значения «у». Затем нанесите точки на координатную плоскость. Чем сложнее функция, тем больше точек нужно найти и нанести. В большинстве случаев подставьте х = -1; х = 0; х = 1, но если функция сложная, найдите по три точки с каждой стороны от начала координат.[5]
- В случае функции
подставьте следующие значения «х»: -1, 0, 1, -2, 2, -10, 10. Вы получите достаточное количество точек.
- Выбирайте значения «х» с умом. В нашем примере несложно понять, что отрицательный знак не играет роли: значение «у» при х = 10 и при х = -10 будет одним и тем же.
- В случае функции
-
5
Определите поведение функции при больших значения переменной «х». Так можно найти общее направление графика функции, который иногда до бесконечности приближается к асимптоте. Например, нетрудно догадаться, что график функции
возрастает до бесконечности: при увеличении огромного значения «х» всего-навсего на 1 (с 1000000 на 1000001), значение «у» увеличится на гораздо большую величину. Определить поведение функции при больших значения «х» можно несколькими способами:
- В функцию подставьте 2-4 больших значения «х» (половину отрицательных и половину положительных), а затем полученные точки нанесите на координатную плоскость.
- Подумайте, что будет, если вместо «х» подставить «бесконечность»? Значение «у» будет бесконечно большим или бесконечно малым?
- Если в функции показатели степени одинаковые (например,
), разделите множители при «х» (
), чтобы найти асимптоту (-0,5).[6]
- Если в функции показатели степени разные, разделите выражение, стоящее в числителе, на выражение, стоящее в знаменателе.
-
6
Соедините точки (5-6 точек), чтобы построить график функции. При этом график не должен пересекать (и касаться) асимптоты. График продолжите в соответствии с найденным поведением функции при больших значениях переменной «х».
-
7
Постройте совершенный график при помощи графического калькулятора. Графические калькуляторы представляют собой мощные карманные компьютеры, при помощи которых можно построить точный график любой функции. Такие калькуляторы способны находить точные координаты точек и угловые коэффициенты прямых, а также быстро строить графики самых сложных функций. Просто введите точную формулу функции (обычно это делается при помощи клавиши «F(х)=») и нажмите соответствующую клавишу, чтобы построить график.
Реклама
Советы
- Практикуйте ваши навыки с использованием графических калькуляторов. Сначала попробуйте построить график вручную, а затем воспользуйтесь калькулятором, чтобы получить точный график и сравнить оба результата.
- Если вы не знаете, что делать, начните с подстановки в функцию различных значений «х», чтобы найти значения «у» (и, следовательно, координаты точек). Теоретически график функции можно построить при помощи только этого метода (если, конечно, подставить бесконечное разнообразие значений «х»).
Реклама
Об этой статье
Эту страницу просматривали 120 687 раз.
Была ли эта статья полезной?
|
13 / 13 / 6 Регистрация: 07.07.2014 Сообщений: 216 |
|
|
1 |
|
|
19.03.2015, 11:31. Показов 17701. Ответов 3
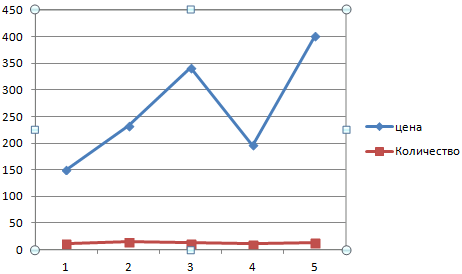
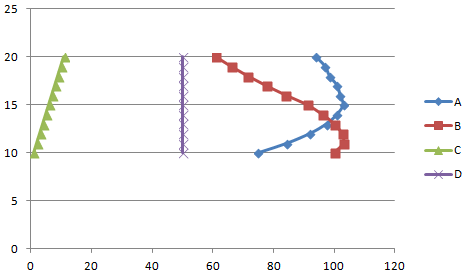
Народ, объясните, почему значение 0 не учитывается при построении графика в моём случае и как это исправить? Миниатюры
0 |
|
3834 / 2260 / 753 Регистрация: 02.11.2012 Сообщений: 5,958 |
|
|
19.03.2015, 13:26 |
2 |
|
по графику вижу что у вас при значении Х=1 Y=0 на всех 3-х графиках. Х=0 не вижу. Какие данные так и строится график.
0 |
|
2635 / 1334 / 256 Регистрация: 25.10.2010 Сообщений: 2,196 |
|
|
19.03.2015, 14:12 |
3 |
|
Решение По скрину видно, что у Вас Excel 2003. В окне Формат оси категорий на вкладке Шкала есть параметр Пересечение с осью Y между категориями, надо снять этот флажок.
3 |
|
13 / 13 / 6 Регистрация: 07.07.2014 Сообщений: 216 |
|
|
19.03.2015, 14:27 [ТС] |
4 |
|
Большое спасибо!
0 |


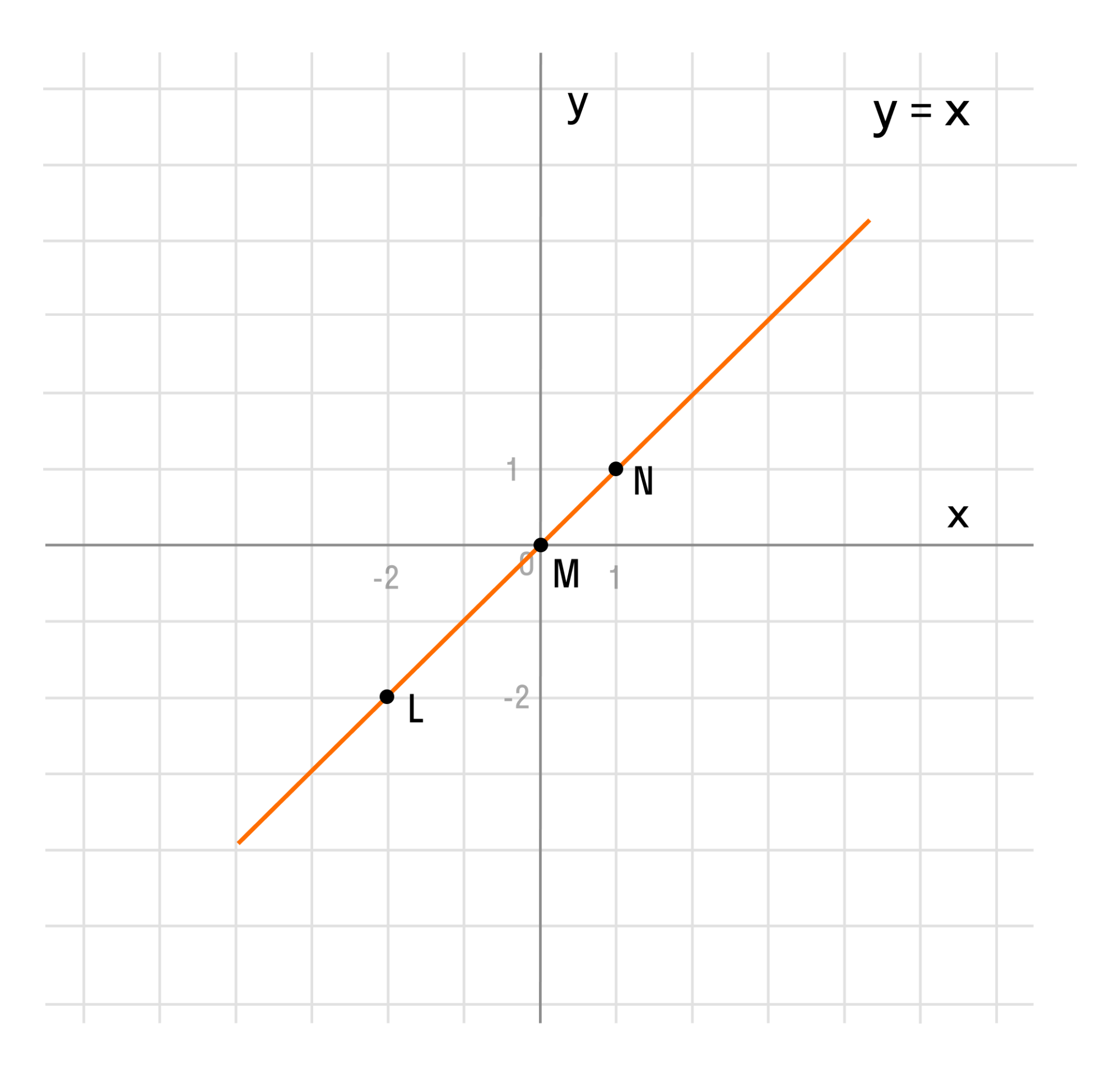
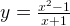
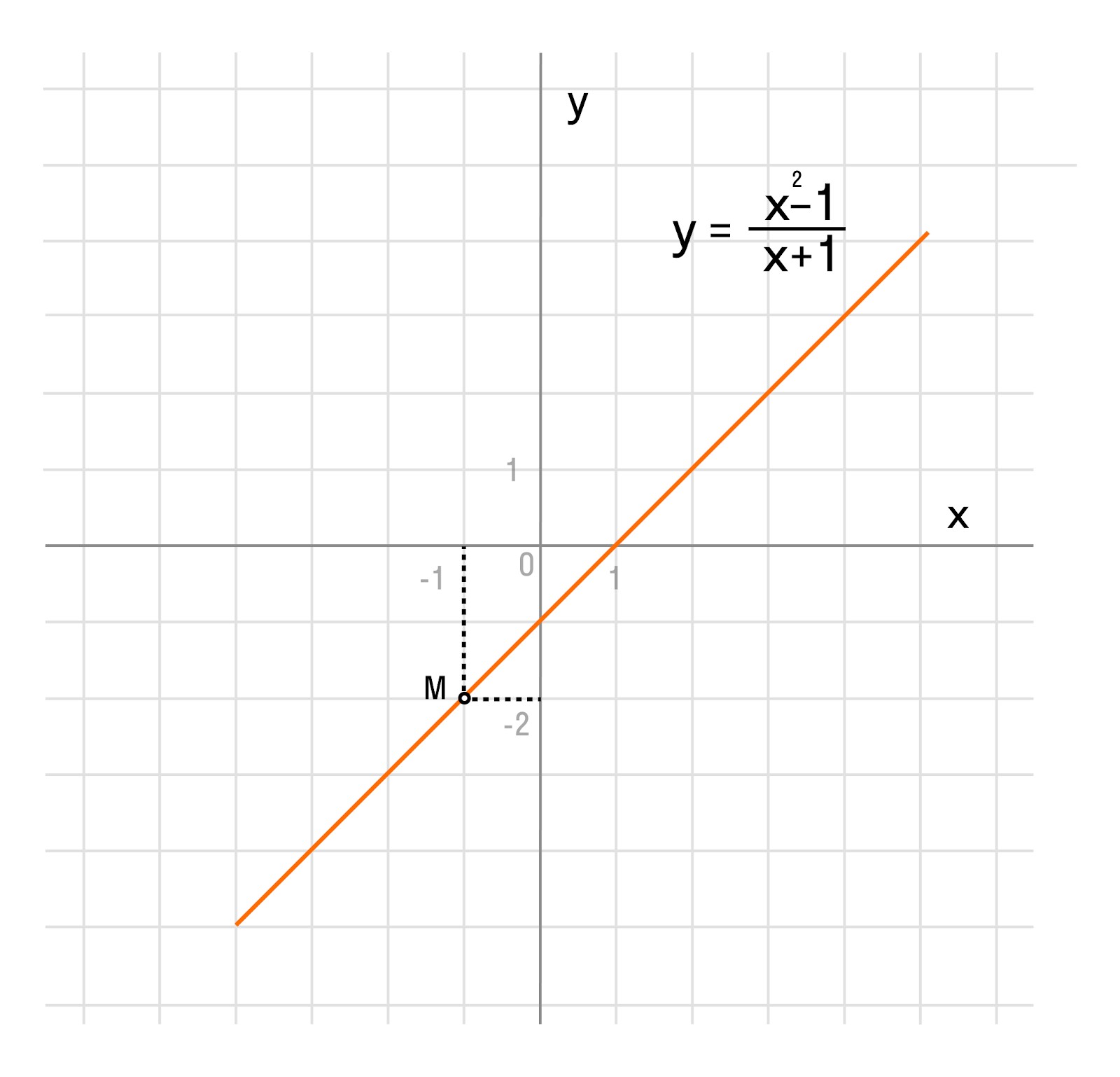
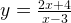
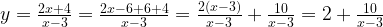
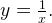
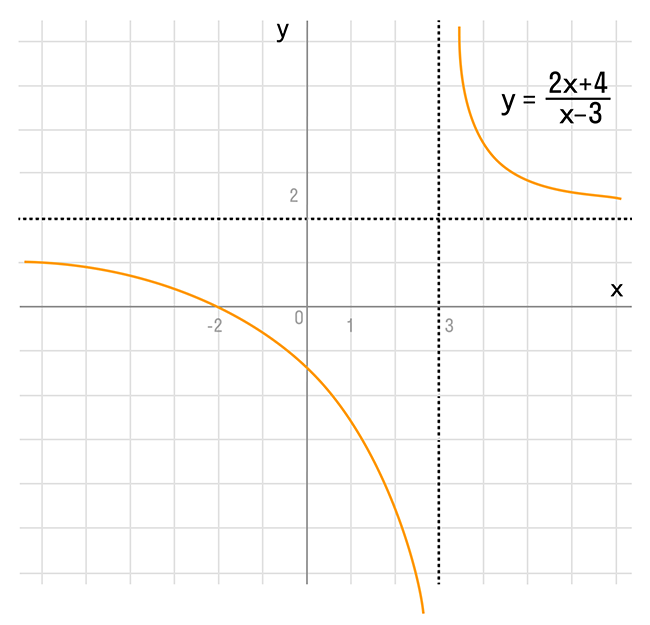
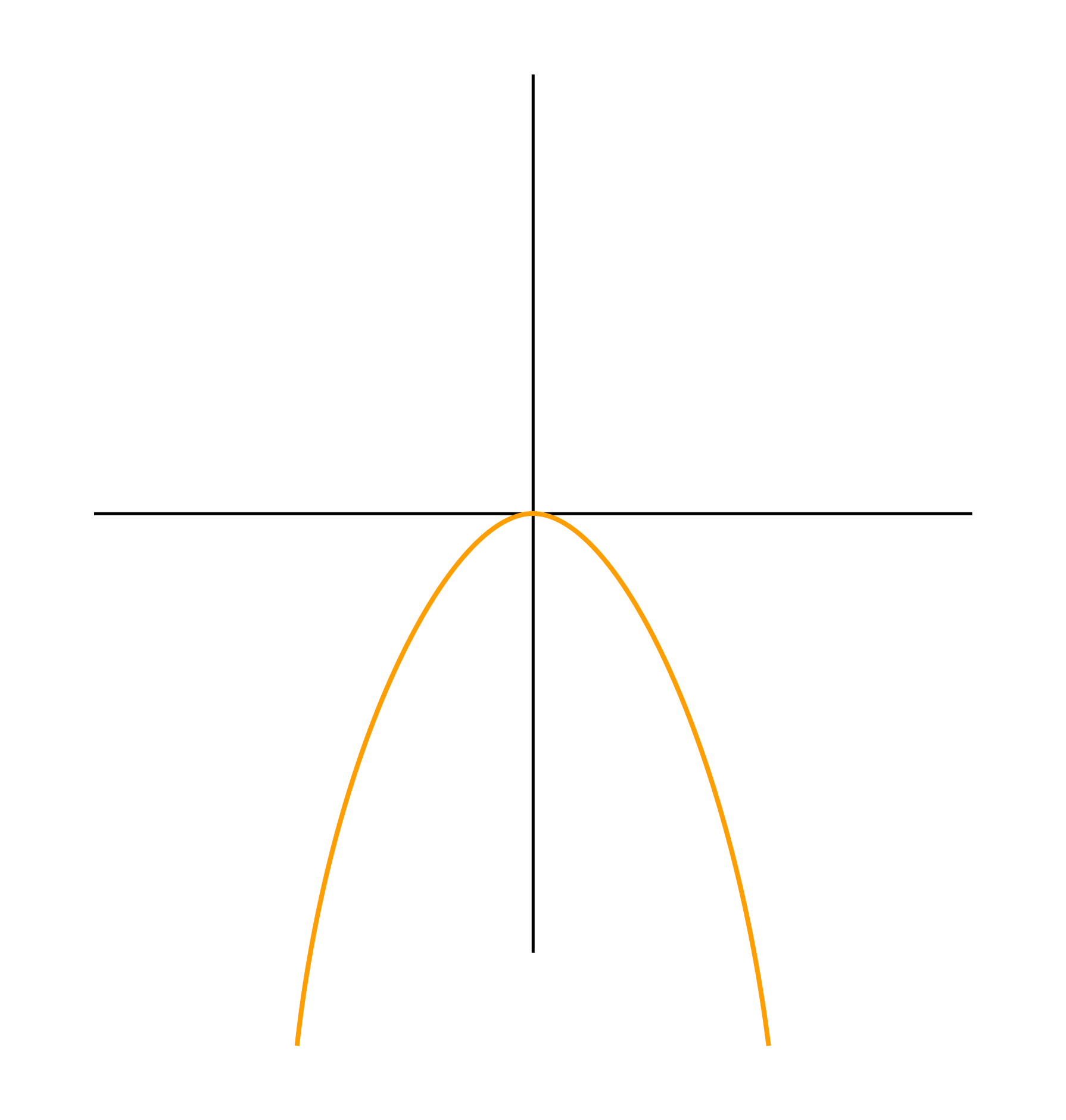
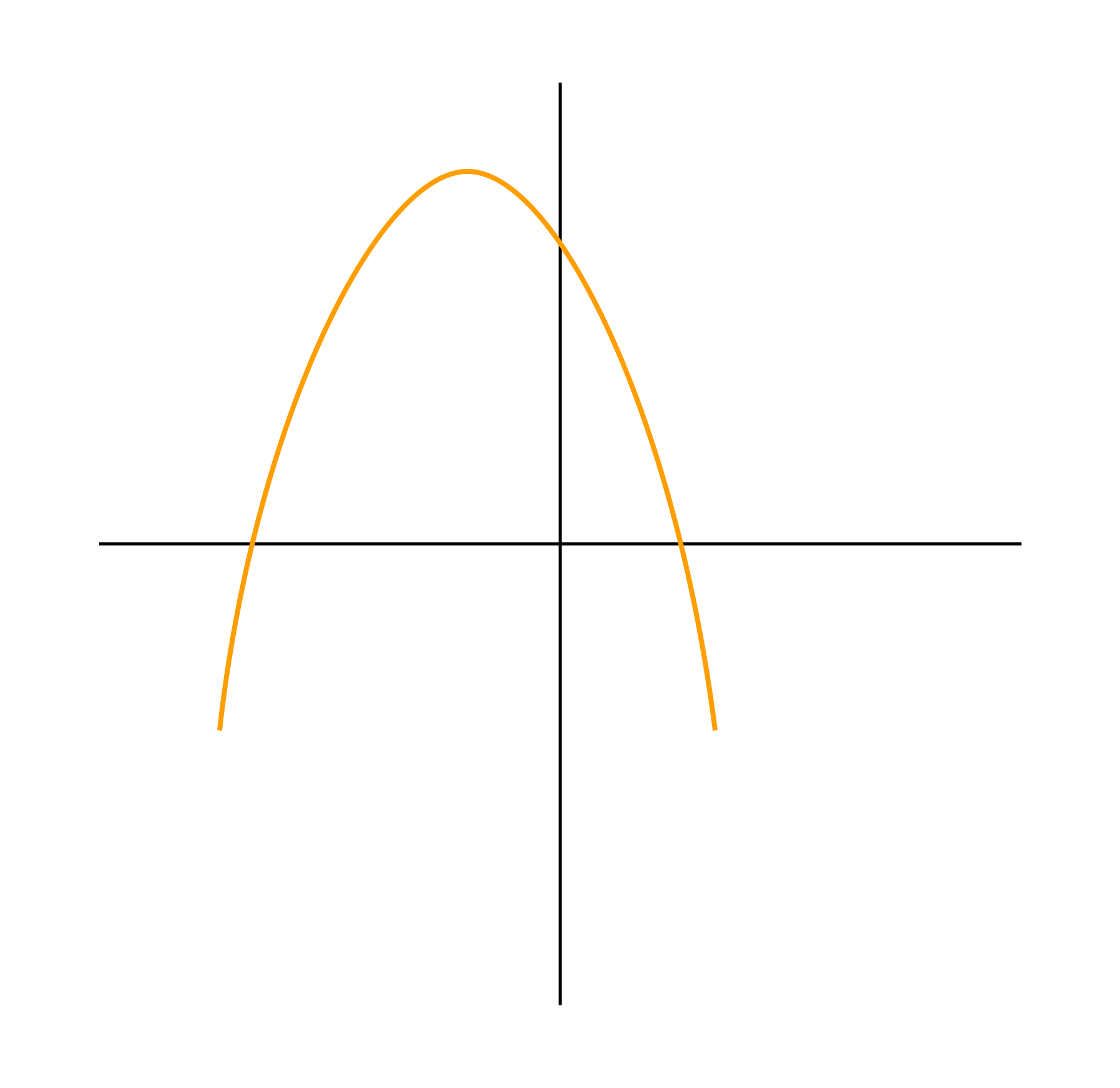
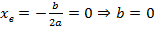
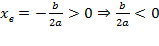 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.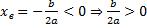 , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.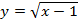
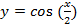
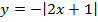
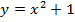
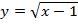
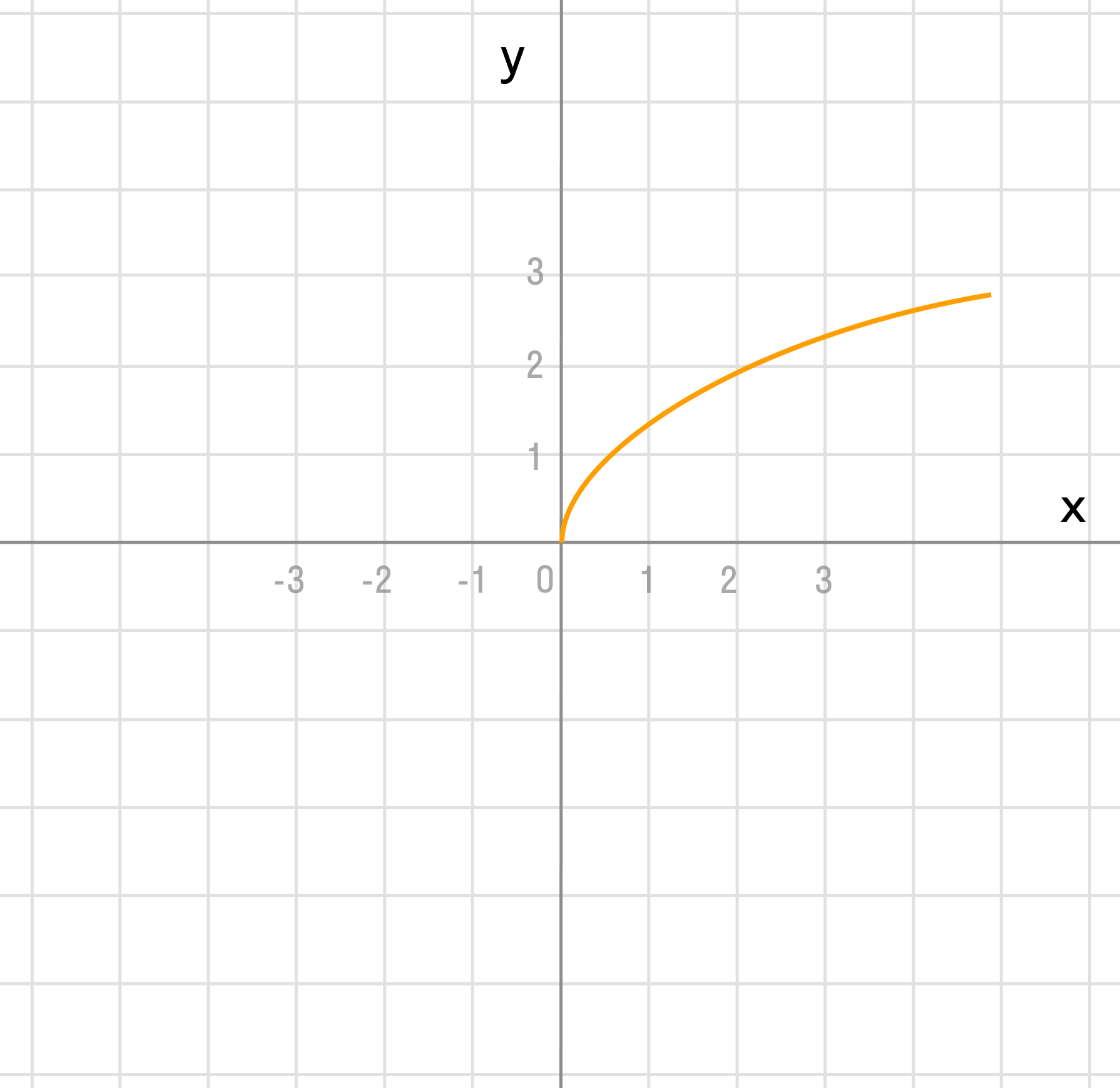
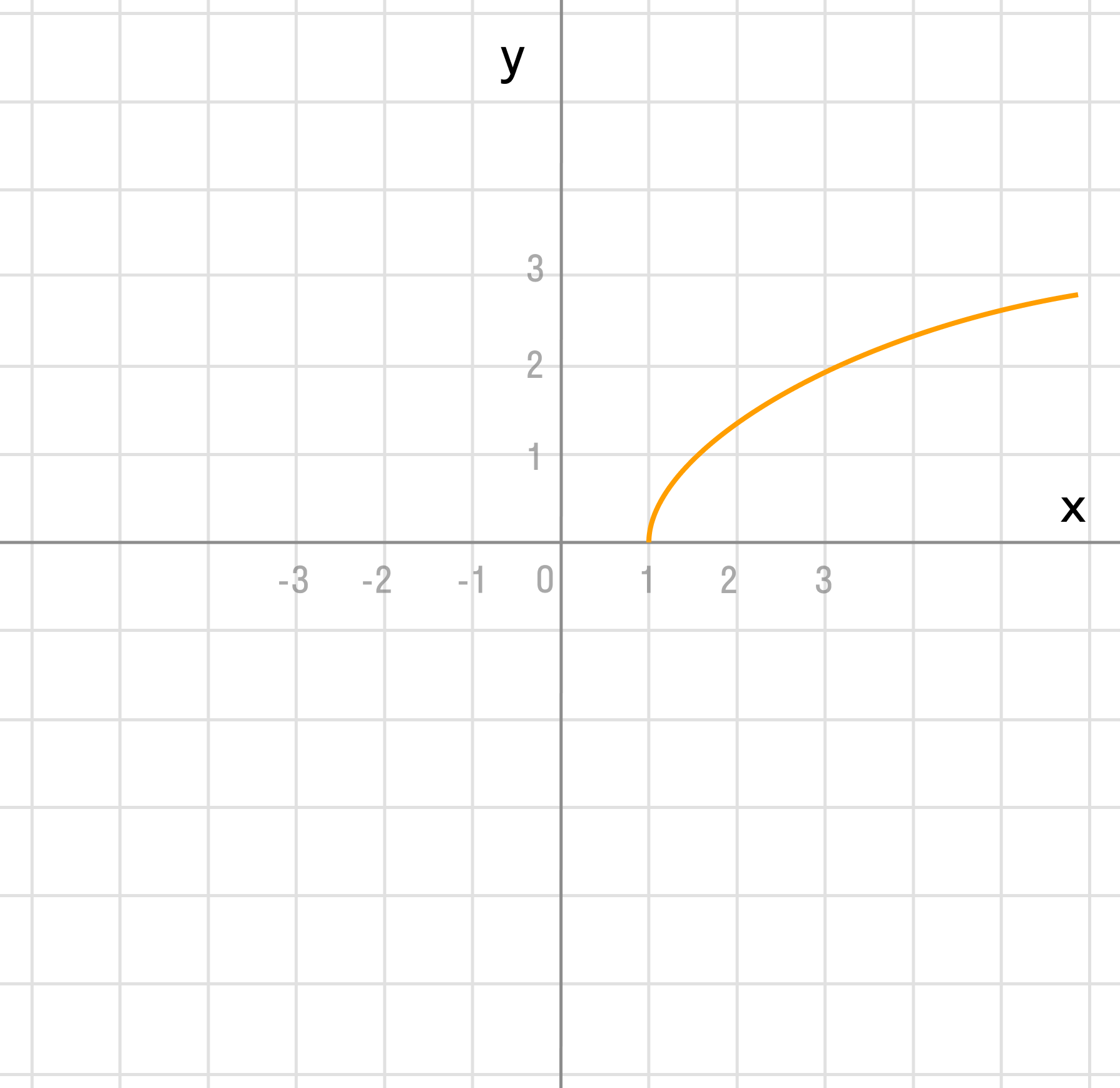
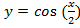
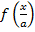
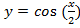
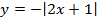
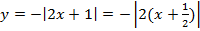
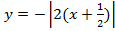





























 Сообщение было отмечено Квас как решение
Сообщение было отмечено Квас как решение