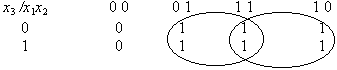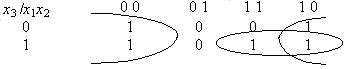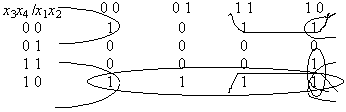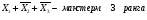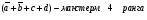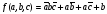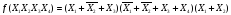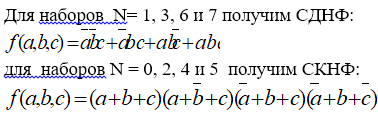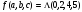Содержание
- 1 ДНФ
- 2 СДНФ
- 3 Алгоритм построения СДНФ по таблице истинности
- 4 Пример построения СДНФ для медианы
- 4.1 Построение СДНФ для медианы от трех аргументов
- 4.2 Построение СДНФ для медианы от пяти аргументов
- 5 Примеры СДНФ для некоторых функций
- 6 См. также
- 7 Источники информации
ДНФ
| Определение: |
| Простой конъюнкцией (англ. inclusive conjunction) или конъюнктом (англ. conjunct) называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза. |
Простая конъюнкция
- полная, если в неё каждая переменная (или её отрицание) входит ровно раз;
- монотонная, если она не содержит отрицаний переменных.
| Определение: |
| Дизъюнктивная нормальная форма, ДНФ (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов. |
Пример ДНФ:
.
СДНФ
| Определение: |
Совершенная дизъюнктивная нормальная форма, СДНФ (англ. perfect disjunctive normal form, PDNF) — ДНФ, удовлетворяющая условиям:
|
Пример СДНФ:
.
| Теорема: |
|
Для любой булевой функции , не равной тождественному нулю, существует СДНФ, ее задающая. |
| Доказательство: |
|
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона: . Данное соотношение легко проверить подстановкой возможных значений ( и ). Эта формула позволяет выносить за знак функции. Последовательно вынося , ,.., за знак , получаем следующую формулу: Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от переменных мы имеем конъюнктов. Каждый из них соответствует значению функции на одном из возможных наборов значений переменных. Если на некотором наборе , то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же , то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ. |
Алгоритм построения СДНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно .
- Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть , то в конъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Пример построения СДНФ для медианы
Построение СДНФ для медианы от трех аргументов
1. В таблице истинности отмечаем те наборы переменных, на которых значение функции равно .
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2. Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть , то в конъюнкцию включаем саму переменную, иначе ее отрицание.
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
3. Все полученные конъюнкции связываем операциями дизъюнкции:
.
Построение СДНФ для медианы от пяти аргументов
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 1 | 1 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
.
Примеры СДНФ для некоторых функций
Стрелка Пирса: .
Исключающее или: .
См. также
- Сокращенная и минимальная ДНФ
- КНФ
Источники информации
- СДНФ — Википедия
- Е.Л Рабкин, Ю.Б. Фарфоровская — Дискретная математика
Доказано,
что любую функцию (кроме тождественного
нуля) можно представить в виде СДНФ. На
практике часто бывает удобно получить
(вместо СДНФ) как можно более “короткую”
ДНФ. Словам “короткая ДНФ” можно придать
разный смысл, а именно:
ДНФ
называется минимальной,
если она содержит наименьшее число букв
(разумеется, среди всех ДНФ ей равносильных);
ДНФ называется кратчайшей,
если она содержит минимальное число
знаков дизъюнкции ; тупиковой,
если уничтожение одной или нескольких
букв в ней приводит к неравной ДНФ
и сокращенной ДНФ,
если ее упрощение проведено с помощью
правила Блейка.
На
практике наиболее важной представляется
нахождение минимальной ДНФ, но алгоритм
ее нахождения по существу является
вариантом перебора всех равносильных
ДНФ. Алгоритмически проще всего находить
сокращенную ДНФ (эти алгоритмы были
даны в разд. 3). Заметим, что если
функция п переменных задана своей таблицей
истинности, то правило
Блейка имеет простой геометрический
смысл. Именно, если все возможные наборы
переменных представить себе как
вершины п-мерного
куба со стороной равной 1 (всего вершин
будет 2п) в
декартовой системе координат, то надо
отметить те вершины, на которых значение
функции равно 1, и если какие-то из этих
единиц лежат на “прямой”, “плоскости”
или “гиперплоскости” в п-мерном
пространстве, то в сокращенную ДНФ будут
входить “уравнения” этих прямых или
гиперплоскостей по известному правилу:
если в это уравнение входило составной
частью х
= 0, то
в сокращенную ДНФ входит ,
если х =
1, то просто х. Разумеется,
геометрически все это изобразить можно
только при п =
2, 3.
Карты
Карно позволяют эти геометрические
идеи использовать при п =
3, 4, 5, для функций, заданных своей таблицей
истинности. При
больших п карты Карно практически не используются.
Рассмотрим отдельно (и более подробно)
случаи п =
3, 4.
Составляем
таблицу истинности для данной конкретной
функции п =
3 в виде таблицы, приведенной в примере
5.1. (Заметим, что для х1 и х2 естественный
порядок набора переменных здесь нарушен.
Это сделано для того, чтобы при переходе
от данного к следующему набору переменных
в этом наборе менялась только одна
цифра). Прямая содержит 2 вершины,
плоскость – 4, гиперплоскости –
8, 16 и т. д. вершин, поэтому объединять
можно 2 рядом стоящие единицы или 4, 8, 16
и т. д. Карты Карно соединяются “по
кругу”, т. е. наборы (10) и (00) считаются
рядом стоящими.
Пример
5.1. Пусть
задана функция:
Видно,
ее СДНФ содержит (по числу 1) 6 дизъюнктных
слагаемых, но ее сокращенная ДНФ содержит
(после объединения единиц) всего 2 буквы
f
= x1x2
Пример
5.2. Следующий
пример показывает, “как соединять
единицы по кругу”.
Здесь
сокращенная ДНФ содержит 2 слагаемых
(СДНФ содержала бы 5):
Пример 5.3.
Пример показывает использование карт
Карно при п = 4.
Здесь
сокращенная ДНФ содержит 4 слагаемых
(СДНФ содержит 8):
При п = 5 использование
карт Карно является несколько более
сложным и здесь не приводится.
6. Полиномы Жегалкина
Полиномом
(многочленом) Жегалкина от п переменных
называется функция
P
=xx2 +
…nxn +n +1xx2 +…+n
+C2nxn-1xn +
…+2n-1xx2..xn
Всего
здесь 2п слагаемых.
Напомним, что + сейчас означает сложение
по модулю 2, коэффициенты , n-1
являются константами (равными нулю или
единице).
Теорема. Любая
функция п переменных может быть
представлена полиномом Жегалкина и это
представление единственно.
Доказательство. Любая
функция f(x1, x2, …, xn) имеет
свою таблицу истинности. Запишем сначала
данную функцию в виде полинома Жегалкина
с неопределенными коэффициентами. Затем
по очереди подставляем всевозможные
наборы переменных и находим коэффициенты.
Легко видеть, что за каждую подстановку
находим только один коэффициент. Так
как число наборов равно числу коэффициентов
(и равно 2п),
отсюда следует утверждение теоремы.
Доказательство
этой теоремы показывает, как по таблице
истинности построить полином Жегалкина.
Имеется
2-й способ нахождения полинома Жегалкина
для функций, заданных в
виде ДНФ.
Этот способ основан на том, что х+1
= .
Если функция задана в виде ДНФ, то сначала
убираем дизъюнкцию, используя при этом
правило де Моргана, а все отрицания
заменяем прибавлением единицы. После
этого раскрываем скобки по обычным
правилам, при этом учитываем, что четное
число одинаковых слагаемых равно нулю
(так как х+
х =
0), а нечетное число одинаковых слагаемых
равно одному такому слагаемому.
Пример.
(
xy + 1)((x + 1)(y + 1) + 1)((y + 1)z + 1) + 1 = (xy + 1)(xy + x +
y)(yz + z + 1) + 1 = (x + y)(yz + z + 1) + 1= xyz + yz + xz +yz + x +
y + 1 = xyz + xz + x +y + 1.
Последнее
выражение и есть полином Жегалкина
данной функции.
Функция f
(x1,x2,…,xn) называется линейной,
если ее полином Жегалкина содержит
только первые степени слагаемых. Более
точно функция называется линейной, если
ее можно представить в виде
f(x1, x2, …, xn)
= a0 + a1 x1 + a2 x2 +…+ an xn.
Класс
линейных функций часто обозначают
через L. (Заметим,
что число линейных функций п переменных
равно 2п+1).
Замечание. Если
п2 то
линейная функция в таблице истинности может
содержать только четное число
единиц. Действительно,
если f(x1,x2,…, xn)
= x1+
x2+…+xn, то
легко видеть что такая функция в таблице
истинности содержит одинаковое число
нулей и единиц а именно 2п /2
единиц и нулей, т. е. число это четно
при п 2.
Столько же нулей и единиц имеет функция
. Добавление же фиктивной переменной
приводит к
увеличению числа единиц (и нулей) в два
раза. Разумеется, нелинейная функция
может иметь в таблице истинности как
четное, так и нечетное число единиц.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
26.11.2018914.43 Кб34дм.doc
- #
- #
- #
- #
- #
Логические функции, СДНФ СКНФ
1.4 Формы представления функций алгебры логики
Функции алгебры логики могут быть заданы различными способами:
— таблицей истинности — в аналитической форме- в числовой форме..
Если функция имеет значения на всех наборах, то она называется полностью определенной.
элементарная дизъюнкция — дизъюнктивный терм или макстерм — это дизъюнктивный терм или макстерм — это дизъюнкция произв числа попарно независимых перем Например,
элементарная конъюнкция — конъюнктивный терм или минтерм — конъюнкция произв числа попарно независимых перем. Напр, Х 1Х 2 Х3 — минтерм 3-его ранг
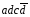
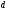
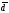
Для аналитической записи функций используют две формы:
1) Дизъюнктивную Нормальную Форму — ДНФ
2) Конъюнктивную Нормальную Форму – КНФ
ДНФ это дизъюнкция минтермов разл ранга
КНФ это конъюнкция макстермов различного ранга
Если все термы, входяшие в нормальную форму имеют одинаковый и максимальный ранг,= числу переменных функции — n, то такая форма называется совершенной. При этом, минтерм называют констинтуентой (составля) 1 (КЕ), а макстерм — конституентой 0 (КН).
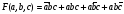
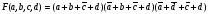
Т е СДНФ есть дизъюнкция конституент 1, а СКНФ — есть конъюнкция конституент 0
Составление совершенных форм по табл истинности
Совершенные формы составляют по табл истинности функции. СДНФ : для каждого набора переменных на которых функция=1, записывают минтерм ранга n , в которых с отрицанием берутся переменные = 0 на данном наборе. Все минтермы объединены дизъюнктивно.
СКНФ =для каждого набора переменных, на которых функция=0, записывают макстерм ранга n, в кот с отрицанием берутся переменные, имеющие значение=1 на данном наборе. Все макстермы объединены конъюнктивно
Для компактной записи функций исп числовую форму, в которой заданы только номера наборов. Числовая форма для СДНФ: 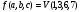
Числовая форма для СКНФ:
Алгоритм преобразованияя в ДНФ
1) Сначала избавляемся от операций импликации, эквивалентности и неравнозначности, выразив их через логические связки ¬, & и ∨ по законам:
2) Доводят знаки отрицания до независимых переменных, используя законы де Моргана:
3) Применяя з-н дистрибутивности
преобразуют формулу к дизъюнкции элементарных конъюнкций
4) 4) Постоянно избавляются от двойных отрицаний:
ДНФ A наз совершенной и обозн СДНФ, если каждая переменная формулы A входит с отрицанием или без отрицания в каждый конъюнкт точно 1 раз.
Алгебраическая форма представления булевых функций используется для минимизации (упрощения формулл) и для построения логических схем. Существукт 2 формы алгебраических функций – дизъюнктивная и конъюнктивн. Дизъюнктивная нормальная форма представляет сумму элементарных произведения аргументов, например
Если кажд слаг содер все арг или их отриц, то получ соверш дизъюнкт норм форму (СДФН), напр
Для перехода от табл истинн к СДНФ учит только те сост, для кот функц= 1. Для каждого такого сост запис элем произв всех ар. Если арг имеет зн «0», то запис его отриц. Для привед примера СДНФ имеет вид (17.4)
Совершенная конъюнктивная нормальная форма (СКНФ) представляет логическое произведение элементарных логических сумм, причем каждая сумма содержит все аргументы или их отрицания, например
ДНФ, но не СДНФ от 3 перем
-ДНФ от 2 перем
-представл импликации в виде ДНФ.
-СДНФ для импликации
-СДНФ для оп эквивалентности
-СДНФ для оп неравнозначности
Прим.1 Привести к ДНФ формулу
Реш.
2. Привести ту же формулу к СДНФ. Начав преобразования с ДНФ
|
Нахождение СДНФ по табл истинности функции |
Нахождение СКНФ по табл истинности функции |
|
1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 1. 2)Выписать для каждой отмеченной строки конъюнкцию всех переменных так: если значение некоторой переменной в данной строке — 1, то в конъюнкцию включать саму эту переменную, если равно 1, то ее отрицание. 3)Все полученные конъюнкции связать в дизъюнкцию. |
1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 0. 2)Выписать для каждой отмеченной строки дизъюнкцию всех переменных так: если значение некоторой переменной в данной строке= 1, то в дизъюнкцию включать саму эту переменную, если равно 0, то ее отрицание. 3)Все полученные дизъюнкции связать в конъюнкцию. |
Прим1
Прим 2
|
построение СДНФ: |
построение СКНФ: |
Для перехода от таблицы истинности к СКНФ учитывают только те состояния, для которых функция= «0». Для каждого такого состояния записывается элементарная сумма аргументов. Если аргуент имеет значение «1», то пишут его отрицание. Для примера СКНФ имеет вид
Примеры
1)Привести к КНФ и СКНФ.
Реш. упростим выражение, используя законы де Моргана и правило x y x y → = ∨
Теперь приводим к КНФ
Приведем к СКНФ:
2) С помощью эквивалентных преобразований построить д.н.ф. функции f (x):
Решение. Преобразуем функцию:
3) Используя СКНФ, найти наиболее простую формулу алгебры высказываний от 4 переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:
Решение. Запишем СКНФ функции по данным задачи
Получили
ЛИТЕРАТУРА и ССЫЛКИ
1)Курилова М.Н. Информатика-логика, СПБ Лес-техн ун-т им.Кирова
https://studfiles.net/preview/2069515/page:5/
2) http://ptca.narod.ru/lec/lec4_3.html
3) https://www.matburo.ru/ex_dm.php?p1=bfpg
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
ДНФ
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
Простая конъюнкция
- полная, если в неё каждая переменная { или её отрицание } входит ровно 1 раз;
- монотонная, если она не содержит отрицаний переменных.
ДНФ { Дизъюнктивная Нормальная Форма } — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
Пример ДНФ: $f(x,y,z) = (x land y) lor (y land neg { z } )$
СДНФ
СДНФ { Совершенная Дизъюнктивная Нормальная Форма } — это такая ДНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых конъюнкций
- каждая простая конъюнкция полная
Пример СДНФ: $f(x,y,z) = (x land neg { y } land z) lor (x land y land neg { z } )$
Теорема: Для любой булевой функции $f(vec { x } )$, не равной тождественному нулю (), существует СДНФ, ее задающая.
Доказательство:
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
$f(vec { x } ) = neg x_i wedge f(x_1, dots ,x_ { i-1 } ,0,x_ { i+1 } , dots ,x_n) vee x_i wedge f(x_1, dots ,x_ { i-1 } ,1,x_ { i+1 } , dots ,x_n)$
Данное соотношение легко проверить подстановкой всевозможных значений $x_i$ { $0$ и $1$ } . Эта формула позволяет выносить $x_i$ за знак функции. Последовательно вынося $x_1$, $x_2$,.., $x_n$ за знак $f(vec { x } )$, получаем следующую формулу :
$ f(vec { x } ) = neg x_1 wedge neg x_2 wedge …wedge neg x_ { n-1 } wedge neg x_n wedge f(0,0,…,0,0)~vee~$
$neg x_1 wedge neg x_2 wedge … wedge neg x_ { n-1 } wedge x_n wedge f(0,0,…,0,1) ~vee~ $ $dots $ $~vee~ x_1 wedge x_2 wedge … wedge x_ { n-1 } wedge neg x_n wedge f(1,1,…,1,0) ~vee~ $ $x_1 wedge x_2 wedge … wedge x_ { n-1 } wedge x_n wedge f(1,1,…,1) $
Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от $n$ переменных мы имеем { { { $2^ { n } $ } } } конъюнктов. Каждый из них соответствует значению функции на одном из { { { $2^ { n } $ } } } возможных наборов значений $n$ переменных. Если на некотором наборе $f(vec { x } )=0$, то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же $ f(vec { x } )=1$, то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.
Алгоритм построения СДНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
- Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Пример построения СДНФ для медианы
-
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
x y z $langle x,y,z rangle$ 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 -
Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
x y z $ langle x,y,z rangle $ 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 $(neg { x } land y land z)$ 1 0 0 0 1 0 1 1 $(x land neg { y } land z)$ 1 1 0 1 $(x land y land neg { z } )$ 1 1 1 1 $(x land y land z)$ -
Все полученные конъюнкции связываем операциями дизъюнкции. $ langle x,y,z rangle = (x land y land z) lor (neg { x } land y land z) lor (x land neg { y } land z) lor (x land y land neg { z } )$
Примеры СДНФ для некоторых функций
Стрелка Пирса: $x downarrow y = (neg { x } land neg { y } )$
Исключающее или: $x oplus y oplus z = (overline { x } land overline { y } land z) lor (overline { x } land y land overline { z } ) lor (x land overline { y } land overline { z } ) lor (x land y land z)$
Совершенной дизъюнктивной нормальной формой формулы $A(x_1,x_2,…,x_n)$ называется ДНФ, обладающая следующими свойствами:
а } в ней нет одинаковых дизъюнктивных элементов;
б } ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в } ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
г } в каждой элементарной конъюнкции содержится либо $X_i$, либо $overline { X } _i$, где $i = 1, n$.
Условие а } – г } являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
1) если какая-нибудь элементарная конъюнкция не содержит высказывание $X_i$, то заменим выражением $Bwedge (X_ivee overline { X } _i) equiv (Bwedge X_i)vee (Bwedge overline { X } _i)$;
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Формула называется дизъюнктивной нормальной формой { ДНФ } , если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде: $A_1vee A_2vee …vee A_n$ , где каждое $A_n$ — элементарная конъюнкция.
Формула $A$ от $k$ переменных называется совершенной дизъюнктивной нормальной формой { СДНФ } , если:
-
$A$ является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция $k$ переменных $x_1,x_2,…,x_k$, причем на $i$-м месте этой конъюнкции стоит либо переменная $x_i$ либо ее отрицание;
-
Все элементарные конъюнкции в такой ДНФ попарно различны.
Например: $A = x_1 wedge$ НЕ $x_2 vee x_1 wedge x_2$
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций { дизъюнктивных членов } в ней.
Она является примером однозначного представления булевой функции в виде формульной { алгебраической } записи.
Теорема о СДНФ: Пусть $f(x_1 x_2, …, x_n)$ – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию $f$.
Алгоритм построения СДНФ по таблице истинности:
- В таблице истинности отмечаем наборы переменных, на которых значение функции $f = 1$.
- Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае – ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Диана Загировна Филиппенкова
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
-
конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $left(Avee overline{B}vee Cright)wedge left(Avee Cright)$;
-
дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $left(Awedge overline{B}wedge Cright)vee left(Bwedge Cright)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных дизъюнкций;
-
ни одна из дизъюнкций не содержит одинаковых переменных;
-
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных конъюнкций;
-
ни одна из конъюнкций не содержит одинаковых переменных;
-
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Пример 1
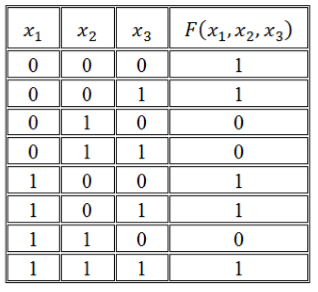
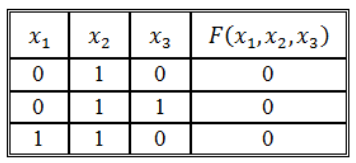
Записать логическую функцию по ее таблице истинности:
Рисунок 1.
Решение:
Воспользуемся правилом построения СДНФ:
Рисунок 2.
Получим СДНФ:
[Fleft(x_1, x_2, x_3right)=left(overline{x_1}wedge overline{x_2}wedge overline{x_3}right)vee left(overline{x_1}wedge overline{x_2}wedge x_3right)vee left(x_1wedge overline{x_2}wedge overline{x_3}right)vee left(x_1wedge overline{x_2}wedge x_3right)vee left(x_1wedge x_2wedge x_3right)]
Воспользуемся правилом построения СКНФ:
Рисунок 3.
Получим СКНФ:
[Fleft(x_1, x_2, x_3right)=left(x_1vee overline{x_2}vee x_3right)wedge left(x_1vee overline{x_2}vee overline{x_3}right)wedge left(overline{x_1}vee overline{x_2}vee x_3right)]
«Построение СКНФ и СДНФ по таблице истинности» 👇
Пример 2
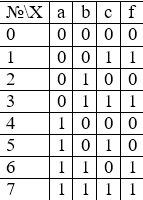
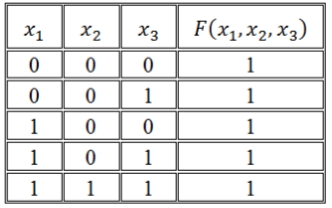
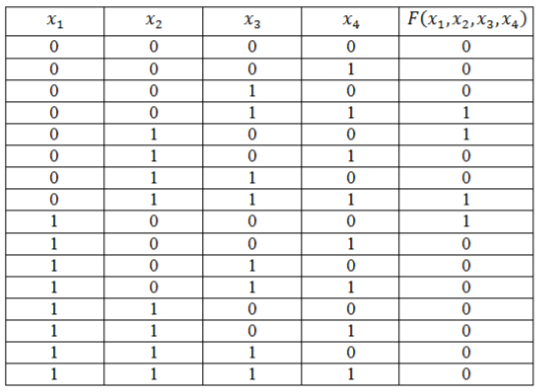
Функция задана таблицей истинности:
Рисунок 4.
Представить эту функцию в виде СДНФ и СКНФ.
Решение:
-
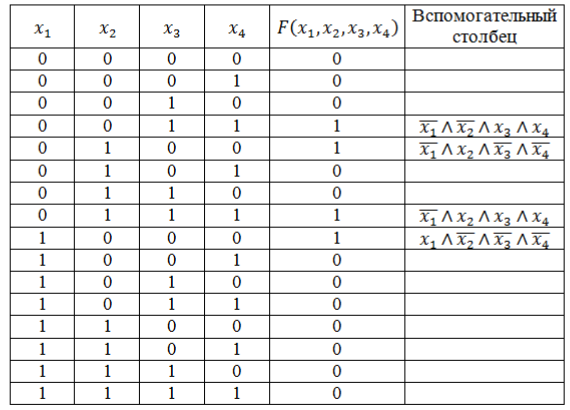
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.
Рисунок 5.
Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(overline{x}wedge overline{y}wedge zwedge fright)vee left(overline{x_1}wedge x_2wedge overline{x_3}wedge overline{x_4}right)vee left(overline{x_1}wedge x_2wedge x_3wedge x_4right)vee left(x_1wedge overline{x_2}wedge overline{x_3}wedge overline{x_4}right).]
-
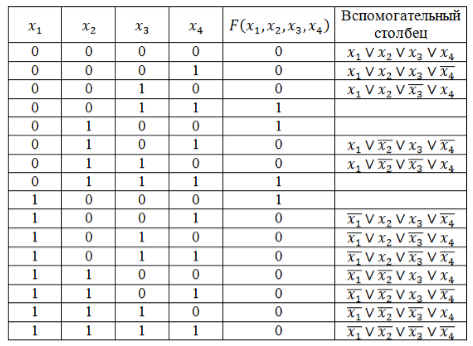
Запишем логическую функцию в СКНФ.
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.
Рисунок 6.
Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(x_1vee x_2vee x_3vee x_4right)wedge left(x_1vee x_2vee x_3vee overline{x_4}right)wedge left(x_1vee x_2vee overline{x_3}vee x_4right)wedge left(x_1vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(x_1vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee overline{x_4}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме