Малюкова Н. И., МОУ «СШИ №2» г. Магнитогорска «Применение метода построения дерева решений при подготовке к ЕГЭ по информатике». 2017
Применение метода построения дерева решений при подготовке к ЕГЭ по информатике
При подготовке к итоговой аттестации по информатике каждый участник – учитель или ученик – выбирает для себя, по возможности, такой способ решения, который можно применить для целого ряда задач. Наиболее приемлемым в этой ситуации является метод построения дерева решений.
В курсе математики метод решения задач с помощью построения дерева решений рассматривается в 5, 6, 7, 8 классах в содержательной линии Г. В. Дорофеева. В 5 классе при изучении главы «Натуральные числа» в теме «Перебор возможных вариантов» [5] автор рассматривает метод построения дерева как удобный способ решения задач с перебором возможных вариантов решений; понятие дерева вводится через понятие специальной схемы. В 6 классе в главе «Комбинаторика. Случайные события» в теме «Логика перебора» [6] в решении задач также используется метод построения дерева решений, рассматривается понятие «обратный ход» в решении логических задач. Комбинаторные задачи, для решения которых можно использовать рассматриваемый метод (построения дерева решений), предлагаются в 7 классе в главе «Свойства степени с натуральным показателем» и в 8 кассе в главе «Вероятность и статистика» [7, 8].
Если мы обратимся к школьному курсу информатики и рассмотрим содержательную линию Л. Л. Босовой (ФГОС), то заметим, что данный метод решения задач также применяется в процессе обучения. В 6 классе в разделе «Информационное моделирование» [1] вводится понятие дерева как графа иерархической структуры, рассматриваются задачи, решение которых оформляется с помощью построения графов и деревьев. В 7, 8, 9 классах [2, 3, 4] метод построения дерева рассматривается подробнее, используется в решении задач различной тематики: двоичное кодирование, файлы и файловая структура, элементы алгебры логики, графические информационные модели, коммуникационные технологии и др.
Метод построения дерева решений подробно рассматривается в школьном курсе и информатики, и математики, часто применяется при решении задач. Таким образом, можно сделать вывод о том, что к моменту окончания основной школы ученики должны достаточно хорошо владеть этим методом и применять при решении задач на ЕГЭ.
Дорофеев Г. В. и Босова Л. Л. по-разному вводят понятие дерева. Мы за основу примем определения, предложенные автором Л. Л. Босовой [1].
Граф – наглядное средство представления состава и структуры системы.
Иерархия — это расположение частей или элементов целого в порядке от высшего к низшему.
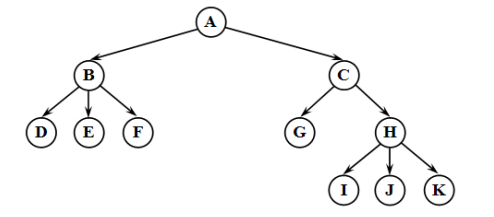
Дерево – граф иерархической структуры. Между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.
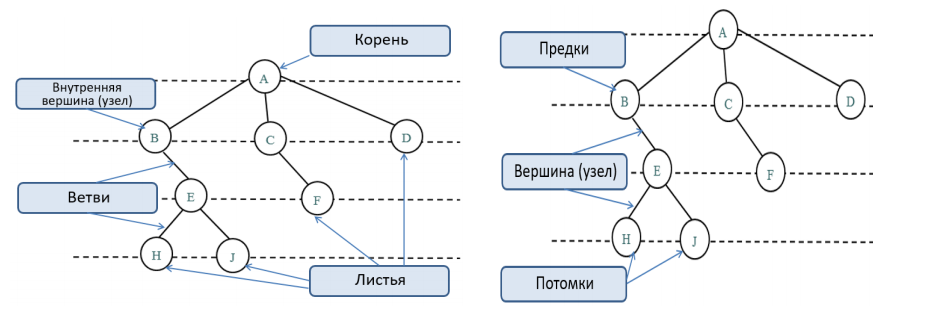
Корень – главная вершина дерева.
Предок – объект верхнего уровня.
Потомок – объект нижнего уровня.
Листья – вершины, не имеющие потомков.
Ниже представлено подробное решение задач, входящих в КИМ ЕГЭ по информатике под номерами 1, 3, 5, 6, 11, 15, 22, 26. Распределим их по тематическим блокам: I блок «Кодирование и декодирование информации»; II блок «Информационное моделирование»; III блок «Алгоритмизация и программирование»; IV блок «Игровые задачи».
I блок «Кодирование и декодирование информации»
При решении таких задач нужно знать, что такое равномерное (все символы кодируются кодами равной длины) и неравномерное (разные символы могут кодироваться кодами разной длины) кодирование, условие Фано (никакое кодовое слово не является началом другого кодового слова) и обратное условие Фано (никакое кодовое слово не является окончанием другого кодового слова).
№1. Демонстрационный вариант ЕГЭ-2015 [11]
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны.
Каким из указанных способов это можно сделать?
1) для буквы В – 101 2) это невозможно
3) для буквы В – 010 4) для буквы Б – 10
Решение
Для решения задачи построим дерево. Учитываем, что коды неравномерные, кодирование однозначное, значит должно выполняться условие Фано. В графическом представлении дерева – это значит, что все кодовые слова должны располагаться в листьях дерева (т.е. при движении по ветке дерева к одной букве не встречаем никакую другую).
В задаче требуется сократить длину кода для одной буквы, это значит, нужно «сократить ветку дерева» — поднять лист на уровень выше. Посмотрим на дерево и найдем такой вариант, при котором не нарушится условие Фано. Искомым вариантом является буква В, ее код можно сократить до 101, подняв «лист» на уровень выше. При этом сохраняется условие, что при движении по ветке к одной букве мы не встретим никакую другую. Например, сократив длину кода буквы Г, мы нарушим условие однозначного декодирования:
Так же, мы не можем сократить коды букв Д и Б.
Ответ: 1) для буквы В – 101
II блок «Информационное моделирование»
Рассмотрим задание по теме «Поиск и сортировка информации в базах данных». Для предотвращения ошибок при решении задач такого типа можно фиксировать пошагово решение в виде дерева.
№ 3. Досрочный вариант ЕГЭ-2015 [11]
Ниже представлены две таблицы из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1.
Определите на основании приведённых данных фамилию и инициалы дяди Ващенко К.Г.
Пояснение: дядей считается родной брат отца или матери.
1) Котий А.В. 2) Котий В.А. 3) Щука А.С. 4) Ващенко И.К.
Решение
Верхним уровнем дерева будет являться запись Ващенко К. Г. В таблице 1находим сведения, необходимые для решения задачи – ID равен 48, указываем на схеме.
Установим по таблицам данные о ее родителях. В таблице 2 для ID_ребенка (48) определяем ID-родителя: 36 и 38. Дополняем дерево этими данными, получаем
Т.к. дядя – это родной брат матери или отца, нужно определить третий уровень, указав бабушек и дедушек, и найти их детей, не отмеченных в схеме.
Используя данные, представленные в таблице, определяем: для 36 родители: 26, 46
Для 38 – родитель 16
У 16, кроме 38, детей нет. У родителей 26 и 46, кроме 36, есть ребенок – 27 (Котий В.А. – пол М) – он и будет являться братом отца для Ващенко К.Г, т.е. ее дядей
Ответ – 2) Котий В.А.
Задачи с маршрутами являются классическим примером задач, для решения которых удобно построить дерево, что, свою очередь, поможет «не потерять» какой-либо из возможных вариантов
№5. Досрочный вариант ЕГЭ-2015 [11]
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
Определите длину кратчайшего пути между пунктами A и F при условии, что передвигаться можно только по указанным в таблице дорогам.
Решение
Для перебора вариантов построим дерево решений, указав направление и протяженность дорог.
Начнем движение из пункта А. Из таблицы видим, что из А можно попасть в пункты В, С, D и F – отмечаем пункты, указывая протяженность дорог – цифры над стрелками:
Получили первый маршрут A-F, протяженность которого равна 16. Далее ищем маршруты. Из пункта B можно попасть в A и D, но возвращаться нецелесообразно, поэтому рассматриваем только пункт D
Из D существуют дороги в C, E и F (пункты A, B не указываем, т.к. это возврат на предыдущие пункты)
Получили еще одну дорогу до F. Чтобы узнать ее длину, нужно сложить протяженность всех промежуточных дорог: AB + BD + DF, 3+5+10 = 15.
Находим маршруты далее. Из С больше дорог нет. Рассмотрим пункт Е. Существует обратный маршрут в пункт D (его не указываем), остается указать только F. И протяженность полученного маршрута будет равна 17:
Остается одна нерассмотренная ветка A-D. Видим, что пункт D уже рассматривали, поэтому фрагмент можно перенести и посчитать протяженность полученных маршрутов
Получим:
Сравнивая полученные результаты, имеем кратчайший путь из А в F равный 13.
Ответ: 13
Рассмотрим еще одну задачу на маршруты
№ 15. Досрочный вариант ЕГЭ-2015 [11]
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М?
Решение
Построим дерево, перебрав все возможные пути из А в М: через Б, В, Г, Д (всего 4 ветки из А). При построении учитываем уже найденные пути и для повторяющихся пунктов указываем только количество возможных дорог (в скобках)
Например, пункт В расписан в первой ветке – всего 2 пути, так же пункт В встречается во второй ветке, и в маршруте из А через Г – в третьей ветке. Так как через пункт В имеем 2 пути, через Ж – 2 пути, то через Г будет в сумме – 4 пути.
Складываем все найденные пути 2+2+2+2+2+2+4+2+2=22.
Ответ: 22
III блок «Алгоритмизация и программирование»
Рассмотрим задачу на построение алгоритма для исполнителя
№6. Демонстрационный вариант ЕГЭ-2015 [11]
Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
-
Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
-
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.
Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.
Решение
Разобьем число 1311 на два числа, которые могут являться результатом суммирования цифр исходного четырехзначного числа: 13 и 11 — единственный возможный вариант, т.к. число 131 не может являться суммой двух цифр. Представим решение в виде дерева, где будут прописаны все возможные варианты слагаемых и показаны все комбинации, за исключением повторяющихся, для четырехзначного числа:
Из чисел, суммы цифр которых равны 13 и 11 выберем наименьшие – такими являются 29 и 49. Составим из них наименьшее число, в результате обработки которого автомат выдает результат 1311 – это будет число 2949.
Ответ: 2949
Иногда метод построения дерева решений удобно применять при решении задач на рекурсивную функцию.
№11. Демонстрационный вариант ЕГЭ-2015 [11]
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(1).
Решение
Решение задачи сводится к тому, чтобы найти сумму всех значений параметров при заданном вызове F(1). Оформим порядок рекурсивных вызовов в виде дерева
Сложим все полученные значения параметров, получим 49.
Ответ: 49
Рассмотрим задачу на построение алгоритма для исполнителя повышенного уровня сложности.
№22. Досрочный вариант ЕГЭ-2015 [11]
Исполнитель Апрель15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Апрель15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 21 и при этом траектория вычислений содержит число 10?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Решение
Для перебора возможных вариантов построим дерево решений. Корнем дерева будет являться 1.
Т.к., применив к 1 команды 1.Прибавить 1 или 2.Умножить на 2, мы получим одинаковые результаты (1+1=2 и 1*2=2), то достаточно рассмотреть одну ветку, а затем полученный результат удвоить. Варианты, не удовлетворяющие условию (траектория вычислений содержит число 10), отбрасываем; для повторяющихся чисел в последовательности вычислений записываем количество программ. Суммируем все найденные программы:
Таким образом, получили 14 программ, удваиваем результат, получаем всего 28 программ.
Ответ: 28
IV блок «Математические задачи-игры»
Рассмотрим задание высокого уровня сложности. Это задача является математической игрой, где у игрока есть выигрышная стратегия.
№26. Досрочный вариант ЕГЭ-2015 [11]
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, то есть первым получивший такую позицию, что в кучах всего будет 55 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 49.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
Задание 1
а) Укажите все такие значения числа S, при которых Петя может выиграть за один ход, и соответствующие выигрывающие ходы. Если при некотором значении S Петя может выиграть несколькими способами, достаточно указать один выигрывающий ход.
б) Сколько существует значений S, при которых Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом?
Задание 2
Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанного значения S опишите выигрышную стратегию Пети.
Задание 3
Укажите значение S, при котором одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рисунке на рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.
Решение
1а) Построим дерево возможных вариантов, указав количество камней в первой и второй кучах после первого хода первого игрока Пети
Т.к. победителем считается тот, после хода которого суммарное количество камней в кучах окажется не менее 55, то нужно найти значение S, при котором первый игрок Петя выиграет своим первым ходом, для этого составим неравенства и решим их.
6+S55; S 49
10+S 55; S 45
5+(S+1) 55; S 49
5+2*S 55; S 25
Видим, что при S 25, 26, 27, 28, …, 49 Петя выигрывает первым ходом – он удваивает количество камней во второй куче. Например, при начальном положении 5, 25 Петя удвоит количество камней во второй куче 25*2=50, т.о. суммарное количество камней 5+50 становится не менее 55. При значениях S 25 невозможно одним ходом (добавить один камень или удвоить количество камней) получить суммарное количество камней в двух кучах не менее 55.
1б) Выясним, есть ли возможность у второго игрока Вани выиграть своим первым ходом при любом ходе первого игрока Пети. Чтобы Петя не выиграл первым ходом, нужно, чтоб после его хода суммарное количество камней составляло менее 55. Решим неравенства:
6+S55; S 49
10+S 55; S 45
5+(S+1) 55; S 49
5+2*S 55; S 25
При S 25 у Вани есть ход после Пети. Продолжим строить дерево возможных вариантов и проверим, является ли первый ход Вани выигрышным. Рассмотрим первый вариант первого хода Пети:
Предположим, что первый ход второго игрока Вани выигрышный, тогда суммарное количество камней в кучах после его хода должно быть не менее 55. Составим и решим неравенства:
7+S55; S 48
12+S 55; S 43
6+(S+1) 55; S 48
6+2*S 55; S 25
При S 25 после хода Пети (6, S) Ваня может выиграть своим первым ходом, удвоив количество камней во второй куче, но при S 25 выигрышная стратегия есть у Пети, поэтому в этом случае Ваня не выиграет. Другие варианты можно уже не рассматривать, т.к. в условии сказано о возможности выигрыша Вани при любом ходе Пети. Значит, значений S, при которых Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первых ходом, не существует.
2) Т.к. Петя не должен выиграть своим первым ходом, то S 25. Построим дерево для начального набора камней (5, 24) и опишем выигрышную стратегию Пети.
Из этого дерева получаем подтверждение, что на первом ходу Петя выиграть не может. Видим, первый вариант хода Пети (6,24) приведет к его выигрышу, значит, эта позиция является проигрышной для второго игрока Вани, т.к. после любого хода Вани Петя выиграет, удвоив количество камней во второй куче. Можно сделать вывод, что при S= 24 первый игрок Петя не может выиграть за один ход, но выигрывает своим вторым ходом независимо от того, как будет ходить Ваня. Выигрышная стратегия первого игрока Петя такова: первым ходом он добавляет 1 камень в первую кучу, затем после любого хода второго игрока удваивает количество камней во второй куче, тем самым – получает количество камней в двух кучах не менее 55.
3) Т.к. первый игрок не должен выиграть первым ходом, значит S 25. При S= 24 есть выигрышная стратегия у первого игрока, поэтому рассмотрим вариант S= 23, построим дерево и опишем стратегию выигравшего игрока.
Из этого дерева видим, что при S=23 если первым ходом первый игрок удваивает количество камней в любой куче (из начальной позиции (5,23), удвоив (5*2, 23), получает (10, 23) или, удвоив (5, 23*2), получает (5, 46), то второй игрок выигрывает своим первым ходом, удвоив количество камней во второй куче ((10, 23*2) получит (10, 46) или (5, 46*2) получит (5, 92)). В первых двух вариантах если первый игрок увеличивает на 1 количество камней в куче своим первым ходом (из начальной позиции (5+1,23) получает (6, 23) или (5, 23+1) получает (5, 24)), то второй игрок переводит игру в проигрышную для соперника позицию (6, 24), добавив 1 камень в первую кучу для позиции (5, 24) или добавив 1 камень во вторую кучу при позиции (6, 23), и при любом ответном ходе первого игрока Пети выигрывает своим вторым ходом, удвоив количество камней во второй куче (из позиции (7,24) получит (7,48); из позиции (6,25) получит (6,50); из позиции (12,24) получит (12,48); из позиции (6,48) получит (6,56)).
В этом дереве указаны все возможные варианты ходов первого игрока Пети, а для второго игрока Вани указаны только ходы, соответствующие его выигрышной стратегии.
Метод построения дерева решений вводится в школьный курс информатики и математики в 5-6 классах, Но, к сожалению, в старшей школе ученики забывают о нем. Тем не менее, применив его в решении, можно свести трудную задачу к более простой. Поэтому можно считать, что метод построения дерева решений будет актуален при сдаче ЕГЭ по информатике
Задания для самостоятельного решения
Кодирование и декодирование информации
1.1. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0, для буквы Б – кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
1) 7 2) 8 3) 9 4) 10
1.2. По каналу связи передаются сообщения, содержащие только 4 буквы П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.
Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
1.3. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
1.4. Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=1, Б=000, В=001. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
1) 00 2) 01 3) 11 4) 010
1.5. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Для букв А, Б, В и Г использовали такие кодовые слова: А — 001, Б — 010, В — 000, Г — 011.
Укажите, каким кодовым словом из перечисленных ниже может быть закодирована буква Д.
Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.
1) 00 2) 01 3) 0000 4) 101
1.6. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 11; Б – 110; В – 101; Г – 000; Д – 010. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?
1) это невозможно 2) для буквы Б – 10
3) для буквы В – 01 4) для буквы Д – 10
1.7. Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К – кодовое слово 10. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
1) 13 2) 14 3) 15 4) 16
Информационное моделирование
3.1. В фрагменте базы данных представлены сведения о родственных отношениях. Определите на основании приведенных данных фамилию и инициалы дяди Леоненко В.С. Пояснение: дядей считается брат отца или матери.
1) Геладзе И.П.
2) Геладзе П.И.
3) Гнейс А.С.
4) Леоненко Н.А.
3.2. В фрагменте базы данных представлены сведения о родственных отношениях. Определите на основании приведенных данных фамилию и инициалы бабушки Ивановой А.И.
1) Иванов Т.М.
2) Черных И.А.
3) Цейс Т.Н.
4) Петренко Н.Н.
3.3. В этом фрагменте базы данных представлены сведения о родственных отношениях. На основании приведённых данных определите фамилию и инициалы внучки Петровой С.М.
1) Басис В.В.
2) Черняк А.П.
3) Павлыш Н.П.
4) Ильченко С.И.
3.4. В фрагменте базы данных представлены сведения о родственных отношениях. На основании приведённых данных определите, сколько всего внуков и внучек есть у Карпец Д.К.
1) 2
2) 3
3) 4
4) 5
3.5. В фрагменте базы данных представлены сведения о родственных отношениях. На основании приведённых данных определите фамилию и инициалы родной сестры Лемешко В.А.
1) Онищенко А.Б.
2) Лемешко Д.А.
3) Корзун П.А.
4) Зельдович М.А.
3.6. В фрагменте базы данных представлены сведения о родственных отношениях. На основании приведенных данных определите, сколько всего двоюродных братьев и сестер есть у Сухорук П.И. Двоюродный брат (сестра) – это сын (дочь) родного брата или сестры матери или отца.
3.7. В фрагменте базы данных представлены сведения о родственных отношениях. На основании приведенных данных определите, сколько прямых потомков (то есть детей и внуков) Кривич Л.П. упомянуто в таблице.
5.1. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
5.2. Между населёнными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Например, из A в B есть дорога длиной 4 км, а из B в A дороги нет.
Сколько существует таких маршрутов из A в Z, которые проходят через 6 и
более населенных пунктов? Пункты A и Z при подсчете учитывать. Два раза проходить через один пункт нельзя.
5.3. Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).
5.4. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт Е и не проходящего через пункт B (при условии, что передвигаться можно только по построенным дорогам).
5.5. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F, не проходящего через пункт C (при условии, что передвигаться можно только по построенным дорогам).
5.6. Между населёнными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Например, из A в B есть дорога длиной 4 км, а из B в A дороги нет.
Курьеру требуется проехать из A в Z, посетив не менее 6 населённых пунктов. Пункты A и Z при подсчёте учитываются, два раза проходить через один пункт нельзя. Какова наименьшая возможная длина маршрута курьера? В ответе запишите натуральное число – длину минимального маршрута.
5.7. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
15.1. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
15.2. На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, I, J, K. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город K?
15.3. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
15.4. На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M, N, Z. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Z?
15.5. На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город M?
15.6. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город М и проходящих через город Г?
15.7. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р, С, Т, У, Ф. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Т?
Алгоритмизация и программирование
6.1. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.
Укажите максимальное число, в результате обработки которого, автомат выдаст число 1412.
6.2. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 411.
Укажите минимальное число, в результате обработки которого, автомат выдаст число 79.
6.3. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.
Укажите минимальное число, в результате обработки которого, автомат выдаст число 1412.
6.4. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и третья, а также вторая и четвёртая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 6 = 9; 1 + 5 = 6. Результат: 69.
Укажите минимальное число, в результате обработки которого, автомат выдаст число 1113.
6.5. Автомат получает на вход трёхзначное число. По этому числу строится новое
число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127.
Укажите наименьшее число, в результате обработки которого автомат выдаст число 157.
6.6. Автомат получает на вход трёхзначное число. По этому числу строится новое
число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127.
Укажите наибольшее число, в результате обработки которого автомат выдаст число 148.
6.7. Автомат получает на вход трёхзначное число. По этому числу строится новое
число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127.
Укажите наименьшее число, в результате обработки которого автомат выдаст число 43.
11.1. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n < 6 then begin
F(n+2);
F(n*3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(1).
11.2. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(‘*’);
if n > 0 then begin
F(n-2);
F(n div 2)
end
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(7)?
11.3. Процедура F(n), где n – натуральное число, задана следующим образом (язык Паскаль):
procedure F(n: integer);
begin
if n < 3 then
write(‘*’)
else begin
F(n-1);
F(n-2);
F(n-2)
end;
end;
Сколько звездочек напечатает эта процедура при вызове F(6)? В ответе запишите только целое число.
11.4. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(‘*’);
if n > 0 then begin
F(n-2);
F(n div 2);
F(n div 2);
end
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(5)?
11.5. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(‘*’);
if n > 0 then begin
F(n-3);
F(n div 2);
end
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(7)?
11.6. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n < 6 then begin
F(n+2);
F(n*3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(2).
11.7. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n > 0 then begin
F(n-1);
F(n-3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(5).
22.1. У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Первая из них увеличивает число на экране на 1, вторая – утраивает его.
Программа для Утроителя – это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 20?
22.2. У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 4
Сколько есть программ, которые число 1 преобразуют в число 55?
22.3. У исполнителя Калькулятор три команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
3. умножь на 4
Сколько есть программ, которые число 1 преобразуют в число 25?
22.4. Исполнитель Хамелеон преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Программа для исполнителя Хамелеон – это последовательность команд. Сколько существует программ, для которых при исходном числе 3 результатом является число 20 и при этом траектория вычислений содержит число 12?
22.5. Исполнитель Калькулятор преобразует целое число, записанное на экране. У исполнителя две команды, каждой команде присвоен номер:
1. Прибавь 1
2. Умножь на 2
Первая команда увеличивает число на экране на 1, вторая увеличивает это число в 2 раза. Сколько существует программ, которые число 3 преобразуют в число 20 и в которых предпоследняя команда 1?
22.6. Исполнитель Калькулятор преобразует целое число, записанное на экране. У исполнителя две команды, каждой команде присвоен номер:
1. Прибавь 1
2. Прибавь 2
Первая команда увеличивает число на экране на 1, вторая увеличивает – на 2. Сколько существует программ, которые число 3 преобразуют в число 18 и в которых предпоследняя команда 2?
22.7. Исполнитель А13S преобразует целое число, записанное на экране. У исполнителя три команды, каждой команде присвоен номер:
1. Прибавь 1
2. Прибавь 3
3. Прибавь предыдущее
Первая команда увеличивает число на экране на 1, вторая увеличивает это число на 3, третья прибавляет к числу на экране число, меньшее на 1 (к числу 3 прибавляется 2, к числу 11 прибавляется 10 и т. д.). Программа для исполнителя А13S – это последовательность команд.
Сколько существует программ, которые число 2 преобразуют в число 10?
Математические задачи-игры
26.1. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу один камень или
увеличить количество камней в куче в три раза и добавить в кучу 1 камень.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 31 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 32. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 32 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 31.
1. При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
2. Назовите два значения S, при которых Петя может выиграть своим вторым ходом?
3. Назовите значение S, при котором Ваня выигрывает своим первым или вторым ходом.
26.2. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) два камня или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 44. Победителем считается игрок, сделавший последний ход, то есть первым получивший такую позицию, что в кучах всего будет 44 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 38.
1. При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
2. Назовите одно любое значение S, при котором Петя может выиграть своим вторым ходом.
3. Назовите значение S, при котором Ваня выигрывает своим первым или вторым ходом.
26.3. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу два камня или
увеличить количество камней в куче в два раза и убрать из кучи 1 камень.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 12 или 29 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 40. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 40 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 39.
1. При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
2. Назовите все значения S, при которых Петя может выиграть своим вторым ходом?
3. Назовите все значения S, при которых Ваня выигрывает своим первым или вторым ходом.
26.4. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) добавить в кучу два камня или
б) увеличить количество камней в куче в три раза и затем добавить в кучу 2 камня.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 12 или 32 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 60. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 60 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 59.
1. При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
2. Назовите все значения S, при которых Петя может выиграть своим вторым ходом?
3. Назовите все значения S, при которых Ваня выигрывает своим первым или вторым ходом.
26.5. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу два камня или увеличить количество камней в куче в три раза. Например, имея кучу из 10 камней, за один ход можно получить кучу из 12 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 50. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 50 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 49.
1. При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
2. Назовите три значения S, при которых Петя может выиграть своим вторым ходом.
3. При каком S Ваня выигрывает своим первым или вторым ходом?
26.6. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу четыре камня или увеличить количество камней в куче в три раза. Например, имея кучу из 10 камней, за один ход можно получить кучу из 14 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 70. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 70 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 69.
1. При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
2. Назовите два значения S, при которых Петя может выиграть своим вторым ходом.
3. При каком S Ваня выигрывает своим первым или вторым ходом?
26.7. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу три камня или увеличить количество камней в куче в четыре раза. Например, имея кучу из 10 камней, за один ход можно получить кучу из 13 или 40 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 75. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 75 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 74.
1. При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
2. Назовите четыре значения S, при которых Петя может выиграть своим вторым ходом.
3. Назовите три значения S, при которых Ваня выигрывает своим первым или вторым ходом.
Ответы
Библиографический список
-
Босова Л. Л. Информатика. 6 класс: учеб. Для общеобразоват. Учреждений/ [Босова Л. Л., Босова А. Ю. ]; ФГОС 2010 (основная школа) – 3 изд. — БИНОМ. Лаборатория знаний, 2015. – 216 с.
-
Босова Л. Л. Информатика. 7 класс: учеб. Для общеобразоват. Учреждений/ [Босова Л. Л., Босова А. Ю. ]; ФГОС 2010 (основная школа) – 3 изд. — БИНОМ. Лаборатория знаний, 2015. – 224 с.
-
Босова Л. Л. Информатика. 8 класс: учеб. Для общеобразоват. Учреждений/ [Босова Л. Л., Босова А. Ю. ]; ФГОС 2010 (основная школа) – 3 изд. — БИНОМ. Лаборатория знаний, 2015. – 160 с.
-
Босова Л. Л. Информатика. 9 класс: учеб. Для общеобразоват. Учреждений/ [Босова Л. Л., Босова А. Ю. ]; ФГОС 2010 (основная школа) – 3 изд. — БИНОМ. Лаборатория знаний, 2015. – 184 с.
-
Дорофеев Г. В. Математика. 5 класс: учеб. Для общеобразоват. Учреждений/ [Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова и др.]; под ред. Г. В. Дорофеева, И.Ф. Шарыгина; Рос. Акад.наук, Рос.акад. образования, изд-во «Просвещение». – 11-е изд. – М.: Просвещение, 2010. – 303 с.: ил. – (Академический школьный учебник).
-
Дорофеев Г. В. Математика. 6 класс: учеб. Для общеобразоват. Учреждений/ [Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова и др.]; под ред. Г. В. Дорофеева, И.Ф. Шарыгина;– М.: Просвещение, 2010.
-
Дорофеев Г. В. Математика. 7 класс: учеб. Для общеобразоват. Учреждений/ [Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова и др.]; под ред. Г. В. Дорофеева, И.Ф. Шарыгина;– М.: Просвещение, 2010.
-
Дорофеев Г. В. Математика: алгебра. Функции. Анализ данных: учеб. для 8 кл. общеобразоват. Учреждений/ [Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович и др.]; под ред. Г. В. Дорофеева. – 3-е изд., с испр. – М.: Просвещение, 2007. – 256 с.
-
Крылов С. С. ЕГЭ 2015. Информатика. Тематические тестовые задания / С. С. Крылов, Д.М. Ушаков. – М.: Издательство «Экзамен», 2015. – 255 с.
-
Поляков К.Ю. Просто графы // Информатика, № 3, 2012, с. 14-21.
Интернет-ресурсы
-
http://www.fipi.ru
-
http://kpolyakov.spb.ru
-
http://reshuege.ru
В этой статье рассмотрим двоичное дерево, как оно строится и варианты обходов.
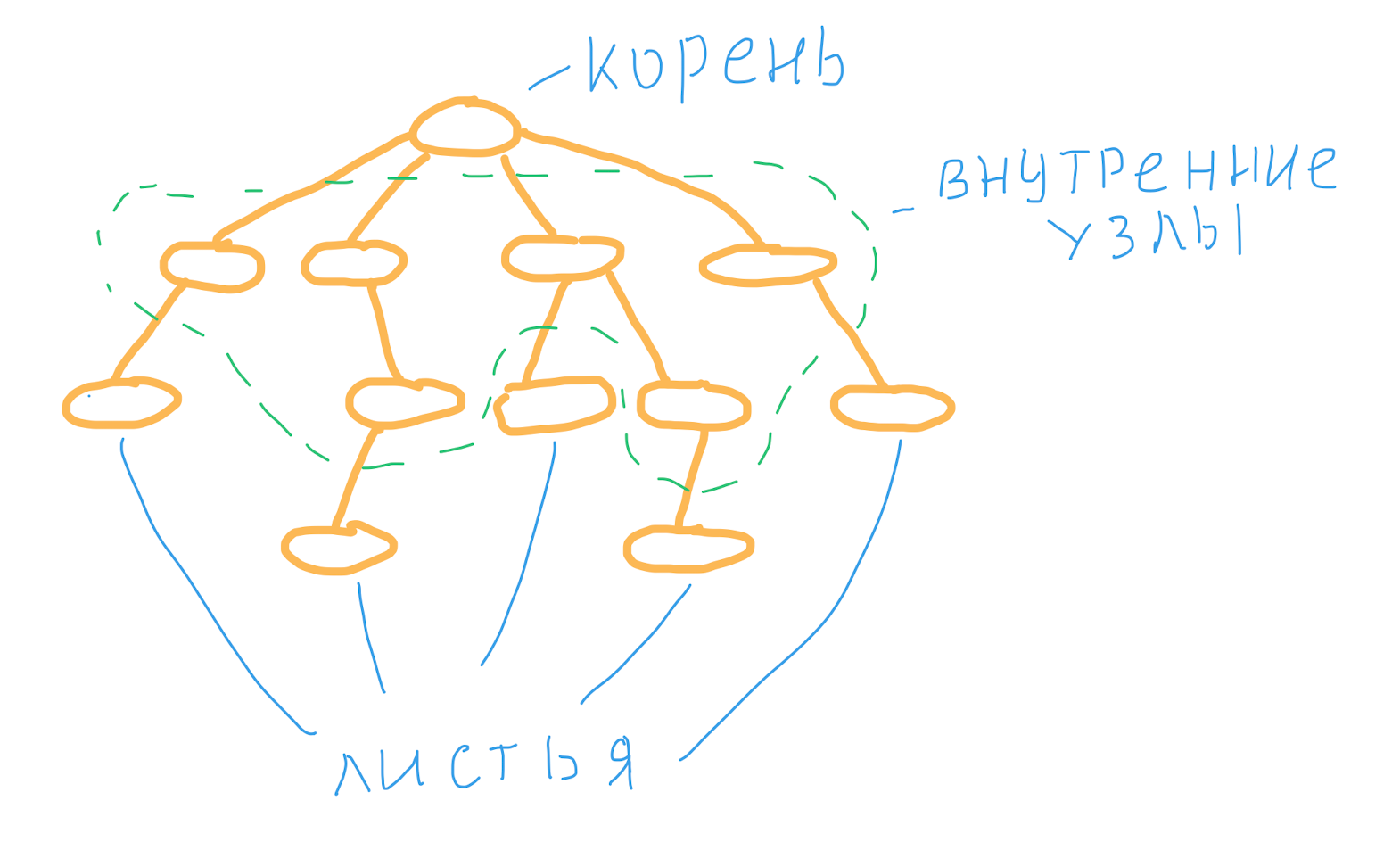
Двоичное дерево в первую очередь дерево. В программировании – структура данных, которая имеет корень и дочерние узлы, без циклических связей. Если рассмотреть отдельно любой узел с дочерними элементами, то получится тоже дерево. Узел называется внутренним, если имеет хотя бы одно поддерево. Cамые нижние элементы, которые не имеют дочерних элементов, называются листами или листовыми узлами.
Дерево обычно рисуется сверху вниз.
В узлах может храниться любая информация, от примитивных типов до объектов. В этой статье, мы рассмотрим реализацию, когда в узле также хранятся ссылки на дочерние элементы. Кроме такого подхода, возможен альтернативный подход для двоичного дерева — хранение в массиве.
Первая особенность двоичного дерева, что любой узел не может иметь более двух детей. Их называют просто — левый и правый потомок, или левое и правое поддерево.
Вторая особенность двоичного дерева, и основное правило его построения, заключается в том что левый потомок меньше текущего узла, а правый потомок больше. Отношение больше/меньше имеет смысл для сравниваемых объектов, например числа, строки, если в дереве содержатся сложные объекты, то для них берётся какая-нибудь процедура сравнения, и она будет отрабатывать при всех операциях работы с деревом.
Создание дерева, вставка
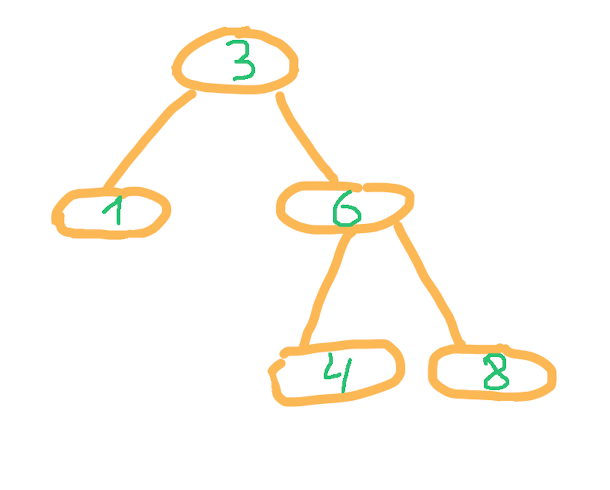
Рассмотрим существующее двоичное дерево. Корень содержит число 3, все узлы в левом поддереве меньше текущего, в правом — больше. Такие же правила действуют для любого рассматриваемого узла и его поддеревьев.
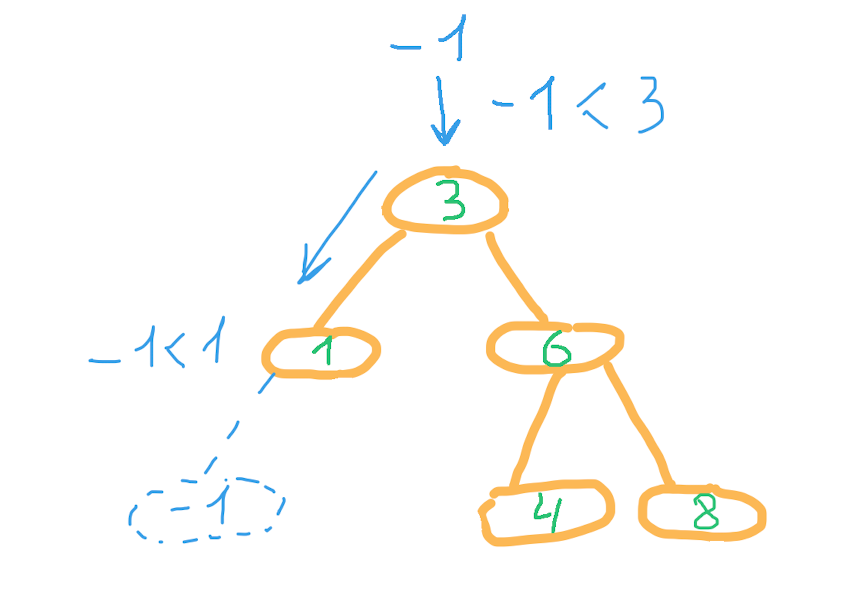
Попробуем вставить в это дерево элемент -1.
Из корня идем в левое поддерево, так как -1 меньше 3. Из узла со значением 1 также идём в левое поддерево. Но в этом узле левое поддерево отсутствует, вставляем в эту позицию элемент, создавая новый узел дерева.
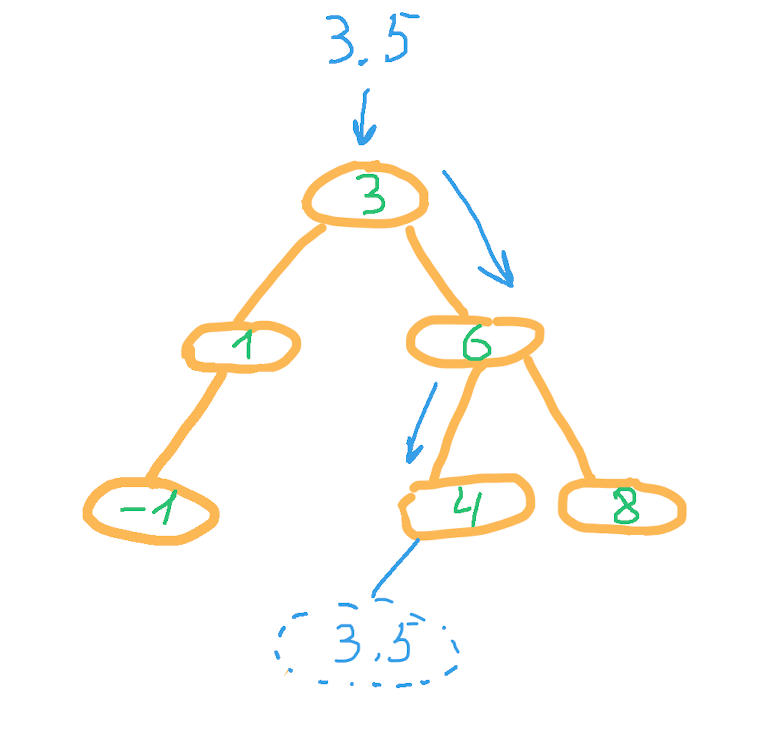
Вставим в получившееся дерево элемент 3.5.
Проходим по дереву, сравнивая на каждом из этапов вставляемое значение с элементом в узле, пока не дойдем до узла, в котором следующий узел для сравнения отсутствует, в эту позицию и вставляем новый узел.
Если дерево не существует, то есть root равен null, то элемент вставляется в корень, после этого проводится вставка по описанному выше алгоритму.
Напишем класс для создания двоичного дерева:
// дополнительный класс для хранения информации узла
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// в начале работы дерево пустое, root отсутствует
constructor() {
this.root = null;
}
insertItem(newItem) {
// создание нового узла дерева
const newNode = new BinaryTreeItem(newItem);
// проверка на пустой root, если пустой, то заполняем
// и завершаем работу
if (this.root === null) {
this.root = newNode;
return;
}
// вызов рекурсивного добавления узла
this._insertItem(this.root, newNode);
}
_insertItem(currentNode, newNode) {
// если значение в добавляемом узле
// меньше текущего рассматриваемого узла
if (newNode.value < currentNode.value) {
// если меньше и левое поддерево отсутствует
// то добавляем
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
// если левое поддерево существует,
// то вызываем для этого поддерева
// процедуру добавления нового узла
this._insertItem(currentNode.left, newNode);
}
}
// для правого поддерева алгоритм аналогичен
// работе с левым поддеревом, кроме операции сравнения
if (newNode.value > currentNode.value) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
// если элемент равен текущему элементу,
// то можно реагировать по разному, например просто
// вывести предупреждение
// возможно стоит добавить проверку на NaN,
// зависит от потребностей пользователей класса
if (newNode.value === currentNode.value) {
console.warn(elementExistMessage);
}
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
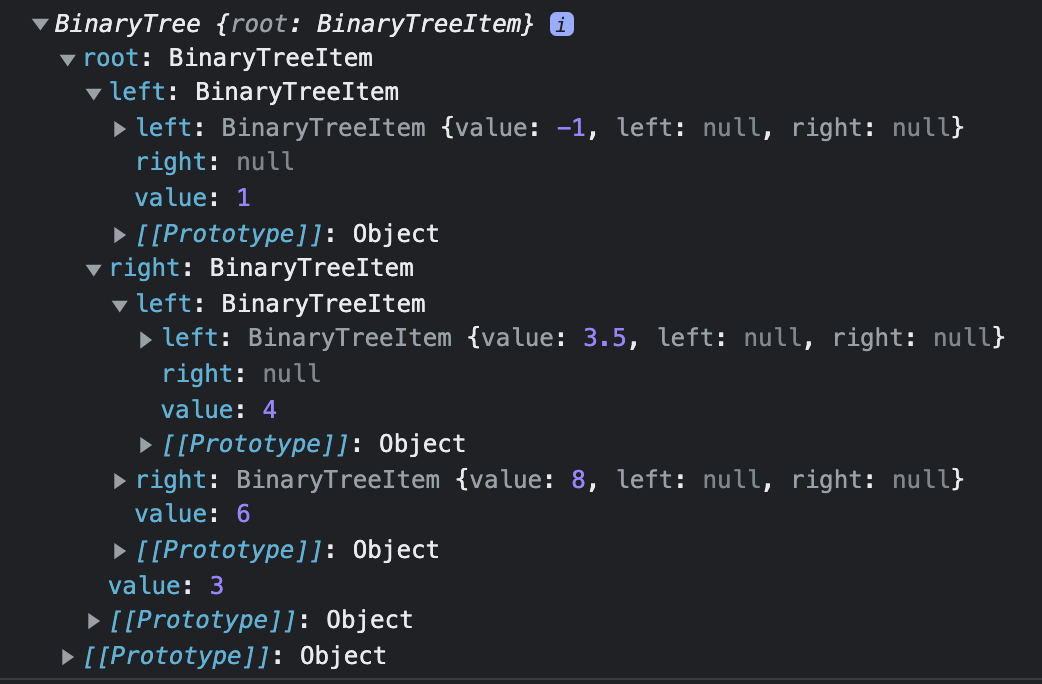
console.log(binaryTree);На скриншоте ниже то, какую информацию хранит в себе binaryTree:
Обход
Рассмотрим несколько алгоритмов обхода/поиска элементов в двоичном дереве.
Мы можем спускаться по дереву, в каждом из узлов есть выбор куда можем пойти в первую очередь и какой из элементов обработать сначала: левое поддерево, корень или право поддерево. Такие варианты обхода называются обходы в глубину (depth first).
Какие возможны варианты обхода (слово поддерево опустим):
- корень, левое, правое (preorder, прямой);
- корень, правое, левое;
- левое, корень, правое (inorder, симметричный, центрированный);
- левое, правое, корень (postorder, обратный);
- правое, корень, левое;
- правое, левое, корень.
Также используется вариант для обхода деревьев по уровням. Уровень в дереве — его удалённость от корня. Сначала обходится корень, после этого узлы первого уровня и так далее. Называется обход в ширину, по уровням, breadth first, BFS — breadth first search или level order traversal.
Выбирается один из этих вариантов, и делается обход, в каждом из узлов применяя выбранную стратегию.
Обычно для обходов в глубину применяется рекурсия. Реализуем один из вариантов, например симметричный: левое поддерево, корень, правое поддерево.
При этом мы обработаем первым самый левый узел, где левое поддерево окажется пустым, но правое может присутствовать. То есть в каждом из узлов будем спускаться ниже и ниже, пока левое поддерево не окажется пустым.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
constructor() {
this.root = null;
}
insertItem(newItem) {
// .....
}
inorder(handlerFunction) {
// просто вызываем функцию с другими параметрами,
// добавляя текущий обрабатываемый узел
// в рекурсивные вызов
this._inorderInternal(this.root, handlerFunction);
}
_insertItem(currentNode, newNode) {
// .....
}
_inorderInternal(currentNode, handlerFunction) {
// если узла нет, то его обрабатывать не нужно
if (currentNode === null) return;
// порядок обхода, для каждого из поддеревьев:
// 1. проваливаемся в левое поддерево
// 2. вызываем обрабатывающую функцию
// 3. проваливаемся в правое поддерево
this._inorderInternal(currentNode.left,
handlerFunction);
handlerFunction(currentNode.value);
this._inorderInternal(currentNode.right,
handlerFunction);
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
binaryTree.inorder(console.log);
// вызов inorder(console.log) выведет
// -1
// 1
// 3
// 3.5
// 4
// 6
// 8
Для реализации других вариантов обхода просто меняем порядок вызова функций в функции _inorderInternal. И нужно не забыть переименовать функцию, чтобы название соответствовало содержимому.
Рассмотрим inorder алгоритм обхода на примере дерева, созданного в предыдущем блоке кода.
// 1
this._inorderInternal(currentNode.left, handlerFunction);
// 2
handlerFunction(currentNode.value);
// 3
this._inorderInternal(currentNode.right, handlerFunction);
Сначала мы спустимся в самое левое поддерево — узел -1. Зайдем в его левое поддерево, которого нет, первая конструкция выполнится, ничего не сделав внутри функции. Вызовется обработчик handlerFunction, на узле -1. После этого произойдёт попытка войти в правое поддерево, которого нет. Работа функции для узла -1 завершится.
В вызов для узла -1 мы пришли через вызов функции _inorderInternal для левого поддерева узла 1. Вызов для левого поддерева -1 завершился, вызовется обработчик для значения узла 1, после этого — для правого поддерева. Правого поддерева нет, функция для узла 1 заканчивает работу. Выходим в обработчик для корня дерева.
Для корня дерева левое поддерево полностью отработало, происходит переход ко второй строке процедуры обхода — вызов обработчика значения узла. После чего вызов функции для обработчика правого поддерева.
Аналогично продолжая рассуждения, и запоминая на какой строке для определенного узла мы вошли в рекурсивный вызов, можем пройти алгоритм «руками», лучше понимая его работу.
Для обходов в ширину используется дополнительный массив.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
constructor() {
this.root = null;
}
insertItem(newItem) {
// .....
}
breadthFirstHandler(handlerFunction) {
if (this.root === null) return;
// массив, в который будем добавлять элементы,
// по мере спускания по дереву
const queue = [this.root];
// используем позицию в массиве для текущего
// обрабатываемого элемента
let queuePosition = 0;
// можем убирать обработанные элементы из очереди
// например функцией shift
// для обработки всегда брать нулевой элемент
// и завершать работу, когда массив пуст
// но shift работает за линейное время, что увеличивает
// скорость работы алгоритма
// while (queue.length > 0) {
// const currentNode = queue.shift();
while (queuePosition < queue.length) {
// текущий обрабатываемый элемент в queuePosition
const currentNode = queue[queuePosition];
handlerFunction(currentNode.value);
// добавляем в список для обработки дочерние узлы
if (currentNode.left !== null) {
queue.push(currentNode.left);
}
if (currentNode.right !== null) {
queue.push(currentNode.right);
}
queuePosition++;
}
}
_insertItem(currentNode, newNode) {
// ......
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
binaryTree.breadthFirstHandler(console.log);
// вызов breadthFirstHandler(console.log) выведет
// 3 корень
// 1 узлы первого уровня
// 6
// -1 узлы второго уровня
// 4
// 8
// 3.5 узел третьего уровня
Поиск
Операция поиска — вернуть true или false, в зависимости от того, содержится элемент в дереве или нет. Может быть реализована на основе поиска в глубину или ширину, посмотрим на реализацию на основе алгоритма обхода в глубину.
search(value) {
return this._search(this.root, value);
}
_search(currentNode, value) {
// дополнительные проверки,
// обрабатывающие завершение поиска
// либо проваливание в несуществующий узел
// либо найденной значение
if (currentNode === null) return false;
if (currentNode.value === value) return true;
// this._search проваливаются в дерево
// когда поиск завершен
// то по цепочке рекурсивных вызовов
// будет возвращен результат
if (value < currentNode.value) {
return this._search(currentNode.left, value);
}
if (value > currentNode.value) {
return this._search(currentNode.right, value);
}
}Функция сравнения или получение ключа
До этого мы рассматривали простые данные, для которых определена операция сравнения между ключами. Не всегда возможно реализовать сравнение таким простым образом.
Можно сделать функцию, которая будет получать ключ из данных, которые хранятся в узле.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// параметр при создании дерева -
// функция получения ключа
// ключи должны быть сравнимы
constructor(getKey) {
this.root = null;
this.getKey = getKey;
}
insertItem(newItem) {
const newNode = new BinaryTreeItem(newItem);
if (this.root === null) {
this.root = newNode;
return;
}
this._insertItem(this.root, newNode);
}
breadthFirstHandler(handlerFunction) {
// .....
}
_insertItem(currentNode, newNode) {
// отличие во всех процедурах сравнения
// вместо просто сравнивания value
// перед этим применяем функцию получения ключа
if (this.getKey(newNode.value) <
this.getKey(currentNode.value)) {
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
this._insertItem(currentNode.left, newNode);
}
}
if (this.getKey(newNode.value) >
this.getKey(currentNode.value)) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
if (this.getKey(newNode.value) ===
this.getKey(currentNode.value)) {
console.warn(elementExistMessage);
}
}
}
const getKey = (element) => element.key;
const binaryTree = new BinaryTree(getKey);
binaryTree.insertItem({ key: 3 });
binaryTree.insertItem({ key: 1 });
binaryTree.insertItem({ key: 6 });
binaryTree.insertItem({ key: 4 });
binaryTree.insertItem({ key: 8 });
binaryTree.insertItem({ key: -1 });
binaryTree.insertItem({ key: 3.5 });
binaryTree.breadthFirstHandler(console.log);Можно передать в конструктор специальную функцию сравнения. Эту функцию можно сделать как обычно делают функции сравнения в программировании, возвращать 0, если ключи равны. Значение больше нуля, если первый переданный объект больше второго, и меньше нуля если меньше. Важно не перепутать когда что возвращается и правильно передать параметры. Например, текущий узел, уже существующий в дереве, первым параметром, а тот, с которым производится текущая операция — вторым.
Для реализации такой возможности потребуется во всех местах сравнения использовать эту функцию
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// в конструкторе передаем функцию сравнения
constructor(compareFunction) {
this.root = null;
this.compareFunction = compareFunction;
}
insertItem(newItem) {
const newNode = new BinaryTreeItem(newItem);
if (this.root === null) {
this.root = newNode;
return;
}
this._insertItem(this.root, newNode);
}
breadthFirstHandler(handlerFunction) {
// .....
}
_insertItem(currentNode, newNode) {
// вместо сравнения value
// вызываем функцию сравнения
// и проверяем больше или меньше нуля
// получился результат сравнения
if (this.compareFunction(currentNode.value,
newNode.value) > 0) {
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
this._insertItem(currentNode.left, newNode);
}
}
// текущий узел меньше нового,
// значит новый узел должен быть отправлен
// в правое поддерево
if (this.compareFunction(currentNode.value,
newNode.value) < 0) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
if (this.compareFunction(currentNode.value,
newNode.value) === 0) {
console.warn(elementExistMessage);
}
}
}
const compare = (object1, object2) => {
return object1.key - object2.key;
};
const binaryTree = new BinaryTree(compare);
binaryTree.insertItem({ key: 3 });
binaryTree.insertItem({ key: 1 });
binaryTree.insertItem({ key: 6 });
binaryTree.insertItem({ key: 4 });
binaryTree.insertItem({ key: 8 });
binaryTree.insertItem({ key: -1 });
binaryTree.insertItem({ key: 3.5 });
binaryTree.breadthFirstHandler(console.log);Заключение
Мы познакомились с концепцией двоичных деревьев и операциями для создания такого типа дерева. Эти операции интуитивно понятны, в следующей статье рассмотрим процедуру удаления и скорость работы двоичного дерева.
Дерево – структура данных, представляющая собой древовидную структуру в виде набора связанных узлов.
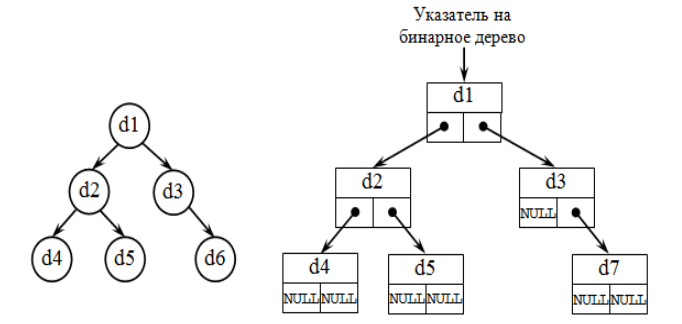
Бинарное дерево — это конечное множество элементов, которое либо пусто, либо содержит элемент (корень), связанный с двумя различными бинарными деревьями, называемыми левым и правым поддеревьями. Каждый элемент бинарного дерева называется узлом. Связи между узлами дерева называются его ветвями.
Способ представления бинарного дерева:
- A — корень дерева
- В — корень левого поддерева
- С — корень правого поддерева
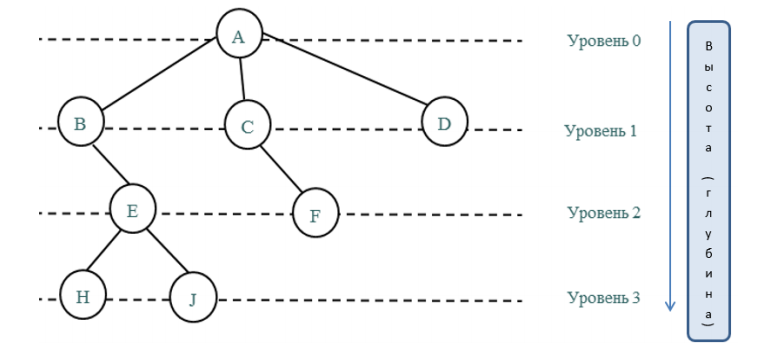
Корень дерева расположен на уровне с минимальным значением.
Узел D, который находится непосредственно под узлом B, называется потомком B. Если D находится на уровне i, то B – на уровне i-1. Узел B называется предком D.
Максимальный уровень какого-либо элемента дерева называется его глубиной или высотой.
Если элемент не имеет потомков, он называется листом или терминальным узлом дерева.
Остальные элементы – внутренние узлы (узлы ветвления).
Число потомков внутреннего узла называется его степенью. Максимальная степень всех узлов есть степень дерева.
Число ветвей, которое нужно пройти от корня к узлу x, называется длиной пути к x. Корень имеет длину пути равную 0; узел на уровне i имеет длину пути равную i.
Бинарное дерево применяется в тех случаях, когда в каждой точке вычислительного процесса должно быть принято одно из двух возможных решений.
Имеется много задач, которые можно выполнять на дереве.
Распространенная задача — выполнение заданной операции p с каждым элементом дерева. Здесь p рассматривается как параметр более общей задачи посещения всех узлов или задачи обхода дерева.
Если рассматривать задачу как единый последовательный процесс, то отдельные узлы посещаются в определенном порядке и могут считаться расположенными линейно.
Способы обхода дерева
Пусть имеем дерево, где A — корень, B и C — левое и правое поддеревья.
Существует три способа обхода дерева:
- Обход дерева сверху вниз (в прямом порядке): A, B, C — префиксная форма.
- Обход дерева в симметричном порядке (слева направо): B, A, C — инфиксная форма.
- Обход дерева в обратном порядке (снизу вверх): B, C, A — постфиксная форма.
Реализация дерева
Узел дерева можно описать как структуру:
1
2
3
4
5
struct tnode {
int field; // поле данных
struct tnode *left; // левый потомок
struct tnode *right; // правый потомок
};
При этом обход дерева в префиксной форме будет иметь вид
1
2
3
4
5
6
7
void treeprint(tnode *tree) {
if (tree!=NULL) { //Пока не встретится пустой узел
cout << tree->field; //Отображаем корень дерева
treeprint(tree->left); //Рекурсивная функция для левого поддерева
treeprint(tree->right); //Рекурсивная функция для правого поддерева
}
}
Обход дерева в инфиксной форме будет иметь вид
1
2
3
4
5
6
7
void treeprint(tnode *tree) {
if (tree!=NULL) { //Пока не встретится пустой узел
treeprint(tree->left); //Рекурсивная функция для левого поддерева
cout << tree->field; //Отображаем корень дерева
treeprint(tree->right); //Рекурсивная функция для правого поддерева
}
}
Обход дерева в постфиксной форме будет иметь вид
1
2
3
4
5
6
7
void treeprint(tnode *tree) {
if (tree!=NULL) { //Пока не встретится пустой узел
treeprint(tree->left); //Рекурсивная функция для левого поддерева
treeprint(tree->right); //Рекурсивная функция для правого поддерева
cout << tree->field; //Отображаем корень дерева
}
}
Бинарное (двоичное) дерево поиска – это бинарное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):
- оба поддерева – левое и правое, являются двоичными деревьями поиска;
- у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, чем значение ключа данных самого узла X;
- у всех узлов правого поддерева произвольного узла X значения ключей данных не меньше, чем значение ключа данных узла X.
Данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.
Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных.
Для составления бинарного дерева поиска рассмотрим функцию добавления узла в дерево.
Добавление узлов в дерево
1
2
3
4
5
6
7
8
9
10
11
12
struct tnode * addnode(int x, tnode *tree) {
if (tree == NULL) { // Если дерева нет, то формируем корень
tree =new tnode; // память под узел
tree->field = x; // поле данных
tree->left = NULL;
tree->right = NULL; // ветви инициализируем пустотой
}else if (x < tree->field) // условие добавление левого потомка
tree->left = addnode(x,tree->left);
else // условие добавление правого потомка
tree->right = addnode(x,tree->right);
return(tree);
}
Удаление поддерева
1
2
3
4
5
6
7
void freemem(tnode *tree) {
if(tree!=NULL) {
freemem(tree->left);
freemem(tree->right);
delete tree;
}
}
Пример Сортировка элементов массива с помощью дерева
Пример Написать программу, подсчитывающую частоту встречаемости слов входного потока.
Поскольку список слов заранее не известен, мы не можем предварительно упорядочить его. Неразумно пользоваться линейным поиском каждого полученного слова, чтобы определять, встречалось оно ранее или нет, т.к. в этом случае программа работает слишком медленно.
Один из способов — постоянно поддерживать упорядоченность уже полученных слов, помещая каждое новое слово в такое место, чтобы не нарушалась имеющаяся упорядоченность. Воспользуемся бинарным деревом.
В дереве каждый узел содержит:
- указатель на текст слова;
- счетчик числа встречаемости;
- указатель на левого потомка;
- указатель на правого потомка.
Рассмотрим выполнение программы на примере фразы
now is the time for all good men to come to the aid of their party
При этом дерево будет иметь следующий вид
Пример реализации
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
//#include <cstddef>
#define MAXWORD 100
struct tnode { // узел дерева
char* word; // указатель на строку (слово)
int count; // число вхождений
struct tnode* left; // левый потомок
struct tnode* right; // правый потомок
};
// Функция добавления узла к дереву
struct tnode* addtree(struct tnode* p, char* w) {
int cond;
if (p == NULL) {
p = (struct tnode*)malloc(sizeof(struct tnode));
p->word = _strdup(w);
p->count = 1;
p->left = p->right = NULL;
}
else if ((cond = strcmp(w, p->word)) == 0)
p->count++;
else if (cond < 0)
p->left = addtree(p->left, w);
else
p->right = addtree(p->right, w);
return p;
}
// Функция удаления поддерева
void freemem(tnode* tree) {
if (tree != NULL) {
freemem(tree->left);
freemem(tree->right);
free(tree->word);
free(tree);
}
}
// Функция вывода дерева
void treeprint(struct tnode* p) {
if (p != NULL) {
treeprint(p->left);
printf(«%d %sn», p->count, p->word);
treeprint(p->right);
}
}
int main() {
struct tnode* root;
char word[MAXWORD];
root = NULL;
do {
scanf_s(«%s», word, MAXWORD);
if (isalpha(word[0]))
root = addtree(root, word);
} while (word[0] != ‘0’); // условие выхода – ввод символа ‘0’
treeprint(root);
freemem(root);
getchar();
getchar();
return 0;
}
Результат выполнения
Назад: Структуры данных
Привет всем, кто проходит курс машинного обучения на Хабре!
В первых двух частях (1, 2) мы попрактиковались в первичном анализе данных с Pandas и в построении картинок, позволяющих делать выводы по данным. Сегодня наконец перейдем к машинному обучению. Поговорим о задачах машинного обучения и рассмотрим 2 простых подхода – деревья решений и метод ближайших соседей. Также обсудим, как с помощью кросс-валидации выбирать модель для конкретных данных.
UPD 01.2022: С февраля 2022 г. ML-курс ODS на русском возрождается под руководством Петра Ермакова couatl. Для русскоязычной аудитории это предпочтительный вариант (c этими статьями на Хабре – в подкрепление), англоговорящим рекомендуется mlcourse.ai в режиме самостоятельного прохождения.
План этой статьи:
- Введение
- Дерево решений
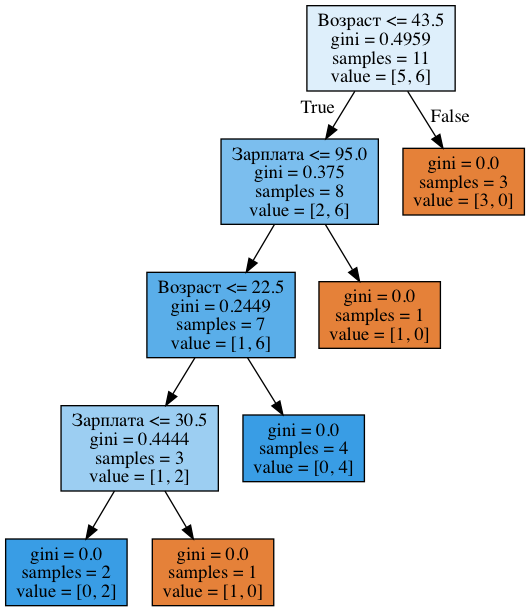
- Как строится дерево решений
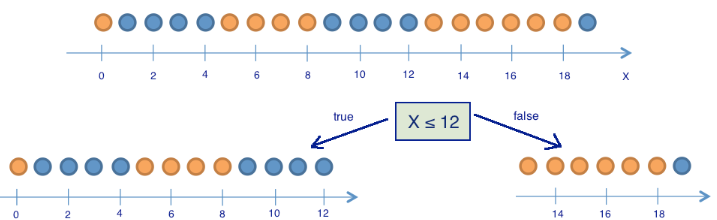
- Как дерево решений работает с количественными признаками
- Основные параметры дерева
- Класс DecisionTreeClassifier в Scikit-learn
- Дерево решений в задаче регрессии
- Метод ближайших соседей
- Метод ближайших соседей в реальных задачах
- Класс KNeighborsClassifier в Scikit-learn
- Выбор параметров модели и кросс-валидация
- Примеры применения
- Деревья решений и метод ближайших соседей в задаче прогнозирования оттока клиентов телеком-оператора
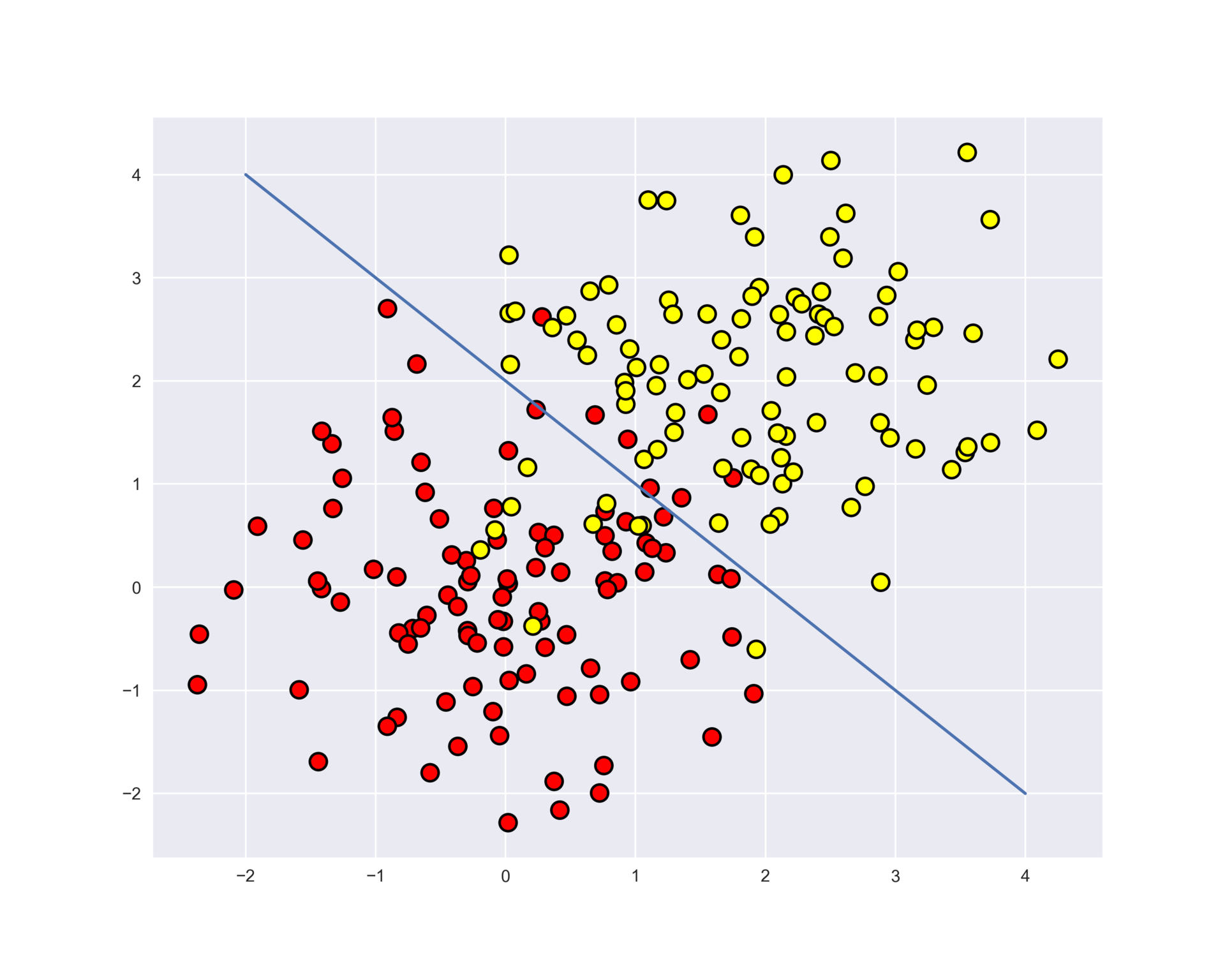
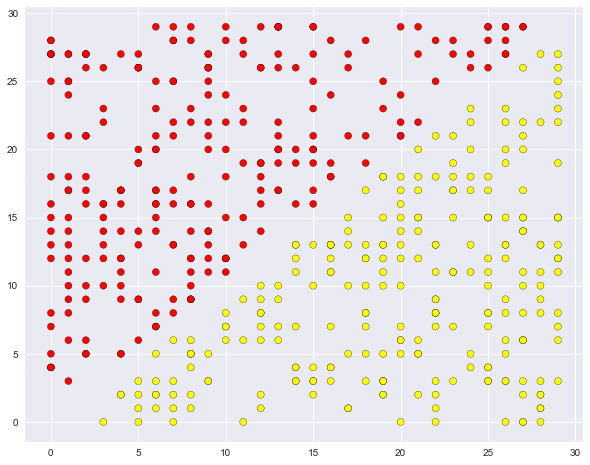
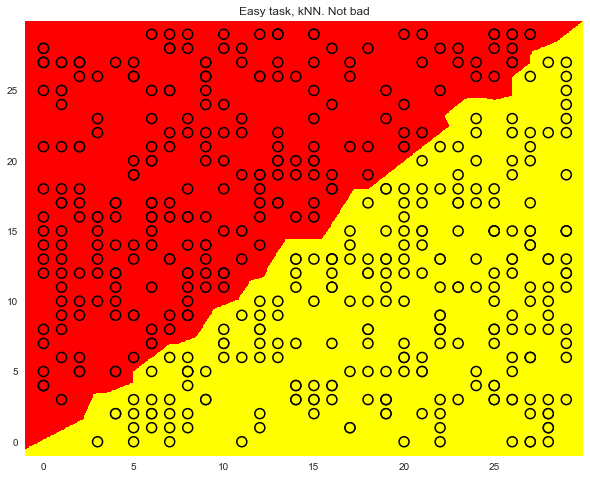
- Сложный случай для деревьев решений
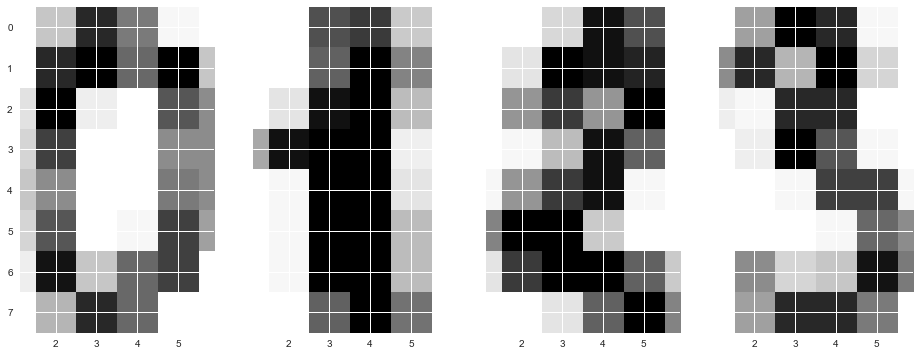
- Деревья решений и метод ближайших соседей в задаче распознавания рукописных цифр MNIST
- Сложный случай для метода ближайших соседей
- Плюсы и минусы деревьев решений и метода ближайших соседей
- Домашнее задание №3
- Полезные ресурсы
Введение
Наверное, хочется сразу рвануть в бой, но сначала поговорим про то, какую именно задачу будем решать и каково ее место в области машинного обучения.
Классическое, общее (и не больно-то строгое) определение машинного обучения звучит так (T. Mitchell «Machine learning», 1997):
говорят, что компьютерная программа обучается при решении какой-то задачи из класса T, если ее производительность, согласно метрике P, улучшается при накоплении опыта E.
Далее в разных сценариях под T, P, и E подразумеваются совершенно разные вещи. Среди самых популярных задач T в машинном обучении:
- классификация – отнесение объекта к одной из категорий на основании его признаков
- регрессия – прогнозирование количественного признака объекта на основании прочих его признаков
- кластеризация – разбиение множества объектов на группы на основании признаков этих объектов так, чтобы внутри групп объекты были похожи между собой, а вне одной группы – менее похожи
- детекция аномалий – поиск объектов, «сильно непохожих» на все остальные в выборке либо на какую-то группу объектов
- и много других, более специфичных. Хороший обзор дан в главе «Machine Learning basics» книги «Deep Learning» (Ian Goodfellow, Yoshua Bengio, Aaron Courville, 2016)
Под опытом E понимаются данные (без них никуда), и в зависимости от этого алгоритмы машинного обучения могут быть поделены на те, что обучаются с учителем и без учителя (supervised & unsupervised learning). В задачах обучения без учителя имеется выборка, состоящая из объектов, описываемых набором признаков. В задачах обучения с учителем вдобавок к этому для каждого объекта некоторой выборки, называемой обучающей, известен целевой признак – по сути это то, что хотелось бы прогнозировать для прочих объектов, не из обучающей выборки.
Пример
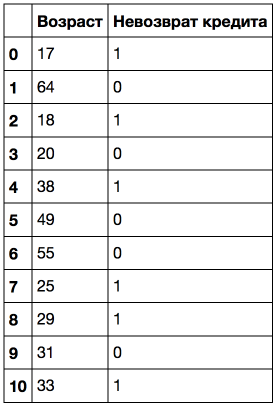
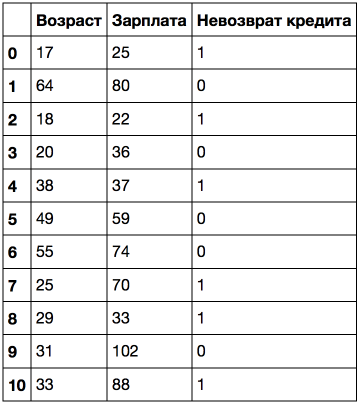
Задачи классификации и регрессии – это задачи обучения с учителем. В качестве примера будем представлять задачу кредитного скоринга: на основе накопленных кредитной организацией данных о своих клиентах хочется прогнозировать невозврат кредита. Здесь для алгоритма опыт E – это имеющаяся обучающая выборка: набор объектов (людей), каждый из которых характеризуется набором признаков (таких как возраст, зарплата, тип кредита, невозвраты в прошлом и т.д.), а также целевым признаком. Если этот целевой признак – просто факт невозврата кредита (1 или 0, т.е. банк знает о своих клиентах, кто вернул кредит, а кто – нет), то это задача (бинарной) классификации. Если известно, на сколько по времени клиент затянул с возвратом кредита и хочется то же самое прогнозировать для новых клиентов, то это будет задачей регрессии.
Наконец, третья абстракция в определении машинного обучения – это метрика оценки производительности алгоритма P. Такие метрики различаются для разных задач и алгоритмов, и про них мы будим говорить по мере изучения алгоритмов. Пока скажем, что самая простая метрика качества алгоритма, решающего задачу классификации – это доля правильных ответов (accuracy, не называйте ее точностью, этот перевод зарезервирован под другую метрику, precision) – то есть попросту доля верных прогнозов алгоритма на тестовой выборке.
Далее будем говорить о двух задачах обучения с учителем: о классификации и регресcии.
Дерево решений
Начнем обзор методов классификации и регрессии с одного из самых популярных – с дерева решений. Деревья решений используются в повседневной жизни в самых разных областях человеческой деятельности, порой и очень далеких от машинного обучения. Деревом решений можно назвать наглядную инструкцию, что делать в какой ситуации. Приведем пример из области консультирования научных сотрудников института. Высшая Школа Экономики выпускает инфо-схемы, облегчающие жизнь своим сотрудникам. Вот фрагмент инструкции по публикации научной статьи на портале института.
В терминах машинного обучения можно сказать, что это элементарный классификатор, который определяет форму публикации на портале (книга, статья, глава книги, препринт, публикация в «НИУ ВШЭ и СМИ») по нескольким признакам: типу публикации (монография, брошюра, статья и т.д.), типу издания, где опубликована статья (научный журнал, сборник трудов и т.д.) и остальным.
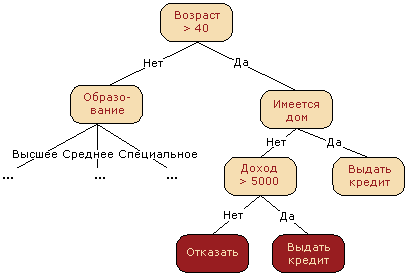
Зачастую дерево решений служит обобщением опыта экспертов, средством передачи знаний будущим сотрудникам или моделью бизнес-процесса компании. Например, до внедрения масштабируемых алгоритмов машинного обучения в банковской сфере задача кредитного скоринга решалась экспертами. Решение о выдаче кредита заемщику принималось на основе некоторых интуитивно (или по опыту) выведенных правил, которые можно представить в виде дерева решений.
В этом случае можно сказать, что решается задача бинарной классификации (целевой класс имеет два значения: «Выдать кредит» и «Отказать») по признакам «Возраст», «Наличие дома», «Доход» и «Образование».
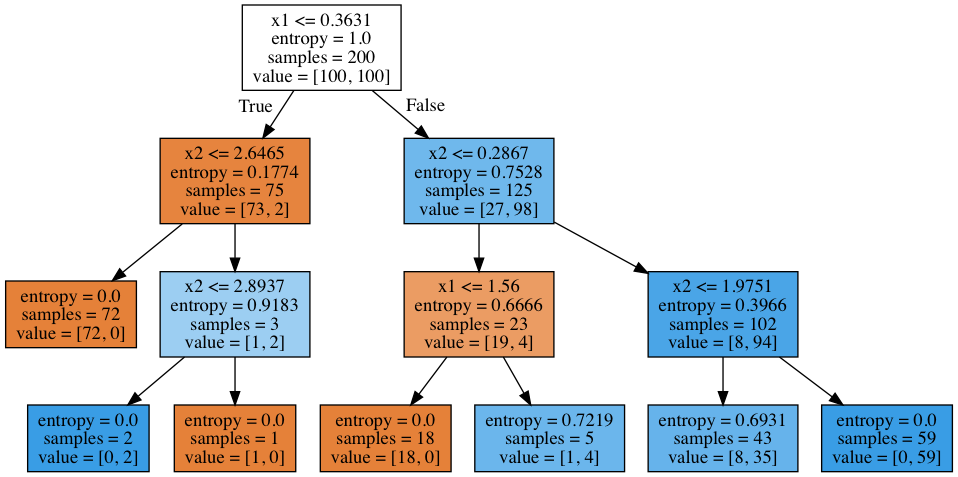
Дерево решений как алгоритм машинного обучения – по сути то же самое: объединение логических правил вида «Значение признака меньше
И Значение признака
меньше
… => Класс 1″ в структуру данных «Дерево». Огромное преимущество деревьев решений в том, что они легко интерпретируемы, понятны человеку. Например, по схеме на рисунке выше можно объяснить заемщику, почему ему было отказано в кредите. Скажем, потому, что у него нет дома и доход меньше 5000. Как мы увидим дальше, многие другие, хоть и более точные, модели не обладают этим свойством и могут рассматриваться скорее как «черный ящик», в который загрузили данные и получили ответ. В связи с этой «понятностью» деревьев решений и их сходством с моделью принятия решений человеком (можно легко объяснять боссу свою модель), деревья решений получили огромную популярность, а один из представителей этой группы методов классификации, С4.5, рассматривается первым в списке 10 лучших алгоритмов интеллектуального анализа данных («Top 10 algorithms in data mining», Knowledge and Information Systems, 2008. PDF).
Как строится дерево решений
В примере с кредитным скорингом мы видели, что решение о выдаче кредита принималось на основе возраста, наличия недвижимости, дохода и других. Но какой признак выбрать первым? Для этого рассмотрим пример попроще, где все признаки бинарные.
Здесь можно вспомнить игру «20 вопросов», которая часто упоминается во введении в деревья решений. Наверняка каждый в нее играл. Один человек загадывает знаменитость, а второй пытается отгадать, задавая только вопросы, на которые можно ответить «Да» или «Нет» (опустим варианты «не знаю» и «не могу сказать»). Какой вопрос отгадывающий задаст первым делом? Конечно, такой, который сильнее всего уменьшит количество оставшихся вариантов. К примеру, вопрос «Это Анджелина Джоли?» в случае отрицательного ответа оставит более 7 миллиардов вариантов для дальнейшего перебора (конечно, поменьше, не каждый человек – знаменитость, но все равно немало), а вот вопрос «Это женщина?» отсечет уже около половины знаменитостей. То есть, признак «пол» намного лучше разделяет выборку людей, чем признак «это Анджелина Джоли», «национальность-испанец» или «любит футбол». Это интуитивно соответствует понятию прироста информации, основанного на энтропии.
Энтропия
Энтропия Шеннона определяется для системы с возможными состояниями следующим образом:
где – вероятности нахождения системы в
-ом состоянии. Это очень важное понятие, используемое в физике, теории информации и других областях. Опуская предпосылки введения (комбинаторные и теоретико-информационные) этого понятия, отметим, что, интуитивно, энтропия соответствует степени хаоса в системе. Чем выше энтропия, тем менее упорядочена система и наоборот. Это поможет нам формализовать «эффективное разделение выборки», про которое мы говорили в контексте игры «20 вопросов».
Пример
Для иллюстрации того, как энтропия поможет определить хорошие признаки для построения дерева, приведем тот же игрушечный пример, что в статье «Энтропия и деревья принятия решений». Будем предсказывать цвет шарика по его координате. Конечно, ничего общего с жизнью это не имеет, но позволяет показать, как энтропия используется для построения дерева решений.
Здесь 9 синих шариков и 11 желтых. Если мы наудачу вытащили шарик, то он с вероятностью будет синим и с вероятностью
– желтым. Значит, энтропия состояния
. Само это значение пока ни о чем нам не говорит. Теперь посмотрим, как изменится энтропия, если разбить шарики на две группы – с координатой меньше либо равной 12 и больше 12.
В левой группе оказалось 13 шаров, из которых 8 синих и 5 желтых. Энтропия этой группы равна . В правой группе оказалось 7 шаров, из которых 1 синий и 6 желтых. Энтропия правой группы равна
. Как видим, энтропия уменьшилась в обеих группах по сравнению с начальным состоянием, хоть в левой и не сильно. Поскольку энтропия – по сути степень хаоса (или неопределенности) в системе, уменьшение энтропии называют приростом информации. Формально прирост информации (information gain, IG) при разбиении выборки по признаку
(в нашем примере это признак «
«) определяется как
где – число групп после разбиения,
– число элементов выборки, у которых признак
имеет
-ое значение. В нашем случае после разделения получилось две группы (
) – одна из 13 элементов (
), вторая – из 7 (
). Прирост информации получился
Получается, разделив шарики на две группы по признаку «координата меньше либо равна 12», мы уже получили более упорядоченную систему, чем в начале. Продолжим деление шариков на группы до тех пор, пока в каждой группе шарики не будут одного цвета.
Для правой группы потребовалось всего одно дополнительное разбиение по признаку «координата меньше либо равна 18», для левой – еще три. Очевидно, энтропия группы с шариками одного цвета равна 0 (), что соответствует представлению, что группа шариков одного цвета – упорядоченная.
В итоге мы построили дерево решений, предсказывающее цвет шарика по его координате. Отметим, что такое дерево решений может плохо работать для новых объектов (определения цвета новых шариков), поскольку оно идеально подстроилось под обучающую выборку (изначальные 20 шариков). Для классификации новых шариков лучше подойдет дерево с меньшим числом «вопросов», или разделений, пусть даже оно и не идеально разбивает по цветам обучающую выборку. Эту проблему, переобучение, мы еще рассмотрим далее.
Алгоритм построения дерева
Можно убедиться в том, что построенное в предыдущем примере дерево является в некотором смысле оптимальным – потребовалось только 5 «вопросов» (условий на признак ), чтобы «подогнать» дерево решений под обучающую выборку, то есть чтобы дерево правильно классифицировало любой обучающий объект. При других условиях разделения выборки дерево получится глубже.
В основе популярных алгоритмов построения дерева решений, таких как ID3 и C4.5, лежит принцип жадной максимизации прироста информации – на каждом шаге выбирается тот признак, при разделении по которому прирост информации оказывается наибольшим. Дальше процедура повторяется рекурсивно, пока энтропия не окажется равной нулю или какой-то малой величине (если дерево не подгоняется идеально под обучающую выборку во избежание переобучения).
В разных алгоритмах применяются разные эвристики для «ранней остановки» или «отсечения», чтобы избежать построения переобученного дерева.
def build(L):
create node t
if the stopping criterion is True:
assign a predictive model to t
else:
Find the best binary split L = L_left + L_right
t.left = build(L_left)
t.right = build(L_right)
return t Другие критерии качества разбиения в задаче классификации
Мы разобрались в том, как понятие энтропии позволяет формализовать представление о качестве разбиения в дереве. Но это всего лишь эвристика, существуют и другие:
На практике ошибка классификации почти не используется, а неопределенность Джини и прирост информации работают почти одинаково.
В случае задачи бинарной классификации (
– вероятность объекта иметь метку +) энтропия и неопределенность Джини примут следующий вид:
Когда мы построим графики этих двух функций от аргумента , то увидим, что график энтропии очень близок к графику удвоенной неопределенности Джини, и поэтому на практике эти два критерия «работают» почти одинаково.
Импорт библиотек
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
%matplotlib inline
import seaborn as sns
from matplotlib import pyplot as pltОтрисовка картинки
plt.rcParams['figure.figsize'] = (6,4)
xx = np.linspace(0,1,50)
plt.plot(xx, [2 * x * (1-x) for x in xx], label='gini')
plt.plot(xx, [4 * x * (1-x) for x in xx], label='2*gini')
plt.plot(xx, [-x * np.log2(x) - (1-x) * np.log2(1 - x) for x in xx], label='entropy')
plt.plot(xx, [1 - max(x, 1-x) for x in xx], label='missclass')
plt.plot(xx, [2 - 2 * max(x, 1-x) for x in xx], label='2*missclass')
plt.xlabel('p+')
plt.ylabel('criterion')
plt.title('Критерии качества как функции от p+ (бинарная классификация)')
plt.legend();Пример
Рассмотрим пример применения дерева решений из библиотеки Scikit-learn для синтетических данных. Два класса будут сгенерированы из двух нормальных распределений с разными средними.
Код для генерации данных
# первый класс
np.random.seed(7)
train_data = np.random.normal(size=(100, 2))
train_labels = np.zeros(100)
# добавляем второй класс
train_data = np.r_[train_data, np.random.normal(size=(100, 2), loc=2)]
train_labels = np.r_[train_labels, np.ones(100)]Отобразим данные. Неформально, задача классификации в этом случае – построить какую-то «хорошую» границу, разделяющую 2 класса (красные точки от желтых). Если утрировать, то машинное обучение в этом случае сводится к тому, как выбрать хорошую разделяющую границу. Возможно, прямая будет слишком простой границей, а какая-то сложная кривая, огибающая каждую красную точку – будет слишком сложной и будем много ошибаться на новых примерах из того же распределения, из которого пришла обучающая выборка. Интуиция подсказывает, что хорошо на новых данных будет работать какая-то гладкая граница, разделяющая 2 класса, или хотя бы просто прямая (в -мерном случае – гиперплоскость).
Отрисовка картинки
plt.rcParams['figure.figsize'] = (10,8)
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5);
plt.plot(range(-2,5), range(4,-3,-1));Попробуем разделить эти два класса, обучив дерево решений. В дереве будем использовать параметр max_depth, ограничивающий глубину дерева. Визуализируем полученную границу разделения классов.
Код для обучения дерева и отрисовки его разделяющей границы
from sklearn.tree import DecisionTreeClassifier
# Напишем вспомогательную функцию, которая будет возвращать решетку для дальнейшей визуализации.
def get_grid(data):
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
return np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
# параметр min_samples_leaf указывает, при каком минимальном количестве
# элементов в узле он будет дальше разделяться
clf_tree = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=17)
# обучаем дерево
clf_tree.fit(train_data, train_labels)
# немного кода для отображения разделяющей поверхности
xx, yy = get_grid(train_data)
predicted = clf_tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5);А как выглядит само построенное дерево? Видим, что дерево «нарезает» пространство на 7 прямоугольников (в дереве 7 листьев). В каждом таком прямоугольнике прогноз дерева будет константным, по превалированию объектов того или иного класса.
Код для отображения дерева
# используем .dot формат для визуализации дерева
from sklearn.tree import export_graphviz
export_graphviz(clf_tree, feature_names=['x1', 'x2'],
out_file='../../img/small_tree.dot', filled=True)
# для этого понадобится библиотека pydot (pip install pydot)
!dot -Tpng '../../img/small_tree.dot' -o '../../img/small_tree.png'Как «читается» такое дерево?
В начале было 200 объектов, 100 — одного класса и 100 – другого. Энтропия начального состояния была максимальной – 1. Затем было сделано разбиение объектов на 2 группы в зависимости от сравнения признака со значением
(найдите этот участок границы на рисунке выше, до дерева). При этом энтропия и в левой, и в правой группе объектов уменьшилась. И так далее, дерево строится до глубины 3. При такой визуализации чем больше объектов одного класса, тем цвет вершины ближе к темно-оранжевому и, наоборот, чем больше объектов второго класса, тем ближе цвет к темно-синему. В начале объектов одного класса поровну, поэтому корневая вершина дерева – белого цвета.
Как дерево решений работает с количественными признаками
Допустим, в выборке имеется количественный признак «Возраст», имеющий много уникальных значений. Дерево решений будет искать лучшее (по критерию типа прироста информации) разбиение выборки, проверяя бинарные признаки типа «Возраст < 17», «Возраст < 22.87» и т.д. Но что если таких «нарезаний» возраста слишком много? А что если есть еще количественный признак «Зарплата», и зарплату тоже можно «нарезать» большим числом способов? Получается слишком много бинарных признаков для выбора лучшего на каждом шаге построения дерева. Для решения этой проблемы применяют эвристики для ограничения числа порогов, с которыми мы сравниваем количественный признак.
Рассмотрим это на игрушечном примере. Пусть имеется следующая выборка:
Отсортируем ее по возрастанию возраста.
Обучим на этих данных дерево решений (без ограничения глубины) и посмотрим на него.
Код для обучения и отрисовки дерева
age_tree = DecisionTreeClassifier(random_state=17)
age_tree.fit(data['Возраст'].values.reshape(-1, 1), data['Невозврат кредита'].values)
export_graphviz(age_tree, feature_names=['Возраст'],
out_file='../../img/age_tree.dot', filled=True)
!dot -Tpng '../../img/age_tree.dot' -o '../../img/age_tree.png'На картинке ниже видим, что дерево задействовало 5 значений, с которыми сравнивается возраст: 43.5, 19, 22.5, 30 и 32 года. Если приглядеться, то это аккурат средние значения между возрастами, при которых целевой класс «меняется» с 1 на 0 или наоборот. Сложная фраза, поэтому пример: 43.5 – это среднее между 38 и 49 годами, клиент, которому 38 лет не вернул кредит, а тот, которому 49 – вернул. Аналогично, 19 лет – среднее между 18 и 20 годами. То есть в качестве порогов для «нарезания» количественного признака, дерево «смотрит» на те значения, при которых целевой класс меняет свое значение.
Подумайте, почему не имеет смысла в данном случае рассматривать признак «Возраст < 17.5».
Рассмотрим пример посложнее: добавим признак «Зарплата» (тыс. рублей/месяц).
Если отсортировать по возрасту, то целевой класс («Невозврат кредита») меняется (с 1 на 0 или наоборот) 5 раз. А если отсортировать по зарплате – то 7 раз. Как теперь дерево будет выбирать признаки? Посмотрим.
Код для обучения и отрисовки дерева
age_sal_tree = DecisionTreeClassifier(random_state=17)
age_sal_tree.fit(data2[['Возраст', 'Зарплата']].values, data2['Невозврат кредита'].values);
export_graphviz(age_sal_tree, feature_names=['Возраст', 'Зарплата'],
out_file='../../img/age_sal_tree.dot', filled=True)
!dot -Tpng '../../img/age_sal_tree.dot' -o '../../img/age_sal_tree.png'Видим, что в дереве задействованы как разбиения по возрасту, так и по зарплате. Причем пороги, с которыми сравниваются признаки: 43.5 и 22.5 года – для возраста и 95 и 30.5 тыс. руб/мес – для зарплаты. И опять можно заметить, что 95 тыс. – это среднее между 88 и 102, при этом человек с зарплатой 88 оказался «плохим», а с 102 – «хорошим». То же самое для 30.5 тыс. То есть перебирались сравнения зарплаты и возраста не со всеми возможными значениями, а только с несколькими. А почему в дереве оказались именно эти признаки? Потому что по ним разбиения оказались лучше (по критерию неопределенности Джини).
Вывод: самая простая эвристика для обработки количественных признаков в дереве решений: количественный признак сортируется по возрастанию, и в дереве проверяются только те пороги, при которых целевой признак меняет значение. Звучит не очень строго, но надеюсь, я донес смысл с помощью игрушечных примеров.
Дополнительно, когда в данных много количественных признаков, и у каждого много уникальных значений, могут отбираться не все пороги, описанные выше, а только топ-N, дающих максимальный прирост все того же критерия. То есть, по сути, для каждого порога строится дерево глубины 1, считается насколько снизилась энтропия (или неопределенность Джини) и выбираются только лучшие пороги, с которыми стоит сравнивать количественный признак.
Для иллюстрации: при разбиении по признаку «Зарплата 34.5″ в левой подгруппе энтропия 0 (все клиенты «плохие»), а в правой – 0.954 (3 «плохих» и 5 «хороших», можете проверить, 1 часть домашнего задания будет как раз на то, чтоб разобраться досконально с построением деревьев). Прирост информации получается примерно 0.3.
А при разбиении по признаку «Зарплата 95″ в левой подгруппе энтропия 0.97 (6 «плохих» и 4 «хороших»), а в правой – 0 (всего один объект). Прирост информации получается примерно 0.11.
Посчитав таким образом прирост информации для каждого разбиения, можно предварительно, до построения большого дерева (по всем признакам) отобрать пороги, с которыми будет сравниваться каждый количественный признак.
Еще примеры дискретизации количественных признаков можно посмотреть в постах, подобных этому или этому. Одна из самых известных научных статей на эту тему – «On the handling of continuous-valued attributes in decision tree generation» (U.M. Fayyad. K.B. Irani, «Machine Learning», 1992).
Основные параметры дерева
В принципе дерево решений можно построить до такой глубины, чтоб в каждом листе был ровно один объект. Но на практике это не делается (если строится только одно дерево) из-за того, что такое дерево будет переобученным – оно слишком настроится на обучающую выборку и будет плохо работать на прогноз на новых данных. Где-то внизу дерева, на большой глубине будут появляться разбиения по менее важным признакам (например, приехал ли клиент из Саратова или Костромы). Если утрировать, может оказаться так, что из всех 4 клиентов, пришедших в банк за кредитом в зеленых штанах, никто не вернул кредит. Но мы не хотим, чтобы наша модель классификации порождала такие специфичные правила.
Есть два исключения, ситуации, когда деревья строятся до максимальной глубины:
- Случайный лес (композиция многих деревьев) усредняет ответы деревьев, построенных до максимальной глубины (почему стоит делать именно так, разберемся позже)
- Стрижка дерева (pruning). При таком подходе дерево сначала строится до максимальной глубины, потом постепенно, снизу вверх, некоторые вершины дерева убираются за счет сравнения по качеству дерева с данным разбиением и без него (сравнение проводится с помощью кросс-валидации, о которой чуть ниже). Подробнее можно почитать в материалах репозитория Евгения Соколова.
Картинка ниже – пример разделяющей границы, построенной переобученным деревом.
Основные способы борьбы с переобучением в случае деревьев решений:
- искусственное ограничение глубины или минимального числа объектов в листе: построение дерева просто в какой-то момент прекращается;
- стрижка дерева
Класс DecisionTreeClassifier в Scikit-learn
Основные параметры класса sklearn.tree.DecisionTreeClassifier:
max_depth– максимальная глубина дереваmax_features— максимальное число признаков, по которым ищется лучшее разбиение в дереве (это нужно потому, что при большом количестве признаков будет «дорого» искать лучшее (по критерию типа прироста информации) разбиение среди всех признаков)min_samples_leaf– минимальное число объектов в листе. У этого параметра есть понятная интерпретация: скажем, если он равен 5, то дерево будет порождать только те классифицирующие правила, которые верны как минимум для 5 объектов
Параметры дерева надо настраивать в зависимости от входных данных, и делается это обычно с помощью кросс-валидации, про нее чуть ниже.
Дерево решений в задаче регрессии
При прогнозировании количественного признака идея построения дерева остается та же, но меняется критерий качества:
Пример
Сгенерируем данные, распределенные вокруг функции c некоторым шумом, обучим на них дерево решений и изобразим, какие прогнозы делает дерево.
Код
n_train = 150
n_test = 1000
noise = 0.1
def f(x):
x = x.ravel()
return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)
def generate(n_samples, noise):
X = np.random.rand(n_samples) * 10 - 5
X = np.sort(X).ravel()
y = np.exp(-X ** 2) + 1.5 * np.exp(-(X - 2) ** 2) +
np.random.normal(0.0, noise, n_samples)
X = X.reshape((n_samples, 1))
return X, y
X_train, y_train = generate(n_samples=n_train, noise=noise)
X_test, y_test = generate(n_samples=n_test, noise=noise)
from sklearn.tree import DecisionTreeRegressor
reg_tree = DecisionTreeRegressor(max_depth=5, random_state=17)
reg_tree.fit(X_train, y_train)
reg_tree_pred = reg_tree.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, reg_tree_pred, "g", lw=2)
plt.xlim([-5, 5])
plt.title("Decision tree regressor, MSE = %.2f" % np.sum((y_test - reg_tree_pred) ** 2))
plt.show()Видим, что дерево решений аппроксимирует зависимость в данных кусочно-постоянной функцией.
Метод ближайших соседей
Метод ближайших соседей (k Nearest Neighbors, или kNN) — тоже очень популярный метод классификации, также иногда используемый в задачах регрессии. Это, наравне с деревом решений, один из самых понятных подходов к классификации. На уровне интуиции суть метода такова: посмотри на соседей, какие преобладают, таков и ты. Формально основой метода является гипотеза компактности: если метрика расстояния между примерами введена достаточно удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных.
Согласно методу ближайших соседей, тестовый пример (зеленый шарик) будет отнесен к классу «синие», а не «красные».
Например, если не знаешь, какой тип товара указать в объявлении для Bluetooth-гарнитуры, можешь найти 5 похожих гарнитур, и если 4 из них отнесены к категории «Аксессуары», и только один — к категории «Техника», то здравый смысл подскажет для своего объявления тоже указать категорию «Аксессуары».
Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:
Под задачу регрессии метод адаптируется довольно легко – на 3 шаге возвращается не метка, а число – среднее (или медианное) значение целевого признака среди соседей.
Примечательное свойство такого подхода – его ленивость. Это значит, что вычисления начинаются только в момент классификации тестового примера, а заранее, только при наличии обучающих примеров, никакая модель не строится. В этом отличие, например, от ранее рассмотренного дерева решений, где сначала на основе обучающей выборки строится дерево, а потом относительно быстро происходит классификация тестовых примеров.
Стоит отметить, что метод ближайших соседей – хорошо изученный подход (в машинном обучении, эконометрике и статистике больше известно, наверное, только про линейную регрессию). Для метода ближайших соседей существует немало важных теорем, утверждающих, что на «бесконечных» выборках это оптимальный метод классификации. Авторы классической книги «The Elements of Statistical Learning» считают kNN теоретически идеальным алгоритмом, применимость которого просто ограничена вычислительными возможностями и проклятием размерностей.
Метод ближайших соседей в реальных задачах
- В чистом виде kNN может послужить хорошим стартом (baseline) в решении какой-либо задачи;
- В соревнованиях Kaggle kNN часто используется для построения мета-признаков (прогноз kNN подается на вход прочим моделям) или в стекинге/блендинге;
- Идея ближайшего соседа расширяется и на другие задачи, например, в рекомендательных системах простым начальным решением может быть рекомендация какого-то товара (или услуги), популярного среди ближайших соседей человека, которому хотим сделать рекомендацию;
- На практике для больших выборок часто пользуются приближенными методами поиска ближайших соседей. Вот лекция Артема Бабенко про эффективные алгоритмы поиска ближайших соседей среди миллиардов объектов в пространствах высокой размерности (поиск по картинкам). Также известны открытые библиотеки, в которых реализованы такие алгоритмы, спасибо компании Spotify за ее библиотеку Annoy.
Качество классификации/регрессии методом ближайших соседей зависит от нескольких параметров:
- число соседей
- метрика расстояния между объектами (часто используются метрика Хэмминга, евклидово расстояние, косинусное расстояние и расстояние Минковского). Отметим, что при использовании большинства метрик значения признаков надо масштабировать. Условно говоря, чтобы признак «Зарплата» с диапазоном значений до 100 тысяч не вносил больший вклад в расстояние, чем «Возраст» со значениями до 100.
- веса соседей (соседи тестового примера могут входить с разными весами, например, чем дальше пример, тем с меньшим коэффициентом учитывается его «голос»)
Класс KNeighborsClassifier в Scikit-learn
Основные параметры класса sklearn.neighbors.KNeighborsClassifier:
- weights: «uniform» (все веса равны), «distance» (вес обратно пропорционален расстоянию до тестового примера) или другая определенная пользователем функция
- algorithm (опционально): «brute», «ball_tree», «KD_tree», или «auto». В первом случае ближайшие соседи для каждого тестового примера считаются перебором обучающей выборки. Во втором и третьем — расстояние между примерами хранятся в дереве, что ускоряет нахождение ближайших соседей. В случае указания параметра «auto» подходящий способ нахождения соседей будет выбран автоматически на основе обучающей выборки.
- leaf_size (опционально): порог переключения на полный перебор в случае выбора BallTree или KDTree для нахождения соседей
- metric: «minkowski», «manhattan», «euclidean», «chebyshev» и другие
Выбор параметров модели и кросс-валидация
Главная задача обучаемых алгоритмов – их способность обобщаться, то есть хорошо работать на новых данных. Поскольку на новых данных мы сразу не можем проверить качество построенной модели (нам ведь надо для них сделать прогноз, то есть истинных значений целевого признака мы для них не знаем), то надо пожертвовать небольшой порцией данных, чтоб на ней проверить качество модели.
Чаще всего это делается одним из 2 способов:
- отложенная выборка (held-out/hold-out set). При таком подходе мы оставляем какую-то долю обучающей выборки (как правило от 20% до 40%), обучаем модель на остальных данных (60-80% исходной выборки) и считаем некоторую метрику качества модели (например, самое простое – долю правильных ответов в задаче классификации) на отложенной выборке.
- кросс-валидация (cross-validation, на русский еще переводят как скользящий или перекрестный контроль). Тут самый частый случай – K-fold кросс-валидация
Тут модель обучается раз на разных (
) подвыборках исходной выборки (белый цвет), а проверяется на одной подвыборке (каждый раз на разной, оранжевый цвет).
Получаются оценок качества модели, которые обычно усредняются, выдавая среднюю оценку качества классификации/регрессии на кросс-валидации.
Кросс-валидация дает лучшую по сравнению с отложенной выборкой оценку качества модели на новых данных. Но кросс-валидация вычислительно дорогостоящая, если данных много.
Кросс-валидация – очень важная техника в машинном обучении (применяемая также в статистике и эконометрике), с ее помощью выбираются гиперпараметры моделей, сравниваются модели между собой, оценивается полезность новых признаков в задаче и т.д. Более подробно можно почитать, например, тут у Sebastian Raschka или в любом классическом учебнике по машинному (статистическому) обучению
Примеры применения
Деревья решений и метод ближайших соседей в задаче прогнозирования оттока клиентов телеком-оператора
Считаем данные в DataFrame и проведем предобработку. Штаты пока сохраним в отдельный объект Series, но удалим из датафрейма. Первую модель будем обучать без штатов, потом посмотрим, помогают ли они.
Считывание и предобработка данных
df = pd.read_csv('../../data/telecom_churn.csv')
df['International plan'] = pd.factorize(df['International plan'])[0]
df['Voice mail plan'] = pd.factorize(df['Voice mail plan'])[0]
df['Churn'] = df['Churn'].astype('int')
states = df['State']
y = df['Churn']
df.drop(['State', 'Churn'], axis=1, inplace=True)Выделим 70% выборки (X_train, y_train) под обучение и 30% будут отложенной выборкой (X_holdout, y_holdout). отложенная выборка никак не будет участвовать в настройке параметров моделей, на ней мы в конце, после этой настройки, оценим качество полученной модели. Обучим 2 модели – дерево решений и kNN, пока не знаем, какие параметры хороши, поэтому наугад: глубину дерева берем 5, число ближайших соседей – 10.
Код
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
X_train, X_holdout, y_train, y_holdout = train_test_split(df.values, y, test_size=0.3,
random_state=17)
tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)
tree.fit(X_train, y_train)
knn.fit(X_train, y_train)Качество прогнозов будем проверять с помощью простой метрики – доли правильных ответов. Сделаем прогнозы для отложенной выборки. Дерево решений справилось лучше: доля правильных ответов около 94% против 88% у kNN. Но это мы пока выбирали параметры наугад.
Код для оценки моделей
from sklearn.metrics import accuracy_score
tree_pred = tree.predict(X_holdout)
accuracy_score(y_holdout, tree_pred) # 0.94knn_pred = knn.predict(X_holdout)
accuracy_score(y_holdout, knn_pred) # 0.88Теперь настроим параметры дерева на кросс-валидации. Настраивать будем максимальную глубину и максимальное используемое на каждом разбиении число признаков. Суть того, как работает GridSearchCV: для каждой уникальной пары значений параметров max_depth и max_features будет проведена 5-кратная кросс-валидация и выберется лучшее сочетание параметров.
Настройка параметров моделей
from sklearn.model_selection import GridSearchCV, cross_val_scoretree_params = {'max_depth': range(1,11),
'max_features': range(4,19)}tree_grid = GridSearchCV(tree, tree_params,
cv=5, n_jobs=-1,
verbose=True)tree_grid.fit(X_train, y_train)Лучшее сочетание параметров и соответствующая средняя доля правильных ответов на кросс-валидации:
tree_grid.best_params_{‘max_depth’: 6, ‘max_features’: 17}
tree_grid.best_score_0.94256322331761677
accuracy_score(y_holdout, tree_grid.predict(X_holdout))0.94599999999999995
Теперь попробуем настроить число соседей в алгоритме kNN.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScalerknn_pipe = Pipeline([('scaler', StandardScaler()), ('knn', KNeighborsClassifier(n_jobs=-1))])knn_params = {'knn__n_neighbors': range(1, 10)}knn_grid = GridSearchCV(knn_pipe, knn_params,
cv=5, n_jobs=-1,
verbose=True)knn_grid.fit(X_train, y_train)knn_grid.best_params_, knn_grid.best_score_({‘knn__n_neighbors’: 7}, 0.88598371195885128)
accuracy_score(y_holdout, knn_grid.predict(X_holdout))0.89000000000000001
В этом примере дерево показало себя лучше, чем метод ближайших соседей: 94.2% правильных ответов на кросс-валидации и 94.6% на отложенной выборке против 88.6% / 89% для kNN. Более того, в данной задаче дерево проявляет себя очень хорошо, и даже случайный лес (который пока представляем просто как кучу деревьев, которые вместе работают почему-то намного лучше, чем одно дерево) в этом примере показывает долю правильных ответов не намного выше (95.1% на кросс-валидации и 95.3% –на отложенной выборке), а обучается намного дольше.
Код для обучения и настройки случайного леса
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=100, n_jobs=-1, random_state=17)
print(np.mean(cross_val_score(forest, X_train, y_train, cv=5))) # 0.949forest_params = {'max_depth': range(1,11),
'max_features': range(4,19)}forest_grid = GridSearchCV(forest, forest_params,
cv=5, n_jobs=-1,
verbose=True)forest_grid.fit(X_train, y_train)forest_grid.best_params_, forest_grid.best_score_ # ({'max_depth': 9, 'max_features': 6}, 0.951)accuracy_score(y_holdout, forest_grid.predict(X_holdout)) # 0.953Нарисуем получившееся дерево. Из-за того, что оно не совсем игрушечное (максимальная глубина – 6), картинка получается уже не маленькой, но по дереву можно «прогуляться», если отдельно открыть рисунок.
Код для отрисовки дерева
export_graphviz(tree_grid.best_estimator_, feature_names=df.columns,
out_file='../../img/churn_tree.dot', filled=True)
!dot -Tpng '../../img/churn_tree.dot' -o '../../img/churn_tree.png'Сложный случай для деревьев решений
В продолжение обсуждения плюсов и минусов обсуждаемых методов приведем очень простой пример задачи классификации, с которым дерево справляется, но делает все как-то «сложнее», чем хотелось бы. Создадим множество точек на плоскости (2 признака), каждая точка будет относиться к одному из классов (+1, красные, или -1 – желтые). Если смотреть на это как на задачу классификации, то вроде все очень просто – классы разделяются прямой.
Код для генерации данных и картинки
def form_linearly_separable_data(n=500, x1_min=0, x1_max=30, x2_min=0, x2_max=30):
data, target = [], []
for i in range(n):
x1, x2 = np.random.randint(x1_min, x1_max), np.random.randint(x2_min, x2_max)
if np.abs(x1 - x2) > 0.5:
data.append([x1, x2])
target.append(np.sign(x1 - x2))
return np.array(data), np.array(target)
X, y = form_linearly_separable_data()
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='autumn', edgecolors='black');Однако дерево решений строит уж больно сложную границу и само по себе оказывается глубоким. Кроме того, представьте, как плохо дерево будет обобщаться на пространство вне представленного квадрата , обрамляющего обучающую выборку.
Код для отрисовки разделяющей поверхности, которую строит дерево
tree = DecisionTreeClassifier(random_state=17).fit(X, y)
xx, yy = get_grid(X, eps=.05)
predicted = tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5)
plt.title('Easy task. Decision tree compexifies everything');Вот такая сложная конструкция, хотя решение (хорошая разделяющая поверхность) – это всего лишь прямая .
Код для отрисовки дерева
export_graphviz(tree, feature_names=['x1', 'x2'],
out_file='../../img/deep_toy_tree.dot', filled=True)
!dot -Tpng '../../img/deep_toy_tree.dot' -o '../../img/deep_toy_tree.png'Метод одного ближайшего соседа здесь справляется вроде лучше дерева, но все же не так хорошо, как линейный классификатор (наша следующая тема).
Код для отрисовки разделяющей поверхности, которую строит kNN
knn = KNeighborsClassifier(n_neighbors=1).fit(X, y)
xx, yy = get_grid(X, eps=.05)
predicted = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5);
plt.title('Easy task, kNN. Not bad');Деревья решений и метод ближайших соседей в задаче распознавания рукописных цифр MNIST
Теперь посмотрим на описанные 2 алгоритма в реальной задаче. Используем «встроенные» в sklearn данные по рукописным цифрам. Эта задача будет примером, когда метод ближайших соседей работает на удивление хорошо.
Картинки здесь представляются матрицей 8 x 8 (интенсивности белого цвета для каждого пикселя). Далее эта матрица «разворачивается» в вектор длины 64, получается признаковое описание объекта.
Нарисуем несколько рукописных цифр, видим, что они угадываются.
Загрузка данных и отрисовка нескольких цифр
from sklearn.datasets import load_digits
data = load_digits()
X, y = data.data, data.target
X[0,:].reshape([8,8])array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])
f, axes = plt.subplots(1, 4, sharey=True, figsize=(16,6))
for i in range(4):
axes[i].imshow(X[i,:].reshape([8,8]));
Далее проведем ровно такой же эксперимент, как и в прошлой задаче, только диапазоны изменения настраиваемых параметров будут немного другие.
Настройка DT и kNN на данных MNIST
Выделим 70% выборки (X_train, y_train) под обучение и 30% будут отложенной выборкой (X_holdout, y_holdout). отложенная выборка никак не будет участвовать в настройке параметров моделей, на ней мы в конце, после этой настройки, оценим качество полученной модели.
X_train, X_holdout, y_train, y_holdout = train_test_split(X, y, test_size=0.3,
random_state=17)Обучим дерево решений и kNN, опять параметры пока наугад берем.
tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)
tree.fit(X_train, y_train)
knn.fit(X_train, y_train)Сделаем прогнозы для отложенной выборки. Видим, что метод ближайших соседей справился намного лучше. Но это мы пока выбирали параметры наугад.
tree_pred = tree.predict(X_holdout)
knn_pred = knn.predict(X_holdout)
accuracy_score(y_holdout, knn_pred), accuracy_score(y_holdout, tree_pred) # (0.97, 0.666)Теперь так же, как раньше настроим параметры моделей на кросс-валидации, только учтем, что признаков сейчас больше, чем в прошлой задаче — 64.
tree_params = {'max_depth': [1, 2, 3, 5, 10, 20, 25, 30, 40, 50, 64],
'max_features': [1, 2, 3, 5, 10, 20 ,30, 50, 64]}
tree_grid = GridSearchCV(tree, tree_params,
cv=5, n_jobs=-1,
verbose=True)
tree_grid.fit(X_train, y_train)Лучшее сочетание параметров и соответствующая средняя доля правильных ответов на кросс-валидации:
tree_grid.best_params_, tree_grid.best_score_ # ({'max_depth': 20, 'max_features': 64}, 0.844)Это уже не 66%, но и не 97%. Метод ближайших соседей на этом наборе данных работает лучше. В случае одного ближайшего соседа на кросс-валидации достигается почти 99% угадываний.
np.mean(cross_val_score(KNeighborsClassifier(n_neighbors=1), X_train, y_train, cv=5)) # 0.987Обучим на этих же данных случайный лес, он на большинстве выборок работает лучше, чем метод ближайших соседей. Но сейчас у нас исключение.
np.mean(cross_val_score(RandomForestClassifier(random_state=17), X_train, y_train, cv=5)) # 0.935Вы будете правы, если возразите, что мы тут не настраивали параметры RandomForestClassifier, но даже с настройкой доля правильных ответов не достигает 98%, как для у метода одного ближайшего соседа.
Результаты эксперимента
(Обозначения: CV и Holdout– средние доли правильных ответов модели на кросс-валидации и отложенной выборке соот-но. DT – дерево решений, kNN – метод ближайших соседей, RF – случайный лес)
Вывод по этому эксперименту (и общий совет): вначале проверяйте на своих данных простые модели – дерево решений и метод ближайших соседей (а в следующий раз сюда добавится логистическая регрессия), может оказаться, что уже они работают достаточно хорошо.
Сложный случай для метода ближайших соседей
Теперь рассмотрим еще один простой пример. В задаче классификации один из признаков будет просто пропорционален вектору ответов, но методу ближайших соседей это не поможет.
Код для генерации шумных данных с паттерном
def form_noisy_data(n_obj=1000, n_feat=100, random_seed=17):
np.random.seed(random_seed)
y = np.random.choice([-1, 1], size=n_obj)
# первый признак пропорционален целевому
x1 = 0.3 * y
# остальные признаки – шум
x_other = np.random.random(size=[n_obj, n_feat - 1])
return np.hstack([x1.reshape([n_obj, 1]), x_other]), y
X, y = form_noisy_data()Как обычно, будем смотреть на долю правильных ответов на кросс-валидации и на отложенной выборке. Построим кривые, отражающие зависимость этих величин от параметра n_neighbors в методе ближайших соседей. Такие кривые называются кривыми валидации.
Видим, что метод ближайших соседей с евклидовой метрикой не справляется с задачей, даже если варьировать число ближайших соседей в широком диапазоне. Напротив, дерево решений легко «обнаруживает» скрытую зависимость в данных при любом ограничении на максимальную глубину.
Построение кривых валидации для kNN
from sklearn.model_selection import cross_val_score
cv_scores, holdout_scores = [], []
n_neighb = [1, 2, 3, 5] + list(range(50, 550, 50))
for k in n_neighb:
knn = KNeighborsClassifier(n_neighbors=k)
cv_scores.append(np.mean(cross_val_score(knn, X_train, y_train, cv=5)))
knn.fit(X_train, y_train)
holdout_scores.append(accuracy_score(y_holdout, knn.predict(X_holdout)))
plt.plot(n_neighb, cv_scores, label='CV')
plt.plot(n_neighb, holdout_scores, label='holdout')
plt.title('Easy task. kNN fails')
plt.legend();Обучение дерева
tree = DecisionTreeClassifier(random_state=17, max_depth=1)
tree_cv_score = np.mean(cross_val_score(tree, X_train, y_train, cv=5))
tree.fit(X_train, y_train)
tree_holdout_score = accuracy_score(y_holdout, tree.predict(X_holdout))
print('Decision tree. CV: {}, holdout: {}'.format(tree_cv_score, tree_holdout_score))Decision tree. CV: 1.0, holdout: 1.0
Итак, во втором примере дерево справилось с задачей идеально, а метод ближайших соседей испытал трудности. Впрочем, это минус скорее не метода, а используемой евклидовой метрики: в данном случае она не позволила выявить, что один признак намного лучше остальных.
Плюсы и минусы деревьев решений и метода ближайших соседей
Плюсы и минусы деревьев решений
Плюсы:
- Порождение четких правил классификации, понятных человеку, например, «если возраст < 25 и интерес к мотоциклам, то отказать в кредите». Это свойство называют интерпретируемостью модели;
- Деревья решений могут легко визуализироваться, то есть может «интерпретироваться» (строгого определения я не видел) как сама модель (дерево), так и прогноз для отдельного взятого тестового объекта (путь в дереве);
- Быстрые процессы обучения и прогнозирования;
- Малое число параметров модели;
- Поддержка и числовых, и категориальных признаков.
Минусы:
- У порождения четких правил классификации есть и другая сторона: деревья очень чувствительны к шумам во входных данных, вся модель может кардинально измениться, если немного изменится обучающая выборка (например, если убрать один из признаков или добавить несколько объектов), поэтому и правила классификации могут сильно изменяться, что ухудшает интерпретируемость модели;
- Разделяющая граница, построенная деревом решений, имеет свои ограничения (состоит из гиперплоскостей, перпендикулярных какой-то из координатной оси), и на практике дерево решений по качеству классификации уступает некоторым другим методам;
- Необходимость отсекать ветви дерева (pruning) или устанавливать минимальное число элементов в листьях дерева или максимальную глубину дерева для борьбы с переобучением. Впрочем, переобучение — проблема всех методов машинного обучения;
- Нестабильность. Небольшие изменения в данных могут существенно изменять построенное дерево решений. С этой проблемой борются с помощью ансамблей деревьев решений (рассмотрим далее);
- Проблема поиска оптимального дерева решений (минимального по размеру и способного без ошибок классифицировать выборку) NP-полна, поэтому на практике используются эвристики типа жадного поиска признака с максимальным приростом информации, которые не гарантируют нахождения глобально оптимального дерева;
- Сложно поддерживаются пропуски в данных. Friedman оценил, что на поддержку пропусков в данных ушло около 50% кода CART (классический алгоритм построения деревьев классификации и регрессии – Classification And Regression Trees, в
sklearnреализована улучшенная версия именно этого алгоритма); - Модель умеет только интерполировать, но не экстраполировать (это же верно и для леса и бустинга на деревьях). То есть дерево решений делает константный прогноз для объектов, находящихся в признаковом пространстве вне параллелепипеда, охватывающего все объекты обучающей выборки. В нашем примере с желтыми и синими шариками это значит, что модель дает одинаковый прогноз для всех шариков с координатой > 19 или < 0.
Плюсы и минусы метода ближайших соседей
Плюсы:
- Простая реализация;
- Неплохо изучен теоретически;
- Как правило, метод хорош для первого решения задачи, причем не только классификации или регрессии, но и, например, рекомендации;
- Можно адаптировать под нужную задачу выбором метрики или ядра (в двух словах: ядро может задавать операцию сходства для сложных объектов типа графов, а сам подход kNN остается тем же). Кстати, профессор ВМК МГУ и опытный участник соревнований по анализу данных Александр Дьяконов любит самый простой kNN, но с настроенной метрикой сходства объектов. Можно почитать про некоторые его решения в этой статье;
- Неплохая интерпретация, можно объяснить, почему тестовый пример был классифицирован именно так. Хотя этот аргумент можно атаковать: если число соседей большое, то интерпретация ухудшается (условно: «мы не дали ему кредит, потому что он похож на 350 клиентов, из которых 70 – плохие, что на 12% больше, чем в среднем по выборке»).
Минусы:
- Метод считается быстрым в сравнении, например, с композициями алгоритмов, но в реальных задачах, как правило, число соседей, используемых для классификации, будет большим (100-150), и в таком случае алгоритм будет работать не так быстро, как дерево решений;
- Если в наборе данных много признаков, то трудно подобрать подходящие веса и определить, какие признаки не важны для классификации/регрессии;
- Зависимость от выбранной метрики расстояния между примерами. Выбор по умолчанию евклидового расстояния чаще всего ничем не обоснован. Можно отыскать хорошее решение перебором параметров, но для большого набора данных это отнимает много времени;
- Нет теоретических оснований выбора определенного числа соседей — только перебор (впрочем, чаще всего это верно для всех гиперпараметров всех моделей). В случае малого числа соседей метод чувствителен к выбросам, то есть склонен переобучаться;
- Как правило, плохо работает, когда признаков много, из-за «прояклятия размерности». Про это хорошо рассказывает известный в ML-сообществе профессор Pedro Domingos – тут в популярной статье «A Few Useful Things to Know about Machine Learning», также «the curse of dimensionality» описывается в книге Deep Learning в главе «Machine Learning basics».
На этом мы подходим к концу, надеемся, этой статьи Вам хватит надолго. К тому же, есть еще и домашнее задание.
Домашнее задание № 3
В качестве закрепления материала предлагаем выполнить это задание – разобраться с тем, как работает дерево решений, на игрушечном примере, затем обучить и настроить деревья в задаче классификации данных Adult репозитория UCI. Проверить себя можно отправив ответы в веб-форме (там же найдете и решение).
Актуальные и обновляемые версии демо-заданий – на английском на сайте курса. Также по подписке на Patreon («Bonus Assignments» tier) доступны расширенные домашние задания по каждой теме (только на англ.)
Полезные ресурсы
- Open Machine Learning Course. Topic 3. Classification, Decision Trees and k Nearest Neighbors (перевод этой статьи на английский)
- Видеозапись лекции по мотивам этой статьи
- Реализация многих алгоритмов машинного обучения с нуля – репозиторий rushter. Полезно, например, посмотреть, как реализованы деревья решений и метод ближайших соседей;
- Курс Евгения Соколова по машинному обучению (материалы на GitHub). Хорошая теория, нужна неплохая математическая подготовка;
- Курс Дмитрия Ефимова на GitHub (англ.). Тоже очень качественные материалы;
- Статья «Энтропия и деревья принятия решений» на Хабре;
- Статья «Машинное обучение и анализ данных. Лекция для Малого ШАДа Яндекса» на Хабре.
Какую выгоду можно извлечь из такой структуры данных, как дерево? В этой статье мы расскажем о данных в виде дерева, рассмотрим основные определения, которые следует знать, а также узнаем, как и зачем используется дерево в программировании. Спойлер: бинарные деревья часто применяют для поиска информации в базах данных, для сортировки данных, для проведения вычислений, для кодирования и в других случаях. Но давайте обо всем по порядку.
Основные термины
Дерево — это, по сути, один из частных случаев графа. Древовидная модель может быть весьма эффективна в случае представления динамических данных, особенно тогда, когда у разработчика стоит цель быстрого поиска информации, в тех же базах данных, к примеру. Еще древом называют структуру данных, которая представляет собой совокупность элементов, а также отношений между этими элементами, что вместе образует иерархическую древовидную структуру.
Каждый элемент — это вершина или узел дерева. Узлы, соединенные направленными дугами, называются ветвями. Начальный узел — это корень дерева (корневой узел). Листья — это узлы, в которые входит 1 ветвь, причем не выходит ни одной.
Общую терминологию можно посмотреть на левой и правой части картинки ниже:
Какие свойства есть у каждого древа:
— существует узел, в который не входит ни одна ветвь;
— в каждый узел, кроме корневого узла, входит 1 ветвь.
На практике деревья нередко применяют, изображая различные иерархии. Очень популярны, к примеру, генеалогические древа — они хорошо известны. Все узлы с ветвями, исходящими из единой общей вершины, являются потомками, а сама вершина называется предком (родительским узлом). Корневой узел не имеет предков, а листья не имеют потомков.
Также у дерева есть высота (глубина). Она определяется числом уровней, на которых располагаются узлы дерева. Глубина пустого древа равняется нулю, а если речь идет о дереве из одного корня, тогда единице. В данном случае на нулевом уровне может быть лишь одна вершина – корень, на 1-м – потомки корня, на 2-м – потомки потомков корня и т. д.
Ниже изображен графический вывод древа с 4-мя уровнями (дерево имеет глубину, равную четырем):
Следующий термин, который стоит рассмотреть, — это поддерево. Поддеревом называют часть древообразной структуры, которую можно представить в виде отдельного дерева.
Идем дальше. Древо может быть упорядоченным — в данном случае ветви, которые исходят из каждого узла, упорядочены по некоторому критерию.
Степень вершины в древе — это число ветвей (дуг), выходящих из этой вершины. Степень равняется максимальной степени вершины, которая входит в дерево. В этом случае листьями будут узлы, имеющие нулевую степень. По величине степени деревья бывают:
— двоичные (степень не больше двух);
— сильноветвящиеся (степень больше двух).
Деревья — это рекурсивные структуры, ведь каждое поддерево тоже является деревом. Каждый элемент такой рекурсивной структуры является или пустой структурой, или компонентом, с которым связано конечное количество поддеревьев.
Когда мы говорим о рекурсивных структурах, то действия с ними удобнее описывать посредством рекурсивных алгоритмов.
Обход древа
Чтобы выполнить конкретную операцию над всеми вершинами, надо все эти узлы просмотреть. Данную задачу называют обходом дерева. То есть обход представляет собой упорядоченную последовательность узлов, в которой каждый узел встречается лишь один раз.
В процессе обхода все узлы должны посещаться в некотором, заранее определенном порядке. Есть ряд способов обхода, вот три основные:
— прямой (префиксный, preorder);
— симметричный (инфиксный, inorder);
— обратный (постфиксный, postorder).
Существует много древовидных структур данных: двоичные (бинарные), красно-черные, В-деревья, матричные, смешанные и пр. Поговорим о бинарных.
Бинарные (двоичные) деревья
Бинарные имеют степень не более двух. То есть двоичным древом можно назвать динамическую структуру данных, где каждый узел имеет не большое 2-х потомков. В результате двоичное дерево состоит из элементов, где каждый из элементов содержит информационное поле, а также не больше 2-х ссылок на различные поддеревья. На каждый элемент древа есть только одна ссылка.
У бинарного древа каждый текущий узел — это структура, которая состоит из 4-х видов полей. Какие это поля:
— информационное (ключ вершины);
— служебное (включена вспомогательная информация, однако таких полей может быть несколько, а может и не быть вовсе);
— указатель на правое поддерево;
— указатель на левое поддерево.
Самый удобный вид бинарного древа — бинарное дерево поиска.
Что значит древо в контексте программирования?
Мы можем долго рассуждать о математическом определении древа, но это вряд ли поможет понять, какие именно выгоды можно извлечь из древовидной структуры данных. Тут важно отметить, что древо является способом организации данных в форме иерархической структуры.
В каких случаях древовидные структуры могут быть полезны при программировании:
- Когда данная иерархия существует в предметной области разрабатываемой программы. К примеру, программа должна обрабатывать генеалогическое древо либо работать со структурой каталогов. В таких ситуациях иногда есть смысл сохранять между объектами программы существующие иерархические отношения. В качестве примера можно вывести древо каталогов операционной системы UNIX:
- Когда между объектами, которые обрабатывает программа, отношения иерархии не заданы явно, но их можно задать, что сделает обработку данных удобнее. Как тут не вспомнить разработку парсеров либо трансляторов, где весьма полезным может быть древо синтаксического разбора?
- А сейчас очевидная вещь: поиск объектов более эффективен, когда объекты упорядочены, будь то те же базы данных. К примеру, поиск значения в неструктурированном наборе из тысячи элементов потребует до тысячи операций, тогда как в упорядоченном наборе может хватить всего дюжины. Вывод прост: раз иерархия — эффективный способ упорядочивания объектов, почему же не использовать древовидную иерархию для ускорения поиска узлов со значениями? Так и происходит: если вспомнить бинарные деревья, то на практике их можно применять в следующих целях:
— поиск данных в базах данных (специально построенных деревьях);
— сортировка и вывод данных;
— вычисления арифметических выражений;
— кодирование по методу Хаффмана и пр.
Источники:
- https://pro-prof.com/archives/682;
- http://e-learning.bmstu.ru/moodle/pluginfile.php/7049/mod_resource/content/1/Бинарные%20деревья_14pt2.pdf.