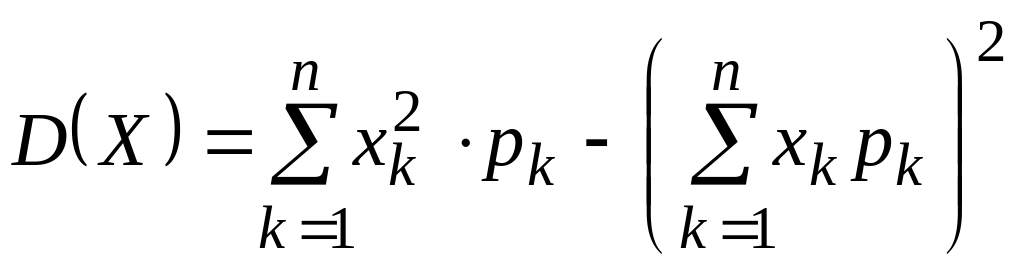Числовые характеристики дискретной случайной величины.
Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
2. Постоянную можно выносить за знак математического ожидания:
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
(для разности аналогично)
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Дисперсию удобно вычислять по формуле:
Свойства дисперсии:
1. Дисперсия постоянной равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:
4.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
Рассмотрим следующие задачи.
1. Математическое ожидание и дисперсия СВ Х соответственно равны 0,5 и 5. Найти математическое ожидание и дисперсию случайной величины .
Решение.
Согласно свойствам математического ожидания и дисперсии, получаем:
2. Случайные величины X и Y независимы, причем 



Решение.
На основании свойств дисперсии получаем:
3. Закон распределения ДСВ Х задан таблицей распределения
 |
1 | 2 | 3 | 4 |
 |
 |
Найти:
1) Так как , т.е.
, следовательно
Т.о. закон распределения примет вид
 |
1 | 2 | 3 | 4 |
 |
2) Для вычисления дисперсии воспользуемся формулой:
Сначала найдем математическое ожидание ДСВ Х2 для этого составим закон распределения этой СВ. Напоминаю, что для этого необходимо каждое значение ДСВ Х возвести в квадрат, а вероятности оставляем прежними. При одинаковых значениях ДСВ вероятности складываем.
3) Найдем среднее квадратическое отклонение:
4)
4. Функция распределения ДСВ Х имеет вид
Найти:
Решение.
Составляем закон распределения ДСВ Х (т.е. выполняем операцию обратную той, которую мы делали в предыдущей статье)
 |
0 | 1 | 2 | 3 |
 |
0,2 | 0,4 | 0,3 | 0,1 |
Составляем закон распределения ДСВ
 |
0 | 1 | 4 | 9 |
 |
0,2 | 0,4 | 0,3 | 0,1 |
5. Независимые случайные величины X и Y заданы таблицами распределения вероятностей
Найти двумя способами:
1. Составив предварительно таблицу распределения СВ ;
2. Используя правило сложения дисперсий.
Решение.
Составим таблицу распределения ДСВ .
Найдем
10+30=40 20+30=50
10+40=50 20+40=60
10+50=60 20+50=70
Т.о. значения ДСВ Z таковы:
Найдем соответствующие им вероятности:
Получаем ряд распределения СВ Z
| 40 | 50 | 60 | 70 | |
 |
0,1 | 0,46 | 0,28 | 0,16 |
2. Используя правило сложения дисперсий:
Если
дискретная случайная величина X
задана законом распределения вероятностей
вида:
то
математическое ожидание
величины
вычисляется по формуле
.
Математическое
ожидание
случайной величины
служит характеристикой среднего
значения величины X.
В задачах
принятия решений математическое
ожидание, например, характеризует
доходность инвестиционного проекта.
Дисперсией
случайной величины
называют математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания:
,
или
.
Дисперсию удобно
вычислять по формулам:
,
или
.
Средним квадратическим
отклонением случайной величины называют
корень квадратный из дисперсии:
.
Дисперсия и среднее
квадратическое отклонение характеризуют
рассеивание возможных значений случайной
величины вокруг ее математического
ожидания (среднего значения). В задачах
принятия решений среднее квадратическое
отклонение служит мерой риска.
№ 70.
Задан закон распределения дискретной
случайной величины X.
-
34
40
42
45
0,3
0,4
0,1
0,2
Найти:
а) математическое ожидание
;
б) дисперсию
и среднее
квадратическое отклонение
.
Решение.
а)
Математическое ожидание
вычислим по формуле:
.
Следовательно,
.
б) Дисперсию
вычислим по формуле
.
Следовательно,
.
И среднее
квадратическое отклонение равно:
.
Ответ:
.
№ 71.
В условиях задачи № 61 найти: условные
математические ожидания составляющие
при
,
и Y
при
.
Решение.
,
.
Ответ:
2,8;
5.
Понятие математического
ожидания широко используется в
микроэкономике при принятии решений в
условиях неопределенности, с использованием
понятия ожидаемой полезности инвестора
или лица, принимающего решение (ЛПР).
Рассмотрим в качестве иллюстрации
следующий пример.
№ 72.
Пусть
ЛПР с функцией полезности
обладает начальным капиталом в 10000 руб.
-
ЛПР может принять
участие в игре, в которой он с вероятностью
0,5 может выиграть или проиграть 2000 руб.
Имеет ли ему смысл покупать страховой
полис, устраняющий риск, за 500 руб., или
не играть. -
ЛПР рискнул, принял
участие в игре и проиграл. Следует ли
ему снова принять участие в игре, или
застраховать свой риск на прежних
условиях.
Решение.
1.
Закон распределения вероятностей
капитала ЛПР при участии в игре без
страховки имеет вид:
|
8000 |
1200 |
|
|
0,5 |
0,5 |
Тогда полезность
такого решения будет равна
ют.
При покупке
страхового полиса закон распределения
вероятностей капитала ЛПР имеет вид:
|
9500 |
11500 |
|
|
0,5 |
0,5 |
с полезностью
ют.
Если вычислить
первоначальную полезность ЛПР:
ют.,
то можно сделать
вывод о том, что ЛПР следует играть,
застраховав свой риск, а без страховки
лучше и не играть.
2.После проигрыша
капитал ЛПР составит 8000 руб., поэтому
его участие в игре второй раз будет
иметь следующую полезность:
а) без страховки
ют.;
б) со страховкой
ют.
Если вычислить
полезность ЛПР после первого проигрыша
ют.,
то можно сделать
вывод о том, что ЛПР может играть и во
второй раз, если полностью застрахует
свой риск.
№ 73
— 74.
Задан закон распределения вероятностей
дискретной случайной величины. Найти
числовые характеристики.
№ 73. №
74.
-
19
21
22
24
7
10
12
14
0,1
0,2
0,3
0,4
0,3
0,2
0,4
0,1
№ 75.
Дан
перечень возможных значений дискретной
случайной величины
:
,
,
,
а
так же известны
,
.
Найти вероятности, соответствующие
возможным значениям X.
№ 76.
Проводятся многократные испытания
некоторого элемента на надежность до
тех пор, пока элемент не откажет. Найти
математическое ожидание и дисперсию
дискретной величины
–
числа испытаний, которое надо провести.
Вероятность отказа элемента в каждом
опыте равна 0,2.
№ 77.
В условиях задачи № 68 найти условные
математические ожидания составляющей
.
№ 78.
В
условиях задачи № 69 найти условные
математические ожидания составляющей
.
№ 79.
Дано следующее состояние рынка ценных
бумаг трех видов
:
-
Состояние
рынка (
)Вероятность
Доходность
ценных бумаг (в %)(хорошее)
0,5
30
20
40
(среднее)
0,3
20
20
10
(плохое)
0,2
-5
-10
-20
Определить, какая из ценных бумаг
является: а) наиболее доходной; б) наименее
рисковой.
№ 80. Летом цена угля за 1 т равна 6
у.е. и у Вас есть место для хранения 6 т
угля. Весь уголь, который не будет
использован в течение зимы, пропадет.
Данные о потребности и ценах на уголь
в зимний период приведены в следующей
таблице:
|
Зима |
Вероятности |
Потребность угля |
Средняя цена за 1 |
|
мягкая |
0,35 |
4 |
7 |
|
обычная |
0,5 |
5 |
7,5 |
|
холодная |
0,15 |
6 |
8 |
Сколько угля Вам следует закупить
летом?
№ 81. В условиях № 72 найдите максимальную
сумму, которую может заплатить ЛПР за
страховку как в первом, так и во втором
случаях.
№ 82. Пусть функция полезности
инвестора имеет вид:
.
Инвестор может вложить в некоторый
проект 25000 руб. и считает, что с одинаковой
вероятностью может получить прибыль в
30000 руб., или потерять все. Определите:
а) следует ли осуществлять инвестирование
проекта; б) какова ожидаемая полезность
инвестирования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Случайной называют величину, которая в результате испытания примет одно и только одно
возможное значение, наперед не известное и зависящее от случайных причин,
которые заранее не могут быть учтены.
Случайные
величины обозначаются прописными буквами
, а их возможные значения – соответствующими строчными буквами
. Например, если случайная величина
имеет три возможных
значения, то они будут обозначены так:
.
Дискретной называют случайную
величину, которая принимает отдельные, изолированные возможные значения с
определенными вероятностями. Число возможных значений дискретной случайной
величины может быть конечным или бесконечным.
Законом распределения дискретной
случайной величины называют соответствие между возможными значениями и их
вероятностями; его можно задать таблично, аналитически (в виде формулы) и
графически.
При табличном задании закона
распределения дискретной случайной величины первая строка таблицы содержит
возможные значения, а вторая – их вероятности:
|
|
|
|
… |
|
|
|
|
|
… |
|
Приняв во внимание, что в одном
испытании случайная величина принимает одно и только одно возможное значение,
заключаем, что события
образуют полную
группу; следовательно, сумма вероятностей этих событий, то есть сумма
вероятностей второй строки таблицы, равна единице:
Если множество возможных значений
бесконечно
(счетно), то ряд
сходится и его
сумма равна единице.
Для наглядности закон распределения
дискретной случайной величины можно изобразить и графически. Для этого в
прямоугольной системе координат строят точки
, а затем соединяют их отрезками прямых. Полученную
фигуру называют многоугольником распределения.
Смежные темы решебника:
- Непрерывная случайная величина
- Функция распределения вероятностей
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Задача 1
В партии
из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Найти закон
распределения числа дефектных курток среди купленных. Построить многоугольник
распределения.
Задача 2
Устройство
состоит из пяти независимых элементов. Вероятность безотказной работы каждого
элемента в одном опыте равна p=0,7. Для случайной
величины X элементов, безотказно работавших в одном опыте,
построить закон распределения, их графики, найти ее числовые характеристики.
Задача 3
С
вероятностью попадания при явном выстреле p=0.88 охотник стреляет по
дичи до первого попадания, но успевает сделать не более n=6
выстрелов.
ДСВ X — число
промахов:
а) Найти
закон распределения X.
б)
Построить многоугольник распределения.
в) Найти
вероятность событий: X<2, X<3,
1<X<3.
Задача 4
Составьте
закон распределения дискретной случайной величины ξ, вычислите ее
математическое ожидание, медиану, дисперсию, среднее квадратическое отклонение,
коэффициенты асимметрии и эксцесса, все моменты, а также начертите ее
многоугольник распределения и график функции распределения. Сделайте выводы по
результатам расчетов.
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор окажется надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8.
ξ – число испытаний, после которых закончится проверка.
Задача 5
В первой урне
6 шаров – 3 белых и 3 черных. Во второй 5 шаров –3 белых и 2 черных. Из первой
урны наудачу переложили во вторую 2 шара, после чего, из второй в первую
переложили 1 шар. Найти закон распределения случайной величины Х – числа белых
шаров в первой урне, после всех перекладываний шаров. Какова вероятность того,
что число белых шаров не больше, чем первоначально. Построить многоугольник
распределения.
Задача 6
В коробке
N=9 карандашей, из которых M=6 красных. Из этой коробки
наудачу извлекается n=5 карандашей.
а) Найти
закон распределения случайной величины X равной числу красных
карандашей в выборке.
б)
Построить многоугольник распределения.
в) Найти
вероятность события: 0<X<4.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор оказался надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8. X – число испытаний, после
которых закончится проверка. Составьте закон распределения случайной величины X,
вычислите ее математическое ожидание, дисперсию, среднее квадратическое
отклонение, а также начертите ее многоугольник распределения и график функции
распределения.
Задача 8
Проведено
n=5 независимых опытов. Вероятность взрыва в каждом опыте равна p=2/7.
Составить закон распределения числа взрывов, вычислить математическое ожидание,
дисперсию, среднеквадратическое отклонение и построить многоугольник
распределения.
Задача 9
Найти закон
распределения указанной дискретной СВ X и ее функции. распределения
F(x). Вычислить математическое ожидание М(Х), дисперсию D(X) и
среднее квадратичное отклонение σ(Х). Построить график
функции распределения F(x).
Вероятность отказа прибора за время испытания
на надежность равна 0,2; СВ Х — число приборов, отказавших в работе, среди 5
испытываемых.
Задача 10
В интернет-магазине
приобретается смартфон. Курьер приносит на дом покупателю 5 одинаковых
смартфонов, среди которых три (заранее неизвестно какие) бракованные.
Покупатель проверяет один за другим, пока не найдет хороший прибор, но делает
не более трех попыток.
Составить
закон распределения случайной величины – числа произведенных попыток.
Найти ее
математическое ожидание, дисперсию, среднее квадратическое отклонение.
Построить
функцию распределения.
Задача 11
В команде
9 спортсменов, из них 4 — первого разряда и 5 — второго. Наудачу отобраны 3
спортсмена. Найти ряд распределения дискретной случайной величины Х — числа
спортсменов второго разряда среди отобранных.
Задача 12
К контролеру с конвейера поступили 4 детали.
Вероятность брака для каждой детали равна 0,1. Детали проверяют одну за другой,
пока не наберут 2 доброкачественные.
Найти закон распределения вероятностей для числа проверенных деталей.
Задача 13
Двое рабочих,
выпускающих однотипную продукцию, допускают производство изделий второго сорта
с вероятностями соответственно равными 0,4 и 0,3. У каждого рабочего взято по 2
изделия. Для случайной величины Х —
числа изделий второго сорта среди отобранных для проверки четырех найти закон
распределения, математическое ожидание и дисперсию.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
На викторине
задаются 3 вопроса. Вероятность правильно ответить на первый – p, на
второй – r, на третий – s. После неправильного
ответа игрок выбывает из игры. Найти распределение числа правильных ответов.
Вычислить математическое ожидание. Решить задачу, если:
а) p=0.7; r=0.6; s=0.3;
б)
p=0.8; r=0.4; s=0.1.
Задача 15
На
некоторой остановке автобус останавливается только по требованию. Вероятность
остановки равна 0,2. За смену автобус проходит мимо этой остановки 5 раз.
Составить закон распределения числа остановки за смену, найти математическое
ожидание и дисперсию этой случайной величины.
Задача 16
Вероятность
того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3.
Аудитору на заключение представлено 3 баланса предприятия. Составить закон
распределения числа положительных заключений на проверяемые балансы.
Задача 17
Два товароведа
проверяют партию изделий. Производительность их труда соотносится как 5:4.
Вероятность определения брака первым товароведом составляет 85%, вторым – 90%.
Из проверенных изделий отбирают четыре. Найти а) математическое ожидание и б)
дисперсию числа годных изделий среди отобранных.
Задача 18
Два
станка выпускают детали с вероятностями брака 0,01 и 0,05 соответственно. В
выборке одна деталь выпущена первым станком и две – вторым. Найти распределение числа бракованных деталей
в выборке.
Задача 19
Монета
подбрасывается до тех пор, пока герб не выпадет 2 раза, но при этом делается не
более 4 бросаний. Найти распределение числа подбрасываний.
Задача 20
Вероятность
сдачи данного экзамена для каждого из n=5 студентов равна p=0.6.
Случайная величина X (СВ X) — число студентов, сдавших экзамен. Найти закон
распределения указанной дискретной СВ X и ее функцию распределения F(x).
Вычислить математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x). Построить график функции распределения F(x).
Содержание:
- Рассмотрим ряд примеров с решением на нахождение математического ожидания.
- Математическое ожидание суммы
- Математическое ожидание произведения
- Дисперсия случайной величины
- Вычисление дисперсии
- Нормированные случайные величины
Числовые характеристики дискретной случайной величины
Исчерпывающей характеристикой дискретной случайной величины является ее закон распределения. Но далеко не в каждой задаче нужно знать весь закон распределения. В ряде случаев можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения. Такого рода числа называют числовыми характеристиками случайной величины (или соответствующего закона распределения).
Их роль в теории вероятностей чрезвычайно велика; многие задачи удается решить до конца, оставляя в стороне законы распределения и оперируя только числовыми характеристиками.
Математическое ожидание случайной величины
Наиболее важное место среди числовых характеристик занимает так называемое математическое ожидание или среднее значение случайной величины.
Чтобы подойти естественным путем к понятию математического ожидания, будем рассуждать следующим образом. Пусть 



и т.д. Найдем среднее арифметическое всех значений, принятых величиной 
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Дробь 







Дадим теперь такое
Определение. Математическим ожиданием или средним значением дискретной случайной величины 
называется число
Таким образом, математическое ожидание дискретной случайной величины 

Смысл числа 


Из определения (4.2) непосредственно вытекает следующий факт.
Математическое ожидание постоянной величины равно ей самой.
Действительно, постоянную величину с можно рассматривать как дискретную случайную величину 

Возможно вам будут полезны данные страницы:
Рассмотрим ряд примеров с решением на нахождение математического ожидания.
Пример 4.1.
Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.
Решение:
Обозначим указанную случайную величину через 
Отсюда
Пример 4.2.
Взнос клиента в страховую компанию составляет 10 руб., а выплата компании при наличии страхового случая 1000 руб. Вероятность страхового случая 0,009. Какую прибыль в среднем имеет компания от одного клиента?
Решение:
Пусть 

Отсюда
Свойства математического ожидания
Ранее был отмечен такой факт: математическое ожидание постоянной величины равно ей самой. Добавим теперь к этому еще одно свойство:
— постоянный множитель с можно вынести за знак математического ожидания.
Для дискретной случайной величины равенство (4.3) очевидно: если 
то 
откуда следует:
Математическое ожидание суммы
Наиболее существенным из всех свойств математического ожидания является следующий факт, который часто называют теоремой сложения математических ожиданий.
Теорема 4.1. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий
Доказательство. Пусть закон распределения системы 
где 




где 


Перепишем формулу (4.5) следующим образом:
Первую сумму правой части можно представить в виде
Выражение 

из событий
т.е. в конечном счете, что 



Аналогично покажем, что
В итоге имеем:
что и требовалось получить.
Нетрудно видеть, что формула (4.4) обобщается на любое число слагаемых:

называют обычно свойствами линейности. Оба свойства линейности можно записать в виде одной формулы:
Математическое ожидание произведения
Доказанная в предыдущем пункте формула (4.4) наводит на мысль о возможности аналогичной формулы для случайной величины
Однако формула (4.6) в общем случае неверна; чтобы в этом убедиться, достаточно взять в качестве 
Тогда 

Докажем, что если случайные величины 

Эту важную теорему часто называют теоремой умножения математических ожиданий. Доказательство. Возможные значения 

Применив такие же рассуждения, как при выводе формулы (4.4), получим равенство
где 
Ввиду независимости величин 
Обозначив

Итак,
Преобразуя полученное равенство, будем иметь:
что и требовалось получить.
Дисперсия случайной величины
Различные случайные величины могут иметь одно и то же математическое ожидание. Рассмотрим, например, величины 
Математические ожидания их одинаковы (равны нулю):
Однако характер распределения величин 


Аналогичных примеров можно привести много. В двух различных географических местностях могут оказаться одинаковые средние уровни осадков, в двух учреждениях с различным соотношением низкооплачиваемых и высокооплачиваемых служащих может оказаться одна и та же средняя заработная плата и т. д.
Укажем еще один пример. Пусть имеются два различных прибора для измерения одной и той же физической величины. Практически результат измерения никогда не совпадает точно с измеряемой величиной: каждое измерение сопровождается случайной ошибкой. Обозначим ошибку при измерении первым прибором через 



Вполне может быть, что для одного из приборов ошибка (по абсолютной величине) принимает в среднем большие значения, чем для другого; проще говоря, один из приборов может оказаться более «разболтанным», давать большее рассеивание результатов измерения, чем другой.
1°. Определение дисперсии и среднего квадратичного отклонения. Рассмотренные в начале параграфа примеры убеждают нас в необходимости вести еще одну числовую характеристику -для измерения степени рассеивания, разброса значений, принимаемых случайной величиной 
Обсудим вопрос о возможных подходах к оценке рассеивания.
На первый взгляд может показаться естественным в качестве характеристики рассеивания взять математическое ожидание разности 



Оказывается, однако, что для характеристики рассеивания число 
В действительности степень рассеивания, т. е. степень удаленности 

меры рассеивания принять не 
линейным отклонением, однако пользоваться ею не очень удобно; читатель по собственному опыту знает, сколь трудно оперировать с формулами, содержащими абсолютные величины. Имеется и другое возражение против числа 
Определение. Дисперсией случайной величины 
Другими словами, дисперсия есть математическое ожидание квадрата отклонения. Из определения (4.8) легко вытекают следующие свойства дисперсии. 1. Дисперсия принимает только неотрицательные значения
Дисперсия дискретной величины 

Действительно, запишем развернутую формулу дисперсии дискретной случайной величины 
Правая часть формулы (4.10) есть сумма неотрицательных слагаемых, причем можно считать, что все вероятности 




2. При умножении случайной величины 
Действительно,
3. Если к случайной величине 

Очевидно,что
т.е. отклонение случайной величины не изменится, следовательно, не изменится и ее дисперсия.
По свойству 1 дисперсия принимает только неотрицательные значения, поэтому определено число
которое носит название среднего квадратичного отклонения величины 

В заключение укажем весьма полезную общую формулу, вытекающую из определения дисперсии:
Доказательство этой формулы основано на известных читателю свойствах математического ожидания. Мы имеем:
Вычисление дисперсии
Наряду с формулой (4.10) часто используют и формулу (4.14). В развернутом виде для дискретной случайной величины 
Пример:
Пусть 

По формуле (4.15), учитывая, что в данном случае 
Нормированные случайные величины
Определение. Случайная величина 
От любой случайной величины 

где 



Лекции:
- Математическое ожидание формула
- Мат ожидание: примеры с решением
- Непрерывные случайные величины примеры с решением
- Числовые характеристики непрерывной случайной величины
- Функция случайной величины
- Дисперсия дискретной случайной величины
- Закон распределении и числовые характеристики непрерывной случайной величины
- Плотность вероятности
- Случайные величины
- Независимые дискретные случайные величины
Дискретная случайная величина: примеры решений задач
На этой странице мы собрали примеры решения учебных задач о дискретных случайных величинах. Это довольно обширный раздел: изучаются разные законы распределения (биномиальный, геометрический, гипергеометрический, Пуассона и другие), свойства и числовые характеристики, для каждого ряда распределения можно строить графические представления: полигон (многоугольник) вероятностей, функцию распределения.
Ниже вы найдете примеры решений о дискретных случайных величинах, в которых требуется применить знания из предыдущих разделов теории вероятностей для составления закона распределения, а затем вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение, построить функцию распределения, дать ответы на вопросы о ДСВ и т.п.
Примеры для популярных законов распределения вероятностей:
- Биномиальный закон распределения
- Гипергеометрический закон распределения
- Геометрический закон распределения
- Закон распределения Пуассона
Лучшее спасибо — порекомендовать эту страницу
Калькуляторы на характеристики ДСВ
- Как найти математическое ожидание случайной величины?
- Как найти дисперсию случайной величины?
- Вычисление математического ожидания, дисперсии и среднего квадратического отклонения ДСВ.
Решенные задачи о ДСВ
Распределения, близкие к геометрическому
Задача 1. На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?
Задача 2. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины.
Задача 3. Стрелок, имея 3 патрона, стреляет в цель до первого попадания. Вероятности попадания при первом, втором и третьем выстрелах соответственно 0,6, 0,5, 0,4. С.В. $xi$ — число оставшихся патронов. Составить ряд распределения случайной величины, найти математическое ожидание, дисперсию, среднее квадратичное отклонение с.в., построить функцию распределения с.в., найти $P(|xi-m| le sigma$.
Задача 4. В ящике содержится 7 стандартных и 3 бракованных детали. Вынимают детали последовательно до появления стандартной, не возвращая их обратно. $xi$ — число извлеченных бракованных деталей.
Составить закон распределения дискретной случайной величины $xi$, вычислить ее математическое ожидание, дисперсию, среднее квадратическое отклонение, начертить многоугольник распределения и график функции распределения.
Задачи с независимыми событиями
Задача 5. На переэкзаменовку по теории вероятностей явились 3 студента. Вероятность того, что первый сдаст экзамен, равна 0,8, второй — 0,7, третий — 0,9. Найдите ряд распределения случайной величины $xi$ числа студентов, сдавших экзамен, постройте график функции распределения, найдите $М(xi), D(xi)$.
Задача 6. Вероятность попадания в цель при одном выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составить закон распределения числа попаданий в цель, если сделано три выстрела. Найти математическое ожидание, дисперсию и С.К.О. этой случайной величины. Построить график функции распределения.
Задача 7. По цели производится 4 выстрела. Вероятность попадания при этом растет так: 0,2, 0,4, 0,6, 0,7. Найти закон распределения случайной величины $X$ — числа попаданий. Найти вероятность того, что $X ge 1$.
Задача 8. Подбрасываются две симметричные монеты, подсчитывается число гербов на обеих верхних сторонах монет. Рассматривается дискретная случайная величина $X$- число выпадений гербов на обеих монетах. Записать закон распределения случайной величины $X$, найти ее математическое ожидание.
Другие задачи и законы распределения ДСВ
Задача 9. Два баскетболиста делают по три броска в корзину. Вероятность попадания для первого баскетболиста равна 0,6, для второго – 0,7. Пусть $X$ — разность между числом удачных бросков первого и второго баскетболистов. Найти ряд распределения, моду и функцию распределения случайной величины $X$. Построить многоугольник распределения и график функции распределения. Вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение. Найти вероятность события $(-2 lt X le 1)$.
Задача 10. Число иногородних судов, прибывающих ежедневно под погрузку в определенный порт – случайная величина $X$, заданная так:
0 1 2 3 4 5
0,1 0,2 0,4 0,1 0,1 0,1
А) убедитесь, что задан ряд распределения,
Б) найдите функцию распределения случайной величины $X$,
В) если в заданный день прибывает больше трех судов, то порт берет на себя ответственность за издержки вследствие необходимости нанимать дополнительных водителей и грузчиков. Чему равна вероятность того, что порт понесет дополнительные расходы?
Г) найдите математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины $X$.
Задача 11. Бросают 4 игральные кости. Найти математическое ожидание суммы числа очков, которые выпадут на всех гранях.
Задача 12. Двое поочередно бросают монету до первого появления герба. Игрок, у которого выпал герб, получает от другого игрока 1 рубль. Найти математическое ожидание выигрыша каждого игрока.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по терверу
Нужны еще решения? Найди в решебнике свое (от 30 рублей и мгновенная доставка):


![Rendered by QuickLaTeX.com [M(C)=C]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-471b40041b6933f0801951cd2c46c645_l3.png)
![Rendered by QuickLaTeX.com [M(CX)=CM(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ded777e15e9adcf8796eeaac76336930_l3.png)
![Rendered by QuickLaTeX.com [M(X_1 cdot X_2 cdot ... cdot X_n)=M(X_1)cdot M(X_2)cdot ... cdot M(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6b30f00123a46fe5905869e2348bdd02_l3.png)
![Rendered by QuickLaTeX.com [M(X_1 + X_2 + ... + X_n)=M(X_1) + M(X_2) + ... + M(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c7b91ac649ba7364f862a40bf8faa91d_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M{[X-M(X)]}^2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-85d713b45963c5757fd071259ac6010f_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M(X^2)-{[M(X)]}^2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0d17db045a4e914ee13c4f6d75c27ea3_l3.png)
![Rendered by QuickLaTeX.com [D(C)=0]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6d535643c4c0b9772d8010dd2bc73943_l3.png)
![Rendered by QuickLaTeX.com [D(CX)=C^2D(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cce0e2900dab2027e7e321a4a122b4a9_l3.png)
![Rendered by QuickLaTeX.com [D(X_1 pm X_2 pm ... pm X_n)=D(X_1) + D(X_2) + ... + D(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-08c51f96c711f2b69dd776944a864ee3_l3.png)
![Rendered by QuickLaTeX.com [D(X+C)=D(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-a915073dccca53c6e5527d0241d183e6_l3.png)
![Rendered by QuickLaTeX.com [sigma (X) =sqrt{D(X)}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-bcacf00d61c4a3f0f69c6d6cfed60d51_l3.png)
![Rendered by QuickLaTeX.com [M(2X-3)=M(2X)+M(-3)=2M(X)-3=2cdot frac12-3=1-3=-2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-010184719e61abad64efd1f6bf166096_l3.png)
![Rendered by QuickLaTeX.com [D(2X-3)=4cdot D(X)=4cdot 5=20]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2a326d2cfcb9cfa50fdee69fe551cee4_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=D(4cdot X- 5 cdot Y +3)=16cdot D(X)+25cdot D(Y)=16cdot 3+25cdot 5=48+125=173]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-72cc99dbd22855f093a923bfe7693994_l3.png)
![Rendered by QuickLaTeX.com [c=1-frac18 -frac14 -frac13=frac{24-3-6-8}{24}=frac{7}{24}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-01420ef852ee1007bd45d93fcbe0b95b_l3.png)
![Rendered by QuickLaTeX.com [M(X)=sum_{i=1}^4 x_i cdot p_i=1cdot frac18+2cdot frac14+3cdot frac13+4cdot frac{7}{24}=frac18+frac12+1+frac76=]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-42c69ea716d0d80a5cc1caa69ef11227_l3.png)
![Rendered by QuickLaTeX.com [M(X^2)=1cdot frac18+4cdot frac14+9cdot frac13+16cdot frac{7}{24}=frac18+1+3+frac{14}{3}=frac{3+96+112}{24}=frac{211}{24};]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-99d6101975deac0f6dbe962de43e23a1_l3.png)
![Rendered by QuickLaTeX.com [D(X)=frac{211}{24}-{left(frac{67}{24}right)}^2=frac{24cdot 211-{67}^2}{{24}^2}=frac{5064-4489}{576}=frac{575}{576};]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cc6b23de18058d53a5ed1fdc11cd9921_l3.png)
![Rendered by QuickLaTeX.com [sigma (X) =sqrt{D(X)}=sqrt{frac{575}{576}}=frac{5sqrt{23}}{24}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-f779e760519df59d8651da0aaa8c2e4b_l3.png)
![Rendered by QuickLaTeX.com [P{X<3}=P{X=1}+P{X=2}=frac18+frac14=frac38]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-65e7c06bd40f6f6cbc44912a49eefda2_l3.png)
![Rendered by QuickLaTeX.com [F(x)={ 0, qquad qquad xle 0 \ 0,2, qquad 0< x le 1, \ 0,6, qquad qquad 1< x le 2 \ 0,9, qquad qquad 2< x le 3 \ 1, qquad qquad x>3]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0947abc5c1ed52fd612642b5b73df2aa_l3.png)
![Rendered by QuickLaTeX.com [M(X), quad M(X^2) quad D(X), quad sigma (X).]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-e2e328ddbafd8e7412cee6e6b7013e8e_l3.png)
![Rendered by QuickLaTeX.com [M(X)=0cdot 0,2+1cdot 0,4+2cdot 0,3+3cdot 0,1=0,4+0,6+0,3=1,3]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-7b7b00dc6dd7147605a5d00f6e4ba120_l3.png)

![Rendered by QuickLaTeX.com [M(X^2)=0cdot 0,2+1cdot 0,4+4cdot 0,3+9cdot 0,1=0,4+1,2+0,9=2,5]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-d3aee42db306199c080afa80f72b3b92_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M(X^2)-{[M(X)]}^2=2,5-{1,3}^2=2,5-1,69=0,81]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cf146049246b3e3f395117bc29116db0_l3.png)
![Rendered by QuickLaTeX.com [sigma (X)=sqrt{0,81}=0,9]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ac025cd6cccf0e250723d48aad978616_l3.png)
![Rendered by QuickLaTeX.com [p_1=P{Z=40}=P{X=10, Y=30}=0,2cdot 0,5=0,1]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-7e1ae4f8b0462f0e7f531d90b468f792_l3.png)
![Rendered by QuickLaTeX.com [p_4=P{Z=70}=P{X=20, Y=50}=0,8cdot 0,2=0,16]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c4ec8e48db0ba1e5f8772cd6e498ea7e_l3.png)
![Rendered by QuickLaTeX.com [M(Z)=sum_{i=1}^4 z_i cdot p_i=40cdot 0,1+50cdot 0,46+60cdot 0,28+70cdot 0,16=4+23+16,8+11,2=55;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ac4878cee852a38e8245022d95b24e00_l3.png)
![Rendered by QuickLaTeX.com [M(Z^2)=sum_{i=1}^4 z_i^2 cdot p_i=1600cdot 0,1+2500cdot 0,46+3600cdot 0,28+4900cdot 0,16=]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ec5b2451d92ebf30458b26e4926d5f63_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=M(Z^2)-{[M(Z)]}^2=3102-3025=77]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-451663c9d742fa3e5fb04afdd7766522_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=D(X+Y)=D(X)+D(Y)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-448a698e43900414c039e2e1e624b053_l3.png)
![Rendered by QuickLaTeX.com [M(X)=10cdot 0,2+20cdot 0,8=2+16=18;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-1ebf2d8b6e0fe85428901ac0b008f5dd_l3.png)
![Rendered by QuickLaTeX.com [M(X^2)=100cdot 0,2+400cdot 0,8=20+320=340;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-32cfe37c5de52468e58eeeadf3e2f766_l3.png)
![Rendered by QuickLaTeX.com [M(Y)=30cdot 0,5+40cdot 0,3+50cdot 0,2=15+12+10=37]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0a5b2478301af6479cd142fcd67c4146_l3.png)
![Rendered by QuickLaTeX.com [M(Y^2)=900cdot 0,5+1600cdot 0,3+2500cdot 0,2=450+480+500=1430]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6b21d4279e597b4488766bf66dc5ec57_l3.png)
![Rendered by QuickLaTeX.com [D(Y)=1430-1369=61]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-641d0e807ce0687edbf79f037574635d_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=16+61=77]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c0e8e4fe96eb97d5374b249328fd738f_l3.png)