При вычислении
суммы или произведения ряда чисел
пользуются соответствующими формулами.
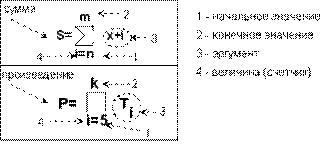
ФОРМУЛА
СУММЫ
Si=Si-1+xi
Сумма равна
предыдущей сумме плюс аргумент. Начальная
сумма равна нулю. При нахождении
количества аргумент равен одному.
ФОРМУЛА
ПРОИЗВЕДЕНИЯ
Pi=Pi-1*xi
Произведение равно
предыдущему произведению, умноженному
на аргумент. Начальное произведение
всегда равно единице.
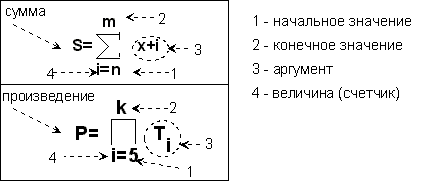
Математически
данные формулы записываются так (рис.
9.14).
Если в аргументе
около имени какой-нибудь величины стоит
индекс
счетчика,
то внутри цикла необходимо поставить
блок ввода этой величины.
Рис.
9. 14. Формулы для вычисления суммы и
произведения
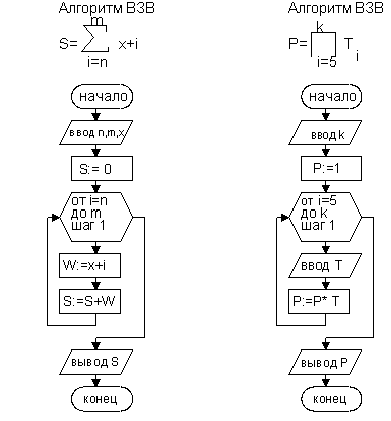
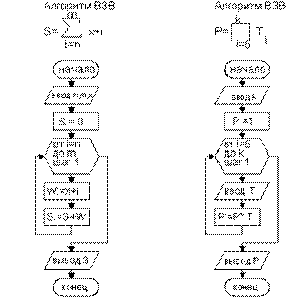
В качестве примера
рассмотрим блок-схемы алгоритмов для
приведенных на рис. 9.14 примеров.
9.3.1.4. Вложенные циклы
Возможны случаи,
когда внутри тела цикла необходимо
повторять некоторую последовательность
операторов, т. е. организовать внутренний
цикл. Такая структура получила название
цикла
в цикле
или вложенных
циклов.
Глубина вложения циклов (то есть
количество вложенных друг в друга
циклов) может быть различной.
Рис.
9. 15. Блок-схемы алгоритмов вычисления
суммы и произведения
При использовании
такой структуры для экономии машинного
времени необходимо выносить из внутреннего
цикла во внешний все операторы, которые
не зависят от параметра внутреннего
цикла.
Рассмотрим два
примера вычисления вложенных циклов.
Рис.
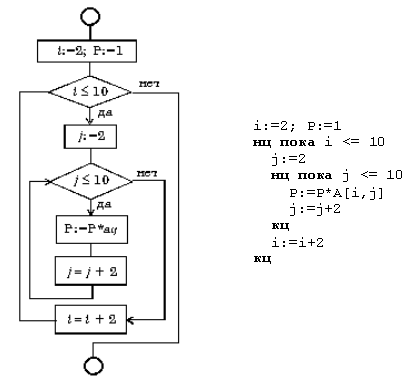
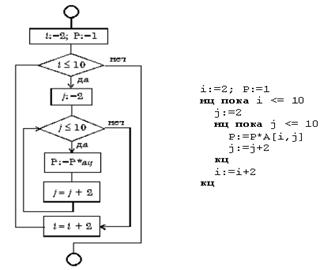
9. 16. Вложенный цикл «до»
Вложенный
цикл «до»
Пример
Вычислите
произведение тех элементов заданной
матрицы A(10,10),
которые расположены на пересечении
четных строк и четных столбцов (рис.
9.16).
Вложенный
цикл «пока»
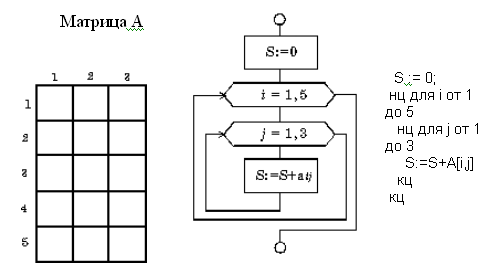
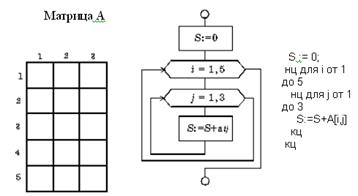
Рис.
9. 17. Вложенный цикл «пока»
Пример
Вычислите сумму
элементов заданной матрицы А(5,3)
– рис. 9.17.
9.4. Языки программирования
9.4.1. Программный способ записи алгоритмов. Уровни языка программирования
При записи алгоритма
в словесной форме, в виде блок-схемы или
на псевдокоде допускается некоторый
произвол при изображении команд. Вместе
с тем такая запись точна настолько, что
позволяет человеку понять суть дела и
исполнить алгоритм.
Однако на практике
в качестве исполнителей алгоритмов
используются специальные автоматы —
компьютеры. Поэтому алгоритм,
предназначенный для исполнения на
компьютере, должен быть записан на
понятном ему языке. И здесь на первый
план выдвигается необходимость точной
записи команд, не оставляющей места для
произвольного толкования их исполнителем.
Следовательно,
язык для
записи алгоритмов должен быть формализован.
Такой язык принято называть языком
программирования,
а запись алгоритма на этом языке —
программой
для компьютера.
В настоящее время
в мире существует несколько сотен
реально используемых языков
программирования. Для каждого есть своя
область применения.
Любой алгоритм
есть последовательность предписаний,
выполнив которые можно за конечное
число шагов перейти от исходных данных
к результату. В зависимости от степени
детализации предписаний обычно
определяется уровень языка программирования
— чем меньше детализация, тем выше
уровень языка.
По этому критерию
можно выделить следующие уровни языков
программирования:
-
машинные;
-
машинно-оpиентиpованные
(ассемблеpы); -
машинно-независимые
(языки высокого уровня).
Машинные языки
и машинно-ориентированные языки —
это языки низкого
уровня,
требующие указания мелких деталей
процесса обработки данных. Языки же
высокого
уровня
имитируют естественные языки, используя
некоторые слова разговорного языка и
общепринятые математические символы.
Эти языки более удобны для человека.
Языки высокого
уровня делятся на:
-
Процедурные
(алгоритмические)
(Basic, Pascal, C и др.), которые предназначены
для однозначного описания алгоритмов;
для решения задачи процедурные языки
требуют в той или иной форме явно
записать процедуру ее решения. -
Логические
(Prolog, Lisp и др.), которые ориентированы
не на разработку алгоритма решения
задачи, а на систематическое и
формализованное описание задачи с тем,
чтобы решение следовало из составленного
описания. -
Объектно-ориентированные
(Object Pascal, C++, Java и др.), в основе которых
лежит понятие
объекта, сочетающего в себе данные и
действия над нами.
Программа на объектно-ориентированном
языке, решая некоторую задачу, по сути,
описывает часть мира, относящуюся к
этой задаче. Описание действительности
в форме системы взаимодействующих
объектов естественнее, чем в форме
взаимодействующих процедур.
При программировании
на машинном
языке программист может держать под
своим контролем каждую команду и каждую
ячейку памяти, использовать все
возможности имеющихся машинных операций.
Но процесс написания
программы на машинном языке очень
трудоемкий
и утомительный.
Программа получается громоздкой,
труднообозримой, ее трудно отлаживать,
изменять и развивать.
Поэтому в случае,
когда нужно
иметь эффективную программу,
в максимальной степени учитывающую
специфику конкретного компьютера,
вместо машинных языков используют
близкие к ним машинно-ориентированные
языки (ассемблеры)
или языки
высокого уровня.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Блок схема вычисления произведения двух чисел
- «Универсальная» блок-схема и 3 типовых алгоритма 🙂
- Алгоритмы вычисления суммы и произведения
- 9.3.1.4. Алгоритмы вычисления суммы и произведения
- 9.3.1.4. Вложенные циклы
- 9.4. Языки программирования
- 9.4.1. Программный способ записи алгоритмов. Уровни языка программирования
- ОАиП | БФЭК
- Учебное пособие
- Составление блок-схем алгоритмов
Блок схема вычисления произведения двух чисел
БлогNot. «Универсальная» блок-схема и 3 типовых алгоритма 🙂
«Универсальная» блок-схема и 3 типовых алгоритма 🙂
Дважды за день заходила речь об одном и том же, да и жаль выкидывать пару картинок, могут ещё понадобиться. Речь шла об изображении базовых типовых алгоритмов, связанных с расчётом какой-либо элементарной характеристики последовательности (массива) — суммы, количества, произведения, максимума, минимума и т.п. В картинках не показаны «начало» и «конец», только содержательная часть.
ГОСТовские «перевёртыши» на практике крайне неудобны, классическое изображение с помощью «ромбика» часто сбивает начинающих с толку похожестью на обычное ветвление (плюс они забывают делать шаг в конце тела цикла), а вот значок «цикла с параметром», если отказаться от паскалевского шага, непременно равного единице, удобен и нормально воспринимается.
I Алгоритм табулирования (составление списка или таблицы)
Что писать в фигурках вместо цифр?
1. Примем, что управляющая переменная цикла называется x , а здесь зададим её начальное ( x1 ) и конечное ( x2 ) значения, а также шаг изменения dx . Это можно записать присваиванием x1=0,x2=1,dx=0.1 или поставить вместо прямоугольника параллелограмм (оператор ввода) с подписью » ввод x1,x2,dx «;
2. Обычно внутри значка «цикл с параметром» (цикл, пределы изменения и шаг управляющей переменной которого известны) пишут что-то вроде псевдокода: » для x от x1 до x2 шаг dx » или то же самое в форме x=x1,x1+dx..x2 или просто x=x1,x2,dx ;
3. Для очередного x вычислить y=f(x) . Этот шаг может включать несколько действий и предполагать вставку дополнительных блоков «расчёт» или условных операторов;
4. Вывести строку таблицы: вывод x, f(x)
II. Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Вместо цифр в элементах блок-схему указываем:
1. Для каждой искомой величины задать по переменной и присвоить ей начальные значения: сумме s=0 , количеству k=0 , произведению p=1 (на самом деле, это не совсем корректно, но для обсуждаемого уровня сойдёт);
2. Выполняется как в задаче I;
3. Считаем очередной элемент последовательности y=f(x) , с тем же замечанием, что к задаче I;
4-5. Если y отвечает условию задачи (проверка на шаге 4), сумма на шаге 5 ищется в виде s=s+f(x) , количество в виде k=k+1 , произведение в виде p=p*f(x) . При нескольких искомых величинах блок вида 4-5 может повторяться несколько раз;
6. По выходе из цикла выводим найденную величину или величины.
III. Алгоритм поиска максимума или минимума
Блок схема задачи II годится и для этого случая.
1. Для каждого максимума или минимума задать по переменной (примем, что минимум обозначен min , а максимум — max ) и присвоить каждой переменной начальные значения: максимуму – заведомо малое значение (например, -10 30 , оператор будет иметь вид Max=-10 30 ) или первый элемент последовательности (массива); минимуму присвоить заведомо большое значение (например, 10 30 ) или первый элемент последовательности;
2-3. Выполняются как в задачах I-II, с теми же замечаниями.
4-5. Для поиска максимума проверяется условие 4 f(x)>max , выполняется действие 5 вида max=f(x) , дли минимума проверяется условие 4 f(x) и выполняется действие 5 вида min=f(x) . С чем сравнивали max или min , то им и присваиваем.Могут понадобиться дополнительные условия, связанные логической операцией «И» либо «ИЛИ» с основным, например, поиск максимального из отрицательных элементов предполагает проверку y max ;
6. По выходе из цикла выводим найденную величину или величины.
Несмотря на обилие средств для рисования блок-схем, удобнее простого Paint из Win7 и выше для этой цели ничего пока не придумали 🙂
IV. Схема ввода и обработки элементов одномерного массива
Как правило, ввод, обработка или вывод одномерного массива (вектора, списка) выполняется поэлементно с помощью цикла с параметром (цикла «for»). Счётчиком цикла служит номер элемента в массиве (обычно применяется нумерация с единицы). Ниже показаны ввод и обработка массива x из 6 элементов.
V. Реализация алгоритма в кратных (вложенных) циклах
Основное отличие – все действия над матрицей (таблицей) выполняются поэлементно в двойном цикле следующего вида:
Здесь показан ввод матрицы A из 6 строк и 4 столбцов, а счётчиками внешнего и внутреннего цикла с параметром служат номера строки ( i ) и столбца ( j ) в матрице. Обработка и вывод элементов матрицы могут быть реализованы аналогичными конструкциями, часто, если элементы обрабатываются последовательно и независимо друг от друга, ввод и обработку или обработку и вывод можно объединить.
Источник
Алгоритмы вычисления суммы и произведения
При вычислении суммы или произведения ряда чисел пользуются соответствующими формулами.
Сумма равна предыдущей сумме плюс аргумент. Начальная сумма равна нулю. При нахождении количества аргумент равен одному.
Произведение равно предыдущему произведению, умноженному на аргумент. Начальное произведение всегда равно единице.
Математически данные формулы записываются так (рис. 9.14).
Если в аргументе около имени какой-нибудь величины стоит индекс счетчика, то внутри цикла необходимо поставить блок ввода этой величины.
Рис. 9. 14. Формулы для вычисления суммы и произведения
В качестве примера рассмотрим блок-схемы алгоритмов для приведенных на рис. 9.14 примеров.
Вложенные циклы
Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.
Рис. 9. 15. Блок-схемы алгоритмов вычисления суммы и произведения
При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.
Рассмотрим два примера вычисления вложенных циклов.
Рис. 9. 16. Вложенный цикл «до»
Вычислите произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов (рис. 9.16).
Рис. 9. 17. Вложенный цикл «пока»
Вычислите сумму элементов заданной матрицы А(5,3) – рис. 9.17.
Источник
9.3.1.4. Алгоритмы вычисления суммы и произведения
При вычислении суммы или произведения ряда чисел пользуются соответствующими формулами.
Сумма равна предыдущей сумме плюс аргумент. Начальная сумма равна нулю. При нахождении количества аргумент равен одному.
Произведение равно предыдущему произведению, умноженному на аргумент. Начальное произведение всегда равно единице.
Математически данные формулы записываются так (рис. 9.14).
Если в аргументе около имени какой-нибудь величины стоит индекс счетчика, то внутри цикла необходимо поставить блок ввода этой величины.
Рис. 9. 14. Формулы для вычисления суммы и произведения
В качестве примера рассмотрим блок-схемы алгоритмов для приведенных на рис. 9.14 примеров.
9.3.1.4. Вложенные циклы
Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.
Рис. 9. 15. Блок-схемы алгоритмов вычисления суммы и произведения
При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.
Рассмотрим два примера вычисления вложенных циклов.
Рис. 9. 16. Вложенный цикл «до»
Вычислите произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов (рис. 9.16).
Рис. 9. 17. Вложенный цикл «пока»
Вычислите сумму элементов заданной матрицы А(5,3) – рис. 9.17.
9.4. Языки программирования
9.4.1. Программный способ записи алгоритмов. Уровни языка программирования
При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается некоторый произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм.
Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы — компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем.
Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке — программой для компьютера.
В настоящее время в мире существует несколько сотен реально используемых языков программирования. Для каждого есть своя область применения.
Любой алгоритм есть последовательность предписаний, выполнив которые можно за конечное число шагов перейти от исходных данных к результату. В зависимости от степени детализации предписаний обычно определяется уровень языка программирования — чем меньше детализация, тем выше уровень языка.
По этому критерию можно выделить следующие уровни языков программирования:
машинно-независимые (языки высокого уровня).
Машинные языки и машинно-ориентированные языки — это языки низкого уровня, требующие указания мелких деталей процесса обработки данных. Языки же высокого уровня имитируют естественные языки, используя некоторые слова разговорного языка и общепринятые математические символы. Эти языки более удобны для человека.
Языки высокого уровня делятся на:
Процедурные (алгоритмические) (Basic, Pascal, C и др.), которые предназначены для однозначного описания алгоритмов; для решения задачи процедурные языки требуют в той или иной форме явно записать процедуру ее решения.
Логические (Prolog, Lisp и др.), которые ориентированы не на разработку алгоритма решения задачи, а на систематическое и формализованное описание задачи с тем, чтобы решение следовало из составленного описания.
Объектно-ориентированные (Object Pascal, C++, Java и др.), в основе которых лежит понятие объекта, сочетающего в себе данные и действия над нами. Программа на объектно-ориентированном языке, решая некоторую задачу, по сути, описывает часть мира, относящуюся к этой задаче. Описание действительности в форме системы взаимодействующих объектов естественнее, чем в форме взаимодействующих процедур.
При программировании на машинном языке программист может держать под своим контролем каждую команду и каждую ячейку памяти, использовать все возможности имеющихся машинных операций.
Но процесс написания программы на машинном языке очень трудоемкий и утомительный. Программа получается громоздкой, труднообозримой, ее трудно отлаживать, изменять и развивать.
Поэтому в случае, когда нужно иметь эффективную программу, в максимальной степени учитывающую специфику конкретного компьютера, вместо машинных языков используют близкие к ним машинно-ориентированные языки (ассемблеры) или языки высокого уровня.
Источник
ОАиП | БФЭК
Учебное пособие
Составление блок-схем алгоритмов
Блок-схемы используются для визуального представления алгоритмов.
Определение:
Алгоритм — это последовательность шагов, ведущая к решению задачи
Определение:
Блок-схема — это схематическое изображение, иллюстрирующее последовательность операторов, которые необходимо выполнить для достижения результата
Инструкции изображаются, используя специальные символы. Символы связываются между собой стрелками, для указания порядка выполнения.
Блок-схемы широко используются при написании программ, так как они:
- Гораздо проще для понимания, чем запись в виде команд.
- Упрощают процесс отладки.
- Позволяют составить эффективную программную документацию.
- Облегчают процесс демонстрации и обсуждения программы.
Блоки, из которых составляются блок-схемы, представлены на Рисунке 1.
Рассмотрим работу с блок-схемами на примере. Для этого нарисуем блок-схему программы нахождения суммы двух чисел:
Блок-схема, показанная на Рисунке 2, иллюстрирует линейную логику. Здесь нет повторений и ветвления.
Способность сравнивать значения и исполнять, в зависимости от полученного результата, различные участки программы превращает компьютер из большого калькулятора в мощное средство решения различных практических задач. Операторы выбора применяются для:
- Сравнения данных
- Выбора одного из альтернативных путей решения задачи.
Например, при снятии денег с банковского счета производится сравнение снимаемой суммы с суммой на счете. Если снимаемая сумма меньше, то заказ выполняется. В противном случае происходит отказ от обслуживания.
Определение:
Ветвление — это процесс выбора из двух, или более альтернативных путей вычисления. Рассмотрим ветвление на следующих примерах:
Пример 1. Посмотрим на то, как будет выглядеть блок-схема алгоритма проверки чисел на четность:
- Ветвление используется в том случае, когда необходимо разделить поток вычислений на два и более альтернативных варианта. Основанием для выбора маршрута является результат проверки истинности условия ветвления.
Пример 2. Рассмотрим блок-схему алгоритма, определяющего максимальное из 3-х чисел (см. рис. 4):
Как мы видим, ветвление производится, когда нам необходимо выбрать дальнейший маршрут в зависимости от истинности некоего условия, называемого также условием ветвления.
Основные типы блок-схем, использующих ветвление, представлены на Рисунке 5:
На Рисунке 5(а) представлена неполная конструкция условного ветвления. Здесь, в зависимости от выбранного маршрута движения, выполняется один или несколько вычислительных шагов, или происходит дальнейшее движение без вычислений, до момента слияния маршрутов.
На Рисунке 5(b) представлен полный вариант условного ветвления. Здесь, в зависимости от выбранного маршрута движения, выполняется одна или другая последовательность вычислений, после чего маршруты вновь сливаются.
Определение:
Цикл — это многократно выполняемый участок алгоритма.
Тело цикла-это последовательность выполняемых в цикле операторов.
Итерация — однократное выполнение тела цикла.
- С фиксированным числом итераций
- С переменным числом итераций
Рассмотрим различия между этими двумя типами на следующих примерах:
Пример 3. Пусть есть данные о расходах за каждый месяц года. Блок-схема алгоритма подсчитывающего расходы за год будет иметь вид:
Рисунок 6 иллюстрирует цикл с фиксированным числом итераций — число месяцев в году известно и последовательность вычислений не может быть повторена более 12 раз.
Мы читаем расходы за один месяц и добавляем их к общему результату. После этого номер месяца сравнивается с 12.
Если номер месяца равен 12, то цикл завершается, и выводятся данные о расходах за год. В противном случае цикл повторяется для следующего месяца.
Пример 4. Пусть есть информация о каждом жителе города (имя, возраст, пол и т.д.). Необходимо составить список жителей старше 50 лет. Блок-схема соответствующего алгоритма будет иметь вид:
Рисунок 7 иллюстрирует цикл с переменным числом итераций — нам заранее неизвестно число жителей города старше 50 лет. Этот цикл выполняется до тех пор, пока есть еще неучтенные люди. Цикл представляется в виде следующей элементарной блок-схемы:
- В цикле с фиксированным числом итераций количество итераций известно заранее. Вычисления, производящиеся внутри цикла, не оказывают никакого влияния на число итераций.
- Цикл с переменным числом итераций выполняется до тех пор, пока не будет выполнено некоторое условие. Количество итераций в таком цикле может варьироваться.
- Циклы обычно выполняются до тех пор, пока какое-либо условие не примет значение true или false.
РАЗДЕЛЕНИЕ БЛОК-СХЕМ НА ЧАСТИ
При работе с блок-схемами мы часто сталкиваемся со следующими проблемами:
- Блок-схема может не поместиться на одной странице.
- Может оказаться сложным связать все элементы блок-схемы друг с другом непосредственно.
Для решения этих проблем блок-схемы обычно разбивают на отдельные части, для состыковки которых используются элементы- соединители.
Соединительный элемент имеет свой собственный, уникальный номер и состоит из двух частей. Эти части изображаются в местах разрыва соединительных линий. Для определения принадлежности частей соединительному элементу, номер элемента записывается на каждой из частей.
Например, разбив на 2 части блок-схему, изображенную на Рисунке 2 мы получим:
- Соединители вставляются в местах разрыва блок-схемы. Расположение каждого объединения указывается с помощью уникального номера.
- В блок-схеме может быть только одна вершина Начало и только одна вершина Конец.
- Используйте машинно-независимые элементы.
- Не обязательно представлять в блок-схеме каждый шаг программы. Можно ограничиться наиболее важными блоками.
- Желательно использовать наглядные названия переменных и блоков.
- Помните, программа должна быть написана так, чтобы любой другой программист смог бы легко понять ее.
МЕТОД ПРОГОНКИ
Метод прогонки используется для проверки правильности работы программы без использования компьютера. Для этого составляется специальная таблица, в которую записываются значения переменных по шагам. Этот метод позволяет эффективно находить и устранять логические ошибки. Проиллюстрируем этот метод следующим примером:
ТАБЛИЦА ПОШАГОВОГО ПРОГОНА
| X | Y | М | |
| Начальные значения | 10 | 5 | 0 |
| после шага 5 | 10 | 5 | 65 |
| после шага 6 | 10 | 9 | 65 |
| после шага 7 | 10 | 9 | 74 |
Таким образом, на 8-м шаге на экран будет выведено: 10, 9 и 74.
Источник
14
CРОЧНО ПОМОГИТЕ
составить блок схему которая вычисляет произведение чисел от 1 до 10
1 ответ:
0
0
Блок-схема — в прилагаемом файле.
Читайте также
Все удачные наборы команд должны включать остановку на отметке 10 футов.
На отметку 1 фут робот может попасть с помощью одной команды A;
на отметку 2 фута — с помощью команд AA и B (всего 2 набора команд);
на отметку 3 фута — с помощью команд AAA, AB, BA и C (4 набора).
Так как за одну команду робот может переместиться на 1, 2 или 3 фута, то для подсчета количества наборов команд, позволяющих роботу попасть на отметки N > 3, можно использовать формулу
K(N) = K(N-1)+K(N-2)+K(N-3).
K(4) = K(3)+K(2)+K(1) = 4+2+1 = 7
K(5) = K(4)+K(3)+K(2) = 7+4+2 = 13
K(6) = K(5)+K(4)+K(3) = 13+7+4 = 24
K(7) = K(6)+K(5)+K(4) = 24+13+7 = 44
K(8) = K(7)+K(6)+K(5) = 44+24+13 = 81
K(9) = K(8)+K(7)+K(6) = 81+44+24 = 149
K(10) = K(9)+K(8)+K(7) = 149+81+44 = 274
Так как вторая часть пути робота также имеет длину 10, то общее количество удачных наборов команд = 274*274 = 75076
Числовая информация — данные, выраженные в виде специальных символов — цифр, чисел. Необходима для, например экономических взаимоотношений. Пример такой информации — ценники в магазинах, данные различных приборов, и пр.
текстовая информация — это перенос речи, мыслей, рассуждений в форму текста — сочетания букв, причем различные языки имеют свой набор символов. Пример такой информации — книги, различные документы, протоколы и пр.
графическая информация — самый, наверное, древний способ отображения и передачи информации. Это — различные изображения. Примеры — наскальная живопись, фрески, картины, диаграммы, чертежи, схемы и пр.
звуковая — информация, в основе которой лежат звуковые колебания. Так же — один из древнейших видов. Примеры — человеческая речь, музыка, различного рода сигнализация и пр.
Видеоинформация — информация, хранящаяся в таком формате, что при воспроизведении ее происходит передача с изменением объекта во времени, информация сменяется информацией — графические объекты «движутся». Пример видеоинформации — кино, телевидение, компьютерные игры и пр…
Количество символов в тексте k=I/i, где I- объем текста, i- количество бит на 1 символ.
i=㏒₂N, где N- количество символов в алфавите.
i=㏒₂64 = 6 бит
k=8190/6= 1365 символов
Зрение
Слух
Вкус
Обоняние
Осязание
A div b -целочисленное деление a на b
a mod b -остаток от деления а на b
после подстановки вместо х числа 3 последовательно получаем = (3+2)*(1+3)/(2)=5*4/2=20/2=10 Ответ 1)
«Универсальная» блок-схема и 3 типовых алгоритма 
Дважды за день заходила речь об одном и том же, да и жаль выкидывать пару картинок, могут ещё понадобиться. Речь шла об изображении базовых типовых алгоритмов, связанных с расчётом какой-либо элементарной характеристики последовательности (массива) — суммы, количества, произведения, максимума, минимума и т.п.
В картинках не показаны «начало» и «конец», только содержательная часть.
ГОСТовские «перевёртыши» на практике крайне неудобны, классическое изображение с помощью «ромбика» часто сбивает начинающих с толку похожестью на обычное ветвление (плюс они забывают делать шаг в конце тела цикла),
а вот значок «цикла с параметром», если отказаться от паскалевского шага, непременно равного единице, удобен и нормально воспринимается.
I Алгоритм табулирования (составление списка или таблицы)
Алгоритм табулирования (составление списка или таблицы)
Что писать в фигурках вместо цифр?
1. Примем, что управляющая переменная цикла называется x, а здесь зададим её начальное (x1) и конечное (x2) значения, а также шаг изменения dx. Это можно записать присваиванием x1=0,x2=1,dx=0.1 или поставить вместо прямоугольника параллелограмм (оператор ввода) с подписью «ввод x1,x2,dx«;
2. Обычно внутри значка «цикл с параметром» (цикл, пределы изменения и шаг управляющей переменной которого известны) пишут что-то вроде псевдокода: «для x от x1 до x2 шаг dx» или то же самое в форме x=x1,x1+dx..x2 или просто x=x1,x2,dx ;
3. Для очередного x вычислить y=f(x). Этот шаг может включать несколько действий и предполагать вставку дополнительных блоков «расчёт» или условных операторов;
4. Вывести строку таблицы: вывод x, f(x)
II. Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Вместо цифр в элементах блок-схему указываем:
1. Для каждой искомой величины задать по переменной и присвоить ей начальные значения: сумме s=0, количеству k=0, произведению p=1 (на самом деле, это не совсем корректно, но для обсуждаемого уровня сойдёт);
2. Выполняется как в задаче I;
3. Считаем очередной элемент последовательности y=f(x), с тем же замечанием, что к задаче I;
4-5. Если y отвечает условию задачи (проверка на шаге 4), сумма на шаге 5 ищется в виде s=s+f(x), количество в виде k=k+1, произведение в виде p=p*f(x). При нескольких искомых величинах блок вида 4-5 может повторяться несколько раз;
6. По выходе из цикла выводим найденную величину или величины.
III. Алгоритм поиска максимума или минимума
Блок схема задачи II годится и для этого случая.
1. Для каждого максимума или минимума задать по переменной (примем, что минимум обозначен min, а максимум — max) и присвоить каждой переменной начальные значения: максимуму – заведомо малое значение (например, -1030, оператор будет иметь вид Max=-1030) или первый элемент последовательности (массива); минимуму присвоить заведомо большое значение (например, 1030) или первый элемент последовательности;
2-3. Выполняются как в задачах I-II, с теми же замечаниями.
4-5. Для поиска максимума проверяется условие 4 f(x)>max, выполняется действие 5 вида max=f(x), дли минимума проверяется условие 4 f(x)<min и выполняется действие 5 вида min=f(x). С чем сравнивали max или min, то им и присваиваем.Могут понадобиться дополнительные условия, связанные логической операцией «И» либо «ИЛИ» с основным, например, поиск максимального из отрицательных элементов предполагает проверку y<0 and y>max;
6. По выходе из цикла выводим найденную величину или величины.
Несмотря на обилие средств для рисования блок-схем, удобнее простого Paint из Win7 и выше для этой цели ничего пока не придумали 
IV. Схема ввода и обработки элементов одномерного массива
Как правило, ввод, обработка или вывод одномерного массива (вектора, списка) выполняется поэлементно с помощью цикла с параметром (цикла «for»). Счётчиком цикла служит номер элемента в массиве (обычно применяется нумерация с единицы). Ниже показаны ввод и обработка массива x из 6 элементов.
Схема ввода и обработки элементов одномерного массива
V. Реализация алгоритма в кратных (вложенных) циклах
Основное отличие – все действия над матрицей (таблицей) выполняются поэлементно в двойном цикле следующего вида:
Блок-схема двойного цикла с параметром
Здесь показан ввод матрицы A из 6 строк и 4 столбцов, а счётчиками внешнего и внутреннего цикла с параметром служат номера строки (i) и столбца (j) в матрице. Обработка и вывод элементов матрицы могут быть реализованы аналогичными конструкциями, часто, если элементы обрабатываются последовательно и независимо друг от друга, ввод и обработку или обработку и вывод можно объединить.
31.10.2016, 21:46 [10939 просмотров]
Ответы с готовыми решениями:

1)Разработать блок-схему и текст программы для вычисления суммы и произведения всех целых чисел в…
Составить блок-схему к программе вычисления произведения
Var i,n,s,p:longint;
Begin
Writeln(‘Введите N:’);
Readln(n);
i:=0;
s:=0;
p:=1;
While i<n do…

1. Составьте блок-схему алгоритма и программу вычисления произведения четных чисел, меньших 15.
…
Вывести сумму чисел, если она больше их произведения — составить блок-схему
№1. Ввести два числа
Вывести их сумму, если она больше произведения этих чисел.
1