На чтение 12 мин Просмотров 4 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
П.6. Методика составления программ на языке программирования Бейсик



Программа на Бэйсике представляет собой последовательность строк, каждая строка снабжается десятичным номером. Выполнение программы осуществляется в порядке возрастания номеров. Причем последовательность номеров строк не обязательно должна состоять из следующих друг за другом натуральных чисел. Для того, чтобы облегчить в процессе составления программы вставление новых строк между уже имеющимися, строки программы обычно нумеруются с шагом в 10 номеров. Каждая строка содержит один или несколько операторов.
Программы могут быть линейными (когда каждый оператор в указанной последовательности выполняется ровно один раз), разветвленные (когда выполнение одной из нескольких групп операторов зависит от соблюдения некоторого условия), циклических (когда какой-то блок операторов выполняется многократно).
Начинать составление программы рекомендуется с составления блок-схемы алгоритма. А написание программы сводится к замене блока алгоритма соответствующими операторами.
Пример 11.6.1 Даны 2 действительных числа. Требуется вычислить в программируемом режиме среднее арифметическое этих чисел и среднее геометрическое их модулей.
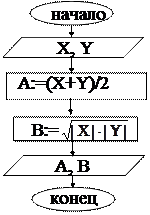
10 REM «Вычисление ср.ар. и ср. геом.»
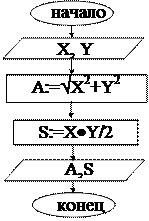
10 REM «Вычисление гипот. и площади»
20 INPUT «Введите значения катетов:»;X,Y
50 PRINT «Гипотенуза=»;A;»Площадь=»;S
| X | Y | A | S |
| 640.3124 | |||
| 728.5307 |
2. Разветвляющиеся программы.
Для реализации логического блока используется оператор условного перехода. Он изменяет ход выполнения программы в зависимости от результата проверки условия. Эта управляющая конструкция называется развилка. На Бейсике развилка выражается с помощью оператора:
IF выражение THEN операторы ELSE операторы
Пример 11.6.3Вычислить действительные корни квадратного уравнения 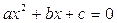
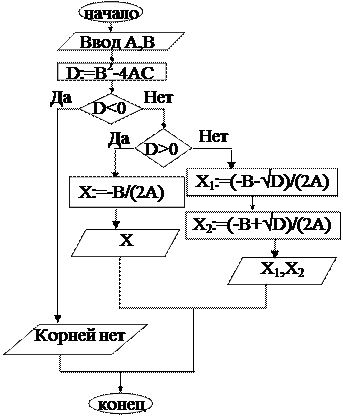
40 IF D 0 THEN 80 ELSE 110

10 REM»ОПРЕДЕЛЕНИЕ ЧЕТНОСТИ»
30 IF X / 2 = INT(X / 2) THEN 30 ELSE 60
Циклы с произвольным числом повторений реализуются с помощью базовых алгоритмических структур цикл-“пока”, цикл-“до”, цикл с параметром
Цикл-“пока” реализуется на Бейсике с помощью операторов
IF … THEN…ELSE и GOTO…
Пример 11.6.5 Дано натуральное число n. Вычислить n!.

50 IF M M THEN 90 ELSE 50

Пример 11.6.8 Дано действительное число а. Найти среди чисел 
10 REM «НАХОЖДЕНИЕ ЭЛЕМЕНТА»
70 IF S > A THEN 80 ELSE 50

FOR счетчик = начало TO конец [STEP приращение]
Пример 11.6.9 Вычислить (для данного n) n!.
10 REM»Вычисление факториала»
Пример 11.6.10 Вычислить значение функции y=4x 3 -2x 2 +5 для значений х, изменяющихся от -3 до 1 с шагом 0,1.
10 REM «Вычисл. значения функции»
30 Y = Y * X ^ 3 — 2 * X ^ 2 + 5
Э. Дийкстр (известный математик) в своей структурной теореме сказал: «Алгоритм любой сложности можно реализовать, используя триаду «следование» — «повторение (циклы)» — «выбор (развилки)».
НОД(56,24) = НОД(24,32) = НОД(24,8) = НОД(8,16) = НОД(8,8) = 8
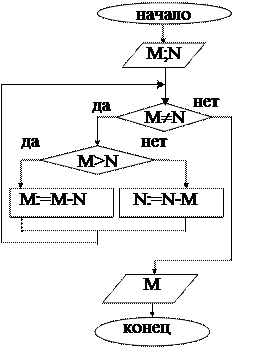
Даны натуральные числа n, m. Используя алгоритм Евклида, найти наибольший общий делитель n и m.
40 IF M>N THEN M=M-N ELSE N=N-M
Пример 11.6.12 Задано n троек чисел a, b, c. Определить, сколько из предложенных троек можно использовать для построения треугольника, если
a, b, c – длины его сторон.
Источник
Как составить блок схему в бейсике
Понятие об алгоритмах. Псевдокод. Блок-схемы.
Вначале пару слов: у нас сегодня радостный день (ну, не знаю, как у вас, а у меня — точно), т.к. у меня появился помошник в написании уроков VB. Прошу любить и жаловать — с сегодняшнего дня с вами — Dusk. Он согласился взять на себя тяжкий труд по подбору и сочинению заданий для уроков. Dusk, большое спасибо, ты значительно мне помогаешь. В том числе-морально.
Ученые проводят опыт. Под потолком подвешен вне досягаемости банан и бутылка водки. Испытуемые — шимпанзе и алкоголик. В углу лежит ящик. Обезьяна пару раз подпрыгивает, останавливается, потом идет к ящику, ставит его под банан, достает и ест. Пьяница прыгает дальше. Ученые сжалились и стали подсказывать: «Да ты погоди, постой, подумай. » На что получили ответ: «Что тут думать! Прыгать надо. «
Этот урок опять общий, так как мы будем говорить о вещах абсолютно не зависящих от какого-то ни было языка программирования. Да и вообще, по сути говоря, ни от чего, не зависящих, кроме наших с вами мозгов.
Для программиста алгоритм всегда был важнее языка, т.к. он показывает как сделать, а язык — как это написать. Непонятно в чем разница? Разберемся.
Язык — это синтаксис, то есть, правильно описанная операция: взяли правильные для этого языка ключевые слова, правильно описали переменную и ее тип, правильно закончили строку, правильно написали операторы и т.д. Чтобы компилятор или интерпретатор — что там с вашим языком работает — поняли в чем дело, что от них требуют и не выдали ошибки.
Алгоритм — это сама операция, которая должна в этом месте выполняться и все равно на каком языке вы ее опишете (если абстрагироваться от некоторых специальных возможностей, плюсов и минусов разных языков).
Если вы не знаете языка, его всегда с большей или меньшей скоростью и желанием можно выучить. Это не принципиально. Если вы не можете создать рабочий алгоритм, каким бы языком вы не владели, программы не будет. Это очень принципиально.
Очень часто начинающие программисты ахают и открывают рты, когда маститые мэтры бросают через плечо: «Да какая разница на чем писать!» Понятно, эту фразу очень трудно понять, когда ты еще путаешься в элементарных синтаксических правилах одного языка, а остальные ощущаются как какие-то неподъемные громады в тумане: нечто неясное и аморфное. И очень неясно зачем писать какие-то алгоритмы непонятные. Код надо писать, код! А если неправильно написали, мы чего-нибудь исправим, и опять запустим, и так пока не заработает.
О! В таком виде работа очень напоминает приведенный эпиграф. Прямо один в один!
НО! Не все так плохо. На самом деле каждый из нас даже тот, кто ни в какую не понимает и зачем это ему/ей алгоритмы, он/она и так все нормально сделает, даже такие кадры где-нибудь про себя, в голове, нет-нет да и подумают: ага, сначала надо будет сделать вот это, а после него — то. Вот тут они и попались, т.к. такие мысли можно смело отнести к алгоритмам.
Итак, алгоритм — это последовательность операций (в обычной жизни — действий). Что за чем мы должны сделать, чтобы получить какой-то результат. На самом деле мы уже знакомились с составлением алгоритмов, во всяком случае те, кто читал Вводную лекцию по курсу программирования для начинающих. Напомню — посмотрите задание 1. То, что в нем предлагалось вам сделать, и было написанием алгоритма.
Мне тут подсказывает Сашок, что можно привести хороший пример для сравнения языка с алгоритмом: сделать то же описание похода на кухню по-русски, по-английски и, скажем, по-японски. Алгоритм один и тот же, языки — разные. Выучил новый язык — можешь описать и на нем. Но если не в силах просто членораздельно описать, как пройти на кухню, тогда за программирование лучше и не браться. Даже на самом простом языке.
Каким должен быть алгоритм?
- Правильным или результативным. То есть, он должен обеспечивать такую последовательность действий, которая позволит вам достичь результата. Если вы, описывая алгоритм утреннего вставания-одевания, опустите операцию «взять одежду в руки», удастся вам одеться? Сомневаюсь, если только вы не фея. Следовательно, такой алгоритм будет неверным без одной-единственной операции.
- Однозначным. Он должен быть написан так, чтобы не было возможности не единственным образом толковать правила и порядок выполнения действий.
- Эффективным. То есть, он должен достигать результата максимально удобным и коротким способом. Например, если взять тот же алгоритм «как дойти до кухни из комнаты», то можно сделать это не одним способом. Можно (коротко говоря) выйти из комнаты в коридор, а из него попасть в кухню. А можно вылезти в окно (если вы живете на первом этаже, а если не на первом, то возможностей масса: вылезти по веревке, спуститься, как Тарзан, по балконам соседей, по пожарной лестнице, или придумать что-нибудь покруче в стиле американских экшенов), пробежать/пройти по земле до подъезда, подняться по лестнице или лифтом, открыть свою дверь ключом или позвонить, чтобы кто-то ее открыл и войти на кухню. Итак, цель достигнута в обоих случаях. А про эффективность, думаю, все ясно А про то, что программа, сделанная по неэффективному алгоритму работает во много раз дольше?
Как записать алгоритм.
записывать алгоритмы можно любым удобным способом, лишь бы понятно было.
- Алгоритмический язык. Хорошо, мы уже выяснили, что алгоритм от языка не зависит. А как же его можно записать? А как мы описывали алгоритм, когда делали задание 1? Правильно, на своем собственном языке. Мы просто описывали — что за чем нужно делать. Обычными словами разговорной речи. Но, наверно, вы заметили, что описания, которые у нас получились — это весьма сдержанный, усеченный вариант речи в котором отсутствуют ненужные красивости и, главное, неоднозначности. Получаем так называемый псевдокод. Это язык описания алгоритмов, искусственный, неформальный (то есть, пишешь так, как тебе удобно, только чтобы другие понимали, если ты работаешь не один).
- Блок-схема. Алгоритм может быть записан графически. Для этого и служит блок-схема. Для изображения операций в ней используются специальные символы. Познакомимся с основными из них.
| Начало или конец. Внутри фигуры пишут начало (или begin — кому как нравится) или конец (end) соответственно. Если вы рисуете не всю схему, а только кусок ее, который нужно расписать подробнее, можете ограничиться маленьким кружочком. | |
|
|
В прямоугольнике находится операция. Можно написать ее словами (например: умножить х на у), а можно кусочком кода с оператором (х*у) |
|
|
Если вы хотите указать, что одно из действий сложное, и его хорошо бы разбить на ряд более простых, и вы выносите его как подзадачу в отдельное место — обозначьте такое действие так. |
|
|
Внутри ромба пишутся проверяемые условия (урок С6, урок VB 8). Обычно после проверки условий последовательность операторов перестает быть конструкцией следования и становится конструкцией выбора либо повторения. (следующие уроки будут посвящены именно этим конструкциям) |
|
|
Так обозначается введение входных параметров, а также выходных. Допустим, вы вынесли отдельно блок операторов и теперь хотите его расшифровать. Но для его работы нужно ввести определенные данные. Их вы напишете справа от этой скобки. То же относится к данным, которые вам нужно получить по окончании работы программы или части кода. |
Вообще-то, есть еще специальные символы блок-схем, но, во-первых, их можно найти в литературе, а во-вторых, для наших учебных целей приведенных выше вполне достаточно.
Последовательность операторов изображается стрелочками, соединяющими блоки. Например вот так:
Это, конечно, самый минимум, только чтобы показать пример. Тренироваться будем дальше по мере того, как будем учить управляющие структуры.
А пока в конце этого урока я хочу предложить вам рассмотреть самостоятельно более сложную блок-схему и описание еще одного алгоритма, которые подготовил для вас Dusk.
- Специальные алгоритмические таблицы. Один из примеров таких таблиц является таблица процедур, которая испрользуется для визуальных сред программирования из-за специфики: изначального разделения программы по процедурам обработки событий. Пишутся они следующим образом: в одном столбце пишется название процедуры, во втором столбце — описание этой процедуры как можно более полное, со всеми названиями компонентов, которые участвуют в этой процедуре. Например, если взять ту маленькую программку, которую вам предлагали сделать в курсе VB, где было 2 кнопки — включение звука и выход их программы, то для нее таблица процедур должна выглядеть так:
| название процедуры | описание этой процедуры |
| CmdSound_Click | При щелчке мышью на кнопке cmdSound вызывается звуковой сигнал |
| CmdEnd_Click | При щелчке мышью на кнопке cmdEnd приложение заканчивает работу. |
Поскольку программа была очень маленькая и суперпростая, то хорошего полного представления о том, как дотошно надо описывать действия она не даст. Поэтому в нескольких уроках позже мы вернемся к этому вопросу. Кроме того, в любом случае к рассмотрению алгоритмов нужно будет возвращаться, т.к. в объектно-ориентированных языках используется несколько другая методика описания алгоритмов, не блок-схема, но пока говорить об этом рано.
Программой называют некую последовательность команд, которую компьютеру нужно выполнить, чтобы решить конкретную задачу. И какой бы сложной ни оказалась задача, программисту придется представить ее в виде последовательности шагов, каждый из которых должен быть прост сам по себе. После этого программисту нужно записать для каждого шага соответствующие команды на языке программирования. Программист должен тщательно следить за тем, чтобы все шаги были описаны абсолютно однозначным образом и шли в правильном порядке. Представьте себе, например, что вам нужно записать все этапы программы замены колеса у автомобиля. В результате у вас может получиться примерно следующее:
- Поставь машину на ручной тормоз
- Достань домкрат
- Сними колпак
- Ослабь болты на колесе
- Подними машину на домкрате
- Выверни болты
- Сними колесо
- Достань запасное колесо
- Одень запасное колесо на место
- Вверни болты
- Опусти домкрат
- Затяни болты
- Одень колпак
- Положи домкрат и спустившееся колесо в багажник
При этом важно помнить, что ослабить болты нужно до того, как мы поставим машину на домкрат. Можете попробовать в качестве упражнения написать аналогичную программу для таких действий, как «перезарядить авторучку» или «заварить чай». Не забудьте, в частности, подумать, когда следует подогревать чайник для заварки.
В представленном виде можно отображать линейную структуру (когда действие происходит одно за другим без выбора). А если на колесах вашей машины нет колпаков, тогда вам эта программа не подойдет. Поэтому в реальных программах часто встречаются механизмы принятия решения, и отображать их лучше в виде блок-схем. Для примера представлена блок-схема «Как поджарить яичницу»:
Задание.
- Написать алгоритмы и блок-схемы программ, которые вы делали в курсе раньше. Для VB — сделать таблицу процедур.
- Попробуйте составить блок-схему программы «Как перейти дорогу».
Источник
2.1 Разработка алгоритма.
2.2 Блок-схема.
2.3 Структуры алгоритмов.
2.1 Разработка алгоритма.
Алгоритм — это
a. описание последовательности действий для решения задачи или достижения поставленной цели;
b. правила выполнения основных операций обработки данных;
c. описание вычислений по математическим формулам.
Перед началом разработки алгоритма необходимо четко уяснить задачу: что требуется получить в качестве результата, какие исходные данные необходимы и какие имеются в наличии, какие существуют ограничения на эти данные. Далее требуется записать, какие действия необходимо предпринять для получения из исходных данных требуемого результата.
На практике наиболее распространены следующие формы представления алгоритмов:




Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Пример. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел.
Алгоритм может быть следующим:
1. задать два числа;
2. если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
3. определить большее из чисел;
4. заменить большее из чисел разностью большего и меньшего из чисел;
5. повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.
Словесный способ не имеет широкого распространения по следующим причинам:



Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой.
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Он занимает промежуточное место между естественным и формальным языками.
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
2.2 Блок-схема.
Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.
Приведем наиболее часто употребляемые символы.
| Название символа | Обозначение и пример заполнения | Пояснение |
| Процесс | Вычислительное действие или последовательность действий | |
| Решение |  |
Проверка условий |
| Модификация |  |
Начало цикла |
| Предопределенный процесс |  |
Вычисления по подпрограмме, стандартной подпрограмме |
| Ввод-вывод |  |
Ввод-вывод в общем виде |
| Пуск-останов |  |
Начало, конец алгоритма, вход и выход в подпрограмму |
| Документ |  |
Вывод результатов на печать |
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Пример. Составить блок-схему алгоритма определения высот ha, hb, hc треугольника со сторонами a, b, c, если
где p = (a + b + c) / 2.
Решение. Введем обозначение 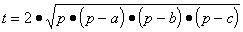
2.3 Структуры алгоритмов.
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
1. Базовая структура следование. Образуется из последовательности действий, следующих одно за другим:
2. Базовая структура ветвление. Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Структура ветвление существует в четырех основных вариантах:




1) если-то если условие то действия конец если2) если-то-иначе если условие то действия 1 иначе действия 2 конец если
3) выбор выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N конец выбора
4) выбор-иначе выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N иначе действия N+1 конец выбора

Пример. Составить блок-схему алгоритма вычисления функции
Базовая структура цикл. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.
Структура цикл существует в трех основных вариантах:
Цикл типа для.
Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.
Цикл типа пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
Цикл типа делать — пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Условие проверяется после выполнения тела цикла.
Заметим, что циклы для и пока называют также циклами с предпроверкой условия а циклы делать — пока — циклами с постпроверкой условия. Иными словами, тела циклов для и пока могут не выполниться ни разу, если условие окончания цикла изначально не верно. Тело цикла делать — пока выполнится как минимум один раз, даже если условие окончания цикла изначально не верно.
цикл для i от i1 до i2 шаг i3 тело цикла (последовательность действий) конец циклацикл пока условие тело цикла (последовательность действий) конец цикла
цикл делать тело цикла (последовательность действий) пока условие конец цикла

Пример. Составить блок-схему алгоритма вычисления функции
yk = sin (kx) + cos (k/x), k = 1, 2, …, 50
Пример. Составить блок-схему вычисления функции
y = a3 / (a2 + x2)
при x, изменяющимся от x = 0 до x = 3 с шагом Dx = 0,1
Итерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата.
Пример. Составить алгоритм вычисления суммы ряда
с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше).
Вычисление сумм — типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.
При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.
Решая эту задачу «в лоб» путем вычисления на каждом i-ом шаге частичной суммы
S:=S+(-1)**(i-1)*x**i/i ,
мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m
будет равно p/i, где i — номер слагаемого.
Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.
Вложенные циклы.
Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.
При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.
Пример вложенных циклов для. Вычислить сумму элементов заданной матрицы А(5,3).
Пример вложенных циклов пока. Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.
Дмитрий Михайлович Беляев
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Общие сведения об алгоритмах
Алгоритмом является конечная очередность операций (действий), которые предназначены для решения поставленной задачи. Операции должны быть точно определены, то есть, разные исполнители алгоритма должны в итоге получить одинаковый результат.
Набор всех начальных данных, к которым алгоритм может быть применен, именуется областью использования алгоритма. Не все математические задачи могут быть решены при помощи алгоритма. Это сопряжено с не вычислимостью определенных областей, на которых выполняется решение этих задач. Задачи, которые не могут быть решены при помощи алгоритма, называются алгоритмически неразрешимыми. Задачи, которые могут решаться алгоритмами, следует отнести к области изучения конструктивной математики.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Запись алгоритмов может быть выполнена на естественном языке, в виде блок-схемы, на каком-либо (специальном) языке программирования. Одним из широко распространенных средств отображения алгоритмов считаются блок-схемы. Блок-схемой является диаграмма специализированного вида, на которой фигуры призваны обозначать операторы, то есть, действия алгоритма, а стрелки обозначают очередность выполнения операторов.
Основными алгоритмическими структурами (операторами) являются конструкции, при помощи которых может быть записан алгоритм. К числу таких основных структур относятся:
- оператор присваивания,
- условные операторы,
- операторы циклов,
- последовательности операторов.
В разных языках программирования данные конструкции могут отображаться по-разному, то есть, обладать разным синтаксисом, но эти различия обычно не являются существенными.
Visual Basic: алгоритмы и блок-схемы
Последовательность операторов означает поочередное их выполнение друг за другом. На блок-схемах эта конструкция отображается при помощи стрелки. В языках программирования поочередно исполняемые операторы должны отделяться друг от друга символом «;» или, как в Visual Basic, символом конца строки (все операторы начинаются с новой строки) или двоеточием.
«Visual Basic: алгоритмы и блок-схемы» 👇
Стандартный синтаксис оператора присваивания выглядит следующим образом:
«переменная» «знак присваивания» «выражение»,
где «знак присваивания» может отображаться как «:=» или «=».
Выполняется присваивание в следующем порядке:
- Определяется выражение в правой части этого оператора.
- Вычисленное значение должно быть присвоено переменной левой части (переменная получает данное значение, удаляя предыдущее).
Рассмотрим пример последовательности операторов присваивания:
а = 4 + 7
а = а + 2
в = 2
а = в*3 + а
Выполняются эти операции в следующем порядке:
- Выполняется суммирование 4+7, результат 11 должен быть присвоен переменной «а». Прежняя величина «а» удаляется, новое значение «а» равно 11.
- Во второй строке к этой величине суммируется 2, результат получается13 (11+2=13). Это значение должно быть присвоено переменной «а», то есть, значение «а» теперь равно 13.
- В третьей строчке «в» присваивается значение 2.
- В четвертой строчке снова выполняется пересчет значения переменной «а», а именно, вычисляется выражение «в3+а» (вместо «в» и «а» используются их значения 13 и 2), итоговый результат 23 + 13 = 19 присваивается переменной «а» (принято говорить, что 19 заносится в переменную «а»).
- Итоговый результат исполнения всей последовательности «а=19, в=2».
Присваивание может трактоваться как сохранение определяемых в процессе выполнения алгоритма значений для последующего их применения. При сохранении в переменной, значение получает имя, к примеру, в рассмотренном примере далее в алгоритме вместо числа 19 может использоваться его (временное) наименование «а», вместо числа 2 может использоваться имя «в». Обратная операция, то есть извлечение значения из переменной, именуется разыменованием.
Условный оператор (ветвление) является алгоритмической структурой, которая представляет разветвление алгоритма в зависимости от значения (истинности или ложности) некоторого условия. В общем виде эта конструкция может быть представлена следующим образом:
«если» «условие» «то» «действия1» «иначе» «действия2»,
и формулируется так:
- Если условие истинно, то выполнить действия1.
- В противном случае, то есть, если условие ложно, то исполнить действия2.
Слова «если», «то», «иначе» в различных языках могут обладать разным синтаксисом, но практически во всех языках это «if», «then», «else». В Visual Basic синтаксис условного оператора представлен ниже:
If «условие» Then «действия1» Else «действия2» End If
Условный оператор может обладать и неполным форматом, то есть, без ветви «иначе» «действия2». В этом случае, если условие ложно, управление должно передаваться следующему в общей очередности оператору. На блок-схемах эти два варианта могут быть представлены следующим образом:
Рисунок 1. Блок-схема. Автор24 — интернет-биржа студенческих работ
Рисунок 2. Блок-схема. Автор24 — интернет-биржа студенческих работ
На этих блок-схемах знаки «+» и «-» служат для обозначения «да», то есть, условие исполняется, и «нет», то есть, условие не исполняется). К примеру, рассмотрим вычисление «у», которое определяется следующими условиями:
$y = x^2$ при x ∠ 0,
$y = x+1$ при x ≥ 0.
Данное вычисление может быть представлено блок-схемой, изображенной на рисунке ниже:
Рисунок 3. Блок-схема. Автор24 — интернет-биржа студенческих работ
На языке программирования Visual Basic данный алгоритм может быть реализован следующим образом:
If x∠0 Then
y=x*x
Else
y=x+1
End If
Следует отметить, что операторы после Then (ветвь «+») и Else (ветвь «-») должны начинаться с новой строки, а сам условный оператор оканчивается строкой End If, то есть, признаком конца операции ветвления.
Приведем пример применения неполного условного оператора:
- Необходимо просуммировать числа, которые вводятся с клавиатуры.
- Когда число является отрицательным, то оно сначала заменяется единицей.
Предположим, что в переменной «а» хранится значение введенного числа, а в переменной S хранится сумма введенных чисел. На рисунке ниже представлен фрагмент блок-схемы решения этой задачи:
Рисунок 4. Фрагмент блок-схемы. Автор24 — интернет-биржа студенческих работ
На языке программирования Visual Basic этот алгоритм может быть реализован следующим образом:
If а∠0 Then
а=1
End If
S=S+a
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Введение
Образованным
культурным человеком, грамотным специалистом в XXI
веке может быть тот, кто хорошо владеет информационными технологиями. Ведь
деятельность людей все в большей степени зависит от информативности,
способности эффективно использовать информацию. Для свободной ориентации в
информационных потоках современный специалист любого профиля должен уметь
получать, обрабатывать и использовать информацию с помощью компьютеров,
телекоммуникаций и других средств связи. Заложить фундамент информационной
культуры призвана дисциплина «Информатика и ИКТ», изучение которой начинается
со школьной скамьи, а затем, приобретая более целенаправленный характер,
продолжается в среднем профессиональном учебном заведении. Эта дисциплина
достаточно новая и своим появлением обязана развитию индустрии информатики,
бурному процессу информатизации, начавшемуся в нашей стране. Об информации
начинают говорить как о стратегическом ресурсе общества, как о ресурсе,
определяющем уровень развития государства.
Информатика, как никакая другая область знаний,
характеризуется чрезвычайно высокой степенью динамики изменений предмета ее
изучения. Сегодня количество компьютеров в мире превышает 500 миллионов единиц
и продолжает удваиваться в среднем каждые три года. При этом в среднем один раз
в полтора года удваиваются основные технические параметры аппаратных средств,
один раз в два-три года меняются поколения программного обеспечения, и один раз
в пять-семь лет меняется база стандартов, интерфейсов и протоколов. Следует
также отметить, что каждая вычислительная система по-своему уникальна. Найти
две системы с одинаковыми аппаратными и программными конфигурациями весьма
сложно, поэтому для эффективной эксплуатации вычислительной техники от
специалиста требуется достаточно широкий уровень знаний и практических навыков.
К
сожалению, до сих пор нет единой точки зрения на область знаний под названием
«Информатика» и соответствующую ей дисциплину. Одни говорят – это веление
времени, дань моде, явление преходящее или считают информатику сложной
премудростью, где к тому же требуется познать характер некоего современного
монстра – персонального компьютера и научиться управлять им. Другие
воспринимают информатику лишь как практическую дисциплину, где учат «правильно
нажимать кнопки» персонального компьютера. Однако не вызывает сомнения, что
современному специалисту, чтобы на должном уровне выполнять свои обязанности,
необходимы инструментарий и методология его применения для обработки
информации. Это сравнимо с использованием средств передвижения: теоретически
человек может пешком преодолеть любое расстояние, но современный темп жизни
просто немыслим без применения автомобиля, поезда, самолета и т. д. То же самое
происходит и в области, связанной с обработкой информации: теоретически человек
сам может переработать без компьютера любую информацию, но сделает это
эффективнее, если он овладеет знаниями и умениями, которыми располагает
информатика.
Информатика
в широком смысле представляет собой единство разнообразных отраслей науки,
техники и производства, связанных с переработкой информации главным образом с
помощью компьютеров и телекоммуникационных средств связи во всех сферах
человеческой деятельности.
Информатику
в узком смысле можно представить как состоящую из трех взаимосвязанных частей —
технических средств (hardware),
программных средств (software),
алгоритмических средств (brainware).
Возможности компьютера
как технической основы обработки данных связаны с используемым программным
обеспечением (программами).
Программа (program, routine)– упорядоченная последовательность команд
(инструкций) компьютеру для решения задачи.
Программы
предназначены для машинной реализации задач. Термин задача и приложение
имеют очень широкое употребление в контексте информатики и программного
обеспечения.
Задача (problem, task)– проблема, подлежащая решению.
Приложение (application)– программная реализация на компьютере
решения задачи.
Таким образом, задача
означает проблему, подлежащую реализации с использованием средств
информационных технологий, а приложение – реализованное на компьютере решение
по задаче. Приложение, являясь синонимом слова «программа», считается более
удачным определением.
Процесс создания
программ можно представить в укрупненном виде как последовательность,
представленную на рис. 1.
Рис. 1. Схема процесса
создания программ
Традиционно наибольшее количество задач
решаемых с помощью компьютера составляют инженерно-технические задачи. В
процессе подготовки и решения их на компьютере можно выделить следующие этапы:
1.
постановка задачи;
2.
моделирование задачи;
3.
алгоритмизация задачи;
4.
разработка, подготовка и отладка
программы;
5.
эксплуатация программы.
Следует
также отметить, что вышеперечисленные этапы тесно связаны друг с другом.
Например, отладка программы может показать необходимость внесения изменений в
программу, алгоритм или даже в постановку задачи.
Данное
учебно-методическое пособие посвящено рассмотрению вопросов алгоритмизации и
программированию на языке Бейсик, что позволяет освоить как логику решения различных
задач, так и использование возможностей компьютера для реализации полученной
логической схемы решения конкретной задачи.
1. Алгоритмизация задач
1.1. Понятие алгоритма
Для
составления программы, предназначенной для решения на компьютере какой-либо
задачи, требуется составление алгоритма ее решения.
Понятие
алгоритма – одно из фундаментальных понятий информатики. Алгоритмизация наряду
с моделированием выступает в качестве общего метода информатики. К реализации
определенных алгоритмов сводятся процессы управления в различных системах, что
делает понятие алгоритма близким к кибернетике.
Алгоритмы
являются объектом систематического исследования пограничной между математикой и
информатикой научной дисциплины, примыкающей к математической логике – теории алгоритмов.
Особенность
положения состоит в том, что при решении практических задач, предполагающих
разработку алгоритмов для реализации на компьютере, и тем более при
использовании на практике информационных технологий, можно, как привило, не
опираться на высокую формализацию данного понятия. Поэтому представляется целесообразным
нижеприведенное определение алгоритма.
Алгоритм
— это система точно сформулированных правил, определяющая процесс преобразования
исходных данных (входной информации) в желаемый результат (выходную информацию).
Алгоритмами,
например, являются правила сложения, умножения, решения алгебраических
уравнений, умножения матриц и т.п. Слово алгоритм происходит от algorithmi,
являющегося латинской транслитерацией арабского имени великого математика IX
века Аль Хорезми. Благодаря латинскому переводу трактата Аль Хорезми европейцы
в XII веке познакомились с позиционной системой счисления, и в средневековой
Европе алгоритмом называлась десятичная позиционная система счисления и правила
счета в ней.
Применительно
к компьютерам алгоритм определяет вычислительный процесс, начинающийся с
обработки некоторой совокупности возможных исходных данных и направленный на
получение определенных этими исходными данными результатов. Термин вычислительный
процесс распространяется и на обработку других видов информации, например,
символьной, графической или звуковой.
Если
вычислительный процесс заканчивается получением результатов, то говорят, что
соответствующий алгоритм применим к рассматриваемой совокупности исходных
данных. В противном случае говорят, что алгоритм неприменим к совокупности
исходных данных. Любой применимый алгоритм имеет ряд обязательных
свойств:
§ дискретность
– разбиение процесса обработки информации на более простые этапы (шаги
выполнения), выполнение которых компьютером или человеком не вызывает затруднений;
§ результативность
(выполнимость) – конечность действий алгоритма
решения задачи, позволяющая получить желаемый результат при допустимых исходных
данных за конечное число шагов;
§ определенность
(детерминированность) – однозначность
выполнения каждого отдельного шага преобразования информации, т.е. совпадении
получаемых результатов независимо от пользователя и применяемых технических средств;
§ формальность
– применение правил выполнения алгоритма механически без выяснения вопроса:
почему надо делать так, а не иначе;
§ массовость
– пригодность алгоритма для решения целого
класса однотипных задач, различающихся конкретными значениями исходных данных.
Для
задания алгоритма необходимо описать следующие его элементы:
•
набор объектов, составляющих совокупность
возможных исходных данных, промежуточных и конечных результатов;
•
правило начала;
•
правило непосредственной переработки
информации (описание последовательности действий);
•
правило окончания;
•
правило извлечения результатов.
Алгоритм
всегда рассчитан на конкретного исполнителя. В нашем случае таким исполнителем
является компьютер. Для обеспечения возможности реализации на компьютере
алгоритм должен быть описан на языке, понятном компьютеру, то есть на языке
программирования.
Таким
образом, можно дать следующее определение программы. Программа для компьютера
представляет собой описание алгоритма и данных на некотором языке
программирования, предназначенное для последующего автоматического выполнения.
1.2. Способы описания алгоритмов
К
основным способам описания алгоритмов можно отнести следующие:
§ словесно-формульный;
§ структурный
или в виде блок–схем;
§ с
помощью граф–схем;
§ с
помощью сетей Петри.
Перед
составлением программ чаще всего используются словесно-формульный и
блок–схемный способы. Иногда перед составлением программ на низкоуровневых
языках программирования типа языка Ассемблера алгоритм программы записывают на
алгоритмическом языке, представляющем в общем случае систему обозначений
и правил для единообразной и точной записи алгоритмов и исполнения их.
Алгоритмический язык удобно использовать для описания алгоритмов
функционирования сложных программных систем, например, для описания принципов
функционирования операционной системы. Отметим, что между понятием
«алгоритмический язык» и «язык программирования» есть различие. Прежде всего,
под исполнителем в алгоритмическом языке может подразумеваться не только
компьютер, но и устройство для работы «в обстановке». Программа, записанная на
алгоритмическом языке, не обязательно предназначена компьютеру. Практическая
реализация алгоритмического языка – отдельный вопрос в каждом конкретном
случае.
Как
и каждый язык, алгоритмический язык имеет свой словарь. Основу этого словаря
составляют слова, употребляемые для записи команд, входящих в систему команд
исполнителя того или иного алгоритма. Такие команды называются простыми
командами. В алгоритмическом языке используются слова, смысл и способ употребления
которых задан раз и навсегда. Эти слова называются служебными. Использование
служебных слов делает запись алгоритма более наглядной, а форму представления
различных алгоритмов – единообразной.
Например,
алгоритм, определяющий движение робота–исполнителя по некоторому маршруту,
может иметь вид:
АЛГ в_склад
НАЧ
вперед
поворот на 90° направо
вперед
КОН
При словесно-формульном
способе алгоритм записывается в виде текста с формулами
по пунктам, определяющим последовательность действий.
Пусть,
например, необходимо найти значение следующего выражения: . Словесно-формульным
способом алгоритм решения этой задачи может быть записан в следующем виде:
1. Ввести значения a
и x.
2.
Сложить x и 6.
3.
Умножить a на 2.
4.
Вычесть из 2a
сумму (х+6).
5.
Вывести y как результат вычисления
выражения.
При блок–схемном
описании алгоритм изображается геометрическими фигурами (блоками), связанными
по управлению линиями со стрелками (направлениями потока данных). В блоках
записывается последовательность действии.
Данный
способ по сравнению с другими способами записи алгоритма имеет ряд преимуществ.
Он наиболее нагляден: каждая операция вычислительного процесса изображается
отдельной геометрической фигурой. Кроме того, графическое изображение алгоритма
наглядно показывает разветвления путей решения задачи в зависимости от
различных условии, повторение отдельных этапов вычислительного процесса и
другие детали.
Оформление
программ должно соответствовать определенным требованиям. В настоящее время
действует единая система программной документации (ЕСПД), которая устанавливает
правила разработки, оформления программ и программной документации. В ЕСПД
определены и правила оформления блок-схем алгоритмов (ГОСТ 19.701-90 ЕСПД,
который действует взамен ГОСТа 19.002-80 ЕСПД, на который до сих пор ссылаются некоторые
авторы учебных и справочных пособий по информатике).
Операции
обработки данных и носители информации изображаются на схеме соответствующими
блоками. В пределах одной схемы рекомендуется изображать блоки
одинаковых размеров. Большая часть блоков по построению условно вписана в прямоугольник
со сторонами a
(высота) и b (длина).
ГОСТ 19.701-90 ЕСПД жестких требований на размеры a
и b не
устанавливает. Но для качественного выполнения блок-схемы, целесообразно
придерживаться рекомендации ГОСТа 19.002-80 ЕСПД: минимальное значение a
равно 10 мм, увеличение a
производится на число, кратное 5 мм; размер b=1,5a;
для отдельных блоков допускается соотношение между a
и b,
равное 1:2. Нумерация блоков сейчас необязательна (по ГОСТу 19.002-80 ЕСПД
порядковый номер блока записывался в разрыве верхней линии в ее левой части).
Виды и назначение основных блоков в соответствии с действующим ГОСТом 19.701-90
ЕСПД приведены в таблице 1.
Таблица 1. Условные обозначения блоков схемы алгоритмов
|
Наименование |
Обозначение |
Функция |
|
|
Выполнение операции или группы |
|
|
|
Преобразование данных в форму, |
|
|
|
Выбор направления выполнения |
|
|
процесс |
Использование ранее созданных и |
|
|
(Пуск–останов) |
Начало, конец, прерывание |
|
|
|
Указание связи между прерванными |
|
|
|
Отображение данных, |
|
|
|
Отображение данных, вводимых вручную |
|
|
(Модификация) |
Выполнение операций, меняющих |
|
|
|
Связь между элементом схемы и |
Линии, соединяющие блоки и указывающие
последовательность связей между ними, должны проводиться параллельно линиям
рамки. Стрелка в конце линии может не ставиться, если линия направлена слева
направо или сверху вниз. В блок может входить несколько линий, то есть блок
может являться преемником любого числа блоков. Из блока (кроме блоков «Решение»
и «Подготовка») может выходить только одна линия. Блок «Решение» может иметь в
качестве продолжения один из двух блоков, и из него выходят две линии. Если на
схеме имеет место слияние линий, то место пересечения выделяется точкой. В
случае, когда одна линия подходит к другой и слияние их явно выражено, точку
можно не ставить.
Схему алгоритма следует выполнять как
единое целое, однако в случае необходимости допускается обрывать линии,
соединяющие блоки.
Если
при обрыве линии продолжение схемы находится на этом же листе, то на одном и
другом конце линии изображается специальный символ соединитель —
окружность диаметром 0,5a.
Внутри парных окружностей указывается один и тот же идентификатор. В качестве
идентификатора, как правило, используется порядковый номер блока, к которому
направлена соединительная линия.
В
ГОСТ 19.701-90 ЕСПД понятие межстраничного соединителя отсутствует,
поэтому если схема занимает более одного листа, то используется описанный
выше соединитель в виде окружности.
1.3. Структурные схемы алгоритмов
Как
уже было отмечено ранее, одним из свойств алгоритма является дискретность, т.
е. возможность расчленения процесса вычислений, предписанных алгоритмом, на
отдельные этапы, возможность выделения участков программы с определенной
структурой. Можно выделить и наглядно представить графически три простейшие
структуры:
• последовательность
двух или более операций;
• выбор направления;
• повторение.
Любой
вычислительный процесс может быть представлен как комбинация этих элементарных
алгоритмических структур (это содержание теоремы Бема–Якопини). Соответственно,
вычислительные процессы, выполняемые на компьютере по заданной программе, можно
разделить на три основных вида:
• линейные;
• разветвляющиеся;
• циклические.
Линейным
принято называть вычислительный процесс, в котором операции выполняются
последовательно, в порядке их записи. Соответственно, линейный алгоритм
– это алгоритм, в котором действия выполняются одно за другим.
Каждая
операция является самостоятельной, независимой от каких-либо условий. На схеме
блоки, отображающие эти операции, располагаются в линейной последовательности.
Линейные
вычислительные процессы имеют место, например, при вычислении арифметических
выражений, когда имеются конкретные числовые данные и над ними выполняются
соответствующие условию задачи действия.
Рассмотрим пример линейного
вычислительного процесса с соответствующим ему линейным алгоритмом.
Задача: Вычислить
периметр произвольного треугольника по его трем сторонам (вопрос существования
треугольника не рассматривается).
Решение:
1
этап: Постановка задачи.
Исходные
данные: А, B,
C
– стороны произвольного треугольника
Выходные
данные: P
– периметр треугольника.
2
этап: Математическая модель.
P=A+B+С
3 этап: Составление
алгоритма
Рис. 2.
Пример линейного алгоритма
Вычислительный процесс
называется разветвляющимся, если для его реализации предусмотрено
несколько направлений (ветвей). Соответственно, разветвляющийся алгоритм
– это алгоритм, в котором в зависимости от условия выполняется либо
одна, либо другая последовательность действий.
Каждое
отдельное направление процесса обработки данных является отдельной ветвью
вычислений. Разветвление в программе — это выбор одной из нескольких последовательностей
команд при выполнении программы. Выбор направления зависит от заранее
определенного признака, который может относиться к исходным данным, к
промежуточным или конечным результатам. Признак характеризует свойство данных и
имеет два или более значений.
Разветвляющийся
процесс, включающий в себя две ветви, называется простым, более двух ветвей —
сложным. Сложный разветвляющийся процесс можно представить с помощью простых
разветвляющихся процессов.
Направление
ветвления выбирается логической проверкой, в результате которой возможны два
ответа: «да» — условие выполнено и «нет» — условие не выполнено.
Следует
иметь в виду, что, хотя на схеме алгоритма должны быть показаны все возможные
направления вычислений в зависимости от выполнения определенного условия (пли
условий), при однократном прохождении программы процесс реализуется только по
одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются
вычисления, должна приводить к завершению вычислительного процесса.
Разветвляющиеся
алгоритмы могут иметь различную структуру (Рис.3).
Рис. 3. Структуры
разветвляющегося алгоритма
Запись разветвляющегося алгоритма типа
«Развилка» в виде блок-схемы представлена на рисунке 4.
Рис. 4. Блок-схемы
разветвляющихся алгоритмов типа «Развилка»: а) обычная, б) обход
Рассмотрим
пример разветвляющегося вычислительного процесса с соответствующим ему разветвляющимся
алгоритмом.
Задача: Вычислить
значение функции 
заданного x.
Решение:
1
этап: Постановка задачи.
Исходные
данные: x
– значение аргумента функции.
Выходные
данные: y
– искомое значение функции при заданном x.
2
этап: Математическая модель.
3
этап: Составление алгоритма
Рис. 5.
Пример разветвляющегося алгоритма
Циклическими называются
программы, содержащие циклы. Цикл — это многократно повторяемый
участок программы. Циклический алгоритм – это алгоритм, в
котором имеется последовательность действий, выполняющихся многократно.
Последовательность действий, выполняющихся многократно, называется телом
цикла.
В организации цикла можно выделить следующие этапы:
• подготовка
(инициализация) цикла (И);
• выполнение
вычислений цикла (тело цикла) (Т);
• модификация
параметров (М);
• проверка
условия окончания цикла (У).
Порядок
выполнения этих этапов, например, Т и М, может изменяться. В зависимости от
расположения проверки условия окончания цикла различают циклы с нижним и
верхним окончаниями (соответственно: цикл «ДО» или цикл с постусловием и цикл
«ПОКА» или цикл с предусловием) (рис. 6). Для цикла с нижним окончанием (рис. 6–а)
тело цикла выполняется как минимум один раз, так как сначала производятся
вычисления, а затем проверяется условие выхода из цикла. В случае цикла с
верхним окончанием (рис. 6–б) тело цикла может не выполниться ни разу в случае,
если сразу соблюдается условие выхода.
Рис. 6. Блок-схемы
циклических алгоритмов: а) с постусловием, б) с предусловием
Цикл
называется детерминированным, если число повторений тела цикла заранее
известно или определено. Цикл называется итерационным, если число повторений
тела цикла заранее неизвестно, а зависит от значений параметров (некоторых
переменных), участвующих в вычислениях. Для детерминированных циклов, которые
называют также цикл с параметром или цикл со счетчиком, запись в виде
блок-схемы представлена на рисунке 7.
Рис. 7. Блок-схема циклического
алгоритма с параметром
Работу
цикла с параметром можно описать следующим образом (словесный алгоритм):
1.
Вычисление значений выражений, определяющих
NI,
KI
и HI;
2.
I
присваивается значение NI;
3.
I
сравнивается с KI: если I
больше KI
при положительном HI (или, наоборот, I
меньше KI
при отрицательном HI), то переход к пункту
7, иначе к следующему пункту;
4.
Выполняется тело цикла;
5.
I
автоматически изменяется на HI;
6.
Переход к пункту 3;
7.
Конец цикла.
Рассмотрим
пример циклического вычислительного процесса с соответствующим ему циклическим
алгоритмом.
Задача: Требуется
вычислить значение функции y=sin φ
в диапазоне изменения аргумента от 10° до 90° с шагом 10°.
Решение:
1
этап: Постановка задачи.
Исходные
данные: X
– угол φ (аргумент
функции)
NX
– начальное значение угла φ
(10°)
KX
– конечное значение угла φ
(90°)
HX
– шаг изменения угла φ
(10°)
Выходные
данные: Y – значения функции при заданных φ.
2
этап: Математическая модель.
3
этап: Составление алгоритма
Рис. 8. Пример циклического
алгоритма
Алгоритмы
разветвляющихся и циклических структур можно комбинировать одну с другой – как
путем организации их следования, так и путем создания суперпозиций: вложений
одной структуры в другую, – сколь угодно разнообразно для выражения логики
алгоритма решения любой задачи. Умение образовывать из базовых структур их
суперпозиции в соответствии с условиями конкретной задачи – одно из важнейших в
программировании.
2. Основы программирования на языке Basic
Язык
программирования Basic
(Beginner‘s All—purpose Instruction Code
– Всецелевой язык программирования для начинающих) разработан Джоном Кимини и
Томасом Куртцем в Дартмутском университете, США, в 1964 г.
Basic занимает особое место среди всех языков высокого уровня. С самого начала
он задумывался как универсальный язык для начинающих. Средства программирования
на Basic долгое время включались
в комплект поставки ПК как обязательный элемент программного обеспечения. В
настоящее время существует множество версий этого языка, которые иногда очень
сильно отличаются друг от друга. Для учебных заведений самыми распространенными
являются версии MSX, впервые
реализованная на японском компьютере «Ямаха», и версии фирмы Microsoft
для компьютеров IBM. Кроме того, в
нашей стране популярностью пользуется версия Turbo—Basic фирмы Borland.
Без преувеличения можно сказать, что сегодня Бейсик до сих пор является самым
распространенным языком программирования. После появления мощных компиляторов Visual Basic этот язык стал популярен и у профессиональных программистов. Бейсик
относится к языкам программирования высокого уровня. Как и другие языки, этот
язык имеет алфавит, синтаксис и семантику.
К
достоинствам языка программирования QBASIC с точки зрения массового
пользователя следует отнести:
•
простота синтаксиса;
•
простота организации данных и управляющих
структур;
•
большое число встроенных команд и
функций, позволяющих без труда выполнять такие операции, как управление
текстовым и графическим экраном, обработка символьных строк и т.п.
Особым
достоинством QBASIC следует считать
возможность работы в режиме интерпретации, который резко упрощает
процесс отладки программ: исполнение почти каждой команды можно проверить сразу
после написания.
2.1. Алфавит языка программирования
Бейсик
Алфавит
языка Basic базируется на кодировочной таблице символов ASCII, первая половина которой
(символы с кодом 0 – 127) – стандартная, а вторая половина (символы с кодом 128
– 255) – специфична для каждой страны. В этой таблице каждый символ имеет
8-битовое обозначение. Таким образом, в алфавит языка Basic
входят: 1) прописные и заглавные буквы английского алфавита, 2) прописные и заглавные
буквы русского алфавита, 3) десятичные цифры, 4) знаки препинания (точка,
запятая, точка с запятой, кавычки, апостроф и др.), 5) знаки операций (сложение,
деление, больше, равно и др.), 6) набор специальных символов, который имеется
на клавиатуре компьютера (% & ! # $ и др.).
2.2. Константы и переменные языка Бейсик
Из
алфавита языка программирования могут быть сформированы функционально
законченные элементарные конструкции, которые называются синтаксическими единицами.
Если провести аналогию с разговорным языком, например русским, то это отдельные
слова: существительные, глаголы, междометия и т.д.
Синтаксические
единицы условно можно разбить на следующие виды:
–
константы;
–
переменные;
–
ключевые слова;
–
метки.
Константы – это
фиксированные величины, которые в процессе вычислений не изменяют своих
значений. В Бейсике используются константы двух типов – числовые и символьные.
Числовые
константы – это десятичные числа, которые состоят из десятичных цифр или
десятичных цифр и дополнительных символов. В свою очередь, числовые константы
можно разделить на целые и вещественные.
Целые константы
– это целые числа, которые записываются в виде последовательности десятичных
цифр, перед которой может стоять знак + или –. Числа без знака воспринимаются
положительными. Бейсик допускает использование как целых чисел в диапазоне от
–32768 до 32768, так и длинных целых чисел в диапазоне от –2147483648 до
2147483648.
Примеры записи целых
чисел:
|
Математическая |
Запись на языке |
|
41 |
41 или +41 |
|
-39 |
-39 |
|
-2147483648 |
-2147483648 |
Вещественные
числа при переводе в двоичную
систему счисления представляют собой, как правило, бесконечные дроби и
округляются в пределах формы записи. Поэтому эти числа представляются в памяти
приближенно.
Допускается запись
вещественных чисел:
~
в основной форме – числа с
фиксированной точкой;
~ в форме с порядком – числа с плавающей точкой.
Числа с фиксированной
точкой – это дробные десятичные числа,
у которых дробная часть отделяется от целой части десятичной точкой. Они могут
быть записаны следующим образом:
,
где N и М – последовательности десятичных цифр.
Десятичная точка в записи
этого числа обязательна. Знак + или — записываются в начале константы. Число
без знака воспринимается положительным.
Примеры записи чисел с фиксированной точкой:
|
Математическая |
Запись на языке Бейсик |
|
|
Верно |
Неверно |
|
|
0 |
0. или 0.0 или |
0 |
|
4 |
4. или 4.0 |
4 или +.4 |
|
-1,0 |
-1.0 или -1. |
.1 или -1,0 |
|
-1,5 |
-1.5 |
1.5 или -1,5 |
Числа с
плавающей точкой – запись чисел
представленных в математике в показательной форме. На языке бейсик они
записываются:
~
одинарной точности:
~
удвоенной точности:
и имеют в записи отличия по основанию степени и где N и М — последовательность десятичных
цифр.
Для чисел одинарной точности N + М = 6.
Для чисел удвоенной точности N + М = 14.
Е – основание степени для чисел одинарной точности, т.е. число 10.
D – основание степени для чисел удвоенной точности, т.е. число 10.
S – порядок числа, выражается целой константой, состоящей из одной
или двух десятичных цифр.
Положительный знак числа и показателя степени можно не указывать.
Примеры записи чисел с плавающей точкой одинарной точности:
|
Математическая |
Запись на языке Бейсик |
|
|
Верно |
Неверно |
|
|
123,4∙10-2= =1,234= =0,1234∙101 |
123.4Е-2 |
123.4*10**(-2) |
|
1.234Е00 |
1.234*10 |
|
|
0.1234Е1 |
0.1234*Е1 |
Примеры записи чисел с плавающей точкой удвоенной точности:
|
Математическая запись |
Запись на языке Бейсик |
|
|
Верно |
Неверно |
|
|
1234,5678∙10-2= =12345678∙10-6= =0,12345678 |
1234.5678D-2 |
1234.5678*10**(-2) |
|
12345678.D-6 |
12345678D-6 |
|
|
0.12345678D2 |
.12345678E2 |
Символьная константа
представляет собой последовательность любых символов алфавита. Значения
символьных констант заключается в кавычки. Примеры записи символьных констант: ”Кстовский нефтяной техникум”,
”Array”, ”sin(x)= ”.
Переменная – это величина,
которая может меняться при выполнении программы. При изучении алгебры дается
понятие переменной величины. Например, в простом алгебраическом равенстве c
= f + 2b – 5 значение переменной с зависит от значения переменных
f и b, указанных в правой части равенства.
Если f=2 и b=6, тогда с=9.
Такое же равенство можно записать в программе на Бейсике: c
= f
+ 2*b – 5 . В
терминах языка Бейсик c,
f и b
– это имена переменных. Такие имена также называют идентификаторами.
В
языке Бейсик идентификатор (имя переменной) – это произвольный набор
символов для обозначения переменной, который может содержать от 1 до 40
символов, причём первый символ должен быть латинской буквой, а остальные –
латинские буквы или цифры или символы типа @, #, % и.т.д. Примеры имен
переменных: A, Ds, SodRan,
k1, n123, dlina!
Кроме
имени переменная характеризуется типом. Переменные – это величины, которые
имеют определенное значение в каждый момент выполнения программы, а оно может
быть как числовым, так и символьным. Для хранения значения переменной
выделяется поле памяти компьютера.
|
Тип переменной, |
Символ, |
Описание типа |
Объём поля |
Пример значения |
|
Целые числа |
% |
integer |
2 байта |
17; -123 |
|
Вещественные |
! |
single |
4 байта |
314.15; 3.1415Е+2 |
|
Символьный |
$ |
string |
min 1 байт |
язык |
|
Длинные |
& |
long |
4 байт |
—12543786 |
|
Вещественные |
# |
double |
8 байт |
1.2543786 |
Тип переменной в Бейсике опознаётся по
последнему символу в её имени: % – целая переменная; & – длинная целая
переменная; ! – вещественная переменная обычной точности; # — вещественная переменная
двойной точности; $ — символьная переменная, а также может определяться специальным
оператором задания типа.
2.3. Арифметические выражения
Выражением называется
последовательность операций, которые необходимо произвести над данными, чтобы
получить требуемое значение.
В
Бейсике существует четыре вида выражений:
•
арифметические;
•
отношений;
•
логические;
•
строковые.
Арифметическое выражение
– это аналог обычной арифметической (алгебраической, математической) формулы.
Результатом его вычисления является целое или вещественное число. Любое
математическое выражение на Бейсике записывается в виде строки и может
содержать: числовые константы, числовые переменные, математические функции,
знаки математических операций, систему скобок. Понятие числовых констант и
числовых переменных было уже дано выше, поэтому рассмотрим последующие три
составляющие арифметических выражений.
Функция – это заранее
определённая операция над данными, математическая функция – это функция,
значением которой является число. Вот некоторые примеры математических функций
встроенных в транслятор Бейсика:
|
Название функции |
Запись в |
Запись в Бейсике |
Пример в Бейсике |
|
Абсолютная величина |
|x| |
ABS(X) |
ABS(-5) |
|
Экспонента |
ex |
EXP(X) |
EXP(5) |
|
Логарифм натуральный |
ln x |
LOG(X) |
LOG(3) |
|
Квадратный корень |
|
SQR(X) |
SQR(4) |
|
Синус |
sin x |
SIN(X) |
SIN(3.14) |
|
Косинус |
cos x |
COS(X) |
COS(1) |
|
Тангенс |
tg x |
TAN(X) |
TAN(2) |
|
Целая часть числа |
[x] |
INT(X) |
INT(13.5) |
|
Арктангенс |
arctg x |
ATN(X) |
ATN(3) |
|
Знак числа |
|
SGN(X) |
SGN(-5) |
Таким образом, в Бейсике обращение к
функции осуществляется по ее имени, а аргумент обязательно записывается в
скобках. При вычислении арифметического выражения значения функций определяются
в первую очередь еще до выполнения математических операций.
В
Бейсике допустимы следующие арифметические операции:
|
Название |
Знак в математике |
Знак в Бейсике |
Пример в |
Пример в |
|
Возведение в степень |
нет |
^ |
25 |
2^5 |
|
Умножение |
· |
* |
2·5 |
2*5 |
|
Деление |
: |
/ |
10:2 |
10/2 |
|
Сложение |
+ |
+ |
5+10 |
5+10 |
|
Вычитание |
– |
– |
a–b |
a–b |
|
Остаток от деления |
нет |
mod |
нет |
17 mod 3 (результат |
|
Деление нацело |
нет |
|
нет |
173 (результат |
Заметим, что операции указаны в
вышеприведенной таблице в порядке уменьшения приоритета.
Действия в арифметических выражениях
выполняют слева направо в зависимости от их приоритета. Для того чтобы изменить
естественный порядок действий, используются круглые скобки. Выражения в круглых
скобках выполняются в первую очередь. Заметим, что понятие система скобок
означает то, что в выражении всегда должно совпадать количество
открывающихся скобок с количеством закрывающихся скобок.
Примеры записи чисел математических выражений на языке Бейсик:
Математическое
выражение 
Бейсик в виде: ((sin(x^3)–cos(x)^2)/(sqr(x–8.5)+1.75E-6))^(1/5)+exp(x+1)/5/abs(x)
2.4. Операторы языка Бейсик для записи
линейного алгоритма
2.4.1. Оператор очистки экрана
Оператор
очистки экрана состоит из одного ключевого слова: CLS. Название этого оператора
произошло от английских слов Clear Screen,
что в переводе означает очистить экран.
Например,
результатом выполнения операторов:
CLS
? ”Привет”
будет
черный экран монитора, а в левом верхнем углу будет выведено слово Привет.
2.4.2. Оператор ввода
Оператор
ввода начинается с ключевого слова INPUT. INPUT
в переводе с английского языка означает вставлять, вводить. Поэтому
действие этого оператора состоит в ведении значения переменной или значений
переменных с клавиатуры в память компьютера.
Синтаксис оператора ввода:
INPUT
”подсказка”; имя переменной
INPUT
[”подсказка”;] имя1, имя2, …
Отметим,
что конструкция в синтаксисе типа […], означает, что данный параметр является
необязательным, т.е. его можно пропустить. При встрече с оператором ввода
(ключевое слово INPUT)
программа приостанавливает своё действие; на экране появляется знак вопроса «?»
или подсказка со знаком «?», после которого необходимо набрать на клавиатуре
значение переменной, входящий в состав оператора, нажать клавишу Enter.
Если в операторе указано несколько имен переменных, то их значения набираются
на клавиатуре через запятую и потом нажимается клавиша Enter.
Оператор
INPUT можно использовать для присваивания значения как числовым, так и
строковым переменным. Пример его использования будет приведен ниже.
2.4.3. Оператор присваивания
Оператор
присваивания начинается с ключевого слова LET.
LET
в переводе с английского языка означает позволять, допускать. Отметим,
что ключевое слово LET можно опустить,
что почти всегда и делается при написании программы, а отличительным признаком
оператора является присутствие знака «=» в синтаксисе оператора.
Синтаксис оператора присваивания:
Имя
переменной = арифметическое выражение
В
результате выполнения оператора присваивания переменной, стоящей слева от знака
равенства присваивается значение арифметического выражения, которое перед
присваиванием вычисляется. В частном случае арифметическое выражение может состоять
как из какого-либо числа, так и из одной переменной. Для корректного действия оператора
присваивания необходимо, чтобы все переменные в выражении имели некоторые значения
еще до его выполнения.
Например,
результаты выполнения трех операторов присваивания:
|
Оператор |
Действие |
|
X=15 |
присваивание переменной X значения |
|
Y=2 |
присваивание переменной Y |
|
Z=(X-3*Y^2)+7 |
1. 2. |
Отметим, что с помощью оператора можно
задавать значения переменных в самой программе, но это ограничивает возможность
использования программы с различными исходными данными.
2.4.4. Оператор вывода
Оператор
ввода начинается с ключевого слова PRINT.
PRINT
в переводе с английского языка означает печать, оттиск. Поэтому действие
этого оператора состоит в выведении значения переменной или значений
переменных, текста или значений выражений после их вычисления из памяти компьютера
на экран монитора. Вместо слова PRINT
можно набирать знак «?», который после набора оператора транслятор
Бейсик заменяет ключевым словом.
Синтаксис
оператора вывода очень разнообразен. Это связано тем, что визуализация результатов
работы программы должна быть понятна как самому автору программы, так и
сторонним пользователям. Поэтому продемонстрируем работу оператора вывода на
конкретных примерах.
Оператор
вывода на экран позволяет:
1.
Выводить текстовую информацию, заключенную в кавычки, на экран монитора.
Например:
PRINT ”Привет”
2.
Вычислять выражения арифметических выражений.
Например:
PRINT 5.5*4-5^2
3.
Выводить значения переменных на экран монитора.
Например:
SQ1=12*25
DAY$=«понедельник»
PRINT SQ1, DAY$
Разделителем
между выводимыми данными может быть:
запятая
( , ) – данные отделяются друг от друга шагом табуляции, равным 8
пробелам;
точка
с запятой ( ; ) – данные печатаются вплотную друг к другу.
2.4.5. Программа линейного алгоритма
Рассмотрим
реализацию линейного алгоритма на примере задачи, приведенной в разделе 1.3, а
именно: вычислить периметр произвольного треугольника по его трем сторонам.
CLS
INPUT »
Введите значения: А, В, С «; А, В, С
Р = А + В
+ С
? »
Р= «; Р
END
Если записать эти пять строк на русском
языке, то получим:
1. Начало –
очистить экран монитора
2. Ввод трех
чисел А, В, С с клавиатуры
3. Вычислить
сумму Р = А + В + С и присвоить ее значение Р
4. Вывод на
экран дисплея значения Р
5. Конец
В программе использован оператор конца
программы. Его ключевое слово END.
Действие этого оператора заключается в том, что транслятор определяет:
программа завершена, далее операторов нет.
Для самостоятельной работы на построение
блок-схемы и записи программы линейного алгоритма можно предложить следующие
задачи:
Задача 1.
Найти
площадь (S) и длину окружности (L).
R
– радиус вводится с клавиатуры.
Задача 2.
Найти
площадь (S) и периметр
прямоугольного треугольника (Р). Значения катетов А и В вводятся с клавиатуры.
Задача 3.
Найти
общее сопротивление параллельно соединенных проводников (RО).
Значения R1 и R2
вводятся с клавиатуры.
2.5. Операторы языка Бейсик для записи
разветвляющегося алгоритма
Для
записи программы, реализующей разветвляющийся алгоритм, используются операторы
перехода: оператор условного перехода и оператор безусловного перехода. Как уже
выше отмечалось, что при разветвляющемся алгоритме порядок действий зависит от
выполнения или не выполнения некоторого условия. Поэтому в языке Бейсик
предусмотрены специальные выражения либо отношения, либо логические, которые
позволяют записать условия для ветвления.
2.5.1. Выражения отношения
Выражения отношения
образуются из сравнения двух выражений либо арифметических, либо строковых.
Ограничимся рассмотрением выражений отношения, в которых присутствуют
арифметические выражения. По сравнению с арифметическими выражениями в составе
выражения отношения всегда присутствует лишь одна операция отношения
из возможных шести:
|
Операции отношения |
Знак операции |
Выражение в Бейсике |
|
Равенство |
= |
x = y |
|
Неравенство |
< > |
x < > y |
|
Меньше |
< |
x < y |
|
Больше |
> |
x > y |
|
Меньше или равно |
< = |
x < = y |
|
Больше или равно |
> = |
x > = y |
Значением выражения отношения могут быть
лишь TRUE
или FALSE.
TRUE
с английского языка переводится как истина, что обычно ассоциируется с
ответом «ДА», FALSE с английского языка
переводится как ложь, что обычно ассоциируется с ответом «НЕТ». Значение
выражение отношения может быть получено только после того, как получены
значения арифметических выражений, входящих в выражение отношения.
Примеры выражений отношений, для
записи условий на языке Бейсик:
|
A |
SIN(C) |
A$ |
X |
Y/17 |
S+T |
2.5.2. Логические выражения
Сложное
условие записывается с помощью логических выражений, содержащих
операции: NOT – логическое отрицание, AND
– логическое умножение (в переводе с английского языка означает И) – конъюнкция
(название в математике), OR
– логическое сложение (в переводе с английского языка означает ИЛИ) –
дизъюнкция (название в математике). В логическом отношении операции
осуществляются над операциями отношений. Поэтому действие логических операций
можно полностью описать таблицей истинности над двумя выражениями отношений A
и B,
которые принимают значения либо TRUE,
либо FALSE:
|
A |
B |
NOT A |
NOT B |
A AND B |
A OR B |
|
TRUE |
TRUE |
FALSE |
FALSE |
TRUE |
TRUE |
|
TRUE |
FALSE |
FALSE |
TRUE |
FALSE |
TRUE |
|
FALSE |
TRUE |
TRUE |
FALSE |
FALSE |
TRUE |
|
FALSE |
FALSE |
TRUE |
TRUE |
FALSE |
FALSE |
Логическое выражение в общем виде может
содержать несколько логических операций, поэтому определен приоритет их
выполнения: высший приоритет – логическое отрицание (NOT),
затем – логическое умножение (AND),
низший приоритет – логическое сложение (OR).
Для изменения порядка выполнения логических операций используются круглые
скобки (как в арифметических выражениях).
Примеры логических выражений,
для записи условий на языке Бейсик:
1.
Записать на языке Бейсик условие: 1 < C
< 7, т.е. С принадлежит интервалу (1, 7) или графически
Ответ: C>1
AND C<7
2.
Записать на языке Бейсик условие: C ≤ 1 или C ≥7, т.е. С не принадлежит интервалу (1, 7) или графически
Ответ: NOT (C>1
AND C<7) или С<=1
OR C>=7
Следует
отметить следующий порядок вычисления логического выражения: 1. вычисляются
значения арифметических выражений, 2. вычисляются значения выражений отношений,
3. вычисляется значение логического выражения.
2.5.3. Операторы условного перехода
Программирование,
т.е. составление программы на алгоритмическом языке, состоит в написании
последовательности операторов алгоритмического языка, реализующих алгоритм
решения задачи.
Обычно
операторы в программе выполняются последовательно: один за другим. В языке Бейсик,
как и в любом другом языке программирования, имеются такие операторы, которые
могут изменять порядок выполнения операторов в программе. В частности, те
операторы, которые сообщают компьютеру о том, что управление должно быть
передано некоторым другим частям программы, называются операторами передачи
управления. Передача управления может быть условной или безусловной, т. е. управление
будет передаваться в том случае, если некоторое условие истинно, или независимо
от условия.
Условные
операторы служат для изменения последовательности выполнения операторов
программы в зависимости от некоторого условия. Они позволяют описывать
разветвляющийся вычислительный алгоритм типа развилки, который был описан выше.
По своей структуре условные операторы подразделяются на строчные и на блочные.
Однако любой условный оператор начинается с ключевого слова IF,
что в переводе с английского языка означает если. Затем записывается
условие в виде логического выражения или выражения отношения и потом следует
ключевое слове THEN, что в переводе c
английского языка означает тогда. Далее следуют отличия в использовании
блочного или строчного условных операторов, а также учитывается тип разветвляющегося
алгоритма. В условных операторах могут использоваться еще два ключевых слова: ELSE,
что в переводе c английского языка
означает иначе, и ENDIF,
что в переводе c английского языка
означает конец если.
Синтаксис условного строчного оператора для полного варианта
разветвления, т.е. алгоритм предусматривает одно
действие (команду 1) при значении условия TRUE
(истина, «Да») и одно действие (команду 2) при значении условия FALSE
(ложь, «Нет»):
IF
условие THEN
команда 1 ELSE команда
2
Действие
условного оператора состоит в том, что вычисляется значение условия. Если оно
равно TRUE,
то выполняется команда 1, следующая за ключевым словом THEN,
и осуществляется переход к следующему оператору программы. Если оно равно FALSE,
то выполняется команда 2, следующая за ключевым словом ELSE,
и осуществляется переход к следующему оператору программы.
Синтаксис условного строчного оператора для неполного
варианта разветвления («обход»), т.е. алгоритм
предусматривает лишь одно действие (команду) при значении условия TRUE
(истина, «Да»), а при значении условия FALSE
(ложь, «Нет») действий нет:
IF
условие THEN
команда
Действие
условного оператора состоит в том, что вычисляется значение условия. Если оно
равно TRUE,
то выполняется команда, следующая за ключевым словом THEN,
и осуществляется переход к следующему оператору программы. Если оно равно FALSE,
то при отсутствии ключевого слова ELSE
сразу осуществляется переход к следующему оператору программы.
Синтаксис условного блочного оператора для полного
варианта разветвления, т.е. алгоритм
предусматривает одно или более действий (серию команд 1) при значении
условия TRUE
(истина, «Да») и одно или более действий (серию команд 2) при значении
условия FALSE
(ложь, «Нет»):
IF
условие THEN
серия команд 1
ELSE
серия команд 2
ENDIF
Действие
условного оператора состоит в том, что вычисляется значение условия. Если оно
равно TRUE,
то выполняется серия команд 1, которые записаны в следующих строках программы
после заголовка условного блочного оператора, закачивающегося ключевым словом THEN.
Сигналом для дальнейшего перехода является ключевое слово ELSE.
Тогда программа анализирует появление ключевого слова ENDIF и осуществляется выполнение следующего оператора за этим ключевым
словом. Если значение условия равно FALSE,
то выполняется серия команд 2, которые записаны в следующих строках программы
после ключевого слова ELSE до ключевого
слова ENDIF,
а осуществляется выполнение следующего оператора за этим ключевым словом.
Синтаксис условного блочного оператора для неполного
варианта разветвления («обход»), т.е. алгоритм
предусматривает лишь одно или более действий (серию команд) при значении
условия TRUE
(истина, «Да»), а при значении условия FALSE
(ложь, «Нет») действий нет:
IF
условие THEN
серия команд
ENDIF
Действие
условного оператора состоит в том, что вычисляется значение условия. Если оно
равно TRUE,
то выполняется серия команд, которые записаны в следующих строках программы
после заголовка условного блочного оператора, закачивающегося ключевым словом THEN.
Не встретив ключевого слова ELSE,
программа анализирует появление ключевого слова ENDIF
и осуществляется выполнение следующего оператора за этим ключевым словом. Если
значение условия равно FALSE,
но, не встретив ключевого слова ELSE,
а, получив для анализа ключевое слово ENDIF,
осуществляется выполнение следующего оператора за этим ключевым словом.
2.5.4. Оператор безусловного перехода
Для
осуществления переходов в программе используется оператор безусловного
перехода. Ключевое слово этого оператора GOTO,
что в переводе с английского языка означает: иди к.
Синтаксис
оператора безусловного перехода:
GOTO N
где
N – номер строки или метки оператора, на который происходит переход в программе.
Этот
оператор служит для перехода из одной строки программы к другой, помеченной номером
или меткой.
Примеры использования
безусловного оператора перехода на языке Бейсик:
|
Пример |
10 20 30 40 |
Пример |
X=3 GOTO Y=2*X W1 |
2.5.5. Программа разветвляющегося алгоритма
Рассмотрим
реализацию разветвляющегося алгоритма на примере задачи, приведенной в разделе
1.3, а именно: вычислить значение функции 
REM
вычисление значения функции y(x)
CLS
INPUT »
Введите значения: X «; X
IF X<=10 THEN
Y=-5 ELSE Y=X^3
? “Y= “; Y
END
В приведенной программе использовался
условный строчный оператор, который можно всегда заменить на условный блочный,
а именно:
IF X<=10 THEN
Y=-5
ELSE
Y=X^3
ENDIF
В программе использован оператор комментария
Его ключевое слово REM (от английского
слова remark
– замечать, отмечать). Транслятор, встретив это ключевое слово, игнорирует эту
строку программы для анализа синтаксиса и выполнения. Этот оператор служит для
внесения пояснений в программу как для ее автора, так и для людей, которые
будут ее читать.
Для самостоятельной работы на построение
блок-схемы и записи программы разветвляющегося алгоритма можно предложить
следующие задачи:
Задача 1.
Даны
катеты одного треугольника (А1, В1) и катеты другого треугольника (А2, В2).
Определить, будут эти треугольники равновеликими, т.е. имеют они равные
площади?
Задача 2.
Найти
общее сопротивление двух проводников R1
и R2,
если они соединены параллельно (R3)
или последовательно (R4). Значения R1
и R2
вводятся с клавиатуры.
2.6. Операторы языка Бейсик для записи
циклического алгоритма
При
рассмотрении вопросов алгоритмизации задач было сказано, что все вычислительные
процессы, выполняемые на компьютере по заданной программе, можно разделить на
три основных вида:
• линейные;
• разветвляющиеся;
• циклические.
Напомним,
что линейным принято называть вычислительный процесс, в котором операции
выполняются последовательно, в порядке их записи в программе.
Вычислительный
процесс называется разветвляющимся, если для его реализации предусмотрено
несколько направлений (ветвей). В программе появляются операторы передачи
управления, которые могут изменять порядок выполнения операторов в программе.
Это рассмотренные ранее оператор безусловного перехода и условные операторы.
Вычислительный
процесс называется циклическим, если он содержит цикл. Цикл – это группа
операторов, которые выполняются многократно путем возврата от последнего
оператора этой группы к её первому оператору, т.е. это многократно повторяемый
участок программы. Цикл может быть организован с использованием оператора безусловного
перехода и условных операторов. Продемонстрируем это на примере.
Пример: Вычислить
сумму
CLS
S=0
N=0
1 N=N+1
S=S+1/N
IF
N<=1000 THEN GOTO 1
PRINT
”Сумма =”; S
END
Это
так называемый цикл «ДО», т. е. проверка условия выхода из цикла осуществляется
после выполнения тела цикла. Для его организации использован условный строчный
оператор и оператор безусловного перехода. Не составит особого труда составить
цикл, в котором проверка условия выхода из цикла осуществляется перед выполнением
тела цикла, т. е. цикл «ПОКА».
Однако
в языке программирования Бейсик, как и в других языках программирования
высокого уровня, существует специальный оператор цикла, обеспечивающий более
удобный способ организации циклов.
2.6.1. Оператор цикла
Оператор
цикла является одним из наиболее важных операторов. Его эффективность особенно
велика при использовании массивов, т. е. работе с элементами массивов.
Оператор
цикла является структурным оператором, имеющим три части: заголовок оператора
цикла, тело цикла, завершающий оператор.
FOR I=NI TO KI STEP HI заголовок
оператора цикла
СЕРИЯ
ОПЕРАТОРОВ тело
цикла
NEXT I завершающий
оператор
Оператор цикла содержит четыре ключевых
слова: FOR,
что
в переводе c английского языка
означает для, TO, что
в переводе c английского языка
означает до, STEP, что
в переводе c английского языка
означает шаг и NEXT, что
в переводе c английского языка
означает следующий.
Тело
цикла состоит из последовательности исполняемых операторов, следующих за
заголовком оператора цикла до завершающего оператора. В частном случае, тело
цикла может состоять из одного оператора.
Напомним,
I
– имя параметра цикла (управляющая переменная цикла, такое определение более
информативно: переменная, которая управляет циклом и входе его выполнения
изменяет свое значение); NI – начальное
значение параметра цикла (управляющей переменной цикла); KI
– конечное значение параметра цикла (управляющей переменной цикла); HI
– шаг изменения параметра цикла (управляющей переменной цикла). NI,
KI
и HI могут
быть представлены любыми арифметическими выражениями, но значения переменных,
которые входят в них, должны быть определены до выполнения цикла.
Работу
оператора цикла можно описать следующим образом:
1.
Вычисление значений выражений, определяющих
NI,
KI
и HI;
2.
I
присваивается значение NI;
3.
I
сравнивается с KI: если I
больше KI
при положительном HI (или, наоборот, I
меньше KI
при отрицательном HI), то переход к выполнению
оператора следующего за завершающим оператором цикла ( NEXT I
), иначе вход в цикл;
4.
Выполняются операторы, входящие в тело
цикла до завершающего оператора цикла ( NEXT I
);
5.
I
автоматически изменяется на HI;
6.
Переход к пункту 3, т.е. как бы переход к
заголовку цикла;
Иначе
говоря, операторы FOR и NEXT обеспечивают изменение значения I от NI до KI
с шагом HI
и выполнение оператора (операторов), заключенных между FOR и NEXT, при каждом
значении I.
Замечания:
1.
Изменять значение величин NI,
KI и HI в процессе
выполнения оператора цикла не рекомендуется.
2.
Вход в цикл, минуя заголовок оператора цикла, в Бейсике запрещен.
3.
Значение HI не должно быть 0 (нуль),
так как цикл будет бесконечным.
4.
Если Значение HI
равно 1, конструкцию STEP 1 можно опустить.
Пример: Вычислить сумму
CLS
S=0
FOR
N=1 TO 1000 STEP 1
S=S+1/N
NEXT
N
PRINT
”Сумма =”;
S
END
2.6.2. Программа циклического алгоритма
Рассмотрим
реализацию разветвляющегося алгоритма на примере задачи, приведенной в разделе
1.3, а именно: вычислить значение y=sin φ
в диапазоне изменения аргумента от 10° до 90° с шагом 10°.
CLS
INPUT »
Введите значения: NX«; NX
INPUT »
Введите значения: KX«; KX
INPUT »
Введите значения: HX«; HX
FOR X=NX TO KX
STEP HX
X1 =
X*3.14/180
Y = SIN(X1)
?
Y;»=sin(«;X;»)»
NEXT X
END
В приведенной программе использовался
оператор цикла, применение которого значительно проще, чем организация цикла с
помощью условного оператора.
Для самостоятельной работы на построение
блок-схемы и записи программы циклического алгоритма можно предложить следующие
задачи:
Задача 1.
Вычислить сумму (S) натуральных
нечетных чисел от 1 до 99 (S=1+3+5+…+99).
Задача 2.
Вычислить произведение (P) натуральных
чисел от 1 до 10 (P=1*2*3*…*10=10! –
это называется 10 факториал).
Список литературы
1.
Гейн А.Г., Сенокосов А.И.,
Юнерман Н.А. Информатика: Учеб. пособие для 10– 11 кл.. общеобразоват.
учреждений. – М.: Просвещение, 2000. – 255 с.
2.
Голицына О.Л., Попов И.И.
Основы алгоритмизации и программирование: Учеб. пособие (серия
«Профессиональное образование»). – М.: ФОРУМ: ИНФРА-М, 2004. – 432 с.
3.
Житкова В.Б., Кудрявцева Е.К.
Алгоритмы и основы программирования. (Тематический контроль по информатике.). –
М.: Интеллект-Центр, 1999. – 64 с.
4.
Кириенко Д.П., Осипов П.О.,
Чернов А.В. ГИА-2013: Экзамен в новой форма: Информатика: 9-й класс:
Тренировочные варианты экзаменационных работ для проведения государственной
(итоговой) аттестации в новой форме. – М.: Астрель, 2013. – 78 с.
5.
Колдаева Н.В. Основы
информатики: Учебное пособие. – Кстово: НФВИУ, 2002. – 60 с.
6.
Коханко В.В., Колдаева Н.В.,
Матвейчук. Основы программирования: Учебное пособие. – Кстово: НВВИКУ (ВИ),
2008. – 244 с.
7.
Кузнецов А.А., Пугач В.И.,
Добудько Т.В., Матвеева Н.В. – 2-е изд., испр. – М.: БИНОМ, Лаборатория знаний,
2003. – 232 с.
8.
Мамонтов Д.В. Quick Basic в задачах и примерах. –
СПб.: Питер, 2006. – 256 с.
9.
Острейковский В.А., Полякова
И.В. Информатика. Теория и практика: Учеб. пособие. – М.: Издательство Оникс,
2008. – 608 с.
10. Островская Е.М., Самылкина Н.Н. ЕГЭ 2013. Информатика. Сдаем без
проблем! – М.: Эксмо, 2012. – 160 с.
11. Самылкина Н.Н.. Островская Е.М., Кузнецова Е.Ю. ЕГЭ 2013.
Информатика: тренировочные задания. – М.: Эксмо, 2012. – 200 с.
12. Светозарова Г.И., Мельников А.А., Козловский А.В. Практикум по
программированию на языке бейсик: Учеб. пособие для вузов. – М.: Наука. Гл.
ред. физ.-мат. лит., 1988. – 368 с.
13. Угренович Н.Д. Информатика и ИКТ. Базовый уровень: учебник для 11
класса. – 5-е изд. – М.: БИНОМ, Лаборатория знаний, 2012. – 187 с.
14. Хлебников А.А. Информатика: учебник (Среднее профессиональное
образование). – Изд. 3-е, стер. – Ростов н/Д.: Феникс, 2012. – 507 с.
15. Цветкова М.С. Информатика и ИКТ: учебник для нач. и сред. проф.
образования. – 3-е изд. стер. – М.: Издательский центр «Академия», 2012. – 352
с.
5
Visual Basic
6.0 Лекция
8
РАЗРаботка
Блок-схемы 1
Использование
MS Word 1
Элементы
блок-схемы 2
Блок-схема
алгоритма вычисления корней квадратного
уравнения 3
Отображение
Блок-схемы 3
Создание
графического файла 3
Добавление
новой формы 4
Отображение
формы 4
Отображение
графического файла 5
РазРаботка Блок-схемы
Любая
вычислительная задача включает в себя
формулировку задачи – описание
требований, которым должно удовлетворять
решение задачи, и алгоритм решения –
последовательность действий, с помощью
которых это решение может быть получено.
В теории алгоритмов доказана теорема
которая гласит: если алгоритм
может выть реализован на каком либо
языке программирования, то он может
быть реализован и на любом другом языке
программирования. Поэтому алгоритм
решения задачи не должен содержать
операторов или приёмов, характерных
для конкретного языка программирования.
Существует
несколько способов описания алгоритма
решения задачи. Приведём некоторые из
них:
-
словесное описание;
-
изображение алгоритма
с помощью блок-схемы; -
описание алгоритма
с помощью псевдокода.
Рассмотрим
второй способ описания алгоритма.
Блок-схема алгоритма включает в себя
определённые геометрические фигуры,
соединённые между собой стрелками.
Каждая фигура содержит словесное или
формульное описание выполняемых действий
или условий. Стрелки определяет
последовательность действий. Блок-схема
может содержать только одну точку входа
(Начало) и только одну
точку выхода (Конец).
Для
создания блок-схемы в настоящий момент
разработано несколько специальных
графических редакторов. Но эту задачу
можно также решить и в популярном
текстовом редакторе MS
Word.
Использование ms Word
При
разработке блок-схемы в текстовом
редакторе MS Word
рекомендуется:
-
о
тобразить
панель инструментов Рисование
с помощью кнопки Рисование
на стандартной панели инструментов -
о
тобразить
сетку (кнопка Действия
команда Сетка флажок
Отображать линии
сетки на
экране) -
установить шаг сетки
равным 0,2 см (кнопка Действия
кнопка Сетка раздел
Шаг сетки
поля По вертикали
и По горизонтали),
что упрощает установку численных
значений размеров объектов -
задавать размеры
объектов кратными двум шагам сетки
(меню Формат команда
Автофигура вкладка
Размер раздел Размер
и поворот поля Высота
и Ширина), что упрощает
симметричную “стыковку” объектов -
привязать объекты
к узлам сетки (кнопка Действия
кнопка Сетка флажок
Привязать к
сетке), что упрощает “стыковку”
объектов -
для перемещения
объектов с шагом сетки используйте
клавиши управления курсором -
для перемещения
объектов с малым шагом используйте
клавиши управления курсором при нажатой
клавише Shift -
для добавления
текста к объекту в контекстное меню и
выберите команду Добавить
текст -
для выравнивания
текста внутри объекта в контекстное
меню и выберите команду Формат
автофигуры и на вкладке Надпись
установите значения внутренних полей -
для выделения
нескольких объектов нажмите кнопку
Выбор объектов
на панели инструментов
Рисование
и протащите указатель по экрану -
для группировки
объектов выделить их и в контекстное
меню выберите команду Группировка
Группировать -
при создании надписей
да , нет
используйте текстовое поле без заливки
и границы (меню Формат
команда Автофигура
вкладка Цвета и линии
разделы Заливка и Линии
поля Цвет ) -
при создании
однотипных фигур используйте копирование
(перетащите объект при нажатой кнопке
Ctrl)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #



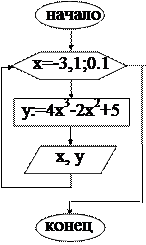
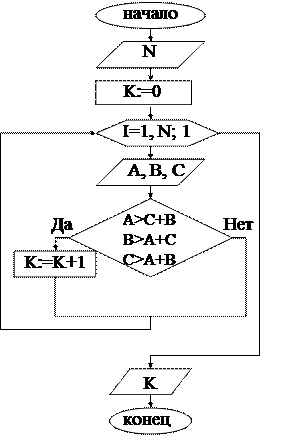




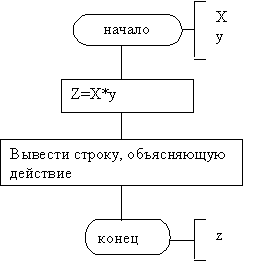
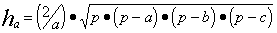
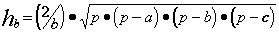
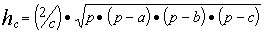
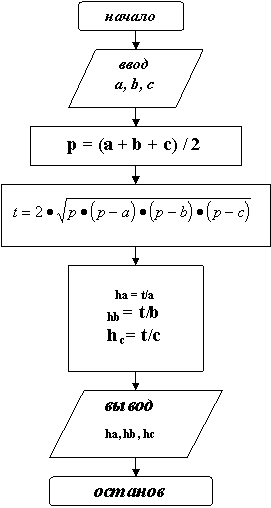

 2) если-то-иначе
если условие
то действия 1
иначе действия 2
конец если
2) если-то-иначе
если условие
то действия 1
иначе действия 2
конец если
 3) выбор
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
конец выбора
3) выбор
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
конец выбора
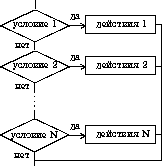 4) выбор-иначе
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1
конец выбора
4) выбор-иначе
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1
конец выбора
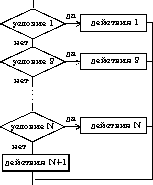

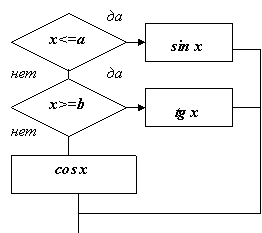
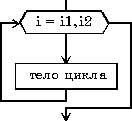 цикл пока условие
тело цикла (последовательность действий)
конец цикла
цикл пока условие
тело цикла (последовательность действий)
конец цикла
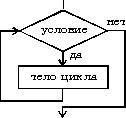 цикл делать
тело цикла (последовательность действий)
пока условие
конец цикла
цикл делать
тело цикла (последовательность действий)
пока условие
конец цикла
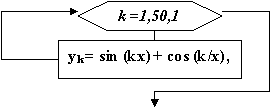
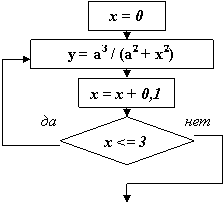
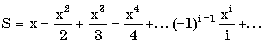
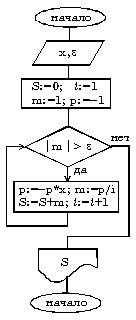
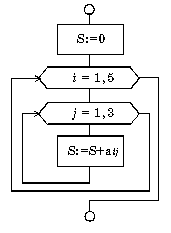
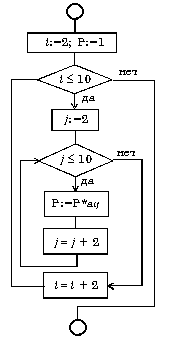





















 тобразить
тобразить