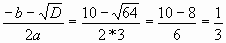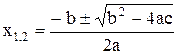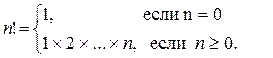Содержание
- Лабораторный практикум по основам языка C/С++
- Справочник
- Правила оформления блок-схем
- Назначение блоков
- Один из методов решения квадратных уравнений
- Составить блок схему алгоритма решения квадратного уравнения
Лабораторный практикум по основам языка C/С++
Справочник
Правила оформления блок-схем
Блок-схема является графическим представлением алгоритма решения задачи. Блок-схема никак не связана с каким-либо языком программирования. Таким образом все выражения в блоках блок-схемы записываются по правилам обычной математики.
В блок-схемах нельзя использовать элементы языка программирования.
- в качестве оператора присваивания в блок-схемах используется двухсимвольный знак «:=»
- в качестве оператора логического сравнения на равенство в блок-схемах используется одинарный символ знак «=»
- в качестве оператора логического сравнения «больше или равно» («меньше или равно») в блок-схемах используется одинарный символ » ≥ » ( » ≤ » )
- в качестве логических операторов используются слова AND , OR
- индексы у элементов массива указываются также, как в математических выражениях: aij .
- математические выражения записываются согласно всем правилам математики. Особенно это касается выражений с дробями, то есть формула должна записываться следующим образом
, а не x1=(-b-sqrt(b*b-4*a*c))/(2*a).
Назначение блоков
| Наименование | Обозначение | Функция |
|---|---|---|
| Терминатор |  |
Элемент отображает выход во внешнюю среду и вход из внешней среды (наиболее частое применение − начало и конец программы). Внутри фигуры записывается соответствующее действие. |
| Процесс |  |
Выполнение одной или нескольких операций, обработка данных любого вида (изменение значения данных, формы представления, расположения). Внутри фигуры записывают непосредственно сами операции, например, операцию: a := 10 b + c  |
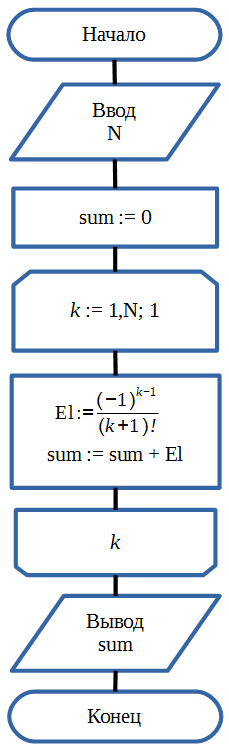
Для вычисления суммы ряда в программе необходимо выполнить следующие действия:
- Описать переменные, которые будут использоваться для хранения текущего значения суммы, текущего значения счетчика элементов цикла, а также общего количества суммируемых элементов.
Примечание: это действие необходимо только для определения количества переменных, которые потребуются алгоритму и потому в блок-схеме эти действия никак не учитываются. - Получить у пользователя число элементов ряда, которые следует просуммировать, то есть ввести данные в программу.
- Обнулить переменную, которая будет хранить сумму ряда.
- Инициализировать счетчик цикла начальным значением.
- Рассчитать значение элемента ряда с номером, равным текущему значению счетчика и прибавить получившееся значение к значению переменной-суммы.
- увеличить значение счетчика на единицу.
- Если значение счетчика меньше количества суммируемых элементов, которое задано пользователем, то перейти к выполнению пункта 5.
- Вывести значение суммы.
Это текстовая запись алгоритма. Теперь реализуем ее в виде графической схемы (блок-схемы).
Если вы не занете при помощи чего создавать блок-схемы, то рекомендуем ознакомиться со следующей статьей:
6 сервисов для работы с блок-схемами
Источник
Один из методов решения квадратных уравнений
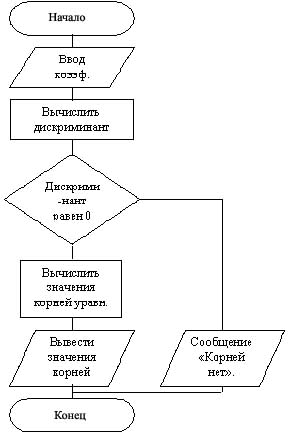
Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:
Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.
После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.
procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
<Ввод исходных данных>a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
< Вычисление дискриминанта >d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin
х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);
Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.
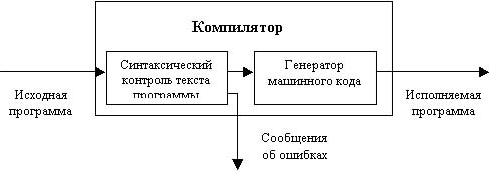
Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа — компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.
Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.
Решение квадратных уравнений средствами Visual Basic
Задача: Дано квадратное уравнение общего вида: ax 2 +bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b 2 -4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.
Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?
Поместим на форму две кнопки: CommandButton1 и CommandButton2.
Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.
Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:
- ввод коэффициентов исходного уравнения a, b, c;
- расчет дискриминанта d=b 2 — 4ac;
- анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
- вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.
Далее рассмотрим процесс решения второго квадратного уравнения: 10x 2 +5x+200=0.
В окне InputBox вводим значение первого коэффициента уравнения a=10.
Ввод первого коэффициента a завершается нажатием кнопки Ok.
Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.
Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.
Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.
Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.
После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.
И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x 2 -8x+16=0.
Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.
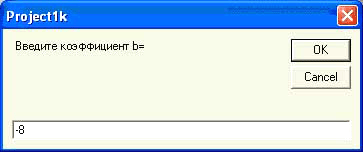
Далее вводим второй коэффициент уравнения b= –8.
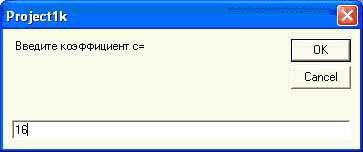
Третий коэффициент уравнения c=16 вводим в последнюю очередь.
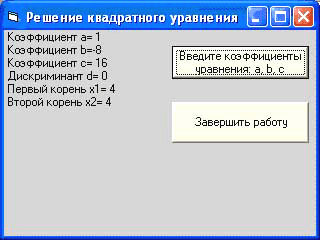
В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.
Источник
Составить блок схему алгоритма решения квадратного уравнения
Задача 1. Составить блок-схему и программу, находящие корни квадратного уравнения
PRINT “Решение квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
THEN Х 1=(-b-sqr(d))/(2*a) : Х 2=(-b+sqr(d))/(2*a) : PRINT “Х1=“, Х1, “ Х2=“, Х2
ELSE PRINT “Действительных корней нет “
Запустите программу на выполнение и решите следующие квадратные уравнения:
б) 502 х 2 – 38,5 х + 12,125 = 0
Задача 2. Составить блок-схему и программу, определяющие количество корней квадратного уравнения
PRINT “Количество корней квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
IF d > 0 THEN PRINT “2 разных корня“ ELSE PRINT “2 одинаковых корня“
ELSE PRINT “Действительных корней нет“
Запустите программу на выполнение и определите количество корней в следующих квадратных уравнениях:
б) 502 х 2 – 38,5 х + 12,125 = 0
Задача 3*. Составить блок-схему и программу, определяющие имеет ли квадратное уравнение ax 2 + bx + c = 0 хотя бы один корень, больший числа m .
Запустите программу на выполнение и определите имеется ли корень в следующих квадратных уравнениях:
а) 1125 х 2 – 45 х – 324 = 0 при m = 0
б) 502 х 2 – 38,5 х + 12,125 = 0 при m = 15
в) 16 х 2 – 256 х + 1024 = 0 при m = 7
Домашнее задание – Составить блок-схемы и программы для следующих задач:
Задача 1. Определить является ли введенное с клавиатуры число корнем квадратного уравнения ax 2 + bx + c = 0 .
До сих пор мы с вами говорили о каких-то отвлечённых задачах из области математики. Сегодня мы поговорим о конкретной задаче, которая встречается у вас почти на каждом уроке. Это решение квадратного уравнения. Я хочу, чтобы вы на примере этой задачи поняли, что программирование – это не просто прихоть учителя, это действительно раздел информатики, который может нам помочь, например, в решении конкретных математических задач. Нужно только уметь разбираться в этом.
Давайте вспомним, что понимают под квадратным уравнением?
Что из себя представляют числа a,b,c и как их называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b 2 -4ac) (Приложение 3)
Как мы решаем далее квадратное уравнение? (сравнение D с нулём)
Какие выводы мы из этого делаем?
Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного уравнения сведу к условию D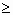
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Найти дискриминант D=b 2 – 4ac.
D=b 2 -4ac=10 2 -4*3*3=100 – 36 =64
Х1=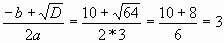
X2 =
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Подпишем основные элементы блок – схемы применительно к языку программирования.
4. Составление программы по блок – схеме.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
Запуск программы – ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
Подсказка: Меню File – Exit или ALT+X.
1. За простое воспроизведение (набор программы) без проверки оценка “3”
2. За проверку работы программы на примерах, представленных учителем оценка “4”
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка “5”
Подсказка: Меню File – Exit или ALT+X.
| № | Х1 | Х2 | |
| 1 | 3,230139 | 0,1031947 | |
| 2 | 1,464102 | -5,464102 | |
| 3 | 1,106107 | -1,356107 | |
| 4 | 5 | 6 | 1,6 |
| 7 | 2 | -1,6 | |
| 8 | 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
1) Напишите программу проверки пароля. Пусть пароль – некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет – сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами – Циклическими.
На сегодня наш урок закончен. До свидания.
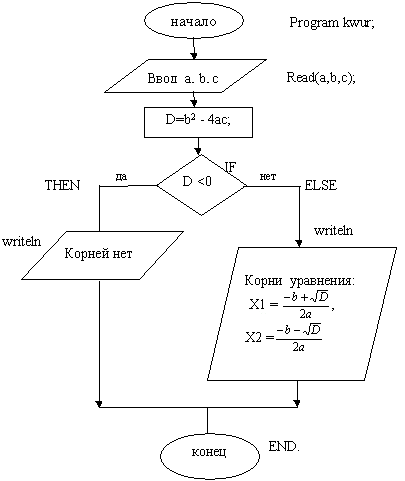
Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты a, b, c. Решением в общем случае являются два корня x1 и x2, которые вычисляются по формулам:
Все величины, используемые в этой программе, имеют вещественный тип.
алг корни квадратного уравнения
вещ a, b, c, x1, x2, d
начввод a, b, c
Слабость такого алгоритма видна «невооруженным глазом». Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам: универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и выходить на конец. Результатом может быть числовой ответ, но может быть и сообщение о том, что при таких данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Это же свойство в литературе по программированию называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).
Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.
Решение уравнения зависит от значений коэффициентов a, b, c. Вот анализ этой задачи (ограничиваемся только поиском вещественных корней):
если a=0, b=0, c=0, то любое х – решение уравнения;
если a=0, b=0, c¹0, то уравнение решений не имеет;
если a=0, b¹0, то это линейное уравнение, которое имеет одно решение: x=–c/b;
если a¹0 и d=b 2 -4ac³0, то уравнение имеет два вещественных корня (формулы приведены выше);
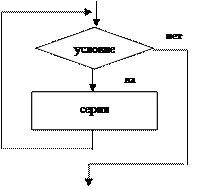
В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий:
еслиусловие то серия 1 иначе серия 2 кв
Вначале проверяется «условие» (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется «серия 1» – последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется «серия 2» (отрицательная ветвь). В АЯ условие записывается после служебного слова «если», положительная ветвь – после слова «то», отрицательная – после слова «иначе». Буквы «кв» обозначают конец ветвления.
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «корни квадратного уравнения». В нем для краткости вместо слов «да» и «нет» использованы соответственно «+» и «–».
Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала.
Ниже приведена блок-схема алгоритма. В нем используются три переменные целого типа: n – аргумент; i – промежуточная переменная; F – результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n=3.
Шаг n F i Условие вывод 1£3, да 2£3, да 3£3, да 4£3, нет
Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.
алгФакториал
нач ввод n
пока i£n, повторять
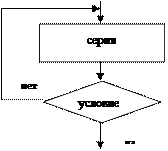
Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда «цикл-пока», или «цикл с предусловием». Общий вид команды «цикл-пока» в блок-схемах и в АЯ следующий:
пока условие, повторять нц серия кц
Повторяется выполнение серии команд (тела цикла), пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова «нц» и «кц» обозначают соответственно начало цикла и конец цикла.
Цикл с предусловием – это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если a=0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля – еще один признак хорошего качества программы.
 |
алгквадратное уравнение вещa, b, c, d, x1, x2 нач повторять ввод a, b, c до a¹0 d:=b 2 –4ac если d³0 тоx1:=(–b+Öd)/(2a) x2:=(–b–Öd)/(2a) вывод x1, x2 иначе вывод “нет вещественных корней” кв кон |
В общем виде структурная команда «цикл с постусловием» или «цикл-до» представляется так:
повторять серия доусловие
Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу.
Составим алгоритм решения следующей задачи: даны два натуральных числа M и N. Требуется вычислить их наибольший общий делитель – НОД(M,N).
Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M>N, то НОД(M N то M:=M–N иначе N:=N–M кв кц кон
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая M=18, N=12. В результате получится НОД=6, что, очевидно, верно.
Источник
Квадратный корень в программах встречается очень часто, при этом его вычисление достаточно трудоемко. Еще в 1950х годах соответствующая операция была вынесена в специальный математический сопроцессор — центральный процессор отправлял в него запрос и пока выполнялись вычисления он успевал обрабатывать другие важные команды.
Я не собирал специально литературу по поводу различных алгоритмов вычисления корня, но мне известны два (достаточно очевидных) способа сделать это. Их и рассмотрим.
Вычисление корня через площадь прямоугольника
В древней Греции было разработано множество алгоритмов с хорошей геометрической интерпретацией. Не удивлюсь, если и этот алгоритм придумали греки. На самом деле, подумайте откуда берется квадратный корень? — известно, что у квадрата со стороной A площадь равна S = A*A. Из этого простого соотношения следует, что если вам надо вычислить корень из S — нужно построить такой квадрат, что его площадь будет равна S, а длина стороны квадрата как раз и будет искомым корнем (a = sqrt(S)).
Кстати, аналогичные рассуждения возможны для кубического корня (но при этом площадь квадрата нужно заменить объемом куба). Это прекрасная геометрическая интерпретация, но как же найти длину стороны такого квадрата? — итеративно. Возьмем для начала прямоугольник одна из сторон которого имеет длину S, а другая — 1. Площадь такого прямоугольника совпадает с площадью исходного квадрата, если при этом длины сторон отличаются на величину допустимой погрешности вычислений — то сторона прямоугольника является ответом. Если же стороны различаются слишком сильно — то самый очевидный алгоритм предлагает усреднить одну из сторон (a), а вторую вычислить как b = S/a . За счет того, что одна сторона усредняется, разница длин сторон сокращается. Вторая сторона вычисляется так, чтобы площадь прямоугольника не изменялась.
Блок-схема такого алгоритма вычисления корня:
Вычисление корня методом половинного деления
Метод половинного деления относится к серии алгоритмов, построенных по принципу «разделяй и властвуй». Он применяется для поиска корней уравнений. Допустим, есть у нас некоторая функция f(x), известно, что функция монотонна на некотором интервале [a,b].
Монотонность — обязательное требование для использования этого алгоритма, оно означает, что функция либо только возрастает на этом интервале, либо — убывает. В общем, на интервале нет перегибов функции, т.е. точек, в которых производная равна нулю.
Тогда, если на концах интервала функция имеет разные знаки — она обязательно пересекает горизонтальную ось, т.е. имеет корень. Если f(a) * f(b) > 0 — значит функция на этом интервале корня не имеет.
Как же найти где именно находится этот корень? — опять же итеративно. Возьмем точку посередине интервала (x = a + (b-a)/2) — по знаку f(x) можно определить где именно находится корень (правее этой точки или левее). Если f(a)*f(x) < 0 — то корень находится на интервале [a,x] при этом заменим b на x и повторим процесс. В противном случае корень находится на [x,b]. Вычисления продолжаются до тех пор, пока интервал поиска корня не сузится достаточно сильно, т.е. пока abs(b-a) > Eps.
Причем же тут корень квадратный? — заметьте, что для его вычисления достаточно решить уравнение типа x*x = S, т.е. f(x) = x*x - S = 0. Начальное значение интервала поиска — [1,S].
Блок-схема такого алгоритма вычисления корня:
Описание алгоритмов с помощью блок-схем.
Для
разработки структуры программы удобнее
пользоваться записью алгоритма в
виде блок-схемы (в
англоязычной литературе используется
термин flow-chart).
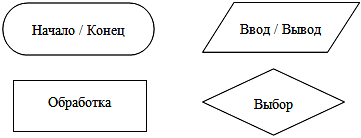
Для изображения основных алгоритмических
структур и блоков на блок-схемах
используют специальные графические
символы. Они приведены на рисунке
Начало/конец
алгоритма
Передача управления
Ввод данных
Блок вычислений
Начало (заголовок)
цикла
Конец цикла
Ветвление
Вывод данных
Составим
алгоритм вычисления квадратного корня
из произвольного положительного
вещественного числа х методом
Герона и запишем его на естественном
языке, а также в виде блок-схемы. Метод
основан на многократном применении
формулы:

при
.
Числовая
последовательность
в
пределе при
сходится
к искомому значению. Выполним только 5
итераций метода, считая, что при этом
будет достигнута достаточно хорошая
точность. Обычно десяти итераций метода
Герона более чем достаточно для достижения
хорошей точность расчёта. Оба варианта
записи алгоритма:
|
|
1. Ввести х.
2. Присвоить
3. Присвоить
4. Присвоить
5. Присвоить 6. |
А
теперь займёмся самым любимым занятием
школьников всех времён и народов –
решением квадратного уравнения:
.
Будем полагать,
что коэффициенты этого
уравнения
,
и
представляют
собой вещественные числа. Простейший
случай предполагает, что все коэффициенты
отличны от нуля. В зависимости от знака
дискриминанта квадратного уравнения
возможны три
случая:
1.
Если
,
то имеются два различных вещественных
корня, которые можно вычислить по
следующим формулам:
,
.
2.
Если
,
то имеется единственный корень (точнее,
двукратный корень):
.
3.
Если
,
то вещественных корней нет.
Блок схема алгоритма
приведена на рисунке:
С
ледует
заметить, что приведённый алгоритм
предназначен для решения узкого класса
задач – квадратных уравнений с «хорошими»
коэффициентами. Если допустить, что
коэффициенты могут принимать произвольные
вещественные значения, есть опасность,
что при определённых значениях
коэффициента (например,
)
возникает аварийная ситуация (деление
на ноль). Качественный алгоритм и
качественная программа должны быть
устойчивыми, то есть при любых входных
параметрах завершение работы программы
должно быть нормальным, хотя, возможно,
и сопровождаться предупреждающим
сообщением о некорректности входных
данных. Свойством устойчивости обладает
алгоритм решения квадратного уравнения.
Разработанный
программистом алгоритм должен давать
правильный ответ. Проверка алгоритма
может оказаться непростым делом. В
простых случаях такая проверка может
быть выполнена с помощью
заполнения трассировочной
таблицы. Каждый столбец такой
таблицы соответствует определённой
переменной, а каждая строка – одному
шагу алгоритма. Для заполнения таблицы
необходимо шаг за шагом проследить
выполнение алгоритма, записывая в
таблицу текущие значения выбранных для
трассировки переменных. Такой метод
позволяет выявить логические ошибки,
допущенные при составлении или записи
алгоритма, и определить, верен ли
окончательный ответ. Составим в качестве
примера трассировочную таблицу для
алгоритма Герона вычисления квадратного
корня из числа 2.
|
i |
z |
|
0 |
1,00000 |
|
1 |
1,50000 |
|
2 |
1,41666 |
|
3 |
1,41421 |
|
4 |
1,41421 |
|
5 |
1,41421 |
Как
видно из таблицы, уже после третьей
итерации приближенное значение
квадратного корня отличается от точного
1,414213 лишь в шестом знаке после запятой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгоритмы
История появления алгоритмов
Появление алгоритмов связывают с зарождением математики. Более 1000 лет назад (в 825 году) ученый из города Хорезма Абдулла (или Абу Джафар) Мухаммед бен Муса аль-Хорезми создал книгу по математике, в которой описал способы выполнения арифметических действий над многозначными числами. Само слово алгоритм возникло в Европе после перевода на латынь книги этого математика.
Понятие алгоритма. Изображение алгоритма в виде блок-схемы.
Алгоритмы линейной и разветвляющейся структуры
1.1. Понятие алгоритма
Алгоритм — четкое описание последовательности действий, которые необходимо выполнить при решении задачи. Можно сказать, что алгоритм описывает процесс преобразования исходных данных в результаты, т.к. для решения любой задачи необходимо:
- Ввести исходные данные.
- Преобразовать исходные данные в результаты (выходные данные).
- Вывести результаты.
Разработка алгоритма решения задачи — это разбиение задачи на последовательно выполняемые этапы, причем результаты выполнения предыдущих этапов могут использоваться при выполнении последующих. При этом должны быть четко указаны как содержание каждого этапа, так и порядок выполнения этапов. Отдельный этап алгоритма представляет собой либо другую, более простую задачу, алгоритм решения которой известен (разработан заранее), либо должен быть достаточно простым и понятным без пояснений. Разработанный алгоритм можно записать несколькими способами:
- на естественном языке;
- в виде блок-схемы;
- в виде R-схемы.
Рассмотрим пример алгоритма на естественном языке:
- Ввести в компьютер числовые значения переменных а, b и с.
- Вычислить d по формуле d = b 2 — 4ас.
- Если d 1 и x 2.
- Прекратить вычисления.
1.2. Изображение алгоритма в виде блок-схемы
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур — блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются следующими геометрическими фигурами:
Блок начала-конца алгоритма (рис. 1.1). Надпись на блоке: «начало» («конец»).
Блок ввода-вывода данных (рис. 1.2). Надпись на блоке: слово «ввод» («вывод» или «печать») и список вводимых (выводимых) переменных.
| Рис. 1.1. Блок начала-конца алгоритма | Рис. 1.2. Блок ввода-вывода данных |
Блок решения или арифметический (рис. 1.3). Надпись на блоке: операция или группа операций.
Условный блок (рис. 1.4). Надпись на блоке: условие. В результате проверки условия осуществляется выбор одного из возможных путей (ветвей) вычислительного процесса. Если условие выполняется, то следующим выполняется этап по ветви «+», если условие не выполняется, то выполняется этап по ветви «–».
| Рис. 1.3. Арифметический блок | Рис. 1.4. Условный блок |
В качестве примера рассмотрим блок-схему алгоритма решения уравнения (рис. 1.5), описанного в предыдущем подразделе.
| Рис. 1.5. Блок-схема алгоритма решения квадратного уравнения |
1.3. Алгоритмы линейной структуры
Линейный алгоритм — это такой, в котором все операции выполняются последовательно одна за другой (рис. 1.6).
| Рис. 1.6 Размещение блоков в линейном алгоритме |
Рассмотрим несколько примеров линейных алгоритмов.
ПРИМЕР 1.1. Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника.
Пусть a, b, c — длины сторон треугольника. Необходимо найти S — площадь треугольника, P — периметр.
| Для нахождения площади можно воспользоваться формулой Герона: | где r — полупериметр. |
Входные данные: a, b, c.
Выходные данные: S, P.
Блок-схема алгоритма представлена на рис. 1.7.
| Рис. 1.7. Алгоритм примера 1.1 |
Внимание. В этих блоках знак «=» означает не математическое равенство, а операцию присваивания. Переменной, стоящей слева от оператора, присваивается значение, указанное справа. Причем это значение может быть уже определено или его необходимо вычислить с помощью выражения. Например, операция r = (a+b+c)/2 — имеет смысл (переменной r присвоить значение r=(a+b+c)/2), а выражение (a+b+c)/2=r — бессмыслица.
ПРИМЕР 1.2. Известны плотность и геометрические размеры цилиндрического слитка, полученного в металлургической лаборатории. Найти объем, массу и площадь основания слитка.
Входные данные: R — радиус основания цилиндра, h — высота цилиндра, ? — плотность материала слитка.
Выходные данные: m — масса слитка, V — объем, S — площадь основания.
Блок-схема представлена на рис. 1.8.
Рис. 1.8. Алгоритм примера 1.2
ПРИМЕР 1.3. Заданы длины двух катетов в прямоугольном треугольнике. Найти длину гипотенузы, площадь треугольника и величину его углов.
Входные данные: a, b — длины катетов.
Выходные данные: с — длина гипотенузы, S — площадь треугольника, ?, ? — углы.
Блок-схема представлена на рис.1.9.
| Рис. 1.9 Алгоритм примера 1.3 |
1.4. Алгоритмы разветвленной структуры
Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. В блок-схемах разветвленные алгоритмы изображаются так, как показано на рис. 1.10 — 1.11.
| Рис. 1.10 Фрагмент алгоритма | Рис. 1.11 Пример разветвления |
Рассмотрим несколько примеров построения алгоритмов разветвленной структуры.
ПРИМЕР 1.4. Известны коэффициенты и с квадратного уравнения. Вычислить корни квадратного уравнения.
Входные данные: a, b, c.
Выходные данные: x 1 , x 2 .
Блок-схема представлена на рис. 1.5.
ПРИМЕР 1.5. Составить программу нахождения действительных и комплексных корней квадратного уравнения. Можно выделить следующие этапы решения задачи:
- Ввод коэффициентов квадратного уравнения a, b и c.
- Вычисление дискриминанта d по формуле d = b 2 — 4ас.
- Проверка знака дискриминанта. Если d >= 0, то вычисление действительных корней по формуле 1.1 и вывод их на экран.
При отрицательном дискриминанте выводится сообщение о том, что действительных корней нет, и вычисляются комплексные корни.Комплексные числа записываются в виде a + ib
a — действительная часть комплексного числа, b — мнимая часть комплексного числа.У обоих комплексных корней действительные части одинаковые, а мнимые отличаются знаком. Поэтому можно в переменной x 1 хранить действительную часть числа -b/2a, в переменной x 2 — модуль мнимой части , а в качестве корней вывести x 1 +ix 2 и x 1 -ix 2.
На рис. 1.12 изображена блок-схема решения задачи. Блок 1 предназначен для ввода коэффициентов квадратного уравнения. В блоке 2 осуществляется вычисление дискриминанта. Блок 3 осуществляет проверку знака дискриминанта, если дискриминант отрицателен, то корни комплексные, их расчет происходит в блоке 4 (действительная часть корня записывается в переменную x 1 , модуль мнимой — в переменную x 2 ), а вывод — в блоке 5 (первый корень x 1 + i x 2 , второй — x 1 — i x 2 ). Если дискриминант положителен, то вычисляются действительные корни уравнения (блок 6) и выводятся на экран (блок 7).
Один из методов решения квадратных уравнений
Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:
Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.
После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.
procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
<Ввод исходных данных>a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
< Вычисление дискриминанта >d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin
х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);
Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.
Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа — компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.
Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.
Решение квадратных уравнений средствами Visual Basic
Задача: Дано квадратное уравнение общего вида: ax 2 +bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b 2 -4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.
Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?
Поместим на форму две кнопки: CommandButton1 и CommandButton2.
Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.
Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:
- ввод коэффициентов исходного уравнения a, b, c;
- расчет дискриминанта d=b 2 — 4ac;
- анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
- вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.
Далее рассмотрим процесс решения второго квадратного уравнения: 10x 2 +5x+200=0.
В окне InputBox вводим значение первого коэффициента уравнения a=10.
Ввод первого коэффициента a завершается нажатием кнопки Ok.
Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.
Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.
Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.
Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.
После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.
И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x 2 -8x+16=0.
Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.
Далее вводим второй коэффициент уравнения b= –8.
Третий коэффициент уравнения c=16 вводим в последнюю очередь.
В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.
Составить блок схему алгоритма решения квадратного уравнения
Задача 1. Составить блок-схему и программу, находящие корни квадратного уравнения
ПРОГРАММА на БЕЙСИК
PRINT “Решение квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
d = b * b – 4 * a * c
THEN Х 1=(-b-sqr(d))/(2*a) : Х 2=(-b+sqr(d))/(2*a) : PRINT “Х1=“, Х1, “ Х2=“, Х2
ELSE PRINT “Действительных корней нет “
Запустите программу на выполнение и решите следующие квадратные уравнения:
а) 1125 х 2 – 45 х – 324 = 0
б) 502 х 2 – 38,5 х + 12,125 = 0
в) 16 х 2 – 256 х + 1024 = 0
Задача 2. Составить блок-схему и программу, определяющие количество корней квадратного уравнения
Если я случай наличия корней квадратного уравнения сведу к условию D0, то что я получу в случае D=0?
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Найти дискриминант D=b 2 – 4ac.
Сравнить его с нулём
D=b 2 -4ac=10 2 -4*3*3=100 – 36 =64
Х1=,
X2 =
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Подпишем основные элементы блок – схемы применительно к языку программирования.
4. Составление программы по блок – схеме.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Var a,b,c,d,x1,x1: real;
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
Запуск программы – ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
1,5х 2 -0,6х – 4,8 = 0
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File – Exit или ALT+X.
1. За простое воспроизведение (набор программы) без проверки оценка “3”
2. За проверку работы программы на примерах, представленных учителем оценка “4”
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка “5”
4. Закрыть программу.
Подсказка: Меню File – Exit или ALT+X.
| № | Х1 | Х2 | |
| 1 | 3,230139 | 0,1031947 | |
| 2 | 1,464102 | -5,464102 | |
| 3 | 1,106107 | -1,356107 | |
| 4 | 5 | 6 | 1,6 |
| 7 | 2 | -1,6 | |
| 8 | 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
1) Напишите программу проверки пароля. Пусть пароль – некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет – сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами – Циклическими.
На сегодня наш урок закончен. До свидания.
Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты a, b, c. Решением в общем случае являются два корня x1 и x2, которые вычисляются по формулам:
Все величины, используемые в этой программе, имеют вещественный тип.
алг корни квадратного уравнения
вещ a, b, c, x1, x2, d
начввод a, b, c
Кон
Слабость такого алгоритма видна «невооруженным глазом». Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам: универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и выходить на конец. Результатом может быть числовой ответ, но может быть и сообщение о том, что при таких данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Это же свойство в литературе по программированию называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).
Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.
Решение уравнения зависит от значений коэффициентов a, b, c. Вот анализ этой задачи (ограничиваемся только поиском вещественных корней):
если a=0, b=0, c=0, то любое х – решение уравнения;
если a=0, b=0, c¹0, то уравнение решений не имеет;
если a=0, b¹0, то это линейное уравнение, которое имеет одно решение: x=–c/b;
если a¹0 и d=b 2 -4ac³0, то уравнение имеет два вещественных корня (формулы приведены выше);
кв
кв
Кон
В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий:
еслиусловие то серия 1 иначе серия 2 кв
Вначале проверяется «условие» (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется «серия 1» – последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется «серия 2» (отрицательная ветвь). В АЯ условие записывается после служебного слова «если», положительная ветвь – после слова «то», отрицательная – после слова «иначе». Буквы «кв» обозначают конец ветвления.
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «корни квадратного уравнения». В нем для краткости вместо слов «да» и «нет» использованы соответственно «+» и «–».
Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала.
Ниже приведена блок-схема алгоритма. В нем используются три переменные целого типа: n – аргумент; i – промежуточная переменная; F – результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n=3.
Шаг
n
F
i
Условие
вывод
1£3, да 2£3, да 3£3, да 4£3, нет
Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.
алгФакториал
целn, i, F
нач ввод n
F:=1; i:=1
пока i£n, повторять
нц F:=F´i
кц
Кон
Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда «цикл-пока», или «цикл с предусловием». Общий вид команды «цикл-пока» в блок-схемах и в АЯ следующий:
пока условие, повторять нц серия кц
Повторяется выполнение серии команд (тела цикла), пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова «нц» и «кц» обозначают соответственно начало цикла и конец цикла.
Цикл с предусловием – это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если a=0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля – еще один признак хорошего качества программы.
| алгквадратное уравнение вещa, b, c, d, x1, x2 нач повторять ввод a, b, c до a¹0 d:=b 2 –4ac если d³0 тоx1:=(–b+Öd)/(2a) x2:=(–b–Öd)/(2a) вывод x1, x2 иначе вывод “нет вещественных корней” кв кон |
В общем виде структурная команда «цикл с постусловием» или «цикл-до» представляется так:
повторять серия доусловие
Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу.
Составим алгоритм решения следующей задачи: даны два натуральных числа M и N. Требуется вычислить их наибольший общий делитель – НОД(M,N).
Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M>N, то НОД(M N то M:=M–N иначе N:=N–M кв кц кон
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая M=18, N=12. В результате получится НОД=6, что, очевидно, верно.
http://urok.1sept.ru/articles/522622
http://4systems.ru/inf/sostavit-blok-shemu-algoritma-reshenija/
Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:
Рисунок 1
Рисунок 2
Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.
После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.
procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real; {Коэффициенты уравнения}
d:real; {Дискриминант}
xl,x2:real; {Корни уравнения}
begin
{Ввод исходных данных} a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
{ Вычисление дискриминанта } d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin
{Вычисление корней}
х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);
{ Вывод результата — значений корней}
Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.
Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа — компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.
Рисунок 3
Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.
Решение квадратных уравнений средствами Visual Basic
Задача: Дано квадратное уравнение общего вида: ax2+bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b2-4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.
Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?
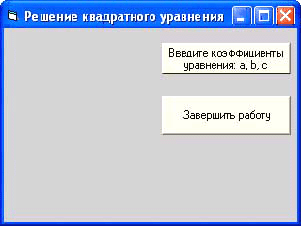
Поместим на форму две кнопки: CommandButton1 и CommandButton2.
Рисунок 4
Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.
Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:
- ввод коэффициентов исходного уравнения a, b, c;
- расчет дискриминанта d=b2 — 4ac;
- анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
- вывод сообщения: «Решений нет», если знак дискриминанта d<0 (отрицательный).
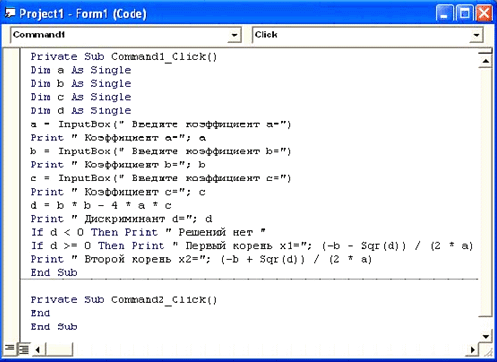
Необходимо написать специальную процедуру события, реагирующую на щелчок мышки по кнопке CommandButton1 на форме, которую назовем: «Введите коэффициенты уравнения a, b, c», и выполняющую названный выше алгоритм.
Рисунок 5
Эта процедура будет иметь название: Command1_Click().
Войдя в компилятор Visual Basic, выберем в главном меню раздел RUN и выполним команду Start. Перед нами появится окно формы нашего проекта задачи «Решение квадратного уравнения». Щелкнем по кнопке «Введите коэффициенты уравнения a, b, c».
Перед нами появится окно InputBox для ввода коэффициента a уравнения.
Рисунок 6
Введем числовое значение, например 1, требуемого коэффициента и нажмите кнопку Ok.
Вслед за этим появится окно для ввода второго коэффициента уравнения b.
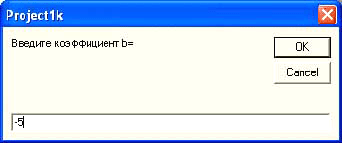
Рисунок 7
Введем коэффициент b (например –5), как это мы сделали для коэффициента a уравнения. Нажмем кнопку Ok.
Проделаем то же самое, чтобы ввести третий коэффициент уравнения c, например с=6.
Рисунок 8
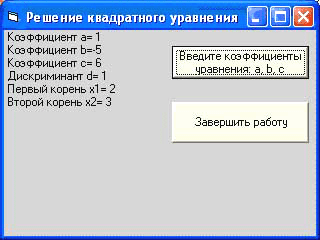
После ввода третьего коэффициента уравнения c перед нами появится окно формы, содержащее решение квадратного уравнения, коэффициенты которого мы ввели.
Рисунок 9
Мы рассмотрели процесс решения квадратного уравнения: x2-5x+6=0.
Далее рассмотрим процесс решения второго квадратного уравнения: 10x2+5x+200=0.
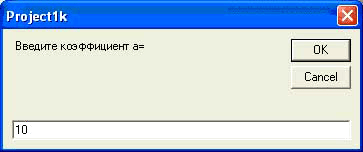
В окне InputBox вводим значение первого коэффициента уравнения a=10.
Рисунок 10
Ввод первого коэффициента a завершается нажатием кнопки Ok.
Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.
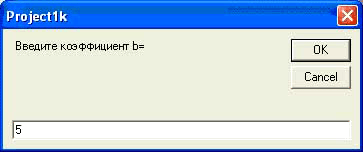
Рисунок 11
Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.
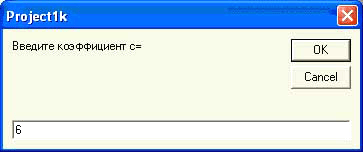
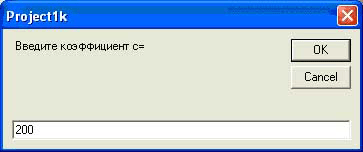
Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.
Рисунок 12
Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.
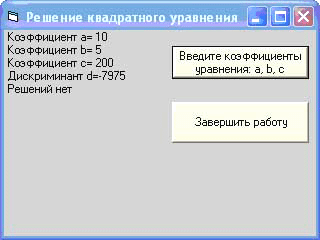
После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.
Рисунок 13
И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x2-8x+16=0.
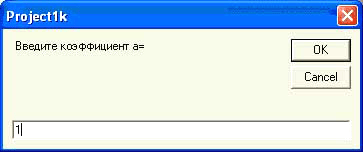
Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.
Рисунок 14
Далее вводим второй коэффициент уравнения b= –8.
Рисунок 15
Третий коэффициент уравнения c=16 вводим в последнюю очередь.
Рисунок 16
В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.
Рисунок 17

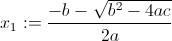 , а не x1=(-b-sqrt(b*b-4*a*c))/(2*a).
, а не x1=(-b-sqrt(b*b-4*a*c))/(2*a).