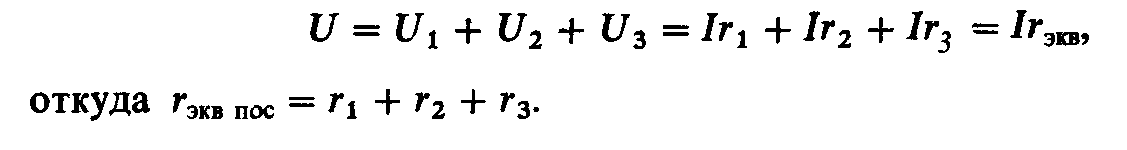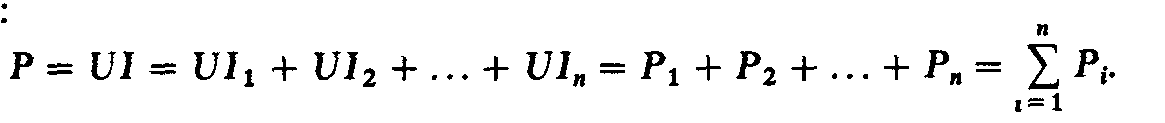Как составить баланс мощностей резисторов

Если имеется схема с известными: сопротивлениями резисторов, ЭДС источников ЭДС и токами источников тока и надо рассчитать токи во всех ветвях, этой схемы, то можно воспользоваться каким либо методом расчёта схем, например методом уравнений Кирхгофа который является самым универсальным и подходит для расчёта любых схем. Для проверки правильности расчёта схемы: рассчитывается мощность потребляемая в схеме Pпр (мощность приёмников), рассчитывается мощность вырабатываемая в этой схеме Pист (мощность источников) после чего эти две рассчитанные мощности сравниваются, если они равны (м.б. с некоторой погрешностью (т.е. различаются но чуть чуть)) то баланс мощностей сошёлся и решение считается верным, если не равны то схема пересчитывается. Рассмотрим схему на рисунке 1:

Рисунок 1 — Схема

В этой схеме есть: 4 резистора R1, R2 ,R3, R4 с сопротивлениями равными R1, R2, R3, R4 (немного неграмотно параметры элементов обозначать также как и сами элементы но так бывает удобней); источник тока J с током равным J и источник ЭДС с напряжением на нём равным по модулю его ЭДС равным E и напряжение на этом источнике противоположно по направлению ЭДС этого источника (направление ЭДС источника ЭДС на схемах указывается внутри этого источника а направление напряжения на нём указывается снаружи). На самом деле источник ЭДС создаёт только ЭДС а напряжение при этом существует на части (имеющей сопротивление) контура подключенной к этому источнику но бывает удобно составлять правильные уравнения считая что существуют напряжения на источниках ЭДС и напряжения на других элементах а ЭДС не учитывать. Для того чтобы рассчитать схему на рисунке 1 пронумеруем в ней узлы (начиная с нуля), выберем направления токов во всех ветвях (можно произвольно), выберем независимые контуры (желательно (для метода контурных токов) в одну сторону и так чтобы они не пересекали ветви на рисунке):

Рисунок 2 — Схема с вспомогательными обозначениями

Уравнения по первому закону (правилу) Кирхгофа составляются для узлов начиная с первого (т.е. для нулевого узла уравнение по первому закону (правилу) Кирхгофа  можно не составлять а для остальных надо). Нулевым узлом можно выбрать любой а все остальные нумеровать по всякому. Уравнения по второму закону (правилу) Кирхгофа составляются для контуров (в количестве = количество ветвей — количество узлов + 1) в которых нет источника тока и есть хотя бы одна ветвь которая не принадлежит другим контурам а для расчёта.

Перенеся в правую часть уравнений токи источников тока и напряжения источников ЭДС можно (а можно в принципе и не переносить) решить систему уравнений и получить токи I1-I4. Но в данном случае можно применить более простые методы нахождения токов нежели метод уравнений Кирхгофа. Например можно использовать метод контурных токов. Уравнения методом контурных токов можно составлять в матричном виде, для схемы на рисунке 2:

Далее если все (даже вспомогательные с источниками тока) контуры направлены в одну сторону и контуры не пересекают ветви на рисунке.
На главной диагонали квадратной матрицы (которая слева) ставятся суммы сопротивлений резисторов входящих в соответствующие контуры, например в ячейке в первой строке и первом столбце ставиться сумма сопротивлений резисторов первого контура (контур I11 с контурным током I11), в ячейке во второй строке и втором столбце ставится сумма сопротивлений второго контура I22 (контур I22 с контурным током I22) и т.д. В остальных ячейках этой матрицы ставятся со знаком минус сопротивления резисторов общих для двух каких либо контуров, например если у первого и второго контура общий резистор с сопротивлением R3 (см. рисунок 2) то -R3 записывается в ячейку в первой строке и втором столбце и также записывается в ячейку во втором столбце и первой строке. Матрица с сопротивлениями умножается на матрицу контурных токов. В правой части уравнения (2) находится матрица источников. В первой строке матрицы источников находится произведение тока источника тока J на сопротивление резистора R1 со знаком плюс. Для того чтобы это записать был выбран дополнительный контур направление которого совпадает с направлением тока источника тока, это произведение записывается со знаком плюс т.к. иначе оно могло быть записано в левой части со знаком минус потому что в левой части со знаком плюс могут быть только суммы сопротивлений контуров без источников токов, но это только при том что все контуры направлены в одну сторону и не пересекают ветви на рисунке. R1 — это резистор общий для первого контура и контура с источником тока. Если бы источник тока был направлен в другую сторону то направление контурного тока J следовало бы выбрать в другую сторону и тогда бы в первой строке матрицы источников стояло произведение J*R1 со знаком минус т.к. контур J был бы направлен через ветвь с резистором R1 в ту же сторону что и контур I11.
Во второй строке матрицы источников находится ЭДС источника ЭДС со знаком минус т.к. эта ЭДС направлена противоположно току (с выбранным направлением) в ветви. Уравнения этим методом можно было составить применяя другой подход.
Контурные токи I11 и I22 находятся при решении уравнения (2). Токи находятся по формулам:

Для ветви с током I1 ток I1=J-I11 т.к. контуру J принадлежит эта ветвь и направление этого контура совпадает с током I1 поэтому J со знаком плюс, контуру I11 принадлежит эта ветвь и направление этого контура не совпадает с током I1 поэтому I11 со знаком минус. Контуру I11 принадлежит только одна ветвь с током I2 и направление этого тока совпадает с направлением контура I11 поэтому I2=+I11. Для других токов аналогично.
Для нахождения токов можно (если нет ветвей с одним источником ЭДС без резистора (или др. элемента с сопротивлением)) также использовать метод узловых потенциалов:

На главной диагонали квадратной матрицы ставятся суммы проводимостей ветвей присоединённых к соответствующим узлам, например в ячейке на первой строке в первом столбце стоит сумма проводимостей присоединённых к первому узлу. К первому узлу присоединено три ветви проводимость ветви с источником тока равна нулю поэтому она не записывается, проводимость ветви с резистором R1 равна 1/R1 (т.к. проводимость — величина обратная сопротивлению), проводимость ветви с резистором R2 равна 1/R2. В ячейке на второй строке во втором столбце записана сумма проводимостей присоединённых ко второму узлу. В остальных ячейках этой матрицы ставятся со знаком минус проводимости ветвей между двумя какими либо узлами кроме нулевого. Проводимость между первым и вторым узлами равна 1/R2 поэтому в ячейке на второй строке и первом столбце ставится -1/R2 и в ячейке на первой строке и втором столбце ставиться -1/R2. Если между узлами нет проводимости то в соответствующую ячейку ставиться ноль. Метод контурных токов и метод узловых потенциалов имеют сходство. Матрица с проводимостями умножается на матрицу с потенциалами узлов. В правой части уравнения (4) стоит одностолбцовая матрица источников. Первая строка матрицы источников соответствует первому узлу, вторая второму и т.д. В первую строку матрицы источников вписывается ток J источника тока J со знаком плюс т.к. ток J источника J направлен к первому узлу (если от то со знаком «-«). Во вторую строку матрицы источников вписано произведение ЭДС E источника ЭДС E на проводимость ветви с этим источником ЭДС со знаком плюс т.к. эта ЭДС направлена ко второму узлу (если от то со знаком «-«). Если к узлу подсоединено несколько источников то все они с соответствующими знаками записываются в соответствующую этому узлу строку. Потенциалы узлов находятся при решении уравнения (4). Токи находятся по формулам:

I1=φ1/R1 т.к. ток на резисторе R1 равен отношению напряжения, на этом резисторе, к сопротивлению этого резистора а напряжение на этом резисторе равно разности потенциалов на этом резисторе, т.к. ток I1 направлен (направление выбранное) от узла 1 к узлу 0 то напряжение на этом резисторе с учётом направления тока находится вычитанием потенциала узла 0 из потенциала узла 1, т.к. потенциал узла 0 равен нулю то он не пишется и получается что напряжение на резисторе R1 с учётом направления тока равно φ1. I4=(E-φ2)/R4 т.к. ток на резисторе R4 равен отношению напряжения, на этом резисторе, к сопротивлению этого резистора а напряжение на этом резисторе равно E-(φ2-φ0) по второму закону Кирхгофа.
 Для примера решим уравнение (2) и примем например что:
J=1
R1=1
R2=1
R3=1
R4=1
E=1
Решить его можно например методом Крамера. Для решения методом Крамера найдём определитель (детерминант) матрицы с сопротивлениями:

Найдём определитель матрицы с сопротивлениями у которой первый столбец заменён на столбец матрицы источников:

Найдём определитель матрицы с сопротивлениями у которой второй столбец заменён на столбец матрицы источников:

Найдём контурные токи:

Найдём токи:

Для проверки правильности расчёта схемы (нахождения токов) рассчитаем мощность потребляемую приёмниками энергии (ими м.б. резисторы или источники (в данном случае только резисторы)):

Мощность (потребителей и источников) равна произведению тока протекающего через элемент (потребитель или источник) на напряжение на нём. Ток в квадрате это ток умноженный на ток, если ток умножить на сопротивление то получиться напряжение поэтому например (I1^2)*R1 это мощность потребляемая резистором R1.
Для резисторов все мощности со знаком плюс, направления токов не учитываются.
Рассчитаем мощность выдаваемую источниками:

Если напряжение на ветви с источником тока направлено согласно току (направление которого указано стрелками в источнике) источника тока то мощность источника тока была бы записана в уравнение (12) со знаком минус и тогда предполагалось бы что источник потребляет энергию или эта мощность была бы записана в уравнение (11) со знаком плюс. Если бы ЭДС источника была направлена в направлении противоположном току (направление которого выбрано и показано на рисунке 2 стрелкой) в этой ветви то мощность этого источника была бы записана в уравнение (12) со знаком минус или в уравнение (11) со знаком плюс. Знаки мощностей записываемых в уравнения для проверки определяются по выбранным в самом начале направлениям токов. Т.к. мощности источников равны мощностям приёмников то можно считать что баланс мощностей сошёлся и расчёт схемы выполнен правильно.

Для расчёта токов I1-I4 в схеме на рисунке 2 с учётом направлений токов (как на рисунке 2) можно воспользоваться программой:

Если вы заметили ошибку то напишите о ней пожалуйста в комментарии

Баланс мощностей

Из
закона сохранения энергии для любой
электрической цепи следует
условие
баланса мощностей.

Суммарная
мощность источников цепи равна суммарной
мощности, потребляемой приемниками.

Знак
мощности будет положителен при совпадении
направлений э.
д. с. E
и тока I,
проходящего через источник, и отрицателен
при взаимно
противоположных направлениях э. д. с. и
тока. Когда направления
тока и э. д. с. совпадают, от источника
за единицу времени в электрическую
цепь поступает мощность, равная EI.
Эта
мощность в
уравнение баланса мощностей входит с
положительным знаком. При
встречном направлении э. д. с. и тока
источник э.
д.
с. потребляет мощность
из цепи. Например, когда источником
является аккумулятор, который
заряжается, или генератор, работающий
в режиме двигателя, мощность EI
расходуется на «химическую» или
механическую работу соответственно. В
этом случае мощность входит в уравнение
баланса с отрицательным знаком. Уравнение
баланса мощностей при питании цепи от
источников э.д.с. имеет вид

(1.19)

Если в электрической
цепи содержатся не только источники
э.д.с., но источники тока, то при составлении
уравнения баланса мощностей необходимо
учитывать энергию, поступающую от
источников тока.

1.4. Методы эквивалентного преобразования схем электрических цепей с пассивными элементами

Часто
при анализе электрических цепей
постоянного тока приходится
иметь дело со сложными разветвленными
цепями. Если такие цепи
состоят из соединения линейных пассивных
элементов, то анализ значительно
упрощается, если в схемах цепей провести
определенные эквивалентные
преобразования. Метод
эквивалентного преобразования схем
заключается
в том, что сложные участки цепи заменяются
более простыми,
им эквивалентными. Преобразование будет
эквивалентным, если
оно не оказывает влияния на режим
остальной, не затронутой преобразованием
части цепи, т. е. если оно не вызывает в
оставшейся части
цепи изменений напряжений и токов.
Примером такого преобразования
может служить замена параллельного или
смешанного соединения
элементов одной ветвью с эквивалентным
сопротивлением.

Рассмотрим
методы эквивалентных преобразований
схем электрических цепей.

Цепь с последовательно
соединенными резисторами. На рис.
1.10,а представлена схема с последовательно
соединенными резисторами. Известно,
что в этом случае через все элементы
цепи проходит одини
тот же ток. Приведем эту схему к
эквивалентной (рис. 1.10,б), в
которой эквивалентное сопротивление
r_{экв
пос} выбрано
таким, чтобы ток в цепи оставался
без изменения. По второму закону Кирхгофаможно записать:

(1.20)

Эквивалентное
сопротивление при последовательном
соединении элементов цепи равно
сумме сопротивлений отдельных элементов.
Напряжение на зажимах последовательно
соединенных приемников распределяется
пропорционально их сопротивлениям.

Ток
в цепи при последовательном соединении
резисторов

(1.21)

а
мощность, подводимая к цепи, равна сумме
мощностей отдельных элементов.

Последовательное
соединение применяют в тех случаях,
когда номи- нальные напряжения приемников
ниже напряжения сети, например в
измерительных приборах для расширения
пределов измерения, в двигателях
постоянного тока для ограничения
пусковых токов и регулирования частоты
вращения и т. д. Однако приемники, как
правило, последовательно не включают,
так как при выходе из строя одного из
них происходит отключение остальных,
что на практике нежелательно. Кроме
того, при последовательном включении
приемников мощность, выделяемая в цепи,
пропорциональна их сопротивлениям, так
как через все приемники проходит один
и тот же ток. Следовательно, прием ники,
рассчитанные на меньшую номинальную
мощность, будут работать с
перегрузкой, а приемники, рассчитанные
на большую номинальную мощность, — с
недогрузкой. Отметим, что приемники с
одинаковыми номинальными
напряжениями и мощностями окажутся в
лучших условиях
работы при последовательном соединении.

Цепь
с параллельно включенными резисторами.
Рассмотрим
парал- лельно
соединенные приемники (рис. 1.11, а),
т. е. случай, когда приемники находятся
под одним и тем же напряжением, что
наиболее часто используют
на практике. Это удобно, так как не
требуется согласовывать
номинальные данные приемников и имеется
возможность их включать
и выключать независимо друг от друга.
Цепь
рис. 1.11,а состоит из трех параллельных
ветвей. По первому закону
Кирхгофа,

(1.22)

где
Тогда
для эквивалентной схемы (рис.
1.11,б)
Подставляя
полученные значения токов в(1.22)
и сокращая на U,
получим

(1.23)

Уравнение (1.23)
можно переписать для проводимости как

(1.24)

или в общем виде

Следовательно,
при параллельном соединении элементов
электрической цепи эквивалентная
проводимость равна сумме проводимостей
ее отдельных параллельно включенных
ветвей.

При увеличении
числа параллельных ветвей эквивалентная
проводимость цепи возрастает, а
эквивалентное сопротивление г_{экв.
пар = =}1/q_{экв.
пар}
уменьшается, вследствие чего ток в
неразветвленной части цепи возрастает.
При этом увеличивается мощность Р всей
цепи. Мощность, подводимая к цепи с
параллельно включенными резисторами,
равна сумме мощностей ее отдельных
параллельно включенных ветвей :

Получим формулы
эквивалентных сопротивлений для двух
частных случаев, представляющих
практический интерес: для цепи с двумя
параллельно включенными резисторами
с сопротивлениями r₁
и г₂
и цепи с тремя параллельно включенными
резисторами с сопротивлениями r₁,r₂,r_3.

Эквивалентное
сопротивление цепи с двумя параллельно
включенными резисторами

(1.25)

Эквивалентное
сопротивление цепи с тремя параллельно
включенными резисторами:

(1.26)

Следует отметить,
что эквивалентное сопротивление при
параллельном соединении резисторов
будет всегда меньше самого
малого
сопротивления, включенного в
цепь.

Смешанное
соединение резисторов.
Рассмотрим простейшую цепь со смешанным
соединением, т. е. содержащую последовательно
и параллельно включенные резисторы,
которая показана на рис. 1.12, а. Эта цепь
может быть приведена к схеме с одним
эквивалентным сопротивлением r_экв.
см = U
/ I
(рис. 1.12,б). Преобразование схемы удобно
проводить в два приема. Вначале заменяют
сопротивления параллельных ветвей на
эквивалентноеЗатем,
зная, что эквивалентное сопротивление
г_экв.
12
включено последовательно с r,
находят эквивалентное сопротивление
всей цепи со смешанным соединением
резисторов:

После
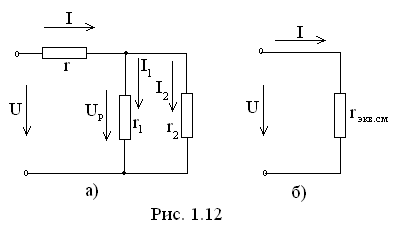
нахождения эквивалентного r_экв
см можно
определить ток в неразветвленной части
цепи:Для
определения токов в параллельных
ветвяхI₁
и I₂
вначале находят напряжение разветвления

затем
записывают токи в ветвях

Последовательное,
параллельное и смешанное соединения
образуют цепи, которые называются
простыми
цепями постоянного тока.
Распределение токов в простых цепях
постоянного тока, если известны э. д.
с. и сопротивления участков цепи,
производится с использованием закона
Ома. Для сложных многоконтурных
разветвленных цепей, в которых произвольно
размещены резисторы и источники э. д.
с., закона Ома для расчета недостаточно.
В этом случае и используют законы
Кирхгофа.

Пример
1.1. К зажимам
а
и с
схемы подключен вольтметр, имеющий
очень большое, теоретически бесконечно
большое сопротивление (следовательно,
его подключение или отключение не влияет
на режим работы цепи).

Если ток I = 10 А
течет от а
к с,
то показание вольтметра Uac = —18
В;

если ток I=10 А течет
от с
к а,
то Uac = —20 В.

Определить величину
сопротивления R и э. д. с. Е.

Решение.

В первом режиме
U’ac = —18 = —Е + IR = —Е + 10R.

Во втором режиме
Uac
= —20 = —Е — IR= —Е — 10R.

Совместное решение
дает Е = 19 В и R = 0,1 Ом.

Баланс мощностей

Содержание:

Баланс мощностей

Для любой электрической цепи суммарная мощность , развиваемая источниками электрической энергии (источниками тока и ЭДС), равна суммарной мощности , расходуемой потребителями (резисторами):

Мощность, рассеиваемая резистором, , мощность источника ЭДС , мощность источника тока .

Мощности, рассеиваемые резисторами, всегда положительные, в то время как мощности источников электрической энергии, в зависимости от соотношения направления падений напряжения и тока в них, могут иметь любой знак. Мощность положительна, когда направление тока через источник тока противоположно падению напряжения на нем. Он питает электрическую цепь. В противном случае источник питания является отрицательным, и вы являетесь потребителем электрической энергии. Следует заметить, что направление падения напряжения всегда противоположно направлению ЭДС, поэтому для источника ЭДС условием положительной мощности является совпадение направлений ЭДС и тока.

Пример расчёта разветвлённой цепи постоянного тока

Рассмотрим решение задачи для цепи, представленной на рис. 1.6, описанными выше методами расчёта.

Дано

1) все неизвестные токи, используя законы Кирхгофа; показать, что баланс мощностей имеет место;

1) Применение законов Кирхгофа. Баланс мощностей.

Всего в схеме семь ветвей =7, ветвей с источниками тока = 1, число неизвестных токов равно , количество узлов — , число уравнений по первому закону Кирхгофа , число уравнений по второму закону Кирхгофа —

Возможно вам будут полезны данные страницы:

Выберем положительные направления токов и обозначим их стрелками. Выберем и обозначим стрелками направления обхода трёх независимых контуров: Составим систему уравнений по законам Кирхгофа

для узла а ;

для узла b

для узла с или ;

для контура ,

для контура

для контура

Полученные уравнения после подстановки в них числовых значений будут иметь следующий вид:

Решение данной системы:

Баланс мощностей для рассматриваемой цепи

Получено тождество 252 Вт = 252 Вт.

Примечание: падение напряжения на источнике тока определено по второму закону Кирхгофа для контура, содержащего и , как

Баланс мощностей

В любой электрической цепи должен соблюдаться энергетический баланс -баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Баланс мощностей электрической цепи

Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.

Определение

Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.

Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.

Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:

Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.

Назначение

Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.

Переменный ток

Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.

1. Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
2. Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
3. Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.

Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.

Постоянный ток

В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.

1. В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
2. I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
3. Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
4. Pист=I×E=1×10=10 Ватт. Это значение для источника.
5. Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
6. Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.

При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.

Заключение

В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.

Видео по теме

Баланс мощностей в цепи постоянного тока

Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.

Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:

С учетом погрешности расчетов баланс мощностей получился.

Какова допустимая погрешность?? У меня выходит 0,561

По идее баланс мощности должен равняться нулю, но так как мы округляем некоторые значения при расчете — возникает погрешность, которая может составлять примерно 0,1 — 5% от потребляемой мощности.

Про знаки ЭДС сказано про знаки мощностей приёмников — нет.