Как составить баланс мощностей для электрической цепи

Баланс мощностей

Составление баланса мощностей.

Из закона сохранения
энергии следует, что вся мощность,
поступающая цепь от источников энергии,
в любой момент времени равна всей
мощности, потребляемой приемниками
данной цепи.

То
есть IPпотр.
= Pист.

Мощность
потребителей, которыми в цепях постоянного
тока являются резисторы, определяется
по формуле

Pпотр.
= I²R

Т.к.
ток входит в данное выражение в квадрате,
то независимо от его направления,
мощность потребления всегда положительна.

Мощность
источников, которыми могут быть источники
напряжения и источники тока, бывает и
положительной и отрицательной.

Мощность источника
э.д.с. определяется по формуле

а)

Pэ.д.с.
= EI

где
I
– ток в ветви с источником э.д.с.

б)

Если
э.д.с. и ток этой ветви совпадают по
направлению (рис.19а), то мощность Pэ.д.с.

входит в
выражение баланса со знаком «+»,

если
не совпадают – то Pэ.д.с.
– величина

Рис.19
отрицательная.

Мощность источника
тока определяется по формуле:

Pи.т.
= IU

Где
I
– значение тока источника, U
— напряжение на его зажимах.

Если
ток I
и напряжение U
действуют так, как показано на рис.19б,
то мощность положительна; в противном
случае она – отрицательна. Следовательно,
при вычислении мощности источника тока
необходимо определять величину и
направление напряжения на его зажимах.

Задача:

Контрольные
вопросы:

1. Что
   представляет собой электрическая
   схема. Что относится к «электрическим»
   и «геометрическим» элементам схемы.

2. Дать
   определение последовательного и
   параллельного соединений элементов
   цепи.

3. Понятие «контур»
   в электрической цепи.

4. Чем отличается
   активная ветвь от пассивной?

5. Потенциальная
   диаграмма, ее назначение.

6. Изложить правило
   выбора знаков при нахождении потенциалов
   точек.

7. Сформулировать
   обобщенный закон Ома. Какова область
   его применения.

8. Сформулируйте
   первый закон Кирхгофа. Как определить
   число узловых уравнений? Правило знаков
   при написании узлового уравнения.

9. Формулировка
   второго закона Кирхгофа. Как определить
   число контурных уравнений. Правило
   знаков при написании контурного
   уравнения.

10. Что понимают под
    балансом мощностей? Как определяется
    мощность источника напряжения, источника
    тока, приемника.

11. Мощность
    каких элементов (активных или пассивных)
    может быть отрицательной и что это
    означает?

Преобразование схем электрических цепей

Цель лекции №3.

Ознакомившись с
данной лекцией, студенты должны знать:

1. Цель преобразования
   электрических цепей.

2. Четко
   различать участки с последовательным
   и параллельным соединениями при
   рассмотрении смешанного соединения
   проводов.

3. Уметь преобразовывать
   соединение треугольник в эквивалентную
   звезду и обратно.

4. Уметь преобразовать
   источник э.д.с. в источник тока и обратно.

Преобразование схем электрических цепей.

Целью
преобразования электрических цепей
является их упрощение, это необходимо
для простоты и удобства расчета.

Одним
из основных видов преобразования
электрических схем является преобразование
схем со смешанным соединением элементов.
Смешанное
соединение элементов
– это совокупность последовательных
и параллельных соединений, которые и
будут рассмотрены в начале данной
лекции.

Последовательное
соединение.

На
рис.20 изображена ветвь электрической
цепи, в которой последовательно включены
сопротивления R₁,
R₂,…,R_n.
Через все эти сопротивления проходит
один и тот же ток I.
Напряжения на отдельных участках цепи
обозначим через U₁,
U₂,…,
U_n.

Рис.20. Последовательное
соединение.

По второму закону
Кирхгофа напряжение на ветви

U=U₁+U₂+…+U_n=
IR₁+IR₂+…+IR_n=I
(R₁+R₂+…R_n)=IRэкв.
(23)

Сумма сопротивлений
всех участков данной ветви

Называется
эквивалентным
последовательным сопротивлением.

Параллельное
соединение.

На
рис.21 изображена схема электрической
цепи с двумя узлами, между которыми
включено n
параллельных ветвей с проводимостями
G₁,
G₂,…,
G_n.
Напряжение между узлами U,
оно одинаково для всех ветвей.

Рис.21. Параллельное
соединение (показать преобразованное).

По первому закону
Кирхгофа ток общей ветви

I=I₁+I₂+…+I_n=G₁U+G₂U+…+G_nU=U
(G₁+G₂+…+G_n)=UGэкв.
(24)

Сумма проводимостей
всех ветвей, соединенных параллельно

называется
эквивалентной
проводимостью.

В
случае параллельного сопротивления
двух ветвей (n=2)
обычно пользуются выражениями, в которые
входят сопротивления
и.

Эквивалентное
сопротивление двух параллельно
соединенных ветвей равно:

.

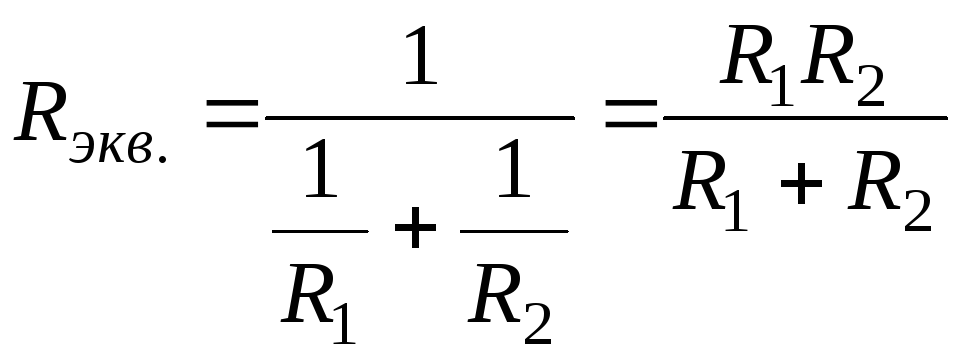
Смешанное
соединение.

На рис.22 показано смешанное соединение
электрической цепи:

Рис.22. Смешанное
соединение.

Эта
схема легко приводится к одноконтурной.
Эквивалентировать схему обычно начинают
с участков наиболее удаленных от входных
зажимов. Для схемы рис.22 – это участок
e-A.
Сопротивления R₅
и R₆
включены параллельно, поэтому необходимо
вычислить эквивалентное сопротивление
данного участка по формуле

Для понимания
полученного результата можно изобразить
промежуточную схему (рис.23).

Рис.23

Сопротивления
R₃,
R₄
и R^/_экв.
соединены последовательно, и эквивалентное
сопротивление участка c-e-f-d
равно:

R_экв.=R₃+
R^/_экв.+R₄.

После этого этапа эквивалентирования
схема приобретает вид рис.24.

Рис.24

Затем
находим эквивалентное сопротивление
участка c-d
и суммируем его с сопротивлением R₁.
Общее эквивалентное сопротивление
равно:

.

Полученное
сопротивление эквивалентно сопротивлению
(рис.25) исходной схемы со смешанным
соединением. Понятие “эквивалентно”
означает, что напряжение U
на входных зажимах и ток I
входной ветви остаются неизменными на
протяжении всех преобразований.

Рис.25

Преобразование
треугольника в эквивалентную звезду.

Преобразованием
треугольника в эквивалентную звезду
называется такая замена части цепи,
соединенной по схеме треугольником,
цепью, соединенной по схеме звезды, при
которой токи и напряжения в остальной
части цепи сохраняются неизменными.

Т.е., под
эквивалентностью треугольника и звезды
понимается то, что при одинаковых
напряжениях между одноименными зажимами
токи, входящие в одноименные выводы,
одинаковы.

Рис.26. Преобразование
треугольника в звезду.

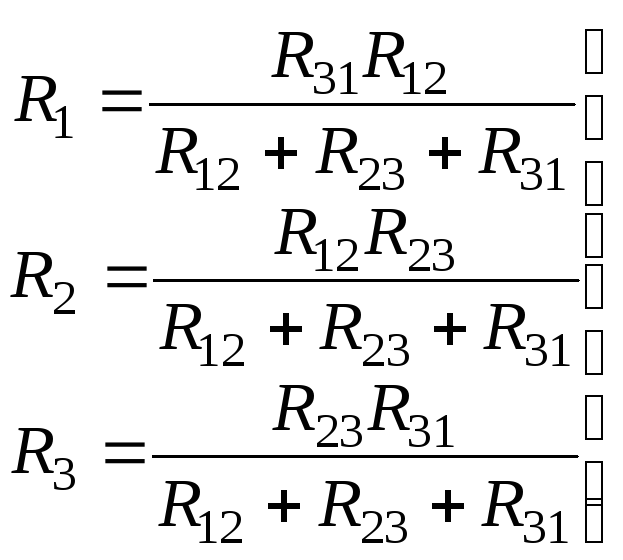
Пусть
R₁₂;
R₂₃;
R₃₁—
сопротивления сторон треугольника;

R₁;
R₂;
R₃—
сопротивления лучей звезды;

I₁₂;
I₂₃;
I₃₁—
токи в ветвях треугольника;

I₁;
I₂;
I₃—
токи, подходящие к зажимам 1, 2, 3.

Выразим
токи в ветвях треугольника через
подходящие токи I₁,
I₂,
I₃.

По
второму закону Кирхгофа сумма падений
напряжений в контуре треугольника равна
нулю:

I₁₂R₁₂+I₂₃R₂₃+I₃₁R₃₁=0

По первому закону
Кирхгофа для узлов 1 и 2

I₃₁=I₁₂-I₁;
I₂₃=I₁₂+I₂

При
решении этих уравнений относительно
I₁₂
получим:

Напряжение между точками 1 и 2 схемы
треугольника:

Напряжение между этими же точками схемы
звезды равно:

U₁₂=I₁R₁-I₂R₂.

Т.к. речь идет об эквивалентном
преобразовании, то необходимо равенство
напряжений между данными точками двух
схем, т.е.

Это возможно при
условии:

(25)

Третье выражение
получено в результате круговой замены
индексов.

Исходя из выражения
(25) формулируется следующее правило:

Сопротивление
луча звезды равно произведению
сопротивлений сторон треугольника,
прилегающих к этому лучу, деленному на
сумму сопротивлений трех сторон
треугольника.

Выше
было получено выражение для тока в
стороне 1-2 треугольника в зависимости
от токов I₁
и I₂.
Круговой заменой индексов можно получить
токи в двух других сторонах треугольника:

Соседние файлы в предмете Теория электрических цепей

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Баланс мощностей

Содержание:

Баланс мощностей

Для любой электрической цепи суммарная мощность , развиваемая источниками электрической энергии (источниками тока и ЭДС), равна суммарной мощности , расходуемой потребителями (резисторами):

Мощность, рассеиваемая резистором, , мощность источника ЭДС , мощность источника тока .

Мощности, рассеиваемые резисторами, всегда положительные, в то время как мощности источников электрической энергии, в зависимости от соотношения направления падений напряжения и тока в них, могут иметь любой знак. Мощность положительна, когда направление тока через источник тока противоположно падению напряжения на нем. Он питает электрическую цепь. В противном случае источник питания является отрицательным, и вы являетесь потребителем электрической энергии. Следует заметить, что направление падения напряжения всегда противоположно направлению ЭДС, поэтому для источника ЭДС условием положительной мощности является совпадение направлений ЭДС и тока.

Пример расчёта разветвлённой цепи постоянного тока

Рассмотрим решение задачи для цепи, представленной на рис. 1.6, описанными выше методами расчёта.

Дано

1) все неизвестные токи, используя законы Кирхгофа; показать, что баланс мощностей имеет место;

1) Применение законов Кирхгофа. Баланс мощностей.

Всего в схеме семь ветвей =7, ветвей с источниками тока = 1, число неизвестных токов равно , количество узлов — , число уравнений по первому закону Кирхгофа , число уравнений по второму закону Кирхгофа —

Возможно вам будут полезны данные страницы:

Выберем положительные направления токов и обозначим их стрелками. Выберем и обозначим стрелками направления обхода трёх независимых контуров: Составим систему уравнений по законам Кирхгофа

для узла а ;

для узла b

для узла с или ;

для контура ,

для контура

для контура

Полученные уравнения после подстановки в них числовых значений будут иметь следующий вид:

Решение данной системы:

Баланс мощностей для рассматриваемой цепи

Получено тождество 252 Вт = 252 Вт.

Примечание: падение напряжения на источнике тока определено по второму закону Кирхгофа для контура, содержащего и , как

Баланс мощностей

В любой электрической цепи должен соблюдаться энергетический баланс -баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Баланс мощностей в цепи постоянного тока

Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.

Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:

С учетом погрешности расчетов баланс мощностей получился.

Какова допустимая погрешность?? У меня выходит 0,561

По идее баланс мощности должен равняться нулю, но так как мы округляем некоторые значения при расчете — возникает погрешность, которая может составлять примерно 0,1 — 5% от потребляемой мощности.

Про знаки ЭДС сказано про знаки мощностей приёмников — нет.

Баланс мощностей электрической цепи

Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.

Определение

Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.

Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.

Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:

Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.

Назначение

Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.

Переменный ток

Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.

1. Комплексная. Состоит из мощностей передаваемых и получаемых. Необходимо будет выполнить расчет, в котором все слагаемые левой части формулы являются положительными (идут со знаками +), при условии, когда совпадает направление заряженных частиц «Ik» с «ЭДС». Должно соблюдаться правило не совпадения «Jk» с направлением напряжения «Uk». Если условия не соответствуют установленным требованиям, все данные левой части формулы становятся отрицательными. Формула приведена ниже.
2. Активные. Значения, отдающиеся источником равны принимаемым потребителями. Вычисление активной мощности полностью зависит от представленной комплексной энергии. Активное значение является расходуемым, невосполнимым, так как уходит на работу приборов. Данный метод вычисления и его формула представлены ниже.
3. Реактивная мощность источника с потребителем равны. Единственное отличие заключается в том, что этот параметр не растрачиваемый. Данный показатель просто циркулирует по схеме. Формула представлена ниже.

Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.

Постоянный ток

В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.

1. В цепи имеется ЭДС «Е» и резистор «R». При расчете должна быть найдена сила тока.
2. I=E/R. Подставляем имеющиеся значения, получаем I=10/10=1 ампер.
3. Так мы нашли силу тока. Теперь нам будет нужен параметр мощности приемника «R» и источника.
4. Pист=I×E=1×10=10 Ватт. Это значение для источника.
5. Теперь для того, чтобы найти Р для приемника делаем расчет как на рисунке ниже.
6. Теперь составим общий баланс — 10 ватт=10 ватт. Данный подсчет показал, что для представленной схемы сохраняется равновесие.

При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.

Заключение

В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.

Видео по теме