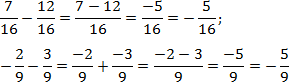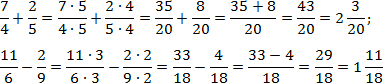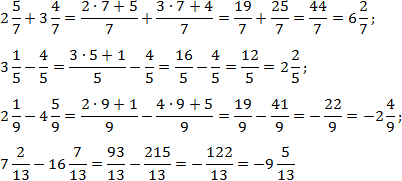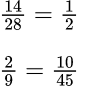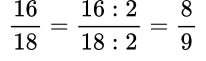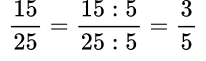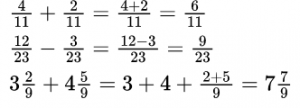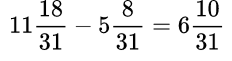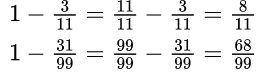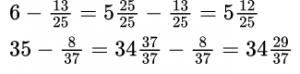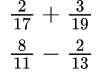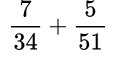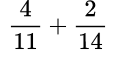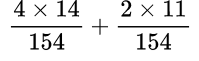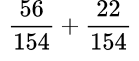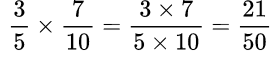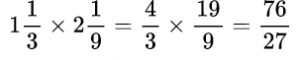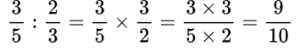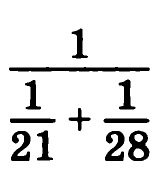Содержание
- Блок схема алгоритма деления обыкновенных дробей
- Обмен значениями двух переменных
- Описание линейного вычислительного алгоритма
- Блок схема алгоритма деления обыкновенных дробей
Блок схема алгоритма деления обыкновенных дробей
Поскольку присваивание является важнейшей операцией в алгоритмах, работающих с величинами, то поговорим о ней более подробно.
Переменная величина получает значение в результате присваивания.
Присваивание производится компьютером при выполнении одной из двух команд из представленной выше системы: команды присваивания или команды ввода.
Рассмотрим последовательность выполнения четырех команд присваивания, в которых участвуют две переменные а и b. В приведенной ниже таблице против каждой команды указываются значения переменных, которые устанавливаются после ее выполнения. Такая таблица называется трассировочной таблицей, а процесс ее заполнения называется трассировкой алгоритма. Компьютер выполняет команды в порядке их записи в алгоритме.
| Команда | а | b |
| а:= 1 | 1 | — |
| b:= 2 х а | 1 | 2 |
| а:= b | 2 | 2 |
| b:= a + b | 2 | 4 |
Прочерк в таблице обозначает неопределенное значение переменной. Конечные значения, которые получают переменные а и b, соответственно равны 2 и 4.
Этот пример иллюстрирует три основных свойства присваивания. Вот эти свойства:
1) пока переменной не присвоено значения, она остается неопределенной;
2) значение, присвоенное переменной, сохраняется вплоть до выполнения следующего присваивания этой переменной нового значения;
3) новое значение, присвоенное переменной, заменяет ее предыдущее значение.
Обмен значениями двух переменных
Рассмотрим еще один очень полезный алгоритм, с которым при программировании часто приходится встречаться. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было: X = 1; Y = 2, то после обмена должно стать: X = 2, У = 1.
Хорошим аналогом для решения такой задачи является следующая: даны два стакана, в первом — молоко, во втором — вода; требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей:
По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная. Назовем ее Z. Тогда задача решается последовательным выполнением трех операторов присваивания (пусть начальные значения 1 и 2 для переменных X и Y задаются вводом):
| Команда | X | Y | Z |
| ввод X, Y | 1 | 2 | — |
| Z:=X | 1 | 2 | 1 |
| Х:=Y | 2 | 2 | 1 |
| Y:=Z | 2 | 1 | 1 |
| вывод X, У | 2 | 1 | 1 |
Действительно, в итоге переменные X и Y поменялись значениями. На экран будут выведены значения X и У в таком порядке: 2, 1. В трассировочной таблице выводимые значения выделены жирным шрифтом.
Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания (X:=Y) переменная, стоящая справа (Y), сохраняет свое значение.
Описание линейного вычислительного алгоритма
И наконец, рассмотрим пример составления алгоритма для решения следующей математической задачи: даны две простые дроби; получить дробь, являющуюся результатом их деления.
В школьном учебнике математики правила деления обыкновенных дробей описаны так:
1. Числитель первой дроби умножить на знаменатель второй.
2. Знаменатель первой дроби умножить на числитель второй.
3. Записать дробь, числителем которой является результат выполнения пункта 1, а знаменателем — результат выполнения пункта 2.
В алгебраической форме это выглядит следующим образом:
Теперь построим алгоритм деления дробей для компьютера. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, b, с, d. Результатом — также целые величины m и n.
Ниже алгоритм представлен в двух формах: в виде блок-схемы и на Алгоритмическом языке (АЯ).
Раньше прямоугольник в схемах алгоритмов управления мы называли блоком простой команды. Для вычислительных алгоритмов такой простой командой является команда присваивания. Прямоугольник будем называть блоком присваивания, или вычислительным блоком. В форме параллелограмма рисуется блок ввода/вывода. Полученный алгоритм имеет линейную структуру (рис. 3.5).
алг Деление дробей
цел а, Ь, с, d, m, n
нач ввод а, Ь, с, d
m:=a х d
n:=b х c
вывод m,n
кон 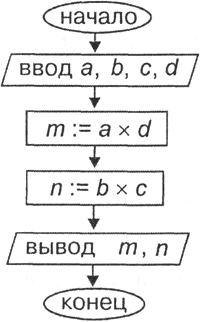
В алгоритме на АЯ строка, стоящая после заголовка алгоритма, называется описанием переменных. Служебное слово цел означает целый тип. Величины этого типа могут иметь только целочисленные значения.
Описание переменных имеет вид:
Список переменных включает все переменные величины данного типа, входящие в алгоритм.
В блок-схемах типы переменных не указываются, но подразумеваются. Запись алгоритма на АЯ ближе по форме к языкам программирования, чем блок-схемы.
1. Из каких команд составляется линейный вычислительный алгоритм?
2. Что такое трассировка? Как она производится?
3. В каком случае значение переменной считается неопределенным?
4. Что происходит с предыдущим значением переменной после присваивания ей нового значения?
5. Как вы думаете, можно ли использовать в арифметическом выражении оператора присваивания неопределенную переменную? К каким последствиям это может привести?
6. Напишите на АЯ алгоритм сложения двух простых дробей (без сокращения дроби).
7. Напишите на АЯ алгоритм вычисления y по формуле
y = (1 — х 2 + 5х 4 ) 2 ,
где х — заданное целое число. Учтите следующие ограничения: 1) в арифметических выражениях можно использовать только операции сложения, вычитания и умножения; 2) выражение может содержать только одну арифметическую операцию. Выполните трассировку алгоритма при х = 2.
8. Пользуясь ограничениями предыдущей задачи, напишите наиболее короткие алгоритмы вычисления выражений: y = х 8 ; y = х 10 ; y = х 15 ; y = х 19 .
Постарайтесь использовать минимальное количество дополнительных переменных. Выполните трассировку алгоритмов.
Источник
Блок схема алгоритма деления обыкновенных дробей
§ 34. Линейные вычислительные алгоритмы
♦ присваивание; свойства присваивания;
♦ обмен значениями двух переменных;
♦ описание линейного вычислительного алгоритма.
Присваивание; свойства присваивания
Поскольку присваивание является важнейшей операцией в алгоритмах, работающих с величинами, то поговорим о ней более подробно.
Переменная величина получает значение в результате присваивания.
Присваивание производится компьютером при выполнении одной из двух команд из представленной выше системы: команды присваивания или команды ввода.
Рассмотрим последовательность выполнения четырех команд присваивания, в которых участвуют две переменные а и b. В приведенной ниже таблице против каждой команды указываются значения переменных, которые устанавливаются после ее выполнения. Такая таблица называется трассировочной таблицей, а процесс ее заполнения называется трассировкой алгоритма. Компьютер выполняет команды в порядке их записи в алгоритме.
| Команда | a | b |
| a:= 1 | 1 | — |
| b:= 2 x a | 1 | 2 |
| a:= b | 2 | 2 |
| b:= a + b | 2 | 4 |
Прочерк в таблице обозначает неопределенное значение переменной. Конечные значения, которые получают переменные а и b, соответственно равны 2 и 4.
Этот пример иллюстрирует три основных свойства присваивания. Вот эти свойства:
1) пока переменной не присвоена значения, она остается неопределенной;
2) значение, присвоенное переменной, сохраняется вплоть до выполнения следующего присваивания этой переменной нового значения;
3) новое значение, присвоенное переменной, заменяет ее предыдущее значение.
Обмен значениями двух переменных
Рассмотрим еще один очень полезный алгоритм, с которым при программировании часто приходится встречаться. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было: X= 1; Y = 2, то после обмена должно стать: X = 2, Y = 1.
Хорошим аналогом для решения такой задачи является следующая: даны два стакана, в первом — молоко, во втором — вода; требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей:
1) перелить из 1-го в 3-й;
2) перелить из 2-го в 1-й;
3) перелить из 3-го во 2-й.
По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная, Назовем ее Z. Тогда задача решается последовательным выполнением трех операторов присваивания (пусть начальные значения 1 и 2 для переменных X и Y задаются вводом):
| Команда | X | Y | Z |
| ввод X, Y | 1 | 2 | — |
| Z:=X | 1 | 2 | 1 |
| X:=Y | 2 | 2 | 1 |
| Y:=Z | 2 | 1 | 1 |
| вывод X, Y | 2 | 1 | 1 |
Действительно, в итоге переменные X и Y поменялись значениями. На экран будут выведены значения X и Y в таком порядке: 2, 1. В трассировочной таблице выводимые значения выделены жирным шрифтом.
Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания (Х:=Y) переменная, стоящая справа (Y), сохраняет свое значение.
Описание линейного вычислительного алгоритма
И наконец, рассмотрим пример составления алгоритма для решения следующей математической задачи: даны две простые дроби; получить дробь, являющуюся результатов их деления.
В школьном учебнике математики правила деления обыкновенных дробей описаны так:
1. Числитель первой дроби умножить на знаменатель второй.
2. Знаменатель первой дроби умножить на числитель второй.
3. Записать дробь, числителем которой является результат выполнения пункта 1, а знаменателем — результат выполнения пункта 2.
В алгебраической форме это выглядит следующим образом:
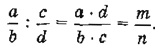
Теперь построим алгоритм деления дробей для компьютера. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, b, с, d. Результатом — также целые величины m и n.
Ниже алгоритм представлен в двух формах; в виде блок-схемы и на Алгоритмическом языке (АЯ).
Раньше прямоугольник в схемах алгоритмов управления мы называли блоком простой команды. Для вычислительных алгоритмов такой простой командой является команда присваивания. Прямоугольник будем называть блоком присваивания, или вычислительным блоком. В форме параллелограмма рисуется блок ввода/вывода. Полученный алгоритм имеет линейную структуру (рис. 6.1).
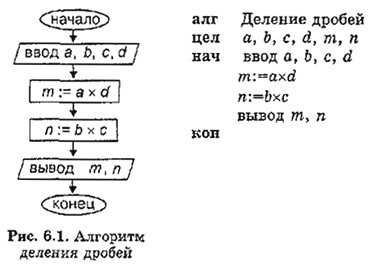
В алгоритме на АЯ строка, стоящая после заголовка алгоритма, называется описанием переменных. Служебное слово цел означает целый тип. Величины этого типа могут иметь только целочисленные значения. Описание переменных имеет вид:
Список переменных включает все переменные величины данного типа, входящие в алгоритм.
В блок-схемах типы переменных не указываются, но подразумеваются. Запись алгоритма на АЯ ближе по форме к языкам программирования, чем блок-схемы.
Основные свойства присваивания:
• значение переменной не определено, если ей не присвоено никакого значения;
• новое значение, присваиваемое переменной, заменяет ее старое значение;
• присвоенное переменной значение сохраняется в ней вплоть до нового присваивания.
Обмен значениями двух переменных производится через третью дополнительную переменную.
Трассировочная таблица используется для «ручного» исполнения алгоритма с целью его проверки.
В алгоритмах на АЯ указываются типы всех переменных. Такое указание называется описанием переменных.
Числовые величины, принимающие только целочисленные значения, описываются с помощью служебного слова цел (целый).
1. Из каких команд составляется линейный вычислительный алгоритм?
2. Что такое трассировка? Как она производится?
3. В каком случае значение переменной считается неопределенным?
4. Что происходит с предыдущим значением переменной после присваивания ей нового значения?
5. Как вы думаете, можно ли использовать в арифметическом выражении оператора присваивания неопределенную переменную? К каким последствиям это может привести?
6. Напишите на АЯ алгоритм сложения двух простых дробей (без сокращения дроби).
7. Напишите на АЯ алгоритм вычисления у по формуле
где х — заданное целое число. Учтите следующие ограничения:
1) в арифметических выражениях можно использовать только операций сложения, вычитания и умножений; 2) выражение может содержать только одну арифметическую операцию. Выполните трассировку алгоритма при х = 2.
8. Пользуясь ограничениями предыдущей задачи, напишите наиболее короткие алгоритмы вычисления выражений:
y = х 8 ; y = x 10 ; y = х 15 ; у = х 19 .
Постарайтесь использовать минимальное количество дополнительных переменных. Выполните трассировку алгоритмов.
9. Запишите алгоритм циклического обмена значениями трех переменных А, В, С. Схема циклического обмена:
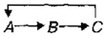
Например, если до обмена было: А = 1, В = 2, С = 3, то после обмена должно стать: А = 3, В = 1, С=2. Выполните трассировку.
И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов
Основы информатики, подборка рефератов к урокам информатики, скачать рефераты, уроки информатики 9 класс онлайн, домашняя работа
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Источник
Сложение и вычитание дробей
30 июля 2011
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Смотрите также:
- Тест к уроку «Сложение и вычитание дробей» (легкий)
- Приведение дробей к общему знаменателю
- Тест к уроку «Десятичные дроби» (1 вариант)
- Метод узлов в задаче B5
- Задача B5: площадь кольца
- Сфера, вписанная в куб
Описание презентации по отдельным слайдам:
-
1 слайд
Презентация работы
учащихся 7 класса «а»
на тему: «Применение алгоритмов при выполнении математических действий»
Работу выполнили:
1.Соболь Павел
2.Устюгова Виктория
3.Булдакова Анастасия
4.Мнацаканян Рубина -
2 слайд
Алгоритм нахождения НОД
нескольких чисел -
3 слайд
Нахождение НОК двух чисел
-
4 слайд
Деление десятичных чисел
-
5 слайд
Умножение десятичных дробей
-
6 слайд
Деление, умножение целых чисел
-
7 слайд
Сложение, вычитание смешанных чисел
-
8 слайд
Деление смешанных чисел
-
9 слайд
Умножение смешанных чисел
-
10 слайд
Сложение обыкновенных дробей
-
11 слайд
Вычитание обыкновенных дробей
-
12 слайд
Умножение обыкновенных дробей
-
13 слайд
Деление обыкновенных дробей
-
Обыкновенная дробь – это запись числа в виде:
где число a называют числителем, а число b – знаменателем дроби.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.
Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.
- Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
- Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.
Сокращение дробей
Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.
Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби – четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.
Пример №4.
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.
Вычитание обыкновенной дроби из целого числа
Вычитание обыкновенной дроби из единицы
Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.
Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).
Вычитание обыкновенной дроби из бóльшего числа
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.
Пример №6.
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.
Нахождение общего знаменателя
Наименьшее общее кратное. Приём №1.
Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7.
1. Нужно разложить на простые множители каждое число:
12=2×2×3
15=3×5
2. Затем найти одинаковые множители (подчеркиваем):
12=2×2×3
15=3×5
В данном случае это только множитель 3.
3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:
12 домножаем на 5: 12×5=60, или
15 домножаем на 2 и 2: 15×2×2=60
Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.
Перемножение знаменателей. Приём №2.
Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.
Пример №8.
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.
Последовательный подбор. Приём №3.
Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.
Пример №9. Возьмем число 51, умножим на 2, получим 102 – видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.
Алгоритм сложения (вычитания)
- Находим общий знаменатель данных дробей.
- Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
- Умножаем каждый числитель на дополнительный множитель.
- Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.
Пример №10.
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 – простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:
Выполняем умножение в числителе:
Выполняем сложение дробей с одинаковыми знаменателями:
Умножение обыкновенных дробей
Как перемножить дроби?
При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).
Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.
Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.
Деление обыкновенных дробей
Как разделить одну дробь на другую?
При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.
Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.
Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.
Пример №14. Делимое умножаем на число, обратное делителю.
Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.
Задание OM2004
Сократите дробь 36n4n−2∙32n−1
Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
(3∙3∙4)n4n−2∙32n−1
Теперь представим каждый множитель в виде степени:
3n∙3n∙4n4n−2∙32n−1
Разложим знаменатель дроби на множители по свойству степеней
3n∙3n∙4n4n∙4−2∙32n∙3−1
Теперь можно сократить числитель и знаменатель на 3n и в 4n степени
Получим дробь, которую преобразуем по свойству степеней:
14−2∙3−1 = 42∙311=16∙3=48
Ответ: 48
pазбирался: Даниил Романович | обсудить разбор
Задание OM1306o
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению:
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b):
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):
Подставим полученные значения в выражение и найдем конечный результат:
Ответ: 39
pазбирался: Даниил Романович | обсудить разбор
Задание OM1305o
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
pазбирался: Даниил Романович | обсудить разбор
Задание OM1304o
Найдите значение выражения
где a = 9, b = 36
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю – это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
9b² + 5a – 9b²
Приведем подобные слагаемые – это 9b² и – 9b², в числителе остается 5a. Запишем конечную дробь:
5a/b
Вычислим её значение, подставив числа из условия:
5•9/36 = 1,25
Ответ: 1,25
pазбирался: Даниил Романович | обсудить разбор
Задание OM1303o
Найдите значение выражения:
при x = √45 , y = 0,5
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель – это 15 x y, для этого необходимо первую дробь домножить на 5 y – и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y – (3 x + 5 y) = 5 y – 3 x – 5 y = – 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: – 1/5 y
Подставим значение y = 0,5: – 1 / (5 • 0,5) = – 1 / 2,5 = – 0,4
Ответ: -0,4
pазбирался: Даниил Романович | обсудить разбор
Задание OM1302o
Найдите значение выражения:
при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Сокращаем (a-b):
И получаем:
a/2
Подставляем значение a = 13:
13 / 2 = 6,5
Ответ: 6,5
pазбирался: Даниил Романович | обсудить разбор
Задание OM0804o
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:
16 – 14 = 2
Суммарно наши действия выглядят так:
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор
Задание OM0603o
Найдите значение выражения:
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Затем складываем:
4/84 + 3/84 = 7/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
84 / 7 = 12
Ответ: 12
pазбирался: Даниил Романович | обсудить разбор
Задание OM0602o
Найдите значение выражения:
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
1/3 • (6 • (1/3) — 17 )
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
1/3 • ( -15 ) = -5
Ответ: -5
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 19.6k
Действия с дробями общего вида
Для дробей общего вида характерно наличие числителя и знаменателя.
Значения которые, которыми выражены данные составляющие дроби, могут быть натуральными и числовыми выражениями.
Если рассмотреть подробно следующие дробные числа:
[frac{5}{4}, frac{3,5}{5}, frac{1+2,6}{4(6-1)}, frac{frac{3}{5}+frac{7}{8}}{2,3-0,9}, frac{1}{2 sqrt{3}}]
можно с уверенностью отметить, что и в числителе и знаменателе дробные выражения могут быть обозначены как:
- десятичная дробь;
- натуральный логарифм;
- сумма и разность выражений;
- дробь с постоянным значением числа.
Алгоритм решения задач с обыкновенной дробью общего вида
- Когда необходимо произвести вычитание дробей с одинаковыми знаменателями, то в процессе решения суммируется только числитель дробей.
[frac{a}{b} pm frac{c}{b}=frac{a pm c}{b}]
Где:
[a, c, d_{0}] и равные некоторым числовым значениям. - При выполнении сложения или вычитания дробей для различных значений в знаменателях, нужно выполнить приведение к общему знаменателю. Далее осуществить сложение или вычитание преобразованных дробей с одинаковыми числовыми значениями.
- При перемножении дробных значений, выполняются следующие действия:
- произведение числителей;
- аналогичные действия , но только с знаменателями.
- При выполнении деления, необходимо первую дробь перемножить на вторую, но в обратном значении. Иными словами произвести замену числителя на значение знаменателя.
Основные показатели и свойства дроби:
- черта в дроби обозначает признак деления;
- деление на числовое значение характеризуется как перемножение его на обратное значение;
- возможность применения свойств, которые относятся для действительных чисел;
- свойства для дробей и различного рода числовых неравенств.
Применяя данные свойства можно произвести преобразование дробных чисел:
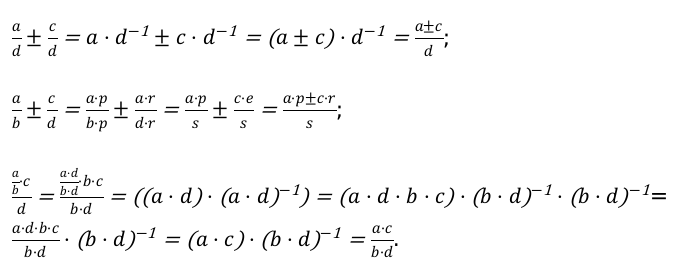
Пример №1:
Для заданных значений дроби: [frac{8}{2,7}] и [frac{1}{2,7}] необходимо выполнить сложение.
используя алгоритм решения, необходимо значения в числителе сложить, а в знаменателе оставить без изменений и переписать.
Выполнив все действия получим дробь: [frac{8+1}{2,7}].
Далее произведем сложение и получим дробное значение:
[frac{8+1}{2,7}=frac{9}{2,7}=frac{90}{27}=3 frac{1}{3}]
Следовательно: [frac{8}{2,7}+frac{1}{2,7}=frac{8+1}{2,7}=frac{9}{2,7}=frac{90}{27}=3 frac{1}{3}]
Ответ задачи: [frac{8}{2,7}+frac{1}{2,7}=3 frac{1}{3}].
Пример №2
Необходимо найти разность дробей:
[frac{1-sqrt{2}}{3 cdotleft(log_{2} 3 cdot log_{2} 5+1right)}]
и
[frac{sqrt[3]{2}}{3 cdotleft(log_{2} 3 cdot log_{2} 5+1right)}]
Так как в знаменателе данные являются равными между собой. вычисление будет производиться по принципу равного знаменателя.
Из этого следует:
[frac{1-sqrt{2}}{3 cdotleft(log {2} 3 cdot log {2} 5+1right)}-frac{sqrt[3]{2}}{3 cdotleft(log {2} 3 cdot log {2} 5+1right)}=frac{1-sqrt{2} sqrt{2}}{3 cdotleft(log {2} 3 cdot log {2} 5+1right)}]
Для решения данного типа задач важно помнить правило приведения к общему знаменателю.
Вычисление дробных значений с переменной
В случае, когда имеются одинаковые значения в знаменателях, то необходимо производить суммирование или вычитание числителей.
Дробь соответствующего вида можно упростить.
После проведения процесса упрощения дробного значения, окончательный вариант значения, если их несколько приводят к общему знаменателю.
Затем суммируют числитель и находят правильный ответ решения.
Вычислительные действия с десятичными дробями
В свою очередь данный вид дробей подразделяется на следующие категории:
- Конечные — если после запятой присутствует окончательное число.
Например: [pm a_{0} a_{1} a_{2} a_{3} ldots . . a_{n}]
[pm sum_{k=0}^{n} a_{k} cdot 10^{-k}] - Бесконечные — количество цифр после запятой, не имеют окончательного значения, то есть они бесконечны.
Например: [pm a_{0} a_{1} a_{2} a_{3}]
[pm sum_{k=0}^{n} a_{k} cdot 10^{-k}]
Основные свойства дробей:
Изменение величины десятичной дроби не произойдет, даже если к ней добавить справа несколько нулей. Это свойство принято считать одним из самых главных для данного вида дробей.
Если в рассматриваемом дробном значении наблюдается множество нулевых значений, тогда их просто исключают, так как никакого влияния на значение они не имеют.
Рассмотрим несколько простых и понятных для ознакомления примеров решения данных дробей
- 0,900 = 0,9;
- 22,10200000 = 22,102;
- 0,45000=0,45;
- 0,12569000=0,12569;
- 0,780=0,78.
Основные характеристики десятичных дробей
- Дробное число, не будет иметь какого-либо значения, если в знаменателе нулевое число. Деление на ноль в математике строго запрещено.
- Нулю будет равна дробь, у которой в числителе значится нулевое значение. В знаменатель — отсутствует.
- Если значения, которые находятся в числителе и знаменателе разделить или перемножить на любое действительное число. То получится дробь равная ей по значении.
- Если взять две дроби: [frac{a}{b}] и [frac{c}{d}] то они называться будут равными при [a cdot d ] или [ b cdot c .]
Принцип умножения десятичных дробей
Для перемножения десятичных дробей необходимо, произвести следующие действия.
- Дробь записать в виде так называемого математического столбика. Далее рассмотреть заданное значение, как обыкновенные действительные числа и подсчитать их;
- Все знаки за запятой подсчитать и сложить сумму;
- Полученную сумму справа налево отложить и поставить запятую.
Для данного вида дробей характерны все те же действия, что и для остальных чисел.
Если переставить местами множители, на окончательный ответ это не повлияет.
если мы хотим умножить число на произведение двух и более. Сначала перемножаем данное число на первый множитель затем полученное значение на второй и так далее.
Чтобы умножить сумму на множитель. Нужно по отдельности перемножить числа и полученную сумму сложить.
Если проводим умножение на разность чисел. Для начала умножаем на уменьшаемое, а затем на вычитаемое. Следовательно, полученные значения вычитаем.
Также процесс умножения можно упростить. Десятичные дроби перемножить как действительные целые числа, и поставить запятую.
Пример №1:
Определить произведение чисел [1,5 cdot 0,75].
Первым делом преобразуем дробь. Заменим десятичную. на обыкновенную.
[0,75 = frac{75}{100}], [1,5=frac{15}{10}]
Затем проводим сокращение дробных значений и выделяем, по уже изученным правилам целую часть.
[frac{125}{1000}] можно преобразовать и получить следующую дробь 1,125.
Ответ: 1,125.
Пример №2:
Определить произведение чисел [5,382 cdot 0,2].
Первое значение является бесконечной дробью. Ее рекомендуется округлить до сотых значений. Получается [5,382 approx 5,38].
Второй множитель округлять не требуется, это не имеет смысла.
[5,38 cdot 0,2=frac{frac{538}{100} cdot 2}{10}=frac{1,076}{1000}=1,076]
Следовательно, получаем ответ к нашей задаче: 1,076.
Пример №3:
Необходимо перемножить две периодические дроби. [0,(3) cdot 2,(36)]
Преобразуем заданные значения в обыкновенную дробь.
[0,(3)=0,3+0,03+0,003+0,003+ldots=frac{0.3}{1-0,1}=frac{0.3}{9}=frac{3}{9}=frac{1}{3}]
[2,(36)=2+(0,36+0,0036+ldots)=2+frac{0,36}{1-0,01}=2+frac{36}{99}=2+frac{4}{11}=frac{2 cdot 4}{11} frac{26}{11}]
[Rightarrow 0,(3) cdot 2,(36)=frac{frac{1}{3} cdot 26}{11}=frac{26}{33}]
Полученную в конечном итоге обыкновенную дробь приводим к десятичной. В столбик разделим числитель на знаменатель.
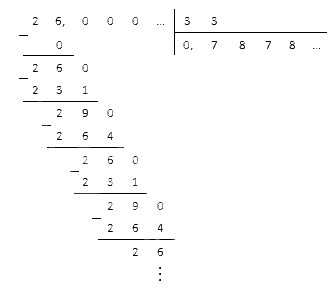
Окончательный ответ : [0,(3) cdot 2,(36)=0,(78)]
Умножение десятичных дробей при помощи столбика
Перемножение столбиком выполняя на условии, что на запятые никакого внимания не уделяется (они игнорируются)
В итоговом результате ставится знак запятой справа. Отделяется столько запятых, сколько множители имеют десятичных знаков вместе.
Если не хватает цифр, то принято в окончательном ответе дописывать нули.
Рассмотрим примеры решения подобных задач.
Пример №1:
Нужно найти значение произведения, следующих чисел: 63,37 и 0,12.
Выполняем умножение, не обращая внимание на запятые.
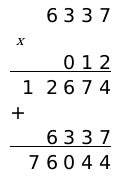
Далее определяемся с запятой, где ее ставить.Она будет через четыре цифры справа. Потому что сумма десятичных знаков двух множителей равна 4.
Нули в данной ситуации не записываются. Это связано с достаточным количеством чисел.
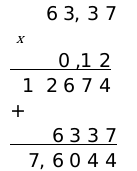
Получаем окончательное значение равное 7,6044.
Пример №2:
Заданные числовые, дробные выражения 3,2601 и 0,0254. необходимо перемножить между собой.
Для этого применим умножение столбиком.

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны. Потому что заданные дроби, вместе, имеют восемь знаков после запятой.
Нули в данной ситуации записываются. Это связано с недостаточным количеством значений.
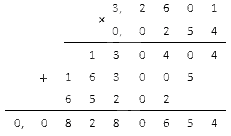
Получаем окончательное значение равное: 0 , 08280654
Нет времени решать самому?
Наши эксперты помогут!
Умножение десятичной дроби с обыкновенной и со смешанной дробью
Чтобы произвести данную операцию, необходимо выполнить следующие требования:
- Десятичную дробь преобразовывают в обыкновенную и перемножаем с нужным числом.
- В десятичную переводим обыкновенную или смешанную дробь и далее перемножаем друг с другом.
Пример 1. Найти произведение [frac{3}{5} text { на 0,9 }].
Поэтапный процесс решения.
- Записываем 0,9 в виде обыкновенной дроби, а именно [0,9=frac{9}{10}].
- Перемножаем цифры по правилам математики.
[frac{frac{3}{5}cdot 9}{10}=frac{27}{50}=0,54]
Ответ: [frac{3}{5} cdot 0,9=0,54]
Пример 2. Найти произведение чисел [0,18 text { на } 3 frac{1}{4}].
Выполняем следующие действия:
- Записываем [3 frac{1}{4}] в виде десятичной дроби:
[3 frac{1}{4}=3,25]. - Вычисляем известные нам значения:
0,18 * 3,25 = 0,585.
Ответ: [0,18 quad 3 frac{1}{4}=0,585].
Пример 3:
Даны следующие значения [0,4 text { и } 3 frac{3}{5} text {. }] По условию задач нужно найти их произведение, иными словами перемножить.
Первым делом 0,4 переведем в десятичную дробь и получим значение: [0,4=frac{4}{10}=frac{2}{5}]
Затем проводим вычисление:
[0,4 quad 3 frac{3}{5}=frac{frac{2}{5} cdot 23}{6}=frac{23}{15}=1 frac{8}{15}]
Полученный ответ является смешанным значением. Его необходимо перевести в значение периодической дроби. А именно: 1,5(3).
Следовательно, это и ответ задачи. 1,5(3).
Возведение в степень дробного числового выражения
Свойство произведения в степень в виде дроби
[frac{left(z^{*} aright)^{m}}{n}=frac{z^{m}}{n} cdot frac{a^{m}}{n}, text { при условии что: } mathrm{z}>0, mathrm{a}>0, frac{m}{n}>0]
В случае если в знаменателе дроби, имеется степень, то ее можно переместить в числитель и при этом необходимо поменять знак на противоположный.
При этом само значение выражения не поменяется.
Данный метод иногда используется при упрощении выражений.
Рассмотрим основные примеры:
Пример 1:
[frac{4^{2}}{4^{2}}=1] — это выражение является верным, так как после преобразования степеней мы получаем [4^{0}]. А как гласят правила алгебры — любое число в нулевой степени равно единице.
Пример 2. Перемещение значения степени из знаменателя дробного выражения [frac{1}{z^{2} x}] в числитель
[frac{1}{z^{2} x}=z^{-2} x z^{-1}]
Пример 3. Записать произведение 3x*(x + y)−4 в виде дроби, которая не имеет степени с отрицательным значением.
Выражение имеет множители 3 и (x + y)−4. Множитель 3 не изменяем, а множители (x + y)−4 заменяем на соответственно равную ему дробь [frac{1}{(x+y)-4}]
[3 *(x+y)-^{4}=3 x frac{1}{(x+y)-4}]
Затем перемножим множитель 3 с числителем дроби [frac{1}{(x+y)-4}].
В результате образуется дробь [frac{3}{}]
Итоговый результат: [3(x+y)-^{4}=3 x frac{1}{(x+y)-4}=frac{3}{(x+y)-4}]
Преобразование дробных значений 0,1, 0,01, 0,001, где основанием степени является число 10
Если степень представлена числами 0,1; 0,01; 0,001 и основание имеет значение 10. Для преобразования необходимо:
- указать отрицательный показатель степени;
- записать основание равным десяти.
Пример 1: Значение 0,01, где основание — число 10.
В числе 0,01 имеется два 0. Значит, оно будет представлено как 10 -2. Значение показателя равно значению нулей в числе 0,01.
0,01 = 10-2
Число 0,01 это значение деления 1/100, или 1/102
Пример 2: Значение 0,00001 в виде степени с основанием 10.
0,00001 = 10-5
Правила деления дробей
Выполнение деления дробных значений по своей аналогии одинаково с умножением.
При делении первую дробь необходимо перемножить со значениями дроби под номером два.
Пример 1:
Дробное значение следующего вида: [frac{sqrt{sqrt{x+2 cdot x}}}{x^{2} cdotleft(operatorname{Ln} x^{2} cdot operatorname{Ln} x+1right)}] необходимо разделить на следующую дробь [frac{3 cdot x^{2.3} cdot(sqrt{x+1})-2}{sin (2 cdot x-sqrt{x})}]
Преобразовывая значения можно записать следующую форму:
[frac{sqrt{sqrt{x+2 cdot x}}}{x^{2} cdotleft(operatorname{Ln} x^{2} cdot operatorname{Ln} x+1right)} / frac{3 cdot x^{2.3} cdot(sqrt{x+1})-2}{sin (2 cdot x-sqrt{x})}]
затем заменить произведением следующего вида
[frac{sqrt{sqrt{x+2 cdot x}}}{x^{2} cdotleft(operatorname{Ln} x^{2} cdot operatorname{Ln} x+1right)} * frac{3 cdot x^{2.3} cdot(sqrt{x+1})-2}{sin (2 cdot x-sqrt{x})}]
Приведение дробей к наименьшему общему знаменателю
Наименьший общий знаменатель дробей
Определение
Общий знаменатель значения — это любое из положительных данных числа, которое является кратным для всех значений дробей.
Иными словами, можно сказать, что общим знаменателем дроби, будет характеризоваться натуральное простое числовое значение. Оно должно делиться без остатка на все значения знаменателей данных дробей.
Натуральные числа имеют свойство бесконечности и поэтому ряд обыкновенных дробных значений имеет характерное множество общих значений знаменателя. Чтобы определить общий знаменатель для дроби, нужно применить его основное определение.
Рассмотри два значения дробных выражений: 16 и 35. Общим дробным знаменателем будет являться любое число с положительным значением. Оно должно быть кратным значениям 6 и 5.
Перечислим подходящие значения: 30,35,65,95,125,155,185,215 и так далее.
Данное определение звучит следующим образом: минимальное значение числа, на которое можно разделить знаменатель дроби, обязательно без остаточного значения.
Аббревиатура данного значения, выглядит как НОК.
В определенном перечне числовых значений, которые являются общими знаменателями данных дробей, будет иметь место наименьшее простое значение. Оно будет характеризоваться, как наименьший общий знаменатель. Сформулируем определение наименьшего общего знаменателя данных дробей.
Как правильно определить наименьший общий знаменатель числа дроби?
Так как НОК, будет иметь значение наименьшего положительного общего делителя данного набора чисел. Тогда НОК знаменателей любых дробей, представлен, как минимальный общий знаменатель дроби.
Из этого следует, что определение наименьшего знаменателя дроби, будет сводиться к определению НОК знаменателя дроби.
Рассмотрим данное правило на примере решения.
Пример 1:
Задано два значения дроби: [frac{3}{10} и frac{277}{28}]
Знаменатели дробей равняются 10 и 28 соответственно.
Наименьший знаменатель будет определяться как НОК чисел 10 и 28.
Разложим числа на простые множители: 10=2*5, 28=2*2*7, следовательно НОК (15 и 28)=2*2*5*7=140.
Ответ задачи: 140
Когда простые обыкновенные дроби, имеют одинаковые по значению знаменатели, то это характеризуется как дроби приведены к общему знаменателю.
Пример 2: значения [frac{45}{76} text { и } frac{143}{76}] приведены к общему знаменателю, числу 76. Рассмотрим еще несколько дробей [frac{1}{3}, frac{3}{3}, frac{17}{3} text { и } frac{1000}{3}] все эти значения приведены к общему знаменателю 3.
В случае, если знаменатели дробных чисел, являются разными по значениям и не равны друг другу. Можно их привести к общему числовому знаменателю. Для этого значение числителя и знаменателя данных значений перемножим с дополнительным множителем.
Например 3: [frac{2}{5} и frac{7}{4}] — эти дроби имеют разные знаменатели, поэтому воспользуемся приведение к общему знаменателю, при помощи дополнительных множителей, а именно 4 и 5.
Применяя данные значения приведем и вычисления и получим общий множитель: значение равное 20.
При перемножении числителя и знаменателя дроби [frac{2}{5}] на значение равное 4, получим дробь вида [frac{8}{20}]. Проводим аналогичные действия, но только с дробью.
При перемножении числителя и знаменателя дроби [frac{7}{4}] на 5 и приведем ее к дроби вида [frac{35}{20}].
Теперь можно сформулировать определение, приведение дробей к общему знаменателю.
Определение
Приведение дробей к знаменателю одинаковых значений – это вычислительный процесс, который включает в себя: умножение числителей и знаменателей любых значений дробей на определенные значения дополнительных множителей, чтобы результаты проведенных вычислений получились дроби с одинаковыми знаменателями.
В математике существует правило, которое помогает привести дроби к общему наименьшему знаменателю.
Данное правило включает в себя три основных пункта.
Принцип приведения дробного значения к наименьшему общему знаменателю:
- Для начала определяется значение наименьшего общего знаменателя дробей.
- Затем для каждой дроби определяется дополнительный множитель. Он должен соответствовать правилу: деление наименьшего общего знаменателя на знаменатель, каждой рассматриваемой при решении, дроби.
- Перемножаем числитель и знаменатель на принятый дополнительный множитель.
Решение задач с приведением к наименьшему знаменателю
Пример 1:
Нужно привести к наименьшему знаменателю следующие дроби:
[frac{5}{14} и frac{7}{18}]
Для решения применим алгоритм решения, рассмотренный вышеприведенном пункте.
Для начала определим наименьшее значение общего знаменателя, который равен минимальному и кратному числу 14 и 18.
Разложим значения знаменателей на множители: 14=2*7, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=126.
Следующим шагом, будет вычисление дополнительных множителей. С их помощью приведем дробные значения [frac{5}{14}] и [frac{7}{18}] будут приведены к числу 126.
Дробному значению [frac{5}{14}] дополнительный множитель будет равняться 12614=9. Для значения второй дроби равной [frac{7}{18}] , аналогичный множитель будет равняться 12918=7.
Числители и знаменатели дробей перемножаем на дополнительный множитель 9 и 7 соответственно.
Записываем следующие выражения:
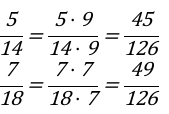
Итоги проведенных вычислений: Заданные дроби [frac{5}{14} и frac{7}{18}] приведены к общему знаменателю. Итоговое значение выражения [frac{45}{126} и frac{49}{126}].
Пример 2:
Нужно привести к наименьшему знаменателю следующие дроби:
[frac{3}{12} и frac{5}{18}]
В этом примере, также применим алгоритм решения, состоящий из трех главным действий.
Используя алгоритм решения, определим наименьшее значение общего знаменателя, который равен самому минимальному значению и кратному числам 12 и 18.
Следующим шагом, разлом данные значения на множители: 12=2*6, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=216.
Произведем вычисление дополнительных множителей. С их помощью приведем дробные значения [frac{3}{12}] и [frac{5}{18}] будут приведены к числу 216.
Дробному значению [frac{3}{12}] дополнительный множитель будет равняться 21612=18. Для значения второй дроби равной [frac{7}{18}], аналогичный множитель будет равняться 21618=12.
Данные значений дробей, нужно перемножить на дополнительный числовой множитель равный числам 9 и 7 соответственно. Подставим эти данные и вычислим составленные выражения.
Записываем следующие выражения:
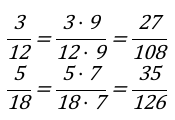
Итоги проведенных вычислений: Заданные дроби [frac{5}{14} и frac{7}{18}] не приведены к общему знаменателю. Окончательное значение выражения [frac{27}{108} и frac{35}{126}] и из этого следует, что знаменатели разные.
Ответ: значение 216 не будет являться наименьшим общем знаменателем.
Аналогичным способом, используя алгоритм решения, можно определить значение наименьшего знаменателя трех и более дробных значений.