Как составить алгоритм по икт

Особенности понятия

Алгоритмы появились вместе с математикой, а первые упоминания о них встречаются в книге математика Мухаммеда бен Мусы аль-Хорезми из города Хорезма. Он описал методы выполнения различных действий с многозначными числами еще в 825 году. Само слово «алгоритм» появилось после того, как книгу ученого перевели на латинский язык в Египте.

Современное определение алгоритма в информатике — это описание действий, последовательное выполнение которых позволяет решить поставленную задачу за конкретное количество шагов.

С этим человек сталкивается каждый день, когда читает рецепты в кулинарных книгах, инструкции к различной технике, правила решения заданий. Но обычно все эти действия выполняются автоматически, без их анализа. Родители сталкиваются с этим понятием, когда объясняют детям, как открыть двери ключом или почистить зубы. Алгоритмов в окружающем мире множество, но есть общие признаки для всех их видов.

Свойства и виды

Для изучения понятия нужно разобраться в свойствах алгоритма в информатике. Их существует несколько:

• дискретность;
• детерминированность или определенность;
• понятность;
• завершаемость или конечность;
• массовость или универсальность;
• результативность.

Согласно свойству дискретности, алгоритмы должны описывать весь процесс решения задания в виде выполнения простых шагов. При этом на пункты отводится определенное количество времени. Каждый шаг должен определяться состоянием системы, то есть при одних и тех же исходных данных результат не меняется. Но есть и вероятностные алгоритмы, где пункты зависят от системы и случайно генерируемых чисел. В этой ситуации понятие становится подвидом обычного.

Понятность заключается в том, что команды алгоритма должны быть доступны конкретному исполнителю и входить в его личную систему. В ходе работы математическая функция при правильно заданных исходных данных выдает результат за определенное количество шагов. Иногда процедура может не завершиться, но вероятность таких случаев стремится к нулю.

Универсальность или массовость позволяет использовать алгоритм с разными наборами начальных данных. Последнее свойство обеспечивает его завершение в виде определенного числа — результата.

У каждого алгоритма есть свои начальные условия, цели и пути решения задачи. Существует большая разница между вычислительными и интерактивными видами. Происхождение первых связано с опытами ученого Тьюринга, они могут преобразовать входные данные в выходные. Вторые предназначены для связи с объектом управления, они работают только под внешним воздействием. Ученые выделяют несколько видов алгоритмов в информатике:

• детерминированные или жесткие;
• гибкие;
• линейные;
• разветвляющиеся;
• циклические;
• вспомогательные;
• структурные блок-схемы.

Жесткие еще называются механическими, так как чаще всего они используются для работы двигателя или машины. Они задают действия в единственно верной последовательности, что приводит к искомому или требуемому результату при условии выполнения процессов, для которых они и разработаны.

Гибкие алгоритмы делятся на эвристические и вероятностные. Первые используются при различных умственных выводах без строгих аргументов, а вторые дают возможность получить один результат несколькими способами.

Линейный тип — это набор команд, которые выполняются в строгой последовательности. Разветвляющийся включает хотя бы одно условие и при проверке дает разделение на несколько блоков. Появляются альтернативные ветвления программы.

В циклических видах несколько раз повторяются одни и те же действия, при этом меняются исходные данные. Сюда относятся переборы вариантов и бо́льшая часть способов расчета. Циклом в этом случае называют последовательность команд, которые нужно выполнить множество раз для достижения требуемого результата.

Подчиненный или вспомогательный вид является ранее разработанным алгоритмом для быстрого решения задачи. Он необходим для сокращения записи, если в структуре есть одинаковые команды. Схемами называются графические изображения с помощью блоков и соединяющих их прямых линий. Их используют перед программированием в качестве наглядных примеров, поскольку зрительное восприятие позволяет быстрее осмыслить процесс обработки информации и выявить возможные ошибки. В блоках отображаются исходные данные, которые вносятся в компьютер для вычислений.

Способы записи

Алгоритмы записываются несколькими методами. В информатике используется всего три:

• словесно-формульный;
• графический;
• программный.

В первом случае алгоритм записывается простым языком — словами и математическими формулами, что необходимо для понимания его теории. Здесь учитываются исходные данные, действия с ними и условия получения результата. Второй тип записи — компьютерное описание. Для этого применяются языки программирования и сами программы — форсы представления расчетов для их выполнения машиной.

Графическое описание состоит из связанных между собой географических фигур. Основные элементы блок-схем:

• прямоугольники;
• эллипсы;
• ромбы;
• шестиугольники;
• стрелки;
• пунктирные линии;
• соединительные фигуры.

В прямоугольниках записывают процессы, они указывают на выполнение операций, которые изменяют форму или значение данных. Ромбы содержат способы решения, здесь выбирается следующее направление в зависимости от поставленных условий. Модификации могут передаваться в шестиугольниках, где записываются операции, меняющие команды.

В блок-схемах можно выделить ручной ввод и предопределенные процессы. Первая фигура позволяет исполнителю ввести данные во время работы алгоритма через устройства, подключенные к компьютеру. Второе понятие заключается в использовании заранее записанных алгоритмов.

Графическое изображение содержит блоки документов и дисплеев. Оператор может вводить данные с бумаги и выводить их на нее, а также с помощью устройств, которые воспроизводят информацию на экране (проекторы для интерактивных досок, подключенные к компьютерам планшеты и ноутбуки).

Линии и соединительные фигуры указывают на связи между разными блоками и их последовательность. В схеме есть блоки начала и конца алгоритма, его прерывания, которое может произойти из-за сбоев в программе. Можно также указывать комментарии и пояснения исполнителя, для этого есть отдельные фигуры.

Правила создания

Существует несколько правил создания алгоритмов. Если их соблюдать, то в ходе работы всегда будет верный результат. Форма должна быть настолько простой, чтобы ее понял тот, кто занимается ее разработкой. Также не должно возникнуть проблем с чтением у того, кто будет выполнять описанные действия.

Объект, который проводит расчеты в алгоритме, называется исполнителем. Идеальными считаются роботы, компьютеры и другие машины. Они работают с программами, то есть схемами, написанными определенным языком программирования.

Разобраться с действиями помогут простые примеры алгоритмов по информатике. Когда есть ряд чисел от 1 до 100 и необходимо найти из них простые, то выбираются те, что делятся на единицу и себя. В этом случае используется циклическая структура:

• сначала нужно взять число 1;
• проверить, меньше ли оно, чем 100;
• если да, то узнать, простое ли оно;
• при выполнении условия записать;
• перейти к числу 2;
• повторить операцию.

Такие действия проводят со всеми числами. При этом первые четыре шага будут постоянно повторяться. Если попадается число, не являющееся простым (4, 6, 8 и т. д. ), то его нужно просто пропустить. Алгоритм в этом случае обладает предусловиями, то есть проверки происходят в начале цикла.

Анализ работы

Распространение информационных технологий привело к увеличению риска сбоев в работе программ. Предотвратить появление ошибок в алгоритмах можно с помощью доказательства их корректности математическими средствами. Такой анализ называется формальным методом, он предусматривает использование специального набора инструментов.

Гипотеза Ричарда Мейса утверждает, что избежать ошибок легче, чем их устранить. Благодаря доказательству корректности программ можно выявить их свойства, применяемые ко всем видам входных данных. Само понятие делится на две разновидности — частичную и полную. При первом типе корректности алгоритм дает правильный результат только для тех случаев, когда он завершается. Во втором случае программа завершает работу корректно для всего диапазона данных.

Исполнители во время проверки сравнивают выдаваемые данные со спецификой требуемого результата. Для доказательства корректности используются предусловия и постусловия. Первые должны выполняться перед включением программы, вторые — после завершения ее работы. Формальные методы успешно применяются для многих задач: верификации программ и микропроцессоров, разработки искусственного интеллекта, электронных схем и автоматических систем для железной дороги, спецификации стандартов.

Для выполнения алгоритма нужно только конкретное количество шагов, но на практике для этого потребуется много времени. В связи с этим введено понятие сложности. Она бывает временной, вычислительной и связанной с размерами алгоритма. Для увеличения эффективности используются быстрые программы, которые появились еще в 50-х годах прошлого века.

Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки

Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании

Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.

■  Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.

Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.

Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.

Свойства алгоритмов

Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:

• Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
• Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
• Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
• Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
• Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.

Способы представления алгоритмов:

• словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
• блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
• формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
• псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.

Словесная запись алгоритма

Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.

■  Пример 1. Записать в словесной форме правило деления обыкновенных дробей.

Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.

Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).

Формальные исполнители алгоритма

Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.

Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).

Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.

■ Пример 2. Исполнитель Крот имеет следующую систему команд:

1. вперед k — продвижение на указанное число шагов вперед;
2. поворот s — поворот на s градусов по часовой стрелке;
3. повторить m [команда1 … командаN] — повторить m раз серию указанных команд.

Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?

Повторить 5 [вперед 10 поворот 72]

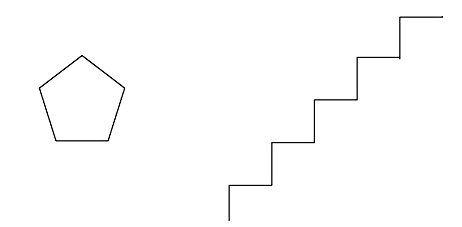
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.

Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).

■ Пример 3.  В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).

Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).

Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]

Блок–схема

Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).

Основные элементы блок–схемы алгоритма:

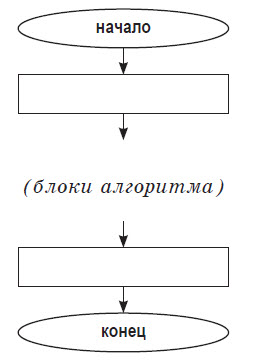
Общий вид блок–схемы алгоритма:

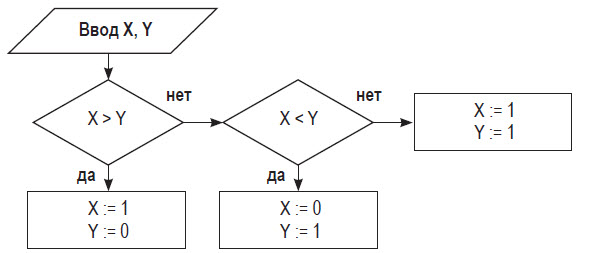
■ Пример 4.  Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.

Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.

Решение.

1. Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
2. В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
3. Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
4. Вычисляется результат выполнения алгоритма: X := 0, Y := 1.

Ответ: X := 0, Y := 1.

Алгоритмические языки

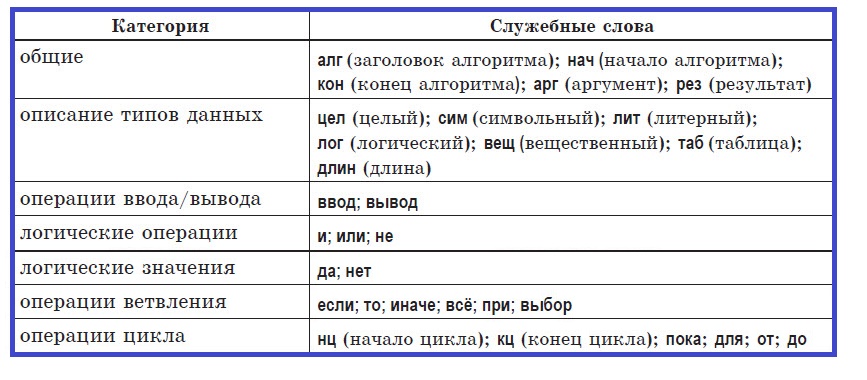
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.

В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.

Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.

Псевдокод

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.

Служебные слова учебного алгоритмического языка:

Стандартная структура алгоритма

Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.

Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.

В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.

Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.

Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.

Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.

Описание величин и действия над ними

При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.

При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.

Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.

В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.

При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.

Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).

Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.

Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.

Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10^-2 и –7,123456*10²).

Над числовыми данными можно выполнять арифметические операции и операции сравнения.

Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.

Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.

Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».

Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.

Команды учебного алгоритмического языка

Учебный алгоритмический язык использует следующие команды для реализации алгоритма:

ОПЕРАЦИЯ ПРИСВАИВАНИЯ

Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.

Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).

Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.

ВВОД И ВЫВОД ДАННЫХ

В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.

При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.

Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.

В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.

Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.

Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).

Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:

Путь 200 м

Тот же результат был бы получен, если бы изменить строку вывода на

вывод «Путь «, v * t, » м»

Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки».

Вернуться к Списку конспектов по информатике.

Составление алгоритмов и блок-схем.

Цели
урока:

          Образовательные:

                   
—
формирование и закрепление навыков по составлению и  выполнению алгоритмов;

                  
—
проверка знаний;
                  — повышение интереса к изучению предмета;
                  — воспитание навыка быстрого мышления.

       Развивающие:

                  
— способствовать развитию умения планировать последовательность действий для
достижения поставленной цели;

 —  способствовать
развитию алгоритмического и логического мышления;

 — развитие
творческой активности учащихся;
                 — развитие познавательных интересов.

      Воспитательная:

               — способствовать
воспитанию в детях ответственности, взаимопомощи и взаимоуважения

Тип урока: 
закрепление полученных знаний

Оборудование:
Раздаточный материал, компьютер, проектор, презентация к уроку

Ход урока

1.   Оргмомент.
Взаимодействие
учителя и учеников

2.   Тема,
цель. На
прошлом уроке вы познакомились с важной темой информатики.

   
— Какой? ( Алгоритмы)

   
— Что такое алгоритм? (Порядок действий или план)

 3.
Устный опрос.

-Кто выполняет
алгоритмы? (Исполнители)

Таблица 1.
Определить соответствие в таблице.

— А каждый ли
исполнитель может исполнить любую команду? Почему?

— Что такое
система команд исполнителя?

— Какие команды
выполняют эти исполнители?

4.     Повторение: Типы алгоритмов. (3 минуты)

·       
Что
такое линейный алгоритм?

·       
Что
такое Разветвляющийся алгоритм?

·       
Что
такое циклический алгоритм?

5.     Практическая
часть.

Составить
алгоритмы и блок-схемы к алгоритмам.

Задание 1.

Написать
алгоритм сбора съедобных грибов, и составить к этому алгоритму блок-схему.

– Какая команда будет
выполняться не всегда? Когда ее нужно пропустить? (команда «сорви гриб» не
выполняется, если гриб несъедобный.) обвести прямоугольник с этой командой
зеленым карандашом.

– Есть ли цикл в этом
алгоритме? Какие команды будут выполняться больше одного раза? («найди гриб»,
«гриб съедобный», «сорви гриб», «все грибы обошел?».)

– Сколько раз будут
выполняться эти 5 команд? («хитрость этого вопроса в том, что команды в цикле
будут выполняться не одинаковое число раз: сорвать гриб нужно столько раз,
сколько будет найдено съедобных грибов, а остальные 4 команды нужно выполнять
столько раз, сколько будет найдено всех грибов.)

– В каком ромбе записано
условие повтора?

(во втором ромбе, который
нужно обвести красным карандашом.)

Задание 2.

Составить
алгоритм разбора фасоли из мешка. Если фасоль белая, то её положить в круглую
корзину, а если не белая, то в овальную корзину.

(Учесть, что задание
допускает разное расположение команд на схеме).

Ответить на вопросы:

– Какие команды будут
выполняться не всегда?

– Какие команды будут
выполняться больше одного раза?

– Сколько раз будет выполнена
каждая из этих команд?

– Какой вопрос на схеме
является условием повтора?

Задание 3.

Составь
блок-схему алгоритма для решения задачи.

Красная Шапочка
гуляла по лесу и собирала цветочки. Она сорвала 5 колокольчиков, 6 незабудок и
4 василька. Вдруг сзади кто-то захихикал. Красная Шапочка оглянулась и увидела
Серого Волка.

— Милая Красная
Шапочка, поделись со мной цветами: если у тебя больше 7
цветочков, дай мне 5, а иначе подари, хотя бы 3.

Сколько цветов
осталось в букете у Красной Шапочки?

6.     Физкультминутка
(3 мин)

7.       Самостоятельная
работа на компьютере по составлению алгоритмов и блок-схем. (15 мин)

8. Домашнее
задание:
составить  текстовый  и графические алгоритмы лепки снеговика.

9.    Подведение
итогов урока

Отлично поработали на
уроке.

Получили «5»

Получили «4»

Чему вы сегодня
научились?

Что вам сегодня
понравилось?

– Закрепили знания о
ветвлениях и циклах в алгоритмах.

– Научились отличать
условие ветвления от условия повтора.

Сегодня вы научились
составлять алгоритмы с ветвлениями и циклами.

Информатика, 11 класс. Урок № 2.

Тема — Базовые алгоритмические структуры

Перечень вопросов, рассматриваемых в теме: алгоритм, блок-схема, следование, линейный алгоритм, ветвление, полная форма ветвления, неполная форма ветвления, разветвляющийся алгоритм, повторение, циклический алгоритм, цикл с предусловием, цикл с постусловием, цикл с параметром, комбинации базовых алгоритмических структур

Глоссарий по теме: следование, ветвление, повторение, цикл с предусловием, цикл с постусловием, цикл с параметром.

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 11 класса

— М.: БИНОМ. Лаборатория знаний, 2017

Дополнительная литература по теме урока:

И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. Информатика и ИКТ. Профильный уровень: учебник для 11 класса — М.: БИНОМ. Лаборатория знаний, 2012

Теоретический материал для самостоятельного изучения

В 1969 году нидерландский ученый Эдсгер Дийкстра доказал важную теорему. Суть ее в том, что для решения любой логической задачи можно составить алгоритм, используя лишь три алгоритмических структуры: следование, ветвление и повторение. Эти структуры называют базовыми.

Самой простой структурой является «следование».

Алгоритм реализован через последовательную алгоритмическую структуру, если все команды этого алгоритма выполняются один раз, причем в том порядке, в котором они записаны.

Алгоритм, основанный на конструкции «следование» называется линейным алгоритмом. Примером такого алгоритма может служить алгоритм вычисления дискриминанта квадратного уравнения, блок-схема которого приведена на рисунке 1.

Рис. 1

Следующей конструкцией является «ветвление». Она встречается, если действия алгоритма зависят от некоторого условия.

Алгоритм реализован через алгоритмическую конструкцию «ветвление», если от входных данных зависит, какие команды будут выполняться. Условие, которое выражает эту зависимость, фактически является вопросом, на который можно ответить либо «да», либо «нет».

Существуют полная и неполная формы ветвления.

В полной форме если условие выполняется, то алгоритм переходит к выполнению первой серии команд, а если не выполняется — то ко второй.

В неполной форме алгоритм выполняет серию команд только если условие истинно. В противном случае ничего не происходит.

Алгоритм, основанный на конструкции «ветвление» называется разветвляющимся алгоритмом. Примером такого алгоритма может служить алгоритм нахождения корней квадратного уравнения, блок-схема которого приведена на рисунке 2.

Рис. 2

И, наконец, последняя алгоритмическая конструкция — «повторение».

Алгоритм реализован с использованием алгоритмической конструкции «повторение», если некая группа подряд идущих шагов алгоритма (она называется телом цикла) может выполняться многократно в зависимости от входных данных.

Алгоритм, содержащий конструкцию «повторение» называется циклическим алгоритмом.

Существует несколько разновидностей циклических алгоритмов.

Первый — цикл с заданным условием продолжения работы (цикл с предусловием или цикл-пока).

Второй — цикл с заданным условием окончания работы (цикл с постусловием или цикл-до).

И третий — цикл с заданным числом повторений (цикл с параметром).

Доказано, что при решении задач можно ограничиться только одним циклом — циклом с предусловием. Но в ряде случаев цикл с постусловием или цикл с параметром делают решение задачи легче.

Примером решения одной и той же задачи с помощью различных циклов может служить задача возведения некоторого числа a в натуральную степень n.

Опубликовано 10.08.20 в 21:36