К настоящему времени внимательным читателям, не пропустившим ни одной статьи, возможно, не терпится. Мы уже перешли к третьей статье — и до сих пор говорим о теории! Когда же мы будем писать SQL код?
Очень скоро! В этой статье рассматривается последняя часть обработки запросов, и в конце у нас будет все необходимое для понимания планов выполнения.
Во второй статье рассказывается о реляционных операциях, и в ней говорится, что для выполнения запросов нужны физические операции, или алгоритмы. Сопоставить эти алгоритмы с логическими операциями непросто; иногда сложная логическая операция заменяется несколькими физическими операциями, или несколько логических операций объединяются в одну физическую.
В этой главе мы описываем эти алгоритмы, начиная с алгоритмов извлечения данных, а затем переходим к алгоритмам для более сложных операций.
Понимание этих алгоритмов позволит нам вернуться к планам выполнения и лучше понять их компоненты. Таким образом, мы будем всего в одном шаге от нашей цели, которая состоит в том, чтобы научиться настраивать запросы.
стоимостные модели алгоритмов
В первой статье упоминалось несколько способов измерения производительности системы, включая время отклика, стоимость и удовлетворенность пользователей. Эти показатели являются внешними по отношению к базе данных, и хотя внешние показатели наиболее ценны, они не доступны оптимизатору запросов.
Вместо этого оптимизатор использует внутренние показатели, основанные на объеме вычислительных ресурсов, необходимых для выполнения запроса или отдельной физической операции в рамках плана. Наиболее важными ресурсами являются те, что влияют на время выполнения, а именно циклы процессора и количество операций ввода-вывода (чтение и запись дисковых блоков). Другие ресурсы, такие как память или дисковое пространство, тоже косвенно влияют на время выполнения; например, количество доступной памяти будет влиять на соотношение циклов процессора и количество операций ввода-вывода. Распределение памяти контролируется параметрами сервера и здесь не рассматривается.
Эти два основных показателя, циклы процессора и количество операций ввода-вывода, напрямую не сопоставимы. Однако для сравнения планов выполнения запросов оптимизатор объединяет их в одну функцию стоимости: чем ниже стоимость, тем лучше план.
В течение нескольких десятилетий количество операций ввода-вывода было доминирующим компонентом стоимости, потому что вращающиеся жесткие диски работают на порядки медленнее, чем процессор. Но для современного оборудования это не обязательно так, поэтому оптимизатор должен быть настроен на использование правильного соотношения. Это также контролируется параметрами сервера.
Стоимостная модель физической операции оценивает ресурсы, необходимые для выполнения операции. Как правило, стоимость зависит от таблиц, указанных в качестве аргументов операции. Для представления стоимостных моделей мы будем использовать простые формулы со следующими обозначениями: для любой таблицы или отношения R символы TR и BR обозначают количество строк в таблице и количество дисковых блоков, занимаемых таблицей, соответственно. Дополнительные обозначения будут вводиться по мере необходимости.
В следующем разделе обсуждаются физические операции и рассматриваются алгоритмы и стоимостные модели для каждой из них. Поскольку относительная скорость процессора и внешнего хранилища может варьироваться в широких пределах, затраты на процессор и ввод-вывод рассматриваются отдельно. Мы не будем говорить про логические операции проекции и фильтрации, которые обсуждали в предыдущей статье. Обычно они объединяются с предшествующей им операцией, потому что могут применяться независимо к каждой строке, не завися от других строк в таблице аргумента.
алгоритмы достуПа к данным
Чтобы начать выполнение запроса, движок должен извлечь сохраненные данные. Этот раздел касается алгоритмов, используемых для чтения данных из объектов базы данных. На практике эти операции часто сочетаются с последующей операцией в плане выполнения запроса. Это выгодно в тех случаях, когда можно сэкономить время выполнения, избегая чтения, которое впоследствии будет отфильтровано.
Эффективность таких операций зависит от соотношения количества строк, составляющих результат операции, к общему количеству строк в сохраненной таблице. Такое соотношение называется селективностью (избирательностью). Выбор алгоритма для определенной операции чтения зависит от селективности фильтров, которые могут применяться одновременно.
Представление данных
Неудивительно, что данные хранятся в файлах на жестких дисках. Любой файл, используемый для объектов базы данных, делится на блоки одинаковой длины; по умолчанию PostgreSQL использует блоки по 8192 байта каждый. Блок — это единица, которая передается между жестким диском и оперативной памятью, а количество операций ввода-вывода, необходимое для выполнения любого доступа к данным, равно количеству блоков, которые читаются или записываются.
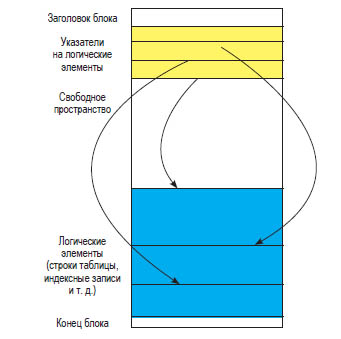
Объекты базы данных состоят из логических элементов (строк таблиц, индексных записей и т. д.). PostgreSQL выделяет место для этих элементов блоками. Несколько мелких элементов могут находиться в одном блоке; более крупные элементы могут быть распределены между несколькими блоками. Общая структура блока показана на рис. 3.1.
Рис. 3.1 ❖ Общая структура блока в PostgreSOL
Распределение элементов по блокам также зависит от типа объекта базы данных. Строки таблицы хранятся с использованием структуры данных, называемой кучей (heap): строка может быть вставлена в любой блок, в котором достаточно свободного места, без специального упорядочивания. Другие объекты (например, индексы) могут использовать блоки иначе.
Полное (последовательное) сканирование
При полном сканировании движок базы данных последовательно считывает все строки в таблице и для каждой строки проверяет условие фильтрации. Чтобы оценить стоимость этого алгоритма, требуется более подробное описание, показанное псевдокодом в листинге 3.1.
Листинг 3.1 ❖ Псевдокод алгоритма доступа к данным полным сканированием
FOR each block IN a_table LOOP
read block
FOR each row IN block LOOP
IF filter_condition (row)
THEN output (row)
END IF
END LOOP
END LOOP
Количество операций ввода-вывода равно BR; общее количество итераций внутреннего цикла равно TR. Нам также необходимо оценить стоимость операций, порождающих выходные строки. Она зависит от селективности (которая обозначается S) и равняется S * TR. Собрав все эти части воедино, мы можем вычислить стоимость полного сканирования:
c1 * BR + c2 * TR + c3 * S * TR,
где константы c1, c2 и c3 представляют характеристики аппаратного обеспечения.
Полностью просканировать можно любую таблицу; для этого не нужны дополнительные структуры данных. Остальные алгоритмы зависят от наличия индексов в таблице, как описано ниже.
Доступ к таблицам на основе индексов
Обратите внимание, что пока мы не перешли к физическим операциям, мы даже не упоминали алгоритмы доступа к данным. Нам не нужно «читать» отношения — это абстрактные объекты. Если следовать идее того, что отношения отображаются в таблицы, нет другого способа получить данные, кроме как прочитать всю таблицу в оперативную память. Как еще мы узнаем, какие значения содержатся в каких строках? Но реляционные базы данных не были бы таким мощным инструментом обработки данных, если бы на этом мы и остановились. Все реляционные базы данных, включая PostgreSQL, позволяют создавать дополнительные, избыточные структуры, значительно ускоряя доступ к данным по сравнению с простым последовательным чтением.
Эти дополнительные структуры называются индексами.
Как создаются индексы, мы рассмотрим позже; пока нам нужно знать два факта, касающихся индексов. Во-первых, индексы — «избыточные» объекты базы данных; они не хранят никакой дополнительной информации, которую нельзя найти в исходной таблице.
Во-вторых, индексы предоставляют дополнительные пути доступа к данным; они позволяют определить, какие значения хранятся в строках таблицы, без необходимости чтения самой таблицы — так работает доступ на основе индексов. И как упоминалось ранее, это происходит полностью прозрачно для приложения.
Если условие (или условия) фильтрации поддерживается индексом в таблице, индекс можно использовать для доступа к данным из этой таблицы. Алгоритм извлекает список указателей на блоки, содержащие строки со значениями, удовлетворяющими условию фильтрации, и только эти блоки читаются из таблицы.
Чтобы получить строку таблицы по указателю, необходимо прочитать блок, содержащий эту строку. Основная структура данных таблицы — это куча, то есть строки хранятся неупорядоченно. Их порядок не гарантирован и не соответствует свойствам данных. Есть две отдельные физические операции, используемые PostgreSQL для получения строк с помощью индексов: индексное сканирование (index scan) и сканирование по битовой карте (bitmap heap scan). При индексном сканировании движок базы данных считывает одну за другой все записи индекса, которые удовлетворяют условию фильтрации, и в этом же порядке извлекает блоки. Поскольку базовая таблица представляет собой кучу, несколько записей индекса могут указывать на один и тот же блок. Чтобы избежать многократного чтения одного и того же блока, в PostgreSQL реализована операция сканирования по битовой карте, которая создает битовую карту блоков, содержащих необходимые строки. Потом все строки в этих блоках фильтруются. Преимущество реализации PostgreSQL состоит в том, что она упрощает использование нескольких индексов в одной и той же таблице в одном запросе, применяя логические операторы «и» и «или» к битовым картам блоков, порождаемым каждым индексом.
Стоимостная модель этого алгоритма намного сложнее. Неформально ее можно описать так: при малых значениях селективности, скорее всего, все строки, удовлетворяющие условиям фильтрации, будут располагаться в разных блоках, и, следовательно, стоимость будет пропорциональна количеству возвращаемых строк. Для больших значений селективности количество обрабатываемых блоков приближается к общему количеству блоков. В последнем случае стоимость становится выше, чем стоимость полного сканирования, поскольку для доступа к индексу необходимы ресурсы.
Сканирование только индекса
Операции доступа к данным не обязательно возвращают полные строки. Если некоторые столбцы не нужны для запроса, их можно опустить, как только строка пройдет условия фильтрации (если таковые имеются). Говоря более формально, это означает, что логическая проекция сочетается с доступом к данным. Такое сочетание особенно полезно, если индекс, используемый для фильтрации, содержит все столбцы, необходимые для запроса.
Алгоритм считывает данные из индекса и применяет оставшиеся условия фильтрации, если это необходимо. Обычно не нужно обращаться к табличным данным, но иногда необходимы дополнительные проверки — мы подробно рассмотрим эту тему в главе 5.
Стоимостная модель сканирования только индекса аналогична модели для доступа к таблице на основе индекса, за исключением того, что не нужно обращаться к данным таблицы. Для малых значений селективности стоимость примерно пропорциональна количеству возвращаемых строк. При больших значениях селективности алгоритм выполняет (почти) полный просмотр индекса. Стоимость просмотра индекса обычно ниже, чем стоимость полного просмотра таблицы, потому что индекс содержит меньше данных.
Сравнение алгоритмов доступа к данным
Выбор лучшего алгоритма доступа к данным в основном зависит от селективности запроса. Отношение стоимости к селективности для различных алгоритмов доступа к данным показано на рис. 3.2. Мы намеренно ограничиваемся качественным сравнением; все числа на этом графике опущены, поскольку они зависят от аппаратного обеспечения и размера таблицы.
Рис. 3.2 ❖ Связь стоимости и селективности запросов для разных алгоритмов доступа к данным
Линия, соответствующая полному сканированию, прямая и почти горизонтальная: ее рост происходит из-за генерации выходных строк. Как правило, стоимость генерации незначительна по сравнению с другими затратами для этого алгоритма.
Линия, обозначающая стоимость доступа к таблице на основе индекса, начинается (почти) с нуля и быстро растет с ростом селективности. Рост замедляется при больших значениях селективности, где стоимость этого алгоритма значительно выше, чем стоимость полного сканирования.
Самым интересным моментом является пересечение двух линий: для меньших значений селективности предпочтительнее доступ на основе индексов, а полное сканирование лучше подходит для больших значений селективности. Точное положение пересечения зависит от аппаратного обеспечения и может зависеть от размера таблицы. Для относительно медленных вращающихся дисков доступ на основе индексов предпочтительнее, только если селективность не превышает 2-5 %. Для твердотельных накопителей или виртуального окружения это значение может быть выше. На старых вращающихся дисках произвольный доступ к блокам может быть на порядок медленнее последовательного доступа, поэтому дополнительные накладные расходы на индексы при той же пропорции строк получаются выше.
Линия, соответствующая сканированию только индекса, располагается в самой нижней части графика, а это означает, что предпочтительно использовать этот алгоритм, если он применим (то есть все необходимые столбцы находятся в индексе).
Оптимизатор запросов оценивает селективность запроса и селективность, соответствующую точке пересечения для данной таблицы и данного индекса. Условие фильтрации запроса, показанного в листинге 3.2, выбирает значительную часть таблицы.
Листинг 3.2 ❖ Фильтрация по диапазону, выполняемая полным сканированием таблицы
SELECT flight_no, departure_airport, arrival_airport
FROM flight
WHERE scheduled_departure BETWEEN ‘2020-05-15’ AND ‘2020-08-31’;
В данном случае оптимизатор выбирает полное сканирование (см. рис. 3.3).
Рис. 3.3 ❖ Последовательное сканирование
Однако меньший диапазон в том же запросе приводит к доступу к таблице на основе индекса. Запрос показан в листинге 3.3, а его план выполнения — на рис. 3.4.
Листинг 3.3 ❖ Фильтрация по диапазону с доступом к таблице на основе индекса
SELECT flight_no, departure_airport, arrival_airport
FROM flight
WHERE scheduled_departure BETWEEN ‘2020-08-12’ AND ‘2020-08-13’;
На самом деле работа оптимизатора запросов намного сложнее: условия фильтрации могут поддерживаться несколькими индексами с разными значениями селективности. Несколько индексов могут быть объединены для создания битовой карты, уменьшая число блоков, которые нужно просканировать. В результате количество вариантов, доступных оптимизатору, значительно превышает выбор из трех алгоритмов.
Рис. 3.4 ❖ Сканирование по битовой карте (доступ на основе индекса)
Таким образом, среди алгоритмов доступа к данным нет победителей и проигравших. Любой алгоритм может выиграть при определенных условиях. Далее, выбор алгоритма зависит от структур хранения и статистических свойств данных. База данных поддерживает для таблиц метаданные, называемые статистикой: информация о кардинальности столбца, разреженности и т. д. Обычно эта статистика неизвестна во время разработки приложения и может изменяться на протяжении жизненного цикла приложения. Следовательно, декларативный характер языка запросов важен для производительности системы. В частности, при изменении статистики таблицы или при корректировке других факторов стоимости для одного и того же запроса может быть выбран другой план выполнения.
индексные структуры
Этот раздел начинается с абстрактного определения того, какую структуру хранения можно назвать индексом; кратко рассматриваются наиболее распространенные индексные структуры, такие как деревья и хеш-индексы, и затрагиваются некоторые особенности PostgreSQL.
Мы покажем, как оценить масштаб улучшений для разных типов индексов и как распознать случаи, когда использование индекса не дает никаких преимуществ в смысле производительности.
Что такое индекс?
Можно предположить, что любой человек, работающий с базами данных, знает, что такое индекс. Увы, удивительно много людей — разработчиков баз данных и составителей отчетов, а в некоторых случаях даже администраторов баз данных — используют индексы и даже создают их, лишь поверхностно представляя, что это за объекты и какова их структура. Во избежание недоразумений мы начнем с определения того, что мы подразумеваем под индексом.
Существует множество типов индексов, поэтому мы ориентируемся не на структурные свойства, а определяем индекс по способу его использования. Структура данных называется индексом, если:
- это избыточная структура данных;
- она невидима для приложения;
- она предназначена для ускорения выбора данных по определенным критериям.
Избыточность означает, что индекс можно удалить без потери данных и восстановить по информации, хранящейся где-то еще (конечно, в таблицах). Невидимость означает, что приложение не может узнать о наличии индекса или о его отсутствии. Иначе говоря, любой запрос дает те же результаты как с индексом, так и без него. И наконец, индекс создается в надежде (или с уверенностью), что это улучшит производительность конкретного запроса или (что еще лучше!) нескольких запросов.
Улучшение производительности не происходит бесплатно. Поскольку индекс избыточен, он должен обновляться при обновлении данных таблицы. Это приводит к накладным расходам для операций обновления, которыми иногда нельзя пренебречь. В частности, индексы PostgreSQL могут оказывать большое влияние на операцию очистки (VACUUM). Однако многие учебники по базам данных переоценивают эти расходы. Современные высокопроизводительные СУБД используют алгоритмы, которые снижают стоимость обновлений индексов, поэтому несколько индексов в таблице — обычное дело.
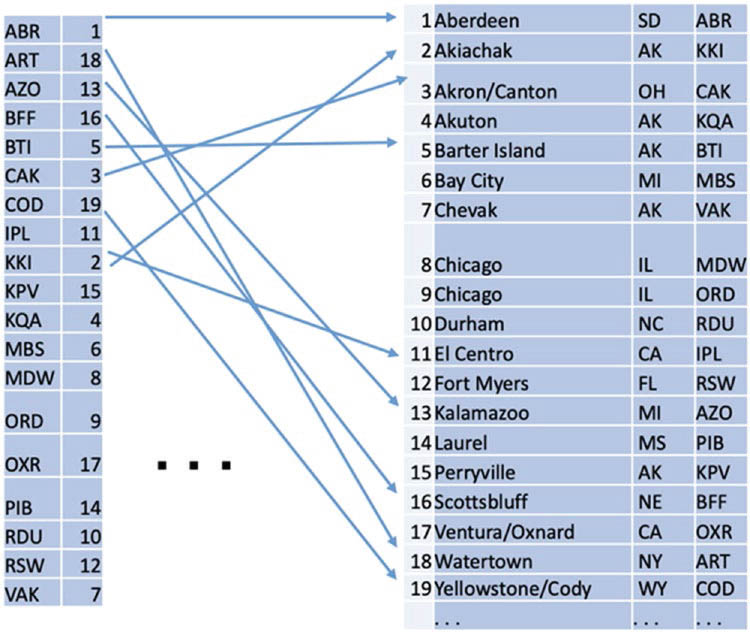
Хотя индексные структуры могут значительно различаться для разных типов индексов, ускорение всегда достигается за счет быстрой проверки некоторых условий фильтрации, указанных в запросе. Такие условия фильтрации устанавливают определенные ограничения на атрибуты таблицы. На рис. 3.5 показана структура наиболее распространенных индексов.
В правой части рисунка показана таблица, а в левой — индекс, который можно рассматривать как особый вид таблицы. Каждая строка индекса состоит из индексного ключа и указателя на строку таблицы. Значение ключа обычно совпадает со значением атрибута таблицы. В примере на рис. 3.5 в качестве значения используется код аэропорта; следовательно, данный индекс поддерживает поиск по коду аэропорта.
У столбца может быть одно и то же значение в нескольких строках таблицы. Если этот столбец индексирован, индекс должен содержать указатели на все строки, содержащие это значение индексного ключа. В PostgreSQL индекс содержит несколько записей, то есть ключ индекса повторяется для каждого указателя на строку таблицы.
Рисунок 3.5 объясняет, как добраться до соответствующей строки таблицы при обнаружении записи индекса; однако он не объясняет, почему строку индекса можно найти намного быстрее, чем строку таблицы. Действительно, это зависит от того, как структурирован индекс, и именно это мы обсуждаем в следующих подразделах.
Рис. 3.5 ❖ Индексная структура
B-деревья
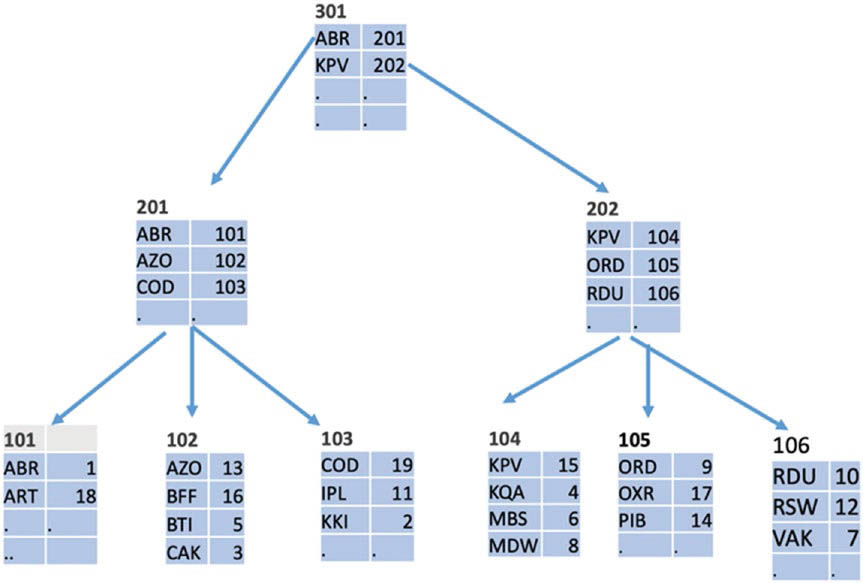
Самая распространенная индексная структура — это B-дерево. Структура B-дерева показана на рис. 3.6; коды аэропортов являются индексными ключами. Дерево состоит из иерархически организованных узлов, связанных с блоками, хранящимися на диске.
Листовые узлы (показанные на рис. 3.6 в нижней строке) содержат точно такие же записи индекса, как на рис. 3.5; эти записи состоят из индексного ключа и указателя на строку таблицы.
Нелистовые узлы (расположенные на всех уровнях, кроме нижнего) содержат записи, состоящие из наименьшего ключа (на рис. 3.5 это наименьшее буквенно-цифровое значение) в блоке, расположенном на следующем уровне, и указателя на этот блок. Все записи во всех блоках упорядочены, и в каждом блоке используется не менее половины доступного объема.
Любой поиск ключа K начинается с корневого узла B-дерева. Во время поиска по блоку будет найден самый большой ключ P, не превышающий K, и затем поиск продолжается в блоке, на который ссылается указатель, связанный с P. Поиск продолжается, пока мы не дойдем до листового узла, где указатели ссылаются на строки таблицы. Количество просмотренных при поиске узлов равно глубине дерева. Конечно, ключ K не обязательно хранится в индексе, но при поиске обнаруживается либо ключ, либо то место, где он мог быть расположен.
Рис. 3.6 ❖ Пример В-дерева
B-деревья также поддерживают поиск по диапазону (представляемый операцией between в SQL). Как только будет найдена нижняя граница диапазона, все индексные ключи диапазона можно получить последовательным сканированием листовых узлов до тех пор, пока не будет достигнута верхняя граница диапазона. Сканирование листовых узлов необходимо также для получения всех указателей, если индекс не является уникальным (то есть значение индексного ключа может соответствовать более чем одной строке).
Почему так часто используются B-деревья?
Из информатики мы знаем, что ни один алгоритм поиска не может найти индексный ключ среди N различных ключей быстрее, чем за время log N (выраженное в инструкциях процессора). Такая производительность достигается с помощью двоичного поиска по упорядоченному списку или с помощью двоичных деревьев. Однако стоимость обновлений (например, вставки новых ключей) может быть очень высока как для упорядоченных списков, так и для двоичных деревьев: вставка одной записи может привести к полной реструктуризации. Это делает обе структуры непригодными для хранения на диске.
Напротив, B-деревья можно изменять без значительных накладных расходов. Когда вы вставляете запись, реструктуризация ограничена одним блоком. Если емкость блока превышена, то он расщепляется на два блока, и обновление распространяется на верхние уровни. Даже в худшем случае количество измененных блоков не будет превышать глубины дерева.
Чтобы оценить стоимость поиска в B-дереве, нужно вычислить его глубину. Если каждый блок содержит f указателей, то количество блоков на каждом уровне в f раз больше, чем в предыдущем. Следовательно, глубина дерева, содержащего N записей, равна log N / log f. Эта формула дает количество обращений к диску, необходимое для поиска по одному ключу. Количество инструкций процессора для каждого блока ограничено, и обычно внутри блока используется двоичный поиск. Следовательно, стоимость ресурсов процессора лишь ненамного хуже теоретически возможного лучшего варианта. Размер блока в PostgreSQL составляет 8 Кбайт. В такой блок помещаются десятки индексных записей; следовательно, индекс с шестью-семью уровнями может вместить миллиарды записей.
В PostgreSOL индекс на основе B-дерева можно создать для любого порядкового типа данных; то есть такого, что из любых двух различных значений этого типа одно значение меньше другого. В эту категорию входят и пользовательские типы.
Битовые карты
Битовая карта — это вспомогательная структура данных, которая используется внутри PostgreSQL с разными целями. Битовые карты можно рассматривать как своего рода индекс: они созданы для облегчения доступа к другим структурам данных, содержащим несколько блоков. Обычно битовые карты используются для компактного представления свойств табличных данных.
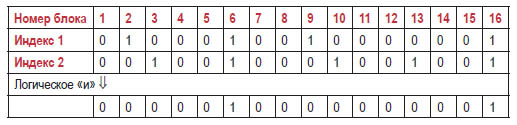
Чаще всего битовая карта содержит по одному биту для каждого блока (8192 байта). Значение бита равно 1, если блок обладает нужным свойством, и 0, если нет. На рис. 3.7 показано, как битовые карты используются для доступа к данным по нескольким индексам.
Рис. 3.7 ❖ Использование битовых карт для доступа к таблицам по нескольким индексам
Движок базы данных начинает со сканирования двух индексов и построения для каждого из них битовой карты, которая указывает на блоки с подходящими табличными строками. Эти битовые карты показаны на рисунке в строках, обозначенных «Индекс 1» и «Индекс 2». Как только битовые карты будут созданы, движок выполняет побитовую операцию «и», чтобы найти блоки, содержащие подходящие значения для обоих критериев отбора. Наконец, сканируются блоки данных, соответствующие единицам в полученной битовой карте. Таким образом, к блокам, которые удовлетворяют только одному из двух критериев, не придется обращаться.
Обратите внимание, что подходящие значения могут находиться в разных строках одного блока. Битовая карта гарантирует, что соответствующие строки не будут пропущены, но не гарантирует, что все просканированные блоки содержат подходящие строки.
Битовые карты очень компактны; однако для очень больших таблиц они могут занимать много блоков.
Другие виды индексов
PostgreSQL предлагает множество индексных структур, поддерживающих разные типы данных и разные классы условий поиска.
Хеш-индекс использует хеш-функцию для вычисления адреса индексного блока, содержащего индексный ключ. Для условия равенства этот тип индекса работает быстрее B-дерева, однако он совершенно бесполезен для запросов по диапазону. Стоимостная оценка поиска по хеш-индексу не зависит от размера индекса (в отличие от логарифмической зависимости для B-деревьев).
R-дерево поддерживает поиск по пространственным данным. Индексный ключ для R-дерева всегда представляет собой прямоугольник в многомерном пространстве. Поиск возвращает все объекты, имеющие непустое пересечение с прямоугольником запроса. Структура R-дерева похожа на структуру B-дерева; однако расщепление переполненных узлов устроено намного сложнее. R-деревья эффективны для небольшого числа измерений (обычно от двух до трех).
Другие типы индексов, доступные в PostgreSQL, полезны для полнотекстового поиска, поиска в очень больших таблицах и многого другого. Дополнительная информация по этим темам представлена в главе 14. Любой из этих индексов можно относительно легко настроить для пользовательских типов данных. Однако в этой книге мы не обсуждаем индексы по пользовательским типам.
сочетание отношений
Настоящая мощь реляционной теории и баз данных SQL основана на сочетании данных из нескольких таблиц.
В этом разделе описываются алгоритмы операций, сочетающие данные, в том числе декартово произведение, соединение, объединение, пересечение и даже группировка. Удивительно, но большинство этих операций можно реализовать с помощью практически идентичных алгоритмов. По этой причине мы обсуждаем алгоритмы, а не операции, которые они реализуют. Мы будем использовать имена R и S для входных таблиц при описании этих алгоритмов.
Вложенные циклы
Первый алгоритм предназначен для получения декартова произведения, то есть множества всех пар строк из входных таблиц. Самый простой способ вычислить произведение — перебрать строки таблицы R и для каждой строки из R перебрать строки таблицы S. Псевдокод этого простого алгоритма представлен в листинге 3.4, а графическое представление алгоритма показано на рис. 3.8.
Листинг 3.4 ❖ Псевдокод для вложенных циклов
FOR row1 IN table1 LOOP
FOR row2 IN table2 LOOP
output (row)
END LOOP
END LOOP
Время, необходимое для этого простого алгоритма, пропорционально произведению размеров таблиц ввода: rows(R)*rows(S).
Интересный теоретический факт состоит в том, что любой алгоритм, вычисляющий декартово произведение, не может работать лучше; то есть стоимость любого алгоритма будет пропорциональна произведению размеров его входов или выше. Конечно, некоторые вариации этого алгоритма могут работать лучше, чем другие, но стоимость остается пропорциональной произведению.
Небольшие модификации алгоритма вложенного цикла позволяют вычислить практически любую логическую операцию, сочетающую данные из двух таблиц. Псевдокод из листинга 3.5 реализует соединение.
Листинг 3.5 ❖ Алгоритм вложенного цикла для соединения
FOR row1 IN table1 LOOP
FOR row2 IN table2 LOOP
IF match(row1,row2) THEN
output (row)
END IF
END LOOP
END LOOP
Обратите внимание, что соединение вложенными циклами является простой реализацией абстрактного определения соединения как декартова произведения, за которым следует фильтр. Поскольку вложенный цикл обрабатывает все пары входных строк, стоимость остается той же, хотя количество выходных строк меньше, чем в случае декартова произведения.
На практике одна или обе входные таблицы являются хранимыми таблицами, а не результатом предыдущей операции. В таком случае алгоритм соединения можно комбинировать с алгоритмом доступа к данным.
Хотя стоимость обработки остается прежней, варианты алгоритма вложенного цикла в сочетании с полным сканированием выполняют вложенные циклы по блокам входных таблиц и еще один уровень вложенных циклов по строкам, содержащимся в этих блоках. Более сложные алгоритмы минимизируют количество обращений к диску, загружая несколько блоков первой таблицы (внешний цикл) и обрабатывая все строки этих блоков за один проход по таблице S .
Рис. 3.8 ❖ Алгоритм вложенного цикла
Вышеупомянутые алгоритмы могут работать с любыми условиями соединения. Тем не менее большинство соединений, которые нужны на практике, являются естественными (natural): их условие соединения требует, чтобы некоторые атрибуты таблицы R были равны соответствующим атрибутам таблицы S.
Алгоритм соединения вложенными циклами также можно комбинировать с индексным доступом к данным, если в таблице S есть индекс по атрибутам, используемым в условии соединения. Для естественных соединений внутренний цикл такого алгоритма сокращается до нескольких строк таблицы S для каждой строки таблицы R. Внутренний цикл может даже полностью исчезнуть, если индекс по таблице S уникален, например атрибут соединения таблицы S является его первичным ключом.
Алгоритм вложенного цикла с индексным доступом обычно предпочтителен, если количество строк в таблице R тоже мало. Однако доступ на основе индекса становится неэффективным, когда количество строк, подлежащих обработке, увеличивается, как описано в этой статье.
Можно формально доказать, что для декартова произведения и соединений с произвольными условиями не существует более производительного алгоритма, чем вложенные циклы. Однако важный вопрос заключается в том, имеется ли более подходящий алгоритм для каждого конкретного типа условий соединения. В следующем разделе показано, что для естественных соединений такой алгоритм есть.
Алгоритмы на основе хеширования
Результат естественного соединения состоит из пар строк из таблиц R и S, которые имеют равные значения атрибутов, по которым выполняется соединение. Идея алгоритма соединения хешированием проста: если значения равны, то и хеш-значения тоже равны.
Алгоритм разбивает обе входные таблицы по корзинам в соответствии со значениями хеш-функции, а затем независимо соединяет строки в каждой корзине. Схема этого алгоритма показана на рис. 3.9.
Рис. 3.9 ❖ Алгоритм соединения хешированием
Базовая версия алгоритма соединения хешированием включает две фазы: 1) на этапе построения все кортежи таблицы R сохраняются в корзинах согласно значениям хеш-функции;
2) на этапе проверки каждая строка таблицы S направляется в соответствующую ей корзину. Если подходящие строки таблицы R находятся в этой корзине, порождаются выходные строки.
Самый простой способ найти подходящие строки в корзине — использовать вложенные циклы (фактически нужно перебирать все строки в корзине для каждой строки таблицы S).
Две фазы алгоритма на основе хеширования показаны как отдельные физические операции в плане выполнения.
Стоимость соединения хешированием приблизительно можно оценить по следующей формуле, где JA — атрибут, по которому выполняется соединение:
cost(hash,R,S) = size(R) + size(S) + size(R)*size(S)/size(JA)
Первое и второе слагаемые в этой формуле приблизительно равны стоимости одного прохода по всем строкам таблиц R и S. Последнее слагаемое обозначает размер порождаемого результата соединения. Конечно, стоимость вывода одинакова для всех алгоритмов соединения, но нам не нужно было включать его в оценку стоимости алгоритма вложенного цикла, потому что она меньше, чем стоимость вложенных циклов.
Эта формула показывает, что алгоритм на основе хеширования значительно лучше вложенных циклов подходит для больших таблиц и большого количества различных значений атрибута соединения. Например, если атрибут соединения в одной из входных таблиц уникален, то последнее слагаемое всего лишь будет равно размеру другой таблицы.
Базовый алгоритм соединения хешированием работает, если все корзины, созданные на этапе построения хеш-таблицы, помещаются в оперативную память. Другой вариант, называемый гибридным соединением хешированием, соединяет таблицы, которые не могут поместиться в оперативную память. Гибридное соединение хешированием разделяет обе таблицы так, чтобы отдельные разделы помещались в память, а затем выполняет базовый алгоритм для каждой пары соответствующих разделов. Стоимость гибридного соединения хешированием выше, потому что разделы временно хранятся на жестком диске и обе таблицы сканируются дважды. Однако стоимость по- прежнему пропорциональна сумме размеров таблиц, а не их произведению.
Сортировка слиянием
Еще один алгоритм для естественных соединений, который называют сортировкой слиянием, показан на рис. 3.10.
Рис. 3.10 ❖ Алгоритм сортировки слиянием
На первом этапе алгоритма обе входные таблицы сортируются в порядке возрастания по атрибутам соединения.
После того как таблицы правильно упорядочены, на этапе слияния обе таблицы сканируются один раз и для каждого значения атрибута соединения вычисляется декартово произведение строк, содержащих это значение. Обратите внимание, что это произведение является необходимой частью результата соединения. Новые строки с таким же значением атрибута не могут появиться в оставшейся части входных данных, потому что таблицы упорядочены.
Стоимость фазы слияния можно выразить той же формулой, что и для соединения хешированием, то есть она пропорциональна сумме размеров входных и выходных данных. Фактическая стоимость несколько ниже, потому что нет необходимости в этапе построения хеш-таблицы.
Стоимость сортировки можно оценить следующей формулой:
size(R)*log(size(R)) + size(S)*log(size(S))
Алгоритм сортировки слиянием особенно эффективен, если одна или обе входные таблицы уже отсортированы. Это может произойти в серии соединений по одним и тем же атрибутам.
Сравнение алгоритмов
Как и в случае с алгоритмами доступа к данным, здесь нет заведомых победителей или проигравших. Любой из алгоритмов может оказаться лучше в зависимости от обстоятельств. Алгоритм вложенного цикла более универсален и лучше всего подходит для небольших соединений с использованием индексов; сортировка слиянием и хеширование более эффективны для больших таблиц, если они применимы.
выводы
Рассмотрев стоимостные модели алгоритмов, алгоритмы доступа к данным, назначение и структуру индексов и алгоритмы для более сложных операций вроде соединения, мы наконец-то набрали достаточно строительных блоков, чтобы взяться за результат работы планировщика запросов — план выполнения.
В следующей статье рассказывается, как читать и понимать планы выполнения и улучшать их.
Вас заинтересует / Intresting for you:
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Бахмад Э.А.
1
Курочкина Е.В.
1
Королева И.Ю.
1
1 ВолгГТУ Волгоградский Государственный Технический Университет
Многие библиотеки высших учебных заведений ведут базу данных публикаций сотрудников, которая поддерживается в локальной сети библиотеки. Поэтому была поставлена задача: реализовать Интернет- версию раздела «Картотека публикаций». В данном разделе должны быть сформированы различные виды фильтров поиска и отчетов по разным типам публикаций (15 видов публикаций, разбитых на 7 групп). Так как база данных была разработана под систему MS DOS и хранит данные о публикациях в формате *.dbf, было необходимо разработать алгоритм конвертирования из формата *.dbf в формат MS SQL. При реализации алгоритма конвертирования удалось в несколько раз сократить время генерации результирующей таблицы. Конечная информация хранится в таблице, работа с которой во многом упрощена, что способствует повышению эффективности и скорости обработки поисковых запросов. Также необходимо было разработать алгоритм для формирования библиографических списков, получаемых в результате поиска, в соответствии с действующим стандартом.
электронная библиотечная система
информационный поиск в базах данных
научная техническая библиотека
публикации сотрудников
библиографическое описание
электронная библиотека
1. Бахмад Э.А. Фундамент электронных библиотек / Э.А. Бахмад, И.Ю. Королева // Журнал научных публикаций аспирантов и докторантов. — 2011. — № 11. — С. 92-95.
2. Белых А.В. Нормализация объектно-ориентированных баз данных на основе N-модели данных / А.В. Белых, С.М. Ковалев, О.В. Ольховик // Известия ВолгГТУ. Серия «Актуальные проблемы управления вычислительной техники иинформатики втехнических системах» : межвуз. сб. науч. ст. / ВолгГТУ. — Волгоград, 2009. — Вып. 7. — № 12. — C. 58-61.
3. Королева И.Ю. Проектирование баз данных : учеб. пособие. — Волгоград : ВолгГТУ, 2008. — 31 с.
4. Методические указания по применению ГОСТ 7.1-2003 «Библиографическая запись. Библиографическое описание. Общие требования и правила составления» / сост. Н.Н. Аржановская; ред. И.М. Рамзина, Н.С. Заруднева. — Волгоград : ВолгГТУ, 2009. — 18 с.
5. Тейбор К. Реализация XML Web-служб на платформе Microsoft NET : пер. с англ. — М. : Вильямс, 2002. — 448 с.
Введение
База данных публикаций сотрудников высших учебных заведений представляет собой уникальную коллекцию библиографических записей. Она успешно используется университетом с целью содействия развитию научных школ и стимулирования труда профессорско-преподавательского состава, сотрудников и аспирантов.
В результате анализа процесса работы пользователей базы данных публикаций было принято решение разработать интернет-версию раздела «Картотека публикаций». В данном разделе должны быть реализованы различные виды фильтров поиска и отчетов по разным типам публикаций. Такая версия работы раздела является востребованной для всех категорий читателей и наиболее эффективна при использовании.
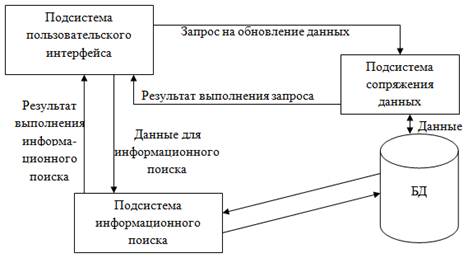
Рис. 1. Архитектура библиотеки.
Информационный обмен между компонентами системы осуществляется посредством программно-информационной сетевой среды. Подсистемы взаимодействуют между собой посредством вызова функций (рис. 1).

Рис. 2. Взаимосвязь электронного каталога со смежными системами.
Электронный каталог взаимодействует со смежными подсистемами через Internet Information Server (IIS), используя платформу Framework.NET (рис. 2) [5].
Загрузка базы данных публикаций
Изначально база данных публикаций разрабатывалась под систему MS DOS. Данные в ней хранятся в формате *.dbf в виде набора из 13 таблиц.
В связи с форматом исходной базы данных, а также большим числом записей о публикациях (около 60000) было необходимо разработать наиболее эффективный способ преобразования данных.
В результате работы был сформирован алгоритм, осуществляющий соединение с базой данных и перенос информации из DBF-таблиц в соответствующие таблицы MS SQL. Были произведены внутренние преобразования базы данных MS SQL [1]. Часть данных была получена с помощью вызовов динамически формируемых SQL-запросов. Другая часть — с помощью программной обработки в памяти, с использованием компонента DataSet для получения итоговой таблицы «_Katalog» [2].
Таблица «_Katalog» хранит сведения об источнике, достаточные для выполнения информационного поиска. Она связана с таблицей «library» полем «reg_n». В таблице «library» хранятся библиографические карточки (рис. 3).
Для преобразования информации понадобилось большое количество промежуточных таблиц, из которых была сформирована результирующая таблица. Для формирования результирующей таблицы было необходимо осуществить несколько операций объединения. Все операции объединения организованны в виде SQL-запросов, что значительно ускоряет обработку данных.
В целом алгоритм загрузки базы данных публикаций выглядит следующим образом.
- 1. Загрузка файлов DBF на сервер.
- 1.1. Подмена бита кодировки.
- 2. Подключение к базе данных на DBF-файлах.
- 3. Перенос данных из DBF в MS SQL.
- 4. Преобразования над данными для получения результирующей таблицы «_Katalog».
- 4.1. Очистка вспомогательных таблиц «KATALOG_N» и «FAK_KAF».
- 4.2. Выборка упорядоченных по индексу публикаций из таблицы «KATALOG».
- 4.3. Выборка упорядоченных по индексу авторов из таблицы «FIO_SP».
- 4.4. Проход по всем публикациям (все записи выборки из таблицы «KATALOG»).
- 4.4.1. Формирование списка авторов, кафедр и факультетов.
- 4.4.1.1. Добавление первого автора из таблицы «KATALOG» и соответствующих автору аббревиатуры кафедры и факультета в списки из таблиц «FAK» и «KAFEDRA».
- 4.4.1.2. Проход по таблице соавторов «FIO_SP», предварительно занесённой в «DataSet» и дополнение списков аббревиатурами кафедр и факультетов из таблиц «FAK» и «KAFEDRA».
- 4.4.2. Формирование таблицы «KATALOG_N» из списков авторов.
- 4.4.3. Формирование таблицы «_FAK_KAF» из списков кафедр и факультетов.
- 4.5. Формирование таблицы «KATALOG_N2» (SQL-запросом), путём объединения таблиц «KATALOG» и сформированной таблицы «KATALOG_N».
- 4.6. Формирование результирующей таблицы «_KATALOG» (SQL-запросом), путём объединения таблиц «KATALOG_N2» и сформированной таблицы «_FAK_KAF».

Рис. 3. Структура БД публикаций.
В результате реализации данного алгоритма удалось в несколько раз сократить время генерации результирующей таблицы, а также снизить временные затраты сервера.
Алгоритм формирования библиографического списка
При выполнении поиска публикаций в базе данных необходимо сначала сформировать его библиографическое описание. Оно создается по ГОСТ 7.1 — 2003 и хранится в отдельной таблице. Такой ход необходим для увеличения производительности системы при поиске [1]. Если результатом поиска будет более 100 документов, и каждый из них требует библиографического описания, то при создании библиографических карточек «на лету» время, затрачиваемое на выполнение одного запроса, существенно возрастает.
Создание библиографического описания (БО) полнотекстового документа выполняется по следующему алгоритму [4].
- 1. Если текущий документ является монографией, учебником или учебным пособием, то
- 1.1. Если число авторов <=3, то
- 1.1.1. Если «ФИО авторов» != «», то
БО = «ФИО авторов» + «.»
- 1.1.2. Если «Название книги» != «», то
БО = БО + «Название книги» + «:»
- 1.1.3. Если «Сведения, поясняющие название (учебник, пособие, методические материалы)» != «», то
БО = БО + «Сведения, поясняющие название (учебник, пособие, методические материалы)» + «/»
- 1.2. Если число авторов >3, то
- 1.2.1. Если «Название книги» != «», то
БО = «Название книги» + «:»
- 1.2.2. Если «Сведения, поясняющие название (учебник, пособие, методические материалы)» != «», то
БО = БО + «Сведения, поясняющие название (учебник, пособие, методические материалы)» + «/»
- 1.2.3. Если «ФИО авторов» != «», то
БО = БО + «ФИО авторов» + «;»
- 1.3. Если «ФИО редактора, переводчика, название организации, ответственной за подготовку книги» != «», то
БО = БО + «ФИО редактора, переводчика, название организации, ответственной за подготовку книги» + «.»
- 1.4. Если «Повторность издания (2-е издание, переработанное и дополненное)» != «», то
БО = БО + «-» + «Повторность издания (2-е издание, переработанное и дополненное)»
- 1.5. Если «Место издания» != «», то
БО = БО + «-» + «Место издания» + «:»
- 1.6. Если «Название издательства» != «», то
БО = БО + «Название издательства» + «,»
- 1.7. Если «Год издания» != «», то
БО = БО + «Год издания» + «.»
- 1.8. Если «Общее количество страниц книги» != «», то
БО = БО + «-» + «Общее количество страниц книги» + «.»
- 2. Если текущий документ является статьей из российского или зарубежного журнала, то
- 2.1. Если число авторов <=3, то
- 2.1.1. Если «ФИО авторов» != «», то
БО = «ФИО авторов» + «.»
- 2.1.2. Если «Название статьи» != «», то
БО = БО + «Название статьи» + «//»
- 2.2. Если число авторов >3, то
- 2.2.1. Если «Название статьи» != «», то
БО = «Название статьи» + «/»
- 2.2.2. Если «ФИО авторов» != «», то
БО = БО + «ФИО авторов» + «//»
- 2.3. Если «Название журнала» != «», то
БО = БО + «Название журнала» + «.»
- 2.4. Если «Год издания» != «», то
БО = БО + «-» + «Год издания» + «.»
- 2.5. Если «Номер журнала, год или номер выпуска» != «», то
БО = БО + «-» + «Номер журнала, год или номер выпуска» + «.»
- 2.6. Если «Страницы, на которых опубликована статья» != «», то
БО = БО + «-» + «Страницы, на которых опубликована статья» + «.»
- 3. Если документ является статьей из сборника, тезисом доклада или известиями, то
- 3.1. Если число авторов <=3, то
- 3.1.1. Если «ФИО авторов» != «», то
БО = «ФИО авторов» + «.»
- 3.1.2. Если «Название статьи» != «», то
БО = БО + «Название статьи» + «//»
- 3.2. Если число авторов >3, то
- 3.2.1. Если «Название статьи» != «», то
БО = «Название статьи» + «/»
- 3.2.2. Если «ФИО авторов» != «», то
БО = БО + «ФИО авторов» + «//»
- 3.3. Если «Название сборника» != «», то
БО = БО + «Название сборника» + «.»
- 3.4. Если «Место издания» != «», то
БО = БО + «-» + «Место издания» + «,»
- 3.5. Если «Год издания» != «», то
БО = БО + «Год издания» + «.»
- 3.6. Если «Страницы, на которых опубликована статья» != «», то
БО = БО + «-» + «Страницы, на которых опубликована статья» + «.»
Алгоритм разбора строки запроса для поиска в базе данных публикаций
Для выполнения поиска в базе данных публикаций необходимо было разработать алгоритм разбора строки записи. Строка записи имеет вид: «name = Название документа <> author = Автор <> PlaceIzd = Место издания <> Year = Год издания <> Str = Количество страниц».
Для разбора строки была использована функция Split [3].
Функция Split(«title», «LogOP», A)
Title — Поле, соответствующее определенной части запроса;
LogOP — логический оператор;
А — элемент массива.
Пока текущий символ строки «a» не равен «», делать
Если текущий символ строки «a» не равен «;», то
tmp=title(i)
Иначе
res = res & Title & » like ‘%» & tmp & «%'»
res = res & » » & LogOP & » »
Возвращаем преобразованную строку
Split = res
SQL-запрос формируется так.
- 1. Разбираем строку записи:
- 1.1. Создаем массив «a» из 5 элементов
- 1.2. Пока количество символов в строке запроса не равно 0, делать
- 1.2.1. Если текущее поле запроса == «name», то
- 1.2.1.1. a(1) = Название документа
- 1.2.1.2. a(1) = Split(«BookValue.FieldValue», «AND», a(1))
- 1.2.2. Если текущее поле запроса == «author «, то
- 1.2.2.1. а(2) = Автор
- 1.2.2.2. a(2) = Split(«BookValue.FieldValue», «AND», a(2))
- 1.2.3. Если текущее поле запроса == «PlaceIzd «, то
- 1.2.3.1. а(3) = Место издания
- 1.2.3.2. a(3) = Split(«BookValue.FieldValue», «AND», a(3))
- 1.2.4. Если текущее поле запроса == » Year», то
- 1.2.4.1. а(4) = Год издания
- 1.2.4.2. a(4) = Split(«BookValue.FieldValue», «AND», a(4))
- 1.2.5. Если текущее поле запроса == » Str», то
- 1.2.5.1. а(5) = Количество страниц
- 1.2.5.2. a(5) = Split(«BookValue.FieldValue», «AND», a(5))
- 2. Составляем строку запроса:
- 2.1. Пока число элементов в массиве «а» не равно 5, делать
- 2.1.1. Если текущий элемент массива «а» не равен «», то
- 2.1.1.1. Если строка запроса не равна «», то
- 2.1.1.1.1. selSQL = selSQL & » OR «
- 2.1.1.1.2. Составляем строку запроса selSQL = selSQL & » ( » & a(i) & » ) «
Заключение
Практическая ценность работы заключается в предоставлении информационного поиска в базе данных публикаций посредством Интернета и в максимальном повышении эффективности этого поиска.
Рецензенты:
- Лукьянов В.С., д.т.н., профессор, зав. кафедрой «ЭВМ и системы», Волгоградский государственный технический университет, г. Волгоград.
- Камаев В.А., д.т.н., профессор, зав. кафедрой «САПР и ПК», Волгоградский государственный технический университет, г. Волгоград.
Библиографическая ссылка
Бахмад Э.А., Курочкина Е.В., Королева И.Ю. РЕАЛИЗАЦИЯ АЛГОРИТМА ОБРАБОТКИ ДАННЫХ ДЛЯ ПРЕДОСТАВЛЕНИЯ ЭФФЕКТИВНОГО ИНФОРМАЦИОННОГО ПОИСКА В БАЗЕ ДАННЫХ ПУБЛИКАЦИЙ // Современные проблемы науки и образования. – 2012. – № 2.
;
URL: https://science-education.ru/ru/article/view?id=5874 (дата обращения: 27.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Уровень сложности
Средний
Время на прочтение
6 мин
Количество просмотров 1.6K
Приветствую Вас, уважаемые читатели! Сегодня хочу поделиться с вами информацией об эффективном алгоритме для обработки больших баз данных MLM-структур, который усовершенствует подход к анализу и управлению данными в многоуровневом маркетинге.
Введение
Многоуровневый маркетинг (MLM) является популярной бизнес-моделью, основанной на сети дистрибьюторов для роста компании. С расширением сети управление клиентами MLM и их взаимоотношениями становится все более сложным, что делает важным поиск эффективного решения для управления постоянно растущим объемом данных. В этой статье мы рассмотрим инновационный подход к обработке больших баз данных MLM-структур, который позволяет оптимизировать анализ и управление данными.
Традиционные методы обработки данных vs представленный алгоритм
Традиционные методы обработки данных в MLM, такие как рекурсивные функции, часто оказываются медленными и неэффективными, особенно при работе с большими объемами данных. Это может привести к длительным задержкам в обработке информации, что негативно сказывается на оперативности и эффективности работы компании.
Допустим, у нас есть бинарная MLM-структура с 10 миллионами пользователей и 23 уровнями. Стандартный подход к обработке таких структур заключается в использовании рекурсивных функций, что может занять значительное время и ресурсы сервера.
Например, для выборки всех пользователей на 23-м уровне с использованием рекурсии. Сложность рекурсии оценивается как O(n * h), где n — количество пользователей на уровне, а h — высота дерева. В данном случае, это равно 2^23 * 24 ≈ 201,326,592 операций. (в которые входят и SQL запросы), что займет очень много времени, даже на мощных серверах. Компания которая обращалась ко мне для оптимизации базы данных, расчеты проводила раз в день по ночам чтобы не прерывать основную работу. Ощутимые задержки вычислений начинаются уже после 50000 пользователей даже на оптимизированной базе данных.
Проблема решилась созданием дополнительной таблицы, в которую начал записывать древовидную структуру в следующем виде:
id |iduser| id_rek| road | level
---|------|-------|-------------|-----
1 | 1 | 0 | |1| | 1
2 | 2 | 1 | |1|2| | 2
3 | 3 | 1 | |1|3| | 2
4 | 4 | 2 | |1|2|4| | 3
5 | 5 | 2 | |1|2|5| | 3
6 | 6 | 3 | |1|3|6| | 3
Теперь мы основную нагрузку перекладываем на SQL запросы (запрос с LIKE не самый эффективный, но по сравнению с рекурсивными методами значительно выигрывает), которые выполняются значительно быстрее и нагляднее, пример на php, одним запросом находит всех последователей пользователя id-3 в порядке иерархии, тогда как рекурсией нам бы пришлось с корневого id обойти всех пользователей.
<?php
class MLMTree {
private $db;
public function __construct($db) {
$this->db = $db;
}
public function getAllDescendants($rootUserId) {
$query = "SELECT * FROM users WHERE road LIKE CONCAT('%|', :root_user_id, '|%') AND id != :root_user_id ORDER BY level";
$stmt = $this->db->prepare($query);
$stmt->bindValue(':root_user_id', $rootUserId, PDO::PARAM_INT);
$stmt->execute();
return $stmt->fetchAll(PDO::FETCH_ASSOC);
}
}
// Пример использования
$db = new PDO('mysql:host=localhost;dbname=mlm_database;charset=utf8', 'username', 'password');
$mlmTree = new MLMTree($db);
$rootUserId = 3;
$descendants = $mlmTree->getAllDescendants($rootUserId);
print_r($descendants);
?>Пример класса пользователя на php, на его основе Вы можете создать свой вариант, по данной методике можно реализовать практически все варианты и виды MLM структур.
<?php
class User
{
private $pdo;
public function __construct($pdo)
{
$this->pdo = $pdo;
}
public function find($userId)
{
$sql = "SELECT * FROM users WHERE id = :id";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id' => $userId]);
return $stmt->fetch(PDO::FETCH_ASSOC);
}
public function create($data)
{
$sql = "INSERT INTO users (username, email, password, id_rek) VALUES (:username, :email, :password, :id_rek)";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([
':username' => $data['username'],
':email' => $data['email'],
':password' => $data['password'],
':id_rek' => $data['id_rek']
]);
$userId = $this->pdo->lastInsertId();
// Create corresponding tree entry
$this->createTreeEntry($userId, $data['id_rek']);
}
private function createTreeEntry($userId, $id_rek)
{
if ($userId == 1) {
$sql = "INSERT INTO tree (id_user, id_rek, col, lvl, road) VALUES (1, 0, 0, 1, '|1|')";
$stmt = $this->pdo->prepare($sql);
$stmt->execute();
} else {
$sql = "SELECT * FROM tree WHERE road LIKE CONCAT('%|', :id_rek, '|%') ORDER BY lvl, col ASC";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id_rek' => $id_rek]);
$treeRow = $stmt->fetch(PDO::FETCH_ASSOC);
if ($treeRow) {
$road = $treeRow['road'] . $userId . "|";
$lvl = count(explode("|", $road)) - 2;
$sql = "INSERT INTO tree (id_user, id_rek, col, lvl, road) VALUES (:id_user, :id_rek, 0, :lvl, :road)";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([
':id_user' => $userId,
':id_rek' => $id_rek,
':lvl' => $lvl,
':road' => $road
]);
$sql = "UPDATE tree SET col = col + 1 WHERE id_user = :id_rek";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id_rek' => $id_rek]);
}
}
}
public function delete($userId)
{
$user = $this->find($userId);
if ($user) {
$sql = "DELETE FROM users WHERE id = :id";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id' => $userId]);
$this->deleteTreeEntry($userId, $user['id_rek']);
$this->updateRoadsAfterDeletion($userId, $user['id_rek']);
$this->updateRekIdAfterDeletion($userId, $user['id_rek']);
}
}
private function deleteTreeEntry($userId, $id_rek)
{
$sql = "DELETE FROM tree WHERE id_user = :id_user";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id_user' => $userId]);
$sql = "UPDATE tree SET col = col - 1 WHERE id_user = :id_rek";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id_rek' => $id_rek]);
}
private function updateRoadsAfterDeletion($userId, $id_rek)
{
$sql = "UPDATE tree SET road = REPLACE(road, '|$userId|', '|'), lvl = lvl - 1 WHERE road LIKE '%|$userId|%'";
$stmt = $this->pdo->prepare($sql);
$stmt->execute();
}
private function updateRekIdAfterDeletion($userId, $id_rek)
{
$sql = "UPDATE users SET id_rek = :id_rek WHERE id_rek = :user_id";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id_rek' => $id_rek, ':user_id' => $userId]);
$sql = "UPDATE tree SET id_rek = :id_rek WHERE id_rek = :user_id";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':id_rek' => $id_rek, ':user_id' => $userId]);
}
public function getUsersByLevel($level)
{
$sql = "SELECT tree.*, users.username, users.email, users.password FROM tree
JOIN users ON tree.id_user = users.id
WHERE tree.lvl = :level";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':level' => $level]);
return $stmt->fetchAll(PDO::FETCH_ASSOC);
}
public function getUsersByRekId($rekId)
{
$sql = "SELECT * FROM tree WHERE id_rek = :rek_id";
$stmt = $this->pdo->prepare($sql);
$stmt->execute([':rek_id' => $rekId]);
return $stmt->fetchAll(PDO::FETCH_ASSOC);
}
// ... другие методы, если необходимо ...
}
?>Преимущества нового алгоритма
-
Ускорение обработки данных: благодаря использованию параллельной древовидной структуры, алгоритм позволяет значительно ускорить процесс обработки информации, сокращая время выполнения запросов.
-
Масштабируемость: новый алгоритм легко масштабируется и может быть применен для работы с базами данных различного размера, от небольших до очень больших.
-
Упрощение процесса управления данными: новый алгоритм предоставляет интуитивно понятный и организованный способ анализа и управления данными MLM-структур, что облегчает работу администраторов и менеджеров.
-
Повышение точности: благодаря оптимизации алгоритма, обработка данных становится более точной, что позволяет избегать ошибок и противоречий в информации.
-
Экономия ресурсов: использование нового алгоритма позволяет снизить нагрузку на сервера и сетевые ресурсы, что сказывается положительно на стабильности системы и снижает затраты на обслуживание.
Подведем итоги
Мы рассмотрели эффективный алгоритм обработки больших баз данных MLM структур и привели примеры его реализации на PHP. Этот подход позволяет значительно сократить время обработки данных и упростить управление MLM структурами.
Вместо использования рекурсии и тяжеловесных запросов, мы предложили способ работы с данными на основе построенного готового пути, что позволяет ускорить выборку информации и облегчить нагрузку на сервер.
Надеемся, что данная статья поможет вам в решении задач, связанных с MLM структурами и позволит оптимизировать процессы ваших проектов. В случае возникновения дополнительных вопросов или предложений, буду рад вашим комментариям и обсуждениям. Удачи вам в реализации вашего MLM проекта!
Исходные коды примеров лежат на https://github.com/infosave2007/fastmlm
Когда речь заходит о реляционных базах данных, становится очевидно, что информации по этой теме не хватает. Базы данных используются повсеместно, и они очень разные — от небольшой, но функциональной SQLite до мощной Teradata. И тем не менее, достойных, подробных статей, объясняющих как они работают, практически нет.
Можете погуглить “как работают реляционные базы данных”, и увидите, как мало результатов поиска. Да и те статьи, что есть, довольно короткие. Если же погуглить что-нибудь из последних трендов (большие данные, базы данных типа NoSQL или JavaScript), вы найдете в разы больше хороших источников информации.
Значит ли это, что реляционные базы данных устарели, и писать о них вне университетских курсов и научных статей уже не модно?
Я разработчик и ненавижу использовать то, чего не понимаю. Раз базы данных используются в разработке вот уже 40 лет, значит, на то есть весомая причина. За эти годы я потратил сотни часов, чтобы понять эти странные ящики пандоры, которые использую каждый день. На самом деле, реляционная база данных – интересная концепция, основанная на полезных, повторяющихся идеях. Если вы всегда хотели углубить ваши знания и понимание баз данных, но не хватало времени или желания разбираться в столь обширной теме, эта статья вам понравится.
Хотя название говорит само за себя, уточню: для понимания данной статьи вам необходимо знать, как написать простой запрос на соединение и базовый CRUD запрос. Только и всего. Всё остальное я объясню.
Начну с таких основ информатики, как временная сложность алгоритма. Наверное, многие из вас эту тему терпеть не могут, но без неё вы не сможете понять всю гениальность баз данных. Поскольку тема большая, я сосредоточусь на том, что считаю наиболее важным: как база данных обрабатывает SQL-запрос. Мы рассмотрим самые простые концепции, так что к концу статьи у вас должно сложиться полное представление о том, что такое БД.
Статья техническая и длинная, в ней много говорится про алгоритмы и структуры данных — не торопитесь дочитать до конца. Какие-то моменты сложнее понять, и пропуская их при первом прочтении, у вас всё равно должна сложиться полноценная картина.
Статья условно разделена на три части:
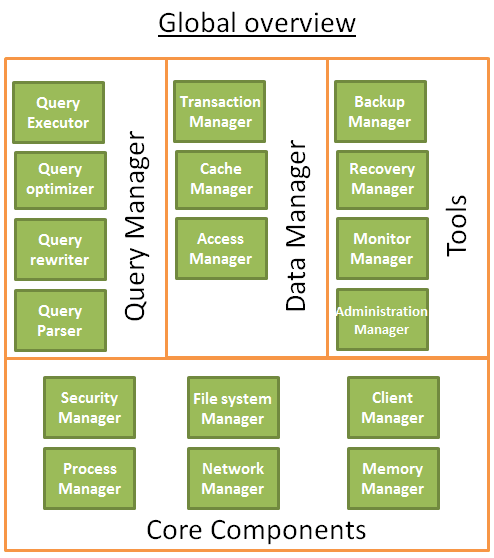
- Обзор низкоуровневых и высокоуровневых компонентов БД;
- Разбор процесса оптимизации запросов;
- Управление транзакциями и буферным пулом БД.
Начнём с азов
Давным-давно (в другой галактике…) разработчикам приходилось запоминать количество совершаемых операций. Они знали наизусть свои алгоритмы и структуры данных, поскольку не могли позволить себе тратить память и мощности своих довольно медленных компьютеров на подобные задачи.
В этой части, я буду напоминать вам о некоторых концепциях из тех далёких времён, поскольку они крайне важны для понимания баз данных. Также мы рассмотрим понятие индекс базы данных.
Временная сложность
O(1)) vs O(n^2)
Сегодня временная сложность алгоритмов не волнует почти никаких разработчиков. Но когда вы начинаете работать с большим объемом данных, или если вам приходится бороться за каждую лишнюю миллисекунду — при работе с базами данных вы рано или поздно столкнётесь и с тем, и с другим, — понимание данной концепции становится очень полезным. Не буду слишком долго утомлять вас разглагольствованиями, только о главном — это поможет нам впоследствии понять принцип оптимизации с учётом затрат.
Временная сложность определяет, сколько времени алгоритм будет обрабатывать конкретный объем данных. Для математического обозначения используется заглавная О и функция, вычисляющая, сколько операций необходимо алгоритму для заданного количества данных.
Проще говоря, формула вида O(некая_функция()) расшифровывается так: для определённого количества данных алгоритму требуется некая_функция(количество_данных) операций.
И важно здесь не количество входных данных, а то, как увеличивается количество необходимых операций с увеличением количества данных. Временная сложность не расчитывает точное число операций, но даёт довольно чёткое представление.
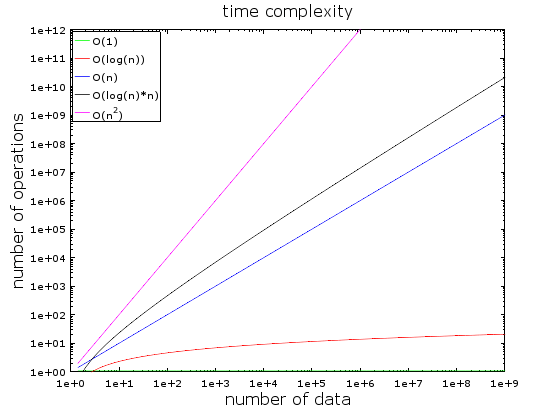
На этом графике вы видите разные временные сложности. Для его создания я использовал логарифмическую шкалу — количество данных резко возрастает от 1 до 1 миллиарда.
Мы видим, что:
- Значение О (1) остается неизменным (поэтому она называется постоянной сложностью);
- Значение О (log(n)) остаётся маленьким даже при больших объёмах данных;
- Хуже всего показатель сложности О (n^2), где количество необходимых операций быстро
возрастает; - Значения двух оставшихся кривых также быстро растут.
Разберём примеры подробнее:
При небольшом объёме данных разницы между О(1) и O(n^2) практически нет. Предположим, у вас есть алгоритм, который должен обработать 2000 элементов.
- Алгоритму O(1) потребуется всего 1 операция;
- Алгоритму O(log(n)) — 7 операций;
- Алгоритм O(n) обойдётся вам в 2 000 операций;
- Алгоритм O(n*log(n)) – уже в 14 000 операций;
- Наконец, алгоритму O(n^2) потребуется 4 000 000 операций.
Разница между O(1) и O(n^2) кажется огромной (4 миллиона), но на самом деле это всего около 2 миллисекунд — и моргнуть не успеете. Современные процессоры способны выполнять сотни миллионов операций в секунду. Поэтому для большинства IT-проектов производительность и оптимизация не являются критическими проблемами.
Однако, когда вы сталкиваетесь с огромным количеством данных, эти знания вам очень пригодятся. Допустим, теперь алгоритм должен обработать 1 000 000 элементов (не так уж много для базы данных):
- Алгоритму O(1), как и прежде, потребуется 1 операция;
- Алгоритму O(log(n)) — 14 операций;
- Алгоритм O(n) займёт 1 000 000 операций;
- Алгоритм O(n*log(n)) – 14 000 000 операций;
- Алгоритм O(n^2) — 1 000 000 000 000 операции.
Точно не считал, но навскидку за время выполнения O(n^2) вы успеете отойти выпить чашку кофе (возможно, две). Добавьте к изначальному количеству элементов ещё один ноль — и на время выполнения последнего алгоритма можно лечь поспать.
Если ближе к практике, можно привести такие примеры:
- Поиск элемента в правильной хеш-таблице занимает O(1) операций;
- Поиск в сбалансированном дереве выдаст результат за O(log(n)) операций;
- Поиск в массиве — пример O(n);
- Лучшие алгоритмы сортировки имеют O(n*log(n)) временную сложность;
- Плохие алгоритмы сортировки — сложность O(n^2).
Временная сложность бывает среднестатистической, а также наилучший и наихудший сценарии. Чаще всего, подразумевается худший сценарий.
Также при выполнении алгоритма учитывается потребление памяти и производительность при чтении и записи на диск.
Конечно, есть сложности и похлеще n^2:
- n^4: это кошмар! я буду упоминать некоторые алгоритмы с такой сложностью;
- 3^n: просто ад; мы встретим один такой алгоритм примерно в середине статьи (и, он, к слову, используется во многих БД);
- факториальный n: результатов вы не дождётесь никогда, даже при небольшом объёме данных;
- n^n: если вы используете алгоритмы такой сложности, возможно, стоит спросить себя, а стоит ли мне дальше работать в IT-сфере.
Я не дал точного определения “большого О”, только общую идею. Изучить подробнее можете в этой Wiki статье.
Сортировка методом слияния
Что вы делаете, когда нужно отсортировать коллекцию? Вызываете функцию sort()? Окей, но для работы с базами данных хорошо бы понимать, как эта функция работает.
Есть несколько хороших алгоритмов сортировки, я остановлюсь на наиболее важном: сортировка методом слияния. Возможно, сейчас вы не очень понимаете, чем так полезна сортировка данных, но когда мы поговорим об оптимизации запросов, вы поймёте. К тому же, понимание этого алгоритма поможет нам позднее понять типичную для БД операцию объединения, которую ещё называют объединение слиянием.
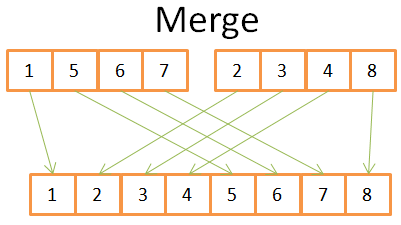
Слияние
Как и многие полезные алгоритмы, сортировка методом слияния основана на хитрости: слияние двух отсортированных массивов размера N/2 в отсортированный массив из N-элементов займёт всего N операций. Эта операция называется слиянием.
Посмотрим на простом примере, что это значит:
По рисунку видно, что для построения отсортированного массива из 8 элементов нам нужно перебрать два массива из 4х элементов всего 1 раз.
Поскольку оба массива из 4 элементов уже отсортированы, мы:
- сравниваем два текущих элемента в 2 массивах (текущий = первый, анализируемый впервые);
- наименьший из них помещаем в массив из 8 элементов;
- и переходим к следующему элементу в массиве, откуда был взят наименьший элемент;
повторяем действия 1-2-3, пока не дойдём до последнего элемента в одном из массивов. Затем уже берём оставшиеся элементы другого массива и помещаем их в наш конечный массив из 8 элементнов.
Оба массива из 4 элементнов изначально отсортированы, поэтому не приходится возвращаться в них.
Таким образом, сортировка методом слияния разбивает задачу на небольшие задачи, и находит результат этих более мелких задач, чтобы в итоге получить результат исходной задачи (такой вид алгоритмов можно назвать «разделяй и властвуй»). Если вдруг алгоритм всё равно вам не понятен, не расстраивайтесь, я не понял его с первого раза. Можете дополнительно ознакомиться со статьёй в википедии.
Я условно разделяю алгоритм на две стадии:
- стадию деления, когда массив делится на более мелкие массивы;
- стадию сортировки, когда небольшие массивы соединяются (слиянием), чтобы сформировать один общий массив.
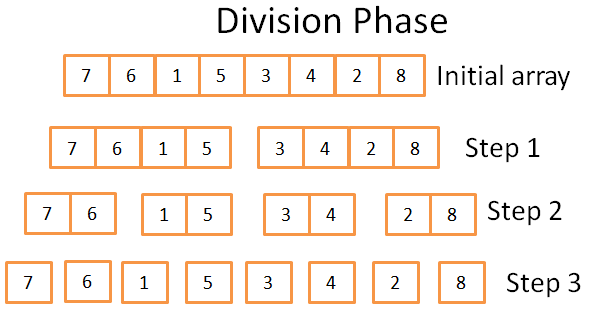
Стадия деления
На стадии деления данный массив разбивается на унитарные массивы в 3 шага. Формальное число шагов можно обозначить как log(N) (т.к. N = 8, log(N) = 3).
Откуда мне это известно?Я гений! Шучу, одним словом — математика. Идея заключается в том, что каждый шаг делит размер исходного массива на 2. Количество шагов отражает, сколько раз можно разделить исходный массив на два. Это определение логарифма (по основанию 2).
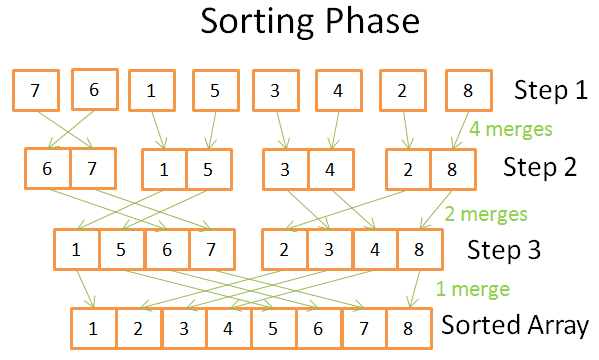
Стадия сортировки
На стадии сортировки мы начинаем с унитарных массивов. На каждом шаге выполняем несколько слияний, и общее число операций составляет N = 8:
Первый этап: 4 слияния, каждое по 2 операции;
Второй этап: 2 слияния, 4 операции каждое;
На третьем этапе: 1 слияние в 8 операций.
Этапов всего log(N), то есть N * log(N) операций.
Преимущества сортировки методом слияния
Так почему же этот алгоритм такой особенный?
Во-первых, его можно изменить, уменьшив тем самым объем занимаемой памяти, так что вам не нужно создавать новые массивы, а лишь непосредственно изменять исходный массив.
Такие алгоритмы называются локальными.
Во-вторых, вы можете изменить его и использовать одновременно дисковое пространство и небольшой объем памяти, без затратных операций чтения и записи на диск. Идея в том, чтобы загружать в память только те части, которые в данный момент обрабатываются. Это очень актуально, когда вам нужно отсортировать многогигабайтную таблицу с буфером памяти лишь 100 Мб. Такие алгоритмы называются внешней сортировкой.
К тому же, можно сделать так, чтобы алгоритм работал на нескольких процессах / потоках / серверах. Например, распределенная сортировка слиянием — один из ключевых компонентов Hadoop (фреймворк для больших данных).
В общем, этот алгоритм может превратить свинец в золото (правда ведь!).
Данный алгоритм сортировки используется в большинстве баз данных (если не во всех), но он не единственный. Если хотите знать больше, можете прочитать эту научную работу, в которой рассматриваются плюсы и минусы основных алгоритмов сортировки в БД.
Массив, дерево и хеш-таблица
Теперь, когда вы знаете о временной сложности и сортировке, я должен рассказать вам о 3 структурах данных. Это важно, так как это основы современных баз данных. Также рассмотрим понятие индекс базы данных.
Массив
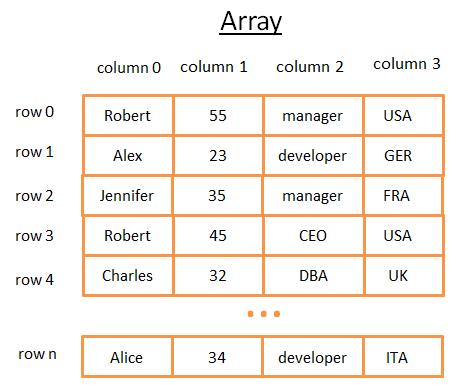
Двумерный массив является простой структурой данных. Таблица может рассматриваться как массив. Например:
Этот двумерный массив представляет собой таблицу со строками и столбцами. Каждая строка представляет собой предмет. Столбцы — признаки, описывающие предметы. Каждый столбец хранит определенный тип данных (целое число, строка, дата …). Для хранения и визуализации данных это удобно, но когда вам нужно найти конкретное значение — это кошмар.
Например, если вам потребуется найти всех людей, работающих в Великобритании, вы должны анализировать каждую строку, чтобы узнать, из Великобритании ли этот человек. Это займёт у вас N операций (где N — число строк), что не плохо, но могло быть и быстрее? Тут-то в игру вступают деревья.
К слову, для более эффективного хранения таблиц большинство современных баз данных обеспечивают расширенные массивы, как таблицы куч или таблицы индексов. Но это не меняет проблемы быстрого поиска по конкретному условию в группе столбцов.
Дерево и индекс БД
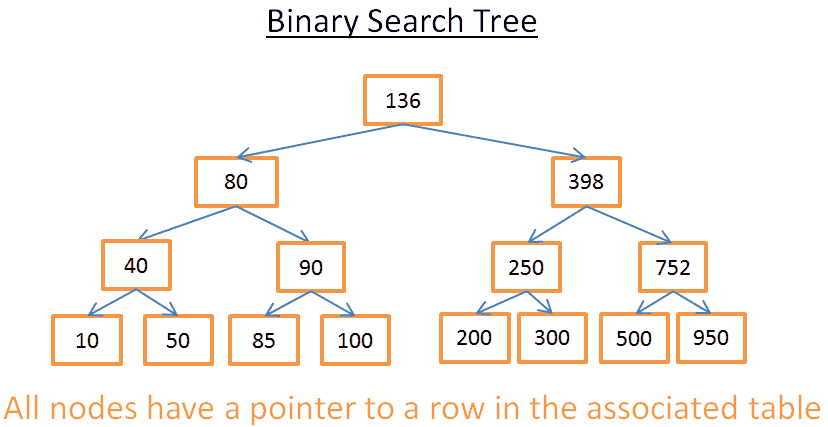
Двоичное дерево поиска — это бинарное дерево с особыми свойствами, ключи в каждом узле должны быть больше всех ключей, хранящихся в левом поддереве, и меньше всех ключей, хранящихся в правом поддереве.
Наглядный пример:
Это дерево состоит из N = 15 элементов. Допустим, я ищу 208:
- Начинаем с корня, у которого ключ 136. Поскольку 136 < 208, ищем в правом поддереве узла 136;
- 398 > 208, поэтому далее ищем в левом поддереве узла 398;
- 250 > 208, поэтому перемещаемся в левое поддерево узла 250;
- 200 < 208, соответственно, надо искать в правом поддереве узла 200. Но 200 не имеет правого поддерева, то есть значение не существует (если бы существовало, оно должно было бы находиться в правом поддереве 200).
Допустим, теперь я ищу 40:
- Начинаем с корня, у которого ключ 136. Поскольку 136 > 40, ищем в левом поддереве узла 136;
- 80 > 40, поэтому далее ищем в левом поддереве узла 80;
- 4 0 = 40, узел существует. Извлекаем id строки внутри узла (на картинке его нет) и ищем в таблице строку с данным id.
Зная id строки, я точно знаю, где именно в таблице находятся нужные данные и могу сразу же их получить.
В итоге, оба поиска заняли количество операций, равных количеству уровней внутри дерева. Если вы внимательно читали раздел о сортировке методом слияния, то увидите, что количество уровней — log(N). Таким образом, сложность поиска — log(N).
Назад к нашей проблеме
Но это всё довольно абстрактные вещи, давайте вернемся к нашей проблеме. Вместо глупого целого числа теперь страну в предыдущей таблице обозначает строка. Предположим, у вас есть дерево, которое содержит столбец таблицы “страна”:
Если задача — узнать, кто работает в Великобритании, вы ищете в дереве узел, представляющий Великобританию, внутри этого узла вы найдете расположение строк работников из Великобритании. Если вы напрямую используете массив, этот поиск потребует log(N) операций (вместо N операций). Это и есть индекс базы данных.
Вы можете построить дерево индекса для любой группы столбцов (строка, целое число, две строки, дата …) при условии, что у вас есть функция для сравнения ключей (т.е. группа столбцов), так что вы можете установить порядок среди ключей (что характерно для большинства БД).
Индекс B+-деревьев
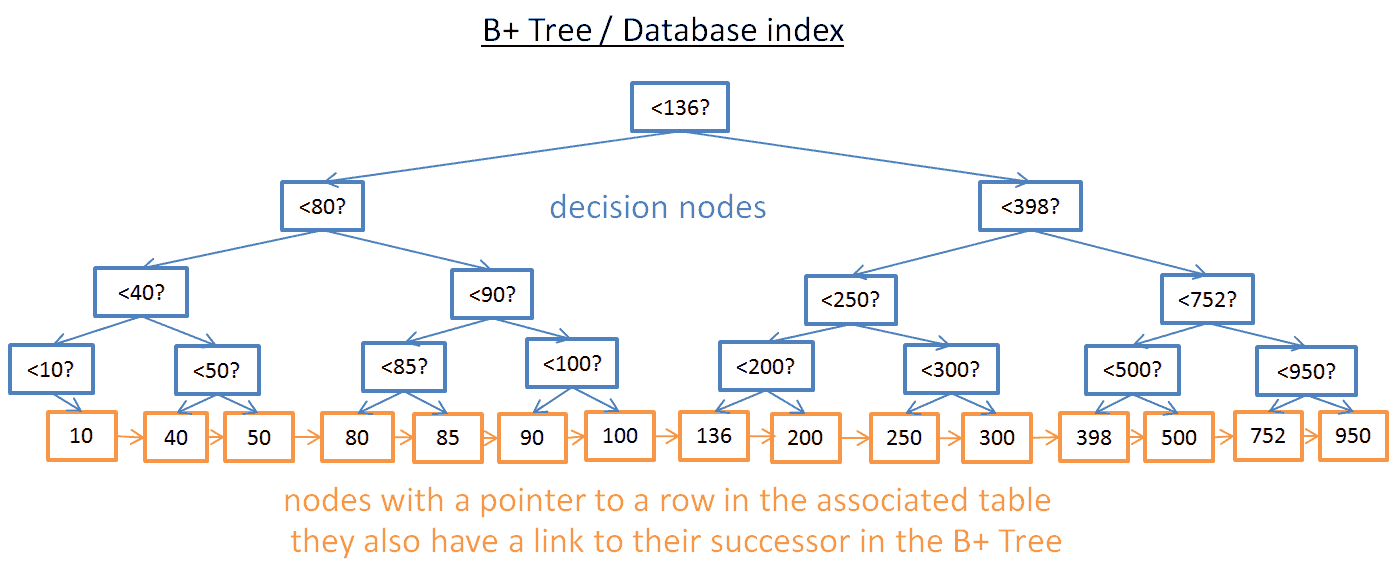
Поиск определённого значения в таком дереве работает неплохо, но проблемы начинаются, когда нужно найти несколько элементов между двумя данными значениями. Это займёт O(N) времени, поскольку вам придется анализировать каждый узел в дереве и проверять, есть ли он между этими двумя значениями (например, обход дерева с порядковой выборкой). Кроме того, эта операция негавтино сказывается на производительности, поскольку вы обрабатываете всё дерево целиком. Неплохо бы найти более эффективный способ запроса диапазона. Для этого современные базы данных используют модифицированную версию дерева под название B+. В таком дереве только нижние узлы (листья) хранят информацию (расположение строк в соответствующей таблице), остальные узлы во время поиска приводят к нужному узлу.
Как видите, узлов больше (в два раза). Действительно, это дополнительные, «решающие» узлы, которые помогут найти нужный узел (хранящий расположение строк в соответствующей таблице). Но сложность поиска все еще O(log(N)) (добавлен лишь ещё один уровень). Большая разница в том, что самые нижние узлы связаны с вышестоящими преемниками.
В таком B+-дереве, если вы ищете значения между 40 и 100:
- Вы просто должны искать 40 (или ближайшие значения после 40, если 40 не существует), как мы делали в предыдущем примере с деревом;
- Затем получить преемников 40, используя прямые ссылки на них, пока не достигнете 100.
Допустим, вы нашли М преемников и дерево имеет N узлов. Поиск конкретного узла займёт log(N) времени, как и в предыдущем дереве. Но, как только у вас есть этот узел, вы находите в M операций М преемников со ссылками на их преемников. Этот поиск стоит всего М+log(N) операций, а не N операций, как в примере с предыдущим деревом. Кроме того, вам не нужно читать полное дерево (только М + log(N) узлов), то есть меньше используется диск. Если значение M невелико (например, 200 строк), а N большое (1 000 000 строк), разница будет существенной.
Но теперь появились новые проблемы! Если добавить или удалить строку в базе данных и, следовательно, в соответствующем индексе B+-дерева:
- вы должны сохранить порядок следования узлов внутри дерева, в противном случае вы не сможете найти узлы внутри беспорядочной массы;
- вы должны стремиться к минимально возможному числу уровней в B+-дереве, иначе временная сложность O(log(N)) превратится в O(N).
Таким образом, В+-дерево должно быть самоупорядоченным и сбалансированным. К счастью, это возможно с помощью смарт-удаления и вставки операций. Но у всего есть своя цена: операции вставки и удаления в B+-деревьях имеют сложность O(log(N)). Поэтому вы, возможно, знаете, что использовать очень много индексов — плохая идея. Вы замедляете быстрые вставку/обновление/удаление строки в таблице, поскольку базе данных нужно обновить индексы таблицы, а это дорогостоящая O(log(N)) операция на каждый индекс. Кроме того, добавление индексов значит больше нагрузки для диспетчера транзакций (мы поговорим о нём в конце статьи).
Более подробную информацию о B+-деревьях можете прочитать в статье в Википедии. Если хотите пример B+-Tree реализации в базе данных, изучите эту статью или эту от главного разработчика MySQL. Обе статьи описывают, как InnoDB (движок MySQL) обрабатывает индексы.
Примечание: один читатель заметил, что из-за низкоуровневой оптимизации В+-дерево должно быть полностью сбалансированным.
Хэш-таблица
Последняя важная структура данных, которую мы рассмотрим, — хеш-таблицы. Они очень полезны, когда нужно быстро получить нужное значение. Понимание хеш-таблиц поможет нам в дальнейшем понять типичную для БД операцию хеш-соединения. Эта структура данных также используется базами данных для хранения внутренних составляющих (например, таблиц блокировок или буферного пула, мы рассмотрим оба понятия позже).
Хеш-таблица — это структура данных, которая быстро находит элемент с ключом. Для построения хеш-таблицы необходимо определить:
- ключ для элементов;
- хеш-функцию для ключей; вычисленные хеши ключей определяют расположение элементов (и называются сегментами (buckets));
- функцию для сравнения ключей; как только вы нашли нужный сегмент, необходимо найти нужный элемент внутри данного сегмента с помощью этой функции.
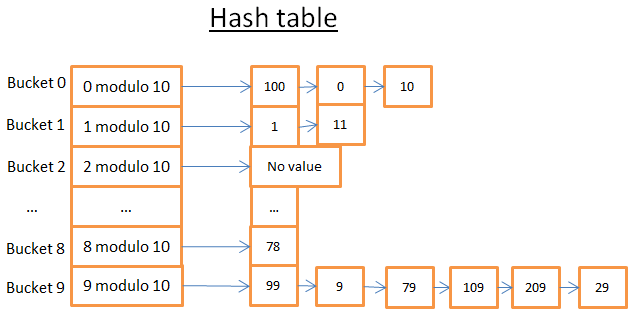
Простой пример
В данной хеш-таблице 10 сегментов. Из-за великой лени я нарисовал всего 5, но уверен, ваше воображение дорисует ещё 5. Я использовал хеш-функцию с ключом по модулю 10. Другими словами, я храню только последнюю цифру ключа элемента, чтобы найти его сегмент.
- если последняя цифра 0, элемент попадает в сегмент 0;
- если последняя цифра 1, элемент попадает в сегмент 1;
- если последняя цифра 2, элемент попадает в сегмент 2, и так далее.
В качестве функции для сравнения я использовал простое равенство двух целых чисел.
Допустим, нам нужен элемент 78:
- хеш-таблица вычисляет хеш код для 78, равный 8;
- первый элемент в сегменте 8 и есть нужный нам элемент 78.
Поиск занимает всего 2 операции – первая вычисляет хеш код, вторая находит элемент в конкретном сегменте.
Например, теперь мы ищем 59:
- хеш-таблица вычисляет хеш код – 9;
- первым элементом в сегменте 9 оказывается 99; поскольку 99 не равно 59, поиск продолжается;
- далее по той же логике анализируется второй элемент (9), и следующий за ним (79) и так далее до последнего элемента в сегменте (29);
- в данном случае необходимого элемента 59 не существует.
Поиск занимает 7 операций.
Правильная хеш-функция
Как видите, количество необходимых операций от поиска к поиску может меняться.
Если я заменю фунцию из предыдущего примера на функцию с ключом по модулю 1 000 000, поиск займёт всего 1 операцию, потому что в сегменте 000059 нет элементов. Главная цель – выбрать такую хеш-функцию, которая создаст сегменты с небольшим количеством элементов.
В моём примере найти подходящую хеш-функцию было не трудно – потому что пример простой. Когда ключом является строка (например, фамилия), 2 строки (фамилия и имя), 2 строки и дата (фамилия, имя и дата рождения), найти хорошую функцию уже гораздо сложнее.
Когда хеш-функция удачная, сложность поиска по хеш-таблице составляет O(1).
Массив или хеш-таблица
А почему бы не использовать только массивы?
Хеш-таблица может быть лишь наполовину загружена в память, остальная половина сегментов будет на диске, а для массива вы должны использовать непрерывное пространство памяти. Если вы работаете с большой таблицей, непрерывного пространства обычно не хватает. С хеш-таблицей вы можете выбрать любой ключ (например, страна и фамилия человека).
Можете также ознакомиться с моей статьёй, где разобран пример эффективной Java хеш-таблицы; вам совсем не обязательно знать Java, чтобы понять статью.
Компоненты БД
Мы посмотрели на основные компоненты БД. Взглянем на всю картину в целом.
База данных это набор информации, которую легко получать и изменять. Но то же самое можно сказать о куче файлов. На самом деле, простейшие базы данных вроде SQLite это и есть куча файлов. Но продуманная и организованная куча файлов, потому что только БД позволяет использовать транзакции, обеспечивающие верную последовательность и безопасность данных, а также обрабатывать данные быстро, даже когда вы имеете дело с миллионами данных.
Общая структура БД выглядит примерно так:
Перед написанием этой части я прочитал немало книг/статей, и каждый источник описывал БД по-своему. Так что не зацикливайтесь особо на том, как я организовал эту базу данных или как назвал процессы, я старался, чтобы данная часть гармонично вписывалась в общий план статьи. Главная идея в том, что БД состоит из нескольких компонентов, которые взаимодействуют друг с другом, а именно:
Ключевые компоненты
- Диспетчер процессов: многие базы данных имеют пул процессов/потоков, которые необходимо контролировать. Кроме того, в целях экономии наносекунд, некоторые современные базы данных используют собственные потоки вместо потоков операционной системы;
- Диспетчер сети: сетевой ввод-вывод — большая проблема, особенно для распределенных баз данных. Поэтому, у некоторых БД есть свой диспетчер сети;
- Менеджер файловой системы: чтение или запись на диск — ещё одно слабое место БД. Поэтому важно иметь менеджер, который будет идеально обрабатывать файловую систему операционки или полностью заменит её;
- Диспетчер памяти: чтобы избежать эпичных зависаний при чтении или записи на диск, требуется большое количество оперативной памяти. Но когда её много, вам неизбежно потребуется эффективный диспетчер памяти. Особенно когда много одновременных запросов, использующих память;
- Диспетчер безопасности учётных записей: для управления аутентификацией и авторизацией пользователей;
- Диспетчер клиентов: управляет клиентскими подключениями.
Утилиты
- Менеджер резервного копирования: для сохранения и восстановления базы данных;
- Диспетчер восстановления: обеспечивает целостность данных при перезапуске БД после падения;
- Диспетчер контроля: ведёт журнал активности базы данных и предоставляет инструменты для её мониторинга;
- Диспетчер администрирования: для хранения метаданных (например, названия и структуры таблиц), а также управления базами данных, схемами, табличными пространствами.
Диспетчер запросов
Парсер запросов: проверяет, является ли запрос допустимым;
Рерайтер: перезаписывает запрос;
Оптимизатор: оптимизирует запрос;
Исполнитель запросов: компилирует и выполняет запрос.
Диспетчер данных
Диспетчер транзакций: обрабатывает транзакции;
Диспетчер кэша: помещает данные в память перед их использованием и записью на диск;
Менеджер доступа к данным: предоставляет доступ к данным на диске.
Далее я подробно остановлюсь на том, как базы данных управляет SQL-запросами с помощью диспетчеров клиентов, запросов и данных (сюда же включу и диспетчера восстановления).
Диспетчер клиентов
Диспетчер клиентов, как несложно догадаться, обрабатывает взиамодействия с клиентом. Клиентом может быть (веб) сервер или приложение конечного пользователя. Диспетчер клиентов предоставляет доступ к базе данных через различные API: JDBC, ODBC, OLE-DB, включая некоторые проприетарные API.
При подключении к БД диспетчер клиентов сначала проверяет аутентификацию (логин и пароль), затем — есть ли у вас полномочия на использование базы данных. Эти права доступа устанавливаются администратором БД. Затем диспетчер проверяет, не перегружена ли БД и есть ли свободный процесс (или поток) для обработки вашего запроса. Пока необходимая информация собирается, диспетчер ожидает. Если ожидание превышает тайм-аут, диспетчер разрывает соединение и возвращает сообщение об ошибке. В дальнейшем ваш запрос перенаправляется к диспетчеру запросов. После получения данных от диспетчера запросов, промежуточные результаты сохраняются в буфер и отправляются вам. В случае каких-то проблем, соединение разрывается, возвращается сообщение, объясняющее проблему, и процесс завершается.
Диспетчер запросов
Вот здесь-то и раскрывается вся сила базы данных. В этой части БД плохо написанный запрос трансформируется в быстрый код, после выполнения которого результаты возвращаются диспетчеру клиентов. Этот процесс состоит из следующих шагов: сначала запрос анализируется на валидность; затем он перезаписывается — это предварительная оптимизация, удаляющая бесполезные операции; далее для улучшения производительности запрос оптимизируется в план исполнения и доступа к данным, который затем компилируется и выполняется.
Если вы хотите лучше понять все вышеописанные процессы, рекомендую почитать:
- Раннее исследование (1979) на тему оптимизации с учётом затрат: выбор пути доступа в реляционной системе управления базами данных. В статье всего 12 страниц, и она будет понятна человеку со средним уровнем компьютерной грамотности;
- А вот очень хорошая и подробная презентация о том, как DB2 9.Х оптимизирует запросы;
- Отличная презентация о том, как PostgreSQL оптимизирует запросы. Не сложная, потому что это презентация не про то, какие алгоритмы используются в PostgreSQL, а о планах запросов, которые создаёт PostgreSQL в разных ситуациях;
- Официальная документация SQLite об оптимизации запросов. Читать тоже не сложно, работают простые правила. Причем, это единственная официальная документация, которая на самом деле объясняет, как оно работает.
- Ещё одна годная презентация о том, как SQL Server 2005 оптимизирует запросы;
- Официальное описание оптимизации в Oracle 12с;
- 2 теоретических курса по оптимизации запросов от авторов книги “Системы управления БД” здесь и здесь. Интересные материалы про оптимизацию чтения и записи на диск, но не для новичков.
- Ещё один теоретический курс, он попроще, но акцент только на операции объединения и ввода-вывода.
Парсер запросов
Каждый SQL-оператор отправляется в парсер, где он проверяется на правильность синтаксиса. Если вы допустили ошибку, парсер отклонит запрос. Например, если вы написали “SLECT” вместо “SELECT”, на этом обработка вашего запроса закончится. Но это ещё не всё. Парсер также проверяет, что ключевые слова используются в правильном порядке. Например, если перед “SELECT” идёт “WHERE”, запрос будет отклонён. Затем анализируются таблицы и поля запроса. Парсер использует метаданные БД, чтобы проверить, существуют ли таблицы, поля в таблице, а также возможны ли операции для конкретных типов полей (например, нельзя сравнивать целое число со строкой, нельзя использовать substring() для целого числа). Затем проверяется, есть ли у вас разрешение на чтение (или редактирование) данных таблиц. Эти права доступа определяются администратором базы данных. Во время парсинга SQL-запрос преобразуется во внутреннее представление (часто дерево). Если все хорошо, внутреннее представление направляет запрос в рерайтер.
Рерайтер запросов
Итак, у нас есть внутреннее представление запроса. Основная цель рерайтера — предварительно оптимизировать запрос, чтобы избежать ненужных операций и помочь оптимизатору найти наилучшее решение. Рерайтер применяет определённый набор правил к запросу. Если запрос подходит под данное правило, правило применяется — запрос переписывается.
Вот неполный список правил:
- Слияние представлений: если вы используете представления, они преобразуются соответствующими алгоритмами SQL;
- Слияние подзапросов: подзапросы очень трудно оптимизировать, поэтому рерайтер попытается изменить запрос, чтобы избавиться от них.
Например:
|
|
будет заменено на:
|
|
- Удаление лишних операторов: например, если вы используете DISTINCT, и одновременно UNIQUE, что не позволяет данным быть неуникальными, оператор DISTINCT удаляется;
- Удаление повторных объединений: если вы дважды использовали одно и то же условие объединения, например, одно из них скрыто в представлении, или если из-за транзитивности объединение повторяется, оно будет удалено;
- Постоянные арифметические вычисления: если ваш запрос требует вычислений, они будут произведены один раз в течение перезаписи. Например, WHERE AGE > 10+2 будет преобразовано в WHERE AGE > 12, а TODATE(“какая-нибудь дата”) преобразуется в дату в формате datetime;
- (дополнительно) Отсечение разделов: если вы используете секционированные таблицы, рерайтер может определить, какие разделы использовать;
- (дополнительно) Перезапись материализованных представлений: если у вас есть материализованное представление, которое соответствует подмножеству предикатов в запросе, рерайтер проверяет, актуально ли представление, и изменяет запрос, чтобы использовать материализованное представление вместо исходных таблиц;
- (дополнительно) Пользовательские правила: если у вас есть пользовательские правила для изменения запроса (например, политика Oracle), рерайтер выполняет эти правила;
- (дополнительно) OLAP преобразования: аналитические функции, звездообразные объединения, агрегирование также преобразуются (не уверен, делает ли это рерайтер или оптимизатор, скорее всего, зависит от конкретной БД).
Наконец, наш переписанный запрос передаётся оптимизатору запросов, где начинается самое интересное!
По мотивам Christophe
To be continued…
Читайте так же статьи по теме:
- Как работает реляционная база данных. Часть 2
- Как работает реляционная база данных. Часть 3
Материал из Кафедра ИУ5 МГТУ им. Н.Э.Баумана — студенческое сообщество
Содержание
- 1 Третья нормальная форма
- 1.1 Пример аномалий у 3НФ
- 1.2 Нормальная форма Бойса-Кодда
- 2 Алгоритм синтеза «хорошей» БД
- 2.1 Пример
Третья нормальная форма
Пример аномалий у 3НФ
$R = (A, B, C, D)$ и $F = (Arightarrow B, Brightarrow A, ACrightarrow D)$
Два ключа:
- первый — $AC$:
- $(AC)^+=ACBD = R$
- $A^+=ABneq R$
- $C^+ = Cneq R$
- второй — $BC$:
- $(BC)^+=BCAD = R$
- $B^+ = BAneq R$
Покажем, что в этом случае $R$ находится в 3НФ:
1)
- неключевой атрибут $H$, $H = D$
2)
- $Yrightarrow H$, $Hnotin Y$, $Y = AC$
3)
- $X = BC$, $X = AC$
Нельзя подобрать нужную тройку, потому $R$ находится в 3НФ. Однако, отношение всё равно обладает аномалиями:
- избыточности: наименование поставщика повторяется для каждой поставляемой делали;
- противоречивости при изменении наименования поставщика надо изменить его во всех записях, куда оно входит;
- включения: нельзя включить информацию о поставщике, если он ничего не поставляет;
- удаления: при удалении детали удаляется информация о поставщике.
Для устранения этого вводится усиленная 3НФ — Бойса-Кодда.
Нормальная форма Бойса-Кодда
ФЗ $Xrightarrow Y$ является неприводимой, если для любого подмножества $Zsubset X$ выполняется $Znrightarrow Y$ или $Zrightarrow Ynotin F^+$
Пусть есть отношение $R$ и $F$ включает в себя нетривиальные неприводимые ФЗ. Тогда отношение $R$ находится в нормальной форме Бойса-Кодда, если для любого $Xrightarrow Yin F$ => $X$ — ключ.
Пример:
$R_1 = AB$, $F_1 = (Arightarrow B, Brightarrow A)$, $A$ — ключ, $B$ — ключ.
или
$R_2 = ACD$, $F_2 = (ACrightarrow D)$, $AC$ — ключ.
Алгоритм синтеза «хорошей» БД
Пусть $U$ — универсальная схема отношения (множество всех атрибутов предметной области) и $F$ — множество ФЗ.
Перед выполнением алгоритма можно привести все ФЗ к одному атрибуту в правой части (по свойству декомпозиции) и удалить лишние ФЗ. Но это не обязательно.
Алгоритм:
- построить УНП для $F$;
- если среди ФЗ в УНП нет ФЗ, включающей все атрибуты из $U$, то добавить в УНП тривиальную ФЗ $Urightarrowvarnothing$. Выполнение этого шага почти всегда обеспечивает свойство соединения без потерь будущей схемы БД;
- привести все нетривиальные ФЗ из УНП к неприводимому виду (удалить лишние атрибуты в левых частях ФЗ);
- разбить полученное множество ФЗ УНП на классы эквивалентности. Две зависимости $X_irightarrow Y_i$ и $X_jrightarrow Y_j$ будем называть эквивалентными, если $X_iY_i = X_jY_j$. Далее введём обозначение $K_r = X_iY_i$ — множество атрибутов в левой и правой частях ФЗ $r$-того класса эквивалентности;
- построить граф иерархии полученных на предыдущем шаге классов эквивалентности (если это возможно). Правило построения: $j$-ый узел соединяем снизу с $i$-ым узлом, если $K_jsubset K_i$. В каждом узле записываются все ФЗ, соответствующего класса эквивалентности;
- из каждого класса эквивалентности в графе иерархии оставить только одну ФЗ. Правила выбора:
- удалить из класса эквивалентности лишние ФЗ;
- если в классе эквивалентности осталось больше одной ФЗ, то выбрать ФЗ с меньшим числом атрибутов в левой части;
- если у оставшихся ФЗ число атрибутов в левой части одинаково, то выбрать ту ФЗ, которая позволит редуцировать (вычеркнуть) атрибуты справа у ФЗ, расположенных выше в графе иерархии;
- если в результате не удалось выбрать ни одной, то выбрать произвольную;
- редуцировать атрибуты справа в оставшихся ФЗ. Для этого просмотреть каждый путь снизу вверх в графе иерархии. Двигаясь по выбранному пути, выполнить следующие действия в каждом узле пути:
- пусть $Xrightarrow Y$ — это ФЗ, записанная в данном узле. Каждый атрибут, принадлежащий правой части, вычеркнуть в правых частях ФЗ, расположенных в узлах этого пути по иерархии выше;
- для тривиальной ФЗ $Urightarrowvarnothing$ атрибуты вычёркиваются слева;
- исключить из рассмотрения ФЗ с пустой правой частью (кроме редуцированной ФЗ $Urightarrowvarnothing$). Исключённые на этом шаге ФЗ являются лишними и выводятся из оставшихся;
- каждую оставшуюся в графе иерархий ФЗ $Vrightarrow W$ заменить на множество $VW$. Получившееся множество схем отношений обозначить как $rho$;
- для полученной на предыдущем шаге схемы БД проверить:
- обладает ли она свойством соединия без потерь. Если не обладает, то добавить ключ универсальной схемы $U$ в эту схему;
- обладает ли $rho$ свойством сохранения ФЗ. Если нет, то, использовать зависимости, не вошедшие в проекцию $Xrightarrow YnotinPi_{R_i}(F)$, для построения новых схем отношений, то есть добавить в $rho$ $XY$.
После выполнения всех шагов полученная схема $rho$:
- обладает свойством соединения без потерь;
- обладает свойством сохранения ФЗ;
- находится в 3НФ или НФБК;
- содержит минимальное число схем отношений.
Пример
$U = (поставщик, фирма, деталь, количество) = (A, B, C, D)$
$F = (Arightarrow B, Brightarrow A, ACrightarrow D, BCrightarrow D)$
Строим $rho$:
1)
- $УНП = (Arightarrow B, Brightarrow A, ACrightarrow BD, BCrightarrow AD)$
2)
- пропускаем этот шаг, так как есть ФЗ (даже не одна), включающая все атрибуты из $U$
3)
- уменьшить число атрибутов не удаётся
4)
- 1 класс: $Arightarrow B$, $Brightarrow A$, $K_1 = AB$
- 2 класс: $ACrightarrow BD$, $BCrightarrow AD$, $K_2 = ABCD$
5)
6)
- для $K_2$:
-
- способ 1 — как во втором семинаре
- можно ли вывести $ACrightarrow BDin(BCrightarrow AD)^+$?
- $(AC)^+=AC$, $BDnsubseteq(AC)^+$, значит нельзя
- можно ли вывести $BCrightarrow ADin(ACrightarrow BD)^+$?
- $(BC)^+=BC$, $ADnsubseteq(BC)^+$, значит нельзя
- способ 1 — как во втором семинаре
-
- способ 2 — вычеркнуть из правых частей ФЗ рассматриваемых классов эквивалентностей общие атрибуты. Если получаются ФЗ с пустой правой частью, то они являются лишними.
- $ACrightarrow B$
- $BCrightarrow A$
- выше по иерархии ничего нет, выбираем $BCrightarrow AD$
- способ 2 — вычеркнуть из правых частей ФЗ рассматриваемых классов эквивалентностей общие атрибуты. Если получаются ФЗ с пустой правой частью, то они являются лишними.
-
- нет лишних ФЗ, потому…
- для $K_1$:

продолжение…